営業活動やマーケティング活動にとって、顧客の離反対策は重要課題の1つでしょう。
顧客の離反などのイベントが発生するまでの期間を扱う分析手法があります。
生存時間分析(survival time analysis)というものです。
小難しい議論はさておき、チャーン分析(顧客の離反分析)やチャーン予測(離反予測)に利用できます。
今回は、「機械学習的チャーン分析(顧客の離反分析)」というお話しをします。
Contents [hide]
機械などが壊れるまでの寿命などを表現する分布
機械などが壊れるまでの寿命などを表現するために考案されたワイブル分布(寿命分布の1つ)というものがあります。
ベアリングボールという部品に対する寿命の分析をワイブルが実施したのが、ことの始まりです。
その後、多くの部品や機械などの寿命の分析で利用されました。さらに、戦争の期間や人間の寿命などの分析にも利用されています。
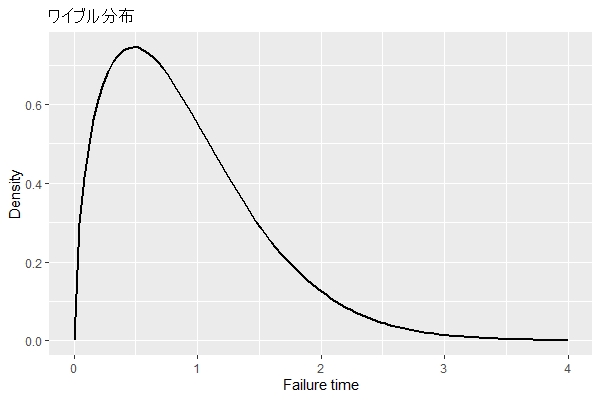
マーケティングの領域では、チャーン分析(顧客の離反分析)や購買間隔の分析などで利用されています。
チャーン分析(顧客の離反分析)の場合ですと……
- ヨコ軸:顧客期間(取引開始から取引停止までの期間)
- タテ軸:相対度数(もしくは度数)
……をヒストグラムで表現したグラフに対する近似曲線(確率密度)です。
バスタブ曲線(故障率曲線)
機械やシステムなどの故障率と時間の関係性を表現したのものに「バスタブ曲線」というものがあります。

3つの故障期における故障率を表現したものです。
- 初期故障期
- 偶発故障期
- 摩耗故障期
実際は、このように綺麗にならないですし、マーケティングや営業系の顧客離反の場合には、別の形状になることでしょう。チャーン分析(顧客の離反分析)の場合には、故障率ではなく離反率になります。
このような故障曲線を表現する関数をハザード関数と言います。
要は、ハザード関数を推定することで、取引期間の長さと離反率の関係性を分析し、例えば累積ハザード確率(その時間までに故障する確率)や生存確率(その時間までに故障しない確率)を求めたり、ある時間までに故障する確率を予測することもできます。
ワイブル分布とハザード関数
チャーン分析(顧客の離反分析)という視点で考えると、ワイブル分布は顧客期間(取引開始から取引停止までの期間)の分布です。
離反率は顧客期間の関数で表現できそうです。それが、ハザード関数です。ある時期までに離反していない人が、次の瞬間に離反する確率です。
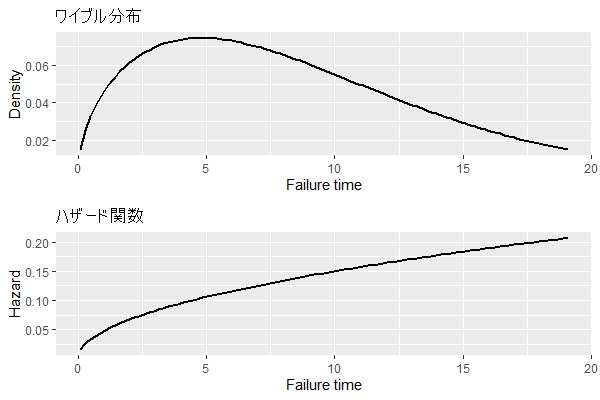
ハザード関数は、場合によっては1の値を超えることがあります。ですので、離反の程度(もしくは密度)ぐらいで考えておいた方がいいかもしれません。
通常は、ハザード関数を使って累積ハザード関数(その時間までに故障する確率)や生存関数(その時間までに故障しない確率)を求め使うことが多いです。こちらは、1の値を超えることはありません。
先ほど紹介したバスタブ曲線は、少なくとも3つのハザード関数を組み合わせて作られます。
バスタブ曲線とワイブル分布とハザード関数
チャーン分析(顧客の離反分析)の場合、バスタブ曲線になることは少ないとは思いますが、ワイブル分布(とハザード関数の組み合わせ)の3つの典型的なパターンが含まれているため、ここで簡単に紹介します。
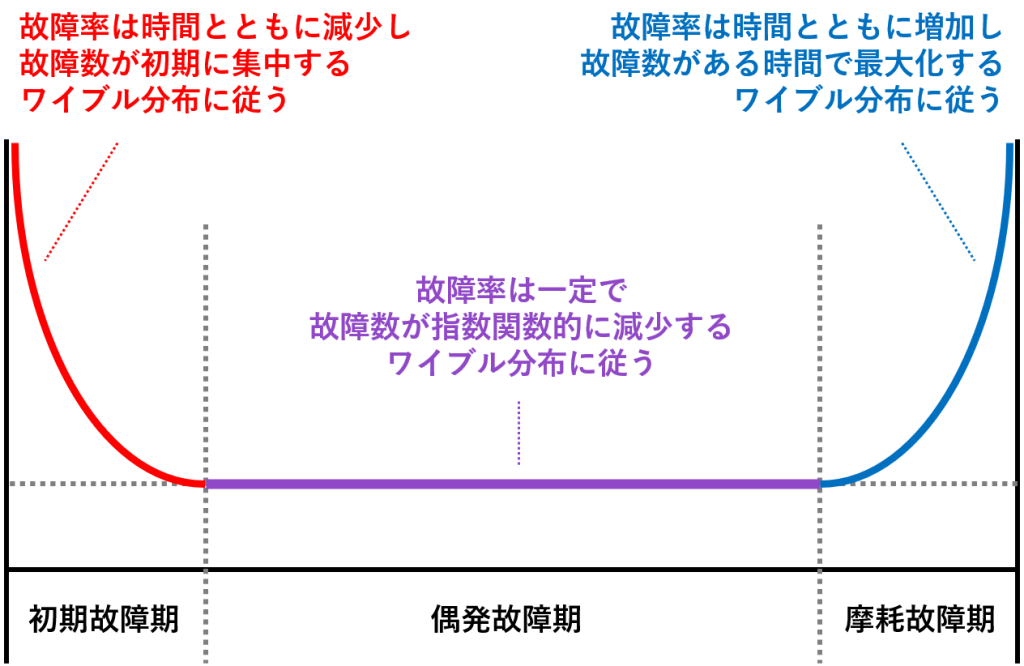
先ほどお話ししたとおり、バスタブ曲線は故障率の曲線で、「初期故障期」「偶発故障期」「摩耗故障期」の3つの期間に分けられ、それぞれで別のワイブル分布(とハザード関数の組み合わせ)になっています。
ワイブル分布の形状パラメータ(shape)を主に変化させることで、形状の異なるワイブル分布を描くことができます。
- 初期故障期:形状パラメータ(shape)<1
- 偶発故障期:形状パラメータ(shape)=1
- 摩耗故障期:形状パラメータ(shape)>1
形状パラメータ(shape)が1より小さいときのハザード関数(故障曲線)がバスタブ曲線の初期故障期で、形状パラメータ(shape)が1のときのハザード関数(故障曲線)がバスタブ曲線の偶発故障期で、形状パラメータ(shape)が1より大きいときのハザード関数(故障曲線)がバスタブ曲線の摩耗期です。
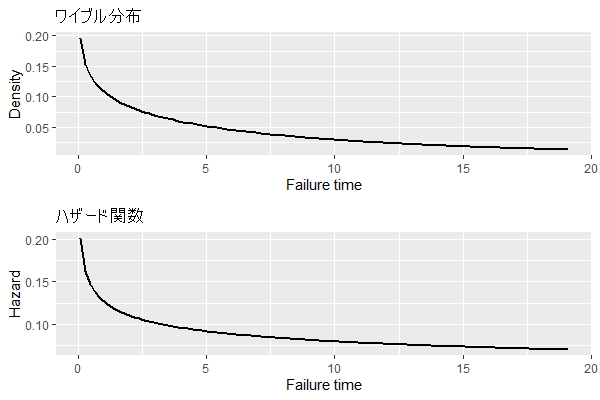
初期故障期:形状パラメータ(shape)<1
以下は、形状パラメータ(shape)が1より小さいときのワイブル曲線(寿命分布)とハザード関数(故障曲線)です。
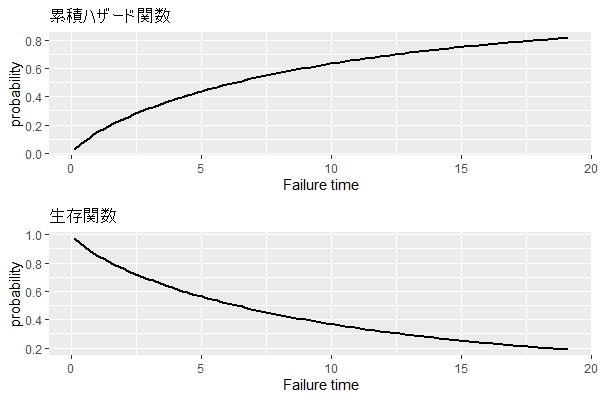
ちなみに、このワイブル分布の累積ハザード関数(その時間までに故障する確率)、生存関数(その時間までに故障しない確率)です。
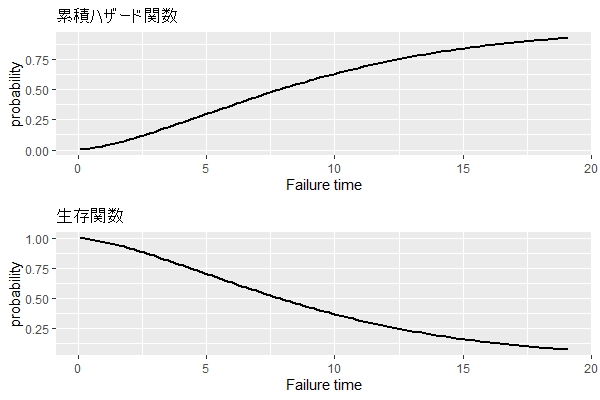
偶発故障期:形状パラメータ(shape)=1
以下は、形状パラメータ(shape)が1のときのワイブル曲線(寿命分布)とハザード関数(故障曲線)です。
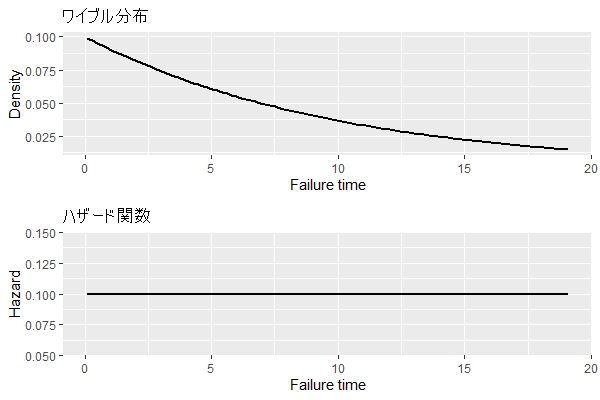
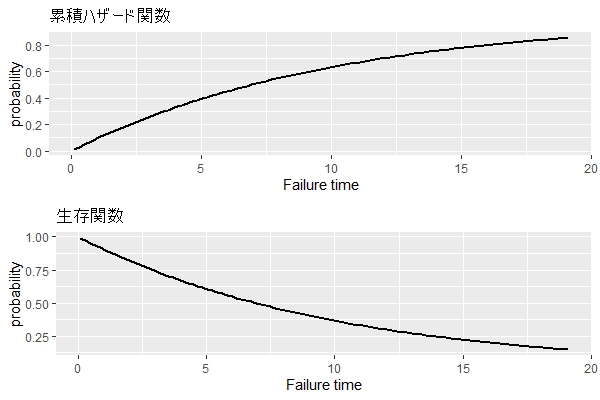
ちなみに、このワイブル分布の累積ハザード関数(その時間までに故障する確率)、生存関数(その時間までに故障しない確率)です。
摩耗故障期:形状パラメータ(shape)>1
以下は、形状パラメータ(shape)が1より大きいときのワイブル曲線(寿命分布)とハザード関数(故障曲線)です。
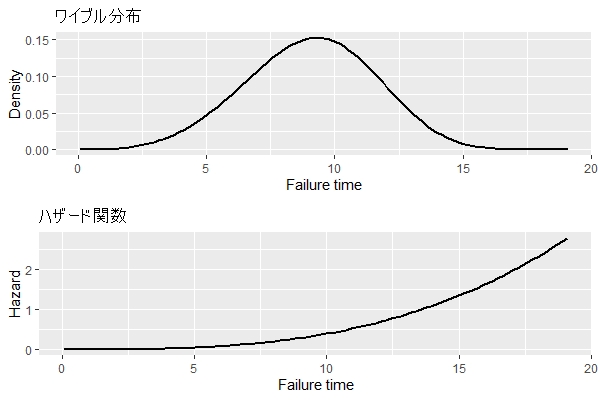
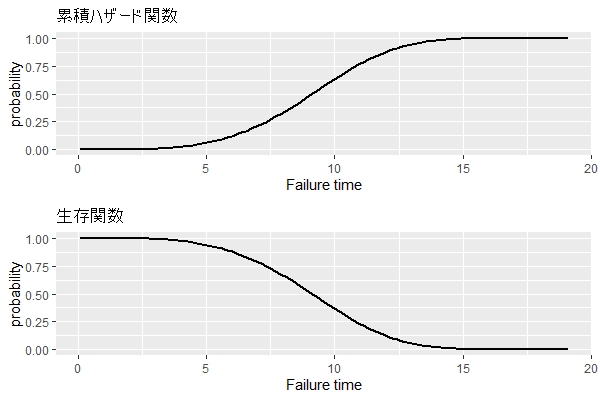
ちなみに、このワイブル分布の累積ハザード関数(その時間までに故障する確率)、生存関数(その時間までに故障しない確率)です。
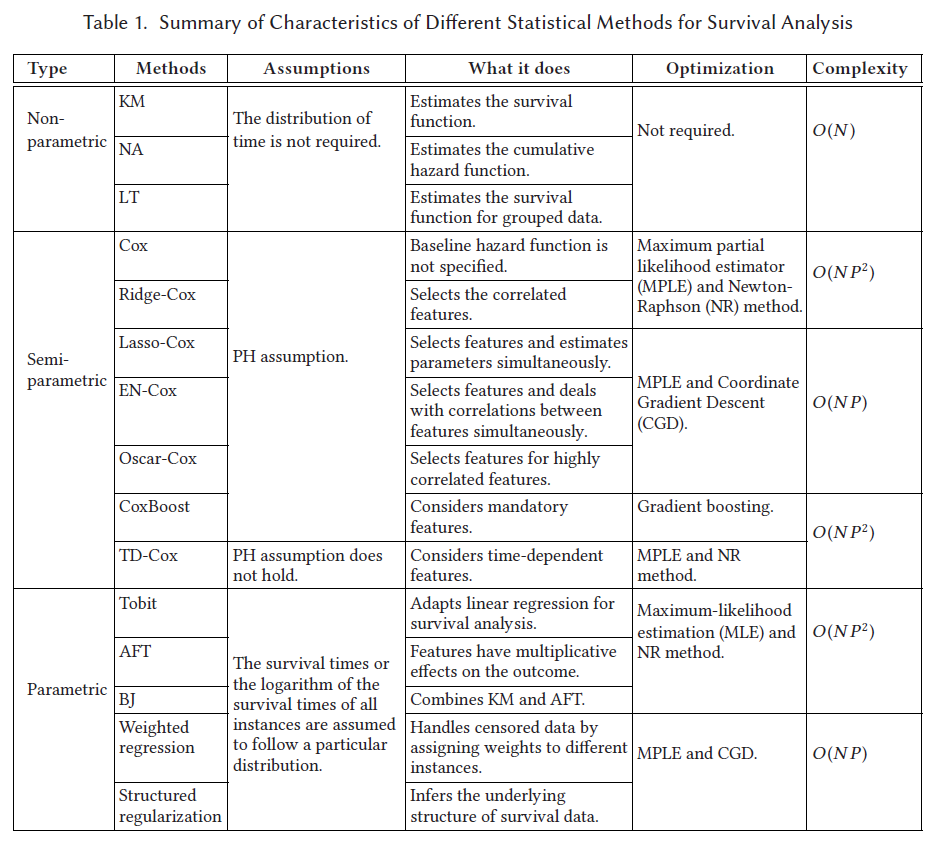
ノンパラ・セミパラで行こう!

バスタブ曲線やワイブル分布、ハザード関数などは、生存時間分析(survival time analysis)と呼ばれるものです。
生存時間分析(survival time analysis)には、色々な考え方やアプローチ、手法があります。
ワイブル分布を使ったアプローチは、パラメトリックなアプローチと呼ばれています。
他には、ノンパラメトリックなアプローチと、セミパラメトリックなアプローチがあります。
- ノンパラメトリックなアプローチ:ワイブル分布などの特定の確率分布を仮定しない。
- セミパラメトリックなアプローチ:ワイブル分布などの特定の確率分布を仮定しない。説明変数Xを使い回帰モデルを作ることができる。
- パラメトリックなアプローチ:ワイブル分布などの特定の確率分布を仮定する。説明変数Xを使い回帰モデルを作ることができる。
出典:Ping Wang, Yan Li, and Chandan K. Reddy. “Machine learning for survival analysis: A survey.” ACM Computing Surveys (CSUR). 51, 6 (2019), 36 pages.
https://github.com/wangpinggl/SurvivalAnalysisSurvey
ノンパラメトリックなアプローチとは、ワイブル分布などの特定の確率分布を仮定せずに実施するアプローチです。
セミパラメトリックなアプローチとは、ワイブル分布などの特定の確率分布を仮定せず、説明変数Xを使い回帰モデルを作るアプローチです。
回帰モデルを作るという目的の場合、このセミパラメトリックなアプローチが主流になっています。よく利用されているのがCox回帰モデルです。
Cox回帰モデルによる予測

Cox回帰の予測モデルを使うことで、顧客それぞれに対し、一定時間経過後までの離脱(取引停止)する確率を出すことができます。
実は、Cox回帰と言っても色々あります。
よく使われているのがCox比例ハザードモデルです。
Cox比例ハザードモデルとは、ハザードが説明変数によって変動するモデルで、ベースランのハザード(通常の回帰モデルで言うところの切片項)を設定することが多いです。
チャーン分析(顧客の離反分析)で考えると、ベースラインの離反率があり、このベースラインとなる離反率をベースに説明変数Xによって増えたり減ったりする、といった感じです。例えば、訪問回数などを説明変数Xとすると、訪問回数Xによって離反率が変化するといった感じです。
このCox回帰も進化し、色々なCox回帰があります。
最近流行りの機械学習っぽい手法
出典:Ping Wang, Yan Li, and Chandan K. Reddy. “Machine learning for survival analysis: A survey.” ACM Computing Surveys (CSUR). 51, 6 (2019), 36 pages.
https://github.com/wangpinggl/SurvivalAnalysisSurvey
統計的機械学習の書籍などでよく登場する、正則化回帰モデル(RidgeやLassoなど)のCox版です。
- Ridge Cox 回帰(説明変数のマルチコ緩和)
- Lasso Cox 回帰(説明変数選択が行われる)
- Elastic Net Cox 回帰(上記2つの中間的なモデル)
- OSCAR Cox 回帰(説明変数Xのクラスタリングが行われる)
説明変数Xも時間的変化をするというモデルが以下です。
- Time-Dependent Cox 回帰
決定木系のモデルが充実してきました。
- Survival Tree
- Bagging Survival Tree
- Random Survival Forest
一様、サポートベクターマシン(SVM)のCox版もあります。
- Support Vector Cox 回帰
今回のまとめ
今回は、「機械学習的チャーン分析(顧客の離反分析)」というお話しをしました。
営業活動やマーケティング活動にとって、顧客の離反対策は重要課題の1つでしょう。
顧客の離反などのイベントが発生するまでの期間を分析手法があります。ワイブル分布や、Cox回帰などを含めた生存時間分析(survival time analysis)というものです。
チャーン分析(顧客の離反分析)という視点で考えると、ワイブル分布は顧客期間の分布です。離反率を顧客期間の関数で表現したのがハザード関数です。
顧客それぞれに対し一定時間経過後までの離脱(取引停止)する確率を出すには、Cox回帰モデルです。Cox回帰と言っても色々あります。
どのようにして、得られたデータからワイブル分布を推定したり、離反確率を予測するモデルの作り方に関しては、別の機会(「[For beginners] がんばれデータサイエンティスト!」)にお話しします。