データ分析では、よく数理統計学の手法が使われます。
その中で、比較的高頻度で登場するのが「相関分析」です。
2つの変量の間の関係性を見るものです。
今回は、「『相関』は曲がったことが大っ嫌い」というお話しをします。
Contents [hide]
相関とは?
2つの変量の間の関係性で、一方が増えたときに他方が増えたり、逆に減ったりする関係性です。
相関係数は-1から+1の間の数値をとります。
- +1に近いほど「正の相関関係がある」(一方が増加すると他方が増加する傾向にある場合)
- -1に近いほど「負の相関関係がある」(一方が増加すると他方が減少する傾向にある場合)
- 0は無相関(正の相関関係も負の相関関係もない)
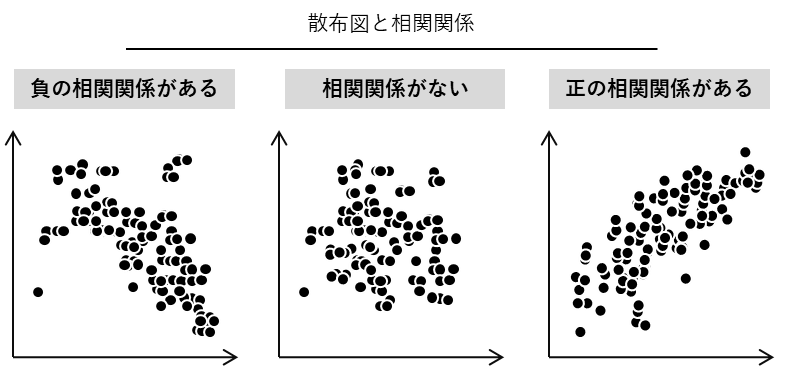
肥満が増えると、長生きも増える???
以下は、男性の肥満者(BMI≧25)の割合の推移です。
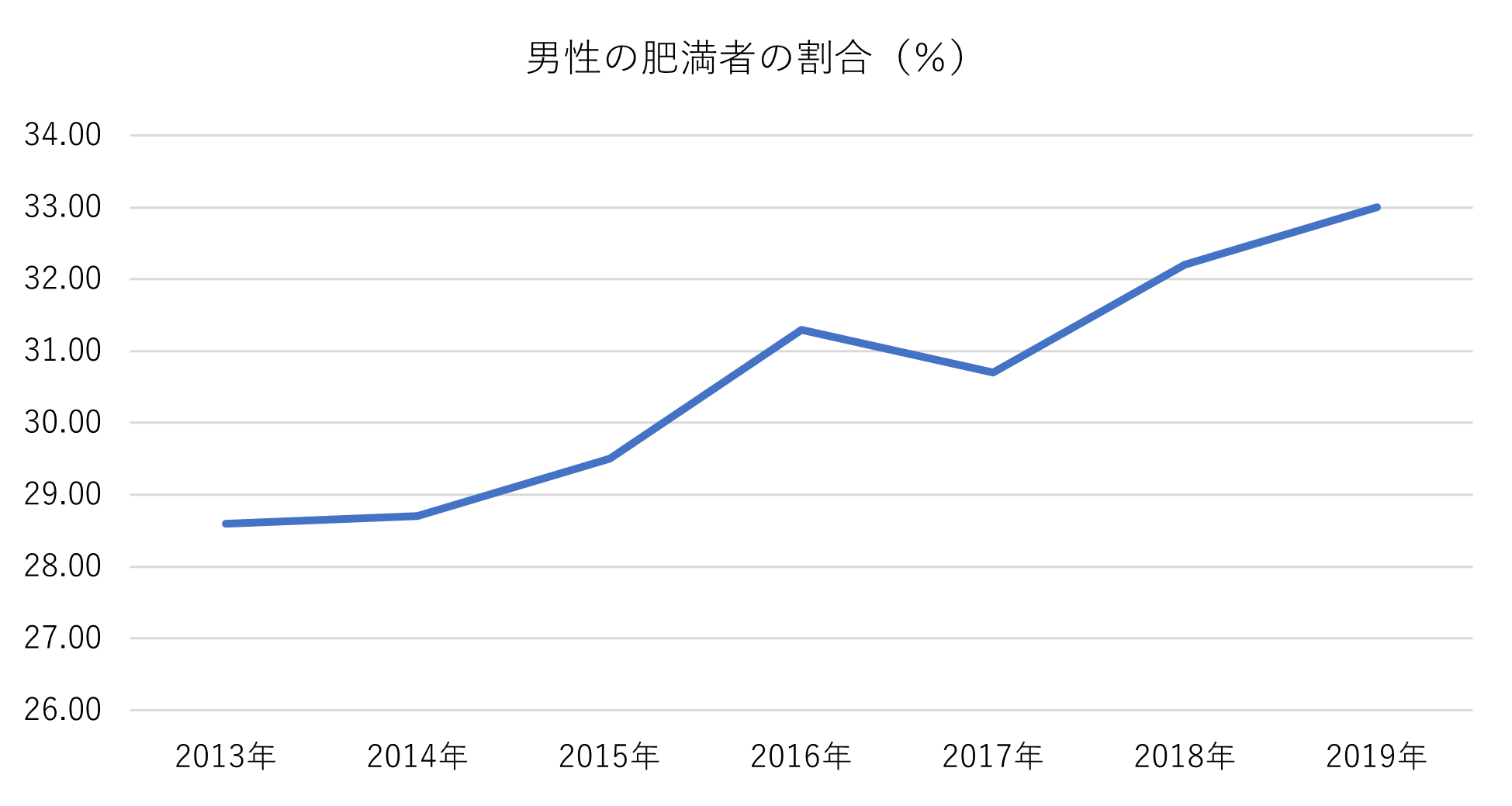
厚生労働省「国民健康・栄養調査報告」
https://www.mhlw.go.jp/bunya/kenkou/kenkou_eiyou_chousa.html
以下は、男性の平均寿命の推移です。
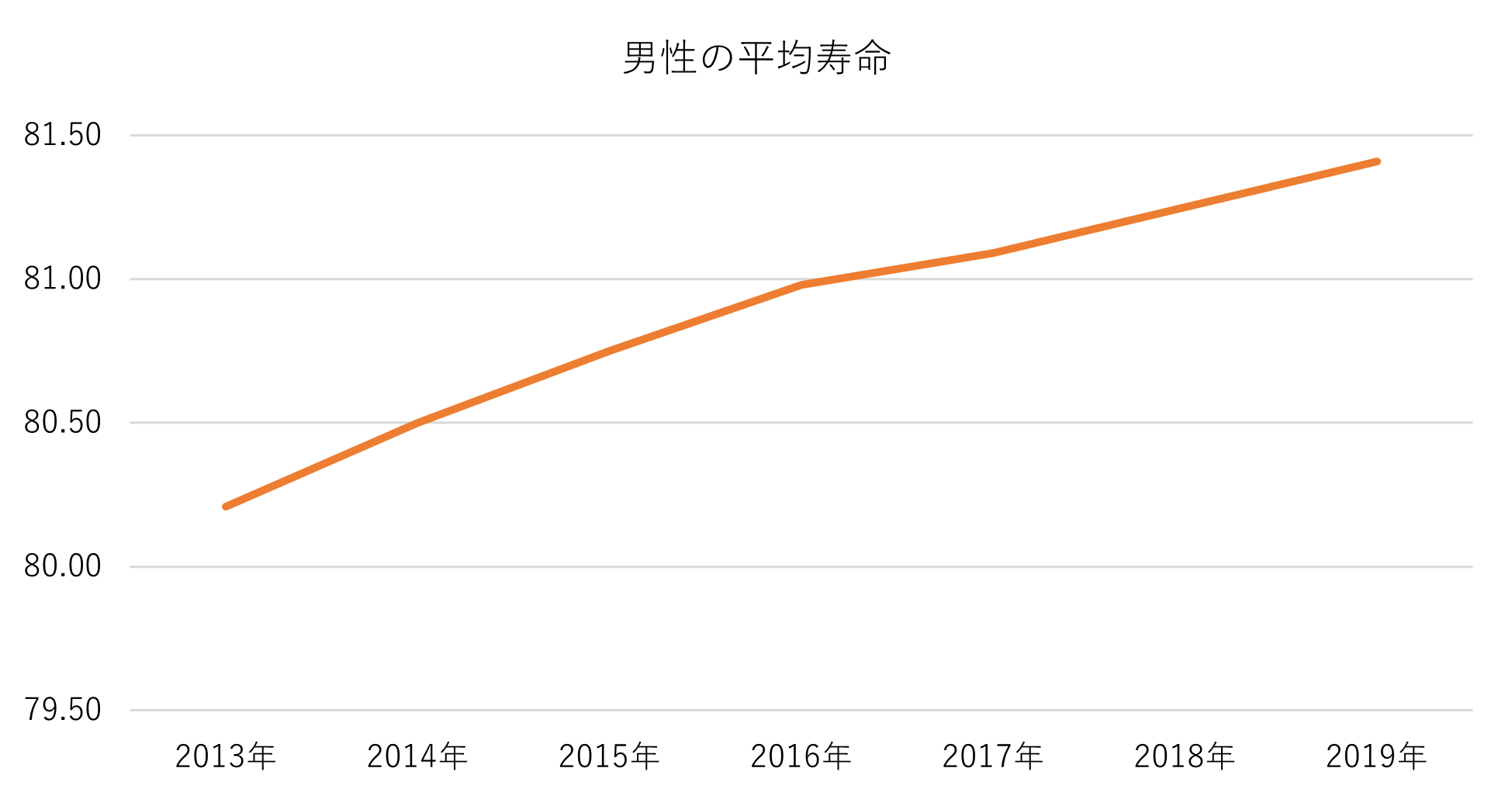
厚生労働省「生命表」
https://www.mhlw.go.jp/toukei/saikin/hw/seimei/list54-57-02.html
ヨコ軸を「男性の肥満者の割合」とし、タテ軸を「男性の平均寿命」とした場合の散布図を描きます。
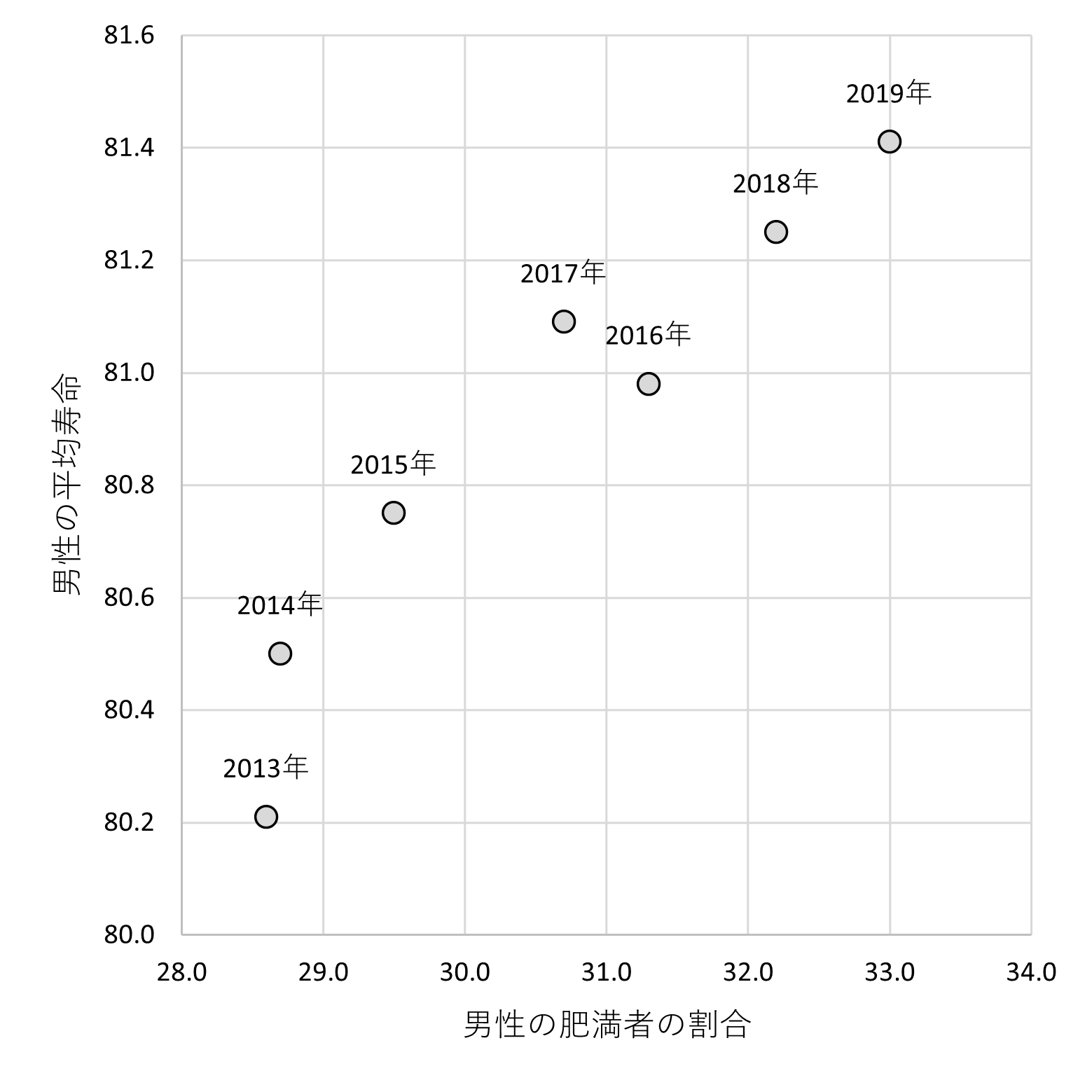
相関係数を計算すると、次のようになります。
- 相関係数:0.953
相関係数がプラスですから、太った人が多いほど寿命が延びる傾向が読み取れます。
本当でしょうか?

線形回帰式
先ほどのプロットに、近似直線を引いてみます。
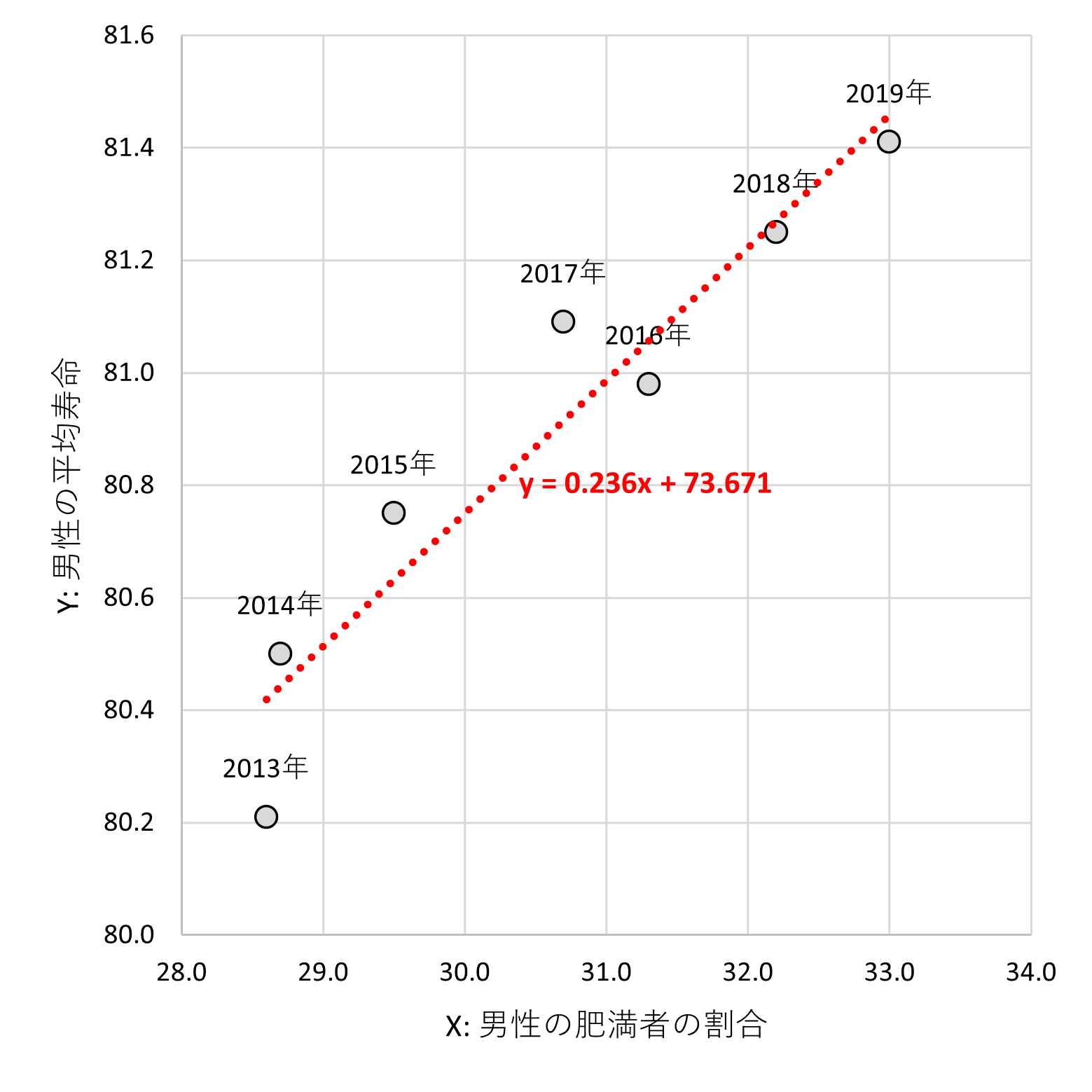
この近似曲線は線形回帰式(単回帰式)と呼ばれるもので、「X:男性の肥満者の割合」をインプットすると、「Y:男性の平均寿命」を計算することができます。
- y = 0.236x + 73.671
このような線形回帰式を予測モデルとして利用したりすることは、少なくありません。
データや数式のレベルでは問題なさそうですが、「実務で活用するにはどうかな?」と違和感を思った方もいたと思います。

この例は分かりやすいですが、ドメイン知識(データ活用をする現場の知識)が欠落していると、このようなことに違和感を持つことなく突き進むことがあります。
直線関係を表現したものに過ぎない
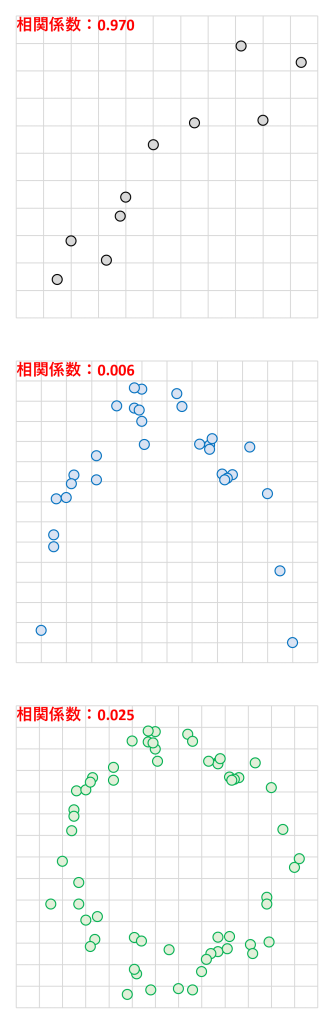
相関は、データ間の直線関係を表現したものに過ぎません。
データ間に曲線関係がある場合には、そのままでは有効に機能しません。線形回帰式も同様で、曲線関係がある場合には、有効な式を表現できません。

何かしら、元のデータを変換して直線関係に近づくようにするか、幾つかの区間に分けて、それぞれの区間で直線関係を作ったりします。
相関は曲がったことが大っ嫌いなのです。
相関は因果ではない
当然ですが、相関は因果ではなく、単なるデータ間の直線関係を表現したものに過ぎません。
直線的な関係性のある因果であれば、正の相関や負の相関として現れます。しかし、正の相関や負の相関であるからと言って、直線的な関係性のある因果であるとまでは言えません。
ましてや、曲線的な関係性のある因果の場合、かなり見極めるのが困難です。
そもそも、データを利用しようがしまいが、明確な因果関係を知ることは非常に難しいと思います。
物事や事象などに蓋然性があるからこそ、データなどを活用するのでしょう。
データで偶然から脱却し、可能な限り必然に近づけることができても、必然にはなりえない、ということなのだと思います。
例えば、離反分析で「離反するも八卦、継続するも八卦」(事前には予期しえない状態)から、データを活用することで、ある程度の離反を予測できる状態にすることは出来ます。

ただ、完璧に予測することはできません。顧客がある行動をとったときの離反確率が90%と予測することはできても、100%の予測はできないということです。
簡易実験(コンピュータ・シミュレーション)
Excelなどで乱数を発生させ、YとXの2つのでたらめなデータを作ります。でたらめなデータ間の関係は、通常はありません。

この例では、相関係数は「-0.014」でした。ほぼ「0」です。
この作業を500回実施し、500個の相関係数を算出します。500個の相関係数の基礎統計量は次のようになりました。
- 相関係数の平均:0.006
- 相関係数の最大:0.840
- 相関係数の最小:-0.867
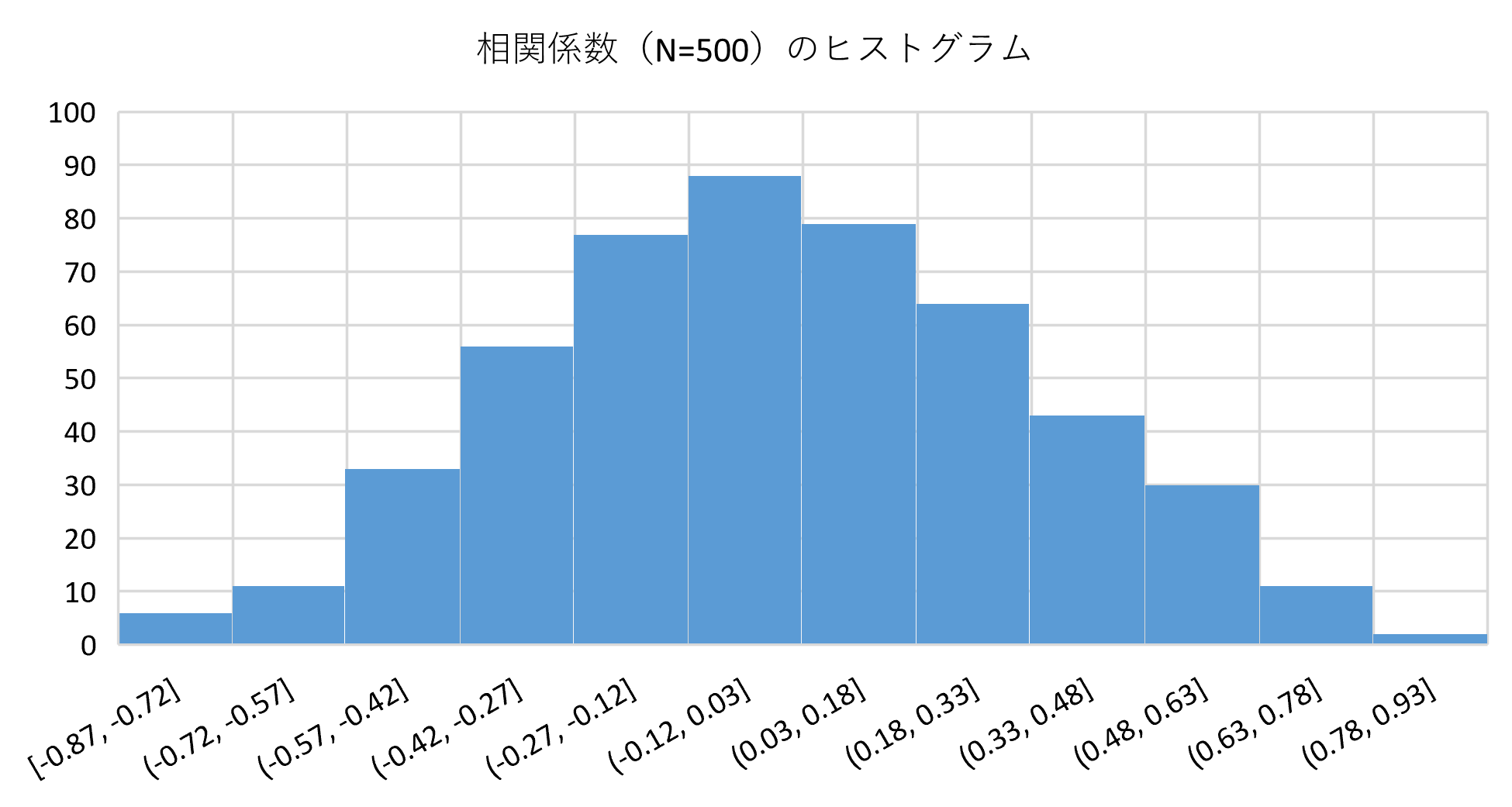
何を言いたいかと言うと、でたらめに作ったデータでも、たまにそれなりの相関係数の値になる(例では、相関係数 0.8ぐらい)ということです。
相関係数の大小や、線形回帰式の係数や精度などに惑わされないことが重要です。
最後にモノを言うのは「ドメイン知識」
先ほど、ドメイン知識(データ活用をする現場の知識)が欠落していると、結果に違和感を持つことなく突き進む危険性について触れました。
データは、所詮過去の事象を記録したモノに過ぎません。しかも、過去のほんの一部分です。
そこから垣間見れるものは非常に多いですが、すべてではありません。すべてどころかほんの少しです。

データ分析の結果や数理モデルの解釈などは、ドメイン知識(データ活用をする現場の知識)が欠落していると、不完全です。
不完全というか、解釈が表面的で非常に浅くなります。
場合には、前提知識が無いばかリに、足りない前提知識を妄想で埋め、そのせいであると勘違いし、間違ったことや的外れなことを堂々と言うことになります。
そのとき、何がファクト(事実)で何が妄想(仮設定)で、そして何を考慮し何を考慮しないのか(データがないから分からない、どっちにも取れるので不透明、など)を、明確に把握しておく必要があります。
妄想(仮設定)部分は、現場のヒアリングや行動観察などで修正しておく必要があることでしょう。

現場ヒアリングは、立場やバックグラウンド、その人の思いなどで、言っていることが変わってくるので、気を付けてファクト(事実)を掴みましょう。最悪は、事実誤認です。
今回のまとめ
今回は、「『相関』は曲がったことが大っ嫌い」というお話しをしました。
データ分析では、よく数理統計学の手法が使われます。
その中で、比較的高頻度で登場するのが「相関分析」です。2つの変量の間の関係性を見るものです。
相関は因果ではなく、単なるデータ間の直線関係を表現したものに過ぎません。データ間に曲線関係がある場合には、そのままでは有効に機能しません。
データ分析の結果や数理モデルの解釈などは、ドメイン知識(データ活用をする現場の知識)が欠落していると、不完全です。不完全というか、解釈が表面的で非常に浅くなります。
「頼まれたことをやっただけ」という感じで、ドメイン(データ活用をする現場)に関しよく分からないという状況のまま、データ分析や数理モデルを構築するのは危険です。
特に、頼んできたのがデータ分析やデータサイエンス、機械学習などの素人であれば、尚更危険です。野球未経験がプロ野球選手に、あーだこーだ注文を付けるようなものです。

