異常とは、標準的な挙動から著しく逸脱した稀なデータのことである。
時系列の多くの異常値は、ある特定の時点における顕著なスパイクや、ある特定の期間だけ傾向が大きく異なるとかです。
そして、異常データの多くは、どのデータが異常でどのデータが正常なのかという正解ラベルの付いたデータではありません。
そのようなとき、教師なし異常検知アプローチが取られます。「教師なし」とは、「異常or正常のラベルがなし」ということです。
時系列異常検知(教師なし)には、大きく3つのアプローチ方法があります。
- 時系列モデルによる信頼区間アプローチ
- 教師なしクラスタリングアプローチ
- 現場専門家×統計学的プロファイリングアプローチ
今回は、「時系列異常検知(教師なし)の3つのアプローチ」というお話しをします。
時系列モデルによる信頼区間アプローチ
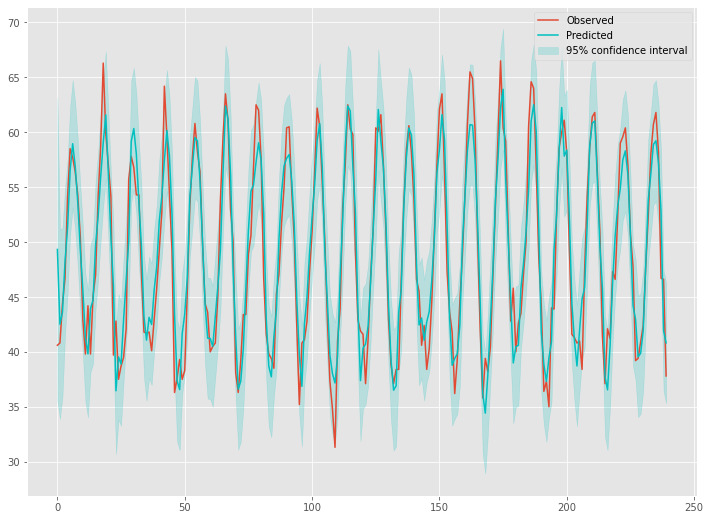 統計学系の数理モデルには、点だけでなく区間を推定することが、多くの場合できます。
統計学系の数理モデルには、点だけでなく区間を推定することが、多くの場合できます。
その区間を信頼区間と言ったりします。
統計学系の時系列モデル(例:ARIMA系など)も、多くの場合、同様に信頼区間を出力することができます。
この信頼区間を利用し、異常検知することができます。
どのように異常検知するのかというと、信頼区間外のデータを異常値と判断します。
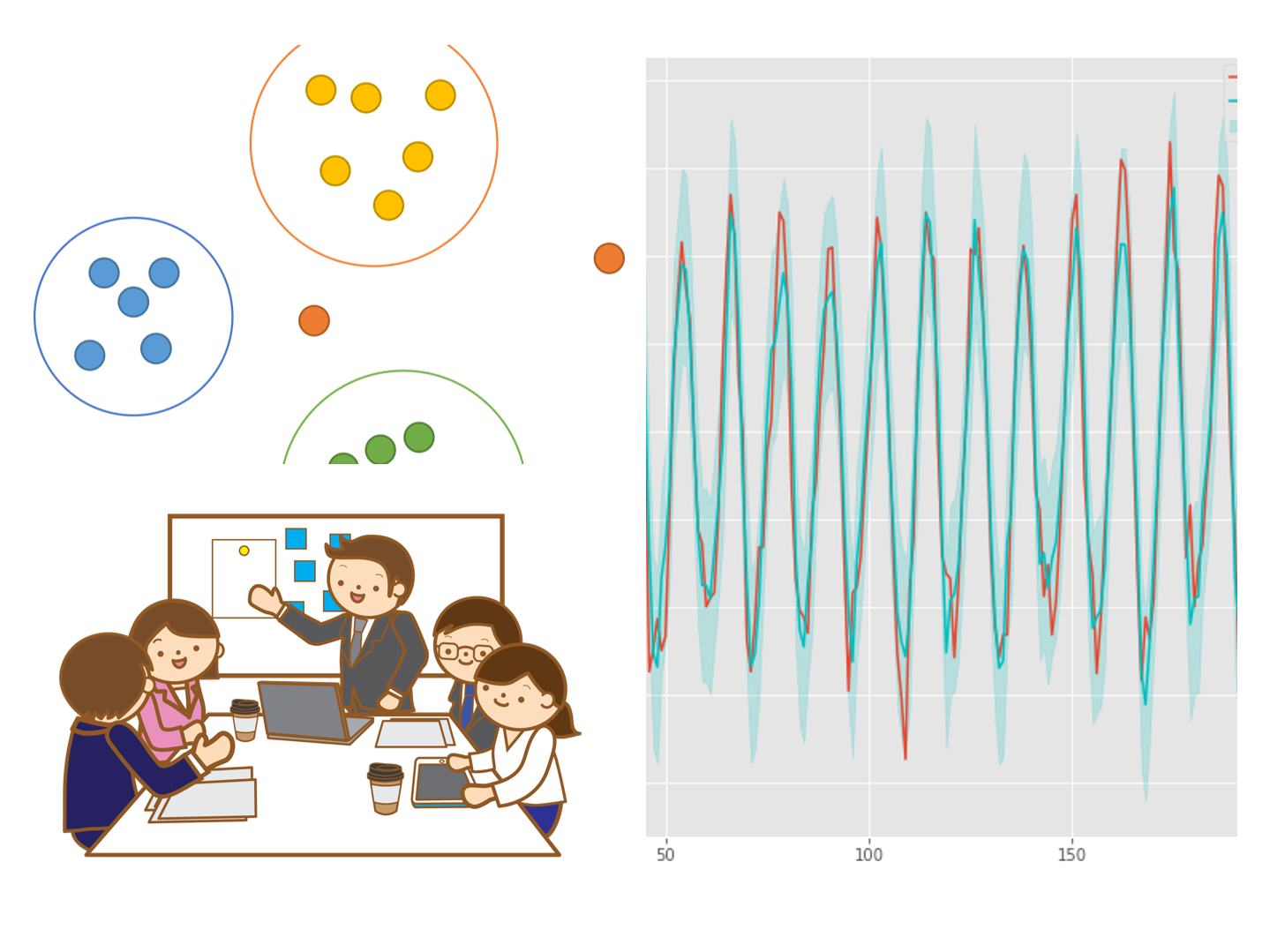
教師なしクラスタリングアプローチ
 教師なし機械学習の1つにクラスタリングという手法があります。
教師なし機械学習の1つにクラスタリングという手法があります。
クラスタリングとは似たようなデータをグルーピングする手法です。
クラスタリングすると異常値はどうなるかというと、極端な場合、どのグループにも所属しません。要は、異常値だけのN=1のクラスターが出来上がります。
クラスタリングと言えばk-means法です。ただ、最初にクラスター数を設定する必要あるのが難点です。最近は、最初にクラスター数を設定する必要のないDBSCAN法を使うケースが増えています。
他にも、教師なし異常検知アルゴリズムIsolation Forestなどもあります。こちらはクラスタリングではなく、ランダムフォレストを応用した異常検知アルゴリズムです。
現場専門家×統計学的プロファイリングアプローチ

時系列モデルによる信頼区間アプローチも教師なしクラスタリングアプローチも、機械的に異常検知するものであり、本当に異常なのか、異常の要因は何か、などは明確になりません。
異常かどうかを考えるきっかけになるに過ぎません。
そこで、現場専門家によるアプローチがものを言います。
統計学的プロファイリングとは、時系列モデルによる信頼区間アプローチや教師なしクラスタリングアプローチで異常と判別されたデータに対し、異常or正常の特徴を把握すること(プロファイリング)です。
具体的には、異常or正常のラベルを目的変数yとした分類問題として検討していきます。
要は、異常データの特徴を、統計学的もしくは機械学習的に洗い出し解釈する、ということです。現場インサイトとデータインサイトの融合です。
多くの場合、現場インサイトとデータインサイトの融合による検討結果をもとにルール化し、異常検知の運用時に活用します。
今回のまとめ
今回は、「時系列異常検知(教師なし)の3つのアプローチ」というお話しをしました。
異常とは、標準的な挙動から著しく逸脱した稀なデータのことである。
時系列の多くの異常値は、ある特定の時点における顕著なスパイクや、ある特定の期間だけ傾向が大きく異なるとかです。
そして、異常データの多くは、どのデータが異常でどのデータが正常なのかという正解ラベルの付いたデータではありません。
そのようなとき、教師なし異常検知アプローチが取られます。「教師なし」とは、「異常or正常のラベルがなし」ということです。
時系列異常検知(教師なし)には、大きく3つのアプローチ方法があります。
- 時系列モデルによる信頼区間アプローチ
- 教師なしクラスタリングアプローチ
- 現場専門家×統計学的プロファイリングアプローチ
上から順番に実施するのがいいでしょう。