昨今、色々な数理モデルが登場してきました。ただ、実用性ではどうでしょうか。
誰もが実務で使えるという観点で考えると、以下の3つの回帰モデルと2つのデータ集約手法で十分なケースが多いです。
- 線形回帰モデル(単回帰/重回帰)
- ポアソン回帰モデル
- ロジスティック回帰モデル
- 主成分分析
- クラスタ分析
今回は、「最低限覚えておきたい5つの数理モデル」というお話しをします。
Contents [hide]
3つの回帰モデル

「線形回帰モデル」「ポアソン回帰モデル」「ロジスティック回帰モデル」は、「〇〇回帰モデル」と呼ばれるもので、「目的変数Y」と「説明変数X」で構成される数理モデルです。
「〇〇回帰モデル」と呼ばれるものは、他にもありますが、使用頻度の高いのはこの3つです。
この3つの違いは、目的変数Yがどのようなデータなのか、によります。通常は、次にようになります。
- 目的変数Yが定量データ(非カウントデータ)→線形回帰モデル
- 目的変数Yが定量データ(カウントデータ)→ポアソン回帰モデル
- 目的変数Yが定性データ(2値)→ロジスティック回帰モデル
カウントデータと非カウントデータ
カウントデータは、1つ2つ3つとカウントするデータで、非負の整数値(0、1、2、3、…)の値をとります。
例えば、訪問件数や受注件数、故障台数などです。
非カウントデータは、カウントデータではない定量データで、負の値をとることもありますし、小数点が付く場合もあります。
例えば、気温や体重などです。
受注金額などの値の大きなカウントデータは、非カウントデータとして扱うことができます。
値が大きいとは、単純に大きな数値という意味でです。
例えば、0円、1円、2円、…ではなく、1,000円、10,000円、100,000円…ということです。
定性データ(2値)とは?

定性データ(2値)は、2つのカテゴリ(例:受注と失注、継続と離反、など)を持つデータです。
2値データと呼んだりします。
例えば、「受注の有無」や「離反の有無」などです。
このときデータは、「1:受注、0:失注」、「1:離反、0:継続」などと数字を割り振ります。
また、「目的変数Y」を「受注の有無」と表現したり、「1:受注、0:失注」と表現したり、簡単に「受注率」と表現したりします。
ちなみに、「目的変数Y」が「受注の有無」のロジスティック回帰モデルで出力されるのは「受注率」になり、受注率が0.5より大きいと予測されたとき「受注」と予測する、といった使い方をします。
主成分分析とクラスタ分析
主成分分析とクラスタ分析は、データを集約(もしくは、グルーピング)する分析技術の1つです。
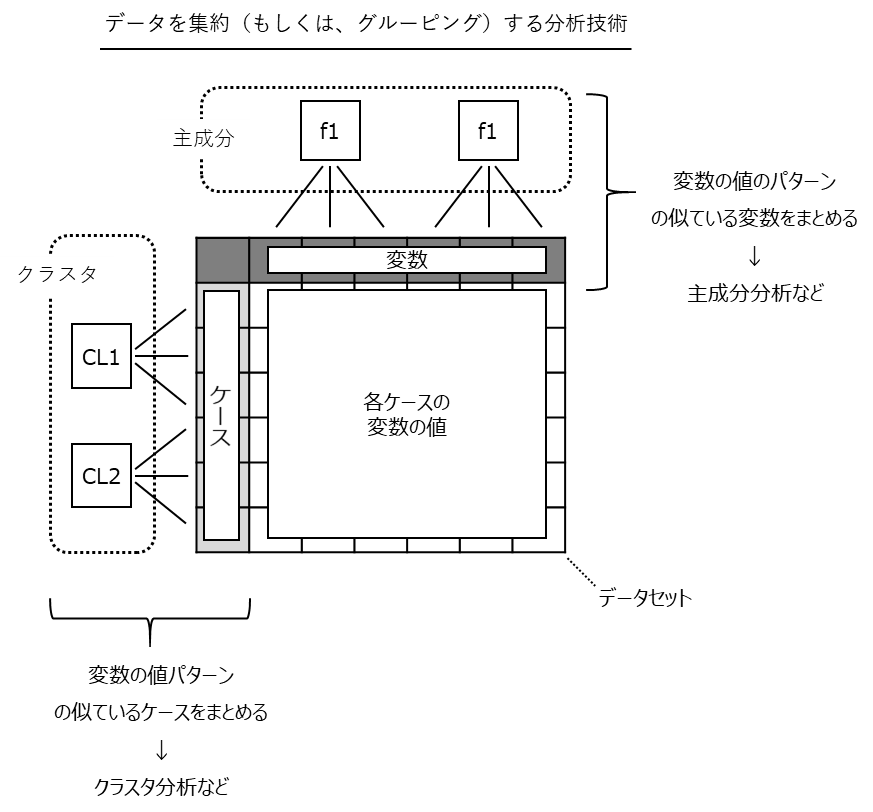
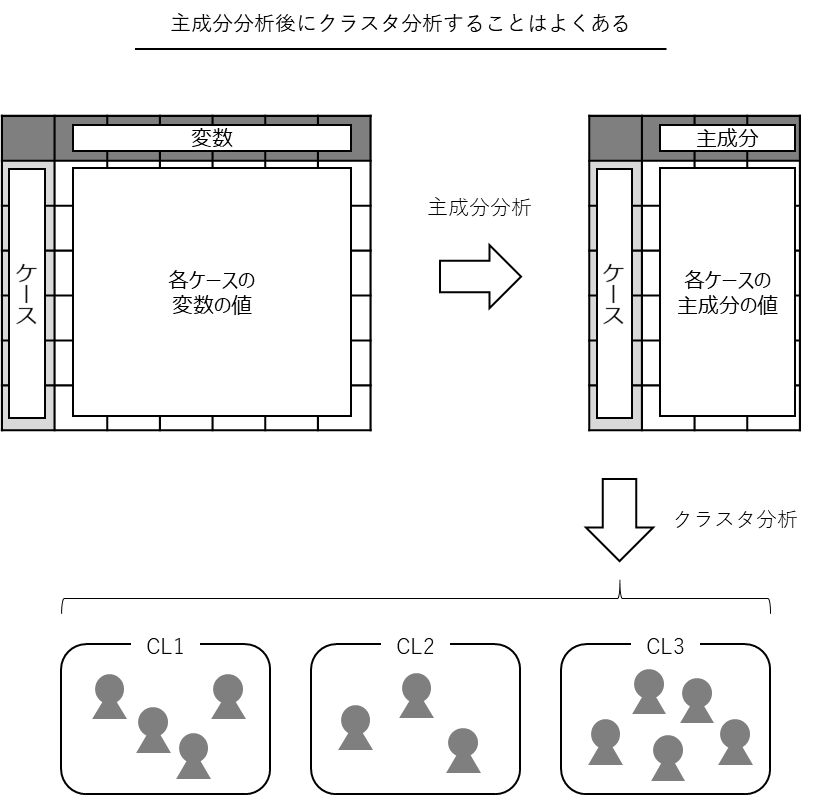
2つの違いは、主成分分析は変数(データセットの列)を集約(もしくは、グルーピング)することで次元縮約(例:1,000変数を10変数にまとめる)するのに対し、クラスタ分析はケース(データセットの行)を集約(もしくは、グルーピング)することで似たようなケースをクラスタ化(同じようなのが集まっている状態)します。
この場合のケースとは、個体(例:個人や店舗、企業など)です。
ちなみに、主成分分析で作られた新たな変数を、「主成分」と呼びます。クラスタ分析で作られたグループを、「クラスタ」もしくは「クラス」と呼びます。
意思決定をサポートするのにそのまま使える回帰モデル

線形回帰モデルやポアソン回帰モデル、ロジスティック回帰モデルなどの「〇〇回帰モデル」と呼ばれるものは、多くの場合、意思決定をサポートするのにそのまま使えます。
例えば、売上を目的変数とする線形回帰モデルを構築すれば、売上の異常を検知することができます。
受注件数を目的変数とするポアソン回帰モデルを構築すれば、受注件数が伸び悩んだときに、その要因を分析することに使えます。
受注の有無を目的変数とするロジスティック回帰モデルを構築すれば、リード(見込み顧客)の受注確率を予測することができます。
一方で、主成分分析やクラスタ分析は、単体で意思決定に役立つとうよりも、仮説発見(どちらかというと、仮説創造)のためや、「〇〇回帰モデル」の前に実施する「前処理」として、実施することが多いようです。
主成分分析とクラスタ分析の活用例
最近のビッグデータ化により、データセットが2方向に延びました。
「横方向の伸び」(変数の数が増える)と「縦方向に伸び」(ケースの数が増える)です。
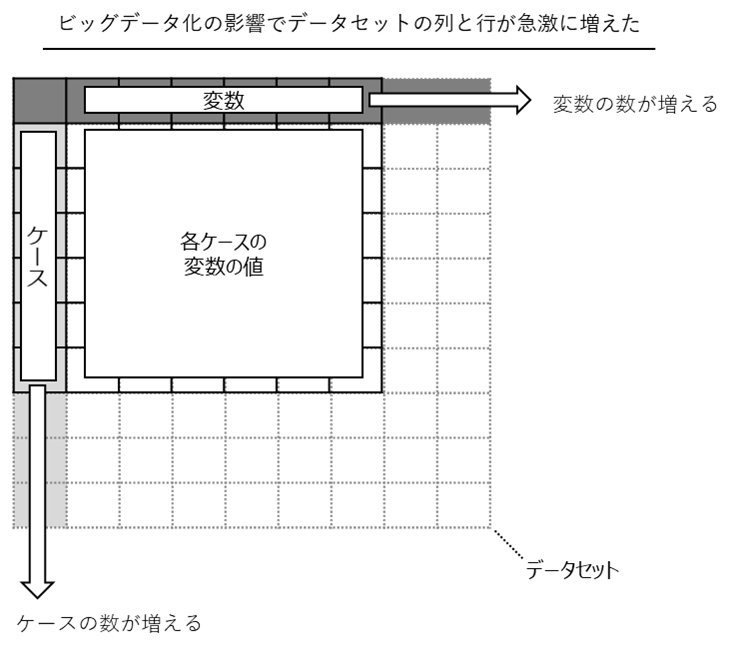
変数の数が急増し、数百変数や数千変数ではなく、場合によっては数万変数や数億変数という状況に陥ることもあります。
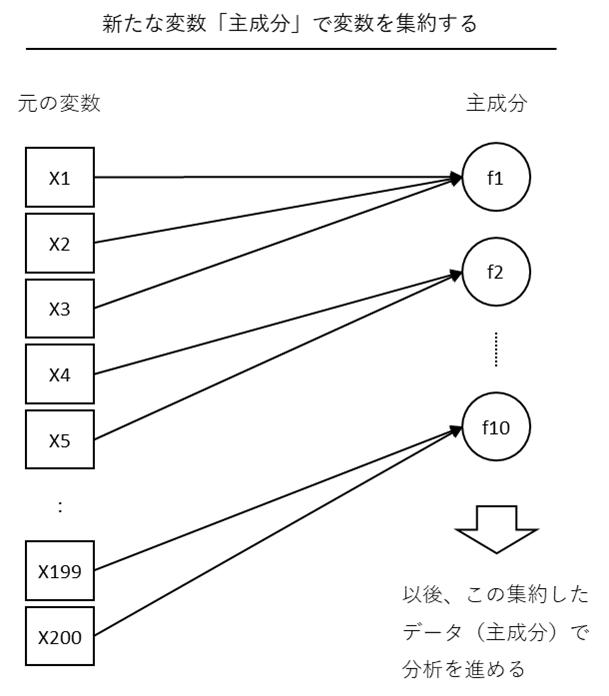
このようなとき、主成分分析を実施することで、データの持つ情報量を出来るだけ失うことなく、「少数の変数」に減らすことができます。
その「少数の変数」は「主成分」と呼ばれ、主成分分析によって作られた「新しい変数」です。
数理モデルを構築するときに、この新しく作られた変数でモデルを構築します。
ちなみに、主成分そのものが、どういった変数なのかは、人の頭で考える必要があります。
例えば、元の変数と主成分の関係性(例:相関係数)などから考えていくことが多いです。
主成分分析は使い勝手のいいので、他にも色々な前処理で利用したり、他の分析手法と組み合わせて利用したりします。
例えば、主成分分析後に「主成分」でクラスタ分析を実施し、似たような主成分を持つケースをグルーピングしたりします。
仮説創造

クラスタ分析の中の「最大の分析」(最も頭を使う)が、「なぜ、そのようなグルーピングがなされたのか? 各クラスタにはどのような特徴があるのか?」を考えるプロファイリングです。
クラスタ別にデータを集計し比較したり、「○○回帰モデル」を構築したりすることで、各クラスタの特徴を把握していきます。
そうして、仮説発見(どちらかというと、仮説創造)をしていきます。
主成分分析やクラスタ分析を実施したからといって、「これが仮説です」という感じで教えてくれることはありません。人の頭を使い仮説を考えていきます。
そして、クラスタ分析の結果を、新たな説明変数Xにしたり、新たな媒介変数Zにすることも多く、そのことで構築した数理モデルの精度が向上したり、説明しやすくなったりします。
今回のまとめ
今回は、「最低限覚えておきたい5つの数理モデル」というお話しをしました。
昨今、色々な数理モデルが登場してきました。ただ、実用性ではどうでしょうか。
誰もが実務で使えるという観点で考えると、以下の3つの回帰モデルと2つのデータ集約手法で十分なケースが多いです。
- 線形回帰モデル(単回帰/重回帰)
- ポアソン回帰モデル
- ロジスティック回帰モデル
- 主成分分析
- クラスタ分析
「線形回帰モデル」「ポアソン回帰モデル」「ロジスティック回帰モデル」は、「〇〇回帰モデル」と呼ばれるもので、「目的変数Y」と「説明変数X」で構成される数理モデルです。
「〇〇回帰モデル」と呼ばれるものは、他にもありますが、使用頻度の高いのはこの3つです。
この3つの違いは、目的変数Yがどのようなデータなのか、によります。通常は、次にようになります。
- 目的変数Yが定量データ(非カウントデータ)→線形回帰モデル
- 目的変数Yが定量データ(カウントデータ)→ポアソン回帰モデル
- 目的変数Yが定性データ(2値)→ロジスティック回帰モデル
「〇〇回帰モデル」と呼ばれるものは、多くの場合、意思決定をサポートするのにそのまま使えます。
主成分分析とクラスタ分析は、データを集約(もしくは、グルーピング)する分析技術の1つです。
主成分分析は変数(データセットの列)を集約(もしくは、グルーピング)することで次元縮約(例:1,000変数を10変数にまとめる)するのに対し、クラスタ分析はケース(データセットの行)を集約(もしくは、グルーピング)することで似たようなケースをクラスタ化(同じようなのが集まっている状態)します。
主成分分析やクラスタ分析は、単体で意思決定に役立つとうよりも、仮説発見(どちらかというと、仮説創造)のためや、「〇〇回帰モデル」の前に実施する「前処理」として、実施することが多いようです。