最もシンプルで始めやすいデータ活用の1つに、ABテストというものがあります。
ABテストでは、統計的仮説検定に纏わる数理統計学の概念を最低限理解して置く必要があります。
初学者にとって、ABテストの最初のハードルは統計的概念の理解です。
今回は、「生まれて初めてのABテスト超入門」というお話しをします。
ABテストのシナリオ例
あなたがECサイトを運営しているとしましょう。
購入ボタンの色を、灰色から橙色に変えようと思っています。

次の3つの仮説が思い浮かびます。
- 橙色のボタンは、灰色のボタンと同じ平均購入数をもたらす
- 橙色のボタンは、灰色のボタンより多くの平均購入数をもたらす
- 橙色のボタンは、灰色のボタンより少ない平均購入数をもたらす
この仮説を次の2つに集約します
- 橙色のボタンは、灰色のボタンと同じ平均購入数をもたらす
- 橙色のボタンは、灰色のボタンの異なる平均購入数をもたらす
この仮説を検証するために、対象者をA群とB群に分けABテストを実施します。
- A群:灰色のボタンを表示する群(統制群/対照群、control group)
- B群:橙色のボタンを表示する群(実験群/処置群、experimental group/treatment group)
A群とB群はランダムに割り付けます。
ある程度のデータが蓄積されたタイミングで、A群とB群の平均購入数を比較し、白黒はきりさせます。
統計的仮説検定
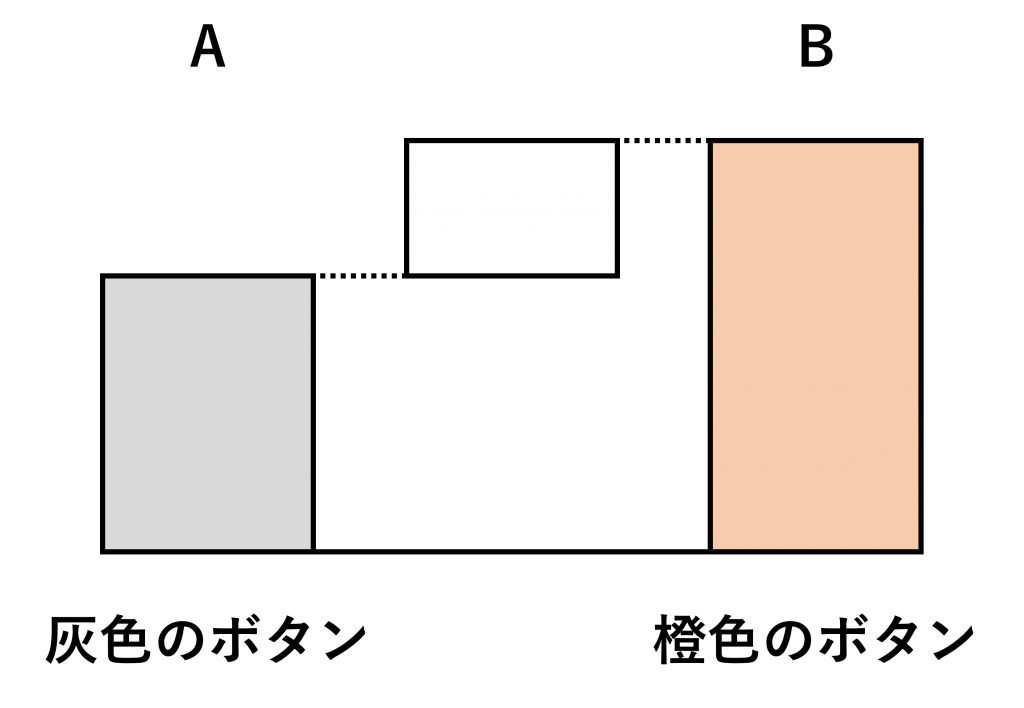
先程、次の2つの仮説を立てました。それぞれ、帰無仮説と対立仮説といいます。
- 帰無仮説H0:橙色のボタンは、灰色のボタンと同じ平均購入数をもたらす
- 対立仮説H1:橙色のボタンは、灰色のボタンの異なる平均購入数をもたらす
統計的仮説検定とは、帰無仮説H0を破棄するに十分な証拠があるかどうかを判断します。
帰無仮説H0を破棄することになって、初めて対立仮説H1を採択します。そうでない場合(帰無仮説H0を破棄できない場合)、実は何も言えません。
要は、帰無仮説H0を破棄し対立仮説H1を採択するかどうかしか、統計的仮説検定はできません。
帰無仮説H0を破棄できない場合、証拠不十分で判定できません。
このあたりが、ややこしいところです。
大数の法則と中心極限定理
今、中学校1年生男子の平均身長を知りたいとします。
この平均身長を知るには、中学校1年生男子全員の身長を測定する必要があります。非常に大変なことです。
そこで登場するのが、中心極限定理です。
中心極限定理によって、全員の身長を測定する手間から開放されます。例えば、中学校1年生男子をランダムに1,000 人のサンプルを集め、この1,000 人の身長の平均をとることで代替できるからです。
全員の身長を測定するよりも、1,000 人の身長を測定する方が、はるかに安価で実現可能です。
大数の法則とは、サンプル数を増やすとサンプルの平均身長 は、中学校1年生男子全員の身長の平均に近くなるということです。
では、中心極限定理とは何なのか?
元のデータが正規分布していなくても、その平均は正規分布に近づく傾向がある、というのが中心極限定理です。
正規分布とは何なのか、という議論もありますが、一旦脇に置いておきます。
重要なことは、正規分布である程度語れる、ということです。
この2つの統計的概念をベースに、統計的仮説検定は成り立っています。
何が嬉しいの?
では、このことで何が嬉しいのでしょうか?
中学校1年生男子全員の身長を測ることなく、1,000 人の身長を測定することで十分なら嬉しいでしょう。
要は、そういうことです。

ABテストを実施するとき、全てのデータを取得すること無く、白黒つけることが可能になるのです。
そう考えると、ABテストの結果を白黒つけるには、ABテストをほぼ半永久的に実施する必要があります。それでは遅すぎます。ある程度のデータ量で白黒つけたいものです。
そのようなことを実現するのが、統計的仮説検定に基づいたABテストです。
白黒はっきりさせるまで、帰無仮説H0を破棄するまでデータを取り続けます。
ただ、時間は有限なため、ある定期までデータを取り続けると計画するのが普通です。
間違うこともある
ABテストは少ないデータ量で白黒はっきりさせようという取り組みのため、間違うことがあります。
以下の2つの間違いです。
- タイプ1過誤:帰無仮説H0が正しいのに、帰無仮説H0を棄却する間違い
- タイプ2過誤:対立仮説H1が正しいのに、帰無仮説H0を棄却しない間違い
意味分からないという方もいるかも知れませんが、このような間違いが起こる可能性があります。

少ないデータで白黒はっきりさせるには、この2つの間違いをある程度許容する必要があります。
この2つの間違いを確率で表現します。
- α:タイプ1過誤の起こる確率、有意水準やp値とも言われる
- β:タイプ2過誤の起こる確率、1-βを検出力と言います
使い方

慣習的に、αである有意水準(p値)を0.05もしくは0.01に設定します。
ECサイトで購入を迷っている訪問者に対し、購入ボタンの色をランダムに表示させます。
灰色の購入ボタンを表示された方をA群、橙色の購入ボタンを表示された方がB群です。
しばらくデータを取得続けると、購入する人が現れ始めます。さらにデータを取得続けると、購入者数に差がつくかもしれません。
その差が意味のある差なのかどうかを、統計的仮説検定で検討します。
- 帰無仮説H0:橙色のボタンは、灰色のボタンと同じ平均購入数をもたらす
- 対立仮説H1:橙色のボタンは、灰色のボタンの異なる平均購入数をもたらす
このとき、出力されたp値の値を見ます。通常の統計学系のツールは、このp値を出力します。
その値が、例えば0.05未満の場合に「有意な差がある」と見なし、帰無仮説H0を棄却し対立仮説H1を採択します。
そして、平均購入数が高い方の購入ボタンの色が良い、と結論付けます。
ただし、この結論は5%(0.05)の間違うリスクがあります。
要は、有意水準(今回の例では5%)分の間違うリスクを許容する代わりに、少ないデータで白黒はっきりさせる、という感じです。
今回のまとめ
今回は、「生まれて初めてのABテスト超入門」というお話しをします。
最もシンプルで始めやすいデータ活用の1つに、ABテストというものがあります。
ABテストでは、統計的仮説検定に纏わる数理統計学の概念を最低限理解して置く必要があります。
初学者にとって、ABテストの最初のハードルは統計的概念の理解です。
大数の法則やら、中心極限定理やら、統計的仮説検定やら、聞き慣れない不思議なワードが並びます。
ABテストは、統計的仮説検定を実施し、少ないデータでA群とB群のどちらの数値が高いのか(低いのか)白黒はっきりさせる手法です。
少ないデータで白黒はっきりさえることで、スピーディに結論に達することができます。
ただし、少ないデータで白黒はっきりさえることで、間違うリスクもあります。
ABテストは、その間違うリスクを許容しつつ、スピーディに結論に達しようというものです。

