ビジネスの意思決定において、不確実性は避けられない課題です。

従来の統計手法では、この不確実性を十分に考慮できないことがあります。そこで注目されているのが、ベイズモデリングです。

ベイズモデリングは、統計学と機械学習の分野で広く用いられている手法で、不確実性を直接モデルに組み込むことができます。

これにより、より現実的で信頼性の高い予測と意思決定が可能になります。

今回は、「ベイズモデリングでビジネスにおける不確実性の把握と活用」というお話しをします。

ベイズモデリングとは何か

ベイズモデリングは、ベイズの定理に基づいて、データから確率的なモデルを構築する手法です。

従来の統計手法とは異なるアプローチを取ることで、より柔軟で現実的なモデリングが可能になります。

　従来の統計手法の限界

従来の統計手法、例えば最尤推定法では、多くの場合パラメータの点推定値を求めることに重点が置かれています。

例えば、広告の効果は常に同じ、予測した値も1点のみ、といった感じです。

しかし、現実のデータには不確実性が内在しており、点推定値だけでは不十分な場合があります。

また、サンプルサイズが小さい場合や、外れ値が存在する場合には、従来の手法では適切なモデリングが難しくなります。

　ベイズモデリングの強み

ベイズモデリングでは、点もしくは区間の推定ではなくパラメータの確率分布を推定します。

これにより、パラメータの不確実性を直接モデルに組み込むことができます。

また、事前分布を設定することで、データ以外の情報や専門家の知見をモデルに反映させることもできます。

ベイズモデリングは、サンプルサイズが小さい場合や外れ値が存在する場合でも、柔軟にモデリングできる点が強みです。

さらに、モデルの比較や選択、予測分布の計算など、様々な応用が可能です。

　ベイズモデリングのメリット

以下のようなメリットがあります。

• パラメータの不確実性を定量化できる
• 事前知識を柔軟にモデルに組み込める
• モデルの比較や選択が容易になる
• 予測分布を直接計算できる

これらのメリットにより、ベイズモデリングは、不確実性を伴うデータに対して、柔軟で現実的なモデリングを可能にします。

ビジネスにおける活用事例

ベイズモデリングは、様々なビジネス領域で活用されています。

ここでは、代表的な活用事例について説明します。

　事例１：需要予測

ABC株式会社は、大手家電メーカーです。多様な製品ラインナップを持ち、国内外で事業を展開しています。

ABC株式会社では、効率的な在庫管理と生産計画の策定が重要な課題となっていました。特に、新製品の需要予測の精度向上が急務でした。

 

従来は、過去の販売実績データを用いた時系列分析により需要予測を行っていましたが、以下のような限界がありました。

• 新製品では過去のデータが少なく、予測精度が低い
• 季節性や経済状況などの外部要因の影響を考慮できない
• 予測の不確実性が定量化できず、リスク評価が困難

これらの課題を解決するため、ABC株式会社では、ベイズモデリングを用いた需要予測を実施しました。

 

ベイズモデリングでは、過去の販売実績データだけでなく、季節性や経済状況などの外部要因を組み合わせて、将来の需要を確率的に予測します。要は、予測結果として1つの数値を示すのではなく、分布を示す、ということです。

また、事前分布を用いることで、新製品に関する専門家の知識や経験を予測に反映させることができます。

事後分布を用いることで、需要の不確実性を定量化し、在庫切れや過剰在庫のリスクを評価できるようになりました。

これにより、適切な在庫水準の設定と、リスクを考慮した生産計画の策定が可能になりました。

 

まとめると、ベイズモデリングを用いた需要予測により、以下のような効果が得られました。

• 新製品の需要予測精度が向上し、在庫切れと過剰在庫のリスクが減少
• 外部要因の影響を考慮した予測により、需要の変動に対する対応力が向上
• 需要の不確実性を定量化することで、リスクを考慮した意思決定が可能に

これらの効果により、ABC株式会社では、在庫管理と生産計画の最適化が実現し、コスト削減と顧客満足度の向上につながりました。

　事例２：価格戦略の最適化

XYZ株式会社は、家具や雑貨を扱うECサイトを運営しています。幅広い商品ラインナップを持ち、価格競争力を強みとしています。

XYZ株式会社では、価格設定が収益に大きな影響を与えるため、最適な価格戦略の立案が重要な課題となっていました。

 

従来は、過去の販売データを用いた回帰分析により、価格弾力性を推定し、利益最大化価格を算出していました。しかし、以下のような限界がありました。

• 価格と需要の関係が線形であると仮定しており、現実の複雑な関係を捉えられない
• 価格変更に伴う不確実性やリスクを考慮できない
• 競合他社の価格変動の影響を反映できない

これらの課題を解決するため、XYZ株式会社では、ベイズモデリングを用いた価格最適化モデルを導入しました。

 

ベイズモデリングでは、価格と需要の関係を柔軟にモデル化することができます。

過去の販売データから、価格弾力性を推定し、利益を最大化する価格を探索します。

また、事前分布を用いることで、競合他社の価格変動など、外部要因の影響を考慮することができます。

事後分布を用いることで、価格変更に伴う不確実性やリスクを定量化し、最適な価格戦略を立案できるようになりました。

これにより、リスクを最小限に抑えつつ、利益最大化を図ることが可能になりました。

 

まとめると、ベイズモデリングを用いた価格最適化により、以下のような効果が得られました。

• 価格と需要の複雑な関係を捉えることで、より現実に即した価格設定が可能に
• 価格変更に伴うリスクを定量化し、リスクを考慮した意思決定が可能に
• 競合他社の価格変動の影響を反映することで、市場環境の変化に迅速に対応可能に

これらの効果により、XYZ株式会社では、価格戦略の最適化が実現し、収益性の向上につながりました。

　事例３：顧客分析

PQR株式会社は、大手小売業者であり、全国に複数の店舗を展開しています。様々な商品カテゴリを扱い、幅広い顧客層を持っています。

PQR株式会社では、効果的なマーケティング戦略の立案のために、顧客分析が重要な役割を果たしていました。

 

従来は、顧客の購買履歴や属性データを用いたクラスター分析により、顧客のセグメンテーションを行っていました。しかし、以下のような限界がありました。

• 顧客の購買行動の変化を捉えられない
• 顧客の多様性を十分に考慮できない
• ドメイン知識を分析に反映させることが困難

これらの課題を解決するため、PQR株式会社では、ベイズモデリングを用いた顧客分析を実施しました。

 

ベイズモデリングでは、顧客の購買行動や属性データを用いて、顧客のセグメンテーションや購買予測を行います。

事後分布を用いることで、顧客の多様性や変化を捉え、個々の顧客に適したアプローチを提案できます。

また、事前分布を通じて、マーケティング担当者の知見やドメイン知識を分析に反映させることができます。

これにより、データだけでは捉えきれない顧客の特性を考慮した分析が可能になります。

 

まとめると、ベイズモデリングを用いた顧客分析により、以下のような効果が得られました。

• 顧客の購買行動の変化を捉えることで、よりタイムリーな施策の立案が可能に
• 顧客の多様性を考慮したセグメンテーションにより、個々の顧客に最適なアプローチが実現
• ドメイン知識を分析に反映させることで、より現実に即した顧客理解が可能に

これらの効果により、PQR株式会社では、マーケティング戦略の精度が大幅に向上し、顧客満足度とロイヤルティの向上につながりました。

　事例４：信用スコアリング

MNO銀行は、全国展開する大手銀行です。個人向けや法人向けの幅広い金融サービスを提供しており、特に個人向け融資に力を入れています。

MNO銀行では、個人向け融資の審査において、信用スコアリングが重要な役割を果たしていました。

 

従来は、顧客の属性情報や過去の取引履歴を用いたロジスティック回帰分析により、デフォルト確率を推定していました。しかし、以下のような限界がありました。

• デフォルトの発生件数が少ないため、モデルの予測精度が低い
• デフォルトリスクの不確実性を定量化できない
• 専門家の知見を反映させることが困難

これらの課題を解決するため、MNO銀行では、ベイズモデリングを用いた信用スコアリングモデルを導入しました。

 

ベイズモデリングでは、顧客の属性情報や過去の取引履歴から、デフォルト確率を推定します。デフォルトの発生件数が少ない場合でも、安定した推定が可能になります。

また、事後分布を用いることで、デフォルトリスクの不確実性を定量化し、適切な融資判断を下すことができます。

これにより、リスクを考慮した意思決定が可能になります。

さらに、事前分布を通じて、融資審査の専門家の知見を反映させることができます。

これにより、データだけでは捉えきれない顧客の特性を考慮した審査が可能になります。

 

まとめると、ベイズモデリングを用いた信用スコアリングにより、以下のような効果が得られました。

• デフォルトの発生件数が少ない場合でも、安定した予測が可能に
• デフォルトリスクの不確実性を定量化することで、リスクを考慮した融資判断が実現
• 専門家の知見を反映させることで、より現実に即した審査が可能に

これらの効果により、MNO銀行では、融資審査の精度が向上し、デフォルト率の低下と融資残高の増加を実現しました。

　事例５：財務分析

RST株式会社は、大手製造業企業であり、複数の事業部門を持つコングロマリットです。

各事業部門の財務状況を把握し、全社的な財務戦略を立案することが重要な課題となっています。

各事業部門の将来業績を予測し、経営資源の配分や投資意思決定を行っていました。

 

従来は、財務諸表データや経済指標を用いた時系列分析により、将来のキャッシュフローや収益性を予測していました。しかし、以下のような限界がありました。

• 予測の不確実性を十分に考慮できない
• 事業部門間の相関関係を捉えられない
• 専門家の見通しを反映させることが困難

これらの課題を解決するため、RST株式会社では、ベイズモデリングを用いた財務分析を実施しました。

 

ベイズモデリングでは、財務諸表データや経済指標を用いて、将来のキャッシュフローや収益性を確率的に予測します。

事後分布を用いることで、予測の不確実性を定量化し、リスクを考慮した意思決定を行うことができます。

また、階層ベイズモデルを用いることで、事業部門間の相関構造を捉えることができます。これにより、全社的な財務戦略の立案が可能になります。

さらに、事前分布を通じて、財務の専門家や事業部門の責任者の見通しを反映させることができます。

これにより、データだけでは捉えきれない事業環境の変化を考慮した予測が可能になります。

 

まとめると、ベイズモデリングを用いた財務分析により、以下のような効果が得られました。

• 予測の不確実性を定量化することで、リスクを考慮した意思決定が可能に
• 事業部門間の相関関係を捉えることで、全社的な財務戦略の立案が実現
• 専門家の見通しを反映させることで、より現実に即した予測が可能に

これらの効果により、RST株式会社では、財務分析の精度が向上し、経営資源の最適配分と投資意思決定の改善につながりました。

ベイズモデリングの基礎

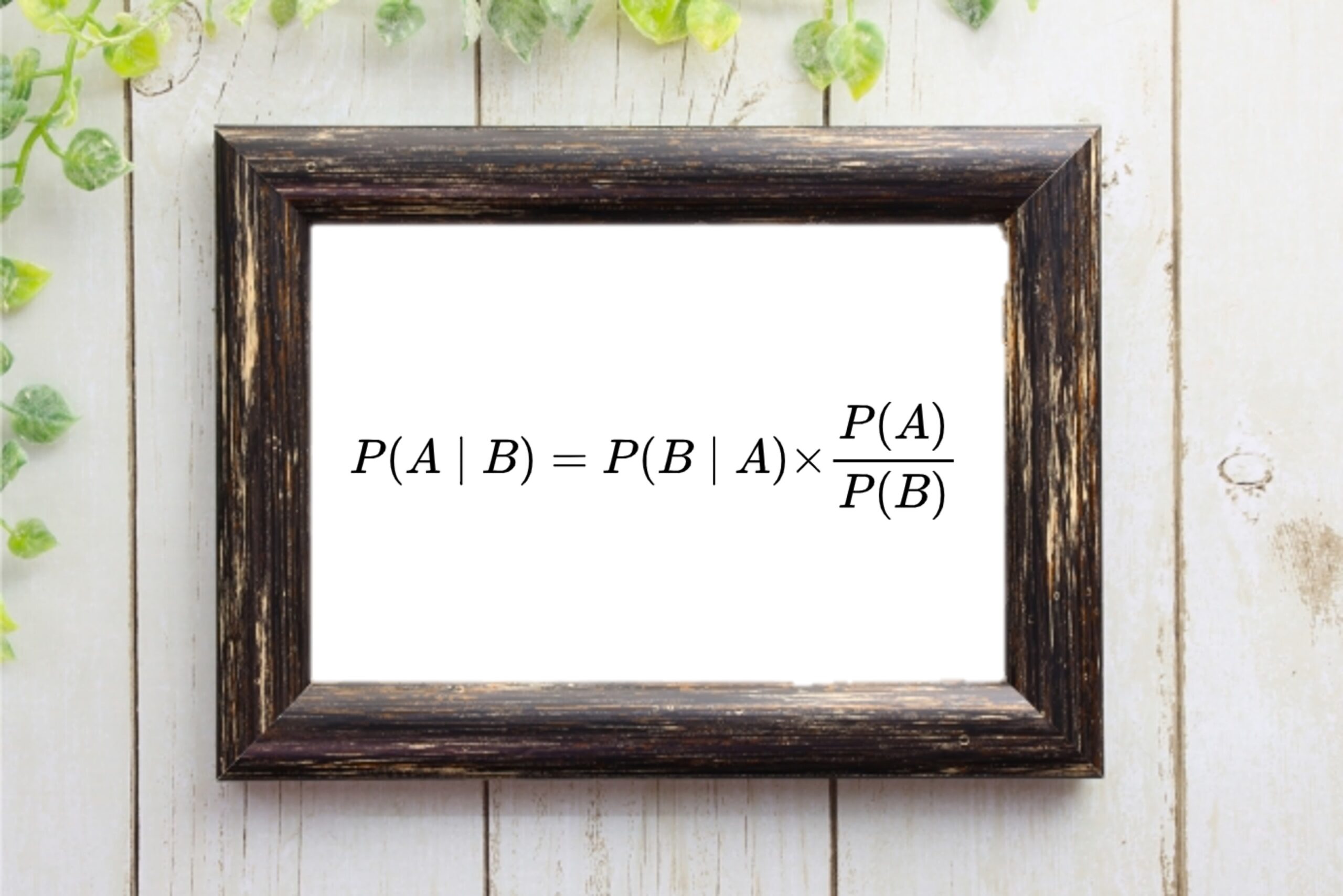
　ベイズの定理

ベイズモデリングの中核をなすのが、ベイズの定理です。

ベイズの定理は、以下の式で表されます。

\displaystyle P(A|B) = P(B|A) \times P(A) / P(B)

• P(A|B)は、事象Bが与えられたときの事象Aの条件付き確率
• P(B|A)は、事象Aが与えられたときの事象Bの条件付き確率
• P(A)は、事象Aの確率
• P(B)は、事象Bの確率

　ベイズモデリング

ベイズモデリングでは、AをパラメータΘ、Bを観測データXとして、以下のように表現します。

\displaystyle P(Θ|X) = P(X|Θ) \times P(Θ) / P(X)

• P(Θ|X)は、事後分布
• P(X|Θ)は、尤度
• P(Θ)は、事前分布
• P(X)は、周辺尤度

　新しい証拠に基づく予測や理論の修正

ベイズの定理は、新しい証拠（データ）が得られたときに、それまでの予測や理論を更新する方法を提供します。

事前分布P(Θ)は、データを観測する前のパラメータΘの確率分布を表し、既存の知識や経験を反映しています。

一方、尤度P(X|Θ)は、パラメータΘのもとでデータXが観測される確率を表します。

ベイズの定理により、事前分布と尤度を組み合わせることで、事後分布P(Θ|X)を計算できます。

事後分布は、データを観測した後のパラメータΘの確率分布を表し、新しい証拠に基づいて更新された知識を反映しています。

ベイズの定理の簡略化

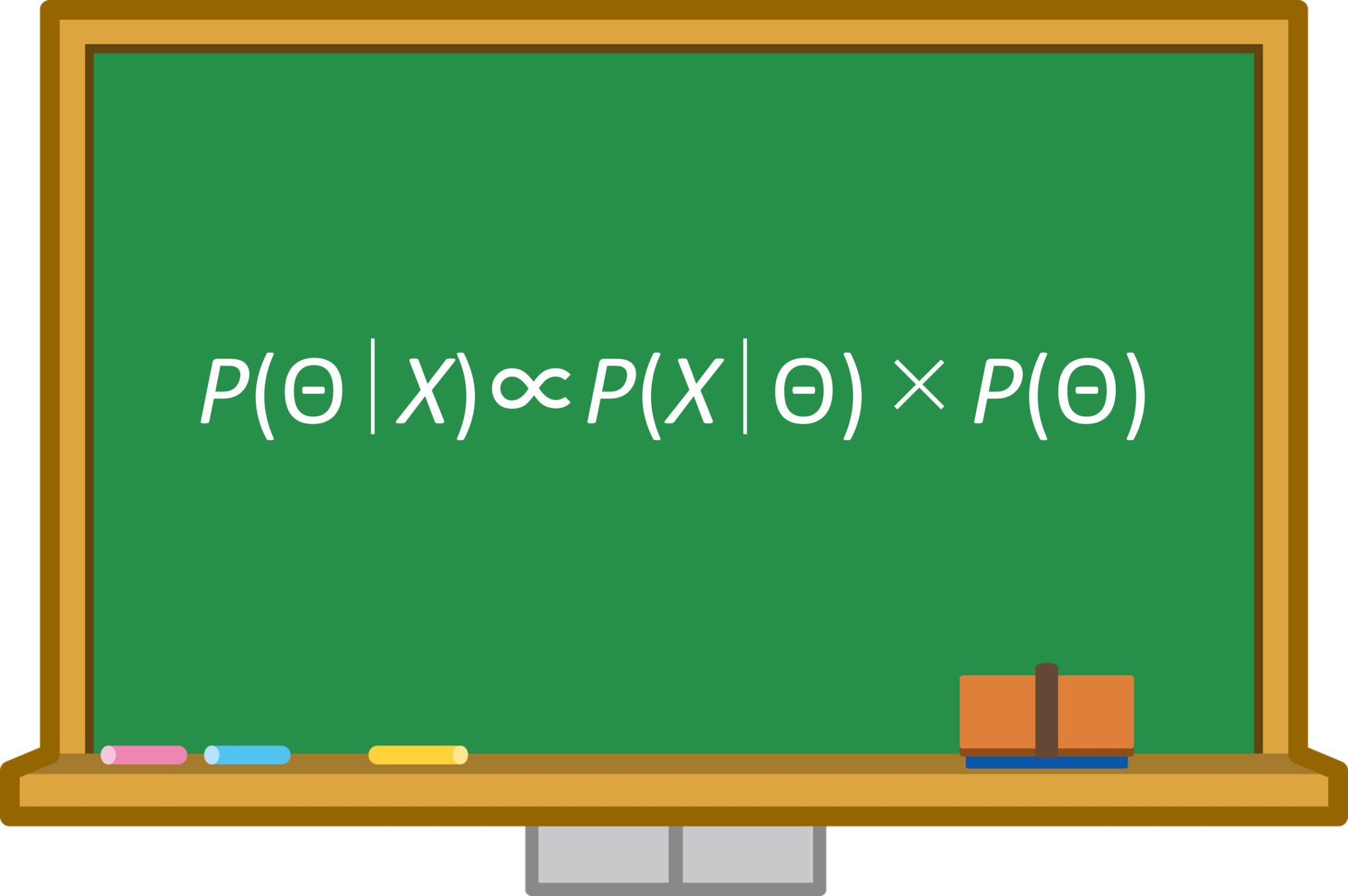
ベイズの定理は、事後分布を計算する上で非常に重要な役割を果たします。

しかし、実際のベイズモデリングでは、定理の簡略化がよく用いられます。

　事後分布、尤度、事前分布の関係

ベイズの定理において、分母のP(X)は、事前分布P(Θ)と尤度P(X|Θ)の積を、パラメータΘについて積分することで計算されます。

\displaystyle P(X) = \int P(X|Θ)  P(Θ) dΘ

この計算は、パラメータΘの次元が高い場合や、複雑な分布を扱う場合に、非常に難しくなります。

　簡略化の考え方

そこで、ベイズモデリングでは、以下の簡略化がよく用いられます。

\displaystyle P(Θ|X) ∝ P(X|Θ) \times P(Θ)

ここで、∝は「比例する」ことを表します。

つまり、事後分布P(Θ|X)は、尤度P(X|Θ)と事前分布P(Θ)の積に比例するということです。

　なぜ簡略化するのか

この簡略化により、分母のP(X)を計算する必要がなくなります。

P(X)は、事後分布の形状には影響しますが、パラメータΘの推定には直接関係しないためです。

簡略化された式を用いることで、事後分布のシミュレーションや最適化が容易になります。

特に、マルコフ連鎖モンテカルロ法（MCMC）などの近似計算手法では、この簡略化が重要な役割を果たします。

ただし、モデル比較や予測分布の計算には、P(X)が必要になる場合があります。

そのような場合には、P(X)を数値的に近似するための手法が用いられます。

ベイズの定理からベイズモデリングへ

ベイズの定理をどのようにしてベイズモデリングに応用するのかを簡単に説明します。

　ベイズモデル構築のプロセス

ベイズモデリングでは、以下の手順でモデルを構築します。線形回帰の例も示します。

 

Step.1　モデルの定式化
確率モデルを定義し、パラメータと変数の関係を明示します。

線形回帰モデルでは、目的変数 y と説明変数 x の関係を以下のように定式化します。

\displaystyle y = β_0 + β_1 \times x + ε

• β_0 は切片
• β_1 は回帰係数
• ε は誤差項であり、ε ~ N(0, σ^2) に従うと仮定

 

Step.2　事前分布の設定
パラメータの事前分布を選択します。事前分布は、パラメータに関する既存の知識や経験を反映します。

線形回帰モデルの例では、パラメータ β_0, β_1, σ^2 に対して事前分布を設定します。

例えば、以下のような事前分布を選択します。

• β_0 \sim N(0, 10^2)
• β_1 \sim N(0, 10^2)
• σ^2 \sim InvGamma(1, 1)

ここで、N は正規分布、InvGamma は逆ガンマ分布を表します。

 

Step.3　尤度の設定
データ (x_i, y_i) が与えられたときのパラメータの尤度を定義します。尤度は、データとパラメータの関係を表します。

線形回帰モデルでは、各観測値 y_i が正規分布 N(β_0 + β_1 \times x_i, σ^2) に従う場合、以下が尤度になります。

\displaystyle N(β_0 + β_1 \times x_i, σ^2)

これは、パラメータ β_0, β_1, σ^2 が与えられたときに、観測値 y_i がどの程度尤もらしいかを表す尤度関数になります。

 

Step.4　事後分布の計算
ベイズの定理を用いて、事前分布と尤度から事後分布を計算します。

線形回帰モデルでは、共役事前分布というものを用いることで、事後分布が解析的に求められます。

• β_0, β_1 の事後分布：β_0, β_1 | y, x, σ^2 ~ MVN(μ_{post}, Σ_{post})
  • データ(y, x)と分散パラメータ(σ^2)が与えられたときの、β_0とβ_1の事後分布
  • この事後分布は多変量正規分布（MVN ）に従う
  • μ_{post}は事後分布の平均ベクトルで、データに基づいて計算
  • Σ_{post}は事後分布の共分散行列で、データに基づいて計算
• σ^2 の事後分布：σ^2 | y, x ~ InvGamma(a_{post}, b_{post})
  • データ(y, x)が与えられたときの、分散パラメータ(σ^2)の事後分布
  • この事後分布は逆ガンマ分布（InvGamma）に従う
  • a_{post} は逆ガンマ分布のシェイプパラメータで、データに基づいて計算
  • b_{post} は逆ガンマ分布のスケールパラメータで、データに基づいて計算

共役事前分布がない場合、事後分布を解析的に求めることができません。

その場合、数値的な近似手法を用いて、事後分布を計算します。代表的な手法として、マルコフ連鎖モンテカルロ法（MCMC）があります。

 

Step.5　モデルの評価と改善
事後分布に基づいて、モデルの性能を評価し、必要に応じて改善します。

例えば、事後予測分布を用いて、新しいデータに対する予測を行うことができます。

また、事後分布の要約統計量（平均値、中央値、信用区間など）を用いて、パラメータの推定値や不確実性を評価することができます。

必要に応じて、モデルの改善（変数選択、事前分布の調整など）を行います。

　尤度と事前分布の組み合わせ

ベイズモデリングでは、尤度と事前分布の組み合わせが重要な役割を果たします。

尤度は、データの生成過程をモデル化したものです。

例えば、線形回帰モデルでは、応答変数が正規分布に従うと仮定します。一方、ロジスティック回帰モデルでは、応答変数がベルヌーイ分布に従うと仮定します。

事前分布は、パラメータの確率分布を表します。

事前分布の選択には、共役事前分布がよく用いられます。共役事前分布を用いると、事後分布が解析的に計算できる場合があります。

尤度と事前分布を適切に組み合わせることで、柔軟かつ現実的なベイズモデリングが可能になります。

事後分布の計算

ベイズモデリングにおいて、事後分布の計算は中心的な役割を果たします。

事後分布は、データを観測した後のパラメータの確率分布を表し、推定や予測に用いられます。

　直接計算法

事後分布を直接計算する方法は、共役事前分布を用いる場合に適用できます。

共役事前分布とは、尤度と同じ関数形を持つ事前分布のことです。

例えば、正規分布の尤度に対しては、正規分布やガンマ分布が共役事前分布になります。

共役事前分布を用いると、事後分布が解析的に求められます。つまり、複雑な計算をせずに、事後分布のパラメータを更新できるのです。

　シミュレーション法（MCMC）

しかし、多くの場合、事後分布を解析的に求めることは困難です。

特に、高次元のパラメータや複雑な確率モデルを扱う場合には、数値的な近似が必要になります。

そこで用いられるのが、マルコフ連鎖モンテカルロ法（MCMC）です。

MCMCは、事後分布からのサンプリングを通じて、事後分布を近似する手法です。代表的なMCMCの手法として、メトロポリス・ヘイスティングス法やギブスサンプリングがあります。

MCMCでは、事後分布に比例する確率分布からサンプルを生成します。十分な数のサンプルを生成することで、事後分布の特徴を捉えることができます。

　ベイズモデリング用ソフトウェア

MCMCの実装には、専門的な知識が必要です。

そこで、ベイズモデリングを行うためのソフトウェアが開発されています。

代表的なソフトウェアとして、以下のようなものがあります。

• Stan: C++で実装された汎用的なベイズモデリング用ソフトウェア、PythonやRからも使える
• PyMC: Pythonで実装されたベイズモデリング用ライブラリ
• JAGS: Rで利用可能なベイズモデリング用ソフトウェア

これらのソフトウェアを利用することで、MCMCを用いた事後分布の計算を容易に行うことができます。

ベイズモデリングの利点

ベイズモデリングは、従来の統計手法と比べて、いくつかの重要な利点を持っています。

　事前知識の直接的な組み込み

ベイズモデリングでは、事前分布を通じて、データ以外の情報を直接モデルに組み込むことができます。

事前分布は、パラメータに関する既存の知識や経験を反映します。

例えば、過去の類似データから得られた知見や、専門家の意見を事前分布に反映させることができます。

この特徴は、サンプルサイズが小さい場合や、データが不完全な場合に特に有用です。

事前知識を活用することで、より現実的で頑健なモデリングが可能になります。

　モデリングステップの透明性

ベイズモデリングでは、モデリングのステップが明示的に記述されます。

確率モデルの定式化、事前分布の設定、尤度の設定など、各ステップが明確に分かれています。

これにより、モデリングのプロセスが透明になり、仮定や選択の妥当性を評価しやすくなります。

また、事後分布の計算に用いられる近似手法も、アルゴリズムとして明示的に記述されます。

これにより、計算の再現性が担保され、結果の解釈がしやすくなります。

　リスク、不確実性、変動性に関する情報の提供

ベイズモデリングでは、パラメータの事後分布を通じて、リスク、不確実性、変動性に関する情報が得られます。

事後分布は、パラメータの推定値だけでなく、その不確実性も表現します。

例えば、事後分布の信用区間を計算することで、パラメータの推定値の信頼性を評価できます。

また、事後予測分布を計算することで、将来の観測値の変動性を定量化できます。

これらの情報は、意思決定やリスク管理において重要な役割を果たします。不確実性を考慮した上で、最適な戦略を立てることができるのです。

今回のまとめ

今回は、「ベイズモデリングでビジネスにおける不確実性の把握と活用」というお話しをしました。

ベイズモデリングは、従来の統計手法では困難だった課題に対して、柔軟で現実的なアプローチを提供します。事前分布を通じて、データ以外の情報を組み込むことができ、事後分布を用いることで、不確実性やリスクを定量化することができます。

需要予測、価格戦略の最適化、顧客分析、信用スコアリング、財務モデリングなど、様々なビジネスの意思決定において、ベイズモデリングは大きな力を発揮します。紹介した事例からもわかるように、ベイズモデリングを活用することで、従来手法の限界を克服し、より精度の高い予測と意思決定が可能になります。

ただし、ベイズモデリングを適切に活用するためには、確率・統計の基礎知識と、モデリングの技術が必要です。また、事前分布の設定や、事後分布の解釈には、一定の経験と専門知識が求められます。

ベイズモデリングに興味を持つビジネスパーソンにとって、一助となれば幸いです。ベイズモデリングの可能性を最大限に引き出し、ビジネスの意思決定の質を高めていくことを期待しています。