第386話｜DAG（因果ダイアグラム）で識別したバイアスの対処手法（前編） – 交絡への対処手法 –

交絡バイアスは、因果関係を探求する上での大きな障害の一つです。

この交絡バイアスは、調査対象の原因と結果の関係に、第三の変数が影響を与えている状況で生じます。

例えば、あるマーケティングキャンペーンが売上に影響を与えたと考える際、季節性や経済状況といった外部要因が実際には大きく影響している可能性があります。

ビジネス意思決定において、このような交絡バイアスを無視すると、誤った結論を導き、戦略の誤方向を引き起こす可能性があります。

例えば、新しい広告戦略を導入した後の売上増加を考えてみましょう。

ここで、導入時期が重要な販売シーズンと重なった場合、売上増加は広告効果によるものなのか、それとも単にシーズン効果なのかを区別する必要があります。

このシナリオでは、季節が交絡変数となり、真の因果関係の識別を難しくします。

今回は、このような交絡への対処法についてお話しをします。

Contents

交絡バイアスの特定：DAGの利用
　DAG（有向非巡回グラフ）を用いた交絡バイアスの特定方法
ランダム化比較試験（RCT）：理想
　RCTとは？
　RCTのアプローチ
　前提条件とメリット、デメリット
　ビジネスシナリオにおける適用事例
　RCTを実施できない場合の考慮事項
マッチング：似た条件を比較する
　マッチングとは？
　マッチングのアプローチ
　前提条件とメリット、デメリット
　ビジネスシナリオにおける適用事例
層別分析：細分化して理解する
　層別分析とは？
　交絡を調整する層別分析のアプローチ
　前提条件とメリット、デメリット
　ビジネスシナリオにおける適用事例
回帰調整：交絡変数を制御する
　回帰調整とは？
　回帰調整のアプローチ
　前提条件とメリット、デメリット
　ビジネスシナリオにおける適用事例
逆確率重み付け（IPW）：効果的な比較のために
　逆確率重み付けとは？
　IPWのアプローチ
　前提条件とメリット、デメリット
　ビジネスシナリオにおける適用事例
調整手法の使い分け
　RCT（ランダム化比較試験）
　マッチング
　層別分析
　回帰調整
　逆確率重み付け（IPW）
交絡バイアスへの感度分析
　感度分析の手法
　実施方法
　交絡の影響の対策
今回のまとめ

交絡バイアスの特定：DAGの利用

　DAG（有向非巡回グラフ）を用いた交絡バイアスの特定方法

DAGは、変数間の因果関係を視覚的に表現するツールで、交絡変数を特定しやすくなります。

以下の記事でやや詳しく説明しています。

例として、ある企業が新製品の広告キャンペーンを開始し、その後の売上増加を観測した場合を考えます。

DAGを用いて、広告キャンペーン（A）、売上（B）、季節（C）の関係を描くと、季節が広告と売上の両方に影響を与えていることが明らかになります。

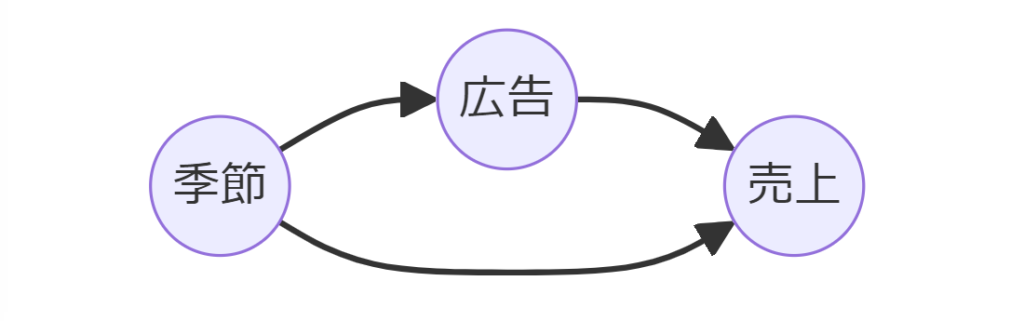
この場合、季節を交絡変数として識別し、その影響を調整する必要があります。

このDAGの利用は、ビジネス上の問題に対する洞察を深めるだけでなく、データ分析計画の策定にも役立ちます。

特に、新しい市場戦略の効果を評価する際や、製品開発における顧客のニーズと反応を理解する際に重要です。

DAGを活用することで、ビジネスリーダーはより精密な意思決定を行い、戦略の有効性を正確に測定できるようになります。

ランダム化比較試験（RCT）：理想

　RCTとは？

ランダム化比較試験（Randomized Controlled Trials、RCT）は、介入の効果を評価する最も信頼性の高い方法の一つです。

参加者を無作為に二つ以上のグループ（例えば、介入グループとコントロールグループ）に割り当て、介入の有無による結果の違いを比較します。

このランダム化プロセスにより、交絡変数の影響を均等に分散させ、介入自体の純粋な効果を明らかにすることができます。

　RCTのアプローチ

RCTの設計は、目的に応じて様々ですが、基本的には次のステップに従います。

Step.1　目標の明確化
何を測定し、何を証明するのかを定義します。

Step.2　参加者の選定
研究に参加する対象者を選びます。

Step.3　ランダム化
参加者を無作為に介入グループとコントロールグループに割り当てます。

Step.4　介入の実施
介入グループに対して特定の介入（例えば、新しい広告戦略の導入）を行います。

Step.5　結果の測定
介入後の効果を測定します。

Step.6　分析と評価
介入グループとコントロールグループの結果を比較し、統計的な差異を評価します。

　前提条件とメリット、デメリット

前提条件：参加者のランダムな割り当てが可能であること、介入と結果の測定が可能であること。
メリット：交絡変数の影響を最小化し、因果関係を強く推定できる。
デメリット：コストが高く、実施に時間がかかること。また、倫理的な制限が存在する場合がある。

　ビジネスシナリオにおける適用事例

ある企業が新しいオンライン広告戦略の効果を評価するために、1,000人の顧客を対象にRCTを実施することにしました。

これらの顧客を無作為に2つのグループに割り当てます。グループA（介入グループ）とグループB（コントロールグループ）にそれぞれ500人ずつ割り当てられます。

グループA（介入グループ）：新しいオンライン広告を表示します。
グループB（コントロールグループ）：通常の広告または広告なしで維持します。

数週間後、企業は両グループの購入率（購入を行った顧客の割合）を求めました。

グループAの購入率： $15%$
グループBの購入率： $5%$

新しい広告戦略の効果は、グループAとグループBの購入率の差として計算されます。この計算により、新しい広告戦略が購入率を10%向上させたことが示されます。

\displaystyle 効果=15\%-5\%=10\%

効果の計算だけでなく、この結果が統計的に有意であるかどうかを評価する必要があります。これは、p値や信頼区間を計算することによって行われます。

このRCTの例では、新しいオンライン広告戦略が購入率を10%向上させるという結果が得られました。この結果は、広告戦略の変更が顧客の購買行動に実質的な影響を与える可能性があることを示唆しています。

しかし、この効果がビジネスの目標と一致するかどうか、さらに投資のリターンが期待通りかどうかを評価するためには、コストや他の因子も考慮に入れる必要があります。

　RCTを実施できない場合の考慮事項

ビジネスでは、RCTを実施するのが非常に困難な場合があります。例えば、倫理的な理由（無作為に割り当てられない、など）やコスト（時間とお金がかかる、など）の問題です。

RCTが実施できない場合、他の手法（例えば、マッチングや傾向スコア分析）を用いて交絡変数の影響を試みて調整する必要があります。

これらの方法はRCTほど強力な証拠を提供するものではありませんが、適切に実施されれば有用な洞察を提供することができます。

マッチング：似た条件を比較する

　マッチングとは？

マッチングは、似たような特性を持つが異なる介入を受けた個体群間での比較を可能にする統計的手法です。

この手法は、ランダム化比較試験（RCT）が実施不可能または不適切な場合に特に有用で、交絡変数の影響を軽減しながら因果関係の推定を改善します。

具体的には、介入群（例えば、新しい広告戦略を見たグループ）とコントロール群（広告戦略を見なかったグループ）の間で、年齢や性別などの基本属性が類似するように個体を選択し、グループ間の比較を行います。

最も一般的な方法の一つは傾向スコアマッチングです。

傾向スコアは、与えられた共変量に基づいて、ある個体が介入群に属する確率を推定するスコアです。ちなみに、共変量には交絡要因もあれば、そうでない要因も含まれますが、交絡要因は必ず含める必要があります

これにより、介入群とコントロール群の間で傾向スコアが類似する個体をマッチングし、両群間の比較を行います。

　マッチングのアプローチ

Step.1　共変量の選定
既知のすべての重要な交絡要因を共変量として含めます。これには、交絡要因以外の影響を与える可能性があるその他の変数も含まれる場合があります。

Step.2　傾向スコアの推定
ロジスティック回帰などの統計的モデルを使用して、各個体が介入群に属する確率（傾向スコア）を推定します。この確率は、選定された共変量に基づいて計算されます。

Step.3　マッチングの実施
計算された傾向スコアを基に、介入群とコントロール群の個体をマッチングします。最も一般的な方法は、1:1マッチングで、介入群の各個体に対して、傾向スコアが最も近いコントロール群の個体を選びます。その他にも、傾向スコア差の範囲を設定した上でのマッチングや、複数のコントロール個体をマッチングする手法もあります。

Step.4　バランスの確認
マッチング後、共変量のバランス（基本統計量や分布がほぼ同じかどうか、など）を確認します。バランスが取れていない場合は、マッチングプロセスを見直す必要があります。

Step.5　効果推定
マッチングされたデータセットを用いて、介入の効果を推定します。この際、介入群とコントロール群間の差を分析し、介入の影響を評価します。

　前提条件とメリット、デメリット

前提条件: 共変量（年齢、性別など）のデータが利用可能で、それに基づいて適切なマッチングペアを作成できること。
メリット: RCTが実施不可能な場合でも、交絡変数の影響を軽減し、因果推論の精度を向上させることができる。
デメリット: 完全なマッチングが常に可能とは限らず、残留交絡の可能性がある。また、マッチングプロセスが複雑で時間を要する場合がある。

　ビジネスシナリオにおける適用事例

あるECサイトが、新しいレコメンデーションエンジンの導入がユーザーの平均購入額にどのような影響を与えたかを明らかにした例です。

このサイトでは、一部のユーザーに対して新しいエンジンを適用し、残りのユーザーは従来のエンジンを使用し続けます。

介入群（新エンジン使用者）：平均購入額 50,000円, ユーザー数 200人
コントロール群（従来エンジン使用者）：平均購入額 45,000円, ユーザー数 200人

共変量（年齢、性別、過去の購入履歴）に基づき、各群から類似したユーザーをペアとして選択します。

例えば、30歳男性で過去1年間に30,000円の購入があるユーザーが介入群にもコントロール群にもいれば、これらをマッチングペアとします。

マッチング後、再び各群の平均購入額を計算します。このプロセスにより、共変量の影響を考慮した上で、新旧のレコメンデーションエンジンの影響をより正確に評価することができます。

介入群（新エンジン使用者）：新しい平均購入額 51,000円, ユーザー数 150人（マッチング後）
コントロール群（従来エンジン使用者）：新しい平均購入額 48,000円, ユーザー数 150人（マッチング後）

\displaystyle 効果=51,000-48,000=3,000

マッチングを行うことで、新しいレコメンデーションエンジンの導入効果（購入額の増加）は初期の5,000円から3,000円に縮小されました。

この差異の縮小は、共変量の影響をより適切に考慮した結果であり、新しいエンジンの導入が購入額の増加に寄与していることを示していますが、当初考えられていたほどの大きな効果は見られませんでした。

この例から、マッチング手法が交絡変数の影響を考慮し、より精確な因果推論を行う上で有効であることがわかります。

層別分析：細分化して理解する

　層別分析とは？

層別分析は、データを特定の層（カテゴリー）に分けて分析する手法です。

この方法は、それぞれの層での介入効果を比較することにより、より正確な因果推論を可能にします。

層別分析により、異なるサブグループ間での効果の違いを明らかにし、交絡変数の影響を理解することができます。

　交絡を調整する層別分析のアプローチ

Step.1　交絡要因の特定
まず、介入とアウトカムの関係に影響を与える可能性がある共変量（交絡要因）を特定します。

Step.2　層の定義
交絡要因に基づいてデータセットを複数の層に分けます。各層が交絡要因の特定の組み合わせを反映するようにします。

Step.3　層ごとの効果推定
次に、各層内で介入群とコントロール群（または比較群）のアウトカムを比較します。各層での介入の効果（差異または比率など）を推定します。

Step.4　結果の集約
最後に、層ごとの効果推定値を集約して全体の効果推定値を得ます。この際、各層の重要性やサイズに応じて重み付けを行う場合があります。

　前提条件とメリット、デメリット

前提条件：交絡変数に基づいて層を明確に定義することができ、各層に十分なデータ点が存在すること。
メリット：交絡変数の影響を個別に評価し、サブグループ間での介入効果の違いを明らかにできる。
デメリット：層が多すぎると、各層のサンプルサイズが小さくなり、統計的なパワーが低下する可能性がある。

　ビジネスシナリオにおける適用事例

ある企業が新しいマーケティングキャンペーンの効果を年齢層（20代、30代、40代）ごとに層別分析を行いました。

初期分析では、キャンペーン後の全体的な平均購入額が20,000円から22,000円に増加しました。

層別分析後の結果は以下の通りです。

20代：平均購入額が18,000円から20,000円に増加
30代：平均購入額が22,000円から25,000円に増加
30代：平均購入額に変化なし

この分析により、マーケティングキャンペーンは特に30代の顧客に対して最も効果的であることが明らかになりました。一方で、40代の層では効果が見られませんでした。

回帰調整：交絡変数を制御する

　回帰調整とは？

回帰調整は、統計的手法を用いて交絡変数の影響を考慮しながら介入（処置）の効果を推定する方法です。

このアプローチでは、アウトカム（結果変数）に対する介入の影響を、交絡変数の効果から分離して評価することを目指します。

回帰モデルを用いることで、交絡変数がアウトカムに与える影響を「調整」し、介入の純粋な効果をより正確に推定することが可能になります。

　回帰調整のアプローチ

Step.1　共変量の選定
影響を与えうるすべての重要な交絡変数を同定し、これらをモデルの共変量として含めます。

Step.2　モデルの構築
適切な回帰モデル（例：線形回帰、ロジスティック回帰）を選択し、介入変数と共変量を含めてモデルを構築します。

Step.3　パラメーターの推定
回帰分析を実施し、介入変数の係数（効果推定値）を推定します。この係数は、他の共変量の影響を調整した上での介入の効果を示します。

Step.4　結果の解釈
推定された介入効果（係数）を解釈し、その統計的有意性を評価します。

　前提条件とメリット、デメリット

前提条件: 分析に必要なデータが利用可能であり、適切な回帰モデルを選択できること。
メリット:複数の交絡変数を同時に考慮できる。モデルの柔軟性が高く、非線形関係や交互作用もモデル化できる。
デメリット:適切なモデル選択と仕様が必要で、誤った仕様はバイアスを導入する可能性がある。観測されていない交絡変数には対処できない。

　ビジネスシナリオにおける適用事例

ある企業が新しいWebマーケティングキャンペーンの効果を評価するために回帰調整を使用した場合を考えます。キャンペーンの目的は、Webサイトへの訪問者数を増やすことです。

共変量: 以前の訪問者数、季節性、競合他社のキャンペーン活動
介入: 新しいマーケティングキャンペーンの導入（介入群 = 1, コントロール群 = 0）

線形回帰モデルを構築し、キャンペーン導入前後の訪問者数の変化を推定します。

モデルの式は以下のようになります。

\displaystyle 訪問者数=\beta_0+\beta_1 \times キャンペーン+β_2 \times 以前の訪問者数+\beta_3 \times 季節性+\beta_4 \times 競合の活動+\epsilon

ここで、 $\beta_1$ の推定値がキャンペーンの効果を示します。

$\beta_1$ の推定値が正であり、統計的に有意であれば、キャンペーンが訪問者数の増加に寄与していることを示します。

この例では、回帰調整を通じて、他の要因の影響を考慮した上で、新しいマーケティングキャンペーンの効果を正確に評価することが可能です。

逆確率重み付け（IPW）：効果的な比較のために

　逆確率重み付けとは？

逆確率重み付け（Inverse Probability Weighting、IPW）は、観察データから因果推論を行う際に使用される手法で、特に交絡の影響を調整する目的で利用されます。

IPWは、個体が介入を受ける確率（傾向スコア）に基づいて重みを計算し、これを用いて分析を行う手法です。

介入群の個体には、介入を受ける逆確率で重み付けを行い、コントロール群の個体には、介入を受けない逆確率で重み付けを行います。

この重み付けにより、分析のバランスを取り、交絡によるバイアスを軽減します。

　IPWのアプローチ

Step.1　傾向スコアの推定
ロジスティック回帰などを用いて、介入を受ける確率（傾向スコア）を各個体に対して推定します。

Step.2　重みの計算
介入群の個体に対する重みは、1 / 傾向スコアで計算され、コントロール群の個体に対する重みは、1 / (1 – 傾向スコア)で計算されます。

Step.3　重み付き分析
計算された重みを用いて、アウトカムの重み付き平均を介入群とコントロール群で比較し、介入効果を推定します。

　前提条件とメリット、デメリット

前提条件：傾向スコアの正確な推定が可能であり、交絡変数が適切に選択されていること。
メリット：共変量のバランスを取りやすく、ランダム化比較試験に近い状態を作り出せる。欠損データやサンプル選択バイアスに対処する際にも有効。
デメリット：傾向スコアの推定が不正確だと、バイアスの除去が不完全になる。極端な重みが生じることがあり、分析の分散が増大する可能性がある。

　ビジネスシナリオにおける適用事例

ある企業が、新しい社員福利厚生プログラムの導入効果を評価する場合を考えます。

社員の職務満足度をアウトカム（結果変数）とし、プログラム導入前後での満足度の変化をIPWを用いて分析します。

共変量：年齢、性別、職歴、過去の職務満足度
介入：福利厚生プログラムの導入

まず、ロジスティック回帰を用いて、福利厚生プログラムに参加する確率（傾向スコア）を推定します。モデルは次のようになります。

\displaystyle logit(P(プログラム参加))=\alpha+\beta_1 \times 年齢+\beta_2 \times 性別+\beta_3 \times 職歴+\beta_4 \times 過去の職務満足度

ここで、各 $\beta_1,\beta_2,\beta_3,\beta_4$ 共変量の効果を表し、 $\alpha$ は切片です。

傾向スコアを用いて、各社員に対する重みを計算します。

プログラム参加群の重み：

\displaystyle w_i = \frac{1}{傾向スコア_i}

非参加群の重み：

\displaystyle w_j = \frac{1}{1-傾向スコア_j}

計算された重みを用いて、職務満足度の重み付き平均を求め、プログラム参加群と非参加群で比較します。

プログラム参加群の重み付き職務満足度平均：

\displaystyle \frac{\displaystyle \sum_{i}w_i\times職務満足度_i}{\displaystyle \sum_{i}w_i}=82

非参加群の重み付き職務満足度平均：

\displaystyle \frac{\displaystyle \sum_{j}w_j\times職務満足度_j}{\displaystyle \sum_{j}w_j}=75

この結果は、重み付き分析を通じて、福利厚生プログラムの参加が職務満足度を有意に向上させる可能性があることを示唆しています。

このアプローチは、観察データを用いた因果推論分析において、ランダム化試験と同等の分析結果を得ることを目指します。

調整手法の使い分け

理想はランダム化比較試験（RCT）です。

ただ、観察研究（Observational Study）などのRCTが実施不可能な場合、マッチング、層別分析、回帰調整、逆確率重み付け（IPW）などの手法が選択肢となります。

ちなみに、観察研究は、自然に発生する条件下で個体やデータを観察し分析する研究手法です。多くのビジネス系のデータは、RCTなどの実験による収集されるデータよりも、こちらのデータの方が圧倒的に多いです。

　RCT（ランダム化比較試験）

データ収集の設計が可能で、倫理的に許容され、参加者を無作為に介入群とコントロール群に割り当てることができる場合に向いています。

RCTは、因果関係を明確にしやすく、交絡バイアスの問題を最小限に抑えることができます。

しかし、実務上は時間やコスト、倫理的な制約により実施が難しい場合があります。

　マッチング

RCTが実施不可能で、既存の観察データを使用する場合や、特定の共変量（交絡要因）に基づいて介入群とコントロール群を類似させたい場合に向いています。

マッチング手法を用いて、似た特性を持つ参加者をペアにします。そのため、上手くマッチングできない場合には向きません。

これにより、選択された共変量に関して交絡の影響を調整し、因果関係をより明確にしますが、観測されていない交絡変数には対応できません。

　層別分析

交絡変数が離散的で、交絡変数の異なるレベルごとに効果を比較したい場合に向いています。

この手法では、データを層に分けて分析し、各層での介入効果を比較することで、交絡要因の影響を個別に調整できます。

しかし、多数の層を作成すると、各層のサンプルサイズが小さくなるリスクがあります。

　回帰調整

複数の交絡変数があり、これらの変数が連続的である、または交絡変数と結果変数（アウトカム）との関係を柔軟にモデル化したい場合に向いています。

回帰モデルを構築して交絡変数の影響を調整することで、介入効果の推定値を得ます。

回帰調整は、モデルが正しく仕様されている限り、因果関係をかなり明確にすることができますが、モデルの選択ミスなどが結果にバイアスをもたらすリスクがあります。

　逆確率重み付け（IPW）

RCTを実施できず、特に交絡変数の影響を全体的にバランスさせたい場合や、観察データに基づいて介入の効果を評価したい場合に向いています。

傾向スコアを計算し、これを用いて各個体に重みを割り当てることで、交絡変数のバランスを取り、介入群とコントロール群が比較可能な状態になるよう調整します。

IPWは、交絡変数に対して適切に設計されていれば、因果関係を明確にすることができますが、傾向スコアの推定誤差や極端な重みによる分散の増加に注意が必要です。

交絡バイアスへの感度分析

感度分析（Sensitivity Analysis）は、統計モデルや意思決定モデルにおいて、入力変数や仮定の変化が結果にどの程度影響を与えるかを評価するための手法です。

感度分析の目的は、モデルの頑健性を評価し、重要な入力変数や仮定を特定することです。

この感度分析は、交絡バイアスの影響を評価し、因果効果の推定値の頑健性を確認するための重要な手法です。

　感度分析の手法

交絡バイアスに対する感度分析には、以下のような手法があります。

E-value（Evidence value）

E-valueは、観測された関連性が未測定の交絡要因によって説明される可能性を評価する指標です。
E-valueが大きいほど、観測された関連性が交絡要因のみでは説明しにくいことを意味し、因果関係の存在をより強く示唆します。
E-valueが小さい場合は、観測された関連性が交絡要因によって容易に説明されてしまう可能性があることを示唆します。

感度分析プロット（Sensitivity analysis plot）

感度分析プロットは、交絡バイアスの影響を視覚的に評価するための手法です。
処置群と対照群の間で交絡要因の分布がどの程度異なるかを示すことで、交絡バイアスの影響の大きさを判断します。
例えば、傾向スコアを用いた分析において、処置群と対照群の傾向スコアの分布を重ねて表示したり、各交絡要因の分布を比較する共変量バランスプロット（例：処置群と対照群の平均値の差を両群の標準偏差で割った標準化差、など）を作成したりすることで、交絡バイアスの影響を評価できます。
処置群と対照群で大きく異なる場合は、交絡バイアスの影響が大きい可能性があります。

シミュレーションベースの感度分析（Simulation-based sensitivity analysis）

シミュレーションベースの感度分析は、交絡バイアスのシナリオをシミュレーションによって生成し、バイアスの影響を評価する手法です。
交絡バイアスのシナリオで利用するデータは、元のデータを基に、シナリオ（例：交絡要因と処置変数の関連性が強い場合と弱い場合、など）に応じて作成（例：交絡要因の値の一部を変更、新しい観測値を追加、ノイズを追加、など）します。
異なる交絡バイアスのシナリオを想定し、それぞれのシナリオにおける因果効果の推定値を比較することで、バイアスの影響の大きさを評価します。

感度パラメータを用いた感度分析（Sensitivity analysis with sensitivity parameters）