機械学習モデルの開発において、モデルの性能を適切に評価することは非常に重要です。

評価指標は、モデルの予測性能を定量的に測定し、モデルの選択、比較、改善に役立ちます。

しかし、多様な評価指標の中から、どの指標を使うべきか判断することは容易ではありません。そもそも、どのような評価指標があるのかを知らないことには、話しになりません。

今回は、回帰問題と分類問題における代表的な10の評価指標について解説します。

各指標の定義、計算方法、特徴、適用場面を説明し、ビジネスケースを通じて評価指標の活用例を示します。

モデル評価の重要性を理解し、適切な評価指標の選択と活用により、機械学習プロジェクトの成功に近づくことができるでしょう。

モデル評価の重要性

　モデルの性能を定量化する必要性

機械学習モデルの開発プロセスにおいて、モデルの性能を定量的に評価することは欠かせません。

評価指標は、モデルがどの程度データに適合しているかを数値で表現し、モデルの良し悪しを判断する基準となります。

これにより、異なるモデルや手法の比較が可能になり、最適なモデルの選択や改善に役立ちます。

また、評価指標を用いることで、モデルの過学習や未学習の問題を検知し、適切な対策を講じることができます。

　ビジネス上の意思決定におけるモデル評価の役割

モデル評価は、ビジネス上の意思決定においても重要な役割を果たします。

機械学習モデルは、様々なビジネス領域で活用されており、その予測結果は重要な意思決定の根拠となります。

例えば、顧客離反予測モデルの性能が低ければ、顧客維持のための施策が適切に行われず、収益に大きな影響を与える可能性があります。

適切な評価指標を用いてモデルの性能を評価し、ビジネス要件に合ったモデルを開発することが、ビジネスの成功につながります。

　モデルの継続的な改善とメンテナンス

モデルの評価は、開発段階だけでなく、運用段階でも継続的に行う必要があります。

データの分布や特性は時間とともに変化する可能性があり、それに伴ってモデルの性能も変化します。

定期的にモデルの性能を評価し、必要に応じて再学習やチューニングを行うことが、モデルの品質維持に不可欠です。

適切な評価指標を用いることで、モデルの劣化を早期に発見し、適切なメンテナンスを行うことができます。

　評価指標の概要

評価指標には、回帰問題用と分類問題用の2種類があります。

回帰問題では、予測値と実際の値の差を測定する指標が用いられます。

一方、分類問題では、予測したクラスと実際のクラスの一致度合いを測定する指標が使われます。

それぞれの評価指標には固有の特徴があり、問題の性質に応じて適切な指標を選択することが重要です。

今回紹介する指標です。

代表的な回帰問題用の評価指標

• 平均絶対誤差（MAE）
• 平均二乗誤差（MSE）
• 平方根平均二乗誤差（RMSE）
• 決定係数（R-squared）
• 平均絶対パーセント誤差（MAPE）

代表的な分類問題用の評価指標

• 正解率（Accuracy）
• 適合率（Precision）
• 再現率（Recall）
• F1スコア
• ROC曲線下面積（AUC）

回帰問題の評価指標とその特徴

　平均絶対誤差 (MAE)

平均絶対誤差（MAE: Mean Absolute Error）は、予測値と実際の値の差分の絶対値の平均を取ることで計算されます。

以下の式で表されます。ここで、nはデータの総数、y_iはi番目の実際の値、\hat{y}_iはi番目の予測値を表します。

\displaystyle MAE = \frac{1}{n}\sum_{i=1}^n |y_i - \hat{y}_i|

 

MAEは、予測値と実際の値の差分の大きさを直接的に表現する指標です。

外れ値の影響を受けにくいという特徴があります。

MAEは、予測誤差の大きさを実際のスケールで解釈できるため、ビジネス上の意思決定に活用しやすい指標といえます。

ただし、誤差の方向（正負）は考慮されないため、過大評価と過小評価が打ち消し合ってしまう可能性があります。

　平均二乗誤差 (MSE)

平均二乗誤差（MSE: Mean Squared Error）は、予測値と実際の値の差分の二乗の平均を取ることで計算されます。

以下の式で表されます。

\displaystyle MSE = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2

 

MSEは、予測値と実際の値の差分の大きさを二乗することで、大きな誤差に対してペナルティを与える指標です。

外れ値の影響を受けやすいという特徴があります。

MSEは、誤差の大きさを強調するため、大きな誤差を特に重視したい場合に適しています。

ただし、誤差の単位が実際のスケールの二乗となるため、解釈が難しくなる場合があります。

　平方根平均二乗誤差 (RMSE)

平方根平均二乗誤差（RMSE: Root Mean Squared Error）は、MSEの平方根を取ることで計算されます。

以下の式で表されます。

\displaystyle RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2}

 

RMSEは、MSEの平方根を取ることで、誤差の単位を実際のスケールに戻した指標です。

MSEと同様に、大きな誤差に対してペナルティを与えますが、解釈がしやすいという利点があります。

RMSEは、誤差の大きさを実際のスケールで表現したい場合に適しています。

　決定係数 (R-squared)

決定係数（R-squared）は、予測値と実際の値の相関の強さを表す指標です。

以下の式で計算されます。ここで、\bar{y}は実際の値の平均を表します。

\displaystyle R^2 = 1 - \frac{\sum_{i=1}^n (y_i - \hat{y}i)^2}{\sum{i=1}^n (y_i - \bar{y})^2}

 

決定係数は、モデルによって説明される目的変数の分散の割合を表します。

値は0から1の間をとり、1に近いほどモデルの当てはまりが良いことを示します。

決定係数は、モデルの説明力を評価するのに適しています。

ただし、モデルの複雑さに応じて決定係数が増加する傾向があるため、モデルの選択においては注意が必要です。

　平均絶対パーセント誤差 (MAPE)

平均絶対パーセント誤差（MAPE: Mean Absolute Percentage Error）は、予測値と実際の値の差分の絶対値を実際の値で割った値の平均を取ることで計算されます。

以下の式で表されます。

\displaystyle MAPE = \frac{1}{n}\sum_{i=1}^n |\frac{y_i - \hat{y}_i}{y_i}|\times 100

 

MAPEは、予測誤差を実際の値に対する割合で表現する指標です。

パーセント表記であるため、誤差の大きさを直感的に理解しやすいという利点があります。

MAPEは、異なるスケールのデータ間で予測誤差を比較する際に有用です。

ただし、実際の値が0に近い場合、MAPEが非常に大きな値をとることがあるため、注意が必要です。

回帰問題の評価指標のビジネス活用例

　需要予測モデルにおけるRMSEの活用

需要予測モデルは、製品やサービスの将来の需要を予測するために使用されます。

このタスクでは、実際の需要と予測値の差を最小限に抑えることが重要です。

RMSEが低いモデルは、予測値と実際の需要の差が小さく、需要予測の精度が高いことを示しています。

\displaystyle RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}

• y_i: 実際の需要
• \hat{y}_i: 予測需要
• n: データ数

 

需要予測モデルの出力を実際の生産計画や在庫管理に活用するには、適切な許容誤差範囲を決定する必要があります。

この許容誤差範囲は、需要予測の誤差による在庫切れや在庫過多のリスクと、それらによる機会損失やコストのバランスを考慮して設定します。

各許容誤差範囲における在庫管理の最適化とコスト削減効果を評価し、最適な許容誤差範囲を決定することが重要です。

 

需要予測モデルの評価指標と在庫管理の最適化を分析することで、適切な在庫量を維持しつつ、在庫関連コストの削減を実現できます。

また、モデルの性能と実際の在庫管理成果の関係を分析することで、モデルの改善点や、より効果的な需要予測方法についての知見が得られます。

 

　住宅価格予測モデルにおけるR2の活用

住宅価格予測モデルは、住宅の特徴や立地条件に基づいて、住宅の価格を予測するために使用されます。

このタスクでは、予測価格と実際の販売価格の差を最小限に抑えることが重要です。

R2が高いモデルは、予測価格と実際の販売価格の差が小さく、住宅価格予測の精度が高いことを示しています。

\displaystyle R^2 = 1 - \frac{\sum_{i}(y_i - \hat{y}_i)^2}{\sum_{i}(y_i - \bar{y})^2}

• y_i: 実際の販売価格
• \hat{y}_i: 予測価格
• \bar{y}: 実際の販売価格の平均

 

住宅価格予測モデルの出力を実際の不動産取引や投資判断に活用するには、適切な価格誤差範囲を決定する必要があります。

この価格誤差範囲は、予測価格と実際の販売価格の乖離による収益性への影響と、不動産市場の変動リスクのバランスを考慮して設定します。

各価格誤差範囲における投資判断の最適化と収益性を評価し、最適な価格誤差範囲を決定することが重要です。

 

住宅価格予測モデルの評価指標と投資判断の最適化を分析することで、適切な不動産投資を行い、収益性の向上を図ることができます。

また、モデルの性能と実際の不動産投資成果の関係を分析することで、モデルの改善点や、より効果的な住宅価格予測方法についての知見が得られます。

 

　株価予測モデルにおけるMAPEの活用

株価予測モデルは、企業の財務データや市場動向に基づいて、将来の株価を予測するために使用されます。

このタスクでは、予測株価と実際の株価の差を最小限に抑えることが重要です。

MAPEが低いモデルは、予測株価と実際の株価の差が小さく、株価予測の精度が高いことを示しています。

\displaystyle MAPE = \frac{100}{n}\sum_{i=1}^{n}|\frac{y_i - \hat{y}_i}{y_i}| \times 100

• y_i: 実際の株価
• \hat{y}_i: 予測株価
• n: データ数

 

株価予測モデルの出力を実際の投資判断に活用するには、適切な株価誤差範囲を決定する必要があります。

この株価誤差範囲は、予測株価と実際の株価の乖離による収益性への影響と、株式市場の変動リスクのバランスを考慮して設定します。

各株価誤差範囲における投資判断の最適化と収益性を評価し、最適な株価誤差範囲を決定することが重要です。

 

株価予測モデルの評価指標と投資判断の最適化を分析することで、適切な株式投資を行い、収益性の向上を図ることができます。

また、モデルの性能と実際の株式投資成果の関係を分析することで、モデルの改善点や、より効果的な株価予測方法についての知見が得られます。

 

分類問題の評価指標とその特徴

　混同行列（confusion matrix）

以下は、混同行列（confusion matrix）を表形式で表現したものです。

	予測クラス 正（positive）	予測クラス 負（negative）
実際のクラス 正（positive）	真陽性 (TP)	偽陰性 (FN)
実際のクラス 負（negative）	偽陽性 (FP)	真陰性 (TN)

• 真陽性 (True Positive, TP): 実際のクラスが正で、予測クラスも正であるケース。
• 偽陰性 (False Negative, FN): 実際のクラスが正だが、予測クラスが負であるケース。
• 偽陽性 (False Positive, FP): 実際のクラスが負だが、予測クラスが正であるケース。
• 真陰性 (True Negative, TN): 実際のクラスが負で、予測クラスも負であるケース。

混同行列は、分類モデルの性能を評価する上で非常に有用なツールです。実際の値と予測結果の関係を明確に示すことで、モデルの強みと弱点を把握することができます。

　正解率 (Accuracy)

正解率（Accuracy）は、全体のデータ数に対する正しく分類されたデータ数の割合を表します。

以下の式で計算されます。

\displaystyle Accuracy = \frac{TP + TN}{TP + TN + FP + FN}

 

正解率は、分類モデルの全体的な性能を評価する指標です。

データセットのクラス分布が均衡している場合に適しています。

ただし、クラス分布が不均衡な場合、多数派クラスに偏った予測を行うことで高い正解率を達成できてしまうため、注意が必要です。

　適合率 (Precision)

適合率（Precision）は、正（positive）と予測されたデータ数に対する、実際に正（positive）であるデータ数の割合を表します。

以下の式で計算されます。

\displaystyle Precision = \frac{TP}{TP + FP}

 

適合率が高いモデルは、正（positive）と予測した場合に、その予測が正（positive）である可能性が高いことを示します。

適合率は、偽陽性（False Positive）を最小限に抑えたい場合に重要な指標となります。

　再現率 (Recall)

再現率（Recall）は、実際の正（positive）の数に対する、正しく正（positive）と予測されたデータ数の割合を表します。

以下の式で計算されます。

\displaystyle Recall = \frac{TP}{TP + FN}

 

再現率が高いモデルは、実際の正（positive）を見逃す可能性が低いことを示します。

再現率は、偽陰性（False Negative）を最小限に抑えたい場合に重要な指標となります。

　F1スコア

F1スコアは、適合率と再現率の調和平均を取ることで計算されます。

以下の式で表されます。

\displaystyle　F1 = 2 \times \frac{Precision \times Recall}{Precision + Recall}

 

F1スコアは、適合率と再現率のバランスを考慮した指標です。

どちらか一方が極端に低い場合、F1スコアは低くなります。

F1スコアは、適合率と再現率の両方をバランス良く同時に高めたい場合に有用です。

特に、クラス分布が不均衡なデータセットにおいて、少数派クラスの分類性能を評価する際によく用いられます。

　ROC曲線下面積 (AUC)

ROC曲線（Receiver Operating Characteristic curve）は、分類モデルの閾値を変化させたときの、真陽性率（True Positive Rate, TPR）と偽陽性率（False Positive Rate, FPR）の関係を表した曲線です。

AUCは、ROC曲線の下部の面積を計算することで得られる指標です。

以下の式で表されます。

\displaystyle AUC = \int_0^1 TPR(FPR) dFPR

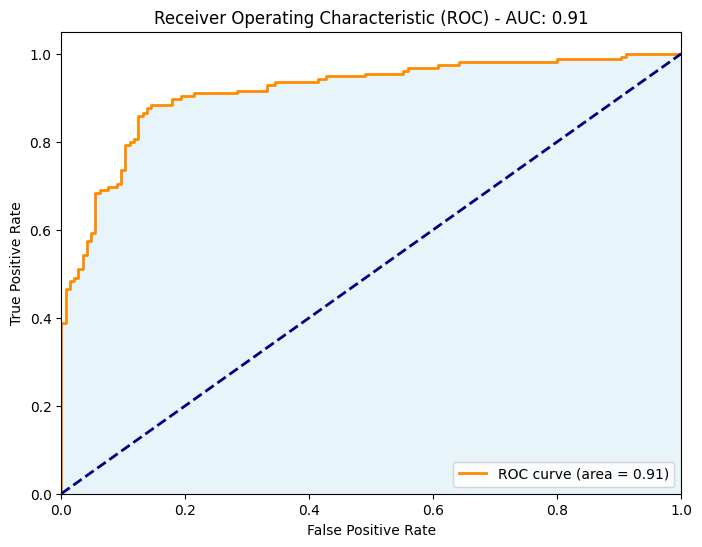
ここで、TPR（True Positive Rate）は再現率（Recall）または感度（Sensitivity）とも呼ばれ、実際の正（positive）の中で正しく正（positive）と予測された割合を表します。

\displaystyle TPR = \frac{TP}{TP + FN}

FPR（False Positive Rate）は偽陽性率または1-特異度（1-Specificity）とも呼ばれ、実際の負（negative）の中で誤って正（positive）と予測された割合を表します。

\displaystyle FPR = \frac{FP}{FP + TN}

 

AUCは、以下のように解釈できます。

• AUC = 1：完璧なモデル。全ての閾値で正（positive）と負（negative）を完全に分離できる。
• 0.9 ≤ AUC < 1：優れたモデル。高い確率で正（positive）と負（negative）を分離できる。
• 0.8 ≤ AUC < 0.9：良好なモデル。正（positive）と負（negative）をある程度分離できる。
• 0.7 ≤ AUC < 0.8：まずまずのモデル。正（positive）と負（negative）の分離性能に改善の余地がある。
• 0.6 ≤ AUC < 0.7：弱いモデル。正（positive）と負（negative）の分離性能が低い。
• 0.5 ≤ AUC < 0.6：ランダムに分類しているのとほとんど変わらない。
• AUC = 0.5：ランダムに分類しているのと同等。
• AUC < 0.5：ランダムに分類するよりも性能が悪い。

 

AUCは、モデルの性能を閾値に依存せずに評価できる指標であり、異なるモデル間の比較やクラス分布が不均衡なデータセットにおけるモデルの評価に適しています。

AUCは、クラス分布が不均衡な場合や、分類の閾値を決定する前にモデルの性能を比較する際に有用です。

分類問題の評価指標のビジネス活用例

　リードスコアリングモデルの最適化

リードスコアリングは、見込み客（リード）の購買可能性を予測するタスクです。

このタスクでは、高い購買可能性を持つリードを正確に特定することが重要です。

	予測: 高購買可能性	予測: 低購買可能性
実際: 高購買可能性	真陽性 (TP)	偽陰性 (FN)
実際: 低購買可能性	偽陽性 (FP)	真陰性 (TN)

• 正（positive）のケース: 高い購買可能性のリード
• 負（nagative）のケース: 低い購買可能性のリード

 

適合率が高いモデルは、セールスチームが優先的に対応すべきリードを絞り込むのに役立ちます。

一方、再現率が高いモデルは、購買可能性の高いリードを見逃すリスクを減らします。

ビジネス上の要件に応じて、適合率と再現率のバランスを考慮してモデルを選択する必要があります。

リードスコアリングモデルの出力を実際のビジネス活動に活用するには、適切な閾値を決定する必要があります。

期待値（Expected Value）は、各閾値におけるベネフィットとコストを定量化し、最適な閾値を決定するのに有用な指標です。

• 適合率: 優先的に対応すべきリードを正確に特定する。
• 再現率: 購買可能性の高いリードを見逃さないようにする。
• 期待値: 最適な閾値を決定し、ビジネス上の利益を最大化する。

期待値（Expected Value）が最大となる閾値を選択することで、ビジネス上の利益を最大化できます。

この閾値は、セールスチームのキャパシティや、見込み客へのアプローチにかかるコストなどを考慮して設定します。

 

リードスコアリングモデルにおける期待値（Expected Value）の計算式は以下のように表すことができます。

\displaystyle EV = (TP \times B_TP) - (FP \times C_FP) - (FN \times C_FN)

 

• TP（True Positive）：正しく高い購買可能性があると予測されたリードの数
• FP（False Positive）：誤って高い購買可能性があると予測されたリードの数
• FN（False Negative）：誤って低い購買可能性があると予測されたリードの数

この計算式で登場する、ベネフィットとコストです。

• TPに対するベネフィット（B_TP）：高い購買可能性のリードを正しく特定し、適切なアプローチを行うことによって得られる利益を表します。
• FPに対するコスト（C_FP）：低い購買可能性のリードに誤ってアプローチすることによる無駄なリソースの投入を表します。
• FNに対するコスト（C_FN）：高い購買可能性のリードを見逃すことによる機会損失を表します。

これらのベネフィットとコストは、ビジネス上の要件や状況に応じて適切に設定する必要があります。

 

リードスコアリングモデルの評価指標と期待値（Expected Value）を活用することで、セールスチームが優先的に対応すべきリードを特定し、リソースの最適化を図ることができます。

また、モデルの性能と実際のビジネス成果の関係を分析することで、モデルの改善点や、より効果的なリード獲得方法についての知見が得られます。

 

　医療診断モデルにおける再現率の重要性

医療診断モデルは、患者の症状やテスト結果に基づいて、疾患の有無を予測するために使用されます。

このタスクでは、実際に疾患を持つ患者を正しく診断することが重要です。

	予測: 疾患あり	予測: 疾患なし
実際: 疾患あり	真陽性 (TP)	偽陰性 (FN)
実際: 疾患なし	偽陽性 (FP)	真陰性 (TN)

• 正（positive）のケース: 疾患あり
• 負（nagative）のケース: 疾患なし

 

再現率が高いモデルは、疾患を持つ患者を見逃すリスクを最小限に抑えることができます。

一方、適合率が高いモデルは、健康な患者が誤って疾患ありと診断されるリスクを減らします。

• 再現率: 疾患を持つ患者を見逃さないようにする。
• 適合率: 健康な患者を誤診しないようにする。

ここで重視したのは再現率です。

\displaystyle \frac{TP}{TP + FN}

 

医療診断モデルの出力を実際の医療現場で活用するには、適切な閾値を決定する必要があります。

この閾値は、疾患を見逃すことによる患者への影響と、不必要な治療や検査による医療リソースの浪費のバランスを考慮して設定します。

各閾値における医療リソースの最適化と患者への影響を評価し、最適な閾値を決定することが重要です。

 

医療診断モデルの評価指標と医療リソースの最適化を分析することで、疾患を持つ患者を正確に診断しつつ、医療リソースの効率的な活用を実現できます。

また、モデルの性能と実際の医療成果の関係を分析することで、モデルの改善点や、より効果的な診断方法についての知見が得られます。

 

　顧客離反予測モデルにおけるF1スコアの活用

顧客離反予測モデルは、顧客が製品やサービスの利用を停止する可能性を予測するために使用されます。

このタスクでは、離反する可能性が高い顧客を正確に特定することが重要です。

	予測: 離反あり	予測: 離反なし
実際: 離反する顧客	真陽性 (TP)	偽陰性 (FN)
実際: 離反しない顧客	偽陽性 (FP)	真陰性 (TN)

• 正（positive）のケース: 離反する顧客
• 負（nagative）のケース: 離反しない顧客

 

F1スコアが高いモデルは、離反する可能性が高い顧客を正確に特定し、同時に、離反しない顧客を誤って特定するリスクを最小限に抑えることができます。

適合率と再現率のバランスを取ることで、顧客維持に関する効果的な意思決定を行うことができます。

\displaystyle 2 \times \frac{Precision \times Recall}{Precision + Recall}

 

顧客離反予測モデルの出力を実際のマーケティング活動に活用するには、適切な閾値を決定する必要があります。

この閾値は、離反する可能性が高い顧客に対する施策のコストと、離反を防ぐことによる利益のバランスを考慮して設定します。

各閾値における顧客維持施策の効果を定量的に評価し、最適な閾値を決定することが重要です。

 

顧客離反予測モデルの評価指標と顧客維持施策の最適化を分析することで、離反リスクの高い顧客に的を絞ったキャンペーンを実施し、顧客維持率の向上を図ることができます。

また、モデルの性能と実際の顧客維持成果の関係を分析することで、モデルの改善点や、より効果的な顧客維持方法についての知見が得られます。

 

評価指標選択の注意点

　ビジネス要件との整合性

評価指標を選択する際は、ビジネス要件との整合性を確認することが重要です。

選択した評価指標がビジネス目標と直結していない場合、モデルの最適化が実際のビジネス成果につながらない可能性があります。

評価指標とビジネス要件の間に乖離がある場合は、評価指標の再検討や、ビジネス要件の明確化が必要です。

モデル開発者とビジネス関係者が緊密に連携し、適切な評価指標を選択することが重要です。

　データの特性を考慮した選択

評価指標の選択は、データの特性にも依存します。

回帰問題では、データの分布や外れ値の存在が評価指標の選択に影響を与える可能性があります。

例えば、外れ値の存在によって平均絶対誤差（MAE）や平均二乗誤差（MSE）が大きく影響を受ける場合、中央絶対誤差（MedAE）などの外れ値の影響を受けにくい指標を使用することが推奨されます。

分類問題では、データのクラス分布が不均衡な場合、正解率のような単一の指標では、モデルの性能を適切に評価できない可能性があります。

このような場合は、適合率、再現率、F1スコアなどの複数の指標を組み合わせて使用することが推奨されます。

また、データの欠損値やノイズの存在も評価指標の選択に影響を与える可能性があります。

データの特性を十分に理解し、それに適した評価指標を選択することが重要です。

　複数の評価指標を組み合わせる重要性

単一の評価指標のみに依存してモデルを評価することは、モデルの性能を適切に把握できない可能性があります。

複数の評価指標を組み合わせて使用することで、モデルの性能をより多角的に評価できます。

回帰問題では、例えば、平均絶対誤差（MAE）と平均二乗誤差（MSE）を組み合わせて使用することで、モデルの予測誤差の大きさと分散を同時に評価できます。

また、決定係数（R^2）を使用することで、モデルの説明力を評価できます。

分類問題では、例えば、適合率と再現率のトレードオフを考慮するために、F1スコアを使用することができます。

また、ROC曲線下面積（AUC）を使用することで、閾値に依存しないモデルの性能評価が可能になります。

ビジネス要件やデータの特性を考慮しつつ、複数の評価指標を組み合わせて使用することが重要です。

今回のまとめ

今回は、機械学習モデルの評価において重要な10の評価指標について解説しました。

回帰問題では、MAE、MSE、RMSE、R-squared、MAPEが広く使用されています。一方、分類問題では、正解率、適合率、再現率、F1スコア、AUCが一般的な評価指標です。

これらの評価指標は、モデルの性能を定量的に評価し、モデルの選択、比較、改善に役立ちます。

ビジネス要件やデータの特性を考慮して、適切な評価指標を選択することが重要です。

• ビジネス要件と評価指標の整合性を確保する
• データの特性を考慮して評価指標を選択する
• 複数の評価指標を組み合わせて使用する
• 評価指標とビジネス成果の関係を分析し、モデルを継続的に改善する

これらのポイントを踏まえることで、モデルの性能を適切に評価し、ビジネス成果の最大化につなげることができます。

機械学習モデルの評価は、今後もデータサイエンスの重要な課題の一つであり続けるでしょう。新たな評価指標の開発や、既存の評価指標の改良が進むことで、より精度の高いモデル評価が可能になると期待されます。

また、説明可能なAI（Explainable AI）の分野での進展により、モデルの予測結果の解釈性が向上し、評価指標の選択やビジネス要件との整合性の確保がより容易になる可能性があります。データサイエンティストは、これらの動向を注視しつつ、適切なモデル評価を行っていくことが重要です。

実務でのモデル開発に役立つ情報を得ていただければ幸いです。