確率分布は、データ分析や統計学の基礎を成す重要な概念です。

ビジネスの世界においても、確率分布を理解し適用することで、さまざまな意思決定や予測が可能になります。

今回は、確率分布の基礎からビジネス応用に至るまでを簡単に解説します。

具体的な分布の定義や数式、ビジネスでの活用例を通じて、確率分布の実践的な利用方法を感覚的に掴みましょう。

はじめに

　確率分布とは何か

確率分布とは、ランダムな変数が特定の値をとる確率を記述する数学的な関数です。

確率分布は、ランダムな現象の結果を予測するためのモデルとして利用されます。

例えば、サイコロを振ったときに出る目の確率や、特定の商品が売れる確率などを表すことができます。

　確率分布の重要性

確率分布は、統計学やデータサイエンスにおいて非常に重要な役割を果たします。

以下のような理由で重要です。

データの理解とモデリング
データがどのように分布しているかを理解することで、より正確な予測や意思決定が可能になります。

リスクの評価
ビジネスにおけるリスク管理や評価に役立ちます。例えば、投資リスクや市場リスクの評価に確率分布が使われます。

統計的検定
統計的な仮説検定を行う際に、確率分布の知識が不可欠です。これにより、データが偶然に生じたかどうかを判断できます。

最適化と意思決定
確率分布を用いたモデリングにより、在庫管理やマーケティング戦略の最適化など、ビジネス上の重要な意思決定をサポートします。

確率分布の分類

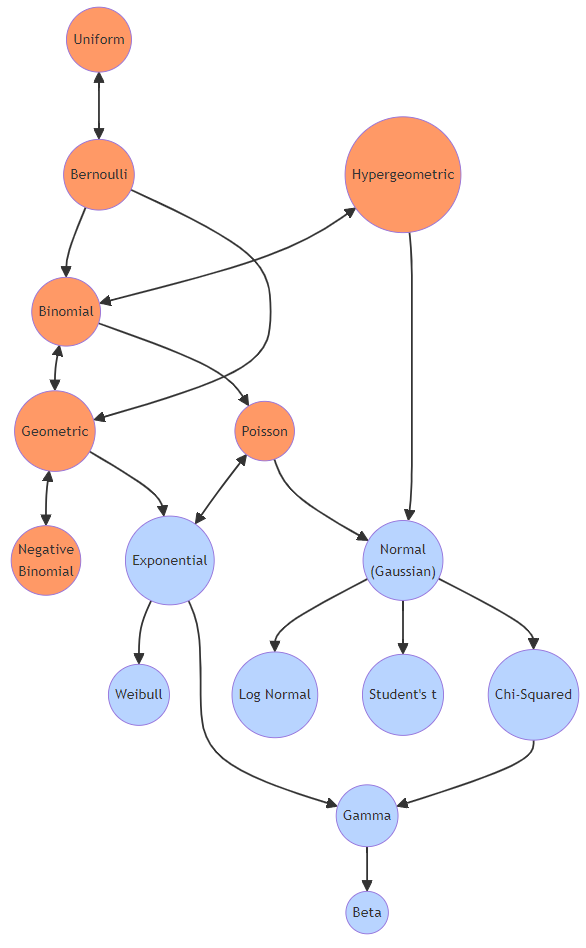
　離散分布と連続分布の違い

確率分布は、大きく分けて離散分布と連続分布の2種類に分類されます。

この分類は、変数がとる値が離散的（有限または可算無限）か連続的（無限の連続体）かに基づきます。

離散分布

• 変数がとる値が個々に分かれたもの。
• 例えば、サイコロの目のように1, 2, 3, 4, 5, 6のように離散的な値をとります。
• 分布例：二項分布、ポアソン分布、幾何分布

連続分布

• 変数がとる値が連続しており、任意の範囲内の任意の値をとりうるもの。
• 例えば、身長や体重のように連続的な値をとります。
• 分布例：正規分布、指数分布、ガンマ分布

　主な確率分布

以下に、ビジネスでよく使われる主要な確率分布の一覧を示します。

離散分布 (Discrete Distributions)

• 離散一様分布 (Discrete Uniform Distribution)
• 二項分布 (Binomial Distribution)
• ポアソン分布 (Poisson Distribution)
• 幾何分布 (Geometric Distribution)
• 負の二項分布 (Negative Binomial Distribution)
• 超幾何分布 (Hypergeometric Distribution)

連続分布 (Continuous Distributions)

• 連続一様分布 (Continuous Uniform Distribution)
• 指数分布 (Exponential Distribution)
• 正規分布 (Normal Distribution)
• カイ二乗分布 (Chi-squared Distribution)
• ガンマ分布 (Gamma Distribution)
• ベータ分布 (Beta Distribution)

今回、これらの離散分布について、それぞれの定義、確率関数、期待値と分散、ビジネス応用例を簡単に解説していきます。

連続分布に関しては、次回お話しいたします。

離散一様分布

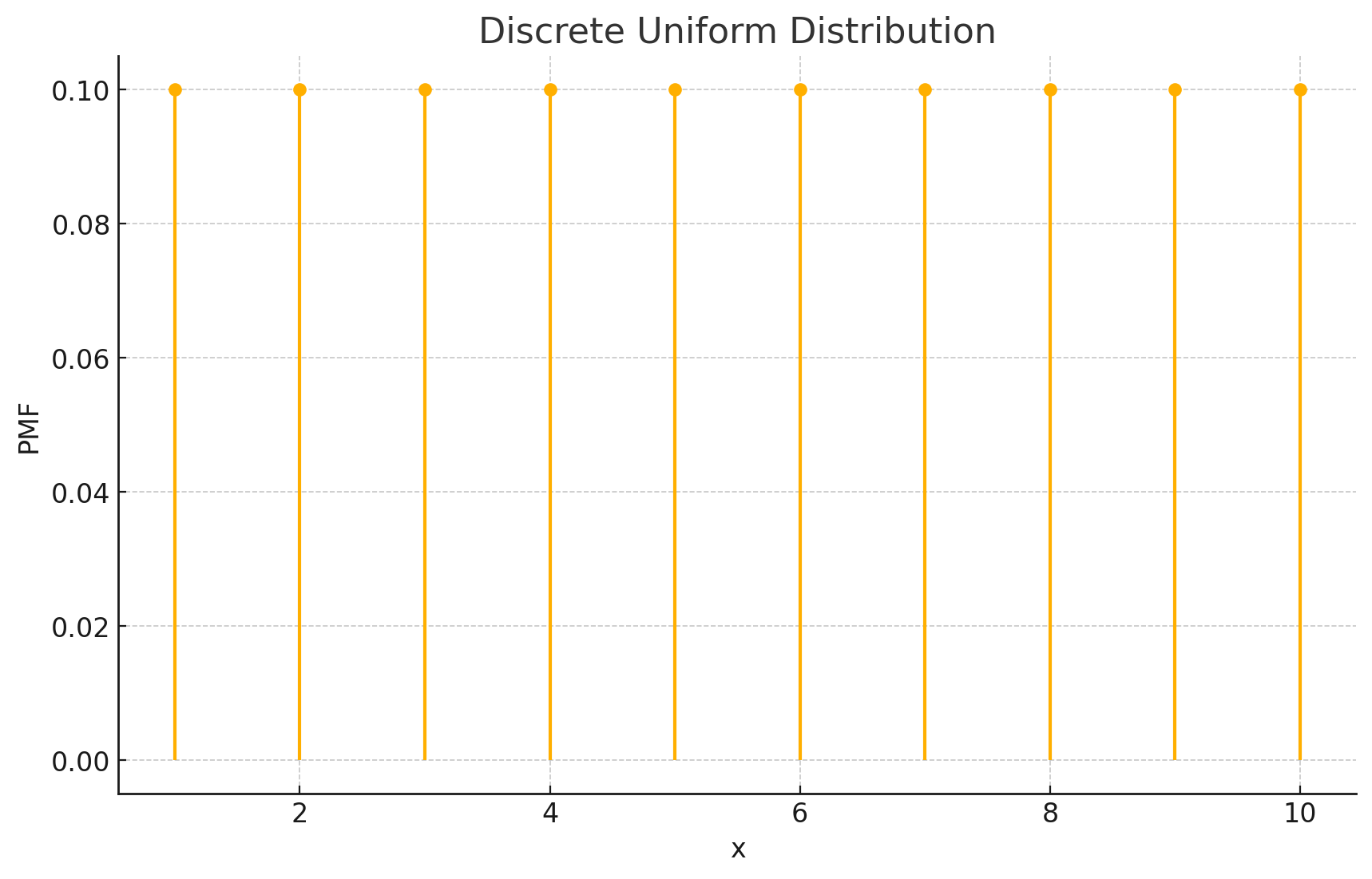
　確率質量関数

離散一様分布は、全ての結果が等しい確率で発生する分布です。n個の異なる結果がある場合、それぞれの結果の発生確率は1/nです。

\displaystyle p(x) = \frac{1}{n}

　期待値と分散

期待値 (E(X))

\displaystyle E(X) = \frac{n+1}{2}

分散 (V(X))

\displaystyle V(X) = \frac{n^2 - 1}{12}

　ビジネス活用事例

　　背景

ある小売業者が、顧客の購買意欲を高めるためにプロモーションキャンペーンを実施しようとしています。

複数のプロモーションオファー（例：割引クーポン、ポイント倍増、無料ギフトなど）をランダムに配布することで、顧客の興味を引き、購入を促進することを目指しています。

　　方法

離散一様分布を用いて、プロモーションオファーをランダムに配布します。

n個の異なるプロモーションオファーがあり、それぞれのオファーが等しい確率で選ばれるようにします。

　　実施手順

ステップ１：オファーリストを作成

以下の5つのプロモーションオファーを用意しました。

• 割引クーポン
• ポイント倍増
• 無料ギフト
• 限定商品の先行販売
• 無料配送

ステップ２：ランダムにオファーを配布

各顧客に対して、5つのオファーの中からランダムに1つを選び、配布します。各オファーが選ばれる確率は1/5（20%）です。

ステップ３：結果の分析

プロモーションキャンペーン後、どのオファーが最も効果的であったかを分析します。顧客の反応率や売上の増加を比較し、今後のキャンペーンに役立てます。

　　期待される効果

公平な機会の提供

全ての顧客が等しくランダムに選ばれたオファーを受け取るため、特定の顧客に偏ることなく、公平な機会を提供できます。

データ収集と分析

異なるプロモーションオファーの効果を比較することで、どのオファーが最も効果的かを特定でき、次回以降のキャンペーンの改善に役立ちます。

　　実施例

ある週末に、1000人の顧客に対してプロモーションキャンペーンを実施しました。

各顧客には、5つのオファーのうち1つがランダムに選ばれて提供されました。その結果、以下のような反応が得られました。

• 割引クーポン：250人が利用
• ポイント倍増：200人が利用
• 無料ギフト：150人が利用
• 限定商品の先行販売：300人が利用
• 無料配送：100人が利用

このデータを基に、最も効果的だったオファー（限定商品の先行販売）を次回のキャンペーンで重点的に活用する計画を立てることができます。

このように、離散一様分布を活用することで、公平で効果的なプロモーションキャンペーンを実施し、顧客の購買意欲を高めることができます。

二項分布

　確率質量関数

二項分布は、固定された回数の試行で成功回数を数える分布です。各試行は成功か失敗のいずれかであり、成功の確率は一定です。

\displaystyle p(x) = \binom{n}{x} p^x (1-p)^{n-x}

　期待値と分散

期待値 (E(X))

\displaystyle E(X) = np

分散 (V(X))

\displaystyle V(X) = np(1-p)

　ビジネス活用事例

　　背景

ある小売りチェーンが、新しいマーケティングキャンペーンを実施しています。

このキャンペーンで、特定のプロモーションメールを顧客に送信し、そのメールを開封した顧客が商品の購入に至るかどうかを確認します。

企業は、このキャンペーンがどの程度効果的かを評価するために、顧客の反応を分析する必要があります。

　　方法

二項分布を用いて、プロモーションメールを受け取った顧客のうち、何人が実際に商品を購入するかをモデル化します。

この分析により、キャンペーンの成功率を評価し、将来のマーケティング戦略を改善するための洞察を得ることができます。

　　実施手順

ステップ１：顧客のリストを準備

キャンペーン対象となる顧客リストを作成します。ここでは、1000人の顧客がプロモーションメールを受け取ることにします。

ステップ２：成功確率の設定

過去のデータに基づき、プロモーションメールを受け取った顧客が商品を購入する確率（成功確率）を推定します。例えば、この確率を0.1（10%）と仮定します。

ステップ３：二項分布の適用

試行回数n=1000、成功確率=0.1を用いて二項分布をモデル化します。

確率関数：

\displaystyle p(x) = \binom{n}{x} p^x (1-p)^{n-x}

期待値：

\displaystyle E(X) = np = 1000 \times 0.1 = 100

分散：

\displaystyle V(X) = np(1-p) = 1000 \times 0.1 \times 0.9 = 90

 

ステップ４：結果の分析

実際のキャンペーン結果を収集し、どの程度の顧客が商品を購入したかを確認します。実際の成功回数が期待値と大きく異なる場合、成功率の改善またはキャンペーン戦略の見直しが必要です。

大きく異なるかどうか（実際の成功回数Xが期待値E(X)と大きく異なるかどうか）を、例えば次のような統計的仮説検定を実施します。

• 帰無仮説H0：成功率が0.1である
• 対立仮説H1：成功率が0.1ではない

検定統計量として、以下の標準化された zスコア を用いたとします。

\displaystyle z = \frac{X - E(X)}{\sqrt{V(X)}}

有意水準αを0.05とすると、両側検定での臨界値は±1.96です。

計算されたz値が臨界値の範囲外にある場合、帰無仮説を棄却し、成功率が0.1ではないと判断します。

　　期待される効果

成功率の評価

キャンペーンの成功率を定量的に評価することで、プロモーションの効果を測定できます。

戦略の改善

期待値と実際の結果を比較することで、成功率が期待値よりも低い場合には、キャンペーンの内容や顧客ターゲティングを改善するための洞察を得ることができます。

費用対効果の分析

キャンペーンにかかるコストと成功率を比較し、費用対効果を評価することができます。これにより、マーケティング予算の最適化が可能になります。

　　実施例

企業が1000人の顧客にプロモーションメールを送り、実際に120人の顧客が商品を購入した場合、期待される成功回数100人（期待値）に対して実際の成功回数120人は、予想よりも高い成功率を示しています。

実際、 zスコア を計算すると、以下のようになりました。

\displaystyle z = \frac{X - E(X)}{\sqrt{V(X)}} = \frac{120 - 100}{\sqrt{90}} \approx 2.11

計算されたz値が臨界値±1.96の範囲外のため帰無仮説を棄却し、成功率が0.1ではないと判断しました。

この結果から、キャンペーンが非常に効果的であったと評価され、同様のプロモーションを将来のマーケティング戦略に組み込むことが推奨されます。

このように、二項分布を活用することで、マーケティングキャンペーンの効果を定量的に評価し、将来の戦略を改善するための貴重な洞察を得ることができます。

ポアソン分布

　確率質量関数

ポアソン分布は、一定の時間または空間内で一定の平均発生率を持つランダムな出来事の発生回数をモデル化します。

\displaystyle p(x) = \frac{\lambda^x e^{-\lambda}}{x!}

　期待値と分散

期待値 (E(X))

\displaystyle E(X) = \lambda

分散 (V(X))

\displaystyle V(X) = \lambda

　ビジネス活用事例

　　背景

ある企業が運営するWebサイトでは、訪問者数の増加が重要な課題となっています。

特定の時間帯や曜日にどれだけの訪問者が訪れるかを予測し、マーケティング戦略やコンテンツの配置を最適化するために、訪問者数の予測が必要です。

Webサイトの訪問者数はランダムな出来事であり、一定の平均発生率に従うと仮定できます。

ポアソン回帰モデルを用いることで、訪問者数を予測し、効果的な対策を講じることができます。

　　方法

ポアソン回帰モデルを用いて、Webサイトの訪問者数を予測します。

このモデルにより、時間帯、曜日、キャンペーン実施の有無などの変数に基づいて訪問者数を予測し、最適なマーケティング戦略を策定します。

　　ポアソン回帰モデルとは？

ポアソン回帰は、ポアソン分布に従うデータの回帰分析を行う手法です。

特に、ある期間内に発生する出来事の回数をモデル化する際に使用されます。

ポアソン回帰モデルは、従属変数（ここでは訪問者数）がポアソン分布に従い、独立変数（例えば時間帯、曜日、キャンペーンの有無など）との関係を推定します。

これにより、特定の条件下での出来事の発生回数を予測することができます。

　　実施手順

ステップ１：データの収集

過去のWebサイト訪問データを収集し、訪問者数、訪問時間、曜日、キャンペーン実施の有無などの変数を含むデータセットを作成します。

ステップ２：ポアソン回帰モデルの設計

収集したデータを基にポアソン回帰モデルを構築します。このモデルでは、訪問者数が従属変数として、訪問時間、曜日、キャンペーン実施の有無などが独立変数として使用されます。

ステップ３：モデルのトレーニング

データをトレーニングセットとテストセットに分割し、トレーニングセットを用いてポアソン回帰モデルをトレーニングし、使えそうかどうかをテストデータで検証します。

実務で使えそうだと判断したら、分割する前のデータセットを使いモデルをトレーニングします。

ステップ４：訪問者数の予測

トレーニングされたモデルを用いて、各時間帯や曜日における訪問者数を予測します。これにより、特定の時間帯や曜日に予想される訪問者数を事前に把握することができます。

ステップ５：マーケティング戦略の最適化

予測された訪問者数に基づいて、キャンペーンの実施タイミングやコンテンツの配置を最適化します。

例えば、予測モデルが特定の曜日に訪問者数が多いと示す場合、その曜日に合わせて新しいコンテンツを公開するなどの対策を講じます。

　　期待される効果

訪問者数の予測精度向上

ポアソン回帰モデルを用いることで、訪問者数の予測精度が向上し、効果的なマーケティング戦略を策定することができます。

マーケティングの最適化

訪問者数の多い時間帯や曜日に合わせてキャンペーンやコンテンツを配置することで、マーケティング効果を最大化できます。

リソースの効率的利用

予測に基づいてリソースを効率的に配置することで、無駄を省き、コスト削減につながります。

　　実施例

企業がポアソン回帰モデルを構築し、次の1週間の訪問者数を予測した結果、金曜日の午後に訪問者数がピークに達することがわかりました。

これに基づいて、企業は金曜日の午後に新しいプロモーションを実施し、特別なコンテンツを公開することを決定しました。

この戦略により、訪問者数がさらに増加し、売上も向上しました。

このように、ポアソン回帰モデルを活用することで、Webサイトの訪問者数を予測し、マーケティング戦略を最適化することができます。

幾何分布

　確率質量関数

幾何分布は、初めて成功するまでの試行回数をモデル化します。各試行は成功か失敗のいずれかであり、成功の確率は一定です。

\displaystyle p(x) = (1-p)^{x-1} p

　期待値と分散

期待値 (E(X))

\displaystyle E(X) = \frac{1}{p}

分散 (V(X))

\displaystyle V(X) = \frac{1-p}{p^2}

　ビジネス活用事例

　　背景

ある企業が新規顧客を獲得するためにマーケティングキャンペーンを展開しています。

顧客が初めて購入するまでに必要なマーケティング接触回数を把握することで、効率的なキャンペーンの設計と予算の最適化が可能になります。

顧客の属性（例えば、年齢、地域、購入履歴など）によって、購入までに必要な接触回数が異なることがあります。

このような状況において、幾何分布を用いることで属性別の接触回数を予測し、最適なマーケティング戦略を策定します。

　　方法

幾何分布を用いて、顧客が初めて購入するまでに必要なマーケティング接触回数を属性別にモデル化します。

これにより、各属性に最適なマーケティング戦略を設計するためのデータに基づいたアプローチを実現します。

　　実施手順

ステップ１：データの収集

過去のマーケティングキャンペーンデータを収集し、各顧客が初めて購入するまでに必要だったマーケティング接触回数と顧客属性（年齢、地域、購入履歴など）を記録します。

ステップ２：属性別の分析

収集したデータを基に、顧客の属性ごとに購入までに必要な平均接触回数を算出します。これにより、各属性がどの程度の接触回数で初回購入に至るかを理解します。

ステップ３：幾何分布の適用

各属性別に必要な接触回数のデータを幾何分布に適用し、成功確率を推定します。この成功確率を基に、各属性ごとの最適なマーケティング接触回数を予測します。

ステップ４：属性別マーケティング戦略の最適化

予測された接触回数に基づき、各属性ごとに異なるマーケティング戦略を設計します。

例えば、若年層の顧客にはソーシャルメディア広告を多用し、高齢層の顧客にはメールや電話を中心としたアプローチを行います。

また、地域ごとの傾向を分析し、特定の地域ではより多くの接触が必要な場合にはその地域に対するマーケティング活動を強化します。

　　期待される効果

マーケティング効果の向上

幾何分布を用いて属性別に適切な接触回数を予測することで、各顧客属性に対して効果的なマーケティング戦略を実施できます。

予算の最適化

最適な接触回数を基にマーケティング活動を計画することで、過剰な広告費用を削減し、予算の最適化が可能になります。

データに基づいた意思決定

幾何分布のモデルに基づいたデータを活用することで、より正確な予測と意思決定が可能になります。

　　実施例

企業が過去のデータを基に、顧客が初めて購入するまでに必要な接触回数を年齢層別に分析した結果……

• 若年層（18-24歳）は平均して8回
• 中年層（25-44歳）は平均して10回
• 高齢層（45歳以上）は平均して12回

……の接触が必要であることがわかりました。

この情報を基に、企業は若年層向けのキャンペーンではソーシャルメディア広告を中心に短期間で多くの接触を計画し、中年層向けにはメールマーケティングと広告を組み合わせ、高齢層向けには電話やダイレクトメールを重視した戦略を実施します。

このように、幾何分布を活用することで、顧客の属性に応じた最適なマーケティング接触回数を予測し、効果的かつ効率的なマーケティング活動を実現することができます。

負の二項分布

　確率質量関数

負の二項分布は、k回目の成功までに必要な試行回数をモデル化します。各試行は成功か失敗のいずれかであり、成功の確率は一定です。

\displaystyle p(x) = \binom{x-1}{k-1} p^k (1-p)^{x-k}

　期待値と分散

期待値 (E(X))

\displaystyle E(X) = \frac{k}{p}

分散 (V(X))

\displaystyle V(X) = \frac{k(1-p)}{p^2}

　ビジネス活用事例

　　背景

あるサブスクリプションサービス企業では、顧客の解約を最小限に抑えることが重要な課題となっています。

顧客の解約を予測し、解約を防ぐためのプロアクティブな施策を講じることが求められています。

顧客の行動データに基づいて、解約のリスクを予測するために、負の二項分布回帰（NBD）モデルを活用します。

　　方法

NBDモデルを用いて、顧客の解約リスクを予測します。

このモデルでは、顧客が特定のイベント（ここでは解約）に至るまでに必要な試行回数（ここでは継続利用の回数）をモデル化します。

これにより、顧客ごとに解約のリスクを評価し、適切な対策を講じることが可能になります。

　　NBDモデルとは

負の二項分布回帰（NBD）モデルは、ある事象が何回目の試行で成功するかをモデル化するための統計手法です。

成功までの試行回数が負の二項分布に従う場合に適用され、サブスクリプションサービスなどの解約予測において非常に有効です。

NBDモデルでは、成功確率が一定であることを前提に、各試行の結果が成功か失敗かを観察し、解約リスクなどを予測します。

　　実施手順

ステップ１：データの収集

過去の顧客行動データを収集します。これには、各顧客の契約開始日、契約期間中の利用回数、解約の有無、およびその他の関連する属性（年齢、地域、利用頻度など）が含まれます。

ステップ２：NBDモデルの設計

収集したデータを基に、NBDモデルを構築します。このモデルでは、顧客の解約までの試行回数（継続利用回数）を予測します。

独立変数として、顧客の属性情報や利用パターン（利用頻度、利用期間、過去の解約履歴など）を使用します。

従属変数として、解約までの継続利用回数を使用します。

ステップ３：モデルのトレーニング

データをトレーニングセットとテストセットに分割し、トレーニングセットを用いてNBDモデルをトレーニングし、使えそうかどうかをテストデータで検証します。

実務で使えそうだと判断したら、分割する前のデータセットを使いモデルをトレーニングします。

ステップ４：解約リスクの予測

トレーニングされたモデルを用いて、各顧客の解約リスクを予測します。これにより、解約の可能性が高い顧客を特定することができます。

ステップ５：プロアクティブな対策の実施

予測された解約リスクに基づいて、高リスク顧客に対してプロアクティブな対策を講じます。

具体的には、パーソナライズされた特典や割引、特別なサポートを提供するなどの施策を実施します。

　　期待される効果

解約率の低減

NBDモデルを用いることで、解約リスクの高い顧客を事前に特定し、適切な対策を講じることで解約率を低減できます。

顧客満足度の向上

プロアクティブな対策により、顧客の満足度が向上し、長期的な顧客ロイヤルティを構築できます。

収益の安定化

解約率の低減により、安定した収益を確保し、ビジネスの成長を促進できます。

　　実施例

この企業がNBDモデルを構築し、次の3ヶ月間の解約リスクを予測した結果、特定の顧客群が高い解約リスクを示していることが判明しました。

この情報を基に、企業はこれらの高リスク顧客に対して特別な割引オファーや追加サービスを提供し、解約を防ぐための施策を実施しました。

その結果、解約率が大幅に低減し、顧客満足度が向上しました。

このように、NBD回帰モデルを活用することで、サブスクリプションサービスの解約予測と防止策を効果的に実施し、顧客ロイヤルティを向上させることができます。

超幾何分布

　確率質量関数

超幾何分布は、有限母集団からサンプリングする際の成功回数をモデル化します。サンプルは置き換えなしで選ばれます。

\displaystyle p(x) = \frac{\binom{M}{x} \binom{N-M}{n-x}}{\binom{N}{n}}

　期待値と分散

期待値 (E(X))

\displaystyle E(X) = n \frac{M}{N}

分散 (V(X))

\displaystyle V(X) = n \frac{M}{N} \left(1 - \frac{M}{N}\right) \frac{N-n}{N-1}

　ビジネス活用事例

　　背景

ある製造企業が製品の品質管理を強化したいと考えています。

生産ラインから出荷される製品の中から、品質基準を満たしているかどうかを確認するために、ランダムにサンプルを抽出し検査を行います。

ここで重要なのは、一度選んだ製品は元に戻さない（非復元抽出）という方法でサンプリングを行うことです。

このような状況で、サンプル中の品質基準を満たしている製品の数をモデル化するために、超幾何分布を用います。

　　方法

超幾何分布を用いて、サンプリングした製品の中で品質基準を満たしている製品の数を予測します。

このモデルにより、製品品質の全体的な評価を行い、品質管理の効果を高めるためのデータに基づいたアプローチを実現します。

　　実施手順

ステップ１：データの収集

製造ラインから一定数の製品を無作為にサンプリングし、各サンプルの品質を検査します。サンプルサイズ、全体の製品数、品質基準を満たしている製品の数を記録します。

ステップ２：超幾何分布の適用

収集したデータを基に、サンプルの中で品質基準を満たしている製品の数を超幾何分布を用いてモデル化します。

このモデルを使用して、サンプル全体に対する品質基準を満たしている製品の割合を推定します。

ステップ３：品質評価の実施

超幾何分布モデルを用いて、サンプリングされた製品の品質評価を行います。

例えば、サンプルの中で品質基準を満たしている製品の割合が一定の基準を下回る場合、製品全体の品質に問題がある可能性が示唆されます。

ステップ４：品質管理の強化：

サンプリング結果に基づき、製造プロセスの改善点を特定し、品質管理の強化策を講じます。

具体的には、製造ラインの調整や品質検査の頻度の見直しなどを行います。

　　期待される効果

品質の安定化

超幾何分布を用いて品質評価を行うことで、製品品質の全体的な安定性を確保できます。

効率的な品質管理

サンプリングによる品質評価を通じて、効率的に品質管理を行い、問題の早期発見と対策が可能になります。

コスト削減

品質基準を満たしていない製品を早期に発見することで、リコールやクレーム対応などのコストを削減できます。

　　実施例

企業が過去のデータを基に、製品の出荷前に毎回100個の製品をサンプリングし、品質検査を実施しているとします。

最近のサンプリングデータでは、品質基準を満たしている製品の数が通常よりも少ないことが判明しました。

この情報を基に、企業は製造プロセスの見直しと改善を行い、品質基準を満たす製品の割合を再び増加させることに成功しました。

このように、超幾何分布を活用することで、製品品質管理の効果を高め、品質の安定性を確保し、製造コストを削減することができます。

今回のまとめ

今回は、確率分布の基礎とビジネス応用について、離散分布を中心に解説しました。

確率分布は、データ分析や統計学の基礎となる重要な概念であり、ビジネスにおける意思決定や予測に幅広く活用されています。

離散分布と連続分布の違いを理解した上で、主要な離散分布である離散一様分布、二項分布、ポアソン分布、幾何分布、負の二項分布、超幾何分布について、それぞれの確率質量関数、期待値、分散を紹介しました。

さらに、各分布のビジネス活用事例を具体的に示し、実際の問題解決にどのように適用できるかを解説しました。

確率分布を理解し、適切に応用することで、データに基づいた意思決定やリスク管理、マーケティング戦略の最適化、品質管理の強化などが可能になります。

次回は、連続分布について解説し、ビジネスにおける確率分布の活用方法をさらに深く探求していきます。

確率分布の理解を深め、ビジネスに活かすことで、より効果的かつ効率的な問題解決とデータ活用が実現できるでしょう。