データ分析の世界に足を踏み入れると、さまざまなグラフや図表に出会います。
その中でも、特に便利でよく使われるものの一つが「ボックスプロット(Boxplot)」です。
ボックスプロットは、データの分布を視覚的に簡単に理解できるツールであり、初心者からプロフェッショナルまで幅広く活用されています。
今回は、ボックスプロットの基本から実際の応用例までを解説します。
Contents [hide]
ボックスプロットの歴史と背景
ジョン・テューキーとボックスプロットの起源
ボックスプロット(Boxplot)は、アメリカの統計学者ジョン・テューキー(John Tukey)によって1969年に発明されました。
テューキーは、データの分布や特徴を簡単に視覚化する方法としてボックスプロットを提案しました。
彼の目標は、複雑な統計モデルを適用する前に、データを理解しやすくするためのシンプルなグラフィカルツールを提供することでした。
テューキーは、探索的データ解析(Exploratory Data Analysis, EDA)の重要性を強調し、ボックスプロットはその一環として開発されました。
EDAは、データの基本的なパターン、異常値、及び仮説を視覚的に把握するための手法です。
テューキーの考え方は、まずデータを視覚的に理解し、その後でより詳細な解析を行うというアプローチを推奨しました。
データ可視化の基本概念
データ可視化(Data Visualization)は、データのパターンや関係性を視覚的に表現する方法であり、データ分析において非常に重要な役割を果たします。
データ可視化の主な目的は以下の通りです。
パターンの発見
データセット全体のトレンドやパターンを迅速に把握することができます。これにより、データの基本的な性質や傾向を理解することができます。
異常値の検出
外れ値(Outliers)や異常なデータポイントを視覚的に発見することができます。これにより、データのクオリティを評価し、必要な修正を行うことができます。
仮説の生成と検証
データの可視化を通じて、新たな仮説を生成し、それを検証するための手がかりを得ることができます。これにより、データ分析のプロセスが効率化されます。
コミュニケーションの向上
データの可視化は、専門家以外の人々にもデータの結果や洞察を伝えるための有効な手段です。グラフや図表を使用することで、複雑なデータを簡潔に説明することができます。
ボックスプロットは、これらの目的を達成するための強力なツールの一つです。
データの分布や特徴を簡潔に視覚化することで、データ分析の初期段階で重要な洞察を得ることができます。
ボックスプロットの基礎知識
ボックスプロットとは何か
ボックスプロット(Boxplot)は、データの分布やばらつきを視覚的に表示するためのグラフの一種です。
これは、データの中心傾向、散布度、及び外れ値を簡単に理解するために非常に有用です。
ボックスプロットは、以下の五数要約(Five-Number Summary)に基づいています。
最小値(Minimum)
最小値はデータセットの中で最も小さい値を示します。ボックスプロットでは、最小値は通常、下側のウィスカーの先端として表示されます。
第一四分位数(Q1, First Quartile)
第一四分位数は、データセットを小さい順に並べたとき、下位25%のデータ点の境界を示します。これにより、データの下位25%がどの範囲にあるかを理解できます。
中央値(Median)
中央値は、データの中央の値で、データセットを二つの等しい部分に分けます。ボックスプロットでは、ボックスの中に引かれた線として表示されます。中央値はデータの代表的な値を示し、平均値と異なり、外れ値に影響されにくい特性を持っています。
第三四分位数(Q3, Third Quartile)
第三四分位数は、データセットの上位25%のデータ点の境界を示します。これにより、データの上位25%がどの範囲にあるかを理解できます。
最大値(Maximum)
最大値はデータセットの中で最も大きい値を示します。ボックスプロットでは、最大値は通常、上側のウィスカーの先端として表示されます。
これらの五数要約は、データの全体的な分布と特性を迅速に把握するための基本的な指標です。
ボックスプロットの読み方
ボックスプロット(Boxplot)はデータの分布や特性を視覚的に把握するための強力なツールです。
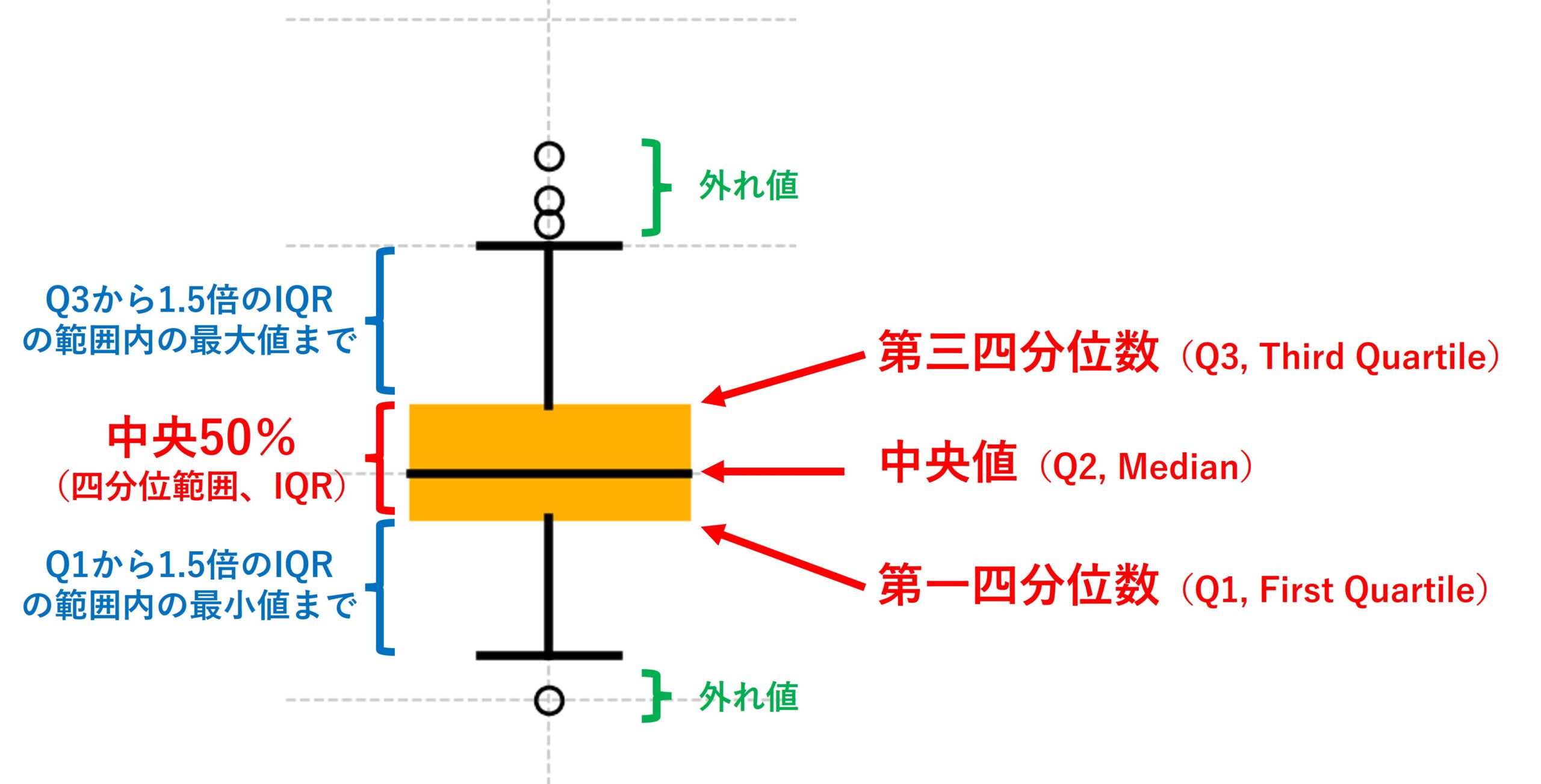
ボックス(Box)
ボックスはデータの中央50%(四分位範囲、IQR)を示します。ボックスの下端は第一四分位数(Q1, First Quartile)、上端は第三四分位数(Q3, Third Quartile)です。ボックス内の線は中央値(Median)を示し、データの中央値を表します。
ウィスカー(Whisker)
ウィスカーはボックスの上下に伸びており、データの範囲を示します。ウィスカーの長さは通常、Q1から1.5倍のIQR、Q3から1.5倍のIQRまでの範囲をカバーします。この範囲内のデータポイントは、通常の範囲内と見なされます。
外れ値(Outliers)
ウィスカーの外に位置するデータポイントは外れ値と呼ばれます。これらは異常値や極端な値であり、ボックスプロットでは個別の点としてプロットされます。外れ値はデータの異常を示すことがあり、詳細な分析が必要な場合があります。
中央値の位置
ボックス内の線がボックスの中央に位置している場合、データは対称的である可能性が高いです。中央値がボックスの上部や下部に偏っている場合、データは偏っている可能性があります(左または右に歪んでいる)。
ボックスの幅
ボックスの幅(IQR)はデータのばらつきを示します。IQRが広い場合、データのばらつきが大きいことを意味し、狭い場合はデータのばらつきが小さいことを示します。
ウィスカーの長さ
ウィスカーの長さが均等である場合、データの分布は対称的である可能性が高いです。ウィスカーの長さが不均等な場合、データは歪んでいる可能性があります。
外れ値の数と位置
外れ値が多い場合、データには多くの異常値が含まれている可能性があります。外れ値の位置は、どの部分に異常が集中しているかを示します。
ボックスプロットの実践的な使い方
ボックスプロット(Boxplot)は、データの分布やばらつきを視覚的に理解するための強力なツールです。
特に、探索的データ解析(Exploratory Data Analysis, EDA)において、その有用性は非常に高いです。
EDA(探索的データ解析)での利用
探索的データ解析(EDA)は、データの基本的な特性を理解するための最初のステップです。
EDAでは、データの概要を把握し、異常値やパターンを見つけることが目的です。ボックスプロットは、このプロセスにおいて非常に有用です。
例:複数のグループ間の比較
例えば、異なるグループのデータ分布を比較する場合、ボックスプロットを使うと非常にわかりやすいです。
以下は、Irisデータセットの「sepal length(がく片の長さ)」の分布を異なる花の品種(species)ごとに比較したボックスプロットです。
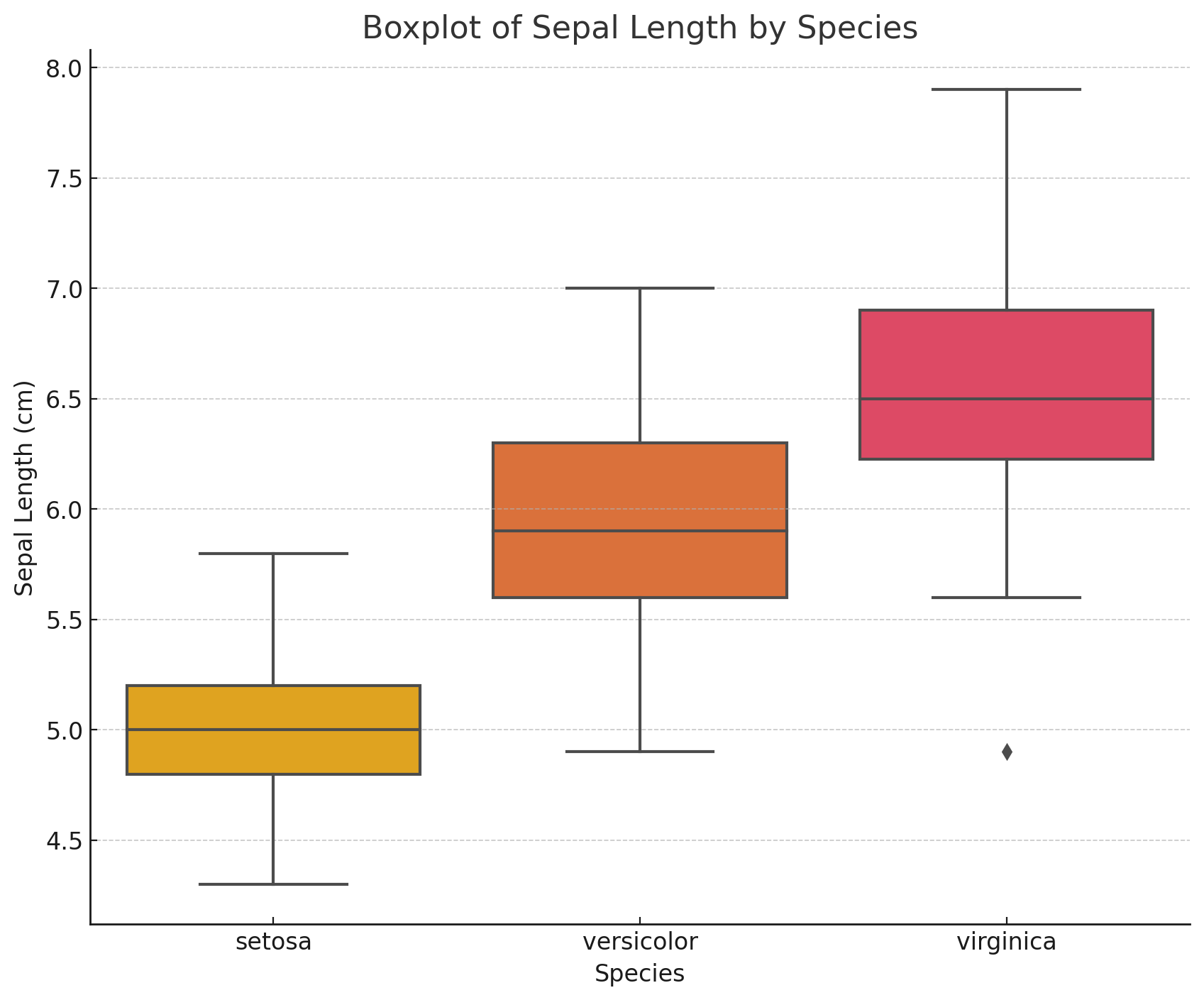
例:データの異常値の検出
ボックスプロットを使用することで、データの異常値(Outliers)を簡単に視覚化できます。
異常値は、ウィスカーの外側に位置するデータポイントとして表示されます。これにより、データの異常値を迅速に特定し、詳細な分析を行うことができます。
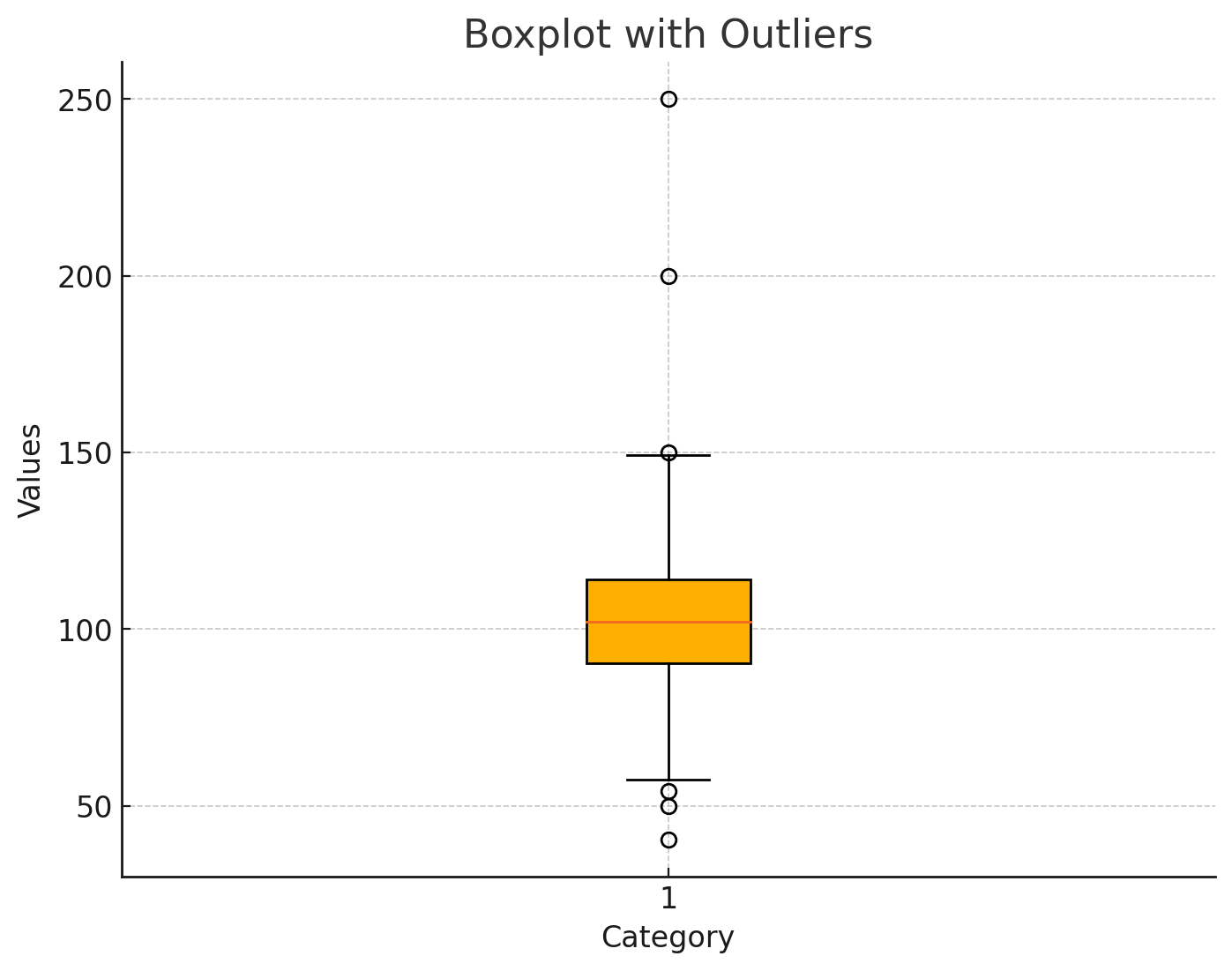
以下は、異常値を含むサンプルデータのボックスプロットです。ウィスカーの外側に異常値が表示されているのがわかります。

データの初期評価における役割
ボックスプロットは、データの初期評価において重要な役割を果たします。
データの中心傾向、ばらつき、及び異常値を迅速に把握することで、データのクオリティや特性を理解するための重要な情報を提供します。
これにより、データの前処理やクリーニングの方針を決定する際に役立ちます。
具体的には、以下のようなポイントでボックスプロットを活用できます。
データの基本的な分布の把握
データの中央値や四分位範囲を把握することで、データの基本的な分布を理解します。
異常値の特定
異常値を迅速に特定し、データのクオリティを評価します。
グループ間の比較
複数のグループ間でデータの分布を比較し、グループ間の違いや共通点を理解します。
ビジネス応用例
ボックスプロット(Boxplot)は、ビジネスデータの分析においても非常に有用です。
例1: 売上データの分析
ある会社が、異なる地域(Region)での月別売上データを分析したいとします。
ボックスプロットを使用することで、各地域ごとの売上の分布や異常値を視覚的に確認できます。
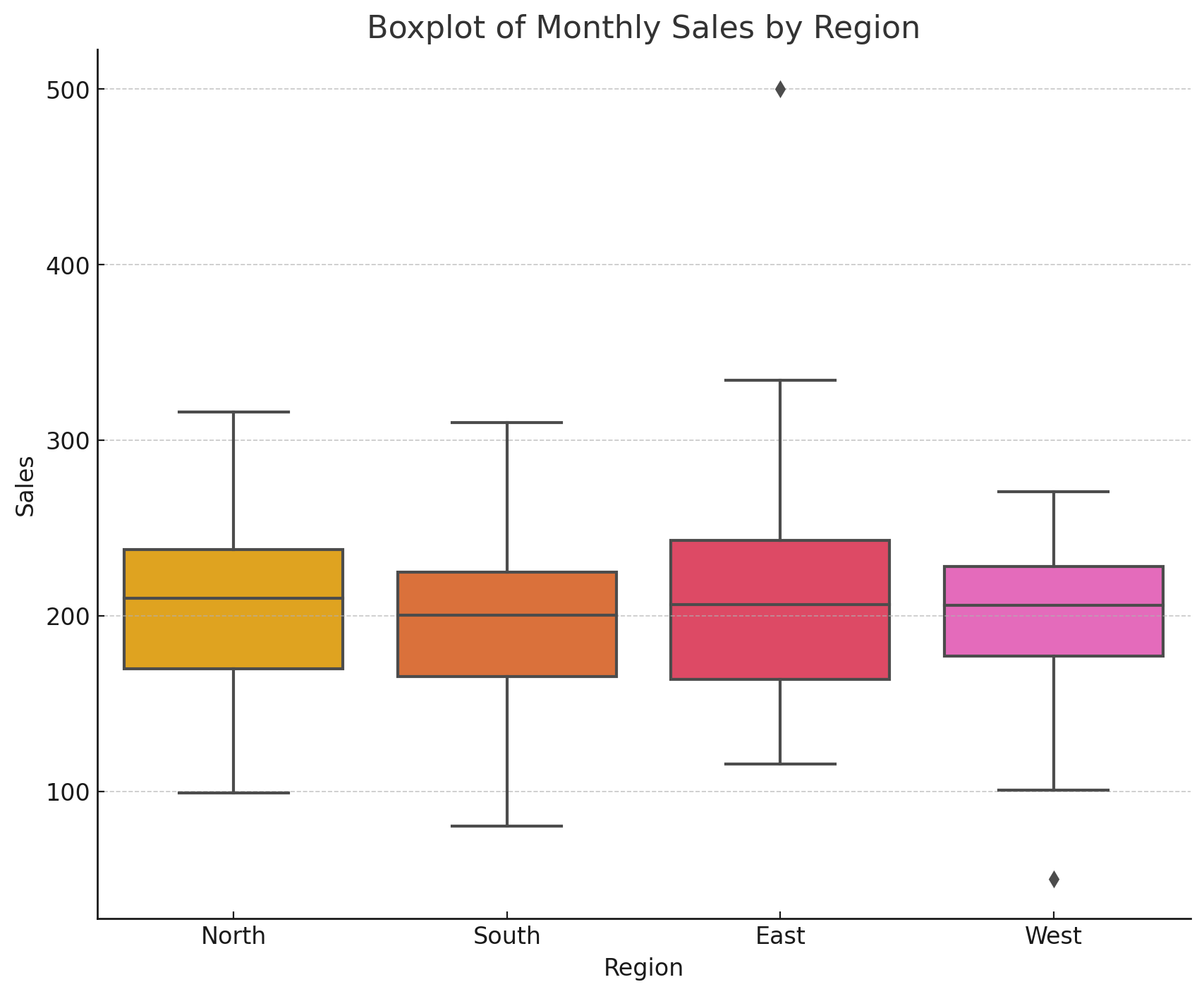
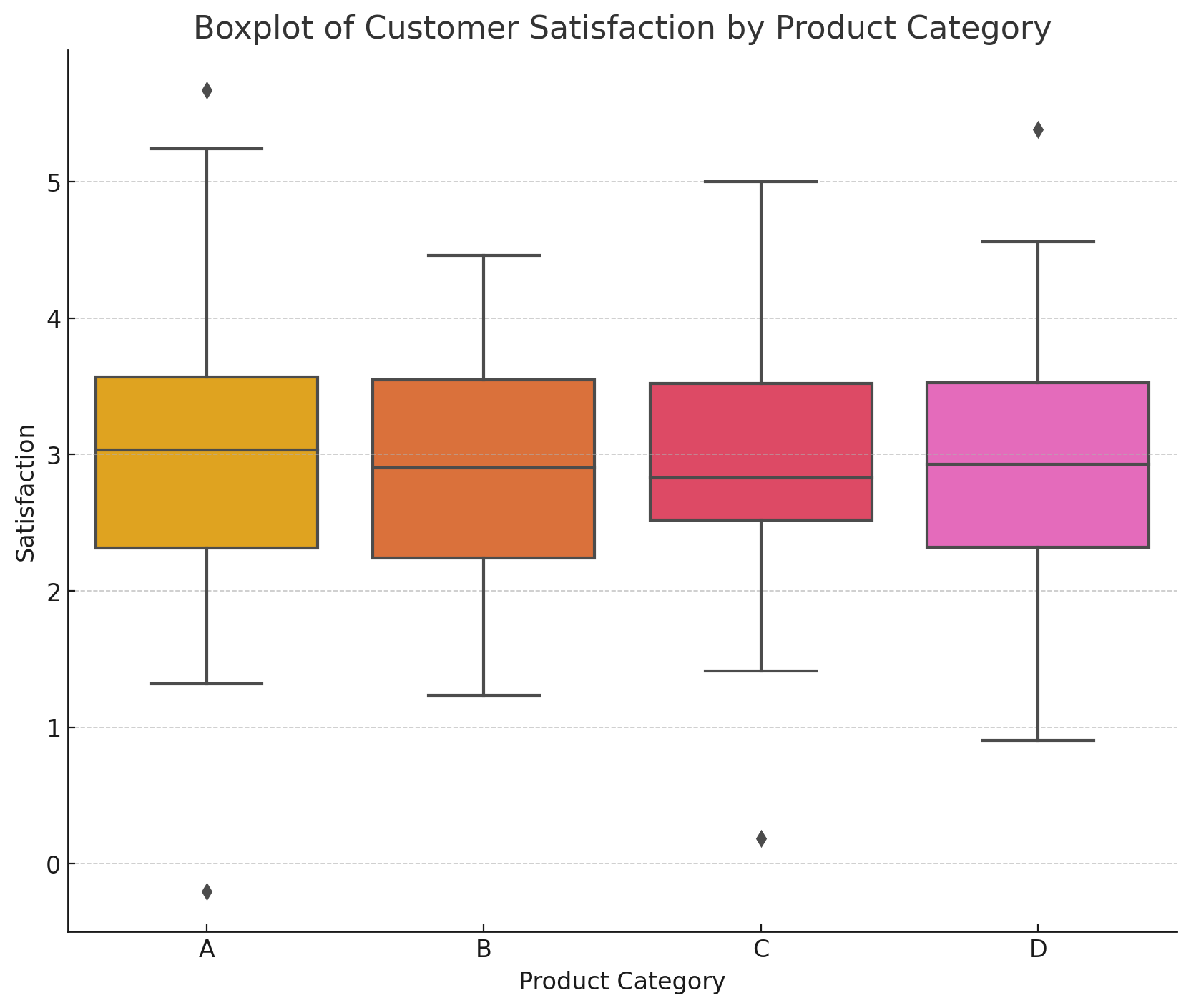
例2: 顧客満足度データの分析
顧客満足度(Customer Satisfaction)を調査したデータを使用します。
異なる製品カテゴリー(Product Category)ごとの満足度の分布をボックスプロットで比較します。
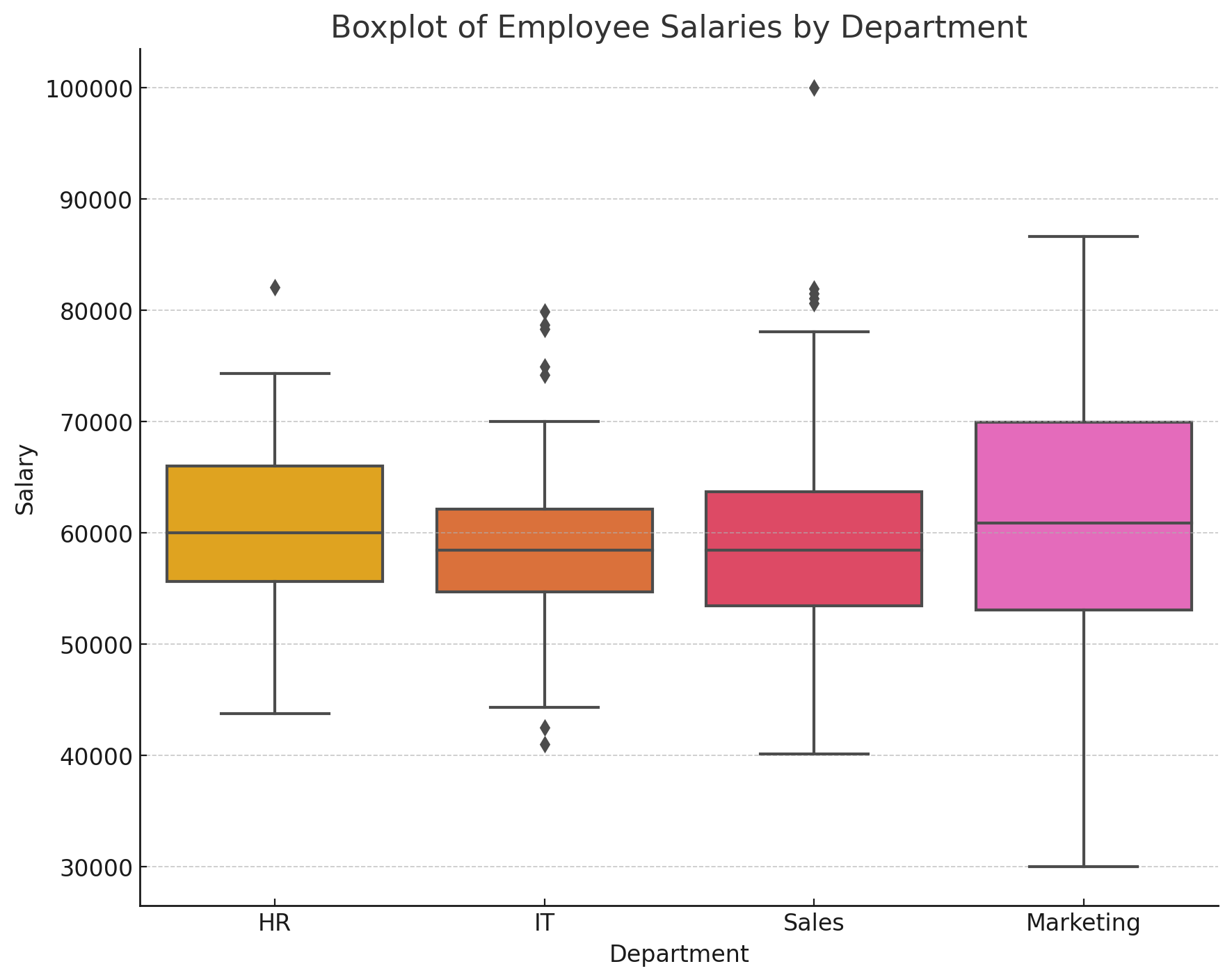
例3: 従業員の給与データの分析
従業員の給与データを使用します。
異なる部門(Department)ごとの給与分布をボックスプロットで比較します。
今回のまとめ
今回は、「取り急ぎボックスプロット」というお話しをしました。
ボックスプロット(Boxplot)は、データの分布やばらつきを視覚的に把握するための強力なツールです。
ボックスプロットを使うことで、データの中心傾向、散布度、及び外れ値を簡単に理解し、異常値やパターンを迅速に特定できます。
ビジネスデータの分析においても、ボックスプロットは非常に有用です。

