ディスク容量が足りなくなった……
システムメモリが逼迫している……

こうした明確な問題は見つけやすいものです。

しかし……

ECサイトの注文数が徐々に減少している
ユーザーの行動パターンが変化している

……といった「通常から逸脱した状態」はどのように検知すればよいのでしょうか？

今回は、複雑な機械学習モデルなしでも実装できる、統計手法を用いた時系列データの異常検知についてお話しします。

はじめに

ウェブサイトやアプリのトラフィック監視、ECサイトの注文数の追跡、システムのパフォーマンス指標の観察、企業が日々モニタリングするメトリクスは多岐にわたります。

これらの数値が「通常」とは異なる動きを見せたとき、いち早く察知できるかどうかが、ビジネスの成功にとって重要な鍵となることがあります。

　異常検知の必要性と課題

ちなみにメトリクスとは、ビジネスやシステムの状態を数値で表した指標のことです。

ビジネスメトリクス例

• ECサイトの1時間あたりの注文数
• アプリの日次アクティブユーザー数
• Webサイトのコンバージョン率（訪問者のうち購入や登録などの目的の行動をとった割合）

システムメトリクス

• サーバーのCPU使用率
• メモリ消費量
• ディスク容量の残り
• ウェブページの読み込み時間

ディスク容量やメモリ使用率のような単純なメトリクスであれば、「残り10%を切ったらアラート」といったシンプルな閾値監視で十分かもしれません。

しかし、ユーザー行動に基づくビジネスメトリクスはどうでしょうか？

例えば、あなたがECサイトを運営しているとします。

「1日の注文数が500件を下回ったらアラート」という監視ルールを設定したとします。

毎日の注文数に対して最低ラインを設定し、1日1回チェックするアプローチは一見合理的に思えます。

しかし、もし何か問題が発生した場合、数時間以内、あるいは数分以内に察知する必要があるとしたら？

ここで問題となるのは、ユーザー活動が一日の中でも時間帯によって大きく変動するという点です。

朝は少なく、昼間にピークを迎え、深夜には減少するといったパターンが一般的です。

　シンプルな閾値監視の限界

このような変動の大きいメトリクスに対して固定の閾値を設けると、例えば次のような問題が生じます。

• 昼間のピーク時に適切な閾値（例：1時間あたり50注文）は、深夜の低活動時間帯では高すぎる基準となる
• 逆に、深夜に対応した低い閾値（例：1時間あたり5注文）では、昼間の小さな変動でも誤検知が増える
• 週末と平日、季節変動、特別なイベントなど、さまざまな要因による変動に対応できない

こうした課題に対処するために、より洗練された異常検知手法が必要になります。

それが統計的手法による異常検知です。

　統計的手法の可能性

統計的手法による異常検知とは、単純な閾値ではなく、過去のデータパターンを分析し、「通常」から外れた状態を特定するアプローチです。

この方法の魅力は、機械学習の専門知識がなくても実装できる点にあります。

例えば……

先週の火曜日のこの時間帯の注文数は平均して40件で、標準偏差が5件だった。
今日の火曜日の同じ時間帯の注文数が25件なら、これは統計的に見て異常である可能性が高い

……といった分析が可能になります。

基本的な統計ツール—標準偏差、Z-スコア、パーセンタイルなど—を活用することで、例えば次のような利点があります。

• 時間帯や曜日ごとの変動を自然に考慮した監視が可能
• 過去の異常データを除外して、より正確な基準を設定できる
• ビジネスに有意義な異常だけを検出し、無駄なアラートを減らせる

よくある間違い

時系列データにおける異常検知に取り組む際、多くの方がまず試みるのが「前週比較」というアプローチです。

これは、今週のメトリクスを先週の同じ曜日・同じ時間帯のメトリクスと比較する方法です。

シンプルで実装も容易なため、一見理にかなっているように思えます。

しかし、この方法にはいくつかの重大な欠点が存在します。

　前週比較手法とその問題点

前週比較の基本的な考え方は次のとおりです。

今週火曜日の13:00の注文数 = 200件
先週火曜日の13:00の注文数 = 300件
変化率 = -33%（大幅減少！→アラート）

このような比較は確かに一部の異常を検出することができます。

例えば、注文処理システムに問題が発生し、急激に注文数が落ち込んだ場合、上記のような単純比較でも異常を検出できるでしょう。

しかし、前週比較には次のような重大な問題があります。

単一の比較ポイント
たった1つの過去データポイントとしか比較しないため、自然な変動と異常を区別する能力が低い

過去の異常が基準になる
前週に異常があった場合、それが今週の基準値になってしまう

長期トレンドの無視
徐々に進行する変化や複数週にわたる傾向を捉えられない

　過去の異常が新しい基準になる危険性

前週比較において最も致命的な問題の一つは、過去の異常データが基準になってしまうことです。

次のような例を考えてみましょう。「週1」（1週目）「週2」（2週目）･･･と週単位の注文データです。

「週1」にサイトで停止が発生し、注文数が大幅に減少しました。その後、「週2」になって注文数は正常に戻り一安心です。

このような場合に前週と比較すると、次のようになっています。

週2の火曜日の13:00の注文数 = 300件（正常）
週1の火曜日の13:00の注文数 = 100件（異常・停止時）
変化率 = +200%（大幅増加！）

これでは「大幅な改善」と誤って解釈してしまいます。ここで問題になるのは、この異常値（週1）が次の週（週2）の比較基準になることです。

不幸にも「週3」に同じような障害が再発したとします。

週3の火曜日の13:00の注文数 = 100件（異常・再発）
週2の火曜日の13:00の注文数 = 300件（正常）
変化率 = -66%（大幅減少！→アラート）

この場合はアラートが発生しますが、さらにその次の週（「週4」）もその状態が継続したとします。

週4の火曜日の13:00の注文数 = 100件（異常・継続）
週3の火曜日の13:00の注文数 = 100件（異常・再発）
変化率 = 0%（変化なし→アラートなし）

これでは、異常状態が継続しているにもかかわらず、アラートが発生しません。

要するに、これは「今週の異常は来週の基準」になってしまうという問題です。

　長期的な傾向を見逃すリスク

もう一つの重要な問題は、前週比較では長期的なトレンドを捉えられないことです。

例えば、次のようなケースを考えてみましょう。

• 週1：注文数 = 1000件
• 週2：注文数 = 980件（-2%、小さな減少）
• 週3：注文数 = 960件（-2%、小さな減少）
• 週4：注文数 = 941件（-2%、小さな減少）
• 週5：注文数 = 922件（-2%、小さな減少）

毎週の変化率は-2%程度と小さいため、単純な前週比較では「正常範囲内」と判断されるかもしれません。

しかし、5週間で見ると累積で約-8%の減少となっており、これはビジネス的に重大な問題である可能性が高いのです。

このような「じわじわと進行する変化」は、前週比較ではほぼ確実に見逃されてしまいます。

　より良いアプローチへ

標準偏差やZ-スコアといった統計的概念を用いることで、例えば次のような改善が期待できます。

• 単一の比較点ではなく、複数週のデータパターンを考慮
• 過去の異常値を検出して除外し、より正確な基準を設定
• 短期的な変動と長期的なトレンドを区別

前週比較という「簡易的な方法」には確かに限界がありますが、適切な統計手法を活用することで、より信頼性の高い異常検知システムを構築することが可能です。

統計手法による異常検知の基礎

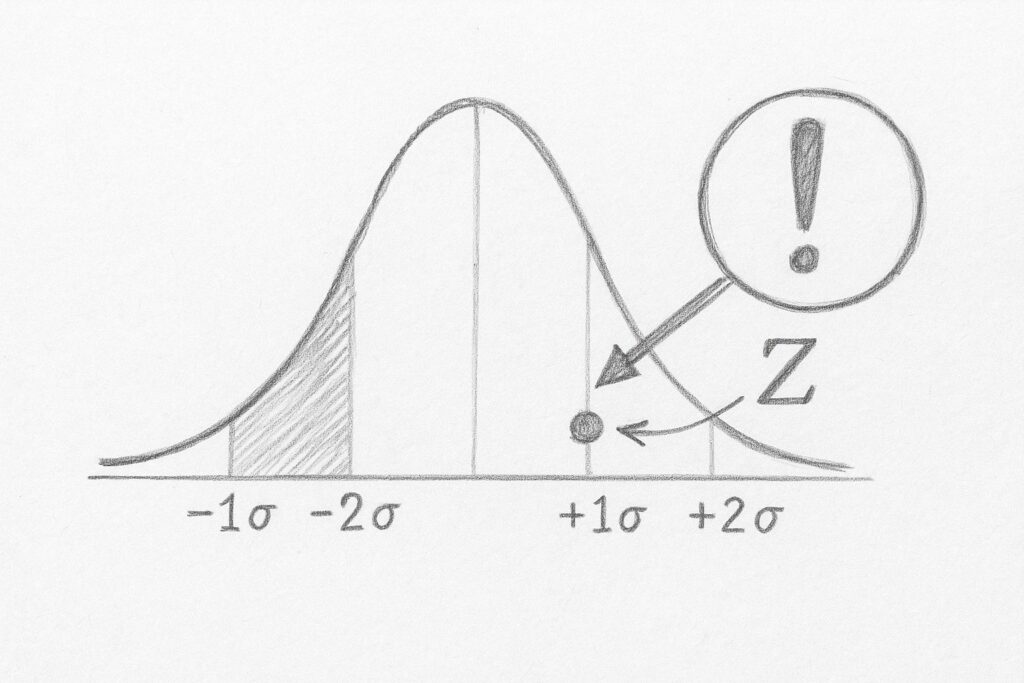
時系列データにおける異常を検出するためには、統計的な考え方が非常に有効です。

特に、標準偏差とZ-スコアは、正常値からの「逸脱の度合い」を数値化する上で重要な概念となります。

　標準偏差の活用方法

標準偏差は、データのばらつき（分散）を測る統計量です。

平均値からデータがどれだけ離れているかを示す指標として、異常検知においては非常に役立ちます。

　　標準偏差とは何か

標準偏差（σ：シグマ）は、以下の数式で表されます。

$$\sigma =\sqrt{\frac{{\displaystyle \sum _{i=1}^N(X_i–\mu {)}^2}}{N}}$$

• $X_i$ は各データポイント
• $\mu$ は平均値
• $N$ はデータの数

標準偏差が大きいほど、データのばらつきが大きいことを意味します。

逆に、標準偏差が小さければ、データは平均値の周りに集中していることになります。

　　標準偏差を用いた予測範囲の作成

標準偏差を使って、時系列データの「正常範囲」を定義することができます。

一般的には、$平均値\pm 標準偏差$（または$平均値\pm 2標準偏差$、$平均値\pm 3標準偏差$）といった形で範囲を設定します。

例えば、直近4週間の火曜日13:00の注文数データで考えていきます。

週1火曜日13:00：290件
週2火曜日13:00：310件
週3火曜日13:00：300件
週4火曜日13:00：280件

これらのデータから、平均値と標準偏差を求めると次のようになります。

• 平均値（μ）= 295件
• 標準偏差（σ）≈ 12.9件

これを用いて正常範囲を定義すると、次のようになります。

• $平均値\pm 標準偏差$：282.1件～307.9件
• $平均値\pm 2\times標準偏差$：269.2件～320.8件
• $平均値\pm 3\times標準偏差$：256.3件～333.7件

これにより、今週の火曜日13:00の注文数が250件だった場合、平均値から約3.5標準偏差以上離れていることになり、「異常」と判断できます。

　Z-スコアとは何か

Z-スコア（標準化得点）は、標準偏差を活用した異常検知のための強力なツールです。

各データポイントが平均からどれだけ離れているかを、標準偏差の単位で表現します。

　　Z-スコアの計算方法

Z-スコアは以下の式で計算されます。

• $x$ は検証したいデータポイント
• $\mu$ は平均値
• $\sigma$ は標準偏差

以下、Z-スコアの特徴です。

• Z-スコアが0の場合、そのデータポイントは平均と同じ値
• Z-スコアが正の場合、平均より大きい値
• Z-スコアが負の場合、平均より小さい値
• Z-スコアの絶対値が大きいほど、平均から離れている（つまり、異常である可能性が高い）

　　Z-スコアによる異常検知

統計学的には、正規分布においてZ-スコアの絶対値が以下の場合に対応する確率が知られています。

• $|Z| > 1$：データポイントは全体の約32%に見られる範囲外（それほど珍しくない）
• $|Z| > 2$：データポイントは全体の約4.6%に見られる範囲外（やや珍しい）
• $|Z| > 3$：データポイントは全体の約0.3%に見られる範囲外（非常に珍しい）

異常検知では、一般的に$|Z|>3$を「異常」とみなすことが多いです。

つまり、データポイントが平均から3標準偏差以上離れている場合、それは偶然とは考えにくく、何らかの特殊な要因があると判断します。

　異常検知アプローチ例

実際のビジネスメトリクスに対して予測範囲を作成する方法を見ていきましょう。

例として、あるECサイトの時間帯別注文数を考えます。

　　ステップ1：過去データの収集

まず、過去4～5週間分の「同じ曜日・同じ時間帯」のデータを収集します。

例えば、火曜日の13:00～14:00の注文数を集めるとします。

　　ステップ2：基本統計量の計算

収集したデータから平均値と標準偏差を計算します。

　　ステップ3：予測範囲の設定

計算された平均値と標準偏差を使って、予測範囲を設定します。

• 上限：$平均値 + 2 × 標準偏差$
• 下限：$平均値 - 2 × 標準偏差$

　　ステップ4：実測値と予測範囲の比較

現在の実測値がこの予測範囲内に収まっているかを確認します。

範囲外であれば「異常」としてアラートを発生させます。

　　視覚化の例

実際にこのアプローチを適用した例を視覚化してみましょう。

この図では、緑の線が実際の注文数、灰色の帯が予測範囲（$平均値\pm 2\times標準偏差$）を表しています。

予測範囲から外れた部分（終盤の下落）が「異常」として検出されています。

　人間中心のアラート設計

統計的手法を実装する際は、単に数学的に正確であるだけでなく、「人間が理解しやすく、行動につながるアラート」を設計することが重要です。

　　絶対値と相対値の併用

Z-スコアのような統計値だけでなく、絶対的な変化量と相対的な変化率を併記することで、アラートの意味をより明確にします。

【警告】注文処理数の低下を検知
- 過去10分間：30件（通常の70件から-57%）
- 過去30分間：120件（通常の190件から-37%）
- 影響見積：約1時間で$5,000の売上減少

　　ビジネスインパクトの評価

技術的なメトリクスを、可能な限りビジネスインパクトに変換して伝えることで、優先度の判断がしやすくなります。

【高優先】決済完了率の低下
- 現在の完了率：85%（通常97%）
- 推定影響：1時間あたり約50件の注文ロスト（250,000円相当）

　　コンテキスト情報の提供

アラートに関連する補足情報を含めることで、トラブルシューティングをするときの助けにします。

【警告】ログイン成功率低下
- 現在の成功率：78%（通常98%）
- 影響地域：欧州のみ（他地域は正常）
- 関連システム：認証サービスApiAuth-3に高負荷

Z-スコアアプローチからの改良

　予測範囲（上限・下限）の構築方法

Z-スコアそのものではなく、予測範囲を中心とした異常検知システムにする方法があります。

予測範囲とは、メトリクスが「正常」とみなされる上限と下限の値のことです。

　　なぜ単純な予測値ではなく範囲なのか

ビジネスメトリクスは本質的に変動しやすいため、単一の予測値だけでは不十分です。

例えば、「火曜日13:00の注文数は300件のはず」という予測は、実際には「290～310件の間に収まるはず」という予測範囲の方が現実的です。

特に変動の大きいメトリクスでは、この範囲を適切に設定することが重要です。

　　予測範囲の計算方法

予測範囲を計算する最もシンプルな方法は、例えば次のようなパーセンタイルによる方法です。

1. 過去N週間分の同じ曜日・同じ時間帯のデータを収集する
2. これらのデータからパーセンタイル値を計算する
3. 下限として低いパーセンタイル値（例：5パーセンタイル）を使用
4. 上限として高いパーセンタイル値（例：95パーセンタイル）を使用

具体的な例を見てみましょう。

ある水曜日の15:00～15:20の時間帯について、例えば次のような過去4週間のデータがあったとします。

週1：150件
週2：162件
週3：145件
週4：158件

これらの値から、5パーセンタイルと95パーセンタイルを概算すると……

• 下限（5パーセンタイル）≈ 145件
• 上限（95パーセンタイル）≈ 162件

この範囲を予測範囲として使用し、現在の値がこの範囲から外れた場合に異常としてアラートを発生させます。

　　滑らかな予測範囲の作成

実際のメトリクスでは、各時間帯のデータ量によって自然な変動幅が異なるため、時間帯ごとに適切な予測範囲が変わります。

これを視覚化すると、例えば以下のようなグラフになります。

このグラフでは、青い帯が予測範囲を示し、緑の線が実際のメトリクスです。

時間帯ごとに予測範囲の幅が異なり、夜間や早朝は変動が大きいため幅広く、日中の安定した時間帯は幅が狭くなっています。

　過去の異常値の除外テクニック

予測範囲を計算する際の重要な課題の一つは、過去のデータに異常値が含まれている場合です。

前週に大きな障害があった場合、その値が今週の予測範囲計算に影響してしまいます。

　　問題点：過去の異常が基準になる

例えば、前週の特定時間に大規模なシステム障害があり、注文数が通常の20%にまで落ち込んだとします。

この異常データを含めて予測範囲を計算すると、下限値が不当に低くなってしまい、同様の問題が発生しても検出できなくなる可能性があります。

　　解決策：アウトライア（外れ値）除外法

この問題を解決するには、予測範囲の計算前に「異常な過去データ」を除外する必要があります。

しかし、「何が異常か」を判断するには予測範囲が必要であり、一見すると循環論法のようです。

この課題に対処するため、例えば次のような統計的外れ値除外手法を採用します。

1. 過去N週間の同時刻データを収集する
2. 各データポイントについてZ-スコアを計算する
3. Z-スコアの中央値（メディアン）を特定する
4. 各Z-スコアから中央値を引いて「正規化Z-スコア」を得る
5. 正規化Z-スコアが一定の閾値（例：0.6）を超えるデータを除外する

このアプローチの利点は、データセット内に明らかな異常値がある場合とない場合の両方に対応できることです。

　　ケース1：明らかな異常値がある場合

例えば、過去4週間の同時刻データが以下のようになっていたとします。

週1：200件（異常値）
週2：580件
週3：600件
週4：580件

通常のZ-スコア計算では、週1のデータが明らかに異常（平均から大きく離れている）と判断できます。

正規化Z-スコア法を使うと、週1は除外され、残りのデータだけで予測範囲が計算されます。

　　ケース2：異常値がない場合

一方、全てのデータが正常範囲内の場合です。データが以下のようになっていたとします。

週1：610件
週2：580件
週3：600件
週4：550件

この場合、どのデータポイントもZ-スコアはそれほど極端ではなく、正規化Z-スコア法によっても除外されません。

全てのデータが予測範囲の計算に使用されます。

このアプローチにより、過去の異常データによる予測範囲の歪みを防ぎながら、正常な変動を適切に反映した予測範囲を構築できます。

　「オフセット」メトリクスの活用

予測範囲を用いた異常検知システムを構築する際の課題の一つは、「どのようにアラートを設定するか」という点です。

　　オフセットメトリクスの概念

この問題を解決するために、「オフセット」という新しいメトリクスを導入します。

オフセットは、実際のメトリクスと予測範囲の差を表す値のことです。

• 実際の値が予測範囲内：オフセット = 0
• 実際の値が上限を超過：オフセット = 実際の値 – 上限値
• 実際の値が下限を下回る：オフセット = 実際の値 – 下限値

オフセットメトリクスを視覚化すると、以下のようなグラフになります：

この図では、オフセット値がゼロから離れるほど、「異常」の度合いが大きいことを示しています。

　　オフセット合計を使ったアラート設定

オフセットメトリクスを使えば、アラート設定が非常にシンプルになります。

1. 一定期間（例：10分間）のオフセット値を合計する
2. その合計が閾値（例：-500）を下回った場合にアラートを発生させる

このアプローチには、次のような利点があります。

• シンプルな条件設定（「X分間のオフセット合計がY未満」）
• 異常の持続時間を考慮できる（短時間の変動ではアラートが発生しない）
• 異常の大きさを定量化できる（オフセットの値が大きいほど重大な異常）

さらに、オフセットとともに、次のような人間が理解しやすいアラートメッセージを添えるといいでしょう。

【警告】注文処理数の低下を検知
- 過去10分間：70件（予測範囲：100〜120件）
- オフセット：-30件（-30%）

特殊なケースへの対応

ここまで紹介した手法は基本的なシナリオ（通常状態）では効果的ですが、現実のビジネスメトリクスにはさらに複雑な状況があります。

それらの特殊なケースへの対応方法についてお話しします。

　イベントや休日の補正方法

ビジネスメトリクスは、特別なイベントや休日によって大きく変動することがあります。

例えば、ECサイトでは以下のような状況が考えられます。

• セール期間中は注文数が通常の2～3倍に増加
• ＧＷなどの大型連休中は法人取引が減少
• スポーツイベント中は関連メディアサイトのトラフィックが急増
• 年末年始や祝日は購買パターンが変化

このような「予測可能な異常」に対応しなければ、誤検知が大量に発生してしまいます。

　　「補正」メトリクスの導入

この問題を解決するため、「補正」メトリクスという新しい概念を導入します。

補正メトリクスは、特定の時間帯において予測範囲を一時的に広げる役割を持ちます。

以下は、補正メトリクスの仕組みの概念的説明です。

1. デフォルトでは補正値 = 0（補正なし）
2. 特別なイベントや休日などでは、補正値 > 0（例：10）
3. 補正値は予測範囲の拡大率（%）として解釈される
   • 補正値 = 10 → 予測範囲を10%拡大
   • 補正値 = 50 → 予測範囲を50%拡大

　　補正値の設定方法

以下は、補正値のよくある簡単な設定方法例です。

• スケジュールベース：休日カレンダーや既知のイベントスケジュールに基づいて、特定の日時に自動的に補正値を適用
• 手動設定：監視チームが必要に応じて特定の期間に補正値を設定
• 過去データベース：過去の同様のイベント時のデータを分析し、適切な補正値を自動算出

例えば、毎年のブラックフライデーセールでは、前年の変動率をもとに補正値を設定できます。

前年のブラックフライデー：通常比200%の注文量
→ 今年のブラックフライデーには補正値 = 100 を設定

　　補正値の活用例

補正メトリクスを活用したモニタリング例を見てみましょう。

通常日（補正なし）

• 予測範囲：900～1100注文/時
• 実測値：850注文/時
• オフセット：-50（予測下限を下回る）
• 結果：アラート発生（異常検知）

特別セール日（補正あり）

• 補正値：30（予測範囲を30%拡大）
• 調整後の予測範囲：770～1230注文/時
• 実測値：850注文/時
• オフセット：0（調整後の範囲内）
• 結果：アラートなし（正常と判断）

このように、補正メトリクスを用いることで、特別な日に発生する「通常とは異なるが問題ない」変動をシステムに理解させることができます。

　好調すぎる場合の異常検知方法

通常、ビジネスメトリクスが予測を下回る場合（例：注文数減少）は問題として検出したい一方、予測を上回る場合（例：注文数増加）はむしろ良いニュースと考えられます。

しかし、場合によっては「予想以上に好調」な状況でも異常を検出する必要があります。

　　好調時に異常を検出する難しさ

例えば、以下のようなシナリオを考えてみましょう。

• あるマーケティングキャンペーンが予想以上に成功し、注文数が通常の120%になった
• そのときある障害が発生していて、本来なら150%の注文数があったものの、120%に抑制されている

この場合、メトリクスは予測範囲を上回っているため、単純なオフセットメトリクスでは異常として検出されません。

しかし、実際には潜在的な機会損失が発生しています。

　　「調整係数」アプローチ

この問題に対処するため、「調整係数」という概念を導入します。

調整係数は、好調なメトリクスの中に隠れた異常を検出するためのツールです。

以下、調整係数の実施イメージです。

1. 直近数時間のメトリクスの挙動を分析
2. 現在のトレンドに基づいた単一の調整係数を計算例：過去4時間のメトリクスが平均して予測上限を20%上回っている場合、調整係数 = 1.2
3. 現在のメトリクスに調整係数を適用して「期待される実測値」を計算
4. 実際の値と「期待される実測値」の差を新たなオフセットとして計算

このことをグラフで表現すると、次のようになります。

このグラフでは、緑の線が実際のメトリクス、黄色の点線が調整係数を適用した「期待される実測値」を示しています。

14:00頃に実測値が大きく低下していますが、予測範囲内に収まっているため、通常のオフセットでは検出できません。

しかし、調整係数アプローチを用いると、「期待される実測値」との乖離として異常を検出できます。

　　調整係数を使ったオフセット計算

調整係数を用いたオフセット計算の例を見てみましょう。

直近4時間のメトリクス平均：予測上限の120%
→ 調整係数 = 1.2

現在の予測範囲：900～1100注文/時
調整後の期待値：1100 × 1.2 = 1320注文/時

実測値：1150注文/時
オフセット：1150 - 1320 = -170

このケースでは、実測値1150は予測上限1100を上回っているため、通常のアプローチでは「好調」と判断されます。

しかし、調整係数を適用すると、期待値1320を下回っているため、オフセット-170として異常が検出されます。

　シミュレーションによる検証

異常検知システムの設計と調整は複雑なプロセスです。

特に上述したような特殊ケースへの対応方法が適切かどうかを、実際の障害が発生する前に検証することが重要です。

　　シミュレーションの重要性

実際のシステムに異常検知を導入する前に、シミュレーションを通じて以下を検証することが推奨されます。

1. 予測範囲の計算が適切か
2. 過去の異常値の除外が効果的に機能するか
3. 補正メトリクスが特殊な日に適切に対応するか
4. 調整係数が「好調の中の異常」を検出できるか

シミュレーションを行わずに本番環境に導入すると、誤検知の多発や重要な異常の見逃しにつながる恐れがあります。

　　シミュレーションツールの構築

効果的なシミュレーションのためには、以下の機能を持つツールが有用です。

• 履歴データ表示：過去数週間のメトリクスデータの視覚化
• パラメータ調整：予測範囲の計算方法やアウトライア除外の閾値などを調整できるUI
• 異常のシミュレーション：人工的な異常データを挿入し、検出能力をテスト
• 結果分析：検出率や誤検知率など、異常検知の性能指標の表示

　　シミュレーションによるフィードバック改善ループ

色々なシミュレーションを実施し、その結果をフィードバックし、異常検知システムの改善に役立てましょう。

以下は、よくある典型的なフィードバック改善ループです。

1. 初期設定のパラメータでシミュレーションを実行
2. 検出漏れや誤検知を分析
3. パラメータを調整（例：予測範囲の計算方法変更）
4. 再度シミュレーションを実行して結果を評価
5. 満足のいく結果が得られるまで繰り返し

このループにより、本番環境への導入前に最適なパラメータセットを見つけることができます。

異常を検知した後のアプローチ

ここまでは、時系列データの異常を検知するための手法についてお話ししてきました。

しかし、異常を検知した後の対応はさらに大きな課題です。

実際のビジネス現場では、アラートが発生しただけでは十分ではなく、その異常の原因を特定し、適切な対応をとることが重要になります。

　異常の原因特定の難しさ

異常検知システムが「異常」を検出したとしても、これはあくまで「何かがいつもと違う」ということを示すだけであり、その原因までは教えてくれません。

特に、次からお話しするような場合は、原因特定が非常に困難です。

　　明確なエラーが存在しない

例えば、ウェブサイトの注文数が過去数時間にわたって予測範囲を10%下回っているとしましょう。

しかし、システムには特にエラーログが出ておらず、サーバー負荷も正常範囲内です。

このような「静かな」異常の原因を特定するには、多角的な視点からの分析が必要となります。

なぜならば、原因となり得る要素はさまざまだからです。

• マーケティングキャンペーンの終了（予定通り、または予定外）
• 競合他社の新たなプロモーション開始
• 検索エンジンやソーシャルメディアからの流入減少
• 季節性の変動（予測モデルでは捉えきれなかった要素）
• ユーザーインターフェースの微細な変更による影響
• 支払いプロセスの変更による影響

　　複合的な要因

多くの場合、異常の原因は単一ではなく、複数の小さな影響が組み合わさった結果として現れます。

例えば……

• 支払い処理の平均応答時間が5%増加
• 特定のブラウザでのバグが一部ユーザーに影響
• プロモーションページへのリンクが正しく機能していない

これらが個別では大きな影響を与えないものの、組み合わさることで全体として10%の注文減少につながるというケースがあります。

　メトリクスの細分化による原因特定

原因を効率的に特定するためには、主要メトリクスを細分化し、より詳細なレベルでモニタリングすることが有効です。

「分割して統治せよ」という原則を適用し、問題領域を徐々に絞り込んでいきます。

　　地域別の分析

グローバルビジネスでは、地域別の分析が非常に重要です。

例えば、全体の注文数が10%減少している場合、地域別に見ると……

• 北米：-2%（ほぼ正常範囲内）
• 欧州：-25%（明らかな異常）
• アジア太平洋：+5%（むしろ好調）

このように分析することで、「欧州地域に特化した問題が発生している」という洞察を得ることができます。

さらに欧州を国別に分析すると、より具体的な問題領域が見えてくるでしょう。

　　デバイス別の分析

ユーザーの利用デバイス別に分析することも、多くの場合で有益です。

• デスクトップ：-3%（ほぼ正常）
• モバイルiOS：-18%（異常）
• モバイルAndroid：-5%（やや低下）
• タブレット：+2%（正常）

この場合、特にiOSデバイスでの問題が浮かび上がります。

ここからさらに、iOS版アプリのバージョン別や、iOS本体のバージョン別に分析を進めることで、より具体的な問題点が見えてきます。

　　マーケティングチャネル別の分析

ユーザー獲得チャネル別の分析も重要です。

• 直接流入：-5%（やや低下）
• 検索エンジン：-30%（大幅減少）
• ソーシャルメディア：+10%（好調）
• 提携サイト：-2%（正常範囲）

この例では、検索エンジンからの流入が大きく減少していることが分かります。

SEOの問題、検索広告の停止、競合の検索順位上昇など、検索エンジン関連の問題にフォーカスして調査を進めることができます。

　段階的なトラブルシューティングアプローチ

異常を検知した後の効果的なアプローチとして、次のような段階的なトラブルシューティング方法が考えられます。

　　ステップ1：全体像の把握

まず、異常の基本的な特徴を把握します。

• 影響の大きさ（通常比でどの程度減少しているか）
• 影響の範囲（広範囲か、局所的か）
• 影響の持続時間（一過性か、継続的か）
• 発生タイミング（特定のイベントや変更と一致するか）

　　ステップ2：メトリクスの細分化

次に、前述のように主要メトリクスを以下の観点から細分化して分析します。

• 地域・国別
• デバイス別（デスクトップ、モバイルOS別、ブラウザ別）
• ユーザーセグメント別（新規・リピーター、会員ランク別など）
• 流入経路別（直接、検索、ソーシャル、広告など）
• 製品カテゴリ別（該当する場合）

　　ステップ3：相関メトリクスの確認

主要メトリクスだけでなく、関連する他のメトリクスも確認します。

• コンバージョンファネル上の前後のステップ（例：カート追加率、決済完了率）
• システムパフォーマンス指標（応答時間、エラー率など）
• ユーザー行動指標（平均セッション時間、離脱率など）

　　ステップ4：変更履歴の確認

システムやビジネス上の変更と異常発生のタイミングを照合します。

• コードデプロイ履歴
• 構成変更履歴
• マーケティングキャンペーンのスケジュール
• 外部依存サービスの状態変化（決済プロバイダなど）

　　ステップ5：外部要因の検討

自社の制御下にない外部要因も検討します。

• 競合他社の動向（新製品、プロモーションなど）
• 業界全体のトレンド
• 季節要因や休日、特別イベント
• 技術的な問題（インターネット障害、CDN問題など）

　ケーススタディ：異常検知から原因特定までの流れ

ECサイトでの事例を紹介します。

　　状況

あるECサイトで、金曜日の午後2時頃から注文数が予測範囲を25%下回るアラートが発生しました。

異常検知システムは、過去4週間の同時間帯と比較して有意な減少があると判断しています。

　　ステップ1：細分化分析

異常が検出された後、まず地域別、デバイス別、マーケティングチャネル別に注文数を分析しました。

地域別分析

• すべての地域で同様の減少（地域特有の問題ではない）

デバイス別分析

• デスクトップ：-5%（やや低下）
• モバイル：-40%（大幅減少）
• タブレット：-10%（やや低下）

マーケティングチャネル別

• 全チャネルで同等の減少傾向（特定チャネルの問題ではない）

　　ステップ2：関連メトリクスの確認

コンバージョンファネルの各ステップを分析したところ……

• サイト訪問数：通常レベル
• 商品ページ閲覧数：通常レベル
• カート追加数：通常の95%
• 決済開始数：通常の60%
• 決済完了数：開始した決済の98%（正常）

この分析から、問題は「決済開始」のステップにあることが判明しました。

　　ステップ3：システム指標の確認

関連するシステム指標を確認しました。

• サーバー応答時間：正常
• APIエラー率：決済関連APIで5%増加（通常は0.5%未満）
• ページロード時間：正常

　　ステップ4：変更履歴の確認

当日の変更履歴を確認しました。

• 午前11時に決済プロバイダとの連携APIに関するマイナーアップデートをデプロイ
• 新しいモバイル決済オプションを追加

　　ステップ5：原因特定と対応

上記の分析結果から、問題はモバイルデバイスでの決済プロセスにあることが特定されました。

具体的には、新しく追加されたモバイル決済オプションに関するコードの問題が、モバイルユーザーの決済開始を妨げていました。

この問題の特定により、開発チームは迅速に修正をデプロイし、モバイルでの注文数は1時間以内に通常レベルに回復しました。

　効果的なトラブルシューティングのためのポイント

異常検知はあくまでも「何かがおかしい」という警告を提供するものであり、実際の業務では原因の特定と対応がさらに重要です。

以下、効果的なトラブルシューティングのためのポイントです。

• メトリクスを細分化する：地域、デバイス、チャネルなど様々な視点から分析
• 関連指標を確認する：コンバージョンファネル全体やシステム指標も確認
• 変更との相関を探る：システム変更や外部要因との時間的相関を分析
• 段階的に問題を絞り込む：広い視点から始め、徐々に具体的な問題領域を特定

異常検知システムとこれらのトラブルシューティング手法を組み合わせることで、ビジネスにおける問題をより早く、より効率的に解決できるようになります。

今回のまとめ

時系列データにおける異常検知は、ビジネスメトリクスの健全性を監視する上で不可欠なプロセスです。

今回は、複雑な機械学習モデルを使わなくても、基本的な統計手法を活用して効果的な異常検知システムを構築できることを説明しました。

単純な前週比較ではなく、標準偏差やZ-スコア、パーセンタイルを用いた予測範囲の作成により、時間帯や曜日による自然な変動を考慮した監視が可能になります。

また、過去の異常値を除外する外れ値検出や、特別なイベントのための補正メトリクス、好調時の隠れた異常を検出するための調整係数など、簡単な実用的なテクニックを紹介しました。

しかし、異常を検知することはあくまで始まりにすぎません。

本当に重要なのは、メトリクスを細分化し、原因を特定して適切に対応することです。

統計的手法による異常検知と体系的なトラブルシューティングアプローチを組み合わせることで、ビジネスにおける問題をより早く、より効率的に解決することが可能になります。