時系列データならRのTSstudioパッケージでサクッと分析

18430
時系列データならRのTSstudioパッケージでサクッと分析

ビジネス系データサイエンスの多くは、時系列データです。

RのTSstudioパッケージを使うと、サクッと時系列解析できます。「TSstudio」の「TS」はTime Series（時系列）の略です。

RのTSstudioパッケージには、時系列データを分析する上で嬉しい機能がてんこ盛りです。

今回は、「時系列データならRのTSstudioパッケージでサクッと分析」というお話しをします。

TSstudioとは？

RのTSstudioには、ざっくりした次のような機能があります。

  • 時系列データの可視化
  • 時系列データの分析
  • 時系列の予測モデル構築

例えば、現在（2021年3月5日現在）は次のような時系列モデルを作ることができます。

  • ARIMAモデル（auto.arima含む）
  • ETS（Error-Trend-Seasonality, Exponential smoothing state space model）
  • Holt-Winters method
  • Neural network autoregression
  • Time series linear model

パッケージのインストール

何はともあれ、TSstudioのインストールです。

以下、コードです。

install.packages("TSstudio", dependencies = TRUE)

 

今回は、「MLmetrics」（精度評価用のライブラリー）と「forecast」（時系列解析のライブラリー）も利用するので、インストールされていない方は、インストールしておいてください。

ライブラリーの読み込み

TSstudioパッケージを使うためには、そのライブラリーを読み込む必要があります。

以下、コードです。

library(TSstudio)
library(MLmetrics)
library(forecast)

 

サンプルデータ

TSstudioの中にあるサンプルデータの1つである「USVSales」を使います。

このデータセットは、1976～2019年の米国の月別総販売台数（単位：千台）です。

以下、コードです。

data(USVSales)

 

どのようなデータなのか、グラフ化し見てみます。

以下、コードです。

# 時系列推移
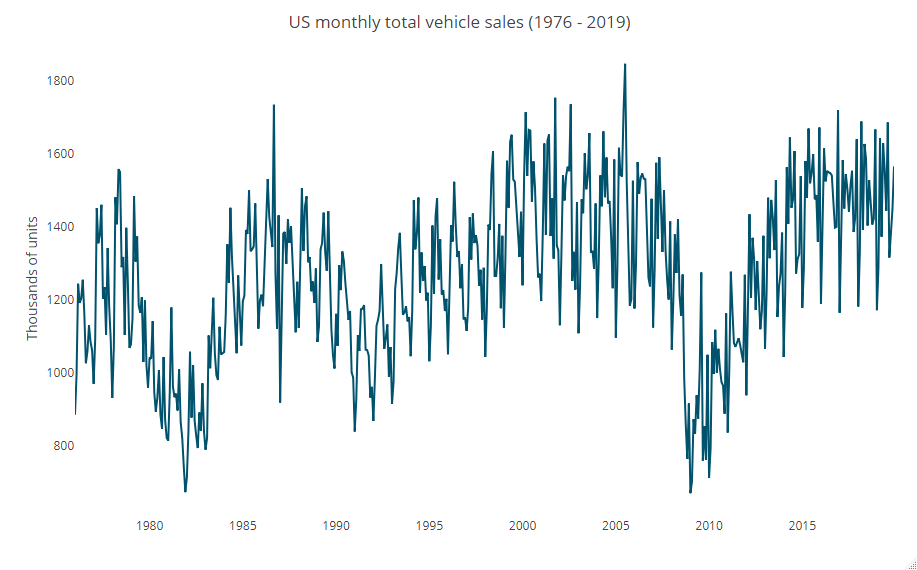
ts_plot(USVSales, 
        title = "US monthly total vehicle sales (1976 - 2019)",
        Ytitle = "Thousands of units")

 

以下、実行結果です。

 

単なる折れ線グラフです。次に、時系列ならではのグラフでデータを見ていきます。

 

時系列ならではのグラフ

トレンドと季節性などに分解してみます。

以下、コードです。

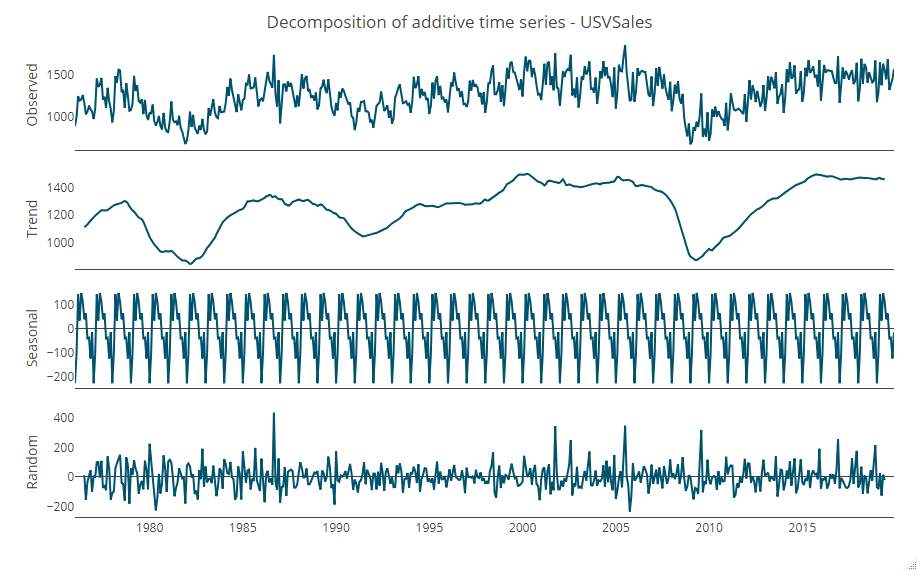
# トレンド・季節性の分解
ts_decompose(USVSales)

 

以下、実行結果です。

Observed(実測値) = Trend(トレンド) + Seasonal(季節性) + Random(残差)

 

次に、月別や年別、ヒートマップなどを作り、トレンドや季節性を視覚的に捉えていきます。

以下、コードです。

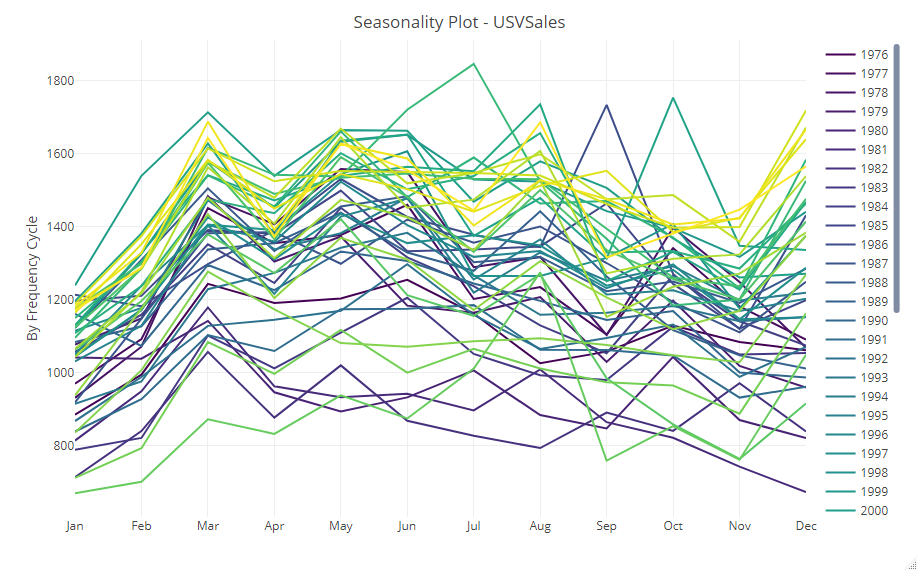
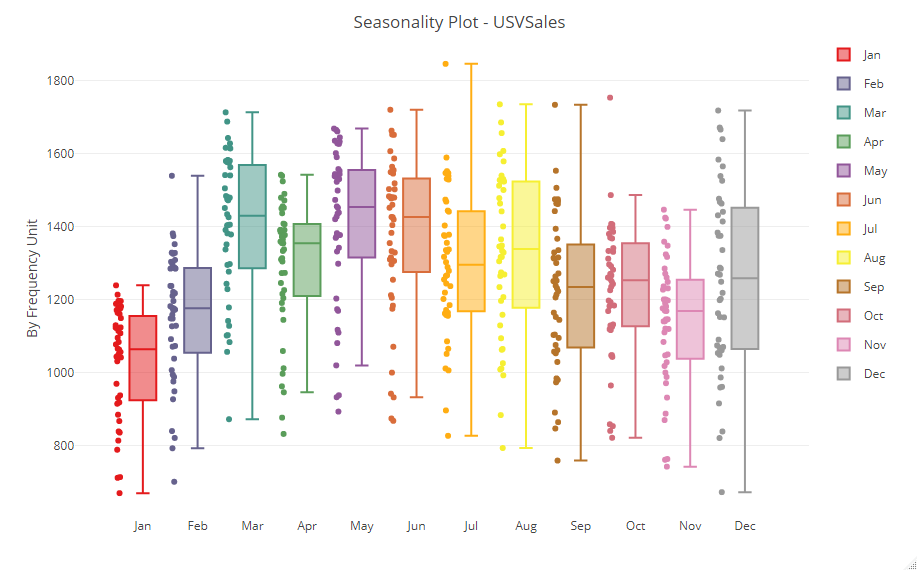
# 季節性やトレンドなどの視覚化
ts_seasonal(USVSales, type = "normal")
ts_seasonal(USVSales, type = "box")
ts_seasonal(USVSales, type = "cycle")
ts_heatmap(USVSales)

 

以下、実行結果です。

 

ヨコ軸が各月で、折れ線が各年になっています。それを集計値で表現したのが次です。

 

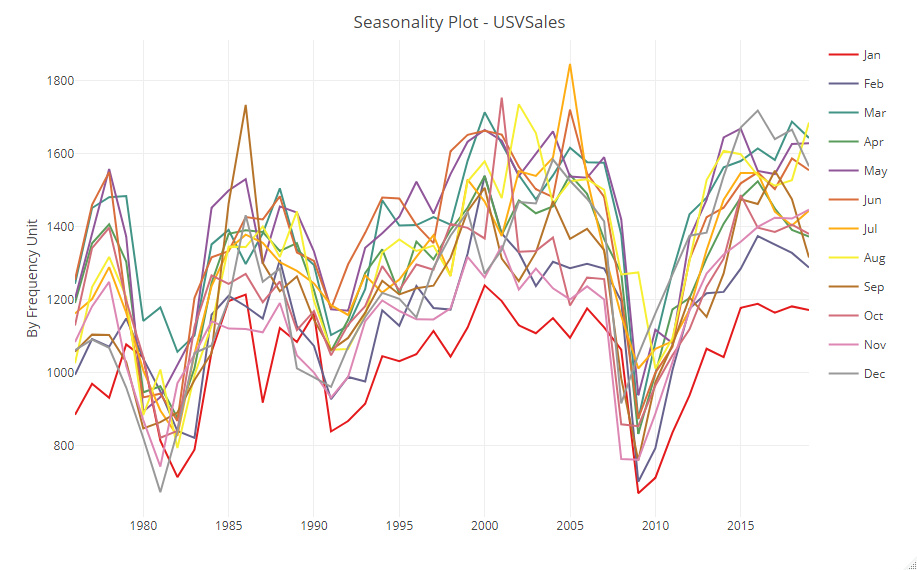
視点を変え、ヨコ軸が各年で、折れ線が各月で表現したのが次です。

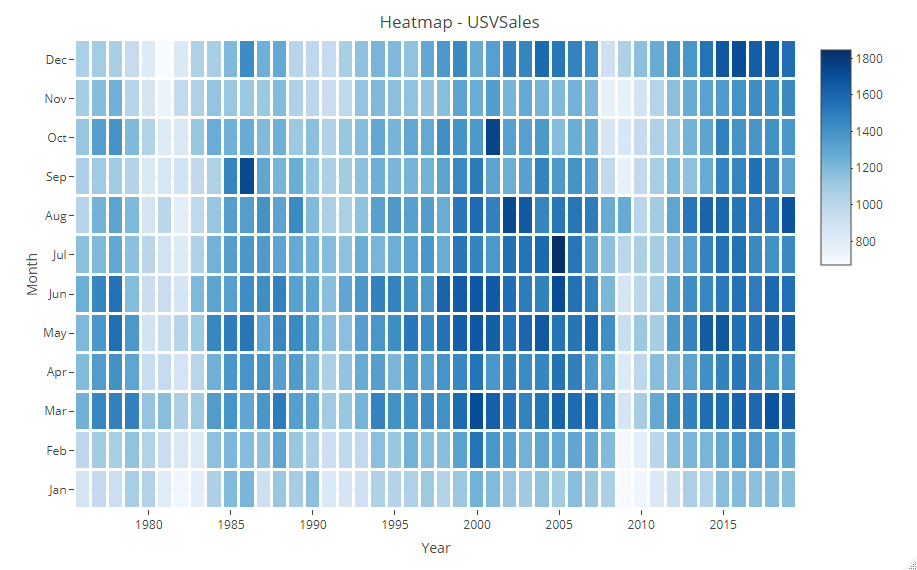
ヒートマップで表現すると、次のようになります。

 

少なくとも、季節性があることは分かります。

 

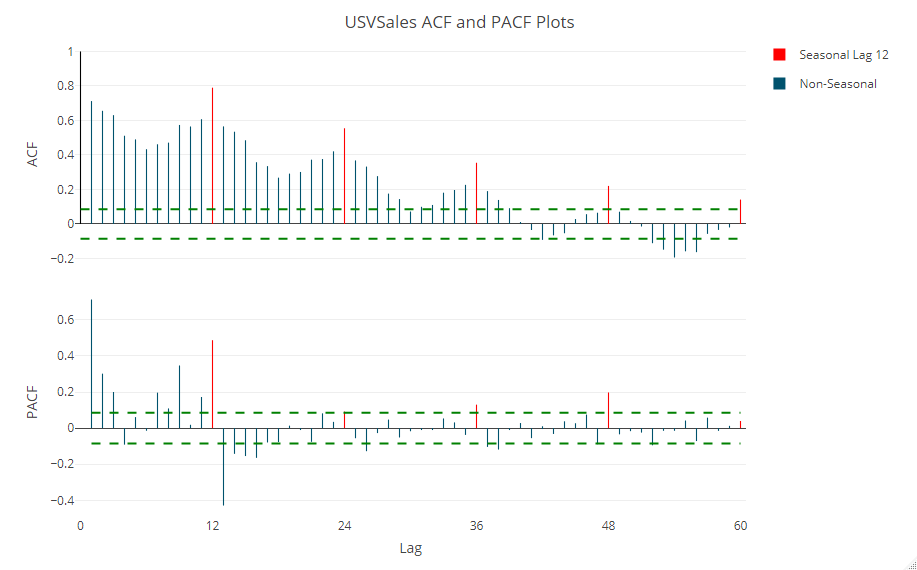
次に、時系列データに対し必ずと言っていいほど出力するであろう、自己相関(ACF)と偏自己相関(PACF)を計算しプロットします。

以下、コードです。

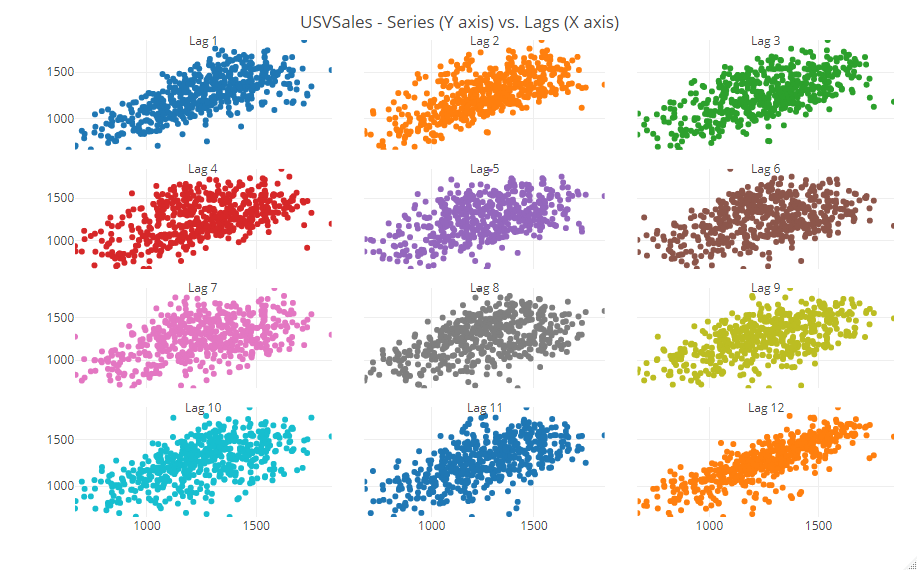
# 自己相関(ACF)と偏自己相関(PACF)
ts_cor(USVSales, lag.max = 60)
ts_lags(USVSales, lags = 1:12)

 

以下、実行結果です。

散布図で表現したのが次です。

 

時系列データでよく見るグラフなどを、このように簡単に出力することができます。

 

時系列のホールドアウト法

時系列データと言えば、時系列予測です。

予測モデルを構築するとき、データセットを学習データとテストデータに分解し、学習データで構築した予測モデルをテストデータで精度検証したりします。

このようなアプローチをホールドアウト法と言います。

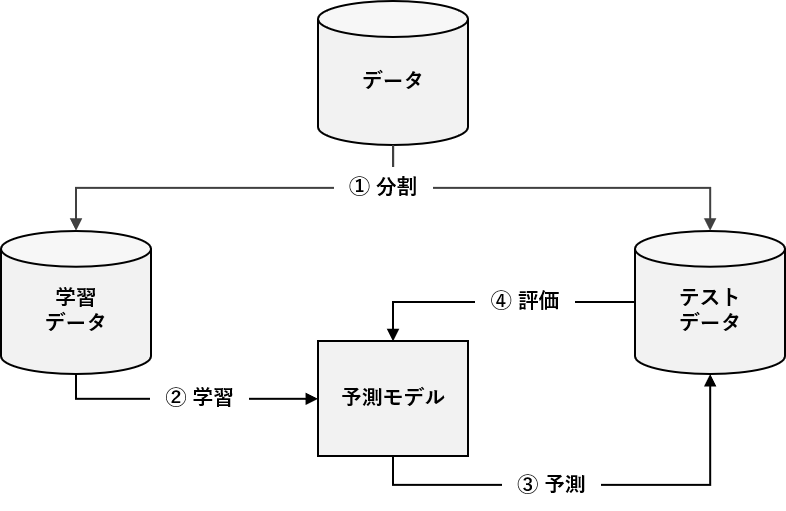
クロスセクショナルデータ（テーブルデータ）の場合、データセットをランダムに学習データとテストデータへ振り分けますが、時系列データの場合そういうわけには行きません。

なぜならば、前後のデータとの関係性（時系列性）をモデル化するためです。そのため、ある時期を境に、学習データとテストデータに分解することが、よく行われます。

ある時期を境に、学習データとテストデータに分解し、予測モデルの精度検証を実施したいと思います。

 

ホールドアウト法で予測モデル構築

先ず、学習データとテストデータに分割します。

以下、コードです。

# 学習データとテストデータに分割
USVSales_s <- ts_split(ts.obj = USVSales,
                       sample.out = 12)

train <- USVSales_s$train #学習データ
test <- USVSales_s$test   #テストデータ（新しい方から12カ月分）
  • train：学習データ（テストデータより前の期間のデータ）
  • test：テストデータ（新しい方から12カ月分）

今回は、ライブラリー「forecast」のARIMAモデルを構築し予測したいと思います。予測期間は、12カ月間です。

以下、コードです。

# ARIMAモデルの構築と予測
md <- auto.arima(train)    #学習データでモデル構築
fc <- forecast(md, h = 12) #12カ月間を予測

 

予測期間（学習期間後の12カ月期間）の予測値をプロットします。

以下、コードです。

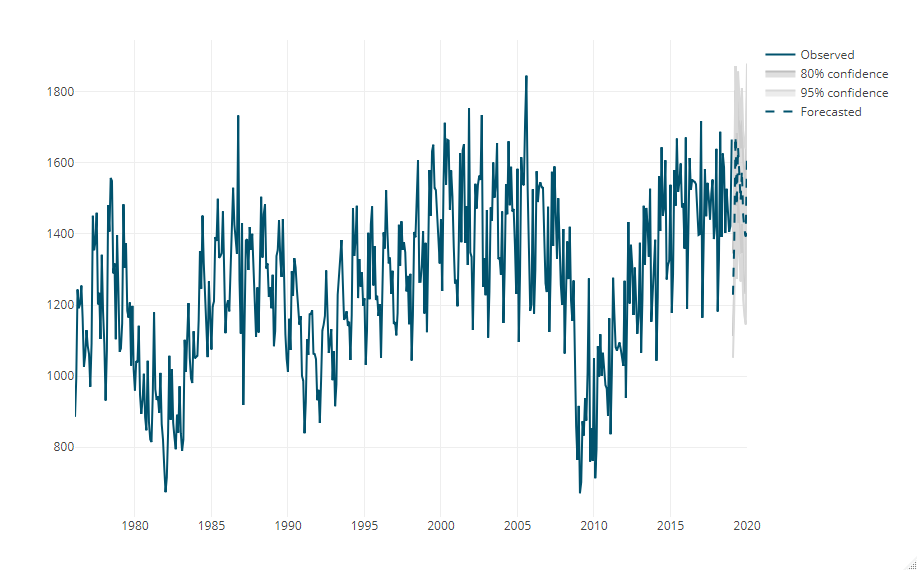
# 予測期間の予測値プロット
plot_forecast(fc)

 

以下、実行結果です。

  • Observed：観測値
  • Forecasted：テストデータ期間の予測値

学習データ期間のデータ（テストデータより前の期間のデータ）の予測状況も併せてプロットします。

以下、コードです。

# 予測値と実測値のプロット
test_forecast(actual = USVSales, 
              forecast.obj = fc, 
              test = test)

 

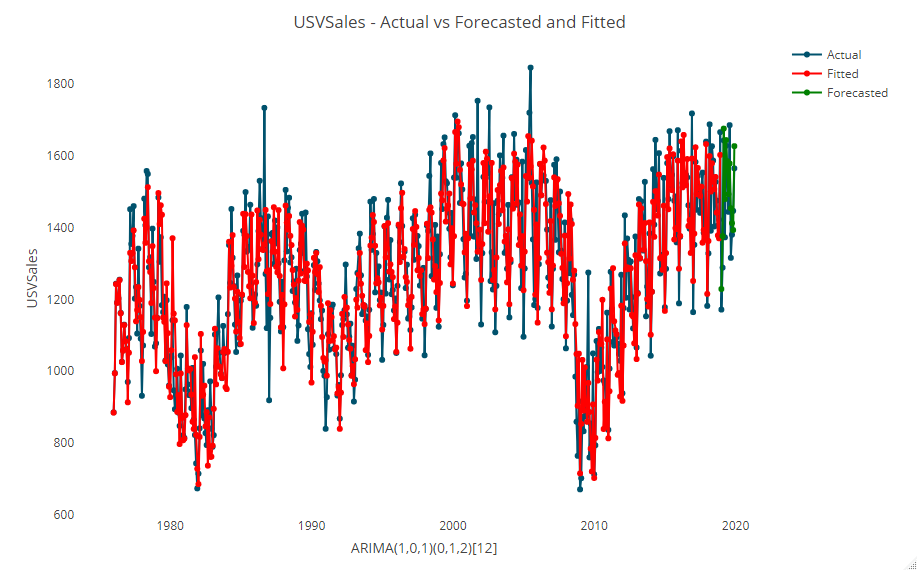
以下、実行結果です。

  • Actual：観測値
  • Fitted：学習データ期間のモデルの予測値
  • Forecasted：テストデータ期間の予測値

テストデータを使い、予測精度を評価したいと思います。

今回は、メインがMAPEで、サブでRMSEとR2も出力します。

以下、コードです。

# 精度評価
MAPE(fc$mean,test)     #MAPE
RMSE(fc$mean,test)     #RMSE
R2_Score(fc$mean,test) #R2

 

以下、実行結果です。

  • MAPE：4.6%
  • RMSE：73.7247
  • R2：77%

 

【参考】精度指標のお話し

以下の記号を使い精度指標の説明をします。

  • y_i^{obs} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • \overline{y^{obs}} ・・・実測値の平均
  • n ・・・実測値・予測値の数

 

指標名 略称 説明
決定係数

coefficient of determination

 R2(R-squared) \frac{\sum_{i=1}^n(y_i^{pred}-\overline{y^{obs}})^2}{\sum_{i=1}^n(y_i^{obs}-\overline{y^{obs}})^2}

目的変数の観測値に対する予測値の説明力を表す指標。1に近いほど良い予測である。
平均平方二乗誤差

Root Mean Squared Error

 RMSE \sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{obs}-{y_i^{pred}})^2}

誤差（実測値と観測値の差）の二乗の平均のルートをとったもの。実測値と観測値の平均はほぼ0になってしまうので、いったん二乗とっている。0に近いほど実測値と予測値の値が近く、良い予測である。
平均絶対誤差

Mean Absolute Error

 MAE \frac{1}{n}\sum_{i=1}^n|y_i^{obs}-{y_i^{pred}}|

誤差（実測値と観測値）の絶対値の平均。誤差をそのまま平均をとるとほぼ0になってしまうので、絶対値をとっている。0に近いほど実測値と予測値の値が近く、良い予測である。
平均二乗誤差

Mean Squared Error

 MSE \frac{1}{n}\sum_{i=1}^n(y_i^{obs}-{y_i^{pred}})^2

誤差（実測値と観測値の差）の二乗の平均。誤差の平均をとるとほぼ0になってしまうため、二乗している。
平均絶対パーセント誤差

Mean Absolute Percentage Error

 MAPE \frac{1}{n}\sum_{i=1}^n|\frac{y_i^{obs}-{y_i^{pred}}}{y_i^{obs}}|

実測値に対して、どれぐらいの誤差が含まれるのかを示す指標。値が0に近いほど実測値と予測値の値が近く、良い予測である。

 

時系列のクロスバリデーション法

ホールドアウト法とは、データセットを学習データとテストデータに分解し、学習データで構築した予測モデルをテストデータで精度検証するアプローチでした。

ホールドアウト法は、1回しか精度検証しません。

この1回が、たまたま悪い結果かもしれませんし、たまたま良い結果かもしれません。このたまたまを払拭するためには、精度検証を複数回実施するのがいいでしょう。

精度検証を複数回実施するアプローチの1つが、クロスバリデーション（CV）法です。

例えば、データセットを10分割し、学習データとテストデータのセットを10組作ります。そうすることで、10回精度検証することができます。多くの場合、精度検証指標の平均値などを計算したりします。

通常のクロスバリデーション法は、例えばデータセットを10分割するとき、データをランダムに割り振り10個のデータセットを作ります。

クロスセクショナルデータ（テーブルデータ）の場合にはそれで問題ないですが、時系列データの場合そういうわけには行きません。前後のデータとの関係性（時系列性）をモデル化するためです。

1つのやり方が、学習データとテストデータの期間をずらし、複数の学習データとテストデータのセットを作る方法です。

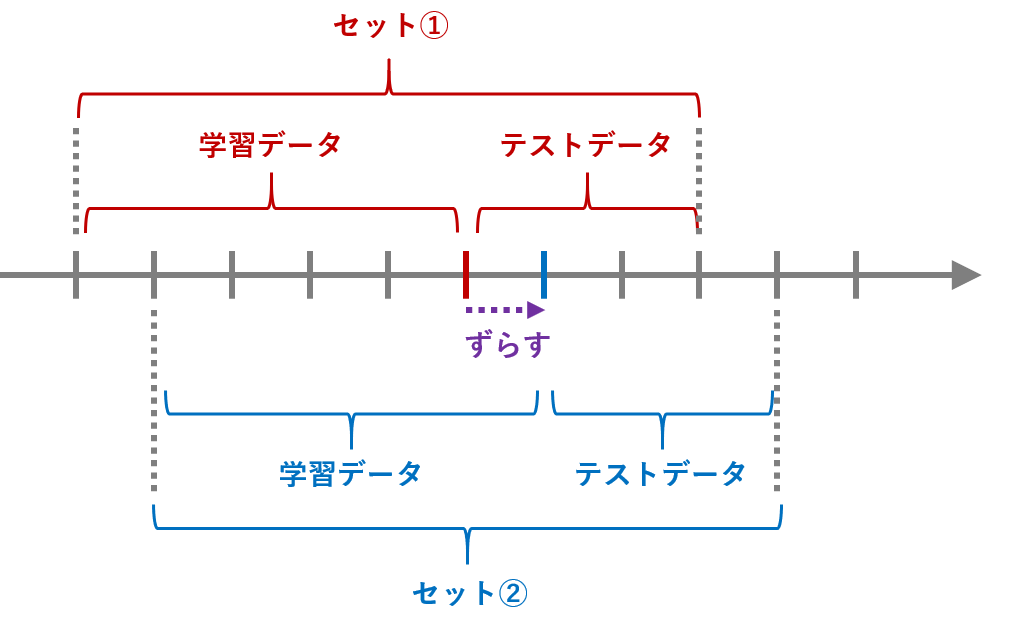
このアプローチの場合、次の4点を定義する必要があります。

  • 学習データとテストデータのセット数（partitions）
  • 各セットの期間のずれ（spase）
  • 学習データの期間（sample in）
  • テストデータの期間（sample out）

学習データとテストデータのセット数（partitions）は、精度検証する回数です。通常のCV法の場合でも設定するものです。例えば、10に設定したら、10セット（組）の学習データとテストデータを使い、精度検証します。

残りの3点は、時系列データ特有のものです。

学習データの期間（sample in）は「学習データ期間の長さ」、テストデータの期間（sample out）は「テストデータ期間の長さ」です。

例えば……

  • 学習データとテストデータのセット数（partitions）：10
  • 学習データの期間（sample in）：60カ月（5年間）
  • テストデータの期間（sample out）12カ月（1年間）

……と設定した場合、学習データ期間の長さが60カ月でテストデータ期間の長さが12カ月の、学習データとテストデータのセットが10組あることになります。

各セットの期間のずれ（spase）は、学習データとテストデータのセットを複数作るときに、学習データとテストデータの境目をどれだけずらすか、というものです。

各セットの期間のずれ（spase）が「1カ月」の場合、1カ月づつずれた学習データとテストデータのセットが作成することになります。各セットの期間のずれ（spase）が「12カ月（1年）」の場合、12カ月（1年）づつずれた学習データとテストデータのセットが作成することになります。

以下、各セットの期間のずれ（spase）が「12カ月（1年）」の場合のイメージです。

No. 学習データ（60カ月） テストデータ（12カ月）
セット1 2007/1/1～2009/12/31 2010/1/1～2010/12/31
セット2 2008/1/1～2010/12/31 2011/1/1～2011/12/31
セット3 2007/1/1～2011/12/31 2012/1/1～2012/12/31
セット4 2008/1/1～2012/12/31 2013/1/1～2013/12/31
セット5 2009/1/1～2013/12/31 2014/1/1～2014/12/31
セット6 2010/1/1～2014/12/31 2015/1/1～2015/12/31
セット7 2011/1/1～2015/12/31 2016/1/1～2016/12/31
セット8 2012/1/1～2016/12/31 2017/1/1～2017/12/31
セット9 2013/1/1～2017/12/31 2018/1/1～2018/12/31
セット10 2014/1/1～2018/12/31 2019/1/1～2019/12/31

 

クロスバリデーション法（単一モデル）で予測モデル構築

先ずは、構築するモデルのアルゴリズムを設定します。今回は、Forecastライブラリーの中にあるARIMAモデルです。

以下、コードです。

# モデルのリスト作成
method <- list(arima = list(method = "auto.arima"))

 

次に、予測モデルの学習と予測を実施します。

以下、コードです。

# 予測モデルの学習と予測
md <- train_model(input = USVSales,                     #データセット
                  methods = method,                     #数理モデル
                  train_method = list(partitions = 30,  #学習データとテストデータのセット数
                                      space = 12,       #各セットの期間のずれ
                                      sample.in = 120,  #学習データの期間
                                      sample.out = 12), #テストデータの期間
                  horizon = 12,                         #予測期間
                  error = "MAPE")                       #ソートする評価指標

 

構築した予測モデルの精度検証します。精度指標はMAPEです。

以下、コードです。

# CVの結果
md$leaderboard   #結果の概要
md$error_summary #各セットの結果（数値）
plot_error(md)   #各セットの結果（グラフ）
plot_model(md)   #グラフ上で視覚的に確認

 

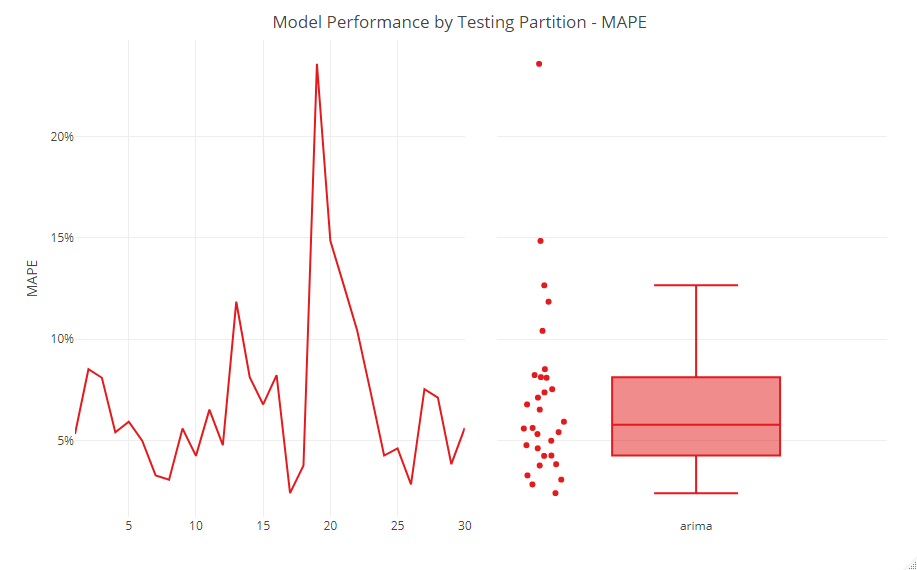
以下、実行結果です。

 

MAPEの平均は7.1%です。ホールドアウト法よりも悪化しています。

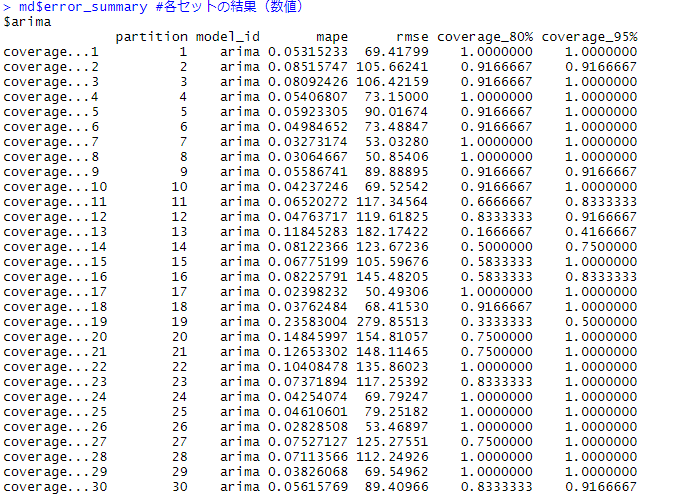
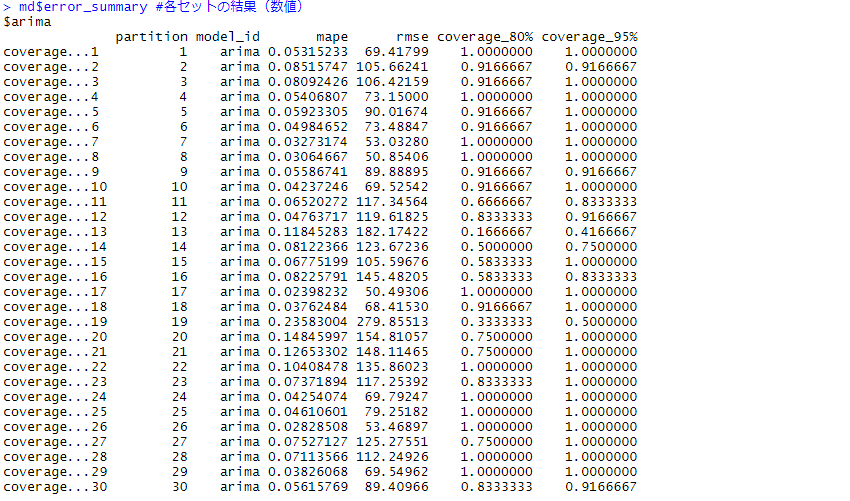
以下は、各セットの結果です。

 

 

幾つか、MAPEの悪いセットがあります。

例えば、No.24のMAPEは23.6%とこの期間の学習データとテストデータの精度は悪いです。

各セットの結果をグラフ化したのが、以下です。

 

No.20のセットのMAPEが、他のセットに比べ大きく悪いことが分かります。

No.20のセットの期間が、特別な時期だったのか、通常の時期ではなく無視しても問題ないのか、などを考慮し検討します。

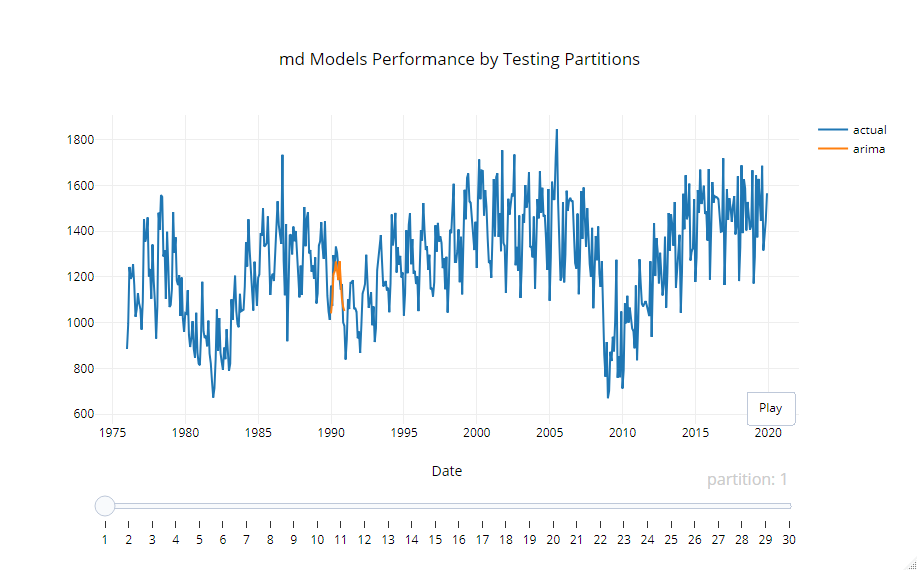
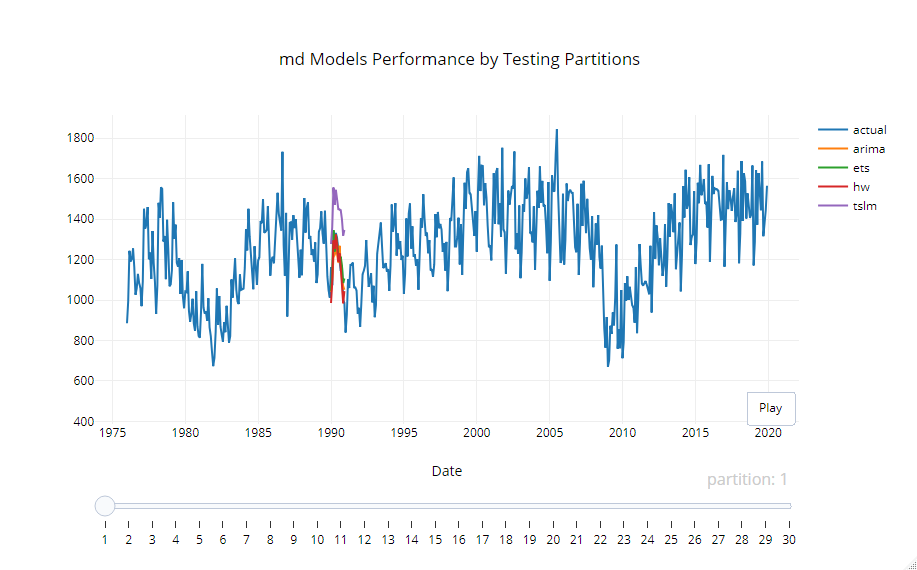
個々のセットがどうだったのかを確認するためのグラフが以下です。

 

クロスバリデーション法（複数モデル）で予測モデル構築

通常、予測モデルを構築するとき、色々なモデルを試し、その中で一番精度の良いものを探ったりします。TSstudioでは、複数のモデルのアルゴリズムを簡単に一緒に検討することができます。

先ず、構築するモデルのアルゴリズムを設定します。

以下、コードです。

# 色々な予測モデルのリスト作成
methods <- list(arima = list(method = "auto.arima",
                             notes = "ARIMA"),
                ets = list(method = "ets",
                           notes = "ETS"),
                hw = list(method = "HoltWinters",
                          notes = "Holt-Winters method"),
                tslm = list(method = "tslm",
                            method_arg = list(formula = input ~ trend + season),
                            notes = "Time series linear model")
                )
  • arima：ARIMAモデル
  • ets：ETSモデル
  • hw：Holt-Winters method
  • tslm：Time series linear model

次に、予測モデルの学習と予測を実施します。

以下、コードです。

# 予測モデルの学習と予測
md <- train_model(input = USVSales,                     #データセット
                  methods = methods,                    #数理モデル
                  train_method = list(partitions = 30,  #セット数
                                      space = 12,       #各セットの期間のずれ
                                      sample.in = 120,  #学習データの期間
                                      sample.out = 12), #テストデータの期間
                  horizon = 12,                         #予測期間
                  error = "MAPE")                       #ソートする評価指標

 

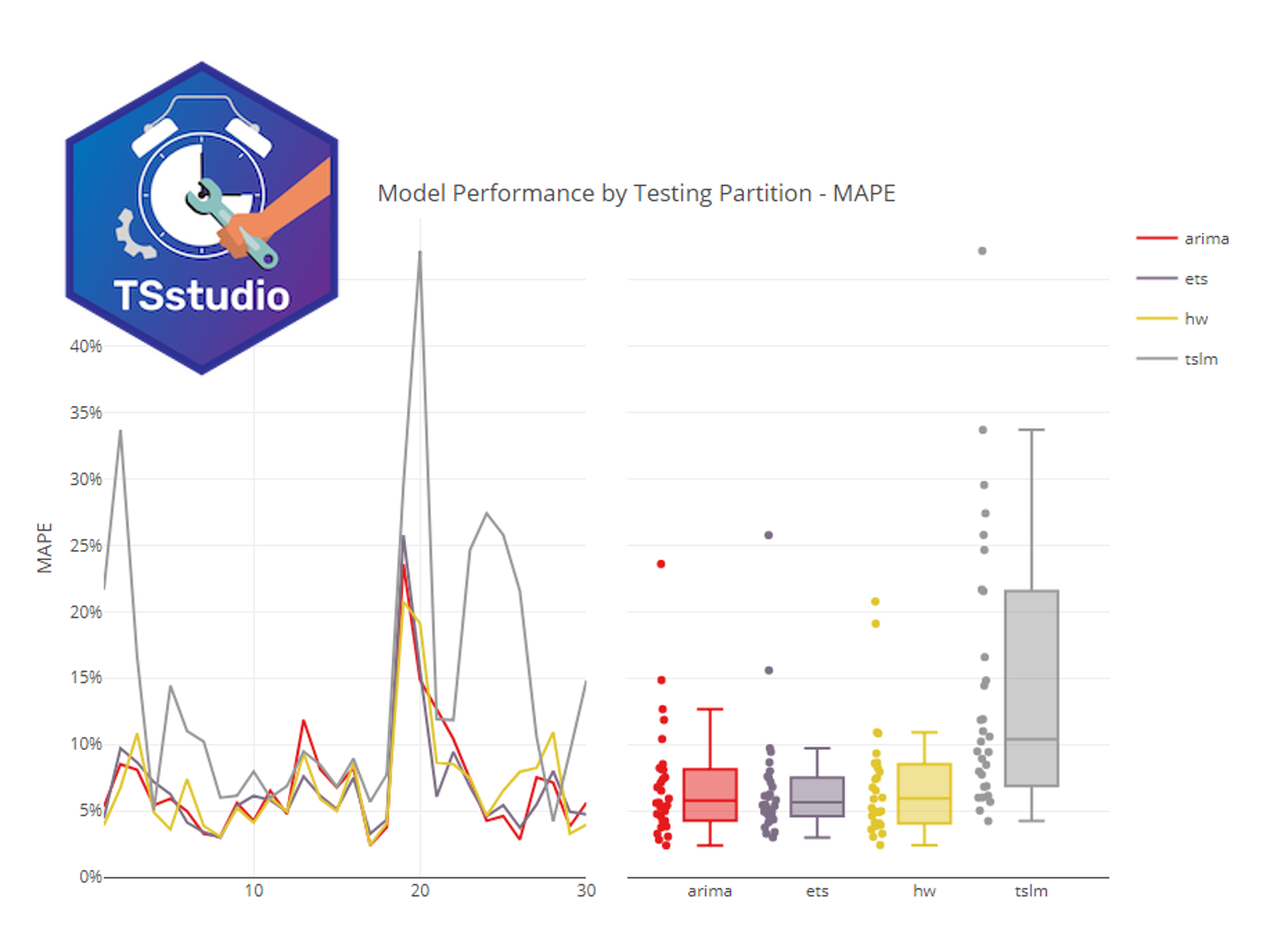
構築した予測モデルの精度検証をします。精度指標はMAPEです。

以下、コードです。

# CVの結果
md$leaderboard   #結果の概要
md$error_summary #各セットの結果（数値）
plot_error(md)   #各セットの結果（グラフ）
plot_model(md)   #グラフ上で視覚的に確認

 

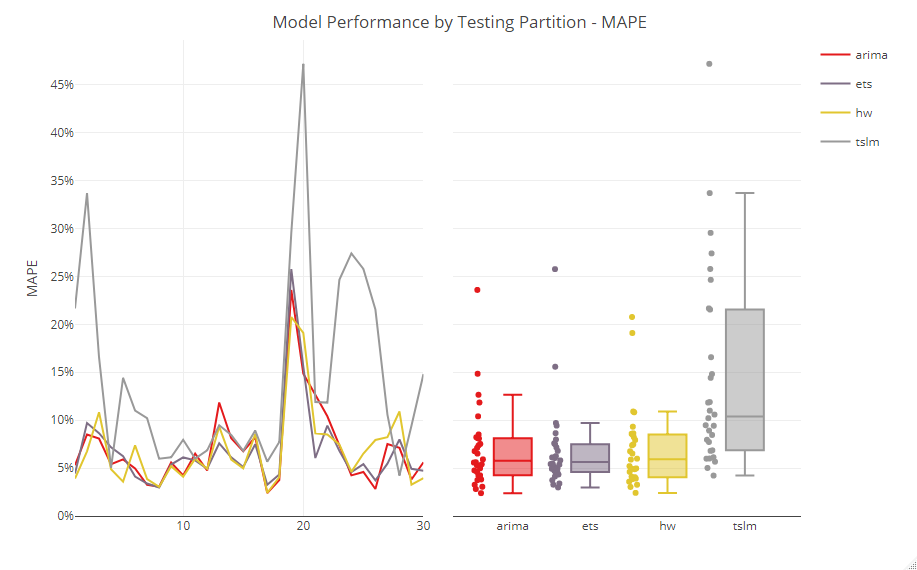
以下、実行結果です。

 

まとめ

今回は、「時系列データならRのTSstudioパッケージでサクッと分析」というお話しをしました。

ビジネス系データサイエンスの多くは、時系列データです。

RのTSstudioパッケージには、時系列データを分析する上で嬉しい機能がてんこ盛りです。

RのTSstudioには、ざっくりした次のような機能があります。

  • 時系列データの可視化
  • 時系列データの分析
  • 時系列の予測モデル構築

時系列データを手にしたら、先ずは試してみてください。