Rにはディープラーニング関連のパッケージは色々あります。R独自のものから、そうでないものもあります。
ディープライニングで有名なKeras(TensorFlow)はRStudio(R)上で使うことができます。
前回は分類問題に対しニューラルネットワーク型のディープラーニングを構築するお話しをしました。
今回は、回帰問題です。Keras(TensorFlow)周りの解説（インストールや諸設定など）は前回の記事を見てください。
Contents
データセット
今回利用するデータセットは、回帰問題でよく登場するみんな大好き「ボストン住宅価格（BostonHousing）」データセットです。似たようなデータセットにカリフォルニアのものがありますが、今回はボストンの方です。
Rのライブラリー「mlbench」にあるサンプルデータです。ライブラリー「mlbench」をインストールし、サンプルデータを利用するときにロードする必要があります。
以下、データ項目です。
- CRIM： 犯罪率
- ZN： 広い家の割合（25,000平方フィートを超える区画に分類される住宅地の割合）
- INDUS： 非小売業の割合
- CHAS： 川と隣接（川に隣接している場合は1、そうでない場合は0）
- NOX： NOx濃度（0.1ppm単位）
- RM： 平均部屋数
- AGE： 古い家の割合（1940年より前に建てられた持ち家の割合）
- DIS： 主要施設への距離（5つあるボストン雇用センターまでの加重距離）
- RAD： 主要高速道路アクセス指数
- TAX： 固定資産税率（10,000ドル当たり）
- PTRATIO： 生徒と先生の比率
- B： 1000×（黒人割合- 0.63）の二乗
- LSTAT： 低所得者人口の割合
- MEDV：住宅価格の中央値（1000ドル単位）
項目数は14。
- 目的変数Y：一番下の「MEDV」（住宅価格）
- 説明変数X（特徴量）：残り13つのデータすべて
要するに、「MEDV」（住宅価格）を他の変数で当てる問題です。
ライブラリーのロード
先ず最初に、必要なライブラリーを読み込みます。
以下、コードです。
# 必要パッケージのロード library(keras) #keras library(tidyverse) #基本ライブラリー library(magrittr) #基本ライブラリー library(mlbench) #サンプルデータ
準備
前処理①：型変換
データセットを整えます。
以下、コードです。
# データセットの読み込み data(BostonHousing) dataset <- BostonHousing str(dataset) #確認用
以下、実行結果です。
データの中に、因子型（factor）が混じっています。数値型へ変換しておく必要があるため、変換します。
以下、コードです。
# 因子型を数値型に変換 dataset %<>% mutate_if(is.factor, as.numeric) str(dataset) #確認用
以下、実行結果です。
さらに、データセットをデータフレームからマトリックに変換します。
以下、コードです。
# Matrix型へ変換 dataset <- as.matrix(dataset) dimnames(dataset) <- NULL
データセットの分割（学習データとテストデータ）
次に、学習データとテストデータに分割します。
モデルは学習データで構築し、その構築したモデルの精度をテストデータで検証します。
以下、コードです。
# 学習データとテストデータに分割 set.seed(123) ind <- sample(2, nrow(dataset), replace = T, prob = c(0.75, 0.25)) ## 学習データ X_train <- dataset[ind==1, 1:13] y_train <- dataset[ind==1, 14] ## テストデータ X_test <- dataset[ind==2, 1:13] y_test <- dataset[ind==2, 14]
- X_train：学習データの説明変数X（特徴量）
- y_train：学習データの目的変数y
- X_test：テストデータの説明変数X（特徴量）
- y_test：テストデータの目的変数y
前処理②：説明変数X（特徴量）の標準化
次に、説明変数X（特徴量）も加工します。標準化です。
以下、コードです。
# 説明変数Xの標準化 m <- apply(X_train, 2, mean) s <- apply(X_train, 2, sd) X_train <- scale(X_train, center = m, scale = s) X_test <- scale(X_test, center = m, scale = s)
これで準備は終了です。
コード全体（ライブラリーの読み込みから前処理まで）
# 必要パッケージのロード library(keras) #keras library(tidyverse) #基本ライブラリー library(magrittr) #基本ライブラリー library(mlbench) #サンプルデータ # データセットの読み込み data(BostonHousing) dataset <- BostonHousing str(dataset) #確認用 # 因子型を数値型に変換 dataset %<>% mutate_if(is.factor, as.numeric) str(dataset) #確認用 # 学習データとテストデータに分割 set.seed(123) ind <- sample(2, nrow(dataset), replace = T, prob = c(0.75, 0.25)) ## 学習データ X_train <- dataset[ind==1, 1:13] y_train <- dataset[ind==1, 14] ## テストデータ X_test <- dataset[ind==2, 1:13] y_test <- dataset[ind==2, 14] # 説明変数Xの標準化 m <- apply(X_train, 2, mean) s <- apply(X_train, 2, sd) X_train <- scale(X_train, center = m, scale = s) X_test <- scale(X_test, center = m, scale = s)
3つの予測モデル
今回は、3つのニューラルネットワーク型のモデルを構築します。
今回は、3つのニューラルネットワーク型のモデルを構築します。
- モデル①：4層型 入力層→隠れ層1→隠れ層2→出力層
- モデル②：5層型 入力層→隠れ層1→隠れ層2→隠れ層3→出力層
- モデル③：Dropout層付き5層型 入力層→隠れ層1→(Dropout層)→隠れ層2→(Dropout層)→隠れ層3→(Dropout層)→出力層
シンプルなもの、やや複雑化したもの、過学習を緩和したものです。
Dropout層とは、過学習を緩和するための工夫で、モデルの学習時に隠れ層から出力される値を設定した割合でゼロにします。適切に設定すると、学習データに対する精度は悪化しますがテストデータに対する精度は良くなります。
モデル①（4層型）
モデル①：学習（学習データ利用）
「入力層→隠れ層1→隠れ層2→出力層」のニューラルネットワーク型のディープラーニングのモデルを構築していきます。
- 入力層のユニット数：13（説明変数Xの数）
- 隠れ層1のユニット数：12
- 隠れ層2のユニット数：7
- 出力層のユニット数：1（目的変数yの数）
各層の活性化関数（activation）は……
- 隠れ層1：selu（Scaled Exponential Linear Unit）
- 隠れ層2：relu（REctified Linear Unit）
以下、コードです。
# モデル構築 ## モデル定義 model <- keras_model_sequential() model %>% layer_dense(units = 12, activation = 'selu', input_shape = c(13)) %>% layer_dense(units = 7, activation = 'relu') %>% layer_dense(units = 1) summary(model) #確認用
以下、実行結果です。
定義通りになっているのか確認しておきましょう。
- 入力層→隠れ層1のパラメータ：(13+1)×12=168
- 隠れ層1→出力層2のパラメータ：(12+1)×7=91
- 隠れ層2→出力層のパラメータ：(7+1)×1=8
次に、コンパイルし学習します。
以下、コードです。
## コンパイル
model %>% compile(loss = 'mse',
optimizer = 'rmsprop',
metrics = 'mae')
## 学習
history <-
model %>% fit(X_train,y_train,
epochs = 100,
batch_size = 10,
validation_split = 0.25)
history
以下、実行中の画像です。
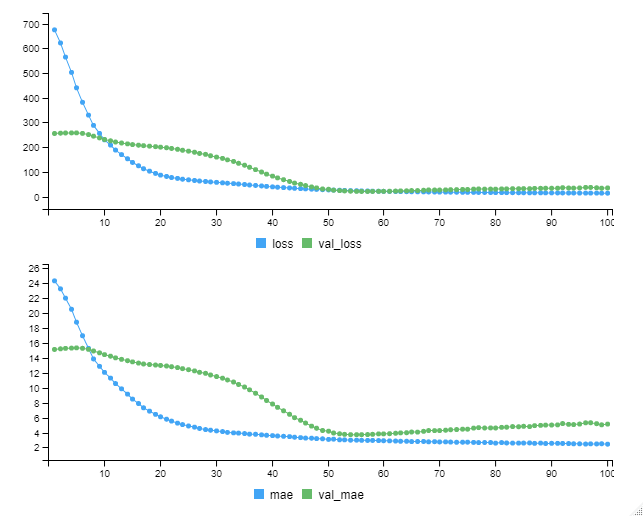
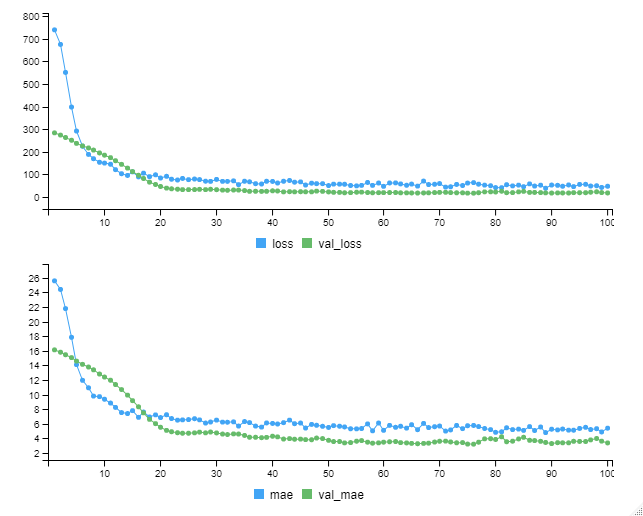
以下、実行結果です。
今回学習したモデルの学習データセットのMAEは……
- train dataのMAE（mae）：2.446
- validation dataのMAE（val_mae）：5.132
validation dataやエポック（epoch）、バッチ（batch）など関しては、前回の記事を参考にしてください。
ちなみに、MAE（Mean Absolute Error）ですが、誤差（実測値と観測値）の絶対値の平均になります。0に近いほど実測値と予測値の値が近く、良い予測であると言えます。
\frac{1}{n}\sum_{i=1}^n|y_i^{obs}-{y_i^{pred}}|- y_i^{obs} ・・・i番目の実測値
- y_i^{pred} ・・・i番目の予測値
- \overline{y^{obs}} ・・・実測値の平均
- n ・・・実測値・予測値の数
モデル①：検証（テストデータ利用）
モデルが構築できたので、テストデータを使い予測し検証していきたいと思います。
先ず、テストデータの説明変数X（特徴量）を使い、目的変数yを予測します。
以下、コードです。
# 予測（検証） ## テストデータの予測 pred_y_test <- model %>% predict(X_test)
どのくらいの精度で当てられたのか、散布図（ヨコ軸：実測値、タテ軸：予測値）を使い見ていきます。回帰線とR2（決定係数）を合わせて表示しています。
以下、コードです。
## 散布図（ヨコ軸：実測値、タテ軸：予測値）
plot(y_test, pred_y_test)
lm.obj<-lm(pred_y_test~y_test)
abline(lm.obj,col=2)
mtext(substitute(paste(R^2,"=",x),
list(x=round(summary(lm.obj)$r.squared,digits=5))),
line=-1,col=2,adj=0)
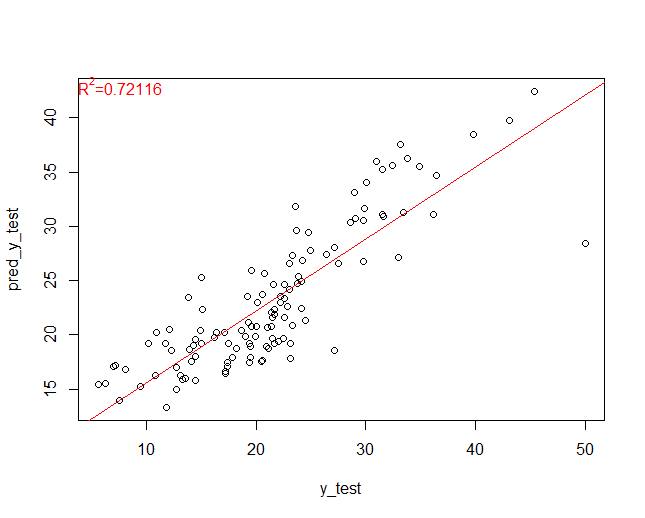
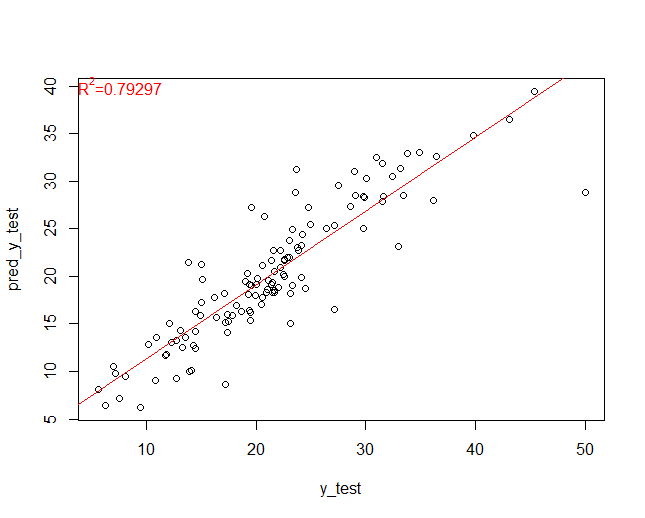
以下、実行結果です。
いい感じで予測できていることが分かります。
では、どのくらい正解したのか、MAEを計算してみます。
以下、コードです。
## 精度 model %>% evaluate(X_test, y_test)
以下、実行結果です。
MAEは3.41でした。
モデル①：コード全体（モデル構築から検証まで）
#
# モデル1
#
# モデル構築
## モデル定義
model <- keras_model_sequential()
model %>%
layer_dense(units = 12, activation = 'selu', input_shape = c(13)) %>%
layer_dense(units = 7, activation = 'relu') %>%
layer_dense(units = 1)
summary(model) #確認用
## コンパイル
model %>% compile(loss = 'mse',
optimizer = 'rmsprop',
metrics = 'mae')
## 学習
history <-
model %>% fit(X_train,y_train,
epochs = 100,
batch_size = 10,
validation_split = 0.25)
history
# 予測（検証）
## テストデータの予測
pred_y_test <-
model %>% predict(X_test)
## 散布図（ヨコ軸：実測値、タテ軸：予測値）
plot(y_test, pred_y_test)
lm.obj<-lm(pred_y_test~y_test)
abline(lm.obj,col=2)
mtext(substitute(paste(R^2,"=",x),
list(x=round(summary(lm.obj)$r.squared,digits=5))),
line=-1,col=2,adj=0)
## 精度
model %>% evaluate(X_test, y_test)
モデル②（5層型）
モデル②：学習（学習データ利用）
「入力層→隠れ層1→隠れ層2→隠れ層3→出力層」のニューラルネットワーク型のディープラーニングのモデルを構築していきます。
- 入力層のユニット数：13（説明変数Xの数）
- 隠れ層1のユニット数：50
- 隠れ層2のユニット数：25
- 隠れ層2のユニット数：10
- 出力層のユニット数：1（目的変数yの数）
各層の活性化関数（activation）は……
- 隠れ層1：selu（Scaled Exponential Linear Unit）
- 隠れ層2：relu（REctified Linear Unit）
- 隠れ層3：relu（REctified Linear Unit）
以下、コードです。
# モデル構築 ## モデル定義 model <- keras_model_sequential() model %>% layer_dense(units = 50, activation = 'selu', input_shape = c(13)) %>% layer_dense(units = 25, activation = 'relu') %>% layer_dense(units = 10, activation = 'relu') %>% layer_dense(units = 1) summary(model) #確認用
定義通りになっているのか確認しておきましょう。
- 入力層→隠れ層1のパラメータ：(13+1)×50=700
- 隠れ層1→出力層2のパラメータ：(50+1)×25=1275
- 隠れ層2→出力層のパラメータ：(25+1)×10=260
- 隠れ層3→出力層のパラメータ：(10+1)×1=11
次に、コンパイルし学習します。
以下、コードです。
## コンパイル
model %>% compile(loss = 'mse',
optimizer = 'rmsprop',
metrics = 'mae')
## 学習
history <-
model %>% fit(X_train,y_train,
epochs = 100,
batch_size = 10,
validation_split = 0.25)
history
以下、実行中の画像です。
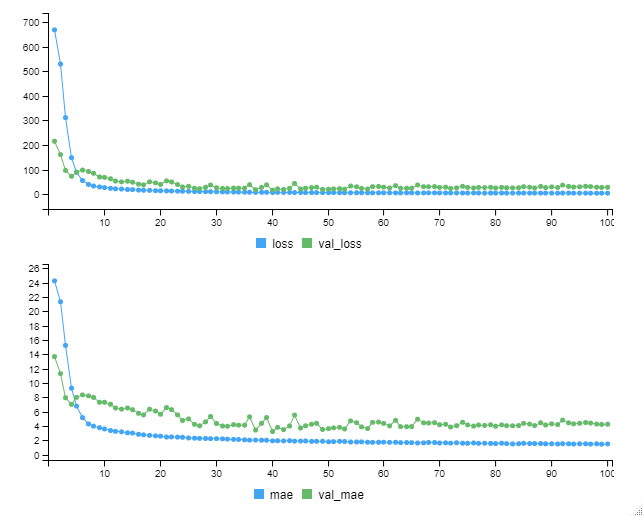
以下、実行結果です。
今回学習したモデルの学習データセットのMAEは……
- train dataのMAE（mae）：1.494
- validation dataのMAE（val_mae）：4.24
モデル②：検証（テストデータ利用）
モデルが構築できたので、テストデータを使い予測し検証していきたいと思います。
先ず、テストデータの説明変数X（特徴量）を使い、目的変数yを予測します。
以下、コードです。
# 予測（検証） ## テストデータの予測 pred_y_test <- model %>% predict(X_test)
どのくらいの精度で当てられたのか、散布図（ヨコ軸：実測値、タテ軸：予測値）を使い見ていきます。回帰線とR2（決定係数）を合わせて表示しています。
以下、コードです。
## 散布図（ヨコ軸：実測値、タテ軸：予測値）
plot(y_test, pred_y_test)
lm.obj<-lm(pred_y_test~y_test)
abline(lm.obj,col=2)
mtext(substitute(paste(R^2,"=",x),
list(x=round(summary(lm.obj)$r.squared,digits=5))),
line=-1,col=2,adj=0)
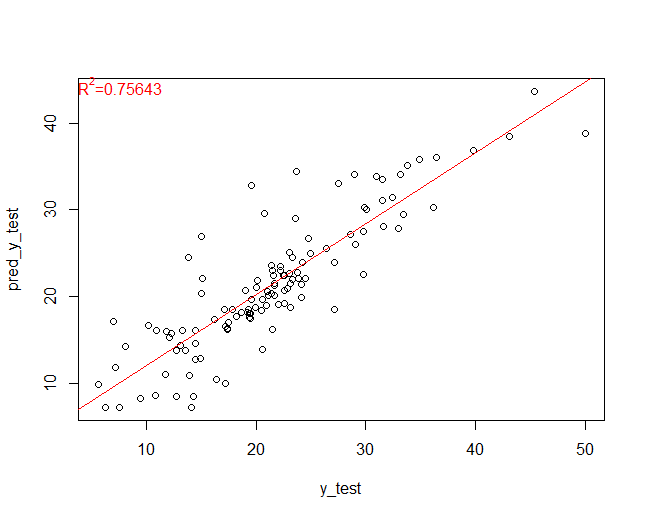
以下、実行結果です。
いい感じで予測できていることが分かります。
では、どのくらい正解したのか、MAEを計算してみます。
以下、コードです。
## 精度 model %>% evaluate(X_test, y_test)
以下、実行結果です。
MAEは2.88でした。
モデル②：コード全体（モデル構築から検証まで）
#
# モデル2
#
# モデル構築
## モデル定義
model <- keras_model_sequential()
model %>%
layer_dense(units = 50, activation = 'selu', input_shape = c(13)) %>%
layer_dense(units = 25, activation = 'relu') %>%
layer_dense(units = 10, activation = 'relu') %>%
layer_dense(units = 1)
summary(model) #確認用
## コンパイル
model %>% compile(loss = 'mse',
optimizer = 'rmsprop',
metrics = 'mae')
## 学習
history <-
model %>% fit(X_train,y_train,
epochs = 100,
batch_size = 10,
validation_split = 0.25)
history
# 予測（検証）
## テストデータの予測
pred_y_test <-
model %>% predict(X_test)
## 散布図（ヨコ軸：実測値、タテ軸：予測値）
plot(y_test, pred_y_test)
lm.obj<-lm(pred_y_test~y_test)
abline(lm.obj,col=2)
mtext(substitute(paste(R^2,"=",x),
list(x=round(summary(lm.obj)$r.squared,digits=5))),
line=-1,col=2,adj=0)
## 精度
model %>% evaluate(X_test, y_test)
モデル③（5層型）
モデル③：学習（学習データ利用）
「入力層→隠れ層1→隠れ層2→隠れ層3→出力層」のニューラルネットワーク型のディープラーニングのモデルを構築していきます。
- 入力層のユニット数：13（説明変数Xの数）
- 隠れ層1のユニット数：50
- 隠れ層2のユニット数：25
- 隠れ層2のユニット数：10
- 出力層のユニット数：1（目的変数yの数）
各層の活性化関数（activation）は……
- 隠れ層1：selu（Scaled Exponential Linear Unit）
- 隠れ層2：relu（REctified Linear Unit）
- 隠れ層3：relu（REctified Linear Unit）
以下、コードです。
# モデル構築 ## モデル定義 model <- keras_model_sequential() model %>% layer_dense(units = 50, activation = 'selu', input_shape = c(13)) %>% layer_dropout(rate=0.4) %>% layer_dense(units =25, activation = 'relu') %>% layer_dropout(rate=0.2) %>% layer_dense(units =10, activation = 'relu') %>% layer_dropout(rate=0.1) %>% layer_dense(units = 1) summary(model) #確認用
以下、実行結果です。
定義通りになっているのか確認しておきましょう。
- 入力層→隠れ層1のパラメータ：(13+1)×50=700
- 隠れ層1→出力層2のパラメータ：(50+1)×25=1275
- 隠れ層2→出力層のパラメータ：(25+1)×10=260
- 隠れ層3→出力層のパラメータ：(10+1)×1=11
次に、コンパイルし学習します。
以下、コードです。
## コンパイル
model %>% compile(loss = 'mse',
optimizer = 'rmsprop',
metrics = 'mae')
## 学習
history <-
model %>% fit(X_train,y_train,
epochs = 100,
batch_size = 10,
validation_split = 0.25)
history
以下、実行中の画像です。
以下、実行結果です。
今回学習したモデルの学習データセットのMAEは……
- train dataのMAE（mae）：5.401
- validation dataのMAE（val_mae）：3.38
モデル③：検証（テストデータ利用）
モデルが構築できたので、テストデータを使い予測し検証していきたいと思います。
先ず、テストデータの説明変数X（特徴量）を使い、目的変数yを予測します。
以下、コードです。
# 予測（検証） ## テストデータの予測 pred_y_test <- model %>% predict(X_test)
どのくらいの精度で当てられたのか、散布図（ヨコ軸：実測値、タテ軸：予測値）を使い見ていきます。回帰線とR2（決定係数）を合わせて表示しています。
以下、コードです。
## 散布図（ヨコ軸：実測値、タテ軸：予測値）
plot(y_test, pred_y_test)
lm.obj<-lm(pred_y_test~y_test)
abline(lm.obj,col=2)
mtext(substitute(paste(R^2,"=",x),
list(x=round(summary(lm.obj)$r.squared,digits=5))),
line=-1,col=2,adj=0)
以下、実行結果です。
いい感じで予測できていることが分かります。
では、どのくらい正解したのか、MAEを計算してみます。
以下、コードです。
## 精度 model %>% evaluate(X_test, y_test)
以下、実行結果です。
MAEは2.71でした。
モデル③：コード全体（モデル構築から検証まで）
#
# モデル3
#
# モデル構築
## モデル定義
model <- keras_model_sequential()
model %>%
layer_dense(units = 50, activation = 'selu', input_shape = c(13)) %>%
layer_dropout(rate=0.4) %>%
layer_dense(units =25, activation = 'relu') %>%
layer_dropout(rate=0.2) %>%
layer_dense(units =10, activation = 'relu') %>%
layer_dropout(rate=0.1) %>%
layer_dense(units = 1)
summary(model) #確認用
## コンパイル
model %>% compile(loss = 'mse',
optimizer = 'rmsprop',
metrics = 'mae')
## 学習
history <-
model %>% fit(X_train,y_train,
epochs = 100,
batch_size = 10,
validation_split = 0.25)
history
# 予測（検証）
## テストデータの予測
pred_y_test <-
model %>% predict(X_test)
## 散布図（ヨコ軸：実測値、タテ軸：予測値）
plot(y_test, pred_y_test)
lm.obj<-lm(pred_y_test~y_test)
abline(lm.obj,col=2)
mtext(substitute(paste(R^2,"=",x),
list(x=round(summary(lm.obj)$r.squared,digits=5))),
line=-1,col=2,adj=0)
## 精度
model %>% evaluate(X_test, y_test)
まとめ
Rにはディープラーニング関連のパッケージは色々あります。R独自のものから、そうでないものもあります。
ディープライニングで有名なKeras(TensorFlow)はRStudio(R)上で使うことができます。
前回は分類問題に対しニューラルネットワーク型のディープラーニングを構築するお話しをしました。今回は回帰問題です。
Keras(TensorFlow)はと言えばPythonですので、どこかの機会でRStudio(Python)上でKeras(TensorFlow)を動かす例を説明したいと思います（あまり…… 面白くはありませんが）。
