時系列解析系の数理モデルは色々ありますが、今も昔も時系列モデルと言えば、ARIMAモデル(SARIMAX含む)です。
ARIMAモデルの人気というか、実務的な活用は根強く、今も昔もメインで使われている気がしています。
要するに、実績十分な数理モデルです。
対象となるデータ(俗に言う目的変数Y)のみでモデルを構築できますし、説明変数Xを組み込むこともできます(ARIMAX)。
しかし、ARIMAの次数を人の知見をフル活用し求める必要があります。
ARIMAの次数を、機械学習的なのりで、予測精度を最大限に高める次数を自動探索し決めようという動きがあります。
Rには、forecastという有名な時系列解析のパッケージがあり、forecastの中にあるauto.arimaという関数を使うことで、予測精度を最大限に高める次数を自動探索することができます。
https://github.com/robjhyndman/forecast
このRのforecastのauto.arimaをPythonへ、ということでpmdarimaというPythonのパッケージが作られ、pmdarimaの中にあるAutoARIMAという関数を使うことで、予測精度を最大限に高める次数を探索することができます。
https://github.com/alkaline-ml/pmdarima
ということで、今回は「Pythonで時系列ARIMAモデルを自動でサクッと作ろう(AutoARIMA)」というお話をします。
ちなみに、ARIMAなどの時系列解析の理論的なお話は出てきません……
Contents [hide]
- pmdarimaのインストール
- 利用するデータセット
- 分析の流れ
- 予測精度評価で利用する指標
- 必要なライブラリーの読み込み
- Australian wine sales(オーストラリアのワイン販売量)
- Australian wine sales|データセットの読み込み
- Australian wine sales|自己相関係数などを確認
- Australian wine sales|学習データとテストデータに分割
- Australian wine sales|ARIMAモデルの自動構築
- Australian wine sales|ARIMAモデルの予測精度評価
- 階差の次数を指定して再構築
- Airline Passengers(飛行機乗客数)
- Airline Passengers|データセットの読み込み
- Airline Passengers|自己相関係数などを確認
- Airline Passengers|学習データとテストデータに分割
- Airline Passengers|ARIMAモデルの自動構築
- Airline Passengers|ARIMAモデルの予測精度評価
- 階差の次数を指定して再構築
- 今回のまとめ
pmdarimaのインストール
コマンドプロンプト上で、condaでインストールするときのコードは以下です。
conda install pmdarima
pipでインストールするときのコードは以下です。
pip install pmdarima
利用するデータセット
Rでも提供されている有名な以下のデータセット2つが、pmdarimaにもサンプルデータとし提供されているので、それを使います。
- Australian wine sales(オーストラリアのワイン販売量) ※月単位の時系列データ
- Airline Passengers(飛行機乗客数) ※月単位の時系列データ
分析の流れ
各データセットに対し、以下の流れで分析していきます。
- データセットの読み込み
- 自己相関係数などを確認
- 学習データとテストデータに分割
- ARIMAモデルの自動構築(学習データ)
- ARIMAモデルの予測精度評価(テストデータ)
予測精度評価で利用する指標
学習データで予測モデルを構築し、テストデータで精度検証していきます。
予測精度評価で利用する指標は、平均絶対誤差(MAE、Mean Absolute Error)と平均絶対パーセント誤差(MAPE、Mean absolute percentage error)です。
以下の記号を使い精度指標の説明をします。
■ 平均絶対誤差(MAE、Mean Absolute Error)
■ 平均絶対パーセント誤差(MAPE、Mean absolute percentage error)
必要なライブラリーの読み込み
先ずは、必要なライブラリー一式を読み込みます。
以下、コードです。
# ライブラリーの読み込み
import numpy as np
import pandas as pd
import pmdarima as pm
from pmdarima import datasets
from pmdarima import utils
from pmdarima import arima
from pmdarima import model_selection
from sklearn.metrics import mean_absolute_error
from statistics import mean
from matplotlib import pyplot as plt
# グラフのスタイルとサイズ
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]
よく利用する標準的なライブラリーが多いです。
- numpy
- pandas
- sklearn
- statistics
- maplotlib
まだインストールしていないパッケージのライブラリーなどがありましたら、インストールしておいてください。
Australian wine sales(オーストラリアのワイン販売量)
Australian wine sales|データセットの読み込み
Australian wine sales(オーストラリアのワイン販売量)は、1980年1月から1994年8月までのオーストラリアのワインメーカーによるワイン販売を記録した月単位のデータです。
先ず、データセットを読み込みます。
以下、コードです。
# データの読み込み data = datasets.load_wineind()
読み込んだデータセットをグラフで確認してみます。
以下、コードです。
# グラフ(折れ線) plt.plot(data)
以下、実行結果です。
Australian wine sales|自己相関係数などを確認
時系列データをトレンド成分や季節成分などへ要素分解します。
以下、コードです。
# 要素分解(tread・seasonal・random)
utils.decomposed_plot(arima.decompose(data,'additive',m=12),
figure_kwargs = {'figsize': (12, 12)} )
以下、実行結果です。
時系列データと言えば自己相関です。自己相関と偏自己相関をグラフで確認します。
以下、コードです。
# グラフのサイズ変更 plt.rcParams['figure.figsize'] = [12, 3] # 自己相関と偏自己相関 utils.plot_acf(data, alpha=.05) utils.plot_pacf(data, alpha=.05)
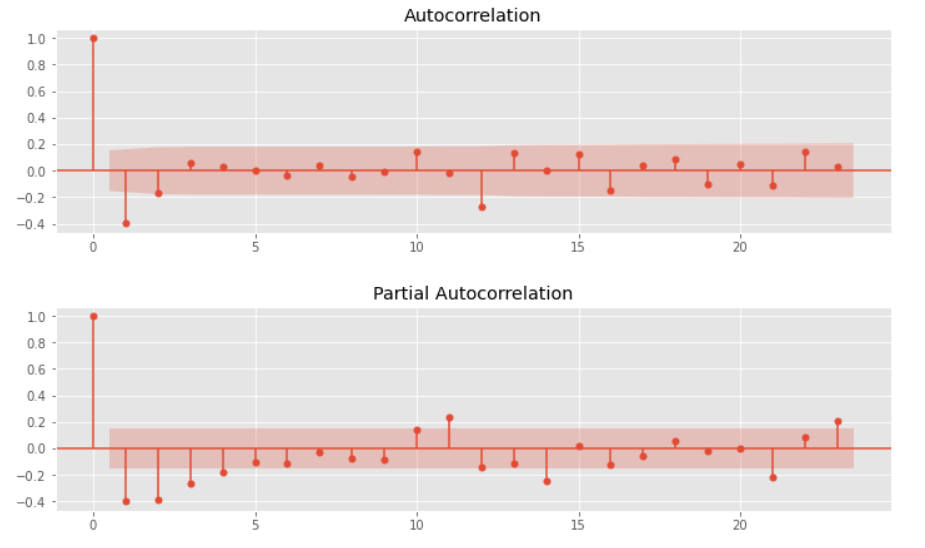
以下、実行結果です。(上:自己相関、下:偏自己相関)
トレンドなどが明らかにある時系列データのため、それらの影響がでています。それらを除去し、再度、自己相関と偏自己相関をグラフで確認します。
そのためには、時系列データの差分をとり階差系列を作る必要があります。
例えば、階差系列とは、前期(今回の場合は先月)との差を計算した時系列データです。季節階差系列とは、1周期前(今回の場合は昨年)との差を計算した時系列データです。このような処理は何回でも可能です。2回このような処理を行ったもの(差分の差分)を2階差系列、3回このような処理を行ったもの(差分の差分の差分)を3階差系列と言います。
問題は、その処理を何回繰り返せばいいのか、です。それを確かめるための機能があります。中で統計的有意差検定を実施しています。
以下、コードです。
# 階差の次数の検討
print('d =', arima.ndiffs(data)) #d(階差)
print('D =', arima.nsdiffs(data,m=12)) #D(季節階差)
以下、実行結果です。
通常の階差処理を1回と季節階差処理を1回実施したほうがいい、という結果です。
通常の階差処理とは、先月との差分を計算することです。季節階差処理とは、1年前との差分を計算することです。
以下、コードです。
# 通常の階差処理を1回しさらに季節階差処理を1回 data_d1_d12 = pd.DataFrame(data).diff(1).diff(12).dropna()
このデータに対し、自己相関と偏自己相関をグラフで確認します。
以下、コードです。
# グラフのサイズ変更 plt.rcParams['figure.figsize'] = [12, 3] # 自己相関と偏自己相関 utils.plot_acf(data_d1_d12, alpha=.05) utils.plot_pacf(data_d1_d12, alpha=.05)
以下、実行結果です。(上:自己相関、下:偏自己相関)
Australian wine sales|学習データとテストデータに分割
予測モデルを構築する学習データと、構築した予測モデルを検証するためのテストデータに分割します。
時系列データですので、ある時期を境に2つのデータに分割します。
今回は、新しい36ヶ月(3年間)のデータをテストデータとし、その前のデータを学習データとします。
- 学習データ:1行目から140行目
- テストデータ:141行目から176行目
では、データを分割します。以下、コードです。
# データ分割(train:学習データ、test:テストデータ) train, test = model_selection.train_test_split(data, train_size=140)
Australian wine sales|ARIMAモデルの自動構築
学習データ(train)を使い、ARIMAモデルを自動構築します。
以下、コードです。
# モデル構築(Auto ARIMA)
arima_model = pm.auto_arima(train,
seasonal=True,
m=12,
trace=True,
n_jobs=-1,
maxiter=10)
以下、実行結果です。
AIC(赤池情報量規準)上のベストモデルは、ARIMA(2,1,1)(1,0,1)[12]です。
Australian wine sales|ARIMAモデルの予測精度評価
構築したモデルをテストデータ(test)を使い精度評価します。
以下、コードです。
# グラフのサイズ変更
plt.rcParams['figure.figsize'] = [12, 9]
# 予測
preds, conf_int = arima_model.predict(n_periods=test.shape[0],
return_conf_int=True)
# 予測精度
print('MAE:')
print(mean_absolute_error(test, preds))
print('MAPE(%):')
print(mean(abs(test - preds)/test) *100)
# 予測と実測の比較(グラフ)
x_axis = np.arange(preds.shape[0])
plt.plot(x_axis,test,label="actual",color='r')
plt.plot(x_axis,preds,label="predicted",color='b')
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1, color='b')
plt.legend()
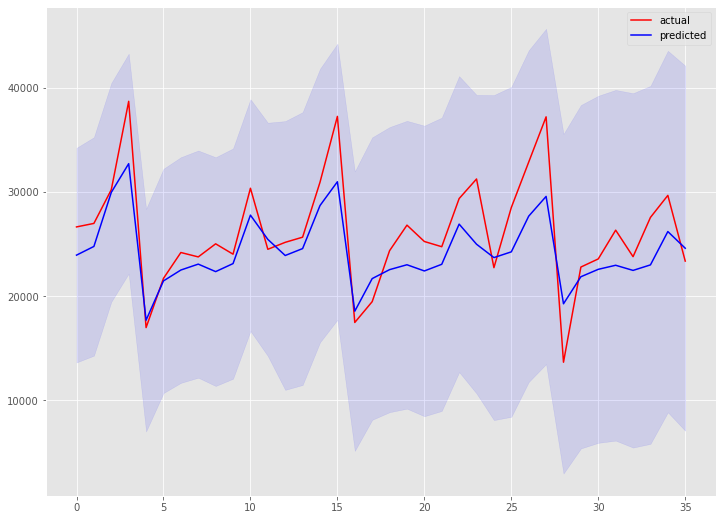
plt.show()
以下、実行結果です。
学習データの期間も含めグラフ化してみます。
以下、コードです。
# グラフ(学習データとテストデータ、予測結果)
x_axis = np.arange(train.shape[0] + preds.shape[0])
plt.plot(x_axis[:train.shape[0]],train,color='r',label="actual")
plt.plot(x_axis[train.shape[0]:],test,color='r')
plt.plot(x_axis[train.shape[0]:],preds,color='b',label="predicted")
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1,color='b')
plt.legend()
plt.show()
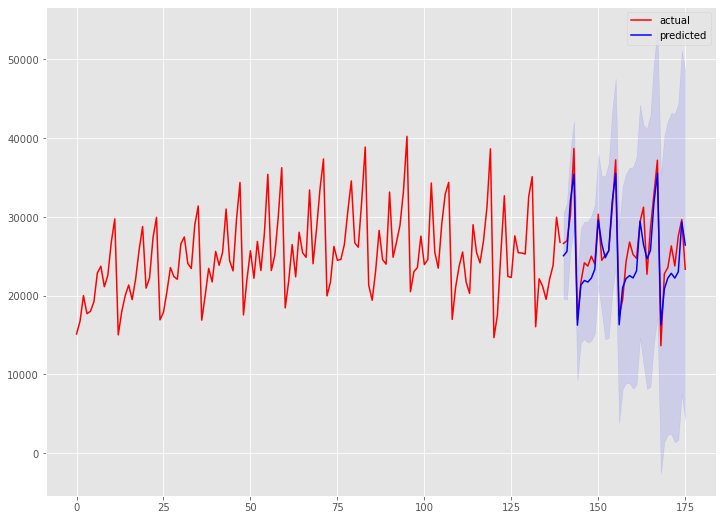
以下、実行結果です。
階差の次数を指定して再構築
先程、通常の階差の次数が1で、季節階差の次数も1であると言いました。この階差の次数を指定しARIMAモデルを自動構築してみます。
以下、コードです。コードで変えた部分に色をつけています。
# モデル構築(Auto ARIMA)
arima_model = pm.auto_arima(train,
seasonal=True,
m=12,
d=1,
D=1,
n_jobs=-1,
maxiter=10)
# グラフのサイズ変更
plt.rcParams['figure.figsize'] = [12, 9]
# 予測
preds, conf_int = arima_model.predict(n_periods=test.shape[0],
return_conf_int=True)
# 予測精度
print('MAE:')
print(mean_absolute_error(test, preds))
print('MAPE(%):')
print(mean(abs(test - preds)/test) *100)
# 予測と実測の比較(グラフ)
x_axis = np.arange(preds.shape[0])
plt.plot(x_axis,test,label="actual",color='r')
plt.plot(x_axis,preds,label="predicted",color='b')
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1, color='b')
plt.legend()
plt.show()
# グラフ(学習データとテストデータ、予測結果)
x_axis = np.arange(train.shape[0] + preds.shape[0])
plt.plot(x_axis[:train.shape[0]],train,color='r',label="actual")
plt.plot(x_axis[train.shape[0]:],test,color='r')
plt.plot(x_axis[train.shape[0]:],preds,color='b',label="predicted")
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1,color='b')
plt.legend()
plt.show()
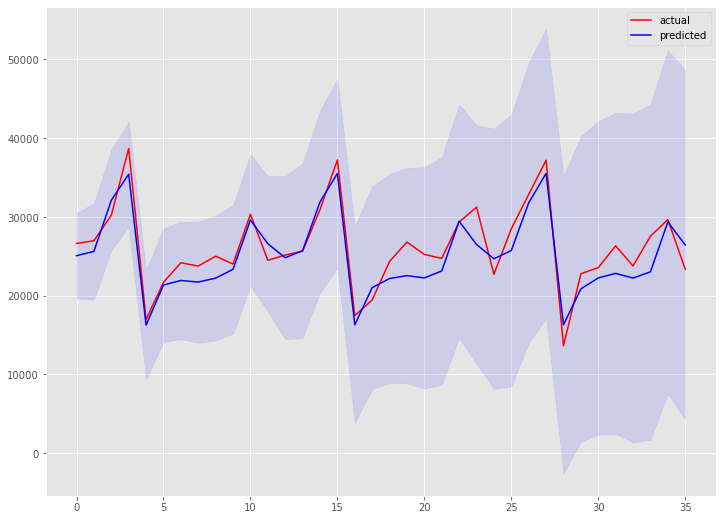
以下、実行結果です。
予測精度は向上しています。全自動は便利ですが、実は手動と自動のハイブリッドが高精度になる傾向があります。
Airline Passengers(飛行機乗客数)
Airline Passengers|データセットの読み込み
Airline Passengers(飛行機乗客数)は、1949年から1960年までの国際航空旅客の月単位のデータです。
先ず、データセットを読み込みます。
以下、コードです。
# データの読み込み data = datasets.load_airpassengers()
読み込んだデータセットをグラフで確認してみます。
以下、コードです。
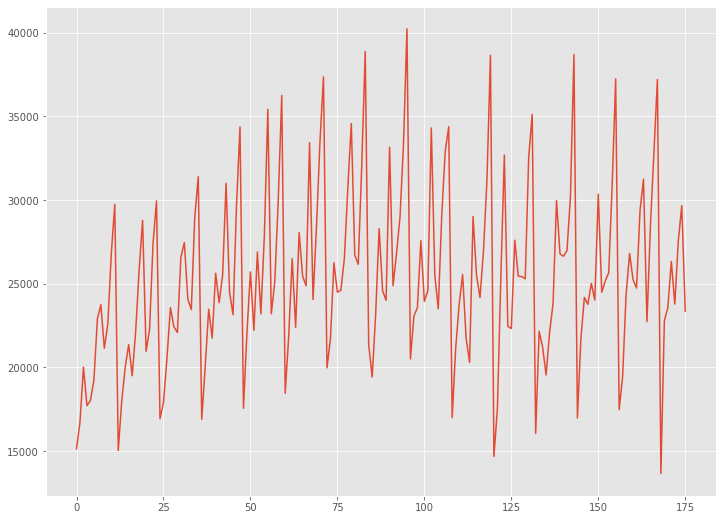
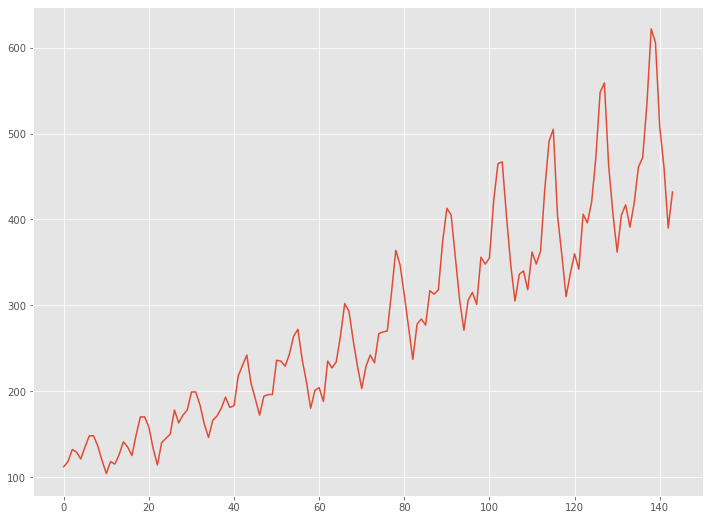
# グラフ(折れ線) plt.plot(data)
以下、実行結果です。
Airline Passengers|自己相関係数などを確認
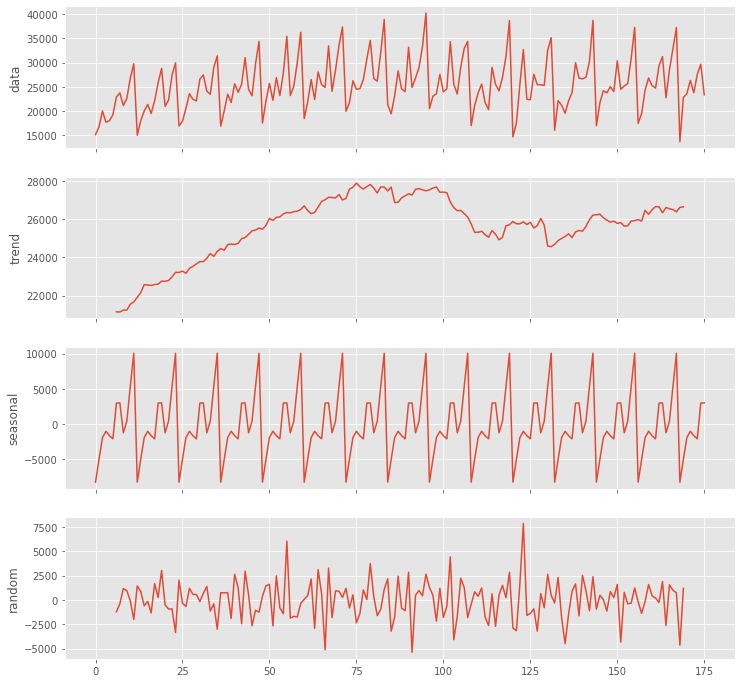
時系列データをトレンド成分や季節成分などへ要素分解します。
以下、コードです。
# 要素分解(tread・seasonal・random)
utils.decomposed_plot(arima.decompose(data,'additive',m=12),
figure_kwargs = {'figsize': (12, 12)} )
以下、実行結果です。
自己相関と偏自己相関をグラフで確認します。
以下、コードです。
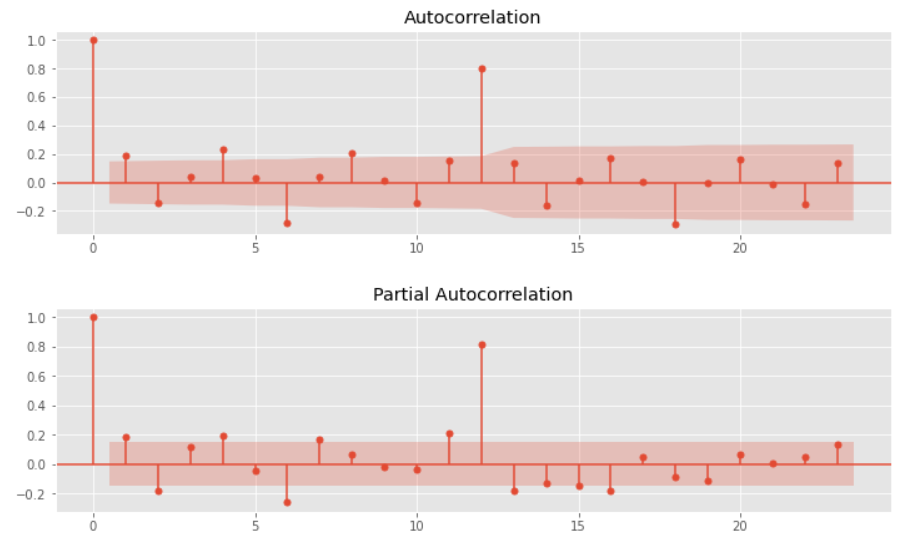
# グラフのサイズ変更 plt.rcParams['figure.figsize'] = [12, 3] # 自己相関と偏自己相関 utils.plot_acf(data, alpha=.05) utils.plot_pacf(data, alpha=.05)
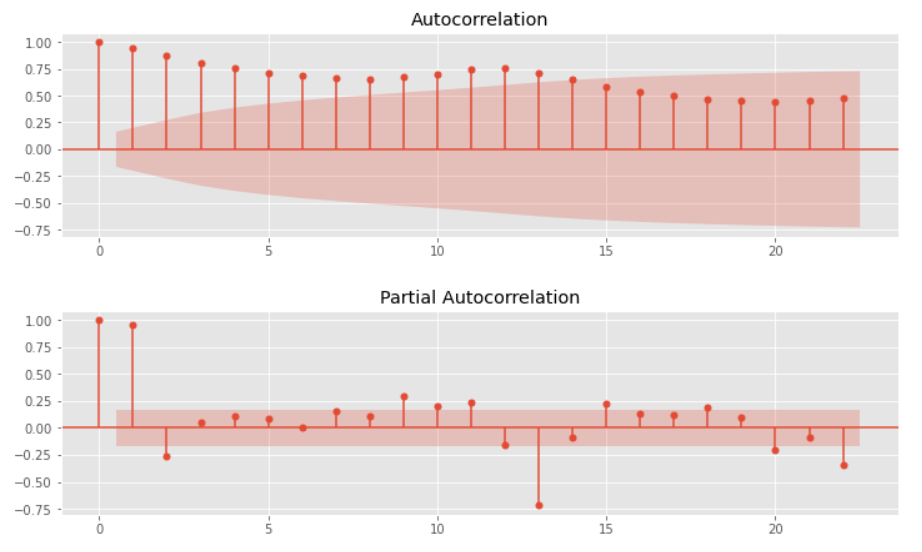
以下、実行結果です。(上:自己相関、下:偏自己相関)
トレンドなどが明らかにある時系列データのため、それらの影響がでています。それらを除去し、再度、自己相関と偏自己相関をグラフで確認します。
そのためには、時系列データの差分をとり階差系列を作る必要があります。
以下、コードです。
# 階差の次数の検討
print('d =', arima.ndiffs(data)) #d(階差)
print('D =', arima.nsdiffs(data,m=12)) #D(季節階差)
以下、実行結果です。
通常の階差処理を1回と季節階差処理を1回実施したほうがいい、という結果です。
通常の階差処理とは、先月との差分を計算することです。季節階差処理とは、1年前との差分を計算することです。
以下、コードです。
# 通常の階差処理を1回しさらに季節階差処理を1回 data_d1_d12 = pd.DataFrame(data).diff(1).diff(12).dropna()
このデータに対し、自己相関と偏自己相関をグラフで確認します。
以下、コードです。
# グラフのサイズ変更 plt.rcParams['figure.figsize'] = [12, 3] # 自己相関と偏自己相関 utils.plot_acf(data_d1_d12, alpha=.05) utils.plot_pacf(data_d1_d12, alpha=.05)
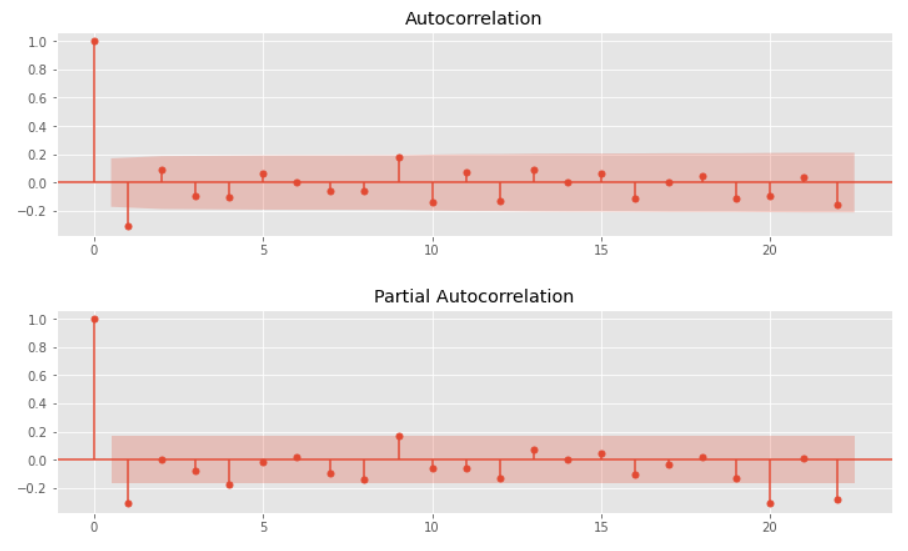
以下、実行結果です。(上:自己相関、下:偏自己相関)
Airline Passengers|学習データとテストデータに分割
予測モデルを構築する学習データと、構築した予測モデルを検証するためのテストデータに分割します。
時系列データですので、ある時期を境に2つのデータに分割します。
今回は、新しい12ヶ月(1年間)のデータをテストデータとし、その前のデータを学習データとします。
- 学習データ:1行目から132行目
- テストデータ:133行目から144行目
では、データを分割します。以下、コードです。
# データ分割(train:学習データ、test:テストデータ) train, test = model_selection.train_test_split(data, train_size=132)
Airline Passengers|ARIMAモデルの自動構築
学習データ(train)を使い、ARIMAモデルを自動構築します。
以下、コードです。
# モデル構築(Auto ARIMA)
arima_model = pm.auto_arima(train,
seasonal=True,
m=12,
trace=True,
n_jobs=-1,
maxiter=10)
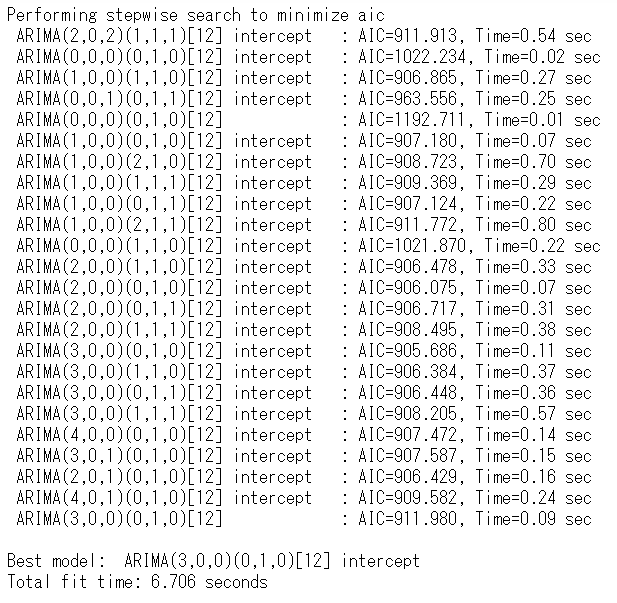
以下、実行結果です。
AIC(赤池情報量規準)上のベストモデルは、ARIMA(3,0,0)(0,1,0)[12]です。
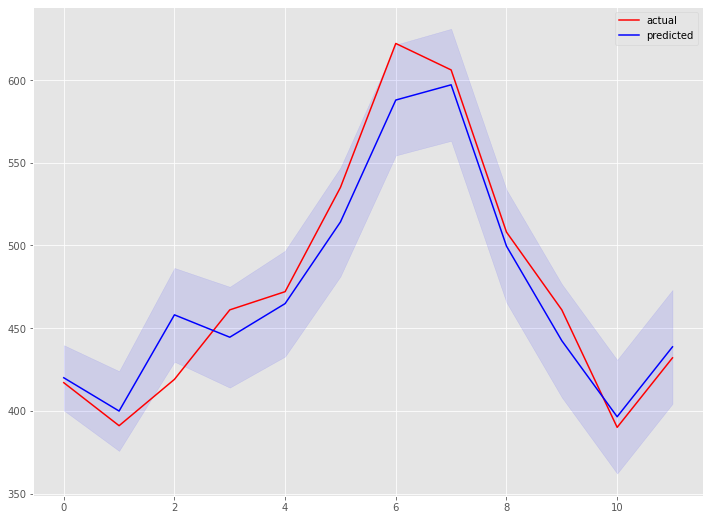
Airline Passengers|ARIMAモデルの予測精度評価
構築したモデルをテストデータ(test)を使い精度評価します。
以下、コードです。
# グラフのサイズ変更
plt.rcParams['figure.figsize'] = [12, 9]
# 予測
preds, conf_int = arima_model.predict(n_periods=test.shape[0],
return_conf_int=True)
# 予測精度
print('MAE:')
print(mean_absolute_error(test, preds))
print('MAPE(%):')
print(mean(abs(test - preds)/test) *100)
# 予測と実測の比較(グラフ)
x_axis = np.arange(preds.shape[0])
plt.plot(x_axis,test,label="actual",color='r')
plt.plot(x_axis,preds,label="predicted",color='b')
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1, color='b')
plt.legend()
plt.show()
以下、実行結果です。
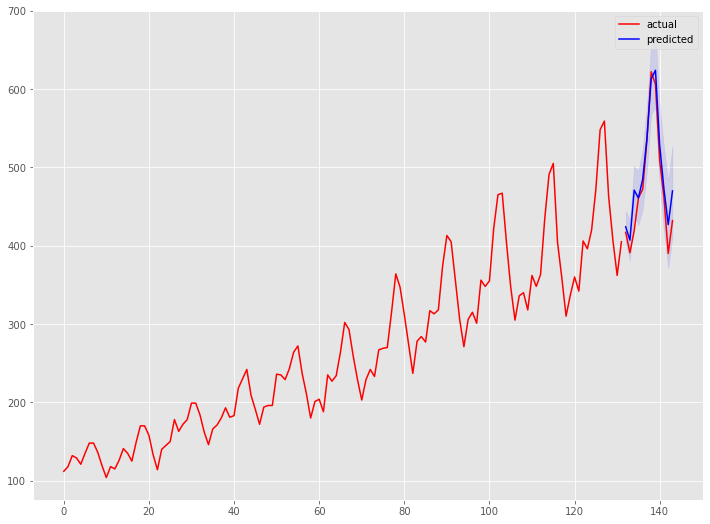
学習データの期間も含めグラフ化してみます。
以下、コードです。
# グラフ(学習データとテストデータ、予測結果)
x_axis = np.arange(train.shape[0] + preds.shape[0])
plt.plot(x_axis[:train.shape[0]],train,color='r',label="actual")
plt.plot(x_axis[train.shape[0]:],test,color='r')
plt.plot(x_axis[train.shape[0]:],preds,color='b',label="predicted")
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1,color='b')
plt.legend()
plt.show()
以下、実行結果です。
階差の次数を指定して再構築
先程、通常の階差の次数が1で、季節階差の次数も1であると言いました。この階差の次数を指定しARIMAモデルを自動構築してみます。
以下、コードです。コードで変えた部分に色をつけています。
# モデル構築(Auto ARIMA)
arima_model = pm.auto_arima(train,
seasonal=True,
m=12,
d=1,
D=1,
n_jobs=-1,
maxiter=10)
# グラフのサイズ変更
plt.rcParams['figure.figsize'] = [12, 9]
# 予測
preds, conf_int = arima_model.predict(n_periods=test.shape[0],
return_conf_int=True)
# 予測精度
print('MAE:')
print(mean_absolute_error(test, preds))
print('MAPE(%):')
print(mean(abs(test - preds)/test) *100)
# 予測と実測の比較(グラフ)
x_axis = np.arange(preds.shape[0])
plt.plot(x_axis,test,label="actual",color='r')
plt.plot(x_axis,preds,label="predicted",color='b')
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1, color='b')
plt.legend()
plt.show()
# グラフ(学習データとテストデータ、予測結果)
x_axis = np.arange(train.shape[0] + preds.shape[0])
plt.plot(x_axis[:train.shape[0]],train,color='r',label="actual")
plt.plot(x_axis[train.shape[0]:],test,color='r')
plt.plot(x_axis[train.shape[0]:],preds,color='b',label="predicted")
plt.fill_between(x_axis[-preds.shape[0]:],
conf_int[:, 0], conf_int[:, 1],
alpha=0.1,color='b')
plt.legend()
plt.show()
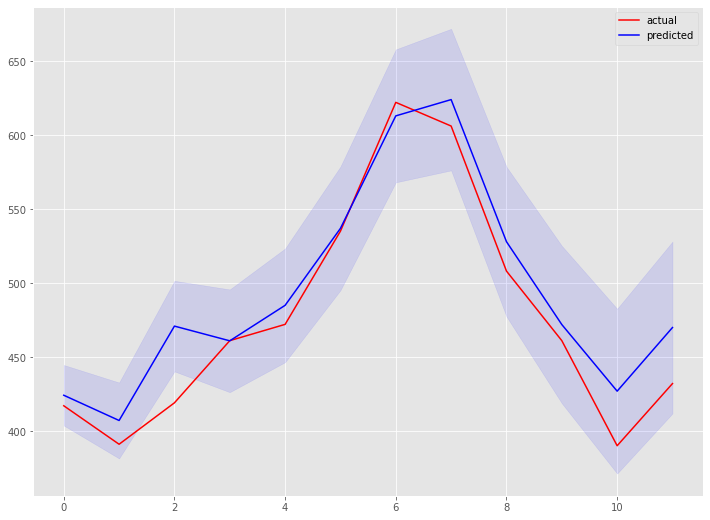
以下、実行結果です。
こちらは、全自動で構築するよりも精度が悪化しました。
今回のまとめ
今回は、「Pythonで時系列ARIMAモデルを自動でサクッと作ろう(AutoARIMA)」というお話をしました。
Rには、forecastという有名な時系列解析のパッケージがあり、forecastの中にあるauto.arimaという関数を使うことで、予測精度を最大限に高める次数を自動探索することができます。
このRのforecastのauto.arimaをPythonへ、ということでpmdarimaというPythonのパッケージが作られ、pmdarimaの中にあるAutoARIMAという関数を使うことで、予測精度を最大限に高める次数を探索することができます。
興味のある方は試してみてください。