顧客別CLTV(Individual CLTV)とは、顧客の金銭的価値のことで、将来行う取引に基づいて算出されます。
個々の顧客が将来どのくらいの利益を生み出すかがわかれば、価値の高い顧客に対し、マーケティング活動などを集中できます。
顧客別CLTV(Individual CLTV)が分かれば、例えば以下の2つの分析につなげることが多いです。
- 離反阻止分析(チャーン分析)
- 出世魚分析(隠れた宝石探し)
価値の高い顧客は、離反阻止すべきですし、取引額拡大に向けて活動すべきです。
要は、短期的な収益ではなく、長期的な収益に視点を当てた活動ができるということです。
では、実際にどのようなデータで、どのようなモデルを構築すれば、CLTV(顧客生涯価値)を求めることができるのか?
今回は、「顧客別CLTV(顧客生涯価値)モデルを Python Lifetimes でサクッと作る方法を事例で学ぶ」というお話しです。
Contents [hide]
リード(見込み顧客)のCLTV(顧客生涯価値)
CLTV(顧客生涯価値)は、取引履歴のある既存顧客に対して見積もります。
取引履歴のないリード(見込み顧客)や1回しか取引していない顧客のCLTV(顧客生涯価値)を見積もるときには、既存顧客のCLTV(顧客生涯価値)を見積もった後に、マッチングの技術などを使い見積もります。
何はともあれ、取引履歴のある既存顧客に対しCLTV(顧客生涯価値)を見積もるところから始まります。
ちなみに、マッチングの方法は色々ありますが、一番簡単なのは、顧客の属性情報などをもとに類似度(もしくは非類似度)を計算し、重み付け平均などで見積もる方法です。このあたりの話題は、別の機会にお話しします。
取引履歴のある既存顧客のCLTV(顧客生涯価値)
既存顧客のCLTV(顧客生涯価値)は、過去の取引状況などをもとに考えていきます。
例えば……
- 購買確率
- 離反確率
- 購買金額
- 購買回数
- 購買間隔
……などを過去の取引状況などをもとに計算し、CLTV(顧客生涯価値)を計算します。
お互いに関係しあっていますので、すべてを計算する必要はありません。例えば、購買回数が0であれば、離反確率は100%です。
今回紹介するCLTV(顧客生涯価値)予測モデルは、以下の2つです。
- 購買回数モデル(BG/NBDモデル)
- 購買金額モデル(GGモデル)
BG/NBDモデル(Beta Geometric/Negative Binomial Distribution)で回数を予測し、金額/回をGGモデル(Gamma-Gamma model)で予測します。
CLTV(顧客生涯価値)モデルは、この2つのモデルを融合したものです。CLTV=回数×金額/回で計算できます。
Pyhtonですと、以下のLifetimesパッケージです。
Lifetimesのインストール
コマンドプロンプト上で、pipでインストールするときのコードは以下です。
pip install lifetimes
サンプルデータ
CLTV(顧客生涯価値)をモデル化するには、トランザクションデータが必要です。
ECサイトのトランザクションデータである購買データ(OnlineRetail.csv)を使います。UCI Machine Learning Repositoryで提供されているOnline Retail Data Setのデータセットです。
必要な方は、以下からダウンロードしてください。
Acquire Valued Shoppers Challenge
https://archive.ics.uci.edu/ml/datasets/Online+Retail弊社サイトからダウンロードする場合は以下から
https://www.salesanalytics.co.jp/jwga
必要なパッケージの読み込み
以下、コードです。
# パッケージ読み込み
import numpy as np
import pandas as pd
import pandas_profiling
from statistics import mean
from sklearn.metrics import mean_absolute_error
from lifetimes.utils import calibration_and_holdout_data
from lifetimes import BetaGeoFitter
from lifetimes import GammaGammaFitter
from lifetimes.utils import summary_data_from_transaction_data
import matplotlib.pyplot as plt
# グラフのスタイルとサイズ
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]
データセットのプロファイリング用のパッケージ(Pandas-Profiling)以外は、特別なパッケージは利用していません。Pandas-Profilingのインストールは、以下を参考にしてください。絶対に必要なものでもないので、無視してしてしまっても問題ありません。
データセット読み込み
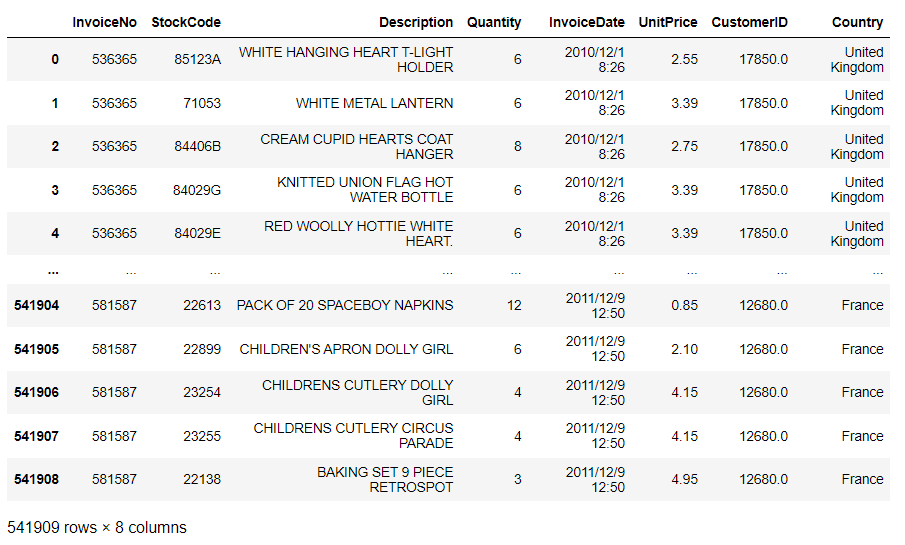
データセットを読み込みます。ECサイトの取引履歴です。
以下、コードです。
# データセット読み込み url = 'https://www.salesanalytics.co.jp/jwga' df = pd.read_csv(url) # データセットの確認 df
以下、実行結果です。
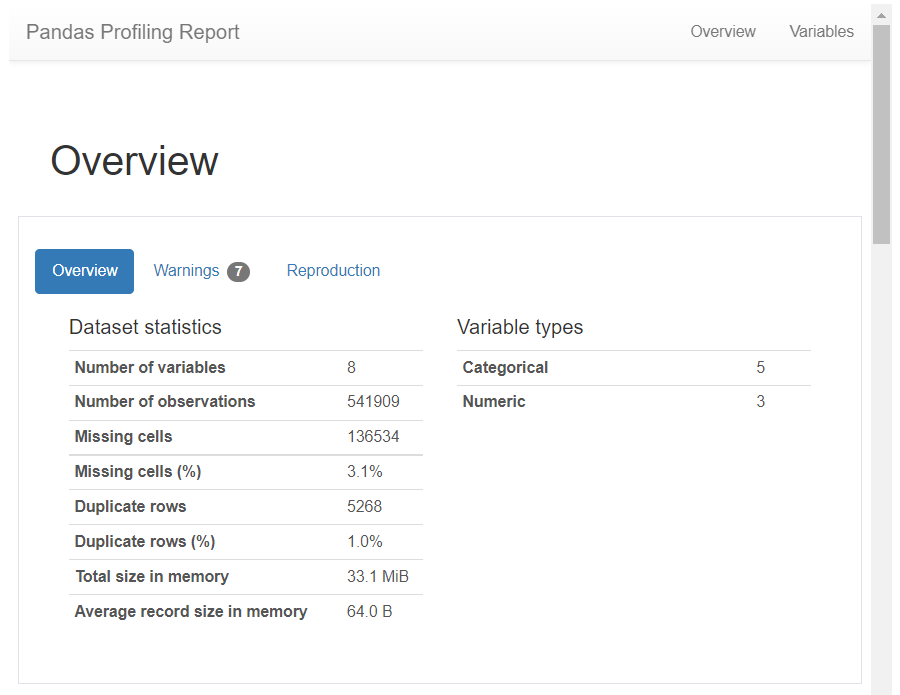
Pandas-Profilingで、読み込んだデータセットをプロファイリングします。
以下、コードです。
# データセットのプロファイリング pandas_profiling.ProfileReport(df, minimal=True)
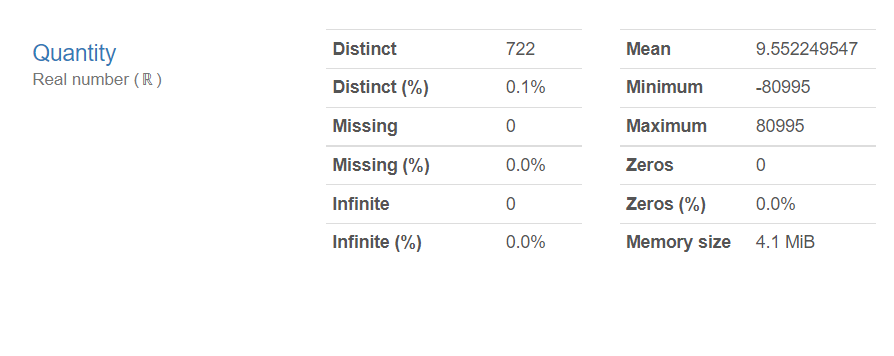
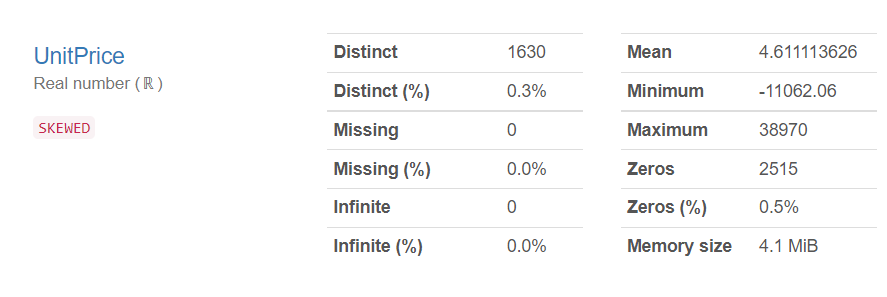
以下、実行結果です。画像をクリックすると別タブで実行結果を見れます。
Quantity(購入数)とUnitPrice(単価)のMinimumを見ると、マイナスの数値になっています。返品などでマイナスの数値になっている取引があることが分かります。
Lifetimesパッケージの扱うトランザクションデータは、以下の3つの変数で構成されるデータセットを前提としています。
- 顧客ID
- 取引日(購入日、注文日など)
- 取引金額(購入金額、注文金額など)
この3つの変数で構成されるトランザクションデータを元に、RFM(frequency・recency・T・monetary_value)の4つの変数を計算し作成したデータセットを使い、モデル構築などを行います。Lifetimesパッケージ独自の定義です。
- frequency:データセット内の、リピート回数( = 購買回数 – 1 )
- recency:データセット内の、アクティブ期間(最初に購入してから最近の購入までの期間)
- T:データセット内で最初に購入してから、そのデータセットが終了するまでの期間
- monetary_value:データセット内のリピート時の平均購入金額
前処理
先ず、以下の3つの変数で構成されるLifetimesパッケージ用のトランザクションデータを作ります。
- CustomerID:顧客ID
- InvoiceDate:購入日
- purchaseamount:購入金額
以下、コードです。
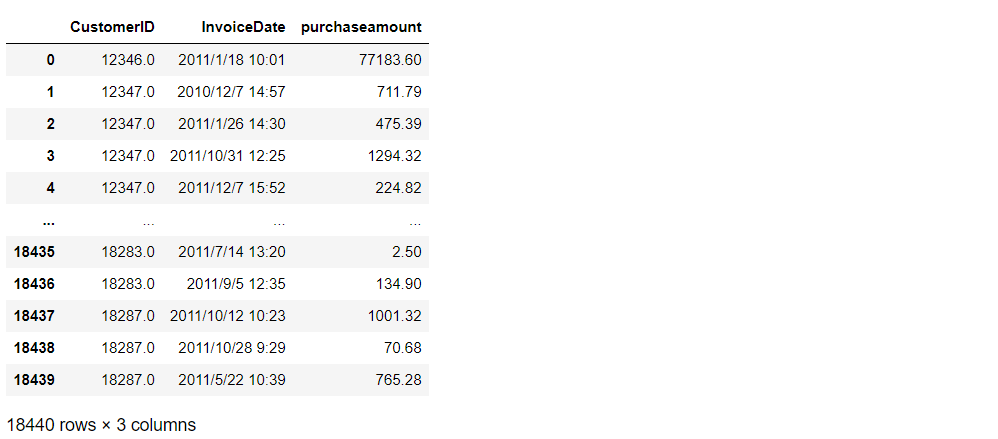
# 合計金額を計算 df['purchaseamount'] = df['Quantity'] * df['UnitPrice'] # 返品処理などを削除 df = df.loc[df['purchaseamount'] > 0.0] # 顧客ID・日時・金額のトランザクションデータを生成 transaction_data = df.groupby(['CustomerID', 'InvoiceDate'])['purchaseamount'].sum().reset_index() # データセットの確認 transaction_data
以下、実行結果です。
この3つの変数で構成されるトランザクションデータを元に、RFM(frequency・recency・T・monetary_value)の4つの変数を計算し、モデル構築用のデータセットを作ります。
以下、コードです。
# RFMデータセット生成
rfm = summary_data_from_transaction_data(
transaction_data,
'CustomerID',
'InvoiceDate',
observation_period_end='2011-11-30',
monetary_value_col = 'purchaseamount'
)
# データセットの確認
rfm
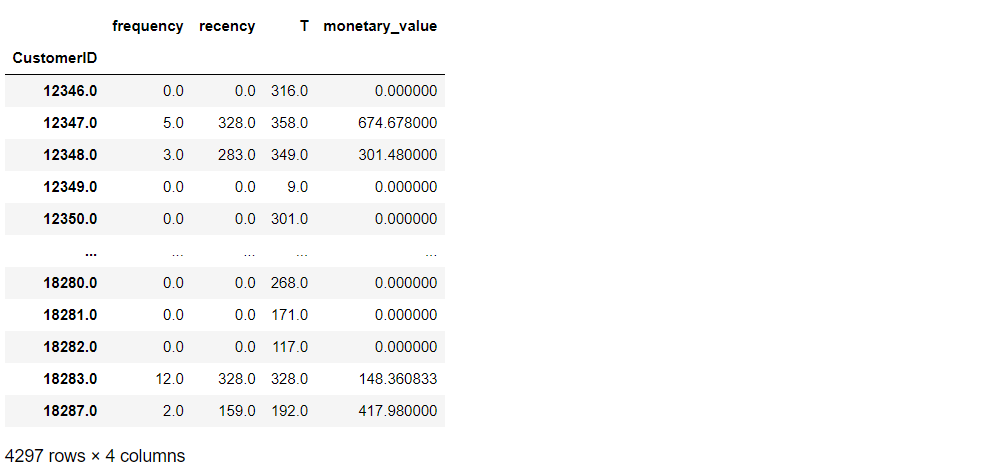
以下、実行結果です。
リピート回数(frequency)が1以上のデータに絞ります。
以下、コードです。
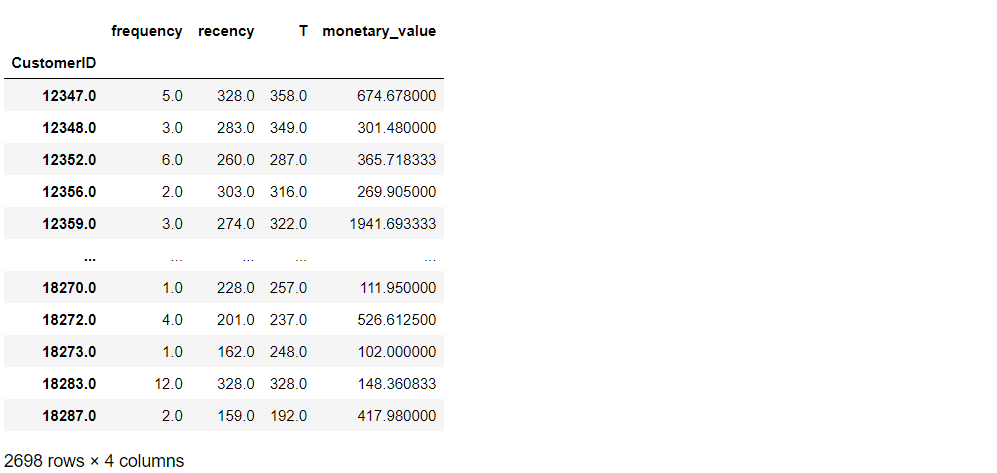
# frequencyが1以上のデータに絞る rfm = rfm.loc[rfm['frequency'] > 0] # データセットの確認 rfm
以下、実行結果です。
ただ、このデータセットを使いモデル構築し検証するわけではありません。通常の機械学習モデルと同様に、学習データとテストデータに分け、学習データでモデル構築し、構築したモデルをテストデータで検証します。
トランザクションデータのような、時系列なデータは、期間で学習データとテストデータを分割します。分割する時期を決め学習データ期間とテストデータ期間に分けます。
今回は、約1年間のデータであるため、前半半年(学習データ期間)と後半半年(テストデータ期間)に分けます。
データ期間分割(学習データ期間とテストデータ期間)
では、先程作成した3つの変数(CustomerID・InvoiceDate・purchaseamount)で構成されたトランザクションデータを、前半半年(学習データ期間)と後半半年(テストデータ期間)に分割します。
以下、コードです。
# データ期間分割(学習データ期間とテストデータ期間)
rfm_train_test = calibration_and_holdout_data(
transaction_data,
'CustomerID',
'InvoiceDate',
calibration_period_end='2011-5-31',
observation_period_end='2011-11-30',
monetary_value_col = 'purchaseamount'
)
# データセットの確認
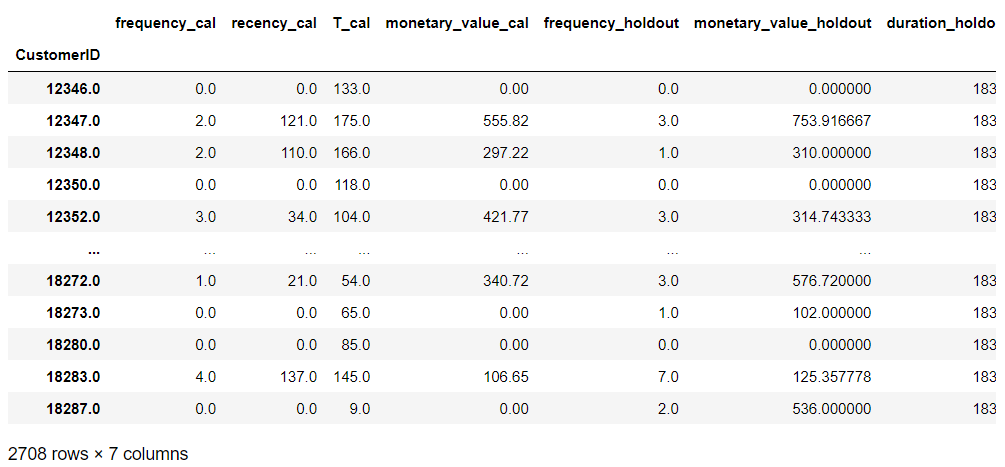
rfm_train_test
以下、実行結果です。
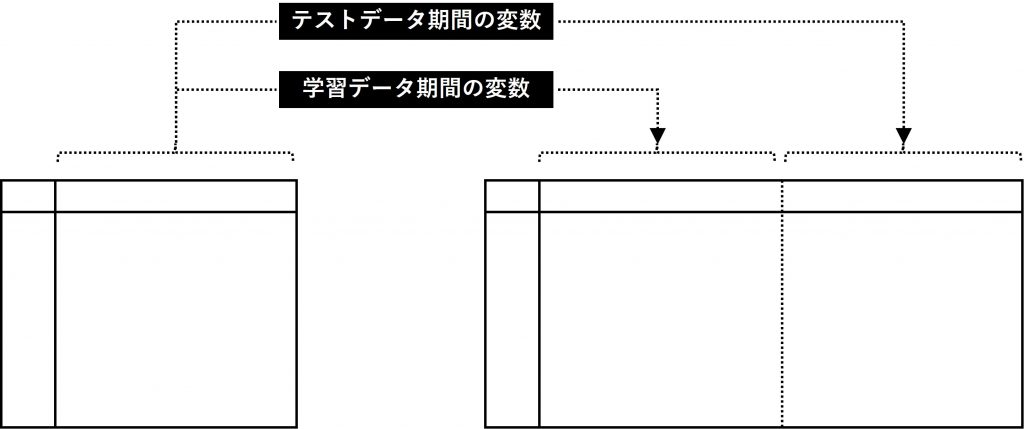
- 学習データ期間のRFM
- frequency_cal:学習データ期間中のリピート回数(購入回数-1)
- recency_cal:学習データ期間のアクティブ期間
- T_cal:学習データ期までのT
- monetary_value_cal:学習データ期間中のリピート平均購入金額
- テストデータ期間のRFM
- frequency_holdout:テストデータ期間中のリピート回数(購入回数)
- monetary_value_holdout:テストデータ期間中のリピート平均購入金額
- duration_holdout:テストデータ期間の日数
通常の機械学習モデルの場合には、学習データとテストデータの2つのデータセットに分けます。しかし、今回の場合は異なります。
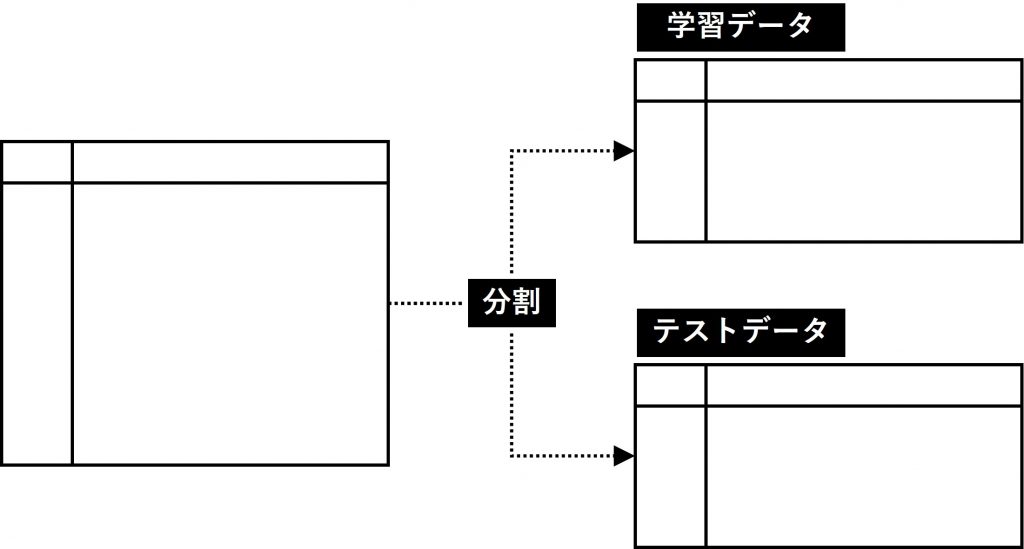
今回の場合は、データセットを2つに分けません。1つのデータセットの中で、変数で表現します。学習データ期間の変数とテストデータ期間の変数を作り表現します。
リピートした既存顧客に絞るために、リピート回数(frequency)が1以上のデータに絞ります。
以下、コードです。
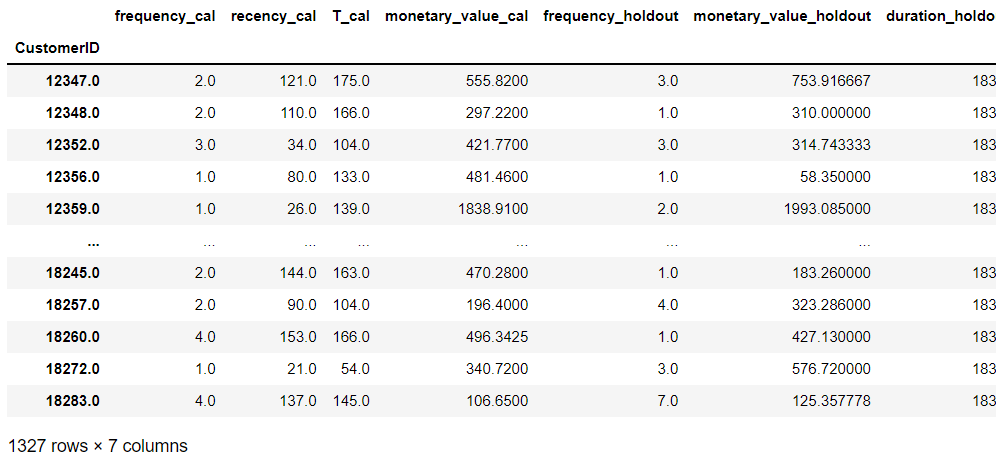
# 学習データ期間のfrequency(frequency_cal)が1以上のデータに絞る rfm_train_test = rfm_train_test.loc[rfm_train_test.frequency_cal > 0, :] # データセットの確認 rfm_train_test
以下、実行結果です。
購買回数モデル(BG/NBDモデル)
BG/NBDモデル(Beta Geometric/Negative Binomial Distribution)で購買回数を予測します。
このモデルは、Faderら(2005)のモデルが元になっています。
Fader, Peter S., Bruce GS Hardie, and Ka Lok Lee. ““Counting your customers” the easy way: An alternative to the Pareto/NBD model.” Marketing science 24.2 (2005): 275-284.
http://brucehardie.com/papers/018/fader_et_al_mksc_05.pdf
この論文の基本的な考え方というアプローチは、顧客の購買確率と離反確率をもとにモデルを考えています。具体的には、購買のガンマ分布と離反のベータ分布です。
では、学習データ期間(前半半年)のデータ(変数)を使ってモデルを構築します。
以下、コードです。
# BG/NBDモデルの学習(学習データ期間)
bgf = BetaGeoFitter(penalizer_coef=0)
bgf.fit(
rfm_train_test['frequency_cal'],
rfm_train_test['recency_cal'],
rfm_train_test['T_cal']
)
構築したモデルを使って、テストデータ期間(後半半年)の予測をします。
以下、コードです。
# 予測期間(半年)
duration_holdout = 183
# 予測(予測データ期間)
predicted_bgf = bgf.predict(
duration_holdout,
rfm_train_test['frequency_cal'],
rfm_train_test['recency_cal'],
rfm_train_test['T_cal']
)
テストデータ期間(後半半年)の実測値(actual)と予測値(predicted)を比較してみます。
以下、コードです。
# 実測値と予測値の代入
actual = rfm_train_test['frequency_holdout']
predicted = predicted_bgf
# 散布図(予測Predict×実測Actual)
xylim = max(max(predicted), max(actual))*1.1
plt.scatter(predicted, actual)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.xlim(0,xylim)
plt.ylim(0,xylim)
plt.plot([0, xylim], [0,xylim], ls="--", c=".3")
plt.show()
# 予測精度
print('RMSE:')
print(mean((actual - predicted)**2)**.5)
print('MAE:')
print(mean_absolute_error(actual, predicted))
print('R:')
print(np.corrcoef(actual, predicted)[0,1])
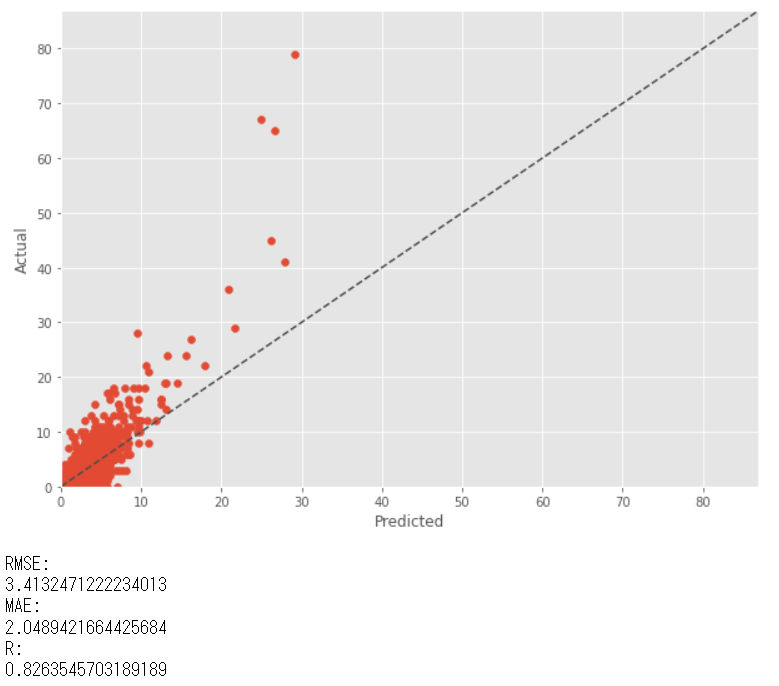
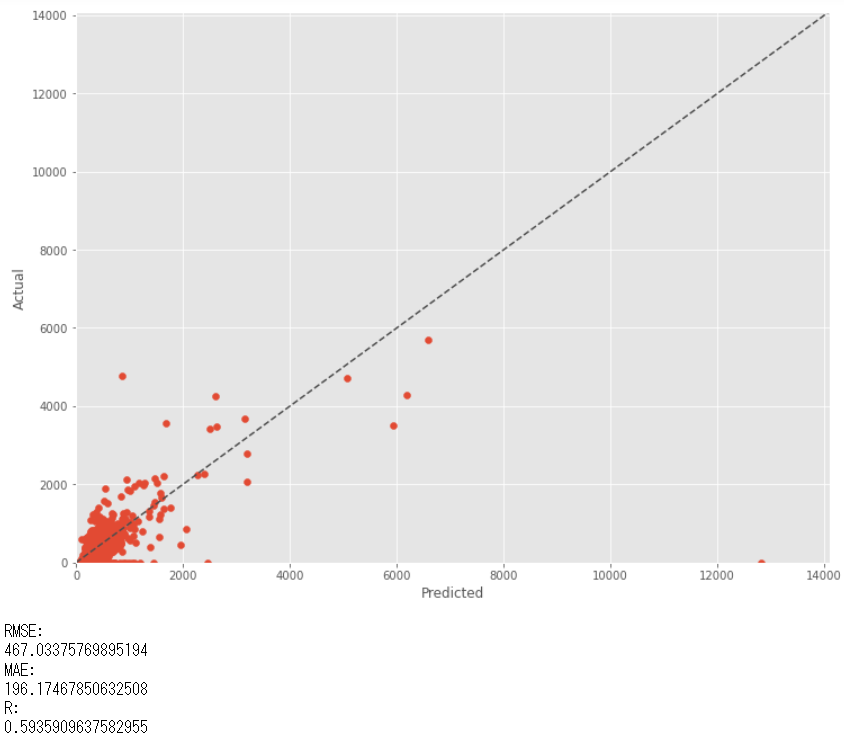
以下、実行結果です。(RMSE:二乗平均平方根誤差、MAE:平均絶対誤差、R:重相関係数)
予測値(predicted)に比べ実測値(actual)の方が値が大きい傾向があります。そもそも、前半半年(学習データ期間)よりも後半半年(テストデータ期間)の方が、実測値(actual)が大きいのかもしれません。脱線しますが確認してみます。
以下、コードです。
rfm_train_test.loc[:,["frequency_cal","frequency_holdout"]].mean()
以下、実行結果です。
前半半年(学習データ期間)よりも後半半年(テストデータ期間)の方が、実測値(actual)が大きいようです。この差分は、季節性が影響しているのかもしれません。本来であれば、半年ではなく「学習データ期間:1年間」「テストデータ期間:1年間」とした方がいいでしょう。
ここで、季節性があるという前提で補正係数を作り、予測値を補正し再度プロットしてみます。
先ず、補正係数(frequency_holdout÷frequency_cal)を求めます。
以下、コードです。
# 補正係数 freq_cal_mean = rfm_train_test["frequency_cal"].mean() freq_holdout_mean = rfm_train_test["frequency_holdout"].mean() correction_coef = freq_holdout_mean / freq_cal_mean correction_coef
この補正係数を使い予測値を補正しプロットします。
以下、コードです。
# 実測値と補正済み予測値の代入
actual = rfm_train_test['frequency_holdout']
predicted = correction_coef * predicted
# 散布図(予測Predict×実測Actual)
xylim = max(max(predicted), max(actual))*1.1
plt.scatter(predicted, actual)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.xlim(0,xylim)
plt.ylim(0,xylim)
plt.plot([0, xylim], [0,xylim], ls="--", c=".3")
plt.show()
# 予測精度
print('RMSE:')
print(mean((actual - predicted)**2)**.5)
print('MAE:')
print(mean_absolute_error(actual, predicted))
print('R:')
print(np.corrcoef(actual, predicted)[0,1])
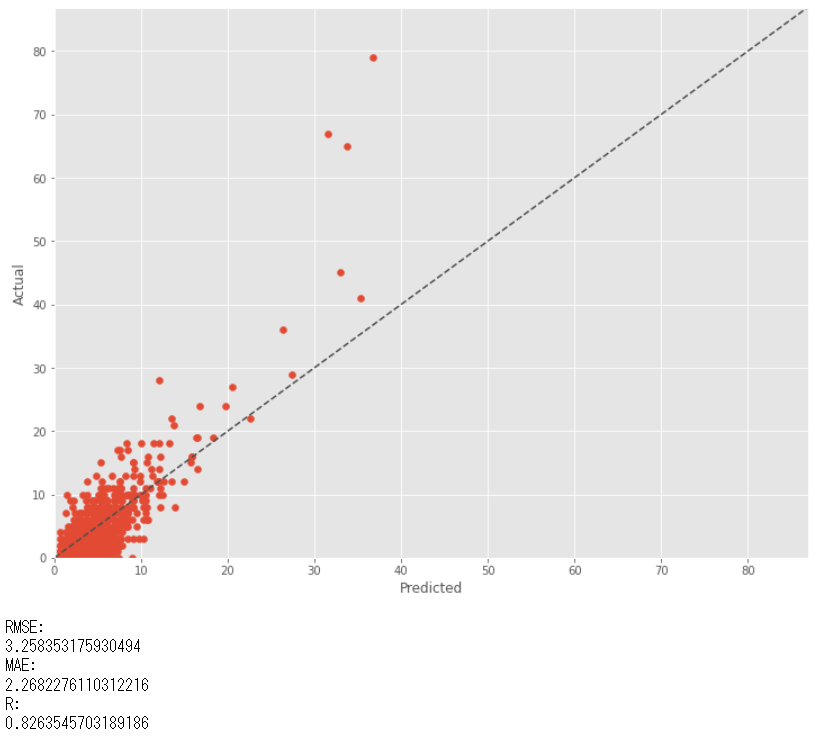
以下、実行結果です。
購買金額モデル(GGモデル)
金額/回をGGモデル(Gamma-Gamma model)で予測します。このモデルも先程登場したFaderら(2005)のモデルが元になっています。
では、学習データ期間(前半半年)のデータ(変数)を使ってモデルを構築します。
以下、コードです。
# GGモデルの学習(学習期間)
ggf = GammaGammaFitter(penalizer_coef=0)
ggf.fit(
rfm_train_test['frequency_cal'],
rfm_train_test['monetary_value_cal']
)
構築したモデルを使って、テストデータ期間(後半半年)の予測をします。
以下、コードです。
#予測
predicted_ggf = ggf.conditional_expected_average_profit(
rfm_train_test['frequency_cal'],
rfm_train_test['monetary_value_cal']
)
テストデータ期間(後半半年)の実測値(actual)と予測値(predicted)を比較してみます。
以下、コードです。
# 実測値と予測値の代入
actual = rfm_train_test['monetary_value_holdout']
predicted = predicted_ggf
# 散布図(予測Predict×実測Actual)
xylim = max(max(predicted), max(actual))*1.1
plt.scatter(predicted, actual)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.xlim(0,xylim)
plt.ylim(0,xylim)
plt.plot([0, xylim], [0,xylim], ls="--", c=".3")
plt.show()
# 予測精度
print('RMSE:')
print(mean((actual - predicted)**2)**.5)
print('MAE:')
print(mean_absolute_error(actual, predicted))
print('R:')
print(np.corrcoef(actual, predicted)[0,1])
以下、実行結果です。(RMSE:二乗平均平方根誤差、MAE:平均絶対誤差、R:重相関係数)
これで、購買回数を予測するBG/NBDモデル(Beta Geometric/Negative Binomial Distribution)と、金額/回を予測するGGモデル(Gamma-Gamma model)ができました。
次に、この2つのモデルを融合しCLTV(顧客生涯価値)モデルを構築します。
CLTV(顧客生涯価値)予測
テストデータ期間(後半半年)のCLTV(顧客生涯価値)を予測します。
以下、コードです。
# CLTV予測
cltv = ggf.customer_lifetime_value(
bgf, #the model to use to predict the number of future transactions
rfm_train_test['frequency_cal'],
rfm_train_test['recency_cal'],
rfm_train_test['T_cal'],
rfm_train_test['monetary_value_cal'],
time=6, # months
discount_rate=0.01
)
# データセットにCLTV追加
rfm_train_test['cltv'] = cltv
timeで予測期間(月)を指定します。月単位です。今回の場合はテストデータ期間が後半半年なのでtime=6としています。timeを変更することで、予測する期間の長さを変化させることができます。
では、テストデータ期間(後半半年)の実測値(actual)と予測値(predicted)を比較してみます。
以下、コードです。
# 実測値と予測値の代入
actual = rfm_train_test['frequency_holdout']*rfm_train_test['monetary_value_holdout']
predicted = rfm_train_test['cltv']
# 散布図(予測Predict×実測Actual)
xylim = max(max(predicted), max(actual))*1.1
plt.scatter(predicted, actual)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.xlim(0,xylim)
plt.ylim(0,xylim)
plt.plot([0, xylim], [0,xylim], ls="--", c=".3")
plt.show()
# 予測精度
print('RMSE:')
print(mean((actual - predicted)**2)**.5)
print('MAE:')
print(mean_absolute_error(actual, predicted))
print('R:')
print(np.corrcoef(actual, predicted)[0,1])
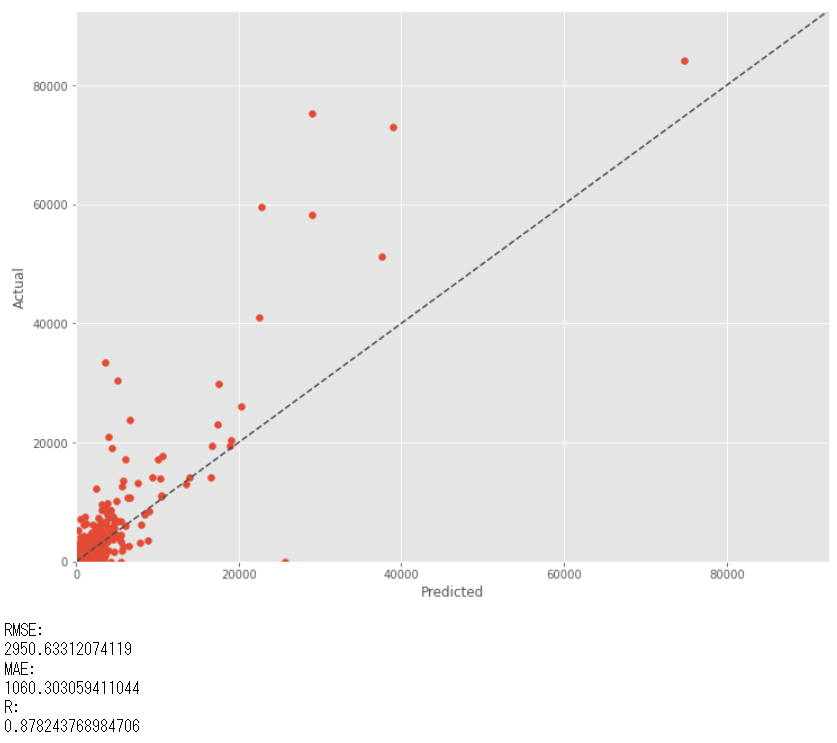
以下、実行結果です。(RMSE:二乗平均平方根誤差、MAE:平均絶対誤差、R:重相関係数)
前半半年(学習データ期間)よりも後半半年(テストデータ期間)の方が、購買回数の実測値(actual)が大きい影響からか、CLTV(顧客生涯価値)の予測値も、前半半年(学習データ期間)よりも後半半年(テストデータ期間)の方が大きくなっています。
この差分は、季節性が影響しているのかもしれません。先程の言いましたが、本来であれば、半年ではなく「学習データ期間:1年間」「テストデータ期間:1年間」とした方がいいでしょう。
購買回数モデル(BG/NBDモデル)のときと同様に、補正係数を使い予測値を補正しプロットします。
以下、コードです。
# 実測値と補正済み予測値の代入
actual = rfm_train_test['frequency_holdout']*rfm_train_test['monetary_value_holdout']
predicted = correction_coef * predicted
# 散布図(予測Predict×実測Actual)
xylim = max(max(predicted), max(actual))*1.1
plt.scatter(predicted, actual)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.xlim(0,xylim)
plt.ylim(0,xylim)
plt.plot([0, xylim], [0,xylim], ls="--", c=".3")
plt.show()
# 予測精度
print('RMSE:')
print(mean((actual - predicted)**2)**.5)
print('MAE:')
print(mean_absolute_error(actual, predicted))
print('R:')
print(np.corrcoef(actual, predicted)[0,1])
以下、実行結果です。
運用時に使うモデルを構築しCLTVを予測
ここまでは、CLTV(顧客生涯価値)予測モデルの検討です。
この結果が満足するものと判断したら、次に実施すべきは実際の運用時に使うモデルの構築です。
実際の運用時に使うモデルは、データを分割せず全データ期間を使い学習し求めます。
要するに、1年間のデータでCLTV(顧客生涯価値)予測モデルを構築し、次年1年間(time=12)の顧客価値を予測します。
以下、コードです。
# BG/NBDモデルの学習
bgf = BetaGeoFitter(penalizer_coef=0)
bgf.fit(
rfm['frequency'],
rfm['recency'],
rfm['T']
)
# GGモデルの学習(学習期間)
ggf = GammaGammaFitter(penalizer_coef=0)
ggf.fit(
rfm['frequency'],
rfm['monetary_value']
)
# CLTV予測
cltv = ggf.customer_lifetime_value(
bgf, #the model to use to predict the number of future transactions
rfm['frequency'],
rfm['recency'],
rfm['T'],
rfm['monetary_value'],
time=12, # months
freq='D',
discount_rate=0.01
)
# データセットにCLTV追加
rfm['cltv'] = cltv
次年1年間の価値の高い順に顧客を出力します(Top10)。
以下、コードです。
# CLTV Top10
rfm.sort_values('cltv', ascending=False).head(10)
以下、実行結果です。
CLTV(顧客生涯価値)と言いながら「1年間だけ???」と思われた方もいることでしょう。
長期間にするためには、幾つか方法があります。1つは顧客ごとに年間購買金額と離反確率を予測し、CLTV(顧客生涯価値)を見積もる(CLTV = 年間購買金額÷離反率)という方法です。
一様、BG/NBDモデルから生存確率を求めることができますので、離反確率( = 1 – 生存確率 )も計算できます。
以下、コードです。
# 生存確率
alive = bgf.conditional_probability_alive(
rfm['frequency'],
rfm['recency'],
rfm['T']
)
# 離反確率(データフレームで出力)
pd.DataFrame(1-alive)
以下、実行結果です。
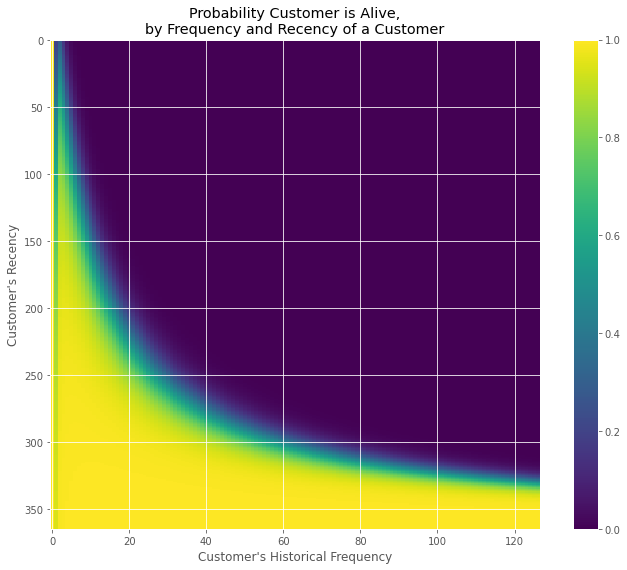
面白いことに、パッケージLifetimesに、生存確率(alive)をグラフ化する関数があります。
以下、コードです。
from lifetimes.plotting import plot_probability_alive_matrix plot_probability_alive_matrix(bgf)
以下、実行結果です。
もっとシンプルに長期間のCLTV(顧客生涯価値)を見積もる方法があります。
予測期間(time)を長くすればいいのです。
先程の予測期間(time)は1年間(12ヶ月間)でした。それを10年間(120ヶ月間)や100年間(1200ヶ月間)などと、長くすればいいのです。
実際に見積もってみます。以下コードです。
# BG/NBDモデルの学習
bgf = BetaGeoFitter(penalizer_coef=0)
bgf.fit(
rfm['frequency'],
rfm['recency'],
rfm['T']
)
# GGモデルの学習(学習期間)
ggf = GammaGammaFitter(penalizer_coef=0)
ggf.fit(
rfm['frequency'],
rfm['monetary_value']
)
# CLTV12予測(1年間)
cltv = ggf.customer_lifetime_value(
bgf,
rfm['frequency'],
rfm['recency'],
rfm['T'],
rfm['monetary_value'],
time=12, # months
freq='D',
discount_rate=0.01
)
# データセットにCLTV12追加
rfm['cltv12'] = cltv
# CLTV120予測(10年間)
cltv = ggf.customer_lifetime_value(
bgf,
rfm['frequency'],
rfm['recency'],
rfm['T'],
rfm['monetary_value'],
time=120, # months
freq='D',
discount_rate=0.01
)
# データセットにCLTV120追加
rfm['cltv120'] = cltv
# CLTV1200予測(100年間)
cltv = ggf.customer_lifetime_value(
bgf,
rfm['frequency'],
rfm['recency'],
rfm['T'],
rfm['monetary_value'],
time=1200, # months
freq='D',
discount_rate=0.01
)
# データセットにCLTV120追加
rfm['cltv1200'] = cltv
# CLTV Top10
rfm.sort_values('cltv12', ascending=False).head(10)
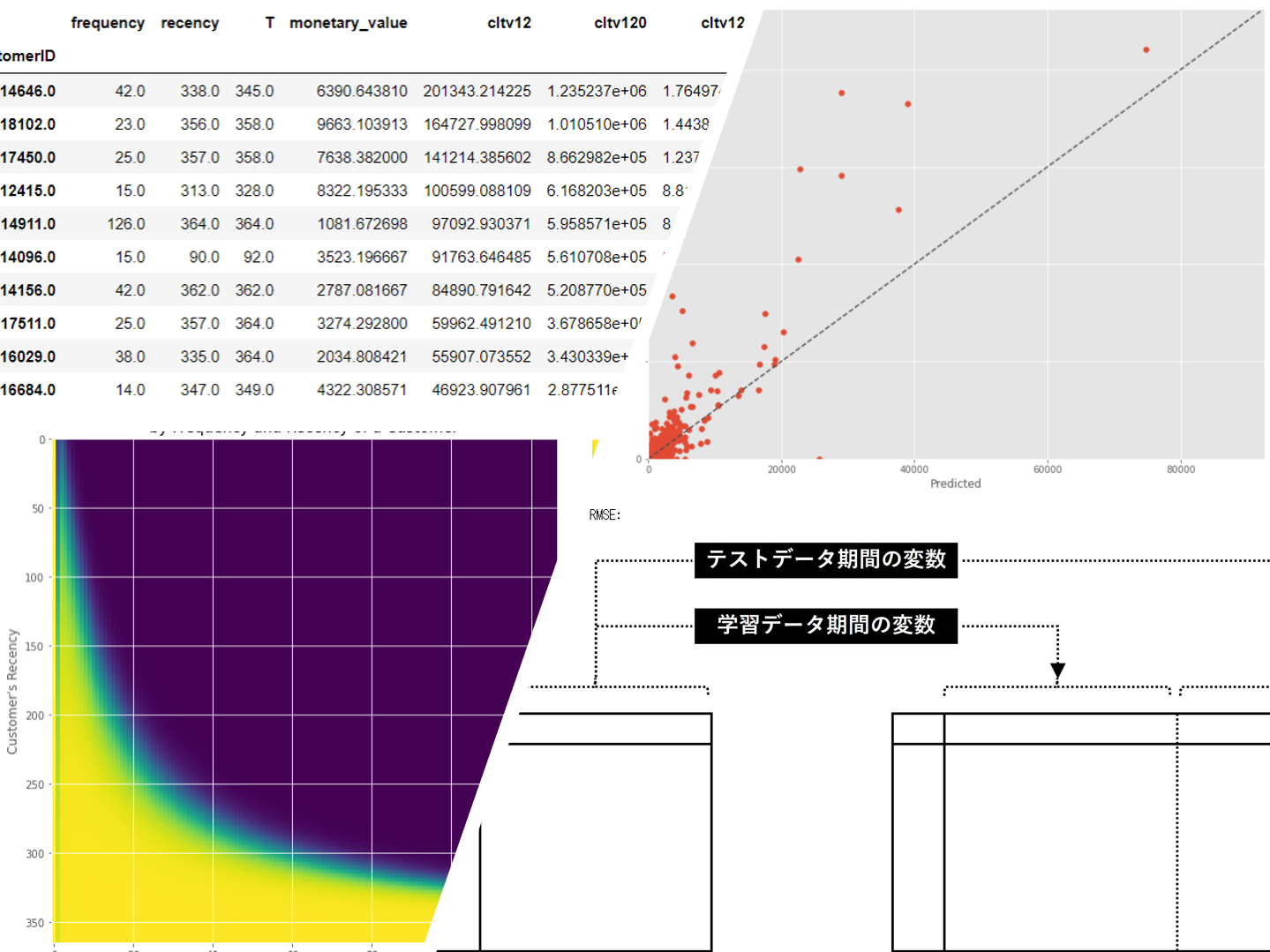
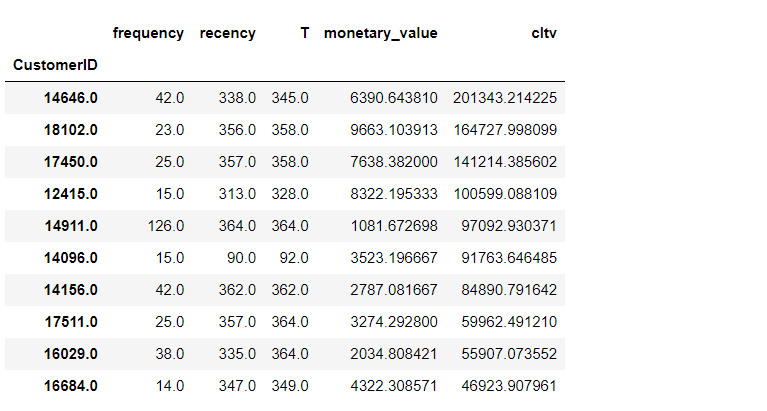
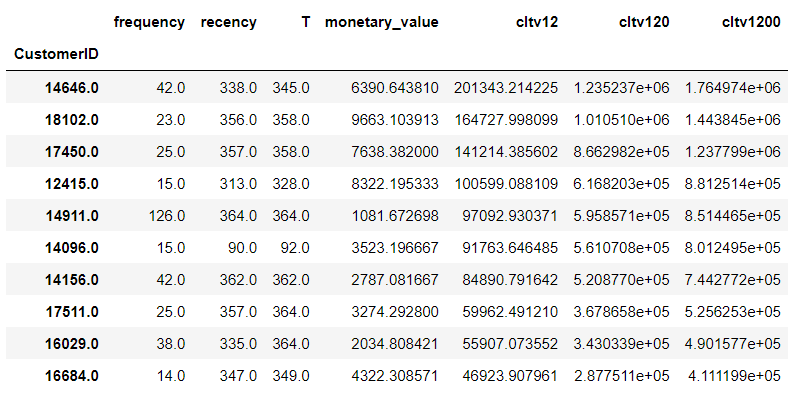
以下、実行結果です。
Top1のCustomerID:14646のCLTV(顧客生涯価値)を見比べてみます。小数点を丸めています。
- CLTV12(1年間): 201,343
- CLTV120(10年間):1,235,237
- CLTV1200(100年間):1,764,974
流石に、CLTV12(1年間)とCLTV120(10年間)は大きく異なりますが、CLTV120(10年間)とCLTV1200(100年間)の差は期間差(90年間)に比べそれほど大きくありません。
CLTV(顧客生涯価値)を考えるビジネスを、どのくらいの先まで考えるかで決めればよいかと思います。
まとめ
今回は、「顧客別CLTV(顧客生涯価値)モデルを Python Lifetimes でサクッと作る方法を事例で学ぶ」というお話しをしました。
Rでも実施できないだろうか? ということで、別の記事でR言語を使ったCLTV(顧客生涯価値)モデルの作り方を解説します。