Python のハイパーパラメータ自動最適化ライブラリー Optuna その4
– 時系列Facebook ProphetモデルをOptunaで自動最適化 –

6145
Python のハイパーパラメータ自動最適化ライブラリー Optuna その4 – 時系列Facebook ProphetモデルをOptunaで自動最適化 –

時系列解析モデルと聞くと、AIRMAモデルや状態空間モデルなどの数理統計学系のモデルをイメージする人も多いことでしょう。そして難しく感じた人も多いことでしょう。

時系列モデルは難しそうなイメージがありますが、あまり数理的なバックボーンが無くても手軽に活用できる、時系列モデルもあります。

Facebookによって開発されたProphetというモデルです。

非常に使い勝手がよく、高度な数理的な前提知識なく使えます。時系列データの外れ値検知や変化点検知、そして将来予測に使えます。

Prophetは、高度な数理的な前提知識なく使え将来予測に使えますが、ハイパーパラメータをチューニングすることで、さらなる予測精度を叩き出します。

ハイパーパラメータのチューニングは、面倒なものです。それをらくらく実施するのが、ハイパーパラメータ自動最適化ライブラリー Optunaです。

Python の ハイパーパラメータ自動最適化ライブラリー Optuna その1 – Optuna のちょっとした使い方 –

正直、Optunaを使うと時間が掛かりますが、単にProphetモデルを構築するよりも、確実により高精度な将来予測モデルを構築することができます。

今回は、デフォルトの設定のまま構築したProphetモデルと、Optunaでハイパーパラメータチューニングして構築したProphetモデルを構築し、その予測精度を比較してみたいと思います。

事前準備

Prophetのライブラリーをまだインストールされていない方は、以下の記事などを参考に、インストールなどの事前準備をして頂ければと思います。

 

利用するサンプルデータ

今回は、以下の3つのサンプルデータを利用します。

  • Peyton ManningのWikipediaのPV（ページビュー数）
  • Airline Passengers（飛行機乗客数）
  • Australian wine sales（オーストラリアのワイン販売量）

 

Peyton ManningのWikipediaのPV（ページビュー数）が日単位の時系列データで、残りの2つは月単位の時系列データになります。

Peyton ManningのWikipediaのPV（ページビュー）は、Prophetで提供されているサンプルデータ（example_wp_log_peyton_manning.csv）の1つです。facebook/prophetのGitHubからダウンロードして使って頂くか、弊社のHPからダウンロードして使って頂ければと思います。

facebook/prophetのGitHub上のデータ
https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/bgr8

 

Airline Passengers（飛行機乗客数）は、Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h

 

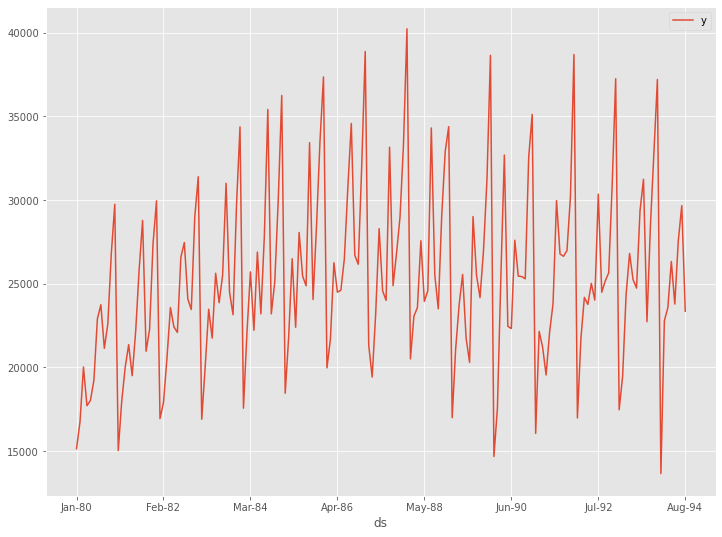
Australian wine sales（オーストラリアのワイン販売量）は、1980年1月から1994年8月までのオーストラリアのワインメーカーによるワイン販売を記録した月単位のデータです。

弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/l6p7

 

精度評価指標

学習データで予測モデルを構築し、テストデータで精度検証していきます。

予測精度評価で利用する指標は、二乗平均平方根誤差（RMSE、Root Mean Squared Error）と平均絶対誤差（MAE、Mean Absolute Error）、平均絶対パーセント誤差（MAPE、Mean absolute percentage error）です。 

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • \overline{y^{actual}} ・・・実測値の平均
  • n ・・・実測値・予測値の数

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

ライブラリーの読み込み

先ず、共通して利用するライブラリーを読み込みます。

以下、コードです。

# ライブラリーの読み込み
import numpy as np
import pandas as pd
import optuna

from prophet import Prophet
from prophet.diagnostics import cross_validation
from prophet.diagnostics import performance_metrics

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ

 

Peyton ManningのWikipediaのPV（ページビュー数）

Peyton Manning｜データ読み込み

データセットを読み込みます。

以下、コードです。

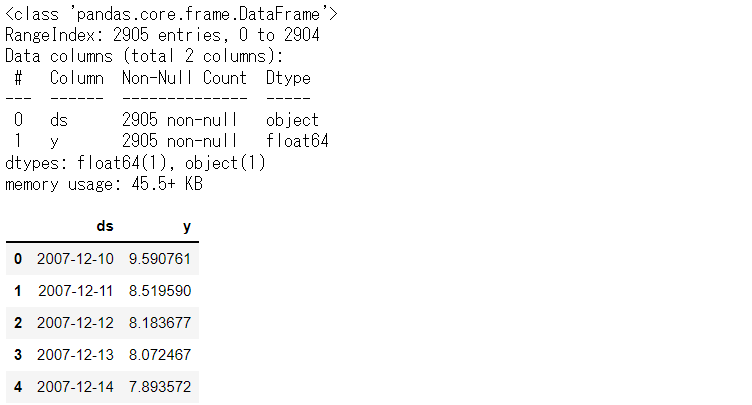
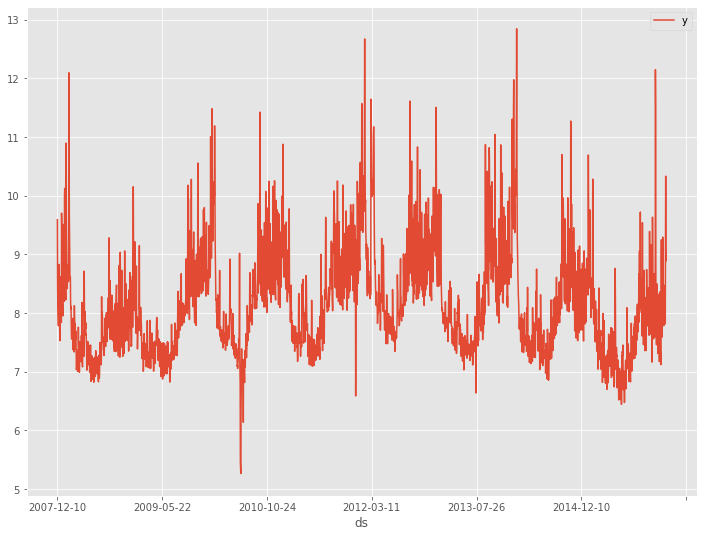
# データセット読み込み
url = 'https://www.salesanalytics.co.jp/bgr8'
df = pd.read_csv(url)
df.columns = ['ds', 'y']

# データ確認
df.plot(kind='line',x='ds', y='y')
df.info() #変数の情報
df.head() #データの一部

 

以下、実行結果です。

 

学習データとテストデータに分割します。直近1年がテストデータで、その前が学習データとします。

以下、コードです。

# 学習データとテストデータの分割
test_length = 365
df_train = df.iloc[:-test_length]
df_test = df.iloc[-test_length:]

 

Peyton Manning｜Prophet（デフォルトのまま）

デフォルトの設定のままで、Prophetの時系列モデルを構築し、構築したモデルをテストデータで精度検証します。

以下、コードです。

# 予測モデル構築
m = Prophet()
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='D')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

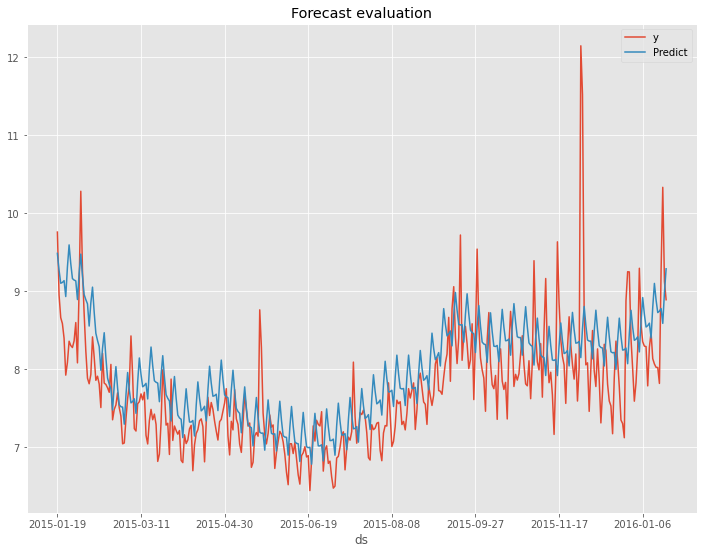
以下、実行結果です。

 

以下が、テストデータの精度評価指標の値です。

  • RMSE: 0.60
  • MAE: 0.46
  • MAPE(%): 5.87%

次から、Optunaで最適化することで、どこまで精度評価指標の値が改善するのかを見ていきます。

 

Peyton Manning｜Prophet（Optunaで最適化）

今回は、以下の3つのハイパーパラメータを対象にします。

  • changepoint_prior_scale
  • seasonality_prior_scale
  • seasonality_mode

changepoint_prior_scaleは、トレンドの柔軟性に関するパラメータで、特にトレンドの変化点でのトレンド変化量を決定します。値が大きいほどトレンドが過剰適合します。0.001～0.5の範囲が適切と言われており、デフォルトは0.05です。

seasonality_prior_scaleは、季節性の柔軟性に関するパラメータで、0.01～10の範囲が妥当と言われており、デフォルトは10です。

seasonality_modeは、周期性の表現の仕方に関するパラメータです。additiveとmultiplicativeの2種類あります。additiveの場合、単純に周期性が追加されるだけです。一方、multiplicativeの場合、トレンドの影響を受ける周期性が追加されます。イメージとしては、「観測値 = トレンド + トレンド × 周期性 + 残差」といった感じです。

 

では、OptunaでProphetモデルの最適パラメータを探します。

以下、コードです。

# 目的関数の設定（ステップ1）
def objective(trial):

    #ハイパーパラメータの集合を定義する

    params = {'changepoint_prior_scale' : 
                 trial.suggest_uniform('changepoint_prior_scale',
                                       0.001,0.5
                                      ),
              'seasonality_prior_scale' : 
                 trial.suggest_uniform('seasonality_prior_scale',
                                       0.01,10
                                      ),
              'seasonality_mode' : 
                 trial.suggest_categorical('seasonality_mode',
                                           ['additive', 'multiplicative']
                                          )
             }

    #良し悪しを判断するメトリクスを定義する

    m = Prophet(**params)
    m.fit(df_train)
    df_future = m.make_future_dataframe(periods=test_length,freq='D')
    df_pred = m.predict(df_future) 
    preds = df_pred.tail(len(df_test))

    val_rmse = np.sqrt(mean_squared_error(df_test.y, preds.yhat))

    return val_rmse

# 目的関数の最適化を実行する（ステップ2）
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)

# 最適パラメータの出力
print(f"The best value is : \n {study.best_value}")
print(f"The best parameters are : \n {study.best_params}")

 

以下、実行結果です。

 

次に、Optunaで算出した最適パラメータを使って予測モデルを構築します。

以下、コードです。

# 最適パラメータで予測モデル構築
m = Prophet(**study.best_params)
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='D')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

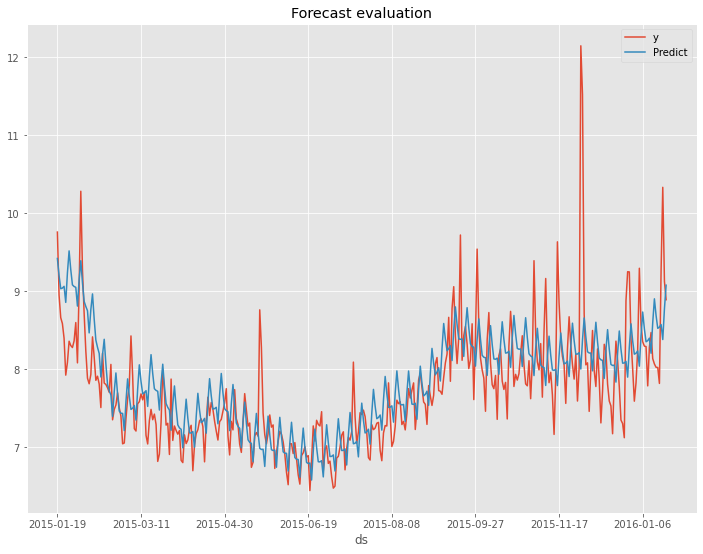
以下、実行結果です。

 

以下が、テストデータの精度評価指標の値の変化です。

  • RMSE: 0.60 → 0.55
  • MAE: 0.46 → 0.38
  • MAPE(%): 5.87% → 4.79%

左の数値がデフォルトの状態で構築したProphetモデルの精度評価指標の値で、右の数値がOptunaで最適化したパラメータで構築したProphetモデルの精度評価指標の値です。

 

Peyton Manning｜Prophet（Optunaで最適化・CV活用）

おまけに、CV（クロスバリデーション）を合わせたOptunaによる最適化の例を示します。Optunaの中の評価指標にCVの評価結果を使っています。

以下、コードです。

# 目的関数の設定（ステップ1）
def objective(trial):

    #ハイパーパラメータの集合を定義する

    params = {'changepoint_prior_scale' : 
                 trial.suggest_uniform('changepoint_prior_scale',
                                       0.001,0.5
                                      ),
              'seasonality_prior_scale' : 
                 trial.suggest_uniform('seasonality_prior_scale',
                                       0.01,10
                                      ),
              'seasonality_mode' : 
                 trial.suggest_categorical('seasonality_mode',
                                           ['additive', 'multiplicative']
                                          )
             }

    #良し悪しを判断するメトリクスを定義する

    m = Prophet(**params)
    m.fit(df_train)
    df_cv = cross_validation(m,
                             initial='730 days',
                             period='180 days',
                             horizon = '365 days',
                             parallel="processes")
    df_p = performance_metrics(df_cv)
    
    return df_p['rmse'].values[0]

# 目的関数の最適化を実行する（ステップ2）
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)

# 最適パラメータの出力
print(f"The best value is : \n {study.best_value}")
print(f"The best parameters are : \n {study.best_params}")

 

以下、実行結果です。

 

次に、Optunaで算出した最適パラメータを使って予測モデルを構築します。

以下、コードです。

# 最適パラメータで予測モデル構築
m = Prophet(**study.best_params)
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='D')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

以下、実行結果です。

 

CVを活用すると非常に時間が掛かります。他の2つのデータセットでは、CVを活用する例は示しません。あくまでもおまけとして紹介しました。

 

Airline Passengers（飛行機乗客数）

Airline Passengers｜データ読み込み

データセットを読み込みます。

以下、コードです。

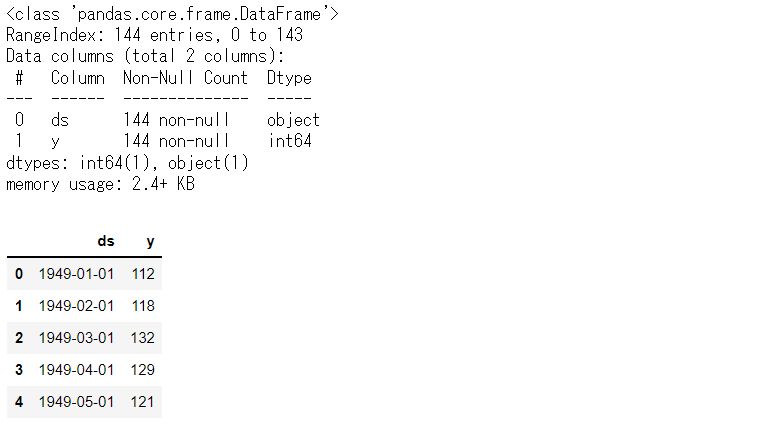
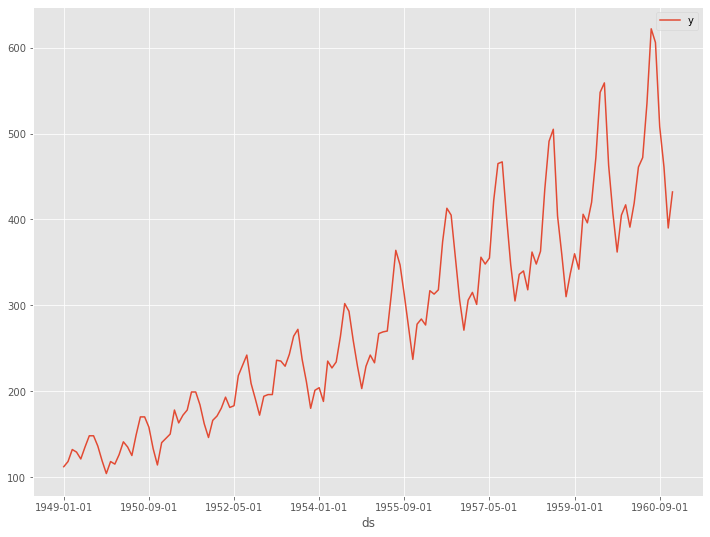
# データセット読み込み
url = 'https://www.salesanalytics.co.jp/591h'
df = pd.read_csv(url)
df.columns = ['ds', 'y']

# データ確認
df.plot(kind='line',x='ds', y='y')
df.info() #変数の情報
df.head() #データの一部

 

以下、実行結果です。

 

学習データとテストデータに分割します。直近1年がテストデータで、その前が学習データとします。

以下、コードです。

# 学習データとテストデータの分割
test_length = 12
df_train = df.iloc[:-test_length]
df_test = df.iloc[-test_length:]

 

Airline Passengers｜Prophet（デフォルトのまま）

デフォルトの設定のままで、Prophetの時系列モデルを構築し、構築したモデルをテストデータで精度検証します。

以下、コードです。

# 予測モデル構築
m = Prophet()
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='M')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

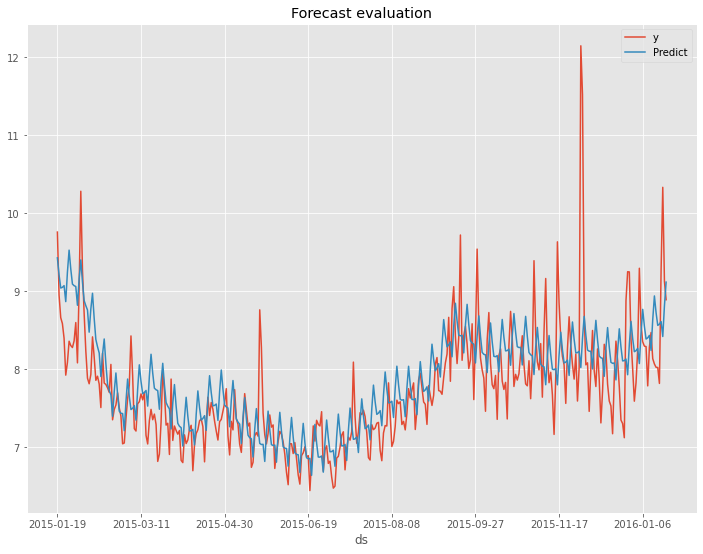
以下、実行結果です。

 

以下が、テストデータの精度評価指標の値です。

  • RMSE: 41.57
  • MAE: 34.02
  • MAPE(%): 6.78%

次に、Optunaで最適化することで、どこまで精度評価指標の値が改善するのかを見ていきます。

 

Airline Passengers｜Prophet（Optunaで最適化）

先ず、OptunaでProphetモデルの最適パラメータを探します。

以下、コードです。

# 目的関数の設定（ステップ1）
def objective(trial):

    #ハイパーパラメータの集合を定義する

    params = {'changepoint_prior_scale' : 
                 trial.suggest_uniform('changepoint_prior_scale',
                                       0.001,0.5
                                      ),
              'seasonality_prior_scale' : 
                 trial.suggest_uniform('seasonality_prior_scale',
                                       0.01,10
                                      ),
              'seasonality_mode' : 
                 trial.suggest_categorical('seasonality_mode',
                                           ['additive', 'multiplicative']
                                          )
             }

    #良し悪しを判断するメトリクスを定義する

    m = Prophet(**params)
    m.fit(df_train)
    df_future = m.make_future_dataframe(periods=test_length,freq='M')
    df_pred = m.predict(df_future) 
    preds = df_pred.tail(len(df_test))

    val_rmse = np.sqrt(mean_squared_error(df_test.y, preds.yhat))
    return val_rmse

# 目的関数の最適化を実行する（ステップ2）
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)

# 最適パラメータの出力
print(f"The best value is : \n {study.best_value}")
print(f"The best parameters are : \n {study.best_params}")

 

以下、実行結果です。

 

次に、Optunaで算出した最適パラメータを使って予測モデルを構築します。

以下、コードです。

# 最適パラメータで予測モデル構築
m = Prophet(**study.best_params)
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='M')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

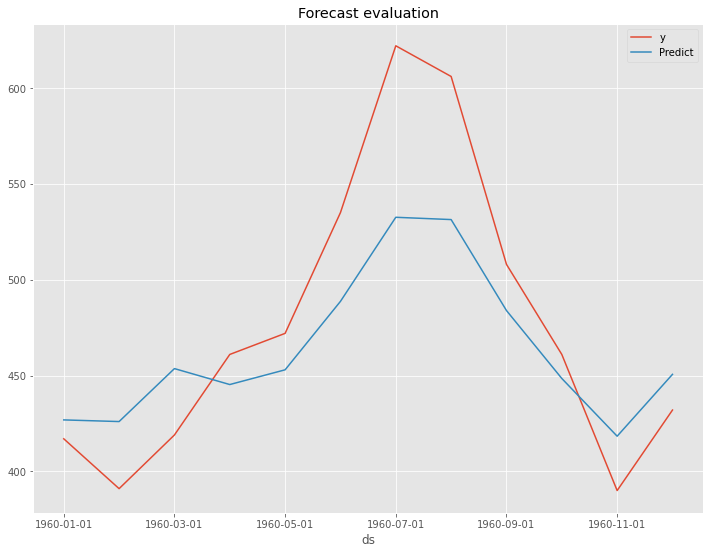
以下、実行結果です。

 

以下が、テストデータの精度評価指標の値の変化です。

  • RMSE: 41.57 → 19.68
  • MAE: 34.02 → 17.39
  • MAPE(%): 6.78% → 3.60%

左の数値がデフォルトの状態で構築したProphetモデルの精度評価指標の値で、右の数値がOptunaで最適化したパラメータで構築したProphetモデルの精度評価指標の値です。

 

Australian wine sales（オーストラリアのワイン販売量）

Australian wine sales｜データ読み込み

データセットを読み込みます。

以下、コードです。

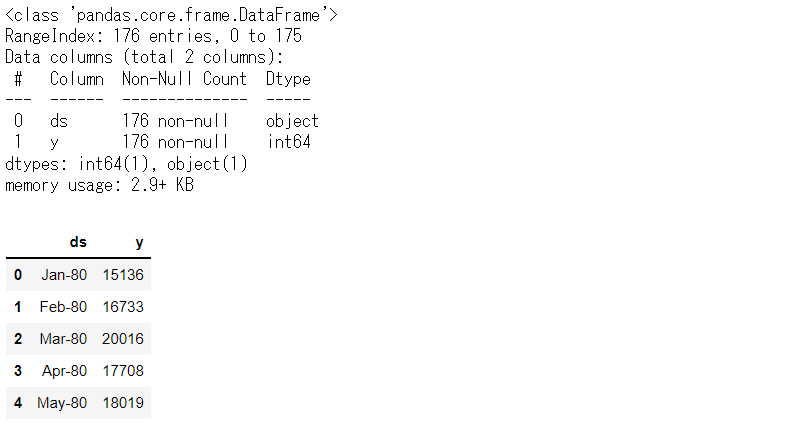
# データセット読み込み
url = 'https://www.salesanalytics.co.jp/l6p7'
df = pd.read_csv(url)
df.columns = ['ds', 'y']

# データ確認
df.plot(kind='line',x='ds', y='y')
df.info() #変数の情報
df.head() #データの一部

 

以下、実行結果です。

 

学習データとテストデータに分割します。直近1年がテストデータで、その前が学習データとします。

以下、コードです。

# 学習データとテストデータの分割
test_length = 12
df_train = df.iloc[:-test_length]
df_test = df.iloc[-test_length:]

 

Australian wine sales｜Prophet（デフォルトのまま）

デフォルトの設定のままで、Prophetの時系列モデルを構築し、構築したモデルをテストデータで精度検証します。

以下、コードです。

# 予測モデル構築
m = Prophet()
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='M')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

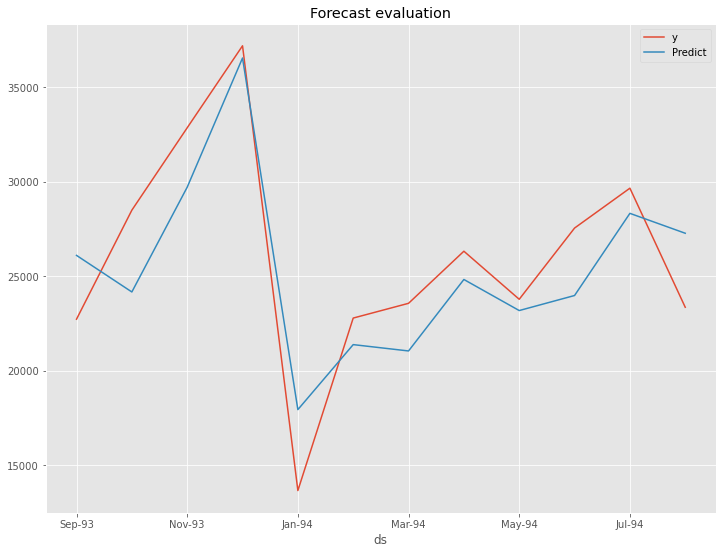
以下、実行結果です。

 

以下が、テストデータの精度評価指標の値です。

  • RMSE: 2881.68
  • MAE: 2552.34
  • MAPE(%): 11.01%

次に、Optunaで最適化することで、どこまで精度評価指標の値が改善するのかを見ていきます。

 

Australian wine sales｜Prophet（Optunaで最適化）

先ず、OptunaでProphetモデルの最適パラメータを探します。

以下、コードです。

# 目的関数の設定（ステップ1）
def objective(trial):

    #ハイパーパラメータの集合を定義する

    params = {'changepoint_prior_scale' : 
                 trial.suggest_uniform('changepoint_prior_scale',
                                       0.001,0.5
                                      ),
              'seasonality_prior_scale' : 
                 trial.suggest_uniform('seasonality_prior_scale',
                                       0.01,10
                                      ),
              'seasonality_mode' : 
                 trial.suggest_categorical('seasonality_mode',
                                           ['additive', 'multiplicative']
                                          )
             }

    #良し悪しを判断するメトリクスを定義する

    m = Prophet(**params)
    m.fit(df_train)
    df_future = m.make_future_dataframe(periods=test_length,freq='M')
    df_pred = m.predict(df_future) 
    preds = df_pred.tail(len(df_test))

    val_rmse = np.sqrt(mean_squared_error(df_test.y, preds.yhat))
    return val_rmse

# 目的関数の最適化を実行する（ステップ2）
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)

# 最適パラメータの出力
print(f"The best value is : \n {study.best_value}")
print(f"The best parameters are : \n {study.best_params}")

 

以下、実行結果です。

 

次に、Optunaで算出した最適パラメータを使って予測モデルを構築します。

以下、コードです。

# 最適パラメータで予測モデル構築
m = Prophet(**study.best_params)
m.fit(df_train)

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='M')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

# 予測精度（テストデータ期間）
## 予測値と実測値
preds = df.iloc[-test_length:].loc[:, 'Predict']
y = df.iloc[-test_length:].loc[:, 'y']

## 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y, preds)))
print('MAE:')
print(mean_absolute_error(y, preds)) 
print('MAPE(%):')
print(np.mean(abs(y - preds)/y)*100)

## グラフ化
df.iloc[-test_length:].plot(kind='line',
                            x='ds',
                            title='Forecast evaluation'
                           )

 

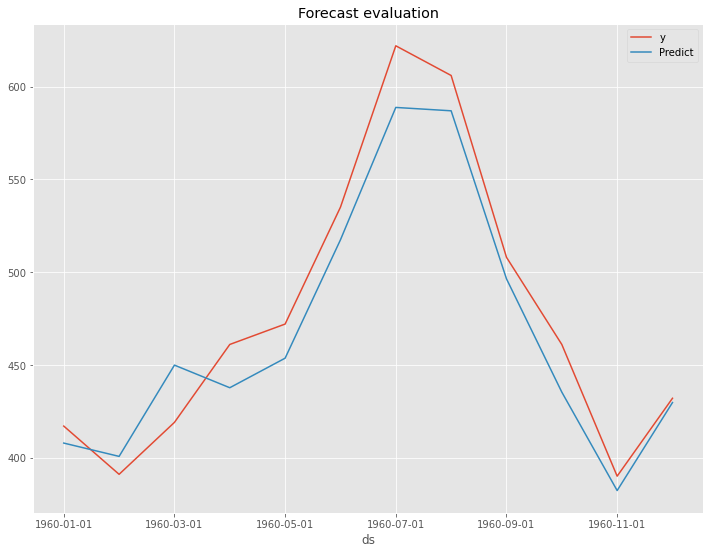
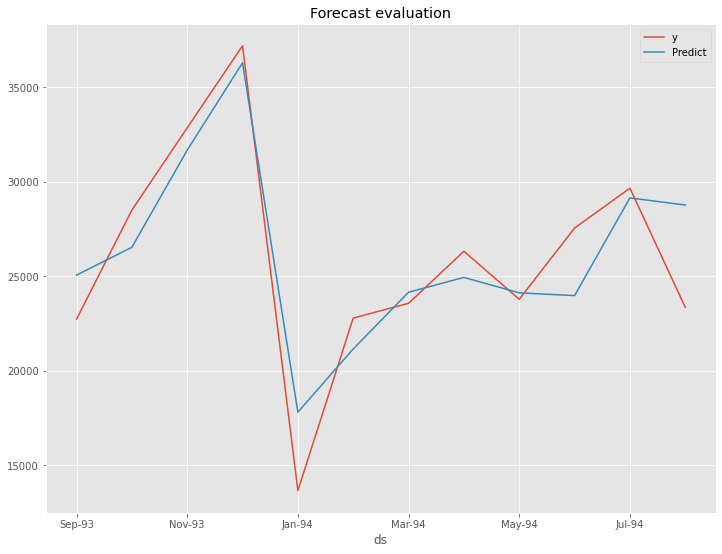
以下、実行結果です。

 

以下が、テストデータの精度評価指標の値です。

  • RMSE: 2881.68 → 2518.94
  • MAE: 2552.34 → 1998.64
  • MAPE(%): 11.01% → 8.99%

左の数値がデフォルトの状態で構築したProphetモデルの精度評価指標の値で、右の数値がOptunaで最適化したパラメータで構築したProphetモデルの精度評価指標の値です。

 

まとめ

今回は、デフォルトの設定のまま構築したProphetモデルと、Optunaでハイパーパラメータチューニングして構築したProphetモデルを構築し、その予測精度を比較しました。

当然ですが、Optunaでハイパーパラメータチューニングして構築したProphetモデルを構築した方が、予測精度が高くなりました。

今回、Optunaでチューニングしたハイパーパラメータは3つでしたが、Prophetのハイパーパラメータはもう少し多いです。

Optunaでチューニングするハイパーパラメータを増やせば増やすほど、時間がかかりますので、そのあたりのバランスを考えながら、興味のある方はチャレンジして頂ければと思います。

Optunaで学ぶベイズハイパーパラメータチューニング超入門 – 第1回: ハイパーパラメータチューニングとは？ –