時系列の深層学習(ディープラーニング)モデルの代表格がRNN(Recurrent Neural Network、リカレントニューラルネットワーク)です。
他には、RNNの長期記憶を保存できないなどの問題点を改善する形で登場したLSTM(Long Short Term Memory)や、LSTMの計算コスト大きい問題を改善する形で登場したGRU(Gated Recurrent Unit)などがあります。
今回は、時系列の深層学習(ディープラーニング)モデルの中で最もシンプルなRNN(Recurrent Neural Network、リカレントニューラルネットワーク)のモデル構築方法と1期先予測(1-Step ahead prediction)についてお話しします。
PythonのKeras(TensorFlow)を使います。
Contents [hide]
- KerasとTensorFlow
- KerasとTensorFlowのインストール
- RNN(Recurrent Neural Network )とは?
- 構築するRNNモデル
- 利用するデータセット
- 予測精度の評価指標
- 準備
- 準備|必要なライブラリーの読み込み
- 準備|データセットの読み込み
- 準備|最低限の前処理とデータ分割
- シンプルRNN(ラグ変数:features)
- シンプルRNN(ラグ変数:features)|データ準備
- シンプルRNN(ラグ変数:features)|モデル生成
- シンプルRNN(ラグ変数:features)|学習
- シンプルRNN(ラグ変数:features)|検証
- シンプルRNN(ラグ変数:time steps)
- シンプルRNN(ラグ変数:time steps)|データ準備
- シンプルRNN(ラグ変数:time steps)|モデル生成
- シンプルRNN(ラグ変数:time steps)|学習
- シンプルRNN(ラグ変数:time steps)|検証
- 深層RNN(ラグ変数:features)
- 深層RNN(ラグ変数:features)|データ準備
- 深層RNN(ラグ変数:features)|モデル生成
- 深層RNN(ラグ変数:features)|学習
- 深層RNN(ラグ変数:features)|検証
- 深層RNN(ラグ変数:time steps)
- 深層RNN(ラグ変数:time steps)|データ準備
- 深層RNN(ラグ変数:time steps)|モデル生成
- 深層RNN(ラグ変数:time steps)|学習
- 深層RNN(ラグ変数:time steps)|検証
- 次回
KerasとTensorFlow
簡単にKerasとTensorFlowについてお話しします。
Kerasは、Pythonで書かれたこのオープンソースの深層学習(ディープラーニング)ライブラリーです。Keras単体でも動作しますが、Tensorflowなどをバックエンドで動作させ使うことが多いです。
Tensorflowは、Googleによって開発されたオープンソースの深層学習(ディープラーニング)フレームワークです。
Tensorflowの名称は「Tensor」と「Flow」を合わせたもので、「Tensor」は数学で登場してくる行列の概念を一般化した「テンソル」(Tensor)です。「Flow」は、Tensorflowでモデル構築するとき、タスクにデータのフローを流しこむ形のフレームワークだからかと思います。
Tensorflowは正直レベルが高く、どちらかというと使い方が分かりにくいです。一方、Kerasは比較的シンプルなため、使い方は分かりやすいです。
ということで、Kerasを使ってTensorflowをバックエンドで動かすのが、いいでしょう。Kerasに頼らずTensorflowのみを使用すると、事前に色々な関数を定義したりと非常に煩雑になります。
KerasとTensorFlowのインストール
KerasとTensorFlowを使うには、ライブラリーをインストールしておく必要があります。
コマンドプロンプト上で、condaでインストールするときのコードは以下です。
conda install tensorflow
TensorflowにKerasが組み込まれていますので、別途Kerasをインストールする必要はありませんが、単体でKerasを使用したい場合には別途インストールしておく必要があります。
以下、condaでインストールするときのコードです。
conda install keras
pipでインストールするときのコードは以下です。
pip install tensorflow pip install keras
Kerasのモデルの可視化機能(plot_model)を活用する場合には、以下のライブラリーをインストールしておく必要があります。
- pydot
- graphviz
コマンドプロンプト上で、condaでインストールするときのコードは以下です。
conda install pydot conda install graphviz
pipでインストールするときのコードは以下です。
pip install pydot pip install graphviz
Windows環境の場合、事前にMicrosoft Visual C++ 再頒布可能パッケージ(Visual Studio 2015、2017、2019、2022)をインストールしておく必要があります。
以下のサイトからMicrosoft Visual C++をダウンロードしPCにインストールして頂ければと思います。
Microsoft Visual C++ のダウンロード サイト
https://docs.microsoft.com/ja-jp/cpp/windows/latest-supported-vc-redist
(x86が32ビット版Windows用、x64が64ビット版Windows用)
RNN(Recurrent Neural Network )とは?
RNNは、「内部に再帰的な構造」(出力が入力に戻るループ構造)を持つニューラルネットワークです。

一般的なニューラルネットワークは、時間依存の特徴量を用いた学習が得意ではありません。ニューラルネットワークの中間層に「内部に再帰的な構造」(出力が入力に戻るループ構造)を導入することで、時間依存の特徴量を用いた学習が可能になります。
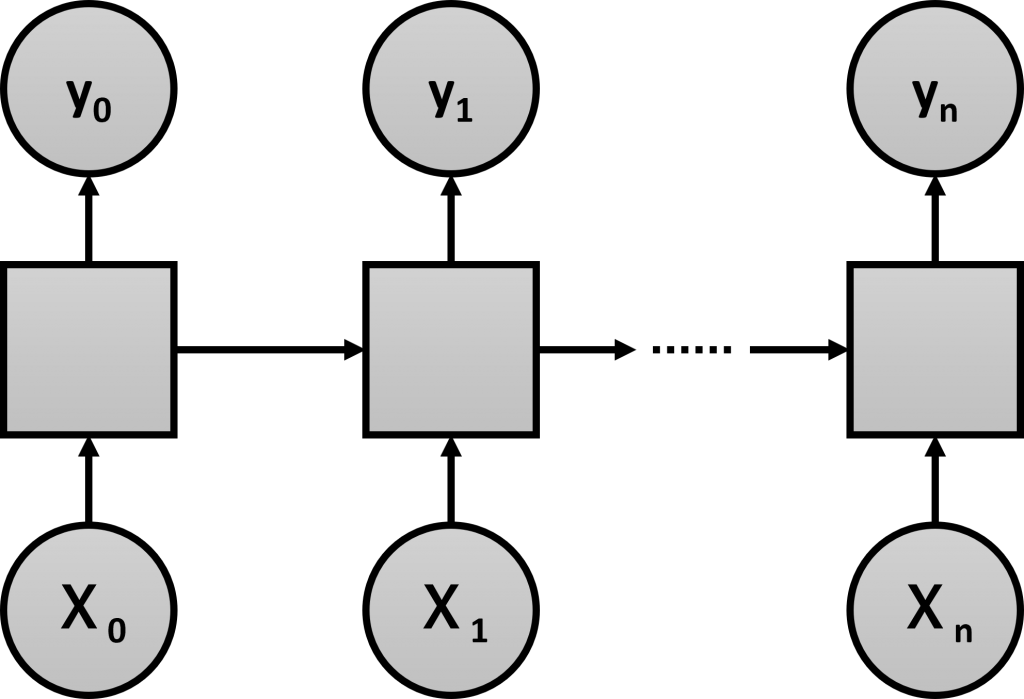
ただRNNは、短期記憶的な学習は得意ですが、長期記憶的な学習は不得意という問題があります。
言い換えると、最近の有用な情報(短期的に有用な情報)を重視するが、将来有用な情報(長期的な有用な情報)をあまり重視しないという問題です。
将来有用な情報(長期的な有用な情報)を考慮すべき場合、RNNでは不十分になります。その場合は、LSTMやGRUを用いることになります。
構築するRNNモデル
今回は、以下の2種類のRNNモデルを構築します。
- シンプルRNN(RNN層が1層)
- 深層RNN(RNN層が2層以上)
Keras(TensorFlow)のRNNのデータセットは、以下のような3元構造が基本になっています。
通常のデータセットは少なくとも2次元構造([samples,features])である必要がりますが、時系列データということもあり少なくとも3次元構造([samples,time_steps,features])である必要があります。
時系列データの特徴量の1つとして、ラグ変数というものがあります。
例えば、日販(1日の売上)であれば、「ラグ1の変数」とは「1日前の日販の変数」、「ラグ2の変数」とは「2日前の日販の変数」などです。
今回は、説明変数のない目的変数が1変量の時系列データを扱います。目的変数のラグ変数を作り説明変数として利用することができます。
このとき、ラグ変数を特徴量(features)として扱うこともできますし、タイムステップ(time steps)として扱うこともできます。
ということで、以下の2種類のデータセットそれぞれで、モデルを試してみます。
- ラグ変数を特徴量(features)とするデータセット
- ラグ変数をタイムステップ(time steps)とするデータセット
要は、以下の4パターンのRNNモデルを構築し、1期先予測(1-Step ahead prediction)を実施し精度検証します。
- シンプルRNN(ラグ変数:features)
- シンプルRNN(ラグ変数:time steps)
- 深層RNN(ラグ変数:features)
- 深層RNN(ラグ変数:time steps)
利用するデータセット
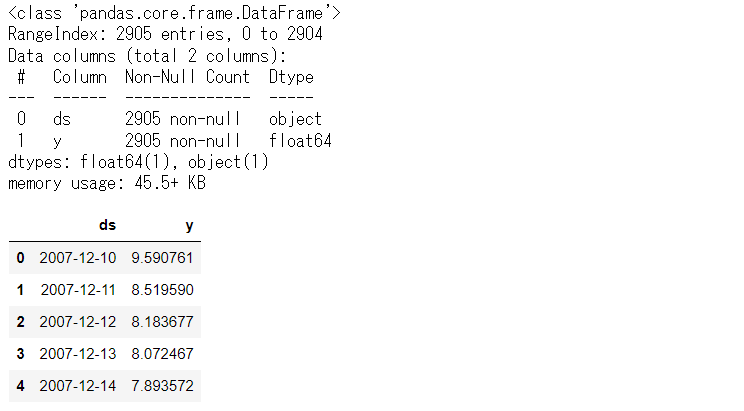
今回利用するのは、Peyton ManningのWikipediaのPV(ページビュー)というProphetで提供されているサンプルデータ(example_wp_log_peyton_manning.csv)の1つです。
facebook/prophetのGitHubからダウンロードして使って頂くか、弊社のHPからダウンロードして使って頂ければと思います。
facebook/prophetのGitHub上のデータ
https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/bgr8
このデータセットは、説明変数のない目的変数が1変量の時系列データです。もちろん、目的変数は、日単位のPV(ページビュー数)です。
PV(ページビュー数)のラグ変数を作り説明変数にします。要するに、過去のPVから未来のPVを予測する、ということです。
予測精度の評価指標
今回は、RMSE(二乗平均平方根誤差、Root Mean Squared Error)とMAE(平均絶対誤差、Mean Absolute Error)、MAPE(平均絶対パーセント誤差、Mean absolute percentage error)を使います。
以下の記号を使い精度指標の説明をします。
■ 二乗平均平方根誤差(RMSE、Root Mean Squared Error)
■ 平均絶対誤差(MAE、Mean Absolute Error)
■ 平均絶対パーセント誤差(MAPE、Mean absolute percentage error)
準備
準備|必要なライブラリーの読み込み
必要なライブラリーを読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
from keras.models import Sequential
from keras.layers import *
from keras.callbacks import EarlyStopping
from tensorflow.keras.utils import plot_model
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
準備|データセットの読み込み
データセットを読み込みます。
以下、コードです。
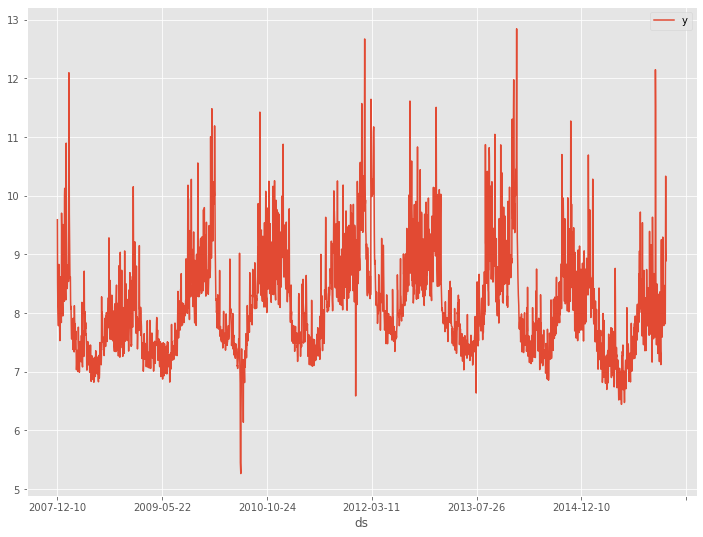
# データセット読み込み url = 'https://www.salesanalytics.co.jp/bgr8' df = pd.read_csv(url) # データ確認 df.plot(kind='line',x='ds', y='y') df.info() #変数の情報 df.head() #データの一部
以下、実行結果です。
準備|最低限の前処理とデータ分割
データセット作成の下準備として、必要な型変換を実施します。
以下、コードです。
# 変換
dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32') #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換
dataset #確認
以下、実行結果です。
今回は、説明変数のない目的変数が1変量の時系列データを扱います。目的変数のラグ変数を作り説明変数として利用することができます。
ということで、先ずラグ変数を作る生成関数を定義し、その生成関数を使いラグ変数を作ります。
以下、ラグ変数を作る生成関数のコードです。
# ラグ付きデータセット生成関数
def gen_dataset(dataset, lag_max):
X, y = [], []
for i in range(len(dataset) - lag_max):
a = i + lag_max
X.append(dataset[i:a, 0]) #ラグ変数
y.append(dataset[a, 0]) #目的変数
return np.array(X), np.array(y)
この関数は、ラグ変数を作り、元のデータは目的変数yに、ラグ変数は説明変数Xとして出力します。
先程準備したデータセットに対し、適用します。ラグの最大値(lag_max)は365日です。
以下、コードです。
# ラグ付きデータセットの生成
lag_max = 365
X, y = gen_dataset(dataset, lag_max)
print('X:',X.shape) #確認
print('y:',y.shape) #確認
以下、実行結果です。

Xは2840行(サンプル)×365列(変数)のデータで、yは2840行(サンプル)×1列(変数)のデータです。
このデータセットXとyを、学習データとテストデータに分割します。直近30日間をテストデータにしています。
以下、コードです。
# データ分割 test_length = 30 #テストデータの期間 X_train_0 = X[:-test_length,:] #学習データ X_test_0 = X[-test_length:,:] #テストデータ y_train_0 = y[:-test_length] #学習データ y_test_0 = y[-test_length:] #テストデータ y_train = y_train_0.reshape(-1,1) y_test = y_test_0.reshape(-1,1)
さらに、各変数を正規化します。今回実施する正規化は0~1の範囲に数値を収めるミニマックススケーリングです。0が最小値で、1が最大値になるように、元のデータを変換します。
以下、コードです。
# 正規化(0-1の範囲にスケーリング) ## 目的変数y scaler_y = MinMaxScaler(feature_range=(0, 1)) y_train = scaler_y.fit_transform(y_train) ## 説明変数X scaler_X = MinMaxScaler(feature_range=(0, 1)) X_train_0 = scaler_X.fit_transform(X_train_0) X_test_0 = scaler_X.transform(X_test_0)
この学習データでモデルを構築し、構築したモデルをテストデータで検証していきます。
シンプルRNN(ラグ変数:features)
中間層にRNN層を1層だけ持ったニューラルネットワークを、ラグ変数Xを特徴量(features)とした学習データで構築していきます。
構築したモデルは、テストデータで検証していきます。
シンプルRNN(ラグ変数:features)|データ準備
ラグ変数Xを特徴量(features)とした学習データとテストデータを準備します。
以下、コードです。
# モデル構築用にデータを再構成(サンプル数、タイムステップ, 特徴量数)
X_train = np.reshape(X_train_0, (X_train_0.shape[0], 1,X_train_0.shape[1]))
X_test = np.reshape(X_test_0, (X_test_0.shape[0], 1,X_test_0.shape[1]))
print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認
以下、実行結果です。
![]()
X_trainが(samples=2510, time_steps=1, features=365)で、X_testが(samples=30, time_steps=1, features=365)ということです。
要は、ラグ変数を特徴量(features)として扱うということです。
シンプルRNN(ラグ変数:features)|モデル生成
ニュラールネットワークモデルを定義し、定義したモデルをコンパイルしモデル生成します。
以下、コードです。
# モデル定義
model = Sequential()
model.add(SimpleRNN(100,
input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(1, activation='linear'))
# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam')
# モデルの視覚化
plot_model(model,show_shapes=True)
以下、実行結果です。
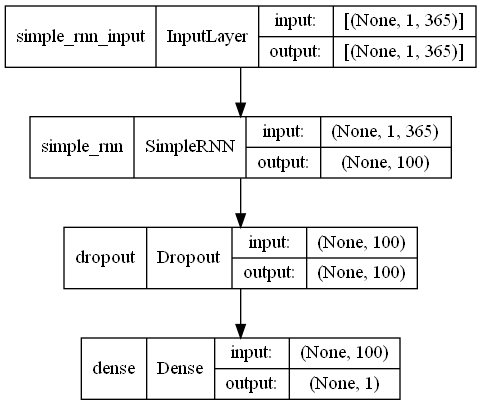
簡単にモデル定義の部分を説明します。
model=Sequential()で、シーケンシャルなニューラルネットワークのインスタンスmodelを生成します。このmodelに、層などを追加するために、model.add()を使います。
model.add(SimpleRNN(100,input_shape=(X_train.shape[1], X_train.shape[2])))で、RNN層をmodelに追加します。 input_shapeで、入力データの次元(time_steps,features)を設定します。
model.add(Dropout(0.2))で、中間層の一部を無効にする層をmodelに追加します。1つ前に追加したRNN層の一部を0.2(20%)無効化することで、ニューラルネットワークモデルの過学習を防ぎます。
model.add(Dense(1, activation=’linear’))で、1つ前の中間層を1つに集約し、予測結果を出力するための層を追加します。このとき活性化関数(activation)を指定します。今回は、単に数量を出力するため「linear」を指定しています。線形回帰式をイメージして頂ければと思います。
要は、Input -> RNN -> Dropout -> Output という非常にシンプルなニューラルネットワークモデルです。
この定義したモデル構造をコンパイル(model.compile)することで、学習できる状態にします。
コンパイルするとき、損失関数(loss)や最適化アルゴリズム(optimizer)などを指定する必要があります。
今回は、損失関数(loss)にMSE(mean_squared_error)を、最適化アルゴリズム(optimizer)にadam(adaptive moment estimation)を指定しています。
シンプルRNN(ラグ変数:features)|学習
学習データを使いモデルを学習します。
以下、コードです。
# EaelyStoppingの設定
early_stopping = EarlyStopping(monitor='val_loss',
min_delta=0.0,
patience=2)
# 学習の実行
history = model.fit(X_train, y_train,
epochs=1000,
batch_size=128,
validation_split=0.2,
callbacks=[early_stopping] ,
verbose=1,
shuffle=False)
最初なので、少し丁寧に説明します。
EarlyStoppingは、学習の更新がほぼないときに学習を止めるために設定します。具体的には、 monitor に設定した値(今回はバリデーションの損失関数の値val_loss)がpatience回(今回は2回)続けてmin_delta(今回は0.0)以上改善しないと学習がストップします。
学習するとき、学習データの一部をバリデーション用のデータとして利用します。今回は、validation_split=0.2と設定していきますので、学習データの20%がバリデーションデータです。
バリデーションデータは、ハイパーパラメータチューニングや特徴量選択などをするときに利用するデータセットで、テストデータと似た感じがしますが、位置づけが大きく異なります。
バリデーションデータとテストデータの大きな違いは、モデル構築中に利用するかどうかにあります。
- バリデーションデータ:モデル構築中に利用
- テストデータ:モデル構築後に利用
テストデータはあくまでも、構築したモデルの精度検証などをするために利用します。モデル構築時のハイパーパラメータチューニングや特徴量選択などには利用しません。
ニューラルネットワークの重要なハイパーパラメータとして、エポック数(epochs)とバッチサイズ(batch_size)というものがあります。
学習するとき、学習用のデータセットをいくつかのサブデータセットに分割し、学習に利用します。分割されたサブデータセットの最小サイズがバッチサイズ(batch_size)です。
学習は、このサブデータセット単位で、順番に実施します。例えば、サブデータセットがN個の場合、N回学習を繰り返すことになります。
このような学習を、エポック数(epochs)回実施します。例えば、エポック数(epochs)が1であれば1回、1000であれば1000回です。
簡単にまとめると……
- 学習用のデータセットをバッチサイズ(batch_size)に従ってN個のサブデータセットに分ける
- サブデータセットごとに学習を実施する(N回学習を繰り返す)
……をエポック数(epochs)回繰り返し実施します。
エポック数(epochs)が多いほどより良いモデルになりますが、あるエポック数(epochs)を超えると、モデルが改善しなくなったり、場合によっては悪化します。
適切なエポック数(epochs)は、実際に学習させてみないと分かりません。ということで、エポック数(epochs)を非常に大きな値に設定し学習してみるのがいいです。
ただ、エポック数(epochs)が非常に大きい値を設定すると、学習がいつまでも終わらないため、今回は先程説明したEarlyStoppingの機能を使いストップさせています。
他には、shuffle=Falseで、データをシャッフルしないようにしています。verbose=1で、ログをプログレスバーで出力するように指定しています。verbose=0にすると出力されなくなります。verbose=2にするとエポックごとに1行のログが出力されます。
今学習したモデルの、学習結果を出力します。
以下、コードです。
# 学習結果の出力
model.summary()
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()
以下、実行結果です。

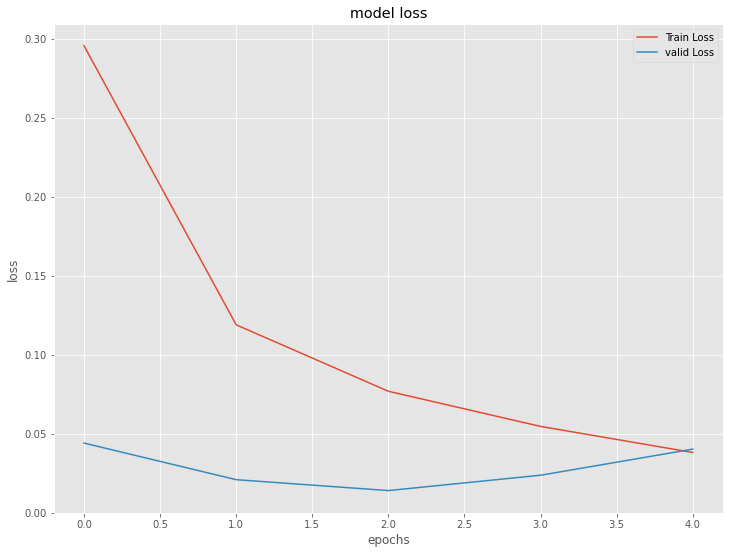
シンプルRNN(ラグ変数:features)|検証
学習したモデルを、テストデータで検証します。
以下、コードです。
# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)
# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)),
columns=['y','Predict'])
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
# グラフ化
df_test.plot(kind='line')
以下、実行結果です。

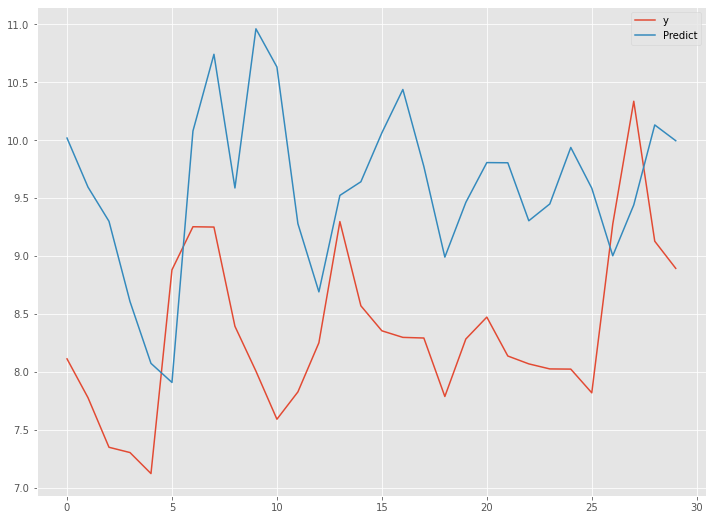
シンプルRNN(ラグ変数:time steps)
中間層にRNN層を1層だけ持ったニューラルネットワークを、ラグ変数Xをタイムステップ(time_steps)とした学習データで構築していきます。
構築したモデルは、テストデータで検証していきます。
シンプルRNN(ラグ変数:time steps)|データ準備
ラグ変数Xをタイムステップ(time_steps)とした学習データとテストデータを準備します。
以下、コードです。
# モデル構築用にデータを再構成(サンプル数、タイムステップ, 特徴量数)
X_train = np.reshape(X_train_0, (X_train_0.shape[0],X_train_0.shape[1], 1))
X_test = np.reshape(X_test_0, (X_test_0.shape[0],X_test_0.shape[1], 1))
print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認
以下、実行結果です。

X_trainが(samples=2510, time_steps=365, features=1)で、X_testが(samples=30, time_steps=365, features=1)ということです。
要は、ラグ変数をタイムステップ(time_steps)として扱うということです。
シンプルRNN(ラグ変数:time steps)|モデル生成
ニュラールネットワークモデルを定義し、定義したモデルをコンパイルしモデル生成します。
以下、コードです。
# モデル定義
model = Sequential()
model.add(SimpleRNN(100,
input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(1, activation='linear'))
# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam')
# モデルの視覚化
plot_model(model,show_shapes=True)
以下、実行結果です。
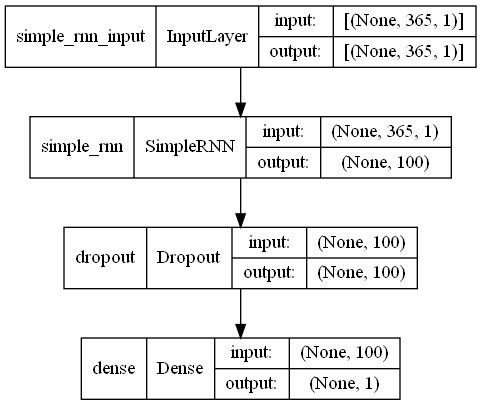
Input -> RNN -> Dropout -> Output という非常にシンプルなニューラルネットワークモデルです。
シンプルRNN(ラグ変数:time steps)|学習
学習データを使いモデルを学習します。
以下、コードです。
# EaelyStoppingの設定
early_stopping = EarlyStopping(monitor='val_loss',
min_delta=0.0,
patience=2)
# 学習の実行
history = model.fit(X_train, y_train,
epochs=1000,
batch_size=128,
validation_split=0.2,
callbacks=[early_stopping] ,
verbose=1,
shuffle=False)
今学習したモデルの、学習結果を出力します。
以下、コードです。
# 学習結果の出力
model.summary()
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()
以下、実行結果です。

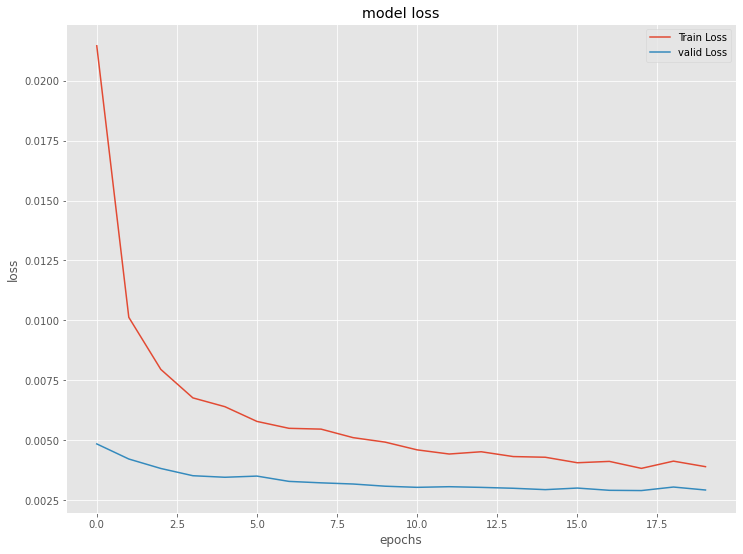
シンプルRNN(ラグ変数:time steps)|検証
学習したモデルを、テストデータで検証します。
以下、コードです。
# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)
# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)),
columns=['y','Predict'])
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
# グラフ化
df_test.plot(kind='line')

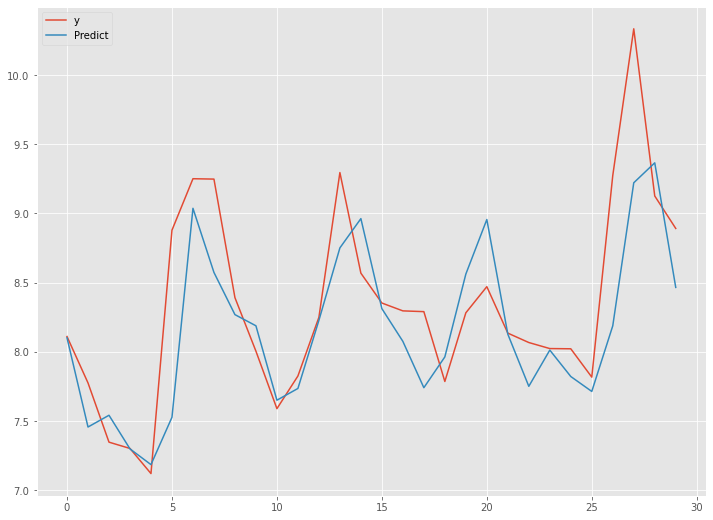
予測精度は、先程のRNNモデルに比べ大分良くなっています。
深層RNN(ラグ変数:features)
中間層にRNN層を2層持ったニューラルネットワークを、ラグ変数Xを特徴量(features)とした学習データで構築していきます。
構築したモデルは、テストデータで検証していきます。
深層RNN(ラグ変数:features)|データ準備
ラグ変数Xを特徴量(features)とした学習データとテストデータを準備します。
以下、コードです。
# モデル構築用にデータを再構成(サンプル数、タイムステップ, 特徴量数)
X_train = np.reshape(X_train_0, (X_train_0.shape[0],1,X_train_0.shape[1]))
X_test = np.reshape(X_test_0, (X_test_0.shape[0],1,X_test_0.shape[1]))
print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認
以下、実行結果です。

X_trainが(samples=2510, time_steps=1, features=365)で、X_testが(samples=30, time_steps=1, features=365)ということです。
要は、ラグ変数を特徴量(features)として扱うということです。
深層RNN(ラグ変数:features)|モデル生成
ニュラールネットワークモデルを定義し、定義したモデルをコンパイルしモデル生成します。
以下、コードです。
# モデル定義
model = Sequential()
model.add(SimpleRNN(100,
return_sequences=True,
input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(SimpleRNN(100))
model.add(Dropout(0.2))
model.add(Dense(1, activation='linear'))
# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam')
# モデルの視覚化
plot_model(model,show_shapes=True)
以下、実行結果です。
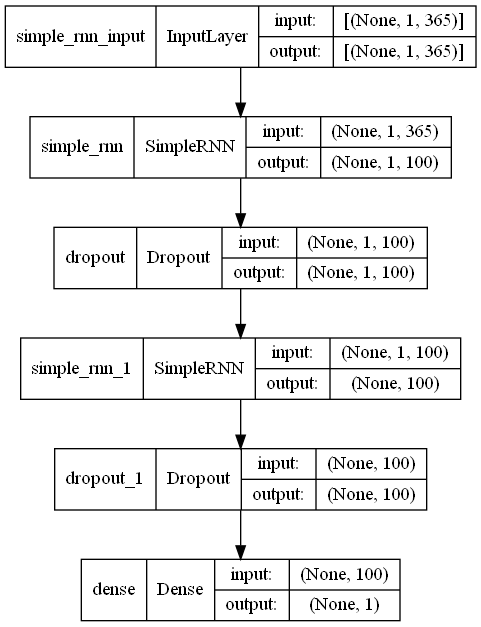
Input -> RNN -> Dropout -> RNN -> Dropout -> Output という中間層がやや深くなったなニューラルネットワークモデルです。
深層RNN(ラグ変数:features)|学習
学習データを使いモデルを学習します。
以下、コードです。
# EaelyStoppingの設定
early_stopping = EarlyStopping(monitor='val_loss',
min_delta=0.0,
patience=2)
# 学習の実行
history = model.fit(X_train, y_train,
epochs=1000,
batch_size=128,
validation_split=0.2,
callbacks=[early_stopping] ,
verbose=1,
shuffle=False)
今学習したモデルの、学習結果を出力します。
以下、コードです。
# 学習結果の出力
model.summary()
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()

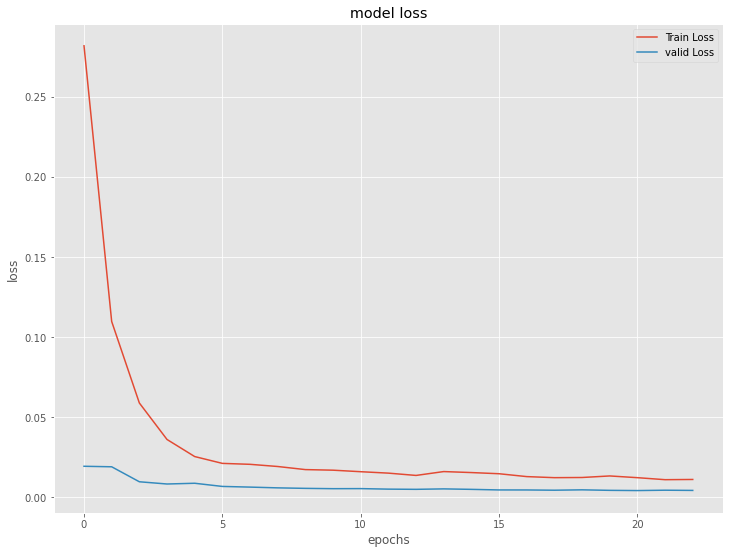
深層RNN(ラグ変数:features)|検証
学習したモデルを、テストデータで検証します。
以下、コードです。
# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)
# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)),
columns=['y','Predict'])
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
# グラフ化
df_test.plot(kind='line')
以下、実行結果です。

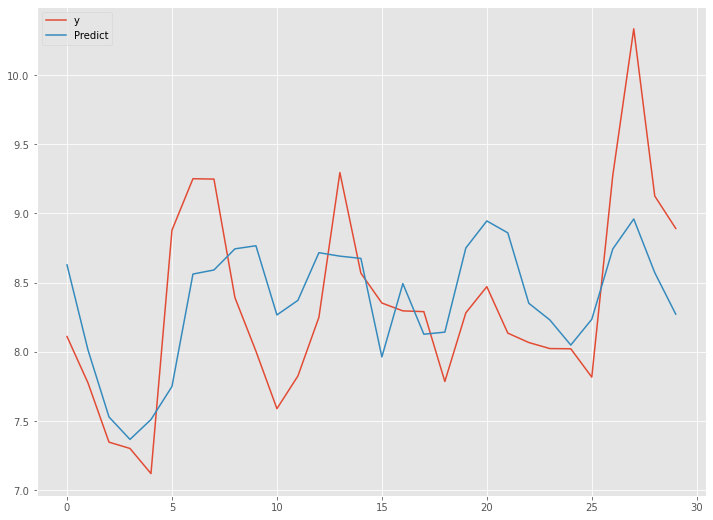
予測精度は、先程のシンプルRNN(ラグ変数:time steps)に比べやや悪化しています。
深層RNN(ラグ変数:time steps)
中間層にRNN層を2層持ったニューラルネットワークを、ラグ変数Xをタイプステップ(time_steps)とした学習データで構築していきます。
構築したモデルは、テストデータで検証していきます。
深層RNN(ラグ変数:time steps)|データ準備
ラグ変数Xをタイプステップ(time_steps)とした学習データとテストデータを準備します。
以下、コードです。
# モデル構築用にデータを再構成(サンプル数、タイムステップ, 特徴量数)
X_train = np.reshape(X_train_0, (X_train_0.shape[0],X_train_0.shape[1],1))
X_test = np.reshape(X_test_0, (X_test_0.shape[0],X_test_0.shape[1],1))
print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認
以下、実行結果です。

X_trainが(samples=2510, time_steps=365, features=1)で、X_testが(samples=30, time_steps=365, features=1)ということです。
要は、ラグ変数をタイプステップ(time_steps)として扱うということです。
深層RNN(ラグ変数:time steps)|モデル生成
ニュラールネットワークモデルを定義し、定義したモデルをコンパイルしモデル生成します。
以下、コードです。
# モデル定義
model = Sequential()
model.add(SimpleRNN(100,
return_sequences=True,
input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(SimpleRNN(100))
model.add(Dropout(0.2))
model.add(Dense(1, activation='linear'))
# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam')
# モデルの視覚化
plot_model(model,show_shapes=True)
以下、実行結果です。
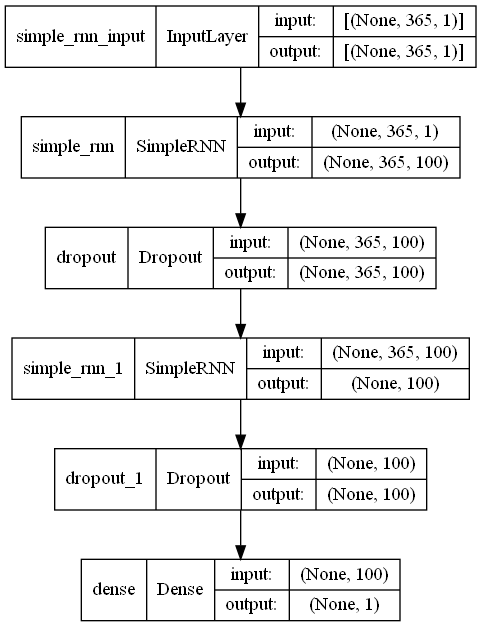
Input -> RNN -> Dropout -> RNN -> Dropout -> Output という中間層がやや深くなったなニューラルネットワークモデルです。
深層RNN(ラグ変数:time steps)|学習
学習データを使いモデルを学習します。
以下、コードです。
# EaelyStoppingの設定
early_stopping = EarlyStopping(monitor='val_loss',
min_delta=0.0,
patience=2)
# 学習の実行
history = model.fit(X_train, y_train,
epochs=1000,
batch_size=128,
validation_split=0.2,
callbacks=[early_stopping] ,
verbose=1,
shuffle=False)
今学習したモデルの、学習結果を出力します。
以下、コードです。
# 学習結果の出力
model.summary()
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()
以下、実行結果です。

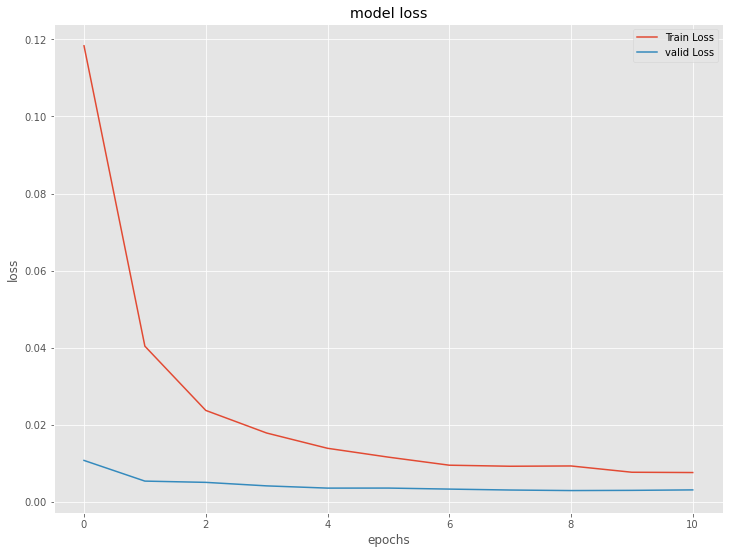
深層RNN(ラグ変数:time steps)|検証
学習したモデルを、テストデータで検証します。
以下、コードです。
# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)
# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)),
columns=['y','Predict'])
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
# グラフ化
df_test.plot(kind='line')
以下、実行結果です。

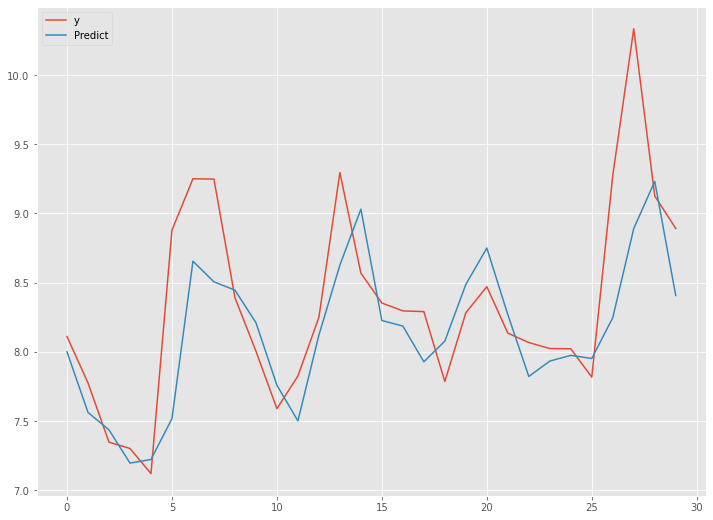
予測精度は、先程のシンプルRNN(ラグ変数:time steps)とほぼ同等です。
次回
今回は、時系列の深層学習(ディープラーニング)モデルの中で最もシンプルなRNN(Recurrent Neural Network、リカレントニューラルネットワーク)のモデル構築方法と1期先予測(1-Step ahead prediction)予測についてお話ししました。
次回は、RNNの長期記憶を保存できないなどの問題点を改善する形で登場したLSTM(Long Short Term Memory)のモデル構築方法と1期先予測(1-Step ahead prediction)予測についてお話しします。
Python Keras(TensorFlow)で作る 深層学習(Deep Learning)時系列予測モデル(その2)LSTMで1期先予測(1-Step ahead prediction)