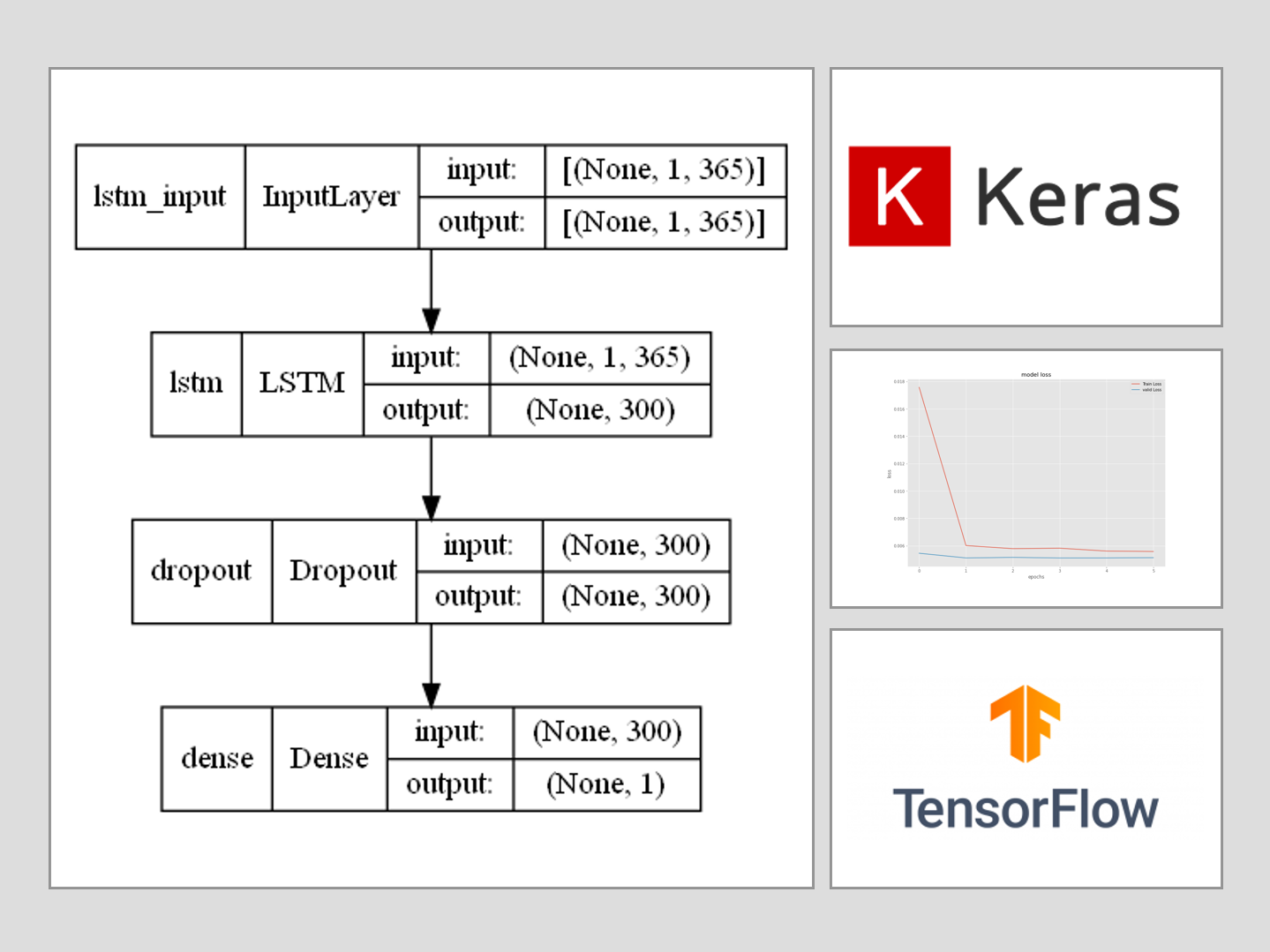
Python Keras(TensorFlow)で作る
深層学習(Deep Learning)時系列予測モデル(その2)

LSTMで1期先予測（1-Step ahead prediction）

27341
Python Keras(TensorFlow)で作る 深層学習(Deep Learning)時系列予測モデル(その2)LSTMで1期先予測（1-Step ahead prediction）

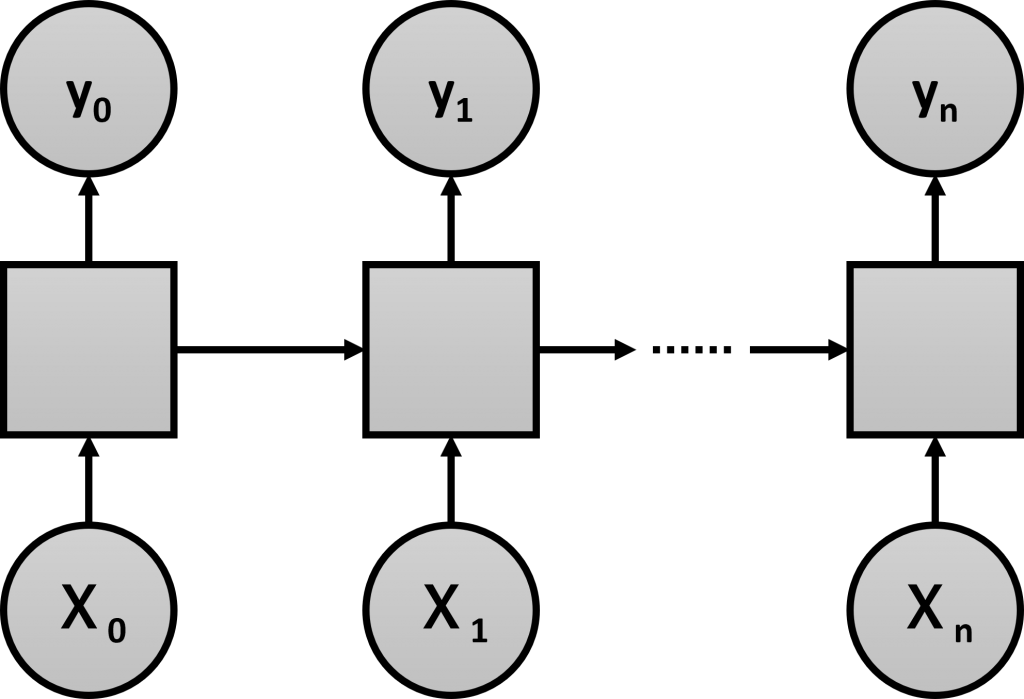
時系列の深層学習（ディープラーニング）モデルの代表格がRNN（Recurrent Neural Network、リカレントニューラルネットワーク）です。

RNNの長期記憶が保持できないなどの問題点を改善する形で登場したLSTM（Long Short Term Memory）です。

今回は、時系列の深層学習（ディープラーニング）モデルで一般的なLSTM（Long Short Term Memory、長・短期記憶）を組み込んだモデル構築の方法と1期先予測（1-Step ahead prediction）についてお話しします。

前回同様、PythonのKeras（TensorFlow）を使います。前回の記事は以下です。

Python Keras(TensorFlow)で作る 深層学習(Deep Learning)時系列予測モデル(その1)RNNで1期先予測（1-Step ahead prediction）

KerasやTensorFlowのインストール方法や基本的な使い方、RNNのモデル構築方法や1期先予測（1-Step ahead prediction）などに関しては、以下の前回の記事を参考にしてください。今回は、前回の記事を前提に記載しています。

LSTM（Long Short Term Memory）とは？

興味ない方は、読み飛ばしてください。

LSTMは、RNNの一種です。前回登場した従来のRNNも今回紹介するLSTMも、どちらもRNNです。区別するために、前回のRNNはシンプルRNNと呼ばれています。

従来のシンプルRNNは、前の時刻の情報を、次の時刻に渡す仕組みでした。この仕組だと、長期記憶を保持できない問題が起こることが分かっています。

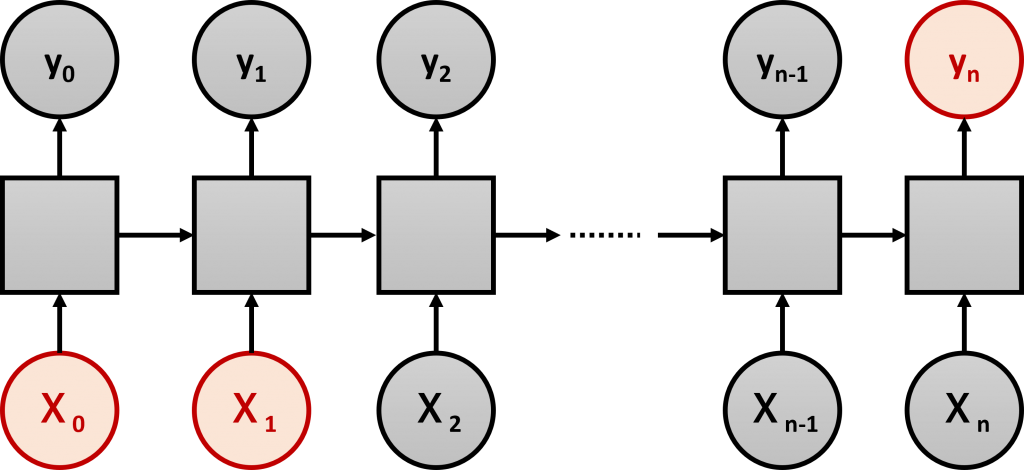
長期記憶を保持できない問題とは、インプット情報の影響が出る時期が離れている場合、その影響を加味できない、という問題です。上の例で考えると、本当は、X_0 とX_1の影響がy_nにあるにも関わらず、時期が離れているために、その影響を加味できないという問題です。

 

この問題を解決するためにLSTMが開発されました。

LSTMでは、中間層の各ユニットが、メモリユニットと呼ばれるものに置き換わります。

 

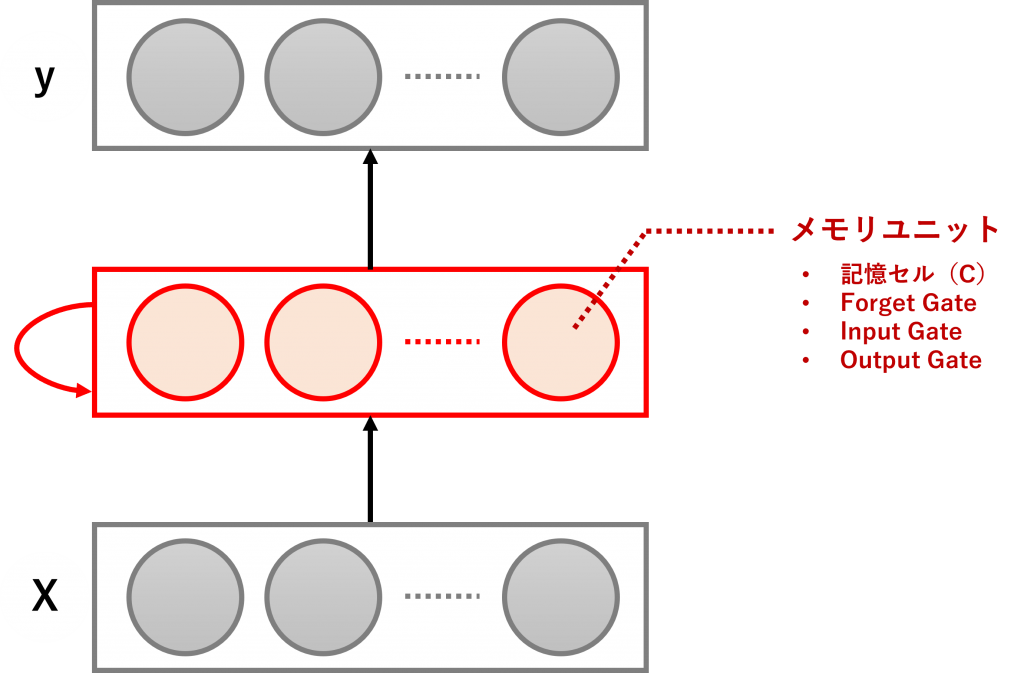
メモリユニットは以下の2つの情報を持ちます。後で説明するゲート（Gate）と呼ばれる情報調整器を使い、新たなインプット情報を時系列に加味しながら更新していきます。

  • ユニットの記憶セル（C）
  • ユニットの出力値（h）

ユニットの出力値（h）は、通常のニューラルネットワークの中間層のユニットの出力値と同じようなもので、次の層に渡す情報です。もちろん、シンプルRNN同様、次の時刻に渡す情報でもあります。

一方、ユニットの記憶セル（C）は、ユニットが保持している情報（記憶のようなもの）で、こちらも次の時刻に渡す情報です。

 

ユニットの記憶セル（C）とユニットの出力値（h）は、ゲート（Gate）と呼ばれる以下の3つの情報調整器を使い調整します。

  • Forget Gate：保持している情報の忘却の取捨選択
  • Input Gate：取り込むインプット情報の取捨選択
  • Output Gate：次の時刻に伝える情報の取捨選択

 

RNNの長期記憶を保持できない問題は、勾配消失問題と重み衝突の２つが関与しています。

勾配消失問題への対策として記憶セル（C）を導入し、重み衝突への対策としてInput GateとOutput Gateを導入する、という感じです。

  • 勾配消失問題：記憶セル（C）を導入
  • 重み衝突：Input GateとOutput Gateを導入

 

勾配消滅問題は、時系列系のニューラルネットワークモデル固有の問題ではなく、中間層が多層のディープニューラルネットワーク（深層ニューラルネットワーク）共通の問題です。1991年にHochreiterが指摘した根深い問題です。

この勾配消失問題により長期にわたる記憶が保持できなくなるため、記憶セルを用意し長期的な記憶を保持可能にしています。

 

一方、重み衝突は、時系列系のニューラルネットワークモデル固有の問題です。

モデルを学習するとき、有用な情報の重みを大きくし、有用でない情報であれば重みを小さくすべきでしょう。しかし、その情報が長期的な特徴をもつものなのか、短期的な特徴を持つものなのか、それが分からない、という問題が起こります。これが、重み衝突の問題です。

シンプルRNNの場合、その時点のインプット情報が有用かどうかの判断しかしないため、結果的に短期的に有用な情報を重視することになります。ということで、必要な情報は残していこう、となりますが、その取捨選択をするのが、Input GateとOutput Gateです。

 

Forget Gateは、Input GateとOutput Gateとはちょっと異なり、忘却するためのゲートです。初期のLSTMには、このゲートはありませんでした。インプット情報ががらりと変わった際に記憶を忘却するためゲートも必要ということで、後で追加されました。

 

この3つのゲート（Input GateとOutput Gate、Forget Gate）をコントロールするにはゲートコントローラーが必要になります。そのために、新たなニューロンが3つ必要になります。ゲートコントローラのニューロンは、一般的には活性化関数としてシグモイド関数が使用されます。

要はLSTMは、シンプルRNNの中間層のユニットが、記憶セルと3つのゲートから構成されるメモリーユニットに置き換わり、ニューロンもさらに3つのニューロン（3つのゲートコントローラー）を導入したものです。

 

従来のシンプルRNNと比べ、若干ややこしくなっていますが、モデル構築時にはそれほど意識することはありません。ただ、ややこしくなっていることもあり、学習時間が長くなるという問題があります。

実は、LSTMには多くのバリエーションがあります。GRU（Gated Recurrent Unit）もその1つで、一般的なLSTMをシンプルにした感じのものです。シンプルにすることで、処理速度が速くなっています。

 

構築するLSTMモデル

Keras（TensorFlow）のLSTMのデータセットは、以下のような3元構造が基本になっています。

[サンプル（samples）,タイムステップ（time_steps）,特徴量（features）]

 

時系列データの特徴量の1つとして、ラグ変数というものがあります。例えば、日販（1日の売上）であれば、「ラグ1の変数」とは「1日前の日販の変数」、「ラグ2の変数」とは「2日前の日販の変数」などです。

今回は、説明変数のない目的変数が1変量の時系列データを扱いますので、目的変数のラグ変数を作り説明変数として利用します。このとき、ラグ変数を特徴量（features）として扱うこともできますし、タイムステップ（time steps）として扱うこともできます。

ということで、以下の2種類のデータセットそれぞれで、LSTMモデルを構築します。

  • ラグ変数を特徴量（features）とするLSTMモデル
  • ラグ変数をタイムステップ（time steps）とするLSTMモデル

 

サンプルデータ（前回と同じです）

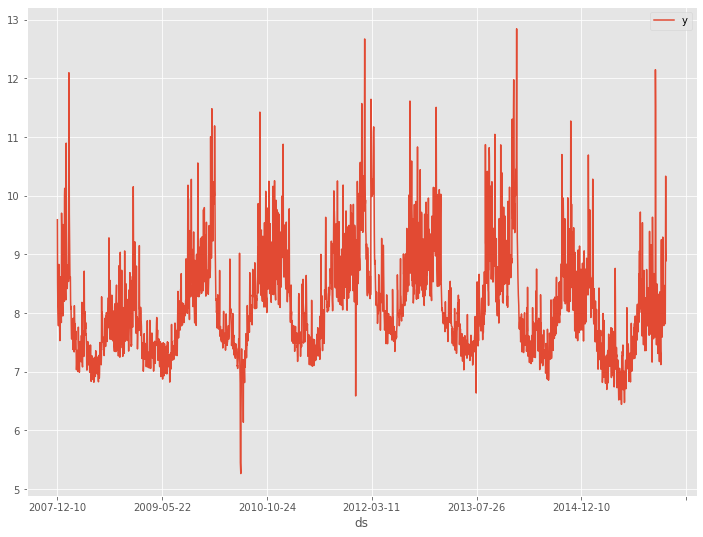
サンプルデータは、前回と同じPeyton ManningのWikipediaのPV（ページビュー）というProphetで提供されているサンプルデータ（example_wp_log_peyton_manning.csv）を使います。

facebook/prophetのGitHubからダウンロードして使って頂くか、弊社のHPからダウンロードして使って頂ければと思います。

facebook/prophetのGitHub上のデータ
https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/bgr8

このデータセットは、説明変数のない目的変数が1変量の時系列データです。もちろん、目的変数は、日単位のPV（ページビュー数）です。

PV（ページビュー数）のラグ変数を作り説明変数にします。要するに、過去のPVから未来のPVを予測する、ということです。

 

予測精度の評価指標（前回と同じです）

今回の予測精度の評価指標も前回と同じで、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。 

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • \overline{y^{actual}} ・・・実測値の平均
  • n ・・・実測値・予測値の数

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

準備（前回と同じです）

もちろん、準備も前回と同じです。説明は、前回の記事を御覧ください。

以下、コードです。

#
# 必要なライブラリーの読み込み
#

import numpy as np
import pandas as pd

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import *
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.utils import plot_model

from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ


#
# データセット読み込み
#

url = 'https://www.salesanalytics.co.jp/bgr8'
df = pd.read_csv(url)

#
# 前処理
#

## 変換
dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32')    #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換

## ラグ付きデータセット生成関数
def gen_dataset(dataset, lag_max):
    X, y = [], []
    for i in range(len(dataset) - lag_max):
        a = i + lag_max
        X.append(dataset[i:a, 0]) #ラグ変数
        y.append(dataset[a, 0])   #目的変数
    return np.array(X), np.array(y)


## 分析用データセットの生成
lag_max = 365
X, y = gen_dataset(dataset, lag_max)


#
# データ分割
#

test_length = 30 #テストデータの期間

X_train_0 = X[:-test_length,:] #学習データ
X_test_0 = X[-test_length:,:]  #テストデータ

y_train_0 = y[:-test_length] #学習データ
y_test_0 = y[-test_length:]  #テストデータ

y_train = y_train_0.reshape(-1,1)
y_test = y_test_0.reshape(-1,1)


#
# 正規化（0-1の範囲にスケーリング）
#
## 目的変数y
scaler_y = MinMaxScaler(feature_range=(0, 1))
y_train = scaler_y.fit_transform(y_train)

## 説明変数X
scaler_X = MinMaxScaler(feature_range=(0, 1))
X_train_0 = scaler_X.fit_transform(X_train_0)
X_test_0 = scaler_X.transform(X_test_0)

 

LSTM（ラグ変数：features）

中間層にLSTM層を持ったニューラルネットワークを、ラグ変数Xを特徴量（features）とした学習データで構築していきます。

構築したモデルは、テストデータで検証していきます。

 

LSTM（ラグ変数：features）｜データ準備

ラグ変数Xを特徴量（features）とした学習データとテストデータを準備します。

以下、コードです。

# モデル構築用にデータを再構成（サンプル数、タイムステップ, 特徴量数）
X_train = np.reshape(X_train_0, (X_train_0.shape[0],1,X_train_0.shape[1]))
X_test = np.reshape(X_test_0, (X_test_0.shape[0],1,X_test_0.shape[1]))

print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認

 

以下、実行結果です。

 

X_trainが(samples=2510, time_steps=1, features=365)で、X_testが(samples=30, time_steps=1, features=365)ということです。

要は、ラグ変数を特徴量（features）として扱うということです。

 

LSTM（ラグ変数：features）｜モデル生成

ニュラールネットワークモデルを定義し、定義したモデルをコンパイルしモデル生成します。

以下、コードです。RNNの違いは3行目がSimpleRNNからLSTMに変わったところです。

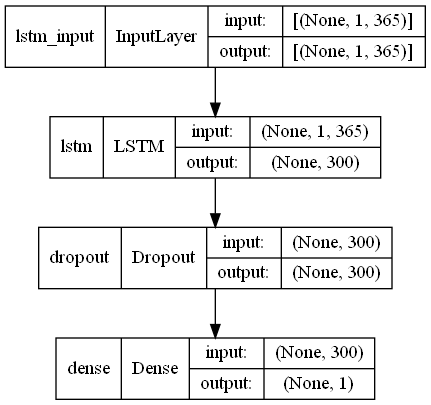
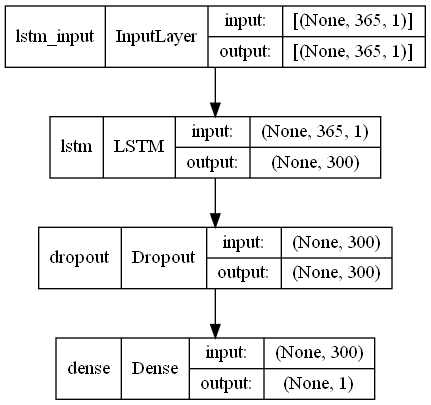
# モデル定義
model = Sequential()
model.add(LSTM(300,input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(1, activation='linear'))

# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam')

# モデルの視覚化
plot_model(model,show_shapes=True)

 

以下、実行結果です。

 

LSTM（ラグ変数：features）｜学習

学習データを使いモデルを学習します。

以下、コードです。

# EaelyStoppingの設定
early_stopping =  EarlyStopping(monitor='val_loss',
                                min_delta=0.0,
                                patience=2)

# 学習の実行
history = model.fit(X_train, y_train,
                    epochs=1000,
                    batch_size=128,
                    validation_split=0.2,
                    callbacks=[early_stopping] ,
                    verbose=1, 
                    shuffle=False)

 

今学習したモデルの、学習結果を出力します。

以下、コードです。

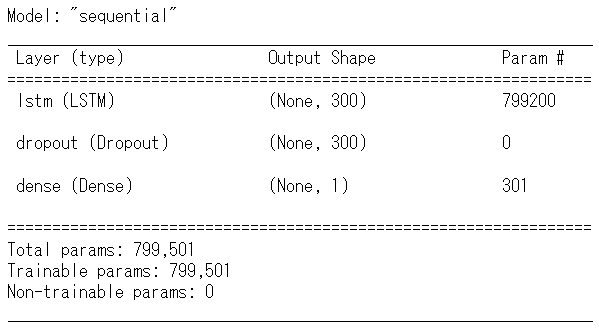
# 学習結果の出力
model.summary()

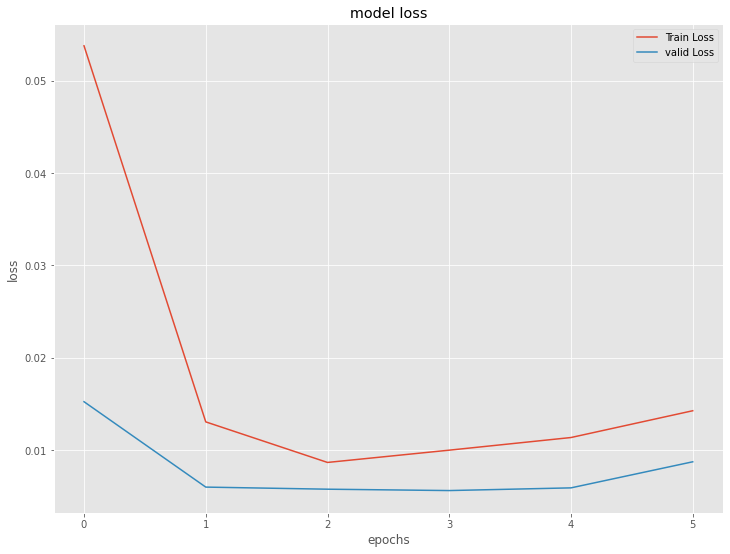
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()

以下、実行結果です。

 

LSTM（ラグ変数：features）｜検証

学習したモデルを、テストデータで検証します。

以下、コードです。

# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)

# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)),
                       columns=['y','Predict'])

# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred)) 

# グラフ化
df_test.plot(kind='line')

 

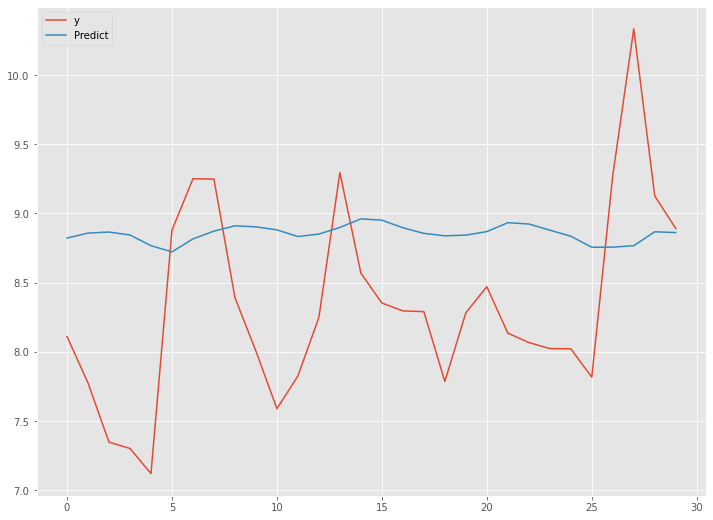
以下、実行結果です。

 

予測精度は、前回のシンプルRNN（ラグ変数：time steps）よりも良くはありません。

 

LSTM（ラグ変数：time steps）

中間層にLSTM層を持ったニューラルネットワークを、ラグ変数Xをタイプステップ（time_steps）とした学習データで構築していきます。

構築したモデルは、テストデータで検証していきます。

 

LSTM（ラグ変数：time steps）｜データ準備

ラグ変数Xをタイプステップ（time_steps）とした学習データとテストデータを準備します。

以下、コードです。

# モデル構築用にデータを再構成（サンプル数、タイムステップ, 特徴量数）
X_train = np.reshape(X_train_0, (X_train_0.shape[0],X_train_0.shape[1],1))
X_test = np.reshape(X_test_0, (X_test_0.shape[0],X_test_0.shape[1],1))

print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認

 

以下、実行結果です。

 

X_trainが(samples=2510, time_steps=365, features=1)で、X_testが(samples=30, time_steps=365, features=1)ということです。

要は、ラグ変数をタイプステップ（time_steps）として扱うということです。

 

LSTM（ラグ変数：time steps）｜モデル生成

ニュラールネットワークモデルを定義し、定義したモデルをコンパイルしモデル生成します。

以下、コードです。

# モデル定義
model = Sequential()
model.add(LSTM(300,input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(1, activation='linear'))

# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam')

# モデルの視覚化
plot_model(model,show_shapes=True)

 

以下、実行結果です。

 

LSTM（ラグ変数：time steps）｜学習

学習データを使いモデルを学習します。

以下、コードです。

# EaelyStoppingの設定
early_stopping =  EarlyStopping(monitor='val_loss',
                                min_delta=0.0,
                                patience=2)

# 学習の実行
history = model.fit(X_train, y_train,
                    epochs=1000,
                    batch_size=128,
                    validation_split=0.2,
                    callbacks=[early_stopping] ,
                    verbose=1, 
                    shuffle=False)

 

今学習したモデルの、学習結果を出力します。

以下、コードです。

# 学習結果の出力
model.summary()

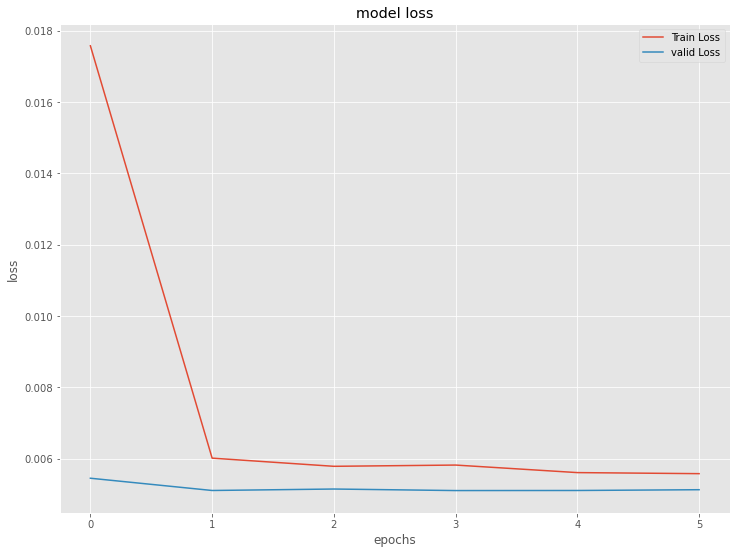
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()

 

以下、実行結果です。

 

LSTM（ラグ変数：time steps）｜検証

学習したモデルを、テストデータで検証します。

以下、コードです。

# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)

# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)),
                       columns=['y','Predict'])

# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred)) 

# グラフ化
df_test.plot(kind='line')

 

以下、実行結果です。

 

予測精度は、先程のLSTM（ラグ変数：features）より良くなっています。

 

次回

今回は、時系列の深層学習（ディープラーニング）モデルで一般的なLSTM（Long Short Term Memory、長・短期記憶）を組み込んだモデル構築の方法と1期先予測（1-Step ahead prediction）についてお話ししました。

次回は、LSTMの計算コスト大きい問題を改善する形で登場したGRU（Gated Recurrent Unit）のモデル構築方法と1期先予測（1-Step ahead prediction）予測についてお話しします。

Python Keras(TensorFlow)で作る深層学習(Deep Learning)時系列予測モデル(その3)GRUで1期先予測（1-Step ahead prediction）