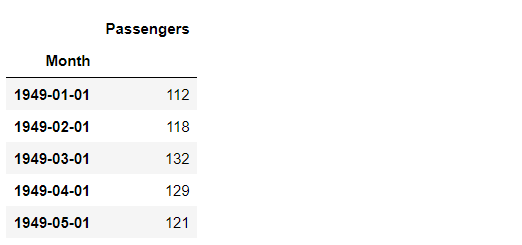ビジネスの世界で発生するデータの多くは、時間的概念の紐付いた時系列データです。
例えば、売上金額や受注件数、販売量、生産量、在庫量、PV(ページビュー)数、見込み顧客数、既存顧客数、離反顧客数、故障件数、広告宣伝費、人件費、従業員数、離職者数、などなど。
このような時系列データから時間的概念を一旦取り除いたり、特定の時間だけを扱うことで、テーブルデータとして扱いデータ分析をしたり、モデル構築することもあります。
ただ、時系列データは、時系列性を考慮しデータ分析したり、モデル構築したりした方が自然でしょう。
ということで、今回は、「時系列データに対する3つの特徴把握方法(変動成分・定常性・コレログラム)」というお話しをします。
Contents [hide]
時系列データの主な4つの変動成分
時系列データの原系列(元の時系列データ)は、主に以下の4つの変動成分で構成されます。
- T:趨勢変動成分
- C:循環変動成分
- S:季節変動成分
- I:不規則変動成分
時系列データの原系列(元の時系列データ)を、簡易的には以下のように表現されます。
もしくは……
1つ目は加法モデル、2つ目は乗法モデルです。乗法モデルも対数変換(log)すると、加法モデルの用に表現されます。
趨勢変動成分とは、データの長期的な増加または減少を表現する成分です。これは、直線である必要はありません。
循環変動成分は、周期的なパターンを表現する成分です。後に説明する季節変動成分と似たような概念ですが、季節変動成分が一定の周期を持っているのに対し、こちらの周期は一定である必要はありません。景気循環などがよい例です。上昇と下降を繰り返すが、上昇している期間が長いときもあれば短いときもある、という感じです。季節変動成分と異なり、2年以上と長くなります。
季節変動成分とは、一定の周期パターンを持った成分です。例えば、データの粒度が1日単位であれば、週周期や年周期などです。循環変動成分と比べ、周期が短く長くても1年程度です。
よく、T(趨勢変動成分)とC(循環変動成分)を一緒くたにTC(趨勢循環変動)とまとめてしまうことが多いです。
その場合、原系列(元の時系列データ)は、以下の3つの変動成分で構成されます。
- TC:趨勢循環変動 → 長期的な上昇または下降の動き
- S:季節変動成分 → 一定の周期パターン(1年以内)
- I:不規則変動成分
以後……
- TC(趨勢循環変動)をトレンド成分
- S(季節変動成)を季節成分
- I(不規則変動成分)を残差成分
……と呼びます。
3つの特徴把握方法
時系列データを手にしたとき、よく実施する3つの特徴把握方法があります。
- 時系列データの変動成分の分解
- 時系列データが定常かどうかの確認
- コレログラム (ACF & PACF)の確認
それぞれについて、データを用いてPythonで実施例を交えて、説明していきます。
準備(必要なライブラリーとデータの読み込み)
主に、ライブラリーはstatsmodelsを使います。
statsmodelsインストールされていない方は、statsmodelsをインストールしてください。
コマンドプロンプト上で、condaでインストールするときのコードは以下です。
conda install -c conda-forge statsmodels
pipでインストールするときのコードは以下です。
pip install statsmodels
では、必要なライブラリーを読み込みます。
以下、コードです。
# ライブラリーの読み込み
import pandas as pd
import numpy as np
from scipy import signal
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.seasonal import STL
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
次に、データセットを読み込みます。
今回利用する時系列データのデータセットは、Airline Passengers(飛行機乗客数)は、Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。
弊社のHPからもダウンロードできます。
弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h
では、データセットを読み込みます。
以下、コードです。
# データセットの読み込み
url='https://www.salesanalytics.co.jp/591h' #データセットのあるURL
df=pd.read_csv(url, #読み込むデータのURL
index_col='Month', #変数「Month」をインデックスに設定
parse_dates=True) #インデックスを日付型に設定
df.head() #確認
以下、実行結果です。
グラフ化し確認します。
以下、コードです。
# プロット
df.plot()
plt.title('Passengers') #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers') #タテ軸のラベル
plt.xlabel('Month') #ヨコ軸のラベル
plt.show()
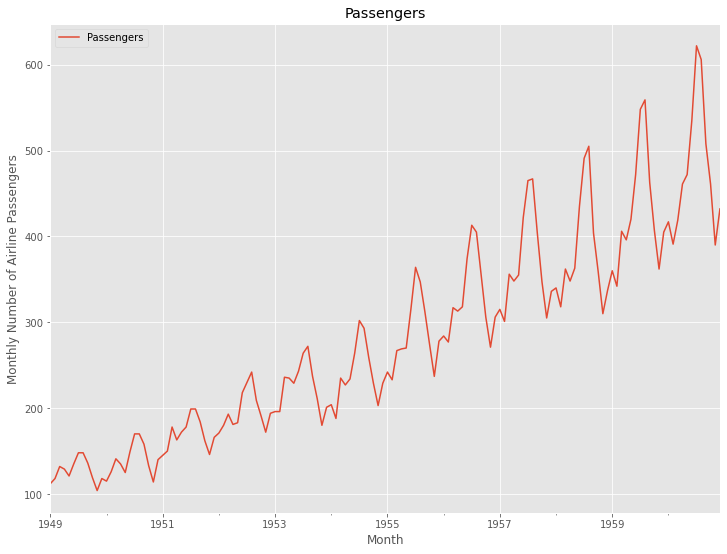
以下、実行結果です。
時系列データの変動成分の分解
時系列データを手にしたら先ずすべきは、以下の3つの変動成分の分解です。どのような時系列データなのか、ざっくり掴めるかと思います。
- トレンド成分
- 季節成分
- 残差成分
成分分解するための方法はいくつかあります。今回は、以下の3つの成分分解方法で実施します。
- 移動平均法を利用した分解(加法モデルを仮定)
- 移動平均法を利用した分解(乗法モデルを仮定)
- STL分解(LOESS平滑化を利用した分解)
移動平均法を利用した分解をするとき、statsmodelsライブラリーのseasonal_decompose()関数を使います。以下のステップで時系列データをトレンド成分と季節成分に分解します。
- 設定した季節性の周期の移動平均を計算しトレンド成分とする
- 原系列からトレンド成分を除去し季節成分(平均値を0に調整)を求める
- 原系列からトレンド成分と季節成分を除去し残差を求める
STL分解(Seasonal Decomposition Of Time Series By Loess)は、statsmodelsライブラリーのSTL()関数を使います。LOESS平滑化(locally estimated scatterplot smoothing)というノンパラメトリック回帰モデルを利用し分解します。
では、それぞれで実施してみます。
以下、移動平均法を利用した分解(加法モデルを仮定)を実施するときのコードです。
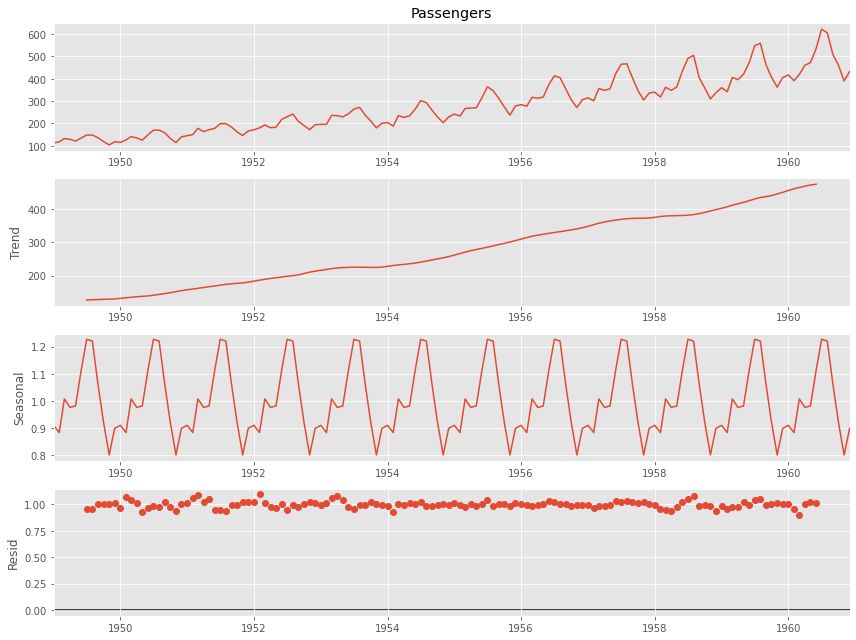
# 成分分解 result=seasonal_decompose(df.Passengers, model='additive', period=12) # グラフ化 result.plot() plt.show()
以下、実行結果です。
以下、移動平均法を利用した分解(乗法モデルを仮定)を実施するときのコードです。
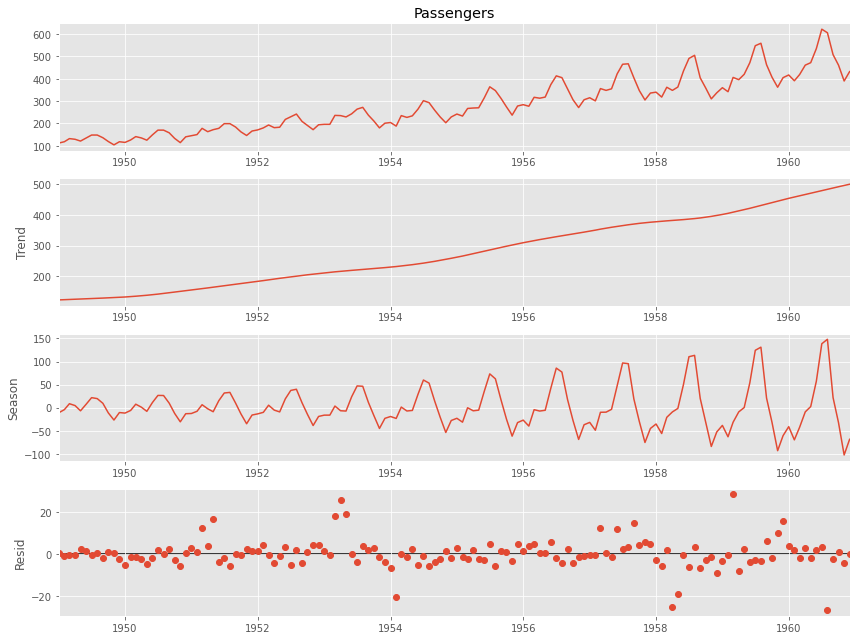
# 成分分解 result=seasonal_decompose(df.Passengers, model='multiplicative', period=12) # グラフ化 result.plot() plt.show()
以下、実行結果です。
以下、STL分解(LOESS平滑化を利用した分解)を実施するときのコードです。
# 成分分解 stl=STL(df.Passengers, period=12, robust=True).fit() # STL分解結果のグラフ化 stl.plot() plt.show()
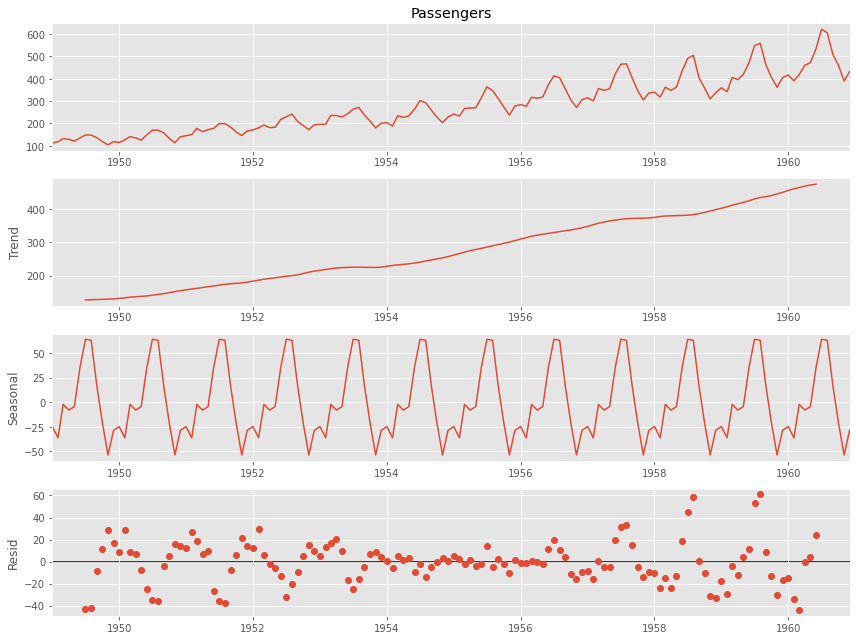
以下、実行結果です。
基本、似たような感じの出力がでるケースが多いです。STL分解が無難でしょう。STL分解は、外れ値に強いなどいくつかの特徴があるからです。
時系列データが定常かどうかの確認
変動成分の分解によって、どのような時系列データなのか、なんとなく掴めたかと思います。
次にすべきは、時系列データが定常かどうかを確認することです。
定常な時系列データは、時間によって平均や分散、共分散などが変化しない時系列データのことです。トレンド成分や季節成分のある時系列データは、非定常と言える可能性が高いです。
わかりやすい例ですと、時間とともにデータの値が大きくなる場合、それは時間に依存していますので非定常な時系列データです。
古典的な時系列解析手法では、どうすれば非定常な時系列データが定常状態になるかを検討するステップを挟みます。そうすることで、トレンド成分を考慮したモデルを作るべきなのか、季節成分を考慮したモデルを作るべきなのかが分かります。
何はともあれ、時系列データが定常かどうかを確認していきます。
定常かどうかを確認する方法の1つに、拡張ディッキー–フラー検定(ADF検定、augmented Dickey–Fuller test)という統計的仮説検定手法があります。
- 帰無仮説H0:時系列は非定常である(単位根をもつ)
- 対立仮説H1:時系列は定常である(単位根をもたない)
単位根をもつ時系列データを単位根過程と呼びます。
単位根過程は、原系列は非定常だが、差分をとると定常になるデータです。差分をとるとは、例えば1期前のデータとの差分を計算し、新たな時系列データを作ることです。
単位根の有無を検定する方法の1つがディッキー–フラー検定(DF検定、Dickey–Fuller test)です。それを拡張したのが拡張ディッキー–フラー検定(ADF検定、augmented Dickey–Fuller test)です。通常は、ADF検定を利用します。
先程、時系列データの変動成分を分解しグラフで確認した限りだと、上昇傾向のトレンドと、12ヶ月周期(季節性)はありそうです。
今回は、次の4つADF検定を実施します。
- 原系列に対するADF検定
- 原系列を対数変換し得た対数系列に対するADF検定
- 対数系列の階差系列(次数1)に対するADF検定
- 対数系列の階差系列(次数1)の季節階差系列(次数1)に対するADF検定
原系列に対するADF検定は、原系列そのものに対するADF検定です。通常は、ここで定常であるという検定結果がでることはありません。
原系列を対数変換した対数系列に対するADF検定は、原系列を対数変換することで得た時系列データ(対数系列)に対するADF検定です。原系列は、時間を経るごとに上下の振れ幅が大きく分散が大きくなっています。対数変換をすることで、分散が大きくなる現象を抑えることができます。
対数系列の階差系列(次数1)に対するADF検定は、原系列を対数変化し得た対数系列に対し、1期前との差分を計算し新たな時系列データを作り、その新たな時系列データに対するADF検定です。線形トレンドは、階差系列(次数1)を作ることで除去できます。
対数系列の階差系列(次数1)の季節階差系列(次数1)に対するADF検定は、原系列の対数系列の階差系列(次数1)に対し、12期前(1年前)との差分を計算し新たな時系列データを作り、その新たな時系列データに対するADF検定です。
先ず、原系列に対するADF検定をします。
以下、コードです。
# ADF検定(原系列)
dftest = adfuller(df.Passengers)
print('ADF Statistic: %f' % dftest[0])
print('p-value: %f' % dftest[1])
print('Critical values :')
for k, v in dftest[4].items():
print('\t', k, v)
以下、実行結果です。
簡単に見方について説明します。
p値(p-value)が0.01より小さいとき1%有意、0.05より小さいとき5%有意、0.1より小さいとき10%有意と呼ばれます。
有意の場合、帰無仮説(時系列は非定常である)を棄却し対立仮説(時系列は定常である)を採択します。
このことは、ADF統計量(ADF Statistic)と棄却限界値(critical value)からも見て取れます。ADF統計量(ADF Statistic)が1%棄却限界値(critical value)より小さいとき1%有意、5%棄却限界値(critical value)より小さいとき5%有意、10%棄却限界値(critical value)より小さいとき10%有意です。
どの基準(1%有意、5%有意、10%有意)を使うかという問題があります。1%有意が最も厳しく、10%有意が最もゆるいです。伝統的に、5%有意を使うケースが多いです。
では、今回の結果はどうなのか?
ADF統計量(ADF Statistic)は0.815369で、p値(p-value)は0.991880ということで、1%有意でも5%有意でも10%有意でもありません。
要するに、帰無仮説(時系列は非定常である)は棄却されません。
次に、原系列を対数変換し得た対数系列に対するADF検定をします。
numpyライブラリーのlog()関数で、原系列を対数変換し新しい時系列データ(対数系列)を得ます。
以下、コードです。
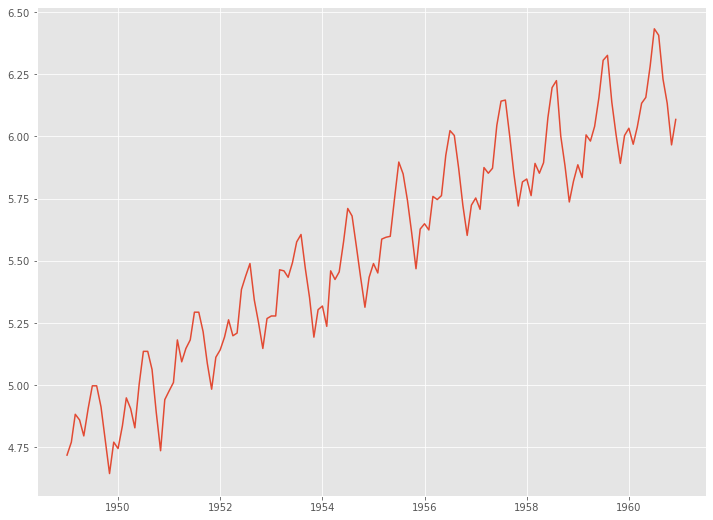
# 対数変換 df_log = np.log(df.Passengers) plt.plot(df_log)
以下、実行結果です。
このデータに対し、ADF検定をします。
以下、コードです。
# ADF検定(対数系列)
dftest = adfuller(df_log)
print('ADF Statistic: %f' % dftest[0])
print('p-value: %f' % dftest[1])
print('Critical values :')
for k, v in dftest[4].items():
print('\t', k, v)
以下、実行結果です。
ADF統計量(ADF Statistic)は-1.717017で、p値(p-value)は0.422367ということで、帰無仮説(時系列は非定常である)は棄却できませんでした。
階差系列(次数1)を作ることで線形トレンドを除去します。階差系列(次数1)とは、1期前のデータとの差分を計算し求めた時系列データです。
以下、コードです。
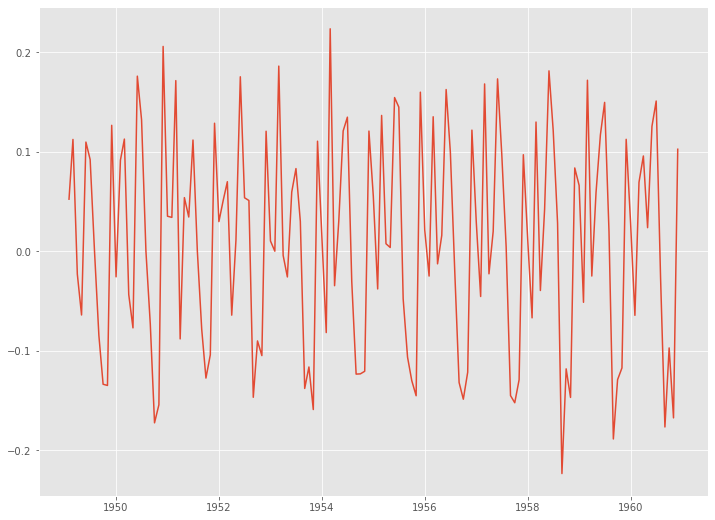
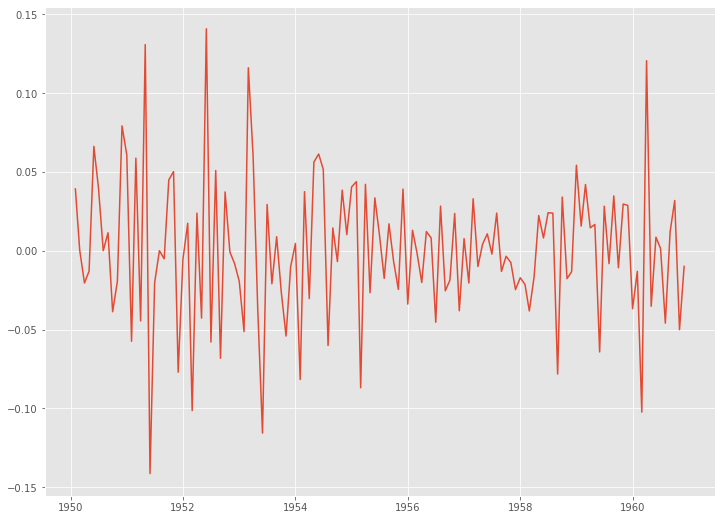
# 階差 df_log_diff1 = df_log.diff(1).dropna() plt.plot(df_log_diff1)
以下、実行結果です。
うまくトレンド除去できているようです。
このデータに対し、ADF検定をします。
以下、コードです。
# ADF検定
dftest = adfuller(df_log_diff1)
print('ADF Statistic: %f' % dftest[0])
print('p-value: %f' % dftest[1])
print('Critical values :')
for k, v in dftest[4].items():
print('\t', k, v)
以下、実行結果です。
ADF統計量(ADF Statistic)は-2.717131で、p値(p-value)は0.071121ということで、帰無仮説(時系列は非定常である)を棄却できませんでした。
この階差系列(次数1)に対し、さらに季節階差(次数1)をとった時系列データを作ります。
以下、コードです。
# 季節階差 df_log_diff1_diff12 = df_log_diff1.diff(12).dropna() plt.plot(df_log_diff1_diff12)
以下、実行結果です。
このデータに対し、ADF検定をします。
以下、コードです。
# ADF検定
dftest = adfuller(df_log_diff1_diff12)
print('ADF Statistic: %f' % dftest[0])
print('p-value: %f' % dftest[1])
print('Critical values :')
for k, v in dftest[4].items():
print('\t', k, v)
以下、実行結果です。
ADF統計量(ADF Statistic)は-4.443325で、p値(p-value)は0.000249ということで、帰無仮説(時系列は非定常である)は棄却され対立仮説(時系列は定常である)が採択されます。要は、定常であるということです。
定常化の3つの方法
すでに登場した方法もありますが、非定常な時系列データを、定常化する場合によく使う3つの方法を紹介します。
- トレンド除去
- 差分化
- Box-Cox変換
トレンド除去とは、トレンド成分を原系列から除去することで定常化を目指します。時間を説明変数にした線形回帰モデルを作ることで、トレンド成分をモデル化するのが最も簡単です。回帰モデルは非線形でなくても構いません。ちなみに、Pythonの回帰モデル構築に対応したライブラリー(statsmodelsやscikit-learnなど)でトレンド成分をモデル化することができます。単に、トレンドを除去した時系列データを求めるには、scipyライブラリーのdetrend()関数で実施できます。
差分化とは、n期前のデータとの差分をとることで定常化を目指します。比較的よく使われます。線形トレンドや季節性のある時系列データに対し有効です。線形トレンドであれば、1期前のデータとの差分をとることで定常化に近づきます。季節的なパターン(n周期)であれば、n期前のデータとの差分をとることで定常化に近づきます。ちなみに、Pythonで差分化するときは、pandasライブラリーのdiff()関数で実施できます。差分化で求めた時系列データを階差系列(差分系列)と言います。
Box-Cox変換とは、原系列に対しBox-Cox変換することで定常化を目指します。Box-Cox変換とは、対数変換(log)を一般化したものです。対数変換(log)を実施することが多いです。対数変換(log)し求めた時系列データを対数系列と言います。ちなみに、PythonでBox-Cox変換するときは、scipyライブラリーのboxcox()関数で実施できます。
コレログラム (ACF & PACF)
コレログラムとは、自己相関 (ACF)と偏自己相関 (PACF)を計算し、それをプロットしたグラフです。
自己相関 (ACF) とは原系列とそのラグとの相関で、偏自己相関 (PACF)とは原系列とそのラグとの偏相関です。
ラグとは、時間をずらしたデータのことです。例えば、日単位の時系列データであれば、1日前のデータをラグ1、2日前のデータをラグ2、などとなります。月単位の時系列データであれば、先月のデータをラグ1、先々月のデータをラグ2、などとなります。
先ず、原系列のコレログラム(ACF & PACF)を見てみます。
以下、コードです。
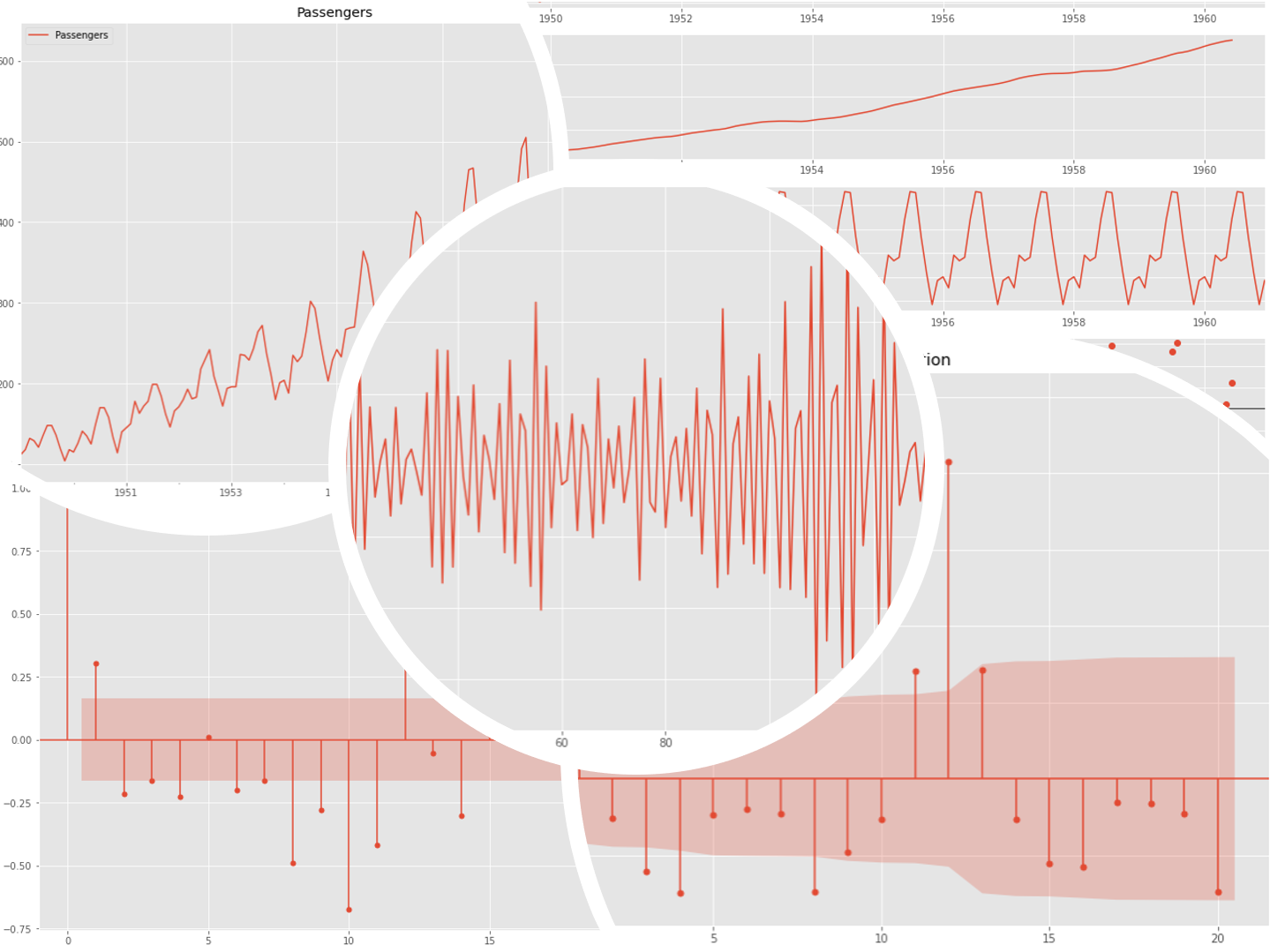
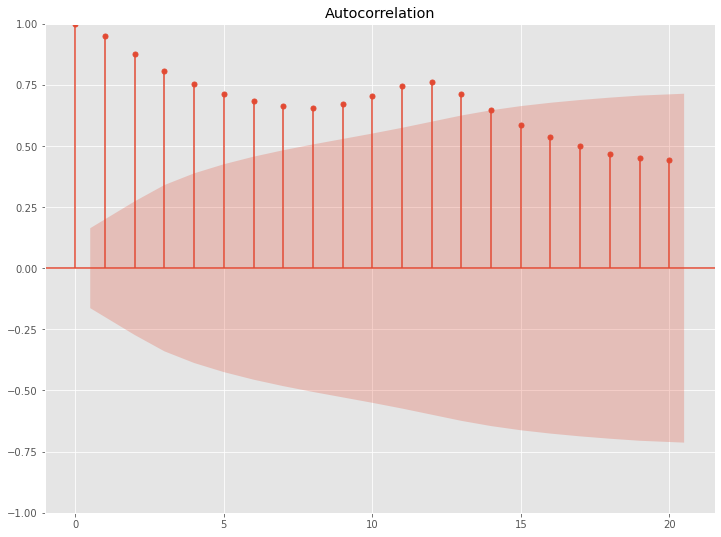
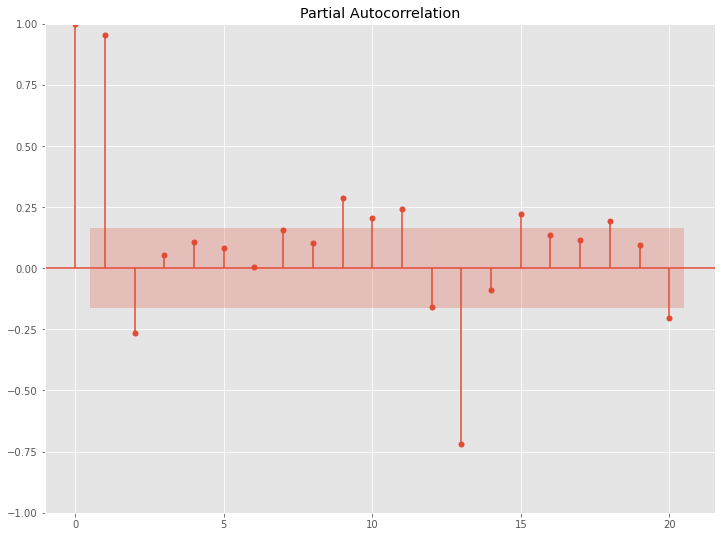
# 自己相関(原系列) acf = plot_acf(df.Passengers, lags=20) pacf = plot_pacf(df.Passengers, lags=20)
以下、実行結果です。
上が自己相関(Autocorrelation)で、下が偏自己相関(Partial Autocorrelation)です。
横軸がラグで、縦軸が相関もしくは偏相関です。ラグ0は、自分自身との相関のため1になっています。
自己相関(ACF)のグラフを見ていただくと分かりますが、原系列のトレンド成分の影響がそのままに出ています。
次に、原系列の対数系列の階差系列(次数1)のコレログラム(ACF & PACF)を見てみます。
以下、コードです。
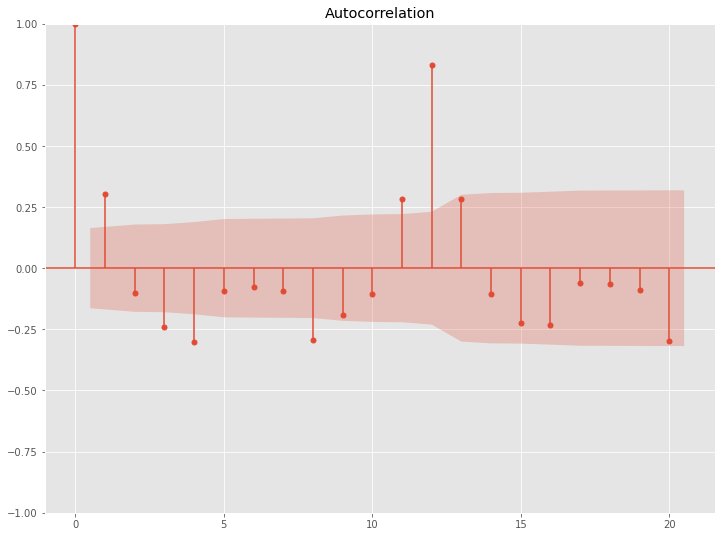
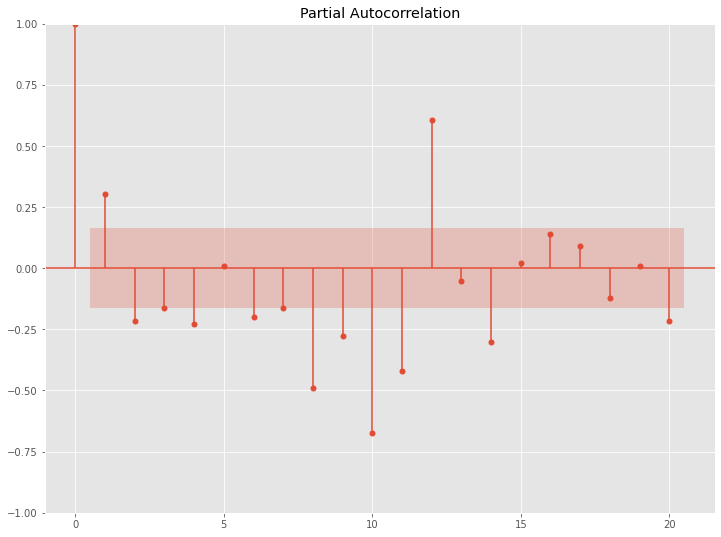
# 自己相関(原系列の対数系列の階差系列(次数1)) acf = plot_acf(np.diff(df.Passengers, 1), lags=20) pacf = plot_pacf(np.diff(df.Passengers, 1), lags=20)
以下、実行結果です。
ラグ12などでコレログラム(ACF & PACF)の数値が跳ねています。解釈例ですが、ラグ12は12ヶ月前を意味しますので、12ヶ月周期の季節性があることが分かります。
コレログラム(ACF & PACF)は、時系列データの特徴を把握するだけでなく、時系列解析の世界で古典的だが優秀なモデルであるARIMA系のモデルを検討する際に、参考にすることが多いです。
古典的な時系列モデル
代表的な古典的な時系列モデルとは、以下の2つです。
- 平滑化法系のモデル
- ARIMA系のモデル
平滑化法系のモデルには色々なものあります。最もシンプルなモデルは、単純指数平滑化(Simple Exponential Smoothing)です。Excelでも簡単にできます。
ARIMA系のモデルにも色々なものがあります。多くの時系列データはARIMA系のモデルで十分に将来予測することができます。経済指標などでARIMA系のモデルはよく登場します。
次回
今回は、「時系列データに対する3つの特徴把握方法(成分分解・定常性・コレログラム)」というお話しをしました。
次回は、平滑化法系の実用的なモデルについて、いくつか説明していきます。
Pythonで時系列解析・超入門(その2)指数平滑化法(Exponential Smoothing model)で予測する方法