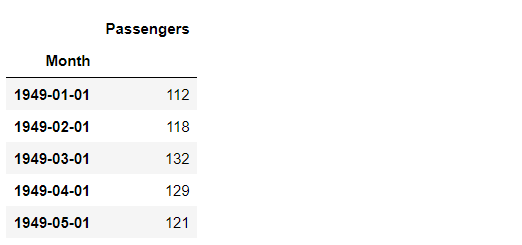Pythonで時系列解析・超入門（その3）

ARIMA系モデルで予測する方法

37808
Pythonで時系列解析・超入門（その3）ARIMA系モデルで予測する方法

ビジネスの世界で発生するデータの多くは、時間的概念の紐付いた時系列データです。

例えば、売上金額や受注件数、販売量、生産量、在庫量、PV（ページビュー）数、見込み顧客数、既存顧客数、離反顧客数、故障件数、広告宣伝費、人件費、従業員数、離職者数、などなど。

前回、「指数平滑化法（Exponential Smoothing model）で予測する方法」というお話しをしました。

Pythonで時系列解析・超入門（その2）指数平滑化法（Exponential Smoothing model）で予測する方法

今回は、「ARIMA系モデルで予測する方法」について説明していきます。

古典的な時系列モデルですが、最も実用的かつ実績のあるモデルです。

ARIMAモデル

ARIMAはAuto-Regressive Integrated Moving Average Modelの頭文字をとったものです。

このモデルは、次の3つの成分から構成されます。

  • AR (Auto-Regressive) component：自己回帰成分
  • I (Integrated) component：和分成分
  • MA (Moving Average) component：移動平均成分

 

時系列データは、上昇傾向や下降傾向などのトレンドが見られ、明らかに定常でない場合があります。

I (Integrated) 成分で定常化を目指します。モデルを構築するというよりも、前処理と表現したほうがいいでしょう。この場合の前処理とは、過去との差分を取り階差系列を作ることです。

例えば、今日の売上と昨日の売上の差分を求め、その差分を新たな時系列データとする、ということです。その新たなデータを階差系列と呼びます。上昇傾向や下降傾向などのトレンドがなくなるまで、この前処理を繰り返します。多くの場合、1,２回で十分です。この繰り返し数を、差分の階数dで表現します。

 

時系列データは、過去の値に依存する場合があります。自己相関があるということです。

例えば、今日の売上が1日前（1期前）と似たような値を取るケースです。AR (Auto-Regressive)で、自己相関をモデル化します。

AR (Auto-Regressive)でモデル化するとき、何期前（p）までのデータを用いるかを考えなくてはなりません。それを自己回帰パラメータpと言います。

 

時系列データは、AR (Auto-Regressive)だけで自己相関を十分にモデル化できません。

自己相関は、MA (Moving Average)でもモデル化することができます。どこまでの過去を考慮するのかを考えなくてはなりません。

それを移動平均パラメータqと言います。移動平均とは、残差の移動平均ですので注意しましょう。

 

要は、以下の3つのパラメータがあります。

  • 自己回帰パラメータp
  • 差分の階数d
  • 移動平均パラメータq

 

どのようにパラメータ設定したかを明示的に示すために、ARIMA(p,d,q)という形式で表現します。

ARIMAモデルでは、これらのパラメータは非負の整数値（0,1,2,…）の値を取ります。パラメータの値を「次数」という表現することも多いです。

問題は、この(p,d,q)の次数の値をどう設定するのか？ ということになります。

 

ARIMAモデルを拡張したSARIMAモデル

ARIMAは、季節性を効果的に捉えることができないという問題があります。この問題を解決するのが、SARIMA（Seasonal ARIMA）モデルです。

SARIMAモデルのパラメータは、以下のようになります。

  • 非季節性パラメータ（p,d,q）
  • 季節性パラメータ (P, D, Q, m)

 

非季節性パラメータ（p,d,q）は、ARIMAモデルのパラメータと同じです。

  • p：ARIMA の AR componentの次数（自己回帰パラメータ）と同じ
  • d：ARIMA の I componentの次数（差分の階数）と同じ
  • q：ARIMA の MA componentの次数（移動平均パラメータ）と同じ

 

ARIMAモデルと大きく異なるのは、以下の季節性パラメータ (P, D, Q, m)の存在です。

  • m (Seasonal Period)：季節性の周期
  • P (Seasonal AR component)：季節性の AR componentの次数
  • D (Seasonal I component)：季節性の I componentの次数
  • Q (Seasonal MA Component)：季節性のMA componentの次数

 

m は季節性の周期です。例えば、月単位の時系列データに対し12ヶ月周期がある場合、m=12 となります。

Pは、季節性の AR componentの次数です。例えば、月単位の時系列データに対しm=12かつP=2の場合、12ヶ月前と24ヶ月前のデータの値を考慮するということです。

Dは、季節性の I componentの次数です。例えば、月単位の時系列データに対しm=12かつD=1の場合、12ヶ月前とデータとの差分をとるということです。

Qは、季節性のMA componentの次数です。例えば、月単位の時系列データに対しm=12かつQ=2の場合、12ヶ月前と24ヶ月前の残差を考慮するということです。

 

どのようにパラメータ設定したかを明示的に示すために、SARIMA(p,d,q)(P, D, Q, m)もしくはSARIMA( p,d,q )( P,D,Q )[m]という形式で表現します。

 

説明変数X付きSARIMAXモデル

SARIMAモデルは、過去の自分（ラグデータ）を使ってモデルを構築します。説明変数Xを導入しモデルに組み込めないだろうか、ということでSARIMAXです。このXは説明変数Xを意味します。

要するに、SARIMAXは、説明変数X付きのSARIMAモデルです。

つまり、ARIMA系のモデルとは、以下のモデル全てを含みます。

  • ARモデル：SARIMA( p,0,0 )( 0,0,0 )[0]
  • MAモデル：SARIMA( 0,0,q )( 0,0,0 )[0]
  • ARMAモデル：SARIMA( p,0,q )( 0,0,0 )[0]
  • ARIMAモデル：SARIMA( p,d,q )( 0,0,0 )[0]
  • SARIMAモデル：SARIMA( p,d,q )( P,D,Q )[m]
  • SARIMAXモデル：SARIMAX( p,d,q )( P,D,Q )[m]

 

パラメータ(p,d,q) (P,D,Q)[m]の設定の仕方

ARIMA系のモデルのパラメータ(p,d,q) (P,D,Q)[m]の次数をどう設定するのかは、非常に大きな問題です。

通常は、周期mを事前に設定した上で、残りのパラメータ(p,d,q)と(P,D,Q)を検討します。

3つの方法があります。

  • 手動構築
  • 自動構築
  • ハイブリッド（自動と手動の組み合わせ）

 

手動構築とは、ADF検定などを使い差分の次数を検討し決めます。その次数で階差系列を求め、その階差系列に対し自己相関 (ACF)と偏自己相関 (PACF)のコレログラムを表示し、ARとMAの次数を検討します。

手動構築の場合、コレログラムが次数を決める上でポイントになります。

以下は、次数を決めるときの考え方です。

Acf
ラグ1,2,3,…		 Pacf
ラグ1,2,3,…
AR(p) 指数関数的に減少 ラグp1の後は0
MA(q) ラグqの後は0 指数関数的に減少
AR(p)+MA(q) 指数関数的に減少 指数関数的に減少
Acf
ラグ1×m,2×m,3×m,…		 Pacf
ラグ1×m,2×m,3×m,…
SAR(P) 指数関数的に減少 ラグP×m1の後は0
SMA(Q) ラグQ×m1の後は0 指数関数的に減少
SAR(P)+SMA(Q) 指数関数的に減少 指数関数的に減少

 

自動構築とは、手動手順の流れを自動化したもので、コレログラムを見て次数を検討するのではなくAICなどの評価基準をもとに次数を検討することです。機械的にモデル構築する場合には、自動構築が向いています。

 

ちなみに、よくあるのは手動構築と自動構築のハイブリッドです。

先ず、自動構築で次数を求め、次に、その次数を参考に手動で次数を検討し決める、という流れや、先ず、階差の次数のみ検討し、次に、その階差の次数以外を自動構築で決める、などなど。

 

必要なライブラリーのインストール

今回は、ARIMAモデル構築用のライブラリーpmdarimaを利用します。

コマンドプロンプト上で、condaでインストールするときのコードは以下です。

conda install pmdarima

 

pipでインストールするときのコードは以下です。

pip install pmdarima

 

ライブラリーpmdarimaに、時系列データを扱う上で便利な道具がいくつか揃っています。例えば、単位根検定やコレログラム、データセットの分割（学習データとテストデータ）、時系列CV（クロスバリデーション）、BoxCox変換などなど。

 

必要なライブラリーの読み込み

では、必要なライブラリーを読み込みます。

以下、コードです。

# ライブラリーの読み込み
import numpy as np
import pandas as pd

import pmdarima as pm
from pmdarima import utils
from pmdarima import arima
from pmdarima import model_selection

from statsmodels.tsa.statespace.sarimax import SARIMAX

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

from matplotlib import pyplot as plt

# グラフのスタイルとサイズ
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]

 

利用するデータ

今回利用する時系列データのデータセットは、Airline Passengers（飛行機乗客数）は、Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h

 

では、データセットを読み込みます。

以下、コードです。

# データセットの読み込み
url='https://www.salesanalytics.co.jp/591h' #データセットのあるURL
df=pd.read_csv(url,                         #読み込むデータのURL
               index_col='Month',           #変数「Month」をインデックスに設定
               parse_dates=True)            #インデックスを日付型に設定

df.head() #確認

 

以下、実行結果です。

 

グラフ化し確認します。

以下、コードです。

# プロット
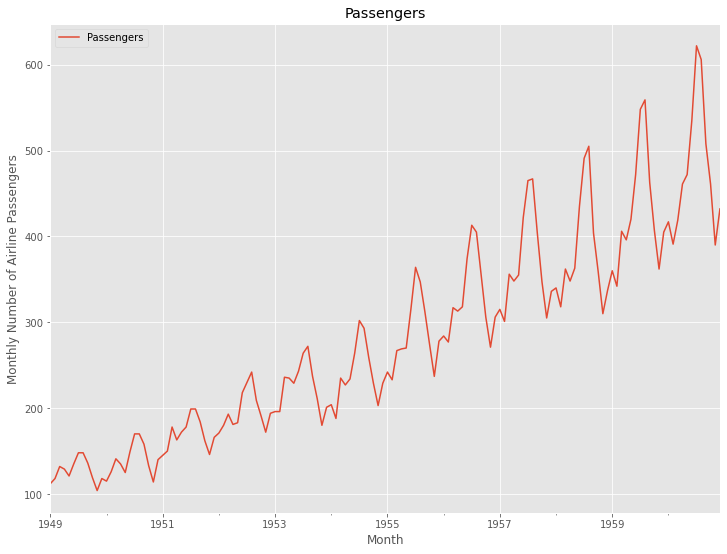
df.plot()
plt.title('Passengers')                            #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers') #タテ軸のラベル
plt.xlabel('Month')                                #ヨコ軸のラベル
plt.show()

 

以下、実行結果です。

 

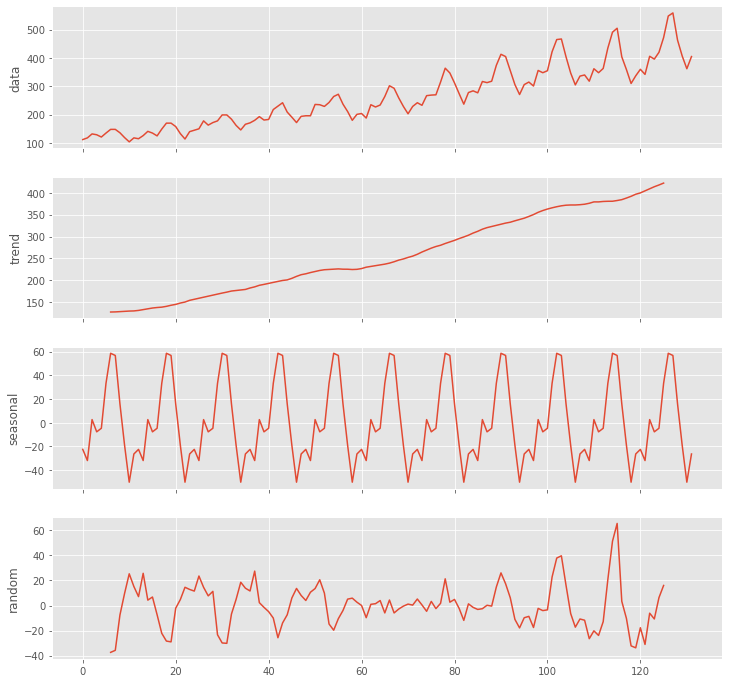
見るからに、トレンド成分と季節成分があるデータです。しかも、季節性の上下変動が時間が経るに従って大きくなっています。

 

今回は2種類の時系列データでモデル構築をしていきます。

  • 原系列：元の時系列データ
  • 対数系列：原系列を対数変換したデータ

 

今回構築するARIMAモデルは以下の3種類です。

  • 手動構築（SARIMAX関数）
  • 自動構築（auto_arima関数）
  • ハイブリッド構築（階差の次数のみ指定）

 

データセットが２種類（原系列と対数系列）で、モデルが３種類なので、合計して6つのARIMA系のモデルを構築します。

 

次に、読み込んだデータセットを、学習データとテストデータに分割します。

以下、コードです。

# 学習データとテストデータ（直近12ヶ月間）に分割
df_train, df_test = model_selection.train_test_split(df, test_size=12)

 

学習データでARIMAモデルを構築し、構築したモデルをテストデータで精度検証します。

 

予測精度の評価指標

今回の予測精度の評価指標は、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。 

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

 

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

原系列

　事前検討

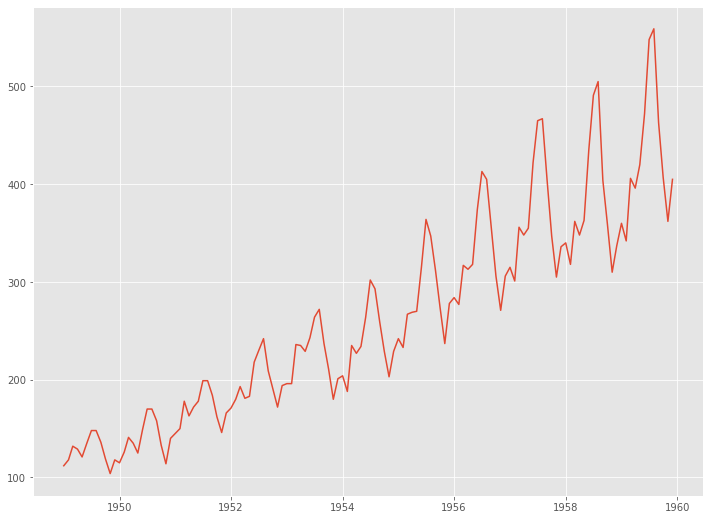
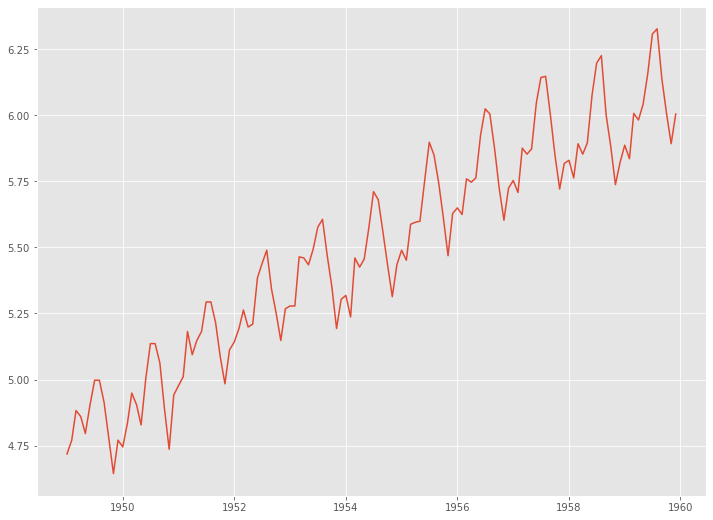
扱うデータを確認します。以下、コードです。

# 系列のプロット
plt.plot(df_train)

 

以下、実行結果です。

 

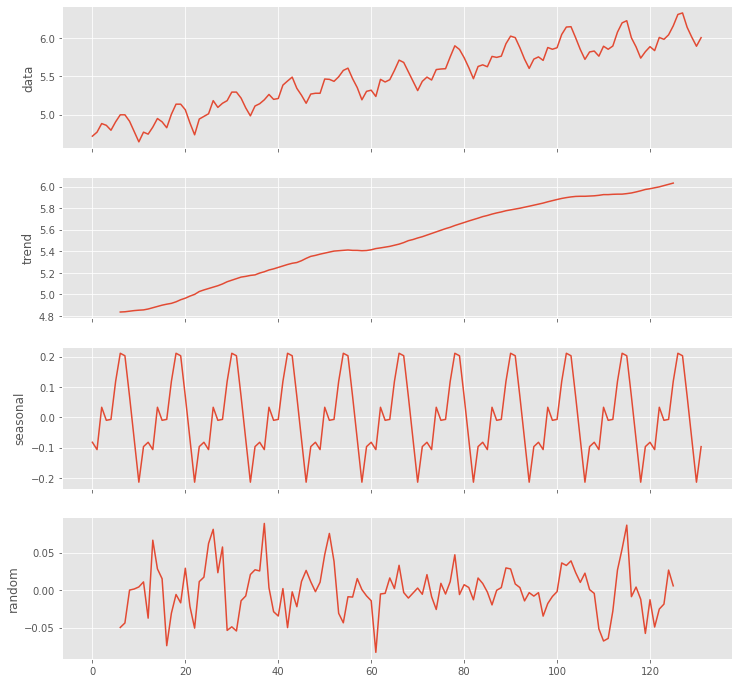
成分分解します。以下、コードです。

# 成分分解（tread・seasonal・random）
data = df_train.Passengers.values

utils.decomposed_plot(arima.decompose(data,'additive',m=12),
                      figure_kwargs = {'figsize': (12, 12)} )

 

以下、実行結果です。

 

階差の次数を検討します。以下、コードです。

# 階差の次数の検討
print('d =', arima.ndiffs(df))      #d
print('D =',arima.nsdiffs(df,m=12)) #D

 

以下、実行結果です。

 

これは、単位根検定などの定常性の統計的仮説検定を実施した結果です。通常の階差の次数は1で、季節階差の次数も1です。

 

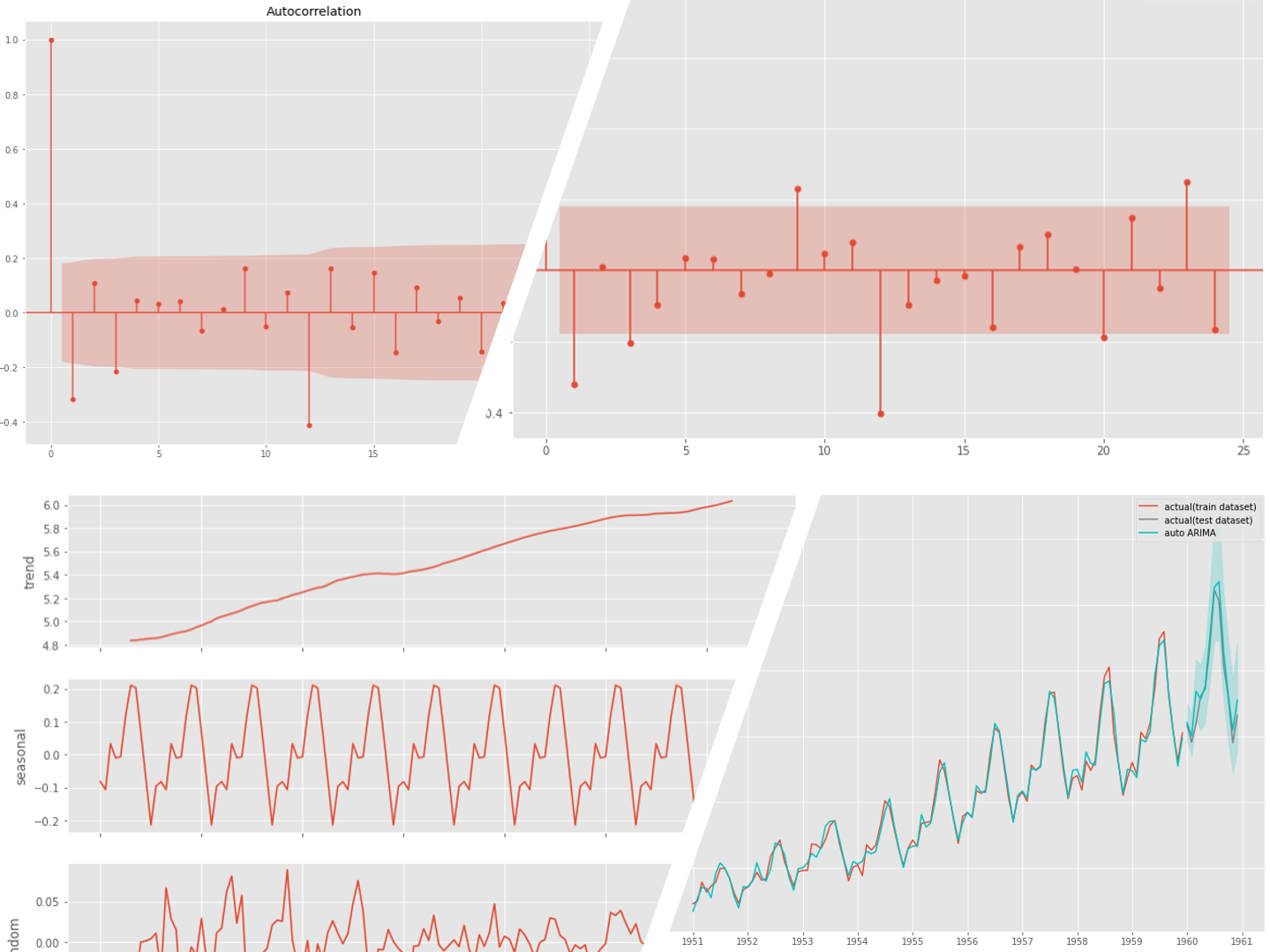
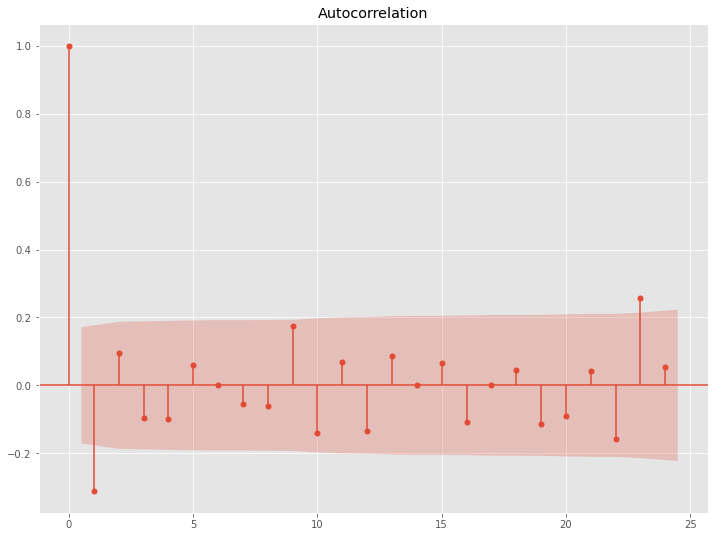
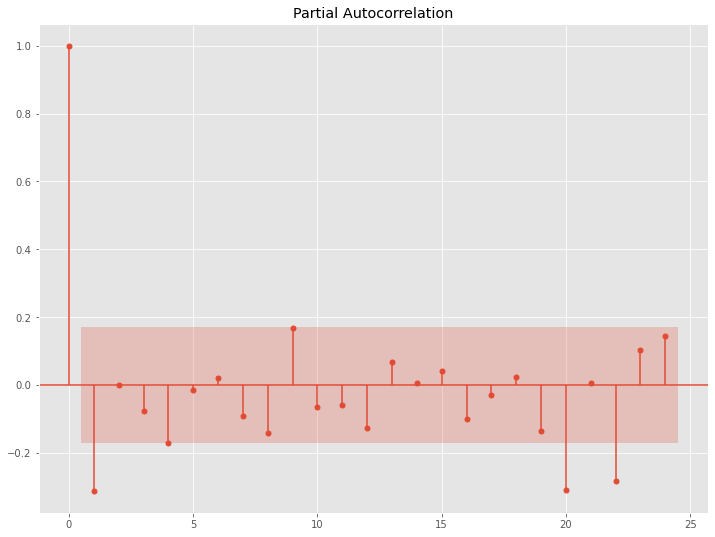
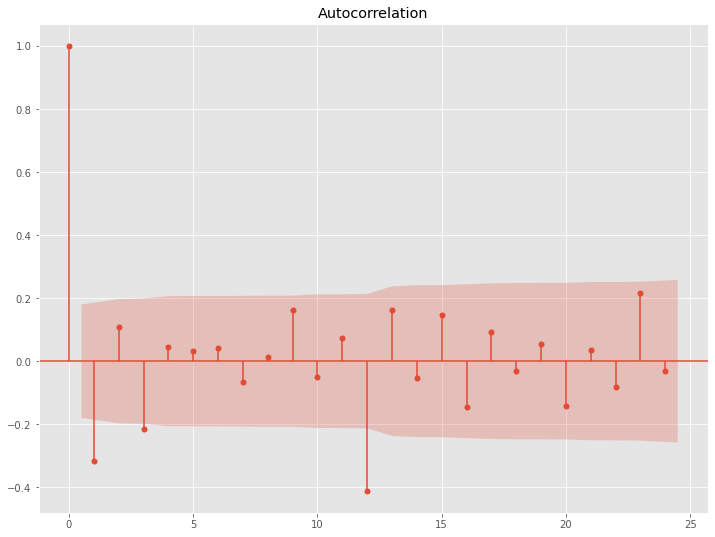
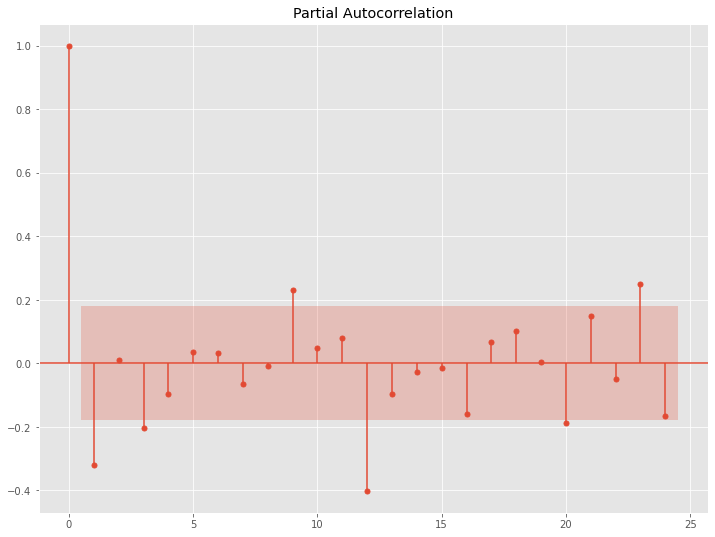
前期との差分から階差系列（1次）を求め、さらに12期前（1年前）との差分から季節階差系列（1次）を求めます。このデータのコレログラムを求めます。

以下、コードです。

# コレログラム（自己相関と偏自己相関）
data = df.diff(1).diff(12).dropna()

utils.plot_acf(data, alpha=.05, lags=24)
utils.plot_pacf(data, alpha=.05, lags=24)

 

以下、実行結果です。

 

このコレログラムをどう読み解くか、という問題はありますが、一旦ARとMAの次数を1とします。

 

　手動構築（SARIMAX関数）

ここまでの結果から、次数を以下のように考えます。

  • 非季節性
    • AR：p=1
    • 階差：d=1
    • MA：q=1
  • 季節性
    • 季節AR：P=0
    • 季節階差：D=1
    • 季節MA：Q=0

 

では、statsmodelsライブラリーのSARIMAX関数を利用し、ARIMAモデルを学習します。

以下、コードです。

# 原系列を学習データとする
train = df_train

# 学習
sarima_model = SARIMAX(train, order=(1, 1, 1), 
                       seasonal_order=(0, 1, 0,12))

sarima_fit = sarima_model.fit()

 

学習し構築したモデルを使い予測をします。

以下、コードです。

# 予測
##学習データの期間の予測値
train_pred = sarima_fit.predict()

##テストデータの期間の予測値
test_pred = sarima_fit.forecast(len(df_test))

##予測区間
test_pred_ci = sarima_fit.get_forecast(len(df_test)).conf_int() 

# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

 

以下、実行結果です。

 

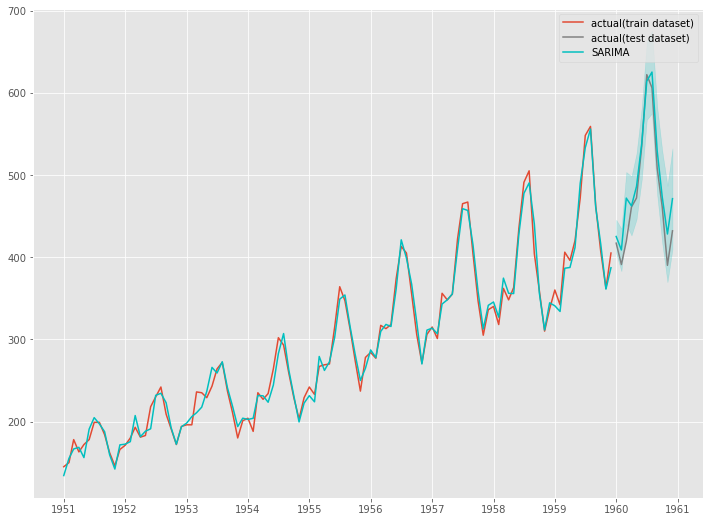
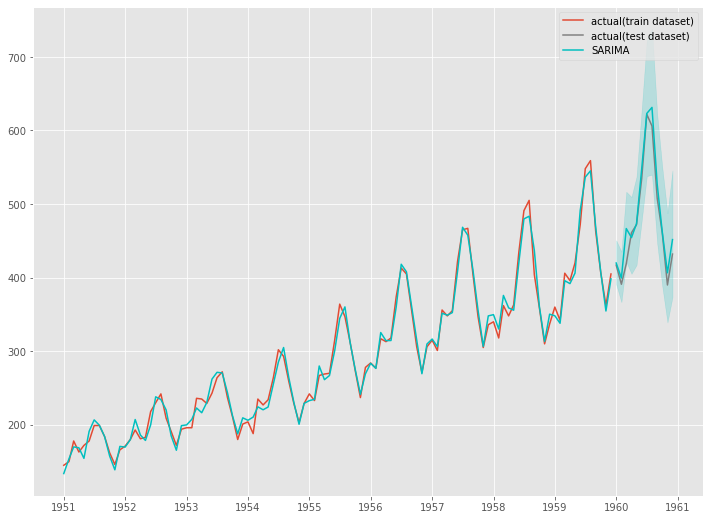
結果をグラフで視覚的に確認します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:].values, color="c")
ax.plot(df_test.index, test_pred.values, label="SARIMA", color="c") 

ax.fill_between(
    df_test.index,
    test_pred_ci.iloc[:, 0],
    test_pred_ci.iloc[:, 1],
    color='c',
    alpha=.2)

ax.legend()

 

以下、実行結果です。

 

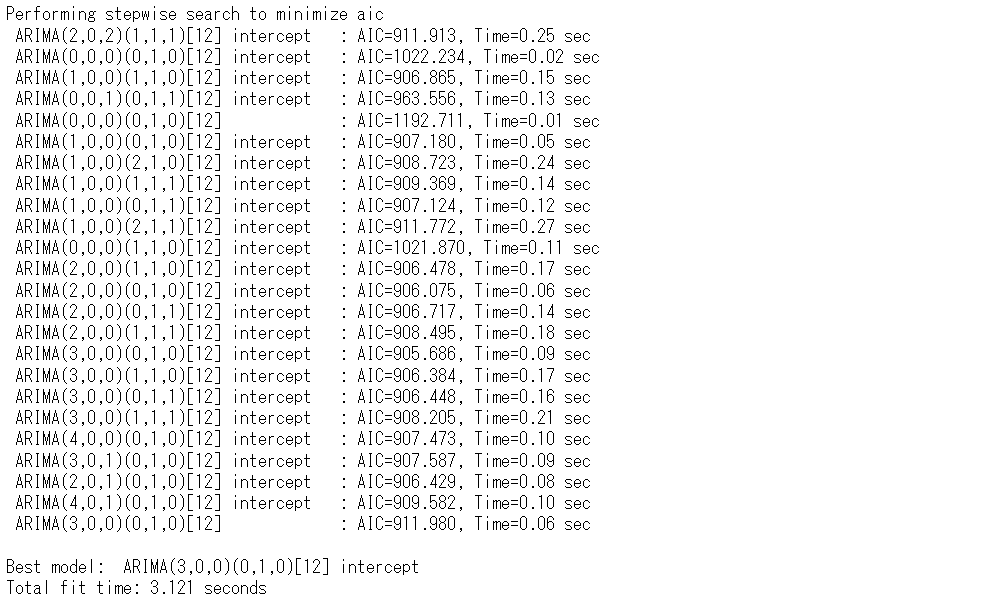
　自動構築（auto_arima関数）

次数を事前に設定せず、pmdarimaライブラリーのauto_arima関数を使い、ARIMAモデルを自動構築します。

以下、コードです。

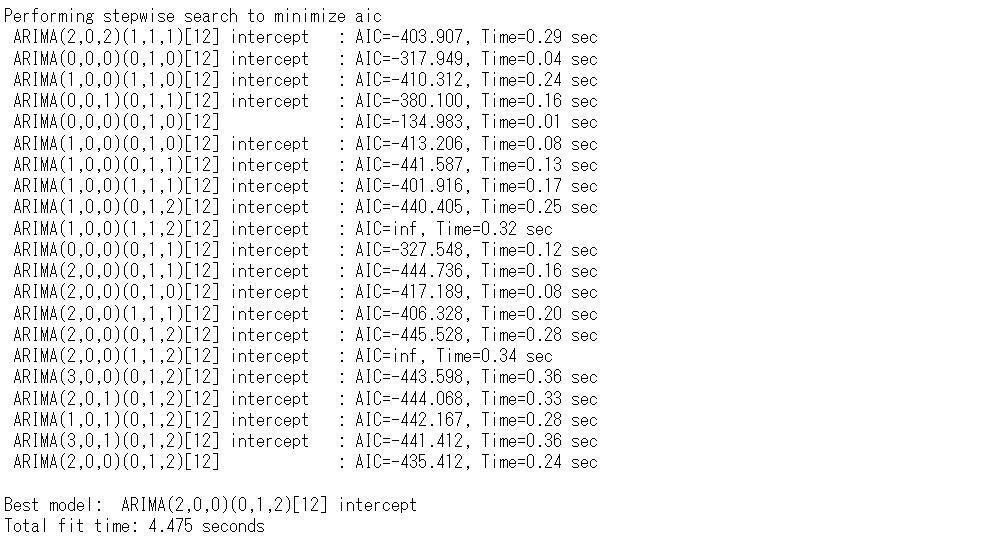
# モデル構築（Auto ARIMA）
arima_model = pm.auto_arima(train, 
                            seasonal=True,
                            m=12,
                            trace=True,
                            n_jobs=-1,
                            maxiter=10)

 

以下、実行結果です。

 

SARIMA(3,0,0)(0,1,0,12)というARIMAモデルが構築されました。このモデルを使い予測をします。

以下、コードです。

# 予測
##学習データの期間の予測値
train_pred = arima_model.predict_in_sample()

##テストデータの期間の予測値
test_pred, test_pred_ci = arima_model.predict(
    n_periods=df_test.shape[0], 
    return_conf_int=True
)

# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

 

以下、実行結果です。

 

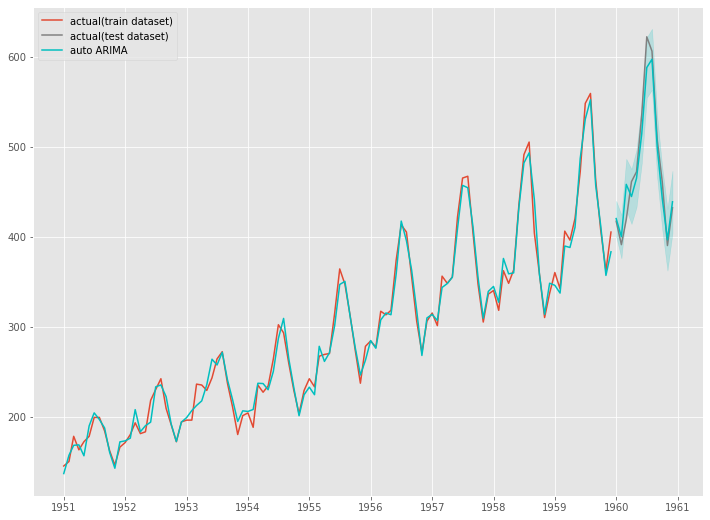
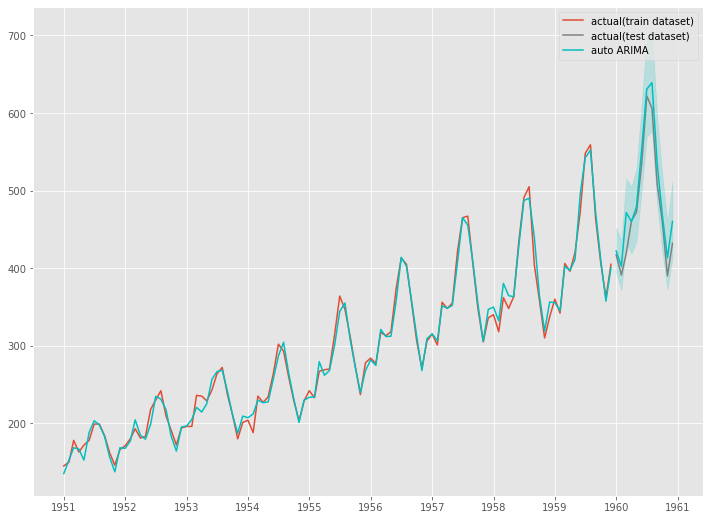
結果をグラフで視覚的に確認します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:], color="c")
ax.plot(df_test.index, test_pred, label="auto ARIMA", color="c") 

ax.fill_between(
    df_test.index,
    test_pred_ci[:, 0],
    test_pred_ci[:, 1],
    color='c',
    alpha=.2)

ax.legend()

 

以下、実行結果です。

 

　ハイブリッド構築（階差の次数のみ指定）

階差の次数のみ指定し、auto_arima関数を使い、ARIMAモデルを構築します。

以下、コードです。

# モデル構築（Auto ARIMA）
arima_model = pm.auto_arima(train, 
                            seasonal=True,
                            m=12,
                            d=1,
                            D=1,
                            trace=True,
                            n_jobs=-1,
                            maxiter=10)

 

以下、実行結果です。

 

SARIMA(1,1,0)(0,1,0,12)というARIMAモデルが構築されました。このモデルを使い予測をします。

以下、コードです。

# 予測
##学習データの期間の予測値
train_pred = arima_model.predict_in_sample()

##テストデータの期間の予測値
test_pred, test_pred_ci = arima_model.predict(
    n_periods=df_test.shape[0], 
    return_conf_int=True
)

# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

 

以下、実行結果です。

 

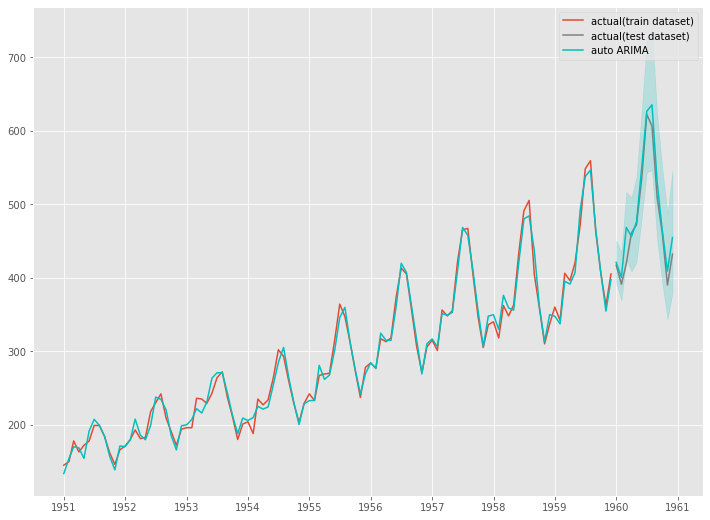
結果をグラフで視覚的に確認します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:], color="c")
ax.plot(df_test.index, test_pred, label="auto ARIMA", color="c") 

ax.fill_between(
    df_test.index,
    test_pred_ci[:, 0],
    test_pred_ci[:, 1],
    color='c',
    alpha=.2)

ax.legend()

 

以下、実行結果です。

 

対数系列

　事前検討

原系列を対数変換し、対数系列を作ります。

以下、コードです。

# 対数変換
df_log = np.log(df_train)

# 系列のプロット
plt.plot(df_log)

 

以下、実行結果です。

 

成分分解します。以下、コードです。

# 成分分解（tread・seasonal・random）
data = df_log.Passengers.values

utils.decomposed_plot(arima.decompose(data,'additive',m=12),
                      figure_kwargs = {'figsize': (12, 12)} )

 

以下、実行結果です。

 

階差の次数を検討します。以下、コードです。

# 階差の次数の検討
print('d =', arima.ndiffs(df_log))
print('D =',arima.nsdiffs(df_log,m=12))

 

以下、実行結果です。

 

これは、単位根検定などの定常性の統計的仮説検定を実施した結果です。通常の階差の次数は1で、季節階差の次数も1です。

 

前期との差分から階差系列（1次）を求め、さらに12期前（1年前）との差分から季節階差系列（1次）を求めます。このデータのコレログラムを求めます。

以下、コードです。

# コレログラム（自己相関と偏自己相関）
data = df_log.diff(1).diff(12).dropna()

utils.plot_acf(data, alpha=.05, lags=24)
utils.plot_pacf(data, alpha=.05, lags=24)

 

以下、実行結果です。

 

このコレログラムをどう読み解くか、という問題はありますが、一旦ARとMAの次数を1、SARとSMAの次数を1とします。

 

　手動構築（SARIMAX関数）

ここまでの結果から、次数を以下のように考えます。

  • 非季節性
    • AR：p=1
    • 階差：d=1
    • MA：q=1
  • 季節性
    • 季節AR：P=1
    • 季節階差：D=1
    • 季節MA：Q=1

 

では、statsmodelsライブラリーのSARIMAX関数を利用し、ARIMAモデルを学習します。

以下、コードです。

# 対数系列を学習データとする
train = df_log

# 学習
sarima_model = SARIMAX(train, order=(1, 1, 1), 
                       seasonal_order=(1, 1, 1,12))

sarima_fit = sarima_model.fit()

 

学習し構築したモデルを使い予測をします。

以下、コードです。

# 予測
##学習データの期間の予測値
train_pred_log = sarima_fit.predict()
train_pred = np.exp(train_pred_log)

##テストデータの期間の予測値
test_pred_log = sarima_fit.forecast(len(df_test))
test_pred = np.exp(test_pred_log)

##予測区間
test_pred_ci_log = sarima_fit.get_forecast(len(df_test)).conf_int() 
test_pred_ci = np.exp(test_pred_ci_log)

# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

 

以下、実行結果です。

 

結果をグラフで視覚的に確認します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:].values, color="c")
ax.plot(df_test.index, test_pred.values, label="SARIMA", color="c") 

ax.fill_between(
    df_test.index,
    test_pred_ci.iloc[:, 0],
    test_pred_ci.iloc[:, 1],
    color='c',
    alpha=.2)

ax.legend()

 

以下、実行結果です。

 

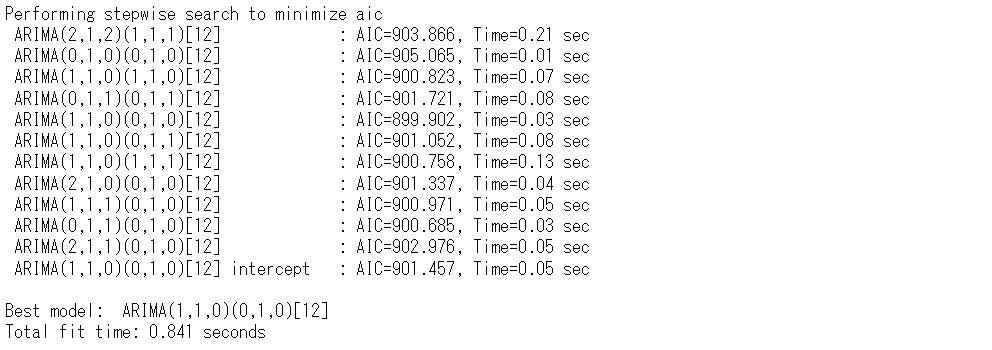
　自動構築（auto_arima関数）

次数を事前に設定せず、pmdarimaライブラリーのauto_arima関数を使い、ARIMAモデルを自動構築します。

以下、コードです。

# モデル構築（Auto ARIMA）
arima_model = pm.auto_arima(train, 
                            seasonal=True,
                            m=12,
                            trace=True,
                            n_jobs=-1,
                            maxiter=10)

 

以下、実行結果です。

 

SARIMA(2,0,0)(0,1,2,12)というARIMAモデルが構築されました。このモデルを使い予測をします。

以下、コードです。

# 予測
##学習データの期間の予測値
train_pred_log = arima_model.predict_in_sample()
train_pred = np.exp(train_pred_log)

##テストデータの期間の予測値
test_pred_log, test_pred_ci_log = arima_model.predict(
    n_periods=df_test.shape[0], 
    return_conf_int=True
)
test_pred = np.exp(test_pred_log)
test_pred_ci = np.exp(test_pred_ci_log)

# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

 

以下、実行結果です。

 

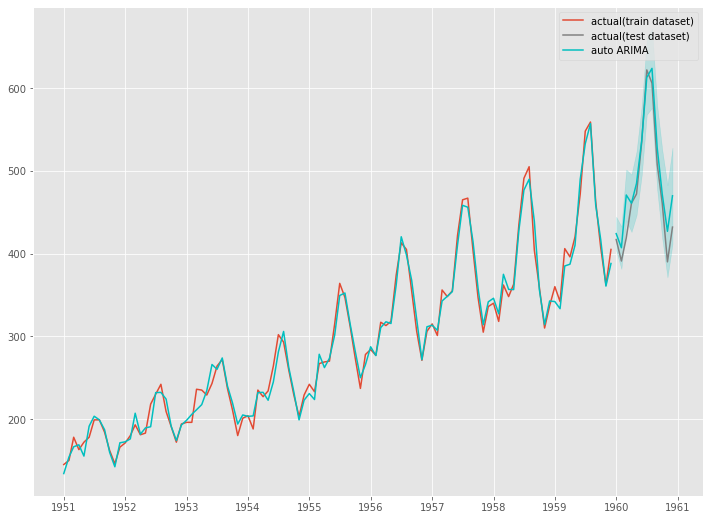
結果をグラフで視覚的に確認します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:], color="c")
ax.plot(df_test.index, test_pred, label="auto ARIMA", color="c") 

ax.fill_between(
    df_test.index,
    test_pred_ci[:, 0],
    test_pred_ci[:, 1],
    color='c',
    alpha=.2)

ax.legend()

 

以下、実行結果です。

 

　ハイブリッド構築（階差の次数のみ指定）

階差の次数のみ指定し、auto_arima関数を使い、ARIMAモデルを構築します。

以下、コードです。

# モデル構築（Auto ARIMA）
arima_model = pm.auto_arima(train, 
                            seasonal=True,
                            m=12,
                            d=1,
                            D=1,
                            trace=True,
                            n_jobs=-1,
                            maxiter=10)

 

以下、実行結果です。

 

SARIMA(1,1,0)(0,1,1,12)というARIMAモデルが構築されました。このモデルを使い予測をします。

以下、コードです。

# 予測
##学習データの期間の予測値
train_pred_log = arima_model.predict_in_sample()
train_pred = np.exp(train_pred_log)

##テストデータの期間の予測値
test_pred_log, test_pred_ci_log = arima_model.predict(
    n_periods=df_test.shape[0], 
    return_conf_int=True
)
test_pred = np.exp(test_pred_log)
test_pred_ci = np.exp(test_pred_ci_log)

# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

 

以下、実行結果です。

 

結果をグラフで視覚的に確認します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:], color="c")
ax.plot(df_test.index, test_pred, label="auto ARIMA", color="c") 

ax.fill_between(
    df_test.index,
    test_pred_ci[:, 0],
    test_pred_ci[:, 1],
    color='c',
    alpha=.2)

ax.legend()

 

以下、実行結果です。

 

次回

今回は、「ARIMA系モデルで予測する方法」について説明しました。

次回は、「Prophetモデルで予測する方法」について説明していきます。

Pythonで時系列解析・超入門（その4）Prophetモデルで予測する方法