前回までは、simpleRNN・LSTM・GTUでモデル構築し1期先予測（1-Step ahead prediction）の方法について説明しました。
以下の記事は、simpleRNNでモデル構築し1期先予測（1-Step ahead prediction）の方法です。
以下の記事は、LSTMでモデル構築し1期先予測（1-Step ahead prediction）の方法です。
以下の記事は、GRUでモデル構築し1期先予測（1-Step ahead prediction）の方法です。
実務的には、1期先予測（1-Step ahead prediction）だけで十分なケースは少なく、複数先予測（Multi-Step ahead prediction）を実施するケースが多いでしょう。
例えば、日単位であれば明日だけでなく明日以降1週間や1ヶ月を予測する、月単位であれば来月だけでなく来月以降3ヶ月間や1年間を予測する、というケースです。
複数先予測（Multi-Step ahead prediction）の方法には、幾つかやり方があります。
その中の1つに、時系列の多変量予測モデルを1つ作る方法があります。言い換えると、目的変数yを多変量化（ベクトル化）し予測モデルを1つ作るということです。
ということで今回は、多変量目的変数で多期先予測（Multi-Step ahead prediction）の方法について説明します。
Contents
データセットとモデル
予測で利用するモデルは以下の3つです。
- シンプルRNN
- LSTM
- GRU
インプットデータXとアウトプットデータyを、データセットをそれぞれ準備する必要があります。
Keras（TensorFlow）のRNN系のインプットデータXは、以下のような3元構造が基本になっています。
前回までは目的変数であるアウトプットデータyが1変量でしたが、今回はn変量になります。
前回までは目的変数であるアウトプットデータyが1変量（1期先）でしたが、今回はn変量（複数先）になります。
時系列データの特徴量の1つとして、ラグ変数というものがあります。
例えば、日販（1日の売上）であれば、「ラグ1の変数」とは「1日前の日販の変数」、「ラグ2の変数」とは「2日前の日販の変数」などです。
目的変数のラグ変数を作り、インプットデータXとアウトプットデータyを作っていきます。
例えば、以下のような日単位の時系列データがあったとします。
y(t=0),y(t=1),y(t=2),…
このとき、過去365日間のデータを使い、近未来30日間を予測するために、以下のようなデータセットを準備します。
| インプットデータX | アウトプットデータy | |||||||
| index | x1 | x2 | … | x365 | y1 | y2 | … | y30 |
| 0 | y(t=394) | y(t=393) | … | y(t=30) | y(t=29) | y(t=28) | … | y(t=0) |
| 1 | y(t=395) | y(t=394) | … | y(t=31) | y(t=30) | y(t=29) | … | y(t=1) |
| 2 | y(t=396) | y(t=395) | … | y(t=32) | y(t=31) | y(t=30) | … | y(t=2) |
| 3 | y(t=397) | y(t=396) | … | y(t=33) | y(t=32) | y(t=31) | … | y(t=3) |
| 4 | y(t=398) | y(t=397) | … | y(t=34) | y(t=33) | y(t=32) | … | y(t=4) |
| 5 | y(t=399) | y(t=398) | … | y(t=35) | y(t=34) | y(t=33) | … | y(t=5) |
| 6 | y(t=400) | y(t=399) | … | y(t=36) | y(t=35) | y(t=34) | … | y(t=6) |
| 7 | y(t=401) | y(t=400) | … | y(t=37) | y(t=36) | y(t=35) | … | y(t=7) |
| 8 | y(t=402) | y(t=401) | … | y(t=38) | y(t=37) | y(t=36) | … | y(t=8) |
| 9 | y(t=403) | y(t=402) | … | y(t=39) | y(t=38) | y(t=37) | … | y(t=9) |
サンプルデータ（前回と同じです）
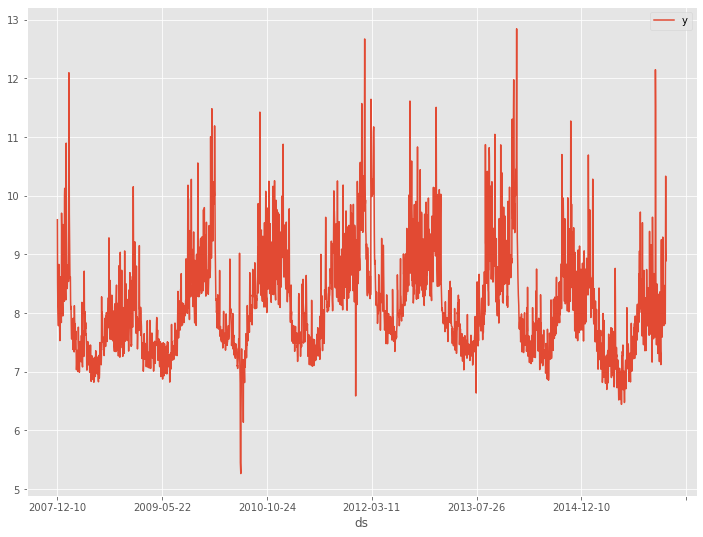
サンプルデータは、前回と同じPeyton ManningのWikipediaのPV（ページビュー）というProphetで提供されているサンプルデータ（example_wp_log_peyton_manning.csv）を使います。
facebook/prophetのGitHubからダウンロードして使って頂くか、弊社のHPからダウンロードして使って頂ければと思います。
facebook/prophetのGitHub上のデータ
https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/bgr8
このデータセットは、説明変数のない目的変数が1変量の時系列データです。もちろん、目的変数は、日単位のPV（ページビュー数）です。
PV（ページビュー数）のラグ変数を作り説明変数にします。要するに、過去のPVから未来のPVを予測する、ということです。
予測精度の評価指標（前回と同じです）
今回の予測精度の評価指標も前回と同じで、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。
以下の記号を使い精度指標の説明をします。
- y_i^{actual} ・・・i番目の実測値
- y_i^{pred} ・・・i番目の予測値
- \overline{y^{actual}} ・・・実測値の平均
- n ・・・実測値・予測値の数
■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）
\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}■ 平均絶対誤差（MAE、Mean Absolute Error）
\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）
\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|
準備
必要なライブラリーなどを読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import *
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.utils import plot_model
from tensorflow.python.keras.models import load_model
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
データセットを読み込みます。
以下、コードです。
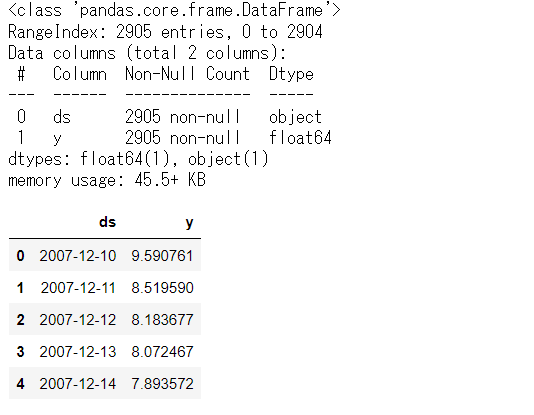
# データセット読み込み url = 'https://www.salesanalytics.co.jp/bgr8' df = pd.read_csv(url) # データ確認 df.info() #変数の情報 df.head() #データの一部
以下、実行結果です。
最低限の前処理とデータ分割
まず、データセットがデータフレームですので、配列へ変換したりします。
以下、コードです。
# 変換
dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32') #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換
dataset #確認
以下、実行結果です。
この時系列データのラグ変数を作り、インプットデータXとアウトプットデータyを作っていきます。
ラグ変数からインプットデータXとアウトプットデータyを作る生成関数を定義します。
以下、インプットデータXとアウトプットデータyを作る生成関数のコードです。
# データセット生成関数
def gen_dataset(dataset, lag_max, forecast_horizon=1):
X, y = [], []
for i in range(len(dataset) - lag_max - forecast_horizon + 1):
a = i + lag_max
b = a + forecast_horizon
X.append(dataset[i:a, 0]) #ラグ特徴量
y.append(dataset[a:b, 0]) #目的変数
return np.array(X), np.array(y)
先程準備した時系列データに対し、適用します。インプットデータXのラグの最大値（lag_max）は365日で、アウトプットデータyの予測期間（forecast_horizon）は30です。
以下、コードです。
# 分析用データセットの生成
lag_max = 365
forecast_horizon = 30
X, y = gen_dataset(dataset, lag_max, forecast_horizon)
print('X:',X.shape) #確認
print('y:',y.shape) #確認
以下、実行結果です。
Xは2511行（サンプル）×365列（変数）のデータで、yは2511行（サンプル）×30列（変数）のデータです。
このデータセットXとyを、学習データとテストデータに分割します。直近100日間をテストデータにしています。
以下、コードです。
# データ分割 test_length = 100 #テストデータの期間 X_train_0 = X[:-test_length,:] #学習データ X_test_0 = X[-test_length:,:] #テストデータ y_train = y[:-test_length,:] #学習データ y_test = y[-test_length:,:] #テストデータ
さらに、各変数を正規化します。今回実施する正規化は0～1の範囲に数値を収めるミニマックススケーリングです。0が最小値で、1が最大値になるように、元のデータを変換します。
以下、コードです。
# 正規化（0-1の範囲にスケーリング） ## 目的変数y scaler_y = MinMaxScaler(feature_range=(0, 1)) y_train = scaler_y.fit_transform(y_train) ## 説明変数X scaler_X = MinMaxScaler(feature_range=(0, 1)) X_train_0 = scaler_X.fit_transform(X_train_0) X_test_0 = scaler_X.transform(X_test_0)
この学習データでモデルを構築し、構築したモデルをテストデータで検証していきます。
RNN/LSTM/GRU（ラグ変数：time steps）
予測で利用するモデルは以下の3つです。
- シンプルRNN
- LSTM
- GRU
どのモデルがいいのかを検討し、最もいいモデルを詳しく見てみます。
データ準備
ラグ変数Xをタイムステップ（time_steps）とした学習データとテストデータを準備します。
以下、コードです。
# モデル構築用にデータを再構成（サンプル数、タイムステップ, 特徴量数）
X_train = np.reshape(X_train_0, (X_train_0.shape[0],X_train_0.shape[1], 1))
X_test = np.reshape(X_test_0, (X_test_0.shape[0],X_test_0.shape[1], 1))
print('X_train:',X_train.shape) #確認
print('X_test:',X_test.shape) #確認
以下、実行結果です。
X_trainが(samples=2411, time_steps=365, features=1)で、X_testが(samples=100, time_steps=365, features=1)ということです。
要は、ラグ変数をタイムステップ（time_steps）として扱うということです。
モデル検討
検討対象の3つのニュラールネットワークモデルを定義します。
以下、コードです。
# 構築するモデル設定
models = [
['SimpleRNN',
Sequential([
SimpleRNN(300,input_shape=(X_train.shape[1], X_train.shape[2])),
Dropout(0.2),
Dense(forecast_horizon, activation='linear'),
])
],
['LSTM',
Sequential([
LSTM(300,input_shape=(X_train.shape[1], X_train.shape[2])),
Dropout(0.2),
Dense(forecast_horizon, activation='linear')
])
],
['GRU',
Sequential([
GRU(300,input_shape=(X_train.shape[1], X_train.shape[2])),
Dropout(0.2),
Dense(forecast_horizon, activation='linear')
])
],
]
定義したモデルをコンパイルしモデル生成します。生成したモデルはファイルとして出力（h5ファイル）していますので、後で呼び出して使えます。
以下、コードです。
for model_name, model in models:
print()
print(model_name)
model.compile(loss='mean_squared_error', optimizer='adam')
# モデルの視覚化
plot_model(model,show_shapes=True)
# EaelyStoppingの設定
early_stopping = EarlyStopping(monitor='val_loss',
min_delta=0.0,
patience=2)
# 学習の実行
history = model.fit(X_train, y_train,
epochs=1000,
batch_size=128,
validation_split=0.2,
callbacks=[early_stopping] ,
verbose=0,
shuffle=False)
# 学習結果の出力
model.summary()
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()
# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)
# テストデータの目的変数と予測結果を結合
df_test = pd.DataFrame(np.hstack((y_test,y_test_pred)))
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
# モデル保存
filename = model_name + '.h5'
model.save(filename)
以下、実行結果です。
simpleRNNが最も予測精度が良い結果になっています。
検討し選択したモデル（simpleRNN）で検証
学習したモデル（simpleRNN）を、テストデータで検証します。
以下、先程生成したモデル（simpleRNN）を読み込むコードです。
# model読み込み filename = 'simpleRNN.h5' model = load_model(filename)
読み込んだモデル（simpleRNN）でテストデータを予測します。
以下、コードです。
# テストデータの目的変数を予測
y_test_pred = model.predict(X_test)
y_test_pred = scaler_y.inverse_transform(y_test_pred)
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
以下、実行結果です。
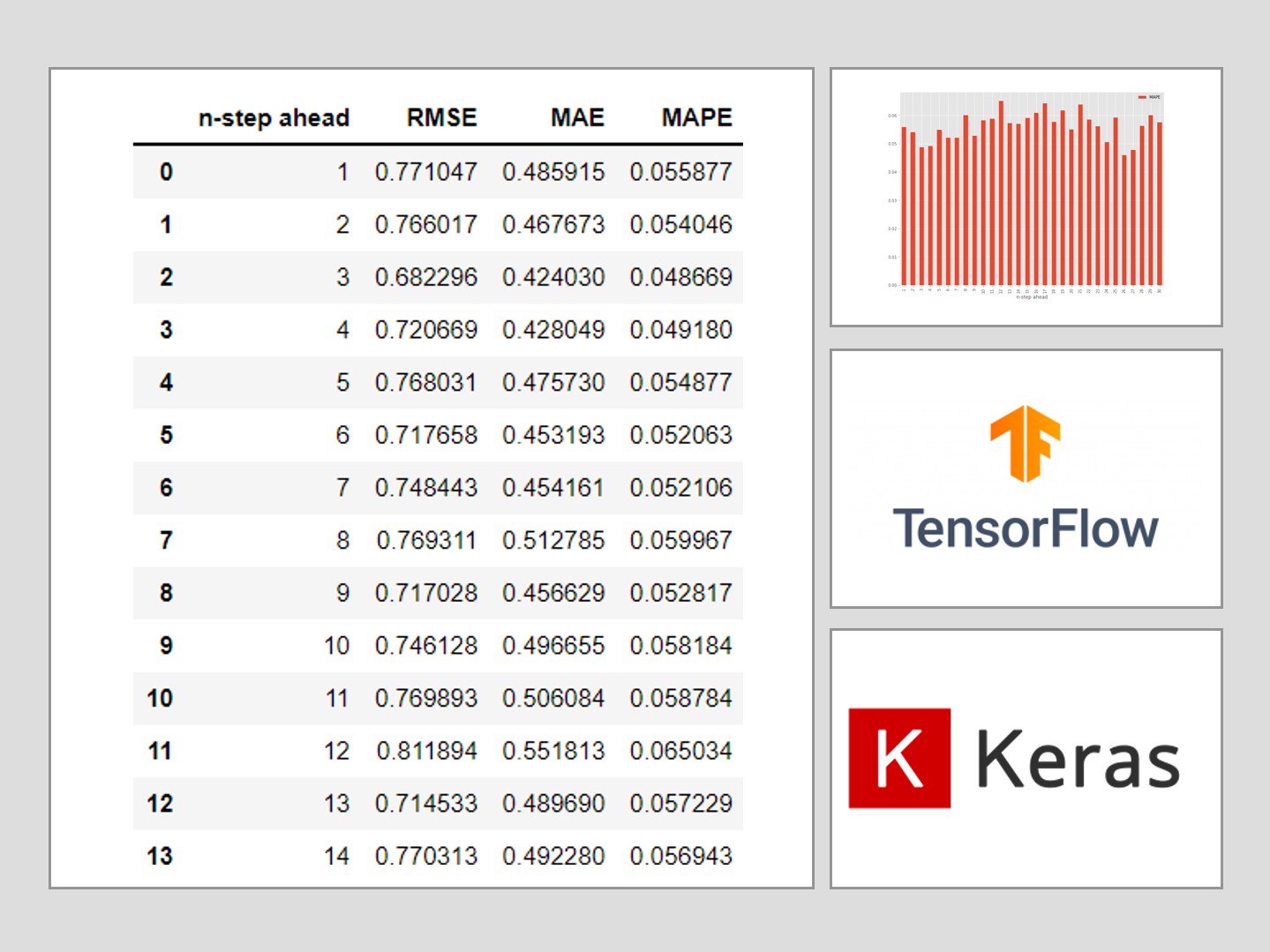
n期先予測別に精度を見てみます。
以下、コードです。
# 精度指標
testResult = []
for i in range(forecast_horizon):
RMSE=np.sqrt(mean_squared_error(y_test[:,i], y_test_pred[:,i]))
MAE=mean_absolute_error(y_test[:,i], y_test_pred[:,i])
MAPE=mean_absolute_percentage_error(y_test[:,i], y_test_pred[:,i])
testResult.append([i+1,RMSE,MAE,MAPE])
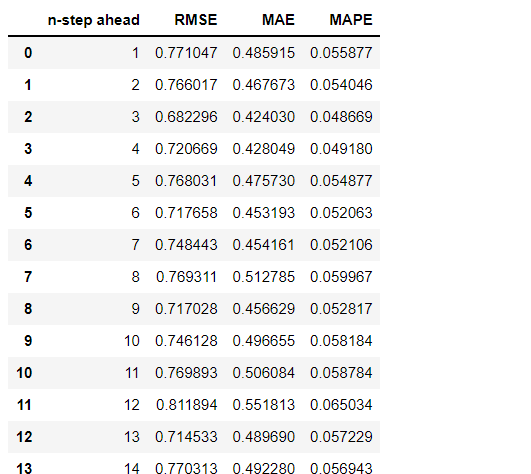
testResult = pd.DataFrame(testResult, columns=(['n-step ahead','RMSE','MAE','MAPE']))
testResult
以下、実行結果です。
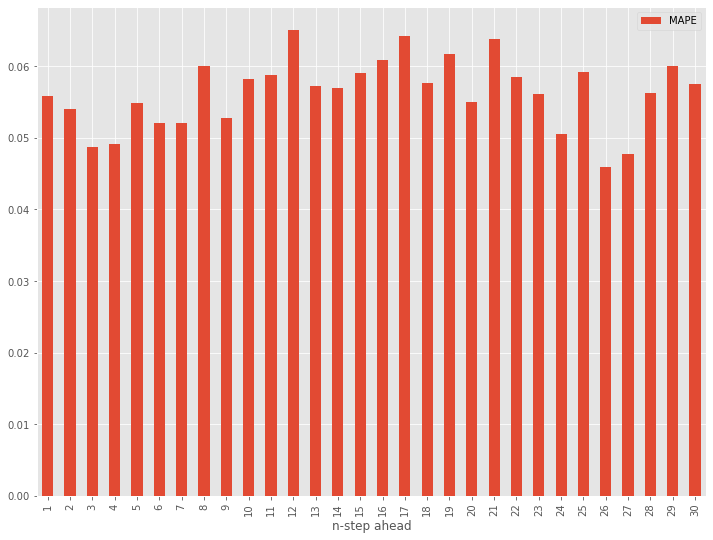
MAPEをグラフ化してみます。
以下、コードです。
# グラフ化 testResult.plot(x='n-step ahead', y='MAPE', kind='bar')
以下、実行結果です。
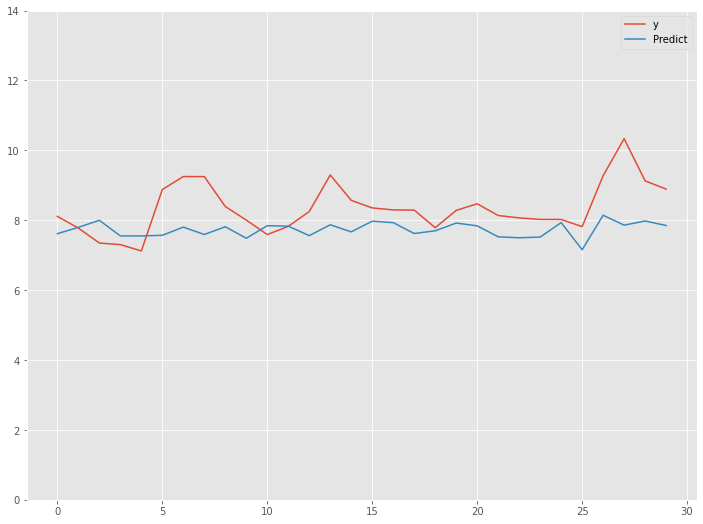
最後に、直近30日の精度を見てみます。
以下、コードです。
# 直近30日の実測値（y）と予測値（Predict）を結合
df_test_last = pd.DataFrame(y_test[test_length-1], columns = ['y'])
df_test_last['Predict'] = pd.DataFrame(y_test_pred[test_length-1])
# 指標出力
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test_last.y, df_test_last.Predict)))
print('MAE:')
print(mean_absolute_error(df_test_last.y, df_test_last.Predict))
print('MAPE:')
print(mean_absolute_percentage_error(df_test_last.y, df_test_last.Predict))
# グラフ化
df_test_last.plot(ylim=[0,14])
以下、実行結果です。
まとめ
今回は、多変量目的変数で多期先予測（Multi-Step ahead prediction）の方法について説明しました。
複数先予測（Multi-Step ahead prediction）の方法には、別のやり方もあります。
その1つが、Seq2Seq とも呼ばれるEncoder-Decoder型RNN（LSTMやGRUを含む）モデルを構築し複数先予測をするというものです。
次回お話しします。
Python Keras(TensorFlow)で作る深層学習(Deep Learning)時系列予測モデル(その5) 時系列Encoder-Decoderモデルで複数時系列予測（解説編）
