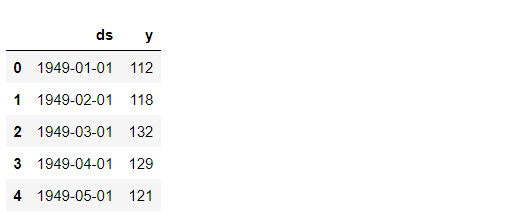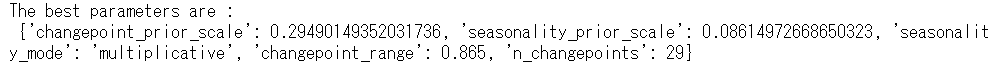Pythonで時系列解析・超入門（その4）

Prophetモデルで予測する方法

22420
Pythonで時系列解析・超入門（その4）Prophetモデルで予測する方法

ビジネスの世界で発生するデータの多くは、時間的概念の紐付いた時系列データです。

例えば、売上金額や受注件数、販売量、生産量、在庫量、PV（ページビュー）数、見込み顧客数、既存顧客数、離反顧客数、故障件数、広告宣伝費、人件費、従業員数、離職者数、などなど。

前回、「ARIMA系モデルで予測する方法」というお話しをしました。

Pythonで時系列解析・超入門（その3）ARIMA系モデルで予測する方法

今回は、「Prophetモデルで予測する方法」について説明していきます。

比較的新しい時系列モデルですが、ARIMAモデル並に使いやすいモデルです。

Prophetモデル

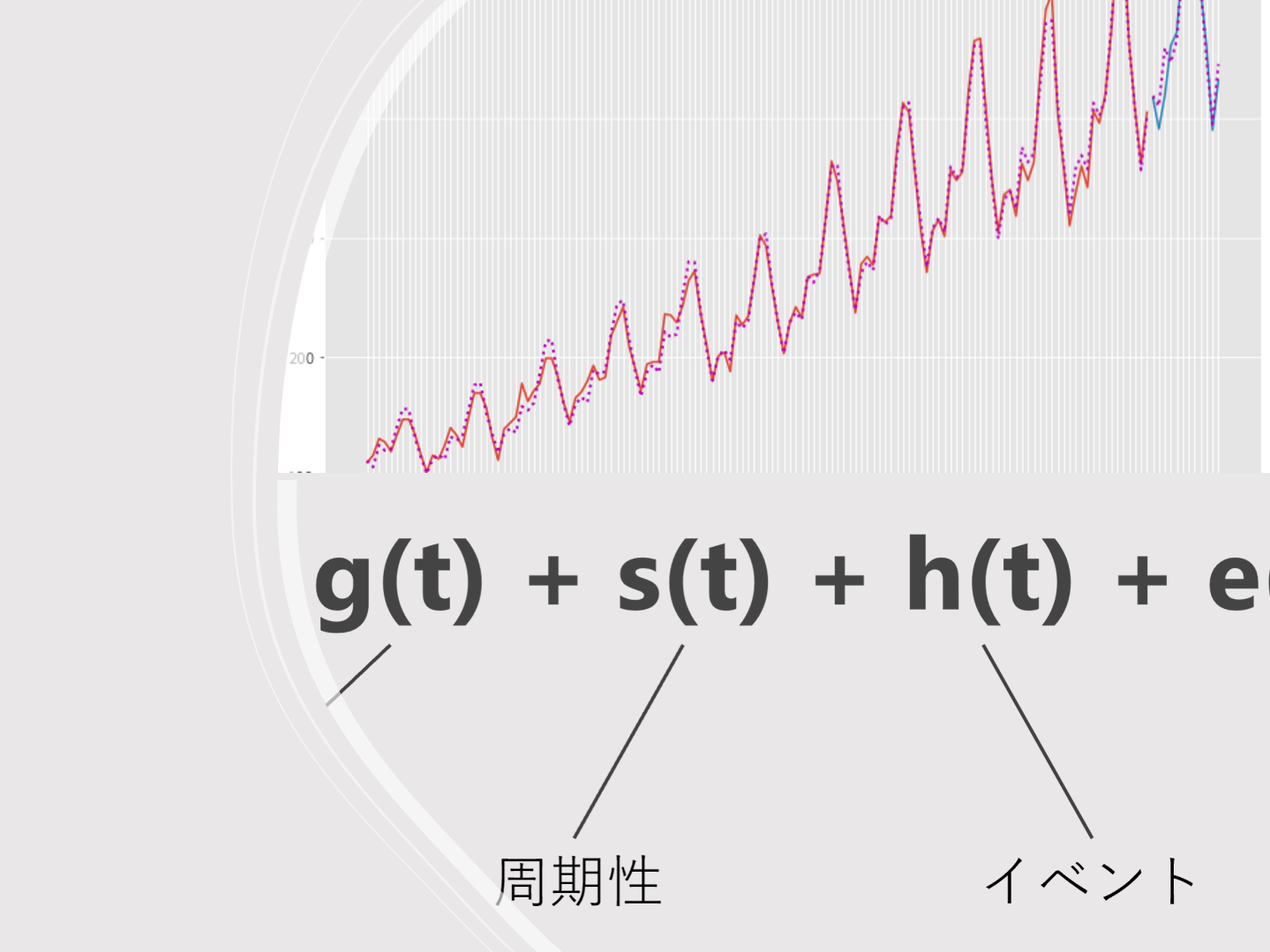
ProphetはMeta社（旧Facebook社）が開発した、一般化加法モデル（Generalized Additive Model）です。

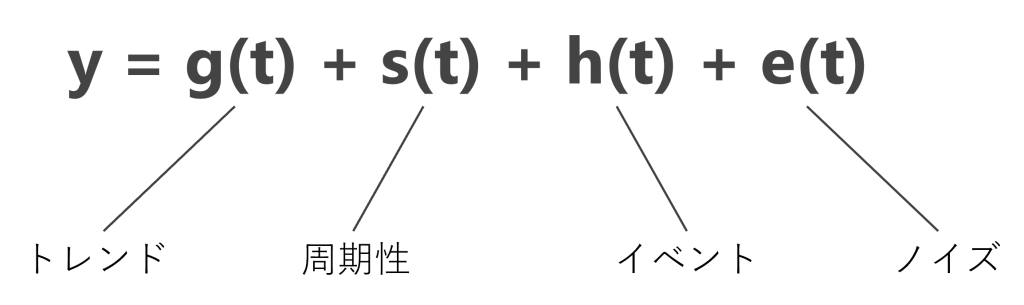
トレンド・周期性・イベント・ノイズをそれぞれでモデル化し足し合わせたモデルです。

Stan（Pythonの場合はPyStan）で動きます。そのため、Pythonで動かすためには、Prophetとともに、PyStanもインストールしておく必要があります。

 

Prophet とPyStanのインストール

コマンドプロンプト上でインストールするときのコードは以下です。

pip install pystan==2.19.1.1
conda install -c conda-forge prophet

 

準備（必要なライブラリーとデータの読み込み）

では、必要なライブラリーを読み込みます。

以下、コードです。

# ライブラリーの読み込み
import numpy as np
import pandas as pd
import optuna

from prophet import Prophet
from prophet.diagnostics import cross_validation
from prophet.diagnostics import performance_metrics

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt

plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ

 

利用するデータ

今回利用する時系列データのデータセットは、Airline Passengers（飛行機乗客数）は、Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h

 

では、データセットを読み込みます。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/591h'
df = pd.read_csv(url)
df.columns = ['ds', 'y'] #日付：DS、目的変数：y

df.head() #確認

 

以下、実行結果です。

 

グラフ化し確認します。

以下、コードです。

# プロット
df.plot(kind='line',x='ds', y='y')

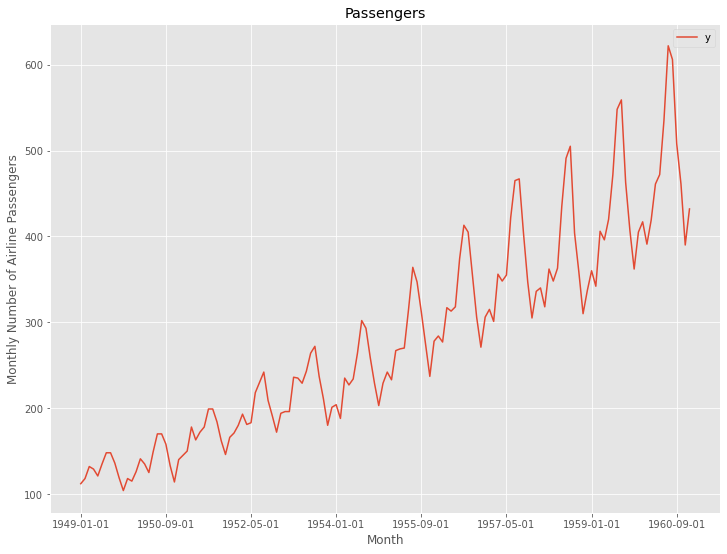
plt.title('Passengers')                            #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers') #タテ軸のラベル
plt.xlabel('Month')                                #ヨコ軸のラベル
plt.show()

 

以下、実行結果です。

 

次に、読み込んだデータセットを、学習データとテストデータに分割します。

以下、コードです。

# 学習データとテストデータの分割
test_length = 12

df_train = df.iloc[:-test_length]
df_test = df.iloc[-test_length:]

 

グラフ化します。

以下、コードです。

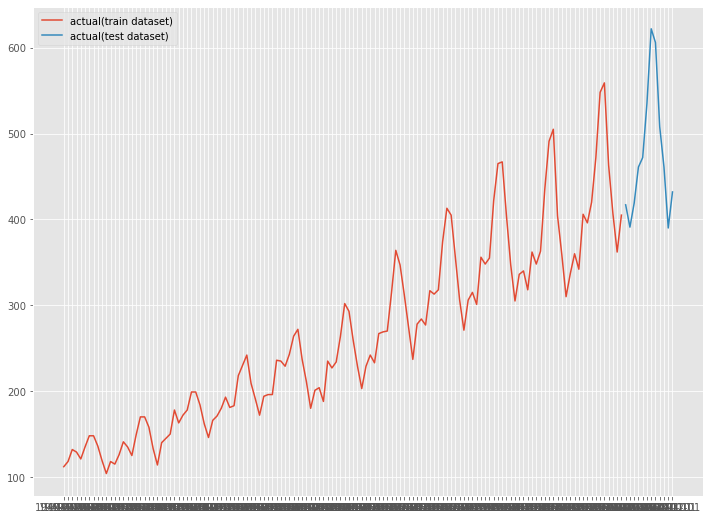
# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train.ds, df_train.y, label="actual(train dataset)")
ax.plot(df_test.ds, df_test.y, label="actual(test dataset)")

plt.legend()

 

以下、実行結果です。

 

学習データでProphetモデルを構築し、構築したモデルをテストデータで精度検証します。

 

予測精度の評価指標

今回の予測精度の評価指標は、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。 

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

 

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

Prophet

以下の2つの方法でProphetモデルを構築します。

  • Prophet（デフォルトのまま）
  • Prophet（Optunaで最適化）

ここではOptunaについて詳しくは説明しません。知りたい方は、以下の一連の記事を参考にしてください。

Python の ハイパーパラメータ自動最適化ライブラリー Optuna その1 – Optuna のちょっとした使い方 –

　Prophet（デフォルトのまま）

学習データを使って、Prophetモデルを学習します。

以下、コードです。

# 予測モデル構築
m = Prophet()
m.fit(df_train)

 

テストデータで精度検証します。

以下、コードです。

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='M')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

#予測値
train_pred = df.iloc[:-test_length].loc[:, 'Predict']
test_pred = df.iloc[-test_length:].loc[:, 'Predict']

#実測値
y_train = df.iloc[:-test_length].loc[:, 'y']
y_test = df.iloc[-test_length:].loc[:, 'y']

# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

グラフ化します。

以下、コードです。

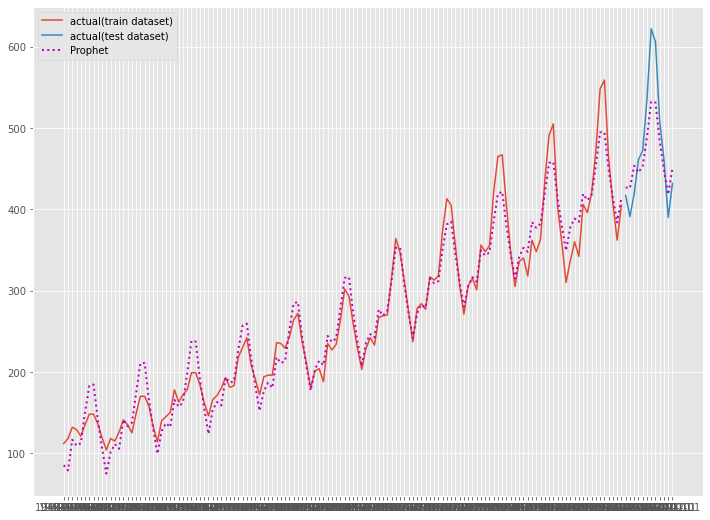
# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train.ds, df_train.y, label="actual(train dataset)")
ax.plot(df_test.ds, df_test.y, label="actual(test dataset)")
ax.plot(df_train.ds, train_pred, linestyle="dotted", lw=2,color="m")
ax.plot(df_test.ds, test_pred, label="Prophet", linestyle="dotted", lw=2, color="m") 

plt.legend()

 

以下、実行結果です。

 

　Prophet（Optunaで最適化）

学習データを使って、Prophetモデルを学習します。Optunaでハイパーパラメータをチューニングします。

先ずは、以下の手順で最適パラメータの探索します。

  1. 目的関数の設定
  2. ハイパーパラメータの探索の実施
  3. 最適パラメータの出力

 

目的関数の設定をします。

以下、コードです。

# 目的関数の設定
def objective(trial):

    params = {'changepoint_prior_scale' : 
                 trial.suggest_uniform('changepoint_prior_scale',
                                       0.001,0.5
                                      ),
              'seasonality_prior_scale' : 
                 trial.suggest_uniform('seasonality_prior_scale',
                                       0.01,10
                                      ),
              'seasonality_mode' : 
                 trial.suggest_categorical('seasonality_mode',
                                           ['additive', 'multiplicative']
                                          ),
              'changepoint_range' : 
                  trial.suggest_discrete_uniform('changepoint_range', 
                                                 0.8, 0.95, 
                                                 0.001),
              'n_changepoints' : 
                  trial.suggest_int('n_changepoints', 
                                    20, 35),
             }
    m = Prophet(**params)

    m.fit(df_train)
    df_future = m.make_future_dataframe(periods=test_length,freq='M')
    df_pred = m.predict(df_future) 
    preds = df_pred.tail(len(df_test))
    
    val_rmse = np.sqrt(mean_squared_error(df_test.y, preds.yhat))
    return val_rmse

 

ハイパーパラメータの探索を実施します。

以下、コードです。

# ハイパーパラメータの探索の実施
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)

 

最適パラメータを出力します。

以下、コードです。

# 最適パラメータの出力
print(f"The best parameters are : \n {study.best_params}")

 

以下、実行結果です。

 

次に、学習データを使って、最適パラメータを設定したProphetモデルを学習します。

以下、コードです。

# 最適パラメータでモデル学習
m = Prophet(**study.best_params)
m.fit(df_train)

 

テストデータで精度検証します。

以下、コードです。

# 予測の実施（学習期間＋テスト期間）
df_future = m.make_future_dataframe(periods=test_length,
                                    freq='M')
df_pred = m.predict(df_future) 

# 元のデータセットに予測値を結合
df['Predict'] = df_pred['yhat']

#予測値
train_pred = df.iloc[:-test_length].loc[:, 'Predict']
test_pred = df.iloc[-test_length:].loc[:, 'Predict']

#実測値
y_train = df.iloc[:-test_length].loc[:, 'y']
y_test = df.iloc[-test_length:].loc[:, 'y']

# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

ハイパーパラメータをチューニングすることで、以下のように改善しました。

  • RMSE : 41.57 → 15.21
  • MAE : 34.02 → 11.31
  • MAPE : 6.78% → 2.53%

 

グラフ化します。

以下、コードです。

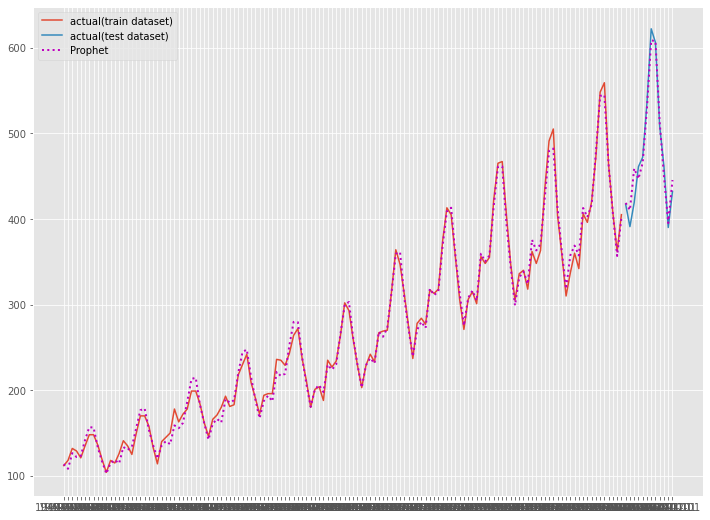
# グラフ化
fig, ax = plt.subplots()

ax.plot(df_train.ds, df_train.y, label="actual(train dataset)")
ax.plot(df_test.ds, df_test.y, label="actual(test dataset)")
ax.plot(df_train.ds, train_pred, linestyle="dotted", lw=2,color="m")
ax.plot(df_test.ds, test_pred, label="Prophet", linestyle="dotted", lw=2, color="m") 

plt.legend()

 

以下、実行結果です。

 

次回

今回は、「Prophetモデルで予測する方法」について説明しました。

多くの人にとって馴染みがあるのは、時系列データ系の数理モデル（アルゴリズム）よりも、テーブルデータ系の数理モデル（アルゴリズム）の方です。

例えば、以下の数理モデル（アルゴリズム）はテーブルデータ系のものです。

  • 線形回帰モデル（単回帰、重回帰、など）
  • 正則化回帰モデル（Ridge回帰、Lasso回帰、など）
  • 一般化線形モデル（GLMM）
  • 一般化加法モデル（GAM）
  • 階層線形モデル、マルチレベルモデル、一般化混合モデル
  • 決定木（ディシジョンツリー）
  • ランダムフォレスト
  • ブースティングモデル（AdaBoost、XGBoost、LightGBMなど）
  • ニューラルネットワークモデル

……などなど。

テーブルデータ系の数理モデル（アルゴリズム）を使い、時系列予測モデルを作るには、時系列特徴量を生成することで、対応できます。

次回は、テーブルデータ系モデルで時系列予測するための準備例を紹介します。

Pythonで時系列解析・超入門（その5）テーブルデータ系の数理モデル（アルゴリズム）で時系列予測するための準備