Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門その1線形回帰モデルでMMMを作ろう！

本当に売上に貢献している広告は、どの広告か？

売上と広告媒体等との関係性をモデリングし、どの広告媒体が売上にどれほど貢献していたのか分析することができます。

それが、マーケティングミックスモデリング（MMM：Marketing Mix Modeling）です。

マーケティングミックスモデリング（MMM：Marketing Mix Modeling）は、単に今までどうだったのかを分析するだけでなく、今後どうなりそうかという近未来分析をすることもできます。

マーケティングミックスモデリング（MMM：Marketing Mix Modeling）で扱うデータは時系列データです。

このような時系列データに対し、時系列系の数理モデルを構築するのもいいですが、線形回帰モデルのような、シンプルなテーブルデータ系の数理モデルでも構築できます。

今回は、「線形回帰モデルでMMMを作ろう！」というお話しをします。

Contents

利用するデータセット
３つの成果物
流れ
MMMの実施
　ライブラリーの読み込み
　データセットの読み込み
　モデル構築
　売上貢献度の算出
次回

利用するデータセット

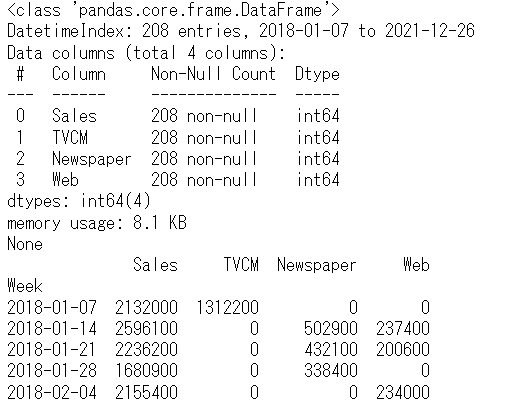
今回利用するデータセットの変数です。

Week：週
Sales：売上
TVCM：TV CMのコスト
Newspaper：新聞の折り込みチラシのコスト
Web：Web広告のコスト

以下からダウンロードできます。

MMM.csv
https://www.salesanalytics.co.jp/4zdt

３つの成果物

マーケティングミックスモデリング（MMM：Marketing Mix Modeling）の、主な3つの成果物です。

売上貢献度
ROI=（売上貢献度－コスト）÷コスト
予測モデル

先ず、どの広告媒体が、どれだけ売上に貢献したのかを見える化できます。

Baseは、広告などに依存しない売上高です。市場に浸透している商品ほどBaseの割合が大きくなります。

広告媒体のコストデータがあれば、ROIを見える化できます。

売上貢献度などを計算する際、数理モデルを構築します。その数理モデルが、そのまま予測モデルとして活用できます。

$Sales = \beta_0 + \beta_{TVCM} \times TVCM + \beta_{Newspaper} \times Newspaper + \beta_{Web} \times Web + \epsilon$

広告媒体の出稿計画などがあれば、未来のシミュレーションに活用できます。

流れ

流れについて簡単に説明します。

先ず、売上であるSalesを目的変数に、TVCMとNewspaper、Webのコストを説明変数に、線形回帰モデルを構築します。

次に、構築した線形回帰モデルを使い、媒体別の売上貢献度を求めます。

売上貢献度を足し合わせると売上の予測値になりますが、通常の予測値は実測値と乖離します。予測値を実測値に合わせるための補正係数を計算し、補正済み売上貢献度を計算します。

最後に、売上貢献度（補正済み）を使い、媒体別のROIを計算します。

MMMの実施

　ライブラリーの読み込み

先ず、必要なライブラリーなどを読み込みます。

以下、コードです。

import pandas as pd
import numpy as np

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score, TimeSeriesSplit

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ

#指数表記しない設定
np.set_printoptions(precision=3,suppress=True)
pd.options.display.float_format = '{:.3f}'.format

　データセットの読み込み

データセットを読み込みます。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(url,
                 parse_dates=['Week'],
                 index_col='Week'
                )

# データ確認
print(df.info()) #変数の情報
print(df.head()) #データの一部

# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']

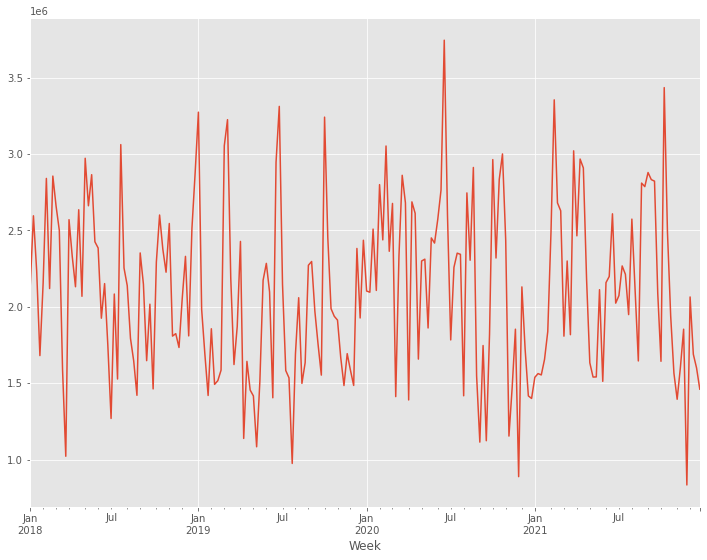
# グラフ化
y.plot()
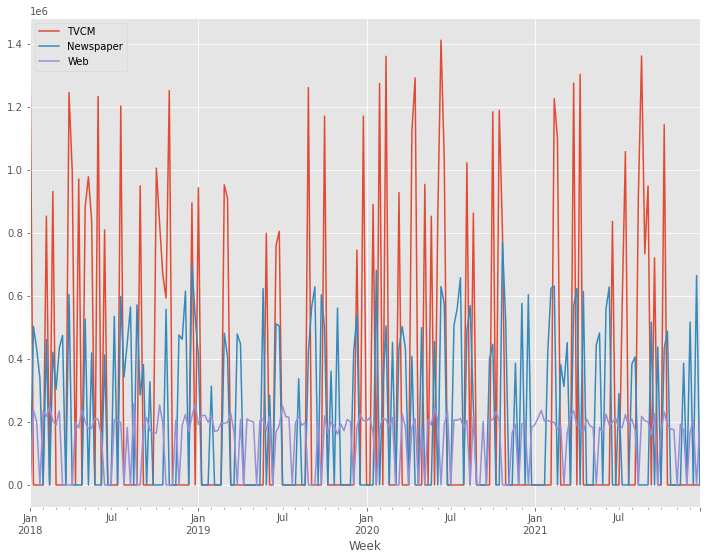
X.plot()

以下、実行結果です。

　モデル構築

線形回帰モデルを構築します。

先ず、線形回帰モデルのインスタンスを作ります。

以下、コードです。

# 線形回帰モデルのインスタンス
lr = LinearRegression()

線形回帰モデルが、どの程度の予測精度を持ったモデルになるのかを確かめるために、時系列のCV（クロスバリデーション）を実施します。今回は、デフォルトの5分割のCVです。

以下、コードです。

# クロスバリデーションで精度検証
np.mean(cross_val_score(lr, 
                        X, y, 
                        cv=TimeSeriesSplit()
                       )
       )

以下、実行結果です。

この実行結果は、5分割CVの結果（決定係数 $R^2$ ）の平均値です。悪くはないですが、ものすごくいいわけでもありません。

では、全てのデータを使い線形回帰モデルを構築します。

以下、コードです。

# 線形回帰モデルの学習
lr.fit(X, y) 

# 回帰係数をデータフレーム化
weights = pd.Series(
    lr.coef_,
    index=X.columns
)

# 結果出力（切片と係数）
print('Intercept:\n', lr.intercept_, sep='')
print()
print('Coefficients:\n',weights, sep='')

以下、結果です。

　売上貢献度の算出

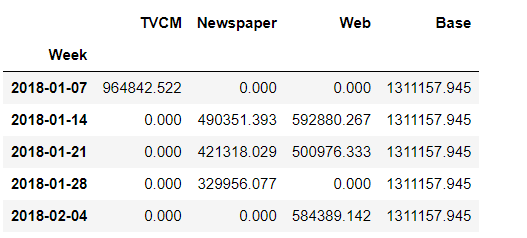
先程求めた線形回帰式を使い、売上貢献度（補正前）を計算します。

以下、コードです。

# 貢献度（補正前）
unadj_contribution = X.mul(weights) #Xと係数を乗算
unadj_contribution = unadj_contribution.assign(Base=lr.intercept_) #切片の追加

unadj_contribution.head() #確認

以下、実行結果です。

週ごとに各媒体の売上貢献度を合計すると、売上の予測値になります。

以下、コードです。

# 貢献度の合計（yの予測値）
y_pred = unadj_contribution.sum(axis=1)

y_pred.head() #確認

以下、実行結果です。

元の売上の実測値を見てみます。

以下、コードです。

y.head() #確認

以下、実行結果です。

予測値と実測値が乖離していることが分かります。この乖離をなくすために、補正係数（correction factor）を計算し、売上貢献度を補正します。

補正係数を計算します。

以下、コードです。

# 補正係数
correction_factor = y.div(y_pred, axis=0)

correction_factor.head() #確認

以下、実行結果です。

この補正係数を使い、売上貢献度を補正します。

以下、コードです。

# 貢献度（補正後）
adj_contribution = (unadj_contribution
                    .mul(correction_factor, axis=0)
                   ) 

# 順番の変更
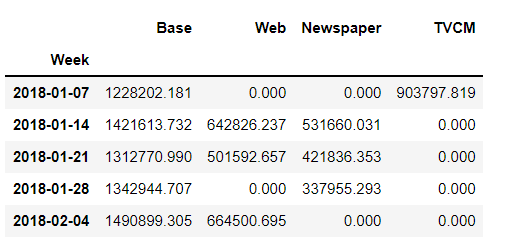
adj_contribution = adj_contribution[['Base', 'Web', 'Newspaper', 'TVCM']]

#確認
adj_contribution.head()

以下、実行結果です。

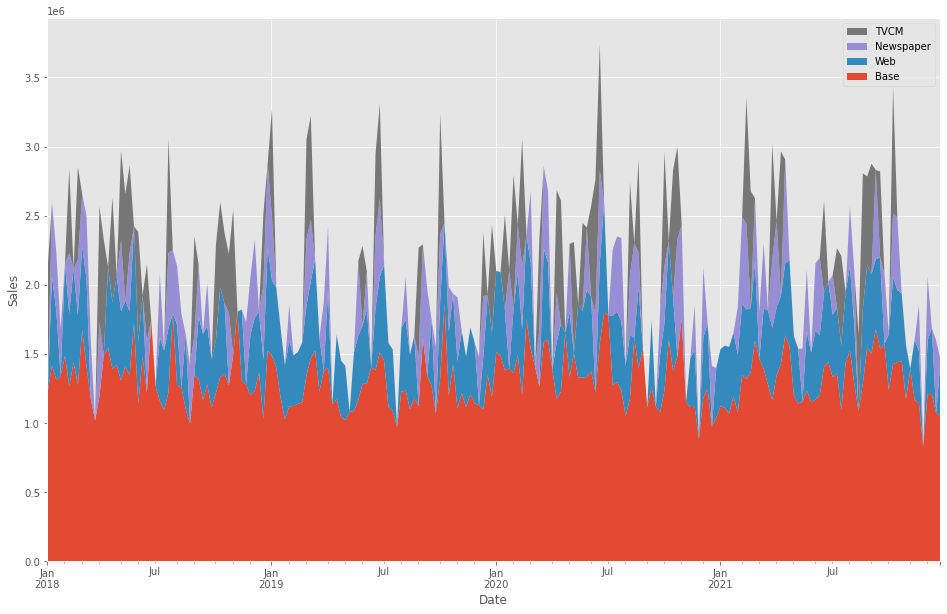
週×媒体別の売上貢献度が求められたので、積み上げグラフを作成し、どのような状況になっているのかを確認してみます。

以下、コードです。

# グラフ化
ax = (adj_contribution
      .plot.area(
          figsize=(16, 10),
          linewidth=0,
          ylabel='Sales',
          xlabel='Date')
     )

handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[::-1], labels[::-1])

以下、実行結果です。

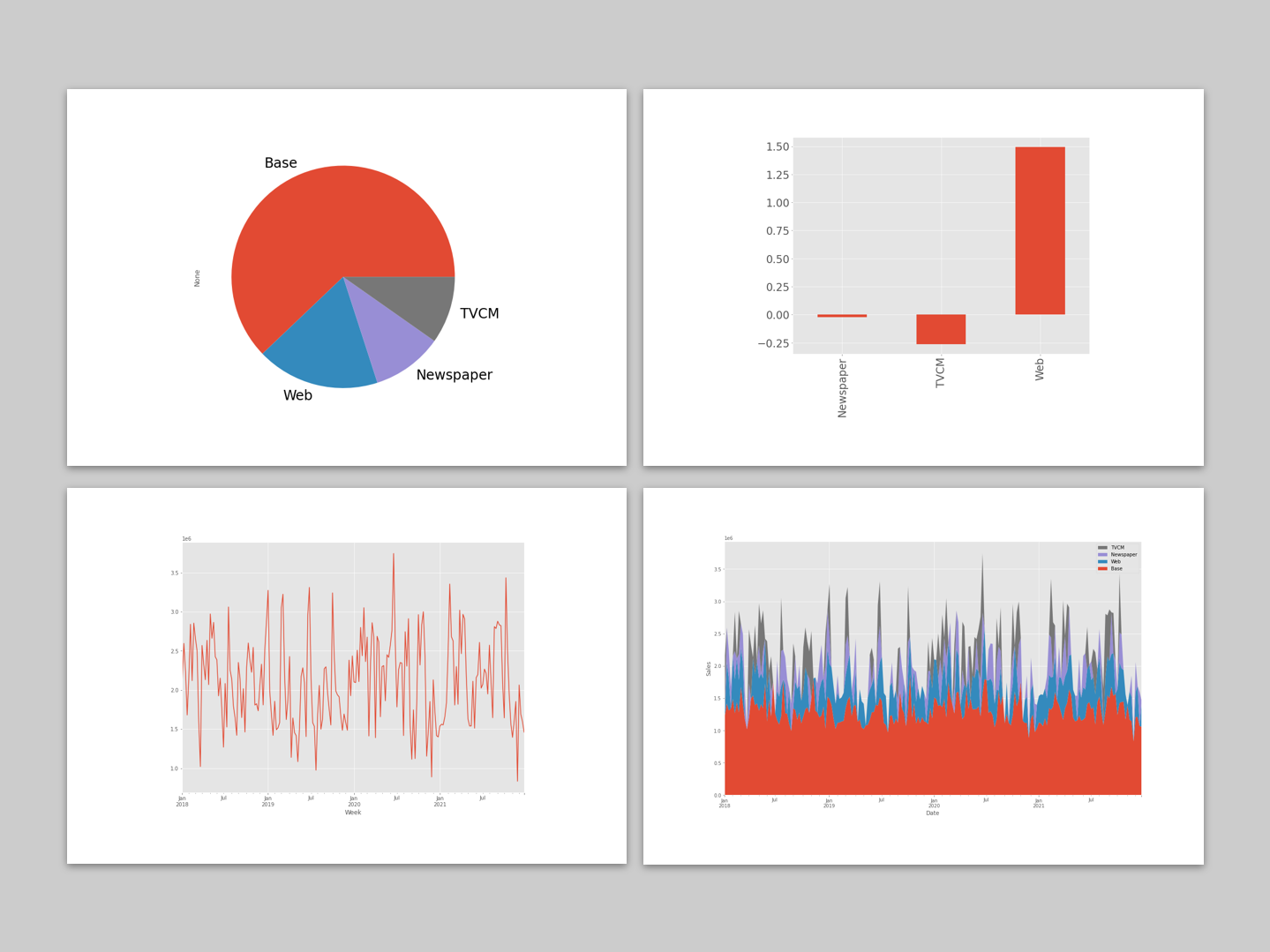
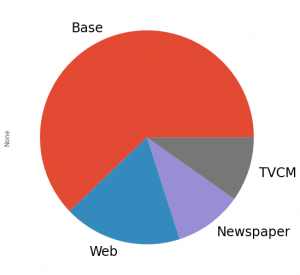
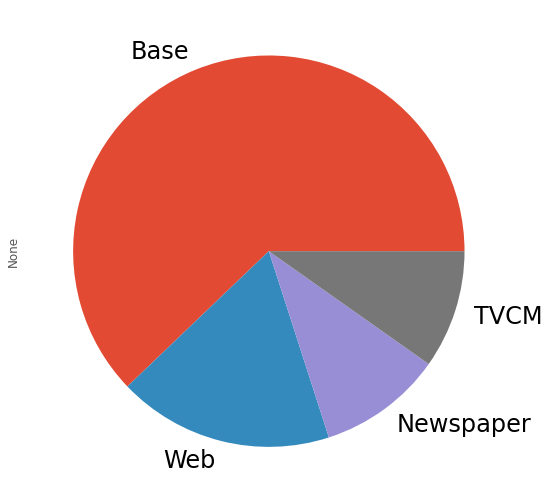
媒体別に全ての週の売上貢献度を合計し、媒体別の売上貢献度（円と構成比％）と、そのグラフを作り、何がどれほど売上に貢献したのかを見てみます。

以下、コードです。

# 媒体別の貢献度の合計
contribution_sum = adj_contribution.sum(axis=0)

#集計結果
print('売上貢献度（円）:\n', 
      contribution_sum, 
      sep=''
     )
print()
print('売上貢献度（構成比）:\n', 
      contribution_sum/contribution_sum.sum(), 
      sep=''
     )

#グラフ化
contribution_sum.plot.pie(fontsize=24)

以下、実行結果です。

費用対効果を見てみます。今回は媒体別にROIを計算します。

先ず、媒体別のコストを集計します。

以下、コードです。

# 各媒体のコストの合計
cost_sum = X.sum(axis=0)

cost_sum #確認

以下、実行結果です。

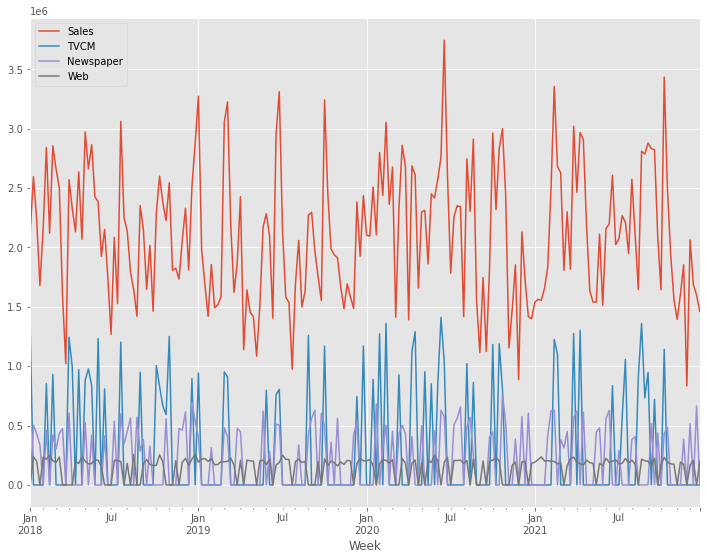
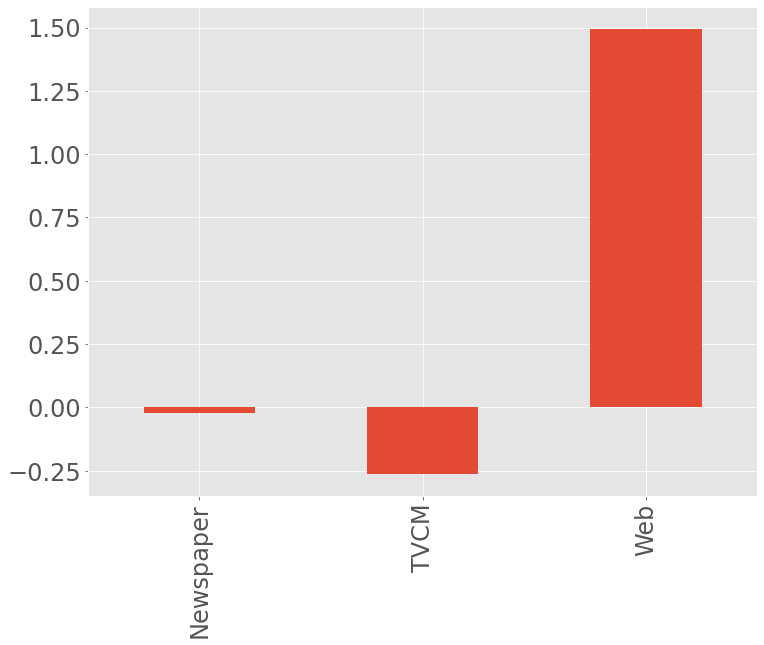
先程求めた売上貢献度を使い、媒体別のROIを計算しグラフ化します。

以下、コードです。

# 各媒体のROIの計算
ROI = (contribution_sum.drop('Base', axis=0) - cost_sum)/cost_sum

#確認
print('ROI:\n', ROI, sep='')

# グラフ化
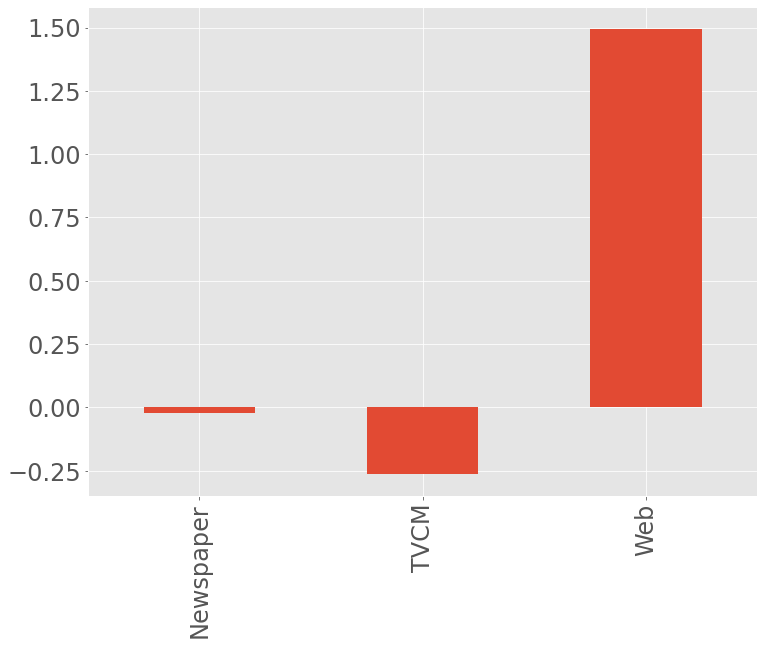
ROI.plot.bar(fontsize=24)

以下、実行結果です。

ROIは、値が大きいほど良く、最低限プラスの値である必要があります。Web広告以外はあまり良くないことが分かります。

このモデルには、ある致命的な欠陥があります。アドストック（Ad Stock）を考慮していないということです。

アドストック（Ad Stock）を考慮したモデルにした方がいいでしょう。

ちなみに、アドストック（Ad Stock）を考慮するとは、残存効果を考慮するということです。ある日の広告宣伝活動が、その日だけに効果があるのではなく、次の日以降もその効果が続くということです。キャリーオーバー（Carryover）効果と表現されることもあります。

次回

今回は、「線形回帰モデルでMMMを作ろう！」というお話しをしました。

次回は、「アドストック（Ad Stock）を考慮した線形回帰モデル」というお話しをします。

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門その2アドストック（Ad Stock）を考慮した線形回帰モデル