VAR(Vector Autoregressive、ベクトル自己回帰)モデルとは、ARモデル(自己回帰モデル)の多変量版です。
VARモデルで、時系列の変数Xと変数Yの間の関係性を検討することができます。
例えば……
- グレンジャー因果性
- インパルス応答
……です。
Pythonの統計解析のライブラリーであるStatsmodelsで実現できます。
![]()
https://www.statsmodels.org/stable/index.html
今回は、「VARモデルによるグレンジャー因果性とインパルス応答」というお話しをします。
Contents [hide]
ちょっとしたお話し
VAR(Vector Autoregressive、ベクトル自己回帰)
通常のARモデルは1変量の時系列データを扱いますが、VARモデルは多変量の時系列データを扱います。
ARモデルの説明変数は過去の自分です。1期前や2既前、3期前、……のデータを説明変数として採用します。
VARモデルも同様に、説明変数は過去の自分達です。1期前や2既前、3期前、……のデータを説明変数として採用します。
VARモデルが扱う時系列データは多変量です。同期の他の時系列データを説明変数として採用しないのだろうか、という疑問が湧いてきます。
答えは、同期の他の時系列データを説明変数として採用しません。1期前や2既前、3期前、……のあくまでも過去を説明変数として採用します。
同時期を含めたい場合には、SVAR(Structural Vector Autoregressive)を利用します。
VARモデルで多変量の時系列データをモデル化することで、グレンジャー因果性を検討することができます。
グレンジャー因果性
グレンジャー因果性は、時系列の変数同士の関係性の1つで、当然ですが因果ではありません。
因果があればグレンジャー因果性を示すでしょうか、グレンジャー因果性を示したからと言って因果があるとは限りません。
今、2つの時系列の変数XとYがあったとします。
次にようなものを、グレンジャー因果性があるといいます。
- Yを予測するとき、過去のXのデータを利用すると予測精度があがる
- Xが、Yの先行指標になっている
- 過去のX(Xのラグ)が、Yと相関している
この3つは、ほぼ同じことを、表現を変えていっています。
例えば、、、
- 売上を予測するとき、1週間前の広告の投入量を利用すると予測精度があがる
- 1週間前の広告の投入量が、売上の先行指標になっている
- 1週間前の広告の投入量が、売上と相関している
、、、といった感じです。
グレンジャー因果性があるかどうかは、そのための統計的仮説検定がありますので、それを活用してもいいでしょう。
- 帰無仮説:グレンジャー因果性がない
- 対立仮説:グレンジャー因果性がある
ただ、「見せかけの回帰」が生じるような場合、このグレンジャー因果性の検討ができません。
「見せかけの回帰」とは、全く無関係な時系列の変数Xと変数Yで回帰モデルを構築(目的変数:Y、説明変数:X)したとき、XとYの間に有意な関係があるとみなされ、予測精度の高い回帰モデルができてしまう現象です。
このような現象は、時系列の変数Xと変数Yが単位根過程である場合に起こります。
単位根過程は、原系列は非定常だが、差分をとると定常になる時系列データです。差分をとるとは、例えば1期前のデータとの差分を計算し、新たな時系列データを作ることです。このような時系列データを階差系列といいます。
単位根過程かどうかを判別するために、統計的仮説検定(単位根検定)などを実施し、単位根過程である時系列の変数は、階差処理(差分計算)を実施し階差系列にした後にグレンジャー因果性の検討を実施したほうがいいでしょう。
他にも、共和分の関係性を見たり、そのための対処をしたりと、厳密性を重視するとやや大変です。共和分の説明や対処方法などは、簡単ではないのでここでは割愛します。
インパルス応答
「ある時系列の変数Xに変動があったとき、他の時系列の変数Yにどう伝わっていくかをモデリングする」ことで、時系列の変数Xと変数Yの関係性を検討したりします。
時系列の変数Xの値を変動させたときの、他の時系列の変数Yの変動を、インパルス応答といいます。
具体的には、VARモデルからインパルス応答関数を求め、インパルス応答をグラフ化したりします。
グレンジャー因果性の統計的仮説検定を実施することなく、インパルス応答のグラフ化から、時系列の変数Xと変数Yの間の関係性がなんとなく見えてきます。
インパルス応答関数には、、、
- 非直交化インパルス応答関数
- 直交化インパルス応答関数
、、、の2種類ありますが、今回は直交化の方を見ていきます。
例えば、「広告の投入量に対する、売上の変動を分析する」ことができます。
Python Statsmodelsで分析してみよう!
Statsmodelsのインストール
Statsmodelsをインストールされていない方は、インストールしておきましょう。
以下、Condaでインストールするときのコードです。
conda install -c conda-forge statsmodels
pipでインストールするときは、以下です。
pip install statsmodels
必要なモジュールを読み込む
先ずは、必要なモジュールを読み込みます。
以下、コードです。
import pandas as pd
import numpy as np
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.vector_ar.var_model import VAR
from matplotlib import mlab
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
利用するデータを読み込む
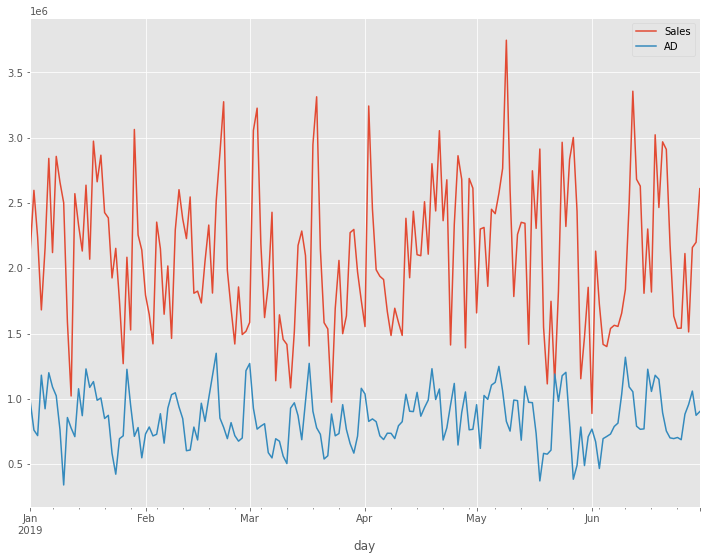
今回利用する時系列データのデータセットは、売上(Sales)と広告(AD)の時系列データです。
弊社のHPからもダウンロードできます。
弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/glrg
では、データセットを読み込みます。
以下、コードです。
# データセット読み込み
url = 'https://www.salesanalytics.co.jp/glrg'
df = pd.read_csv(url,
parse_dates=True,
index_col='day'
)
# グラフ化
df.plot()
以下、実行結果です。
先ず、2つの時系列データの単位根検定から始めます。
ADF単位根検定
2つの時系列データに対し、念のため単位根検定をします。
今回は、以下の3つの対立仮説のADF単位根検定(Augmented Dickey-Fuller 単位根検定)を実施します。
- 対立仮説1:定数項+トレンド+定常過程
- 対立仮説2:定数項+定常過程
- 対立仮説3:定常過程(定数項なし)
帰無仮説は「単位根がある」になります。
p値が0.05未満のとき帰無仮説が棄却されたと考え対立仮説を採択したいと思います。
グラフを見る限り、「対立仮説2:定数項+定常過程」ですが、とりあえず3つとも実施します。
先ず、変数「Sales」に対しADF単位根検定を実施します。
以下、コードです。
# Augmented Dickey-Fuller 単位根検定(帰無仮説:単位根がある) ct_results = adfuller(df['Sales'],regression='ct') #対立仮説:定数項+トレンド+定常過程 c_results = adfuller(df['Sales'],regression='c') #対立仮説:定数項+定常過程 n_results = adfuller(df['Sales'],regression='n') #対立仮説:定常過程(定数項なし) # p値 print(ct_results[1]) print(c_results[1]) print(n_results[1])
以下、実行結果です。
上から2番目が「対立仮説2:定数項+定常過程」です。
p値が0.05未満のため、対立仮説を採択します。したがって、単位根過程ではないとして話しを進めます。
次に、変数「AD」に対しADF単位根検定を実施します。
以下、コードです。
# Augmented Dickey-Fuller 単位根検定(帰無仮説:単位根がある) ct_results = adfuller(df['AD'],regression='ct') #対立仮説:定数項+トレンド+定常過程 c_results = adfuller(df['AD'],regression='c') #対立仮説:定数項+定常過程 n_results = adfuller(df['AD'],regression='n') #対立仮説:定常過程(定数項なし) # p値 print(ct_results[1]) print(c_results[1]) print(n_results[1])
以下、実行結果です。
上から2番目が「対立仮説2:定数項+定常過程」です。
p値が0.05未満のため、対立仮説を採択します。したがって、単位根過程ではないとして話しを進めます。
グレンジャー因果性
VARモデルを構築し、グレンジャー因果性を検討します。
先ず、VARモデルを構築します。
以下、コードです。
# データフレームを配列へ変換
x = df.to_numpy()
# 最大のラグ数
maxlags = 10
# モデルのインスタンス生成
model = VAR(x)
# 最適なラグの探索
lag = model.select_order(maxlags).selected_orders
print('最適なラグ:',lag['aic'],'\n')
# モデルの学習
results = model.fit(lag['aic'])
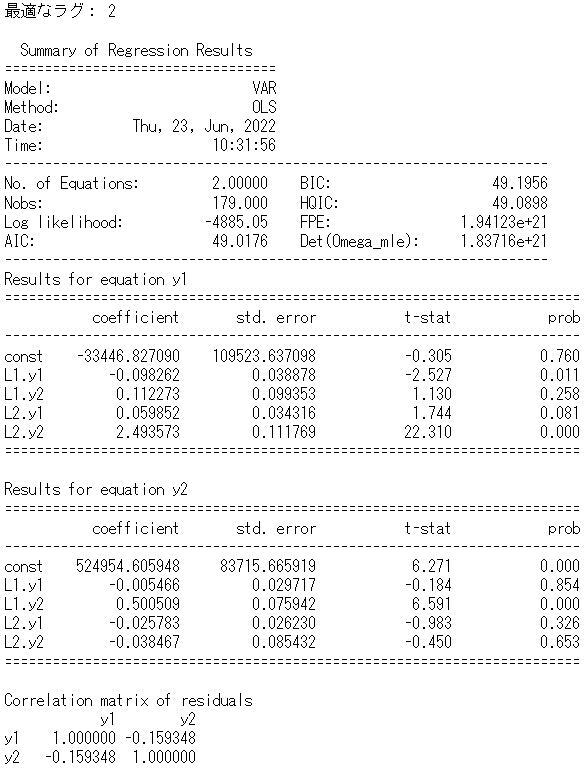
print(results.summary())
以下、実行結果です。
y1がSalesで、y2がADです。L1はラグ1で、L2はラグ2を意味します。
次に、「Sales → AD」と「AD → Sales」のグレンジャー因果性を統計的仮説検定で検討していきます。
- 帰無仮説:グレンジャー因果性がない
- 対立仮説:グレンジャー因果性がある
p値が0.05未満のとき帰無仮説が棄却されたと考え対立仮説を採択します。
「Sales → AD」のグレンジャー因果性の検定を実施します。
以下、コードです。
# Sales -> AD の因果を検定 test_results = results.test_causality(causing=0, caused=1) test_results.pvalue #p値
以下、実行結果です。
p値が0.05以上のため、帰無仮説は棄却されたとはいえず、グレンジャー因果性があるとはいえませんでした。
「AD → Sales」のグレンジャー因果性の検定を実施します。
以下、コードです。
# AD -> Sales の因果を検定 test_results = results.test_causality(causing=1, caused=0) test_results.pvalue #p値
以下、実行結果です。
p値が0.05未満のため、帰無仮説を棄却し対立仮説を採択します。グレンジャー因果性があるいえそうです。
インパルス応答
「ある時系列の変数Xに変動があったとき、他の時系列の変数Yにどう伝わっていくかをモデリング」した「直交化インパルス応答関数」を求めグラフ化し確認したいと思います。
以下、コードです。
# (直行化)インパルス応答関数 period = 7 irf = results.irf(period) irf.plot(orth=True) plt.show()
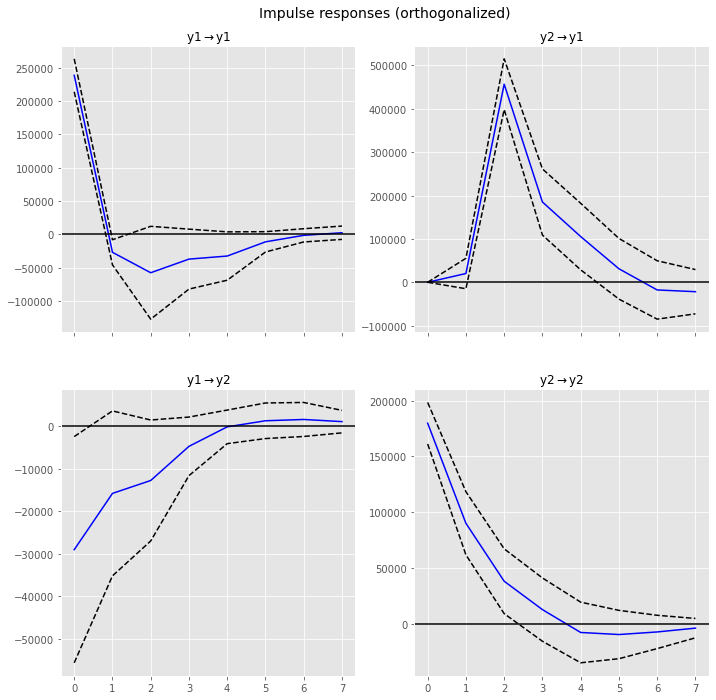
以下、実行結果です。
「y1 → y2」が「Sales → AD」で、「y2 → y1」が「AD → Sales」です。
縦軸のスケールに注意して見ましょう。
明らかに、「y2 → y1」(AD → Sales)の変動が大きいことがわかります。横軸はラグです。ラグ2にピークがきていることがわかります。
まとめ
今回は、「VARモデルによるグレンジャー因果性とインパルス応答」というお話しをしました。
VAR(Vector Autoregressive、ベクトル自己回帰)モデルとは、ARモデル(自己回帰モデル)の多変量版です。
VARモデルで、時系列の変数Xと変数Yの間の関係性を検討することができます。
例えば……
- グレンジャー因果性
- インパルス応答
……です。
Pythonの統計解析のライブラリーであるStatsmodelsで実現できます。もちろんRなどでもできます。
同時期を含めたい場合には、SVAR(Structural Vector Autoregressive)を利用します。
Rでどいうやるのかや、SVARをPythonでどうやるのかなど。別の機会にお話しします。