（Python版）複数季節性を持つ時系列データをモデル化する方法（TBATSモデルとARIMAモデル）

6262
（Python版）複数季節性を持つ時系列データをモデル化する方法（TBATSモデルとARIMAモデル）

時系列データには複数の季節性を持つ場合があります。

例えば、日単位の時系列データであれば週周期と年周期、時単位の時系列データであれば日周期と週周期などです。

時系列データでよく利用されるモデルは、ARIMA系のモデルです。季節性を考慮したARIMA系のモデルをSARIMAモデルといいます。

SARIMAモデルは、季節成分が1つの場合に対応し、複数には対応していません。

では、どうすればいいのか。

複数の季節性をもつ時系列モデルがあります。その1つがTBATSモデルです。

TBATSモデルは次の頭文字をとったものです。頭文字を取ったぐらいなので、それぞれの要素は組み込まれています。

  • 三角関数による季節性表現（Trigonometric seasonality）
  • Box-Cox変換（Box-Cox transformation）
  • ARIMA誤差（ARMA error）
  • トレンド成分（Trend component）
  • 季節成分（Seasonal component）

TBATSモデルは、古典的な時系列モデルの1つである指数平滑モデルをもとにしており、式で記述するとやや難しく見えますので割愛します。

今回は、「複数季節性を持つ時系列データをモデル化する方法（TBATSモデルとARIMAモデル）」というお話しをします。

TBATSモデルの季節性表現方法

　フーリエ級数に基づく三角関数による季節性表現

季節性の表現方法には幾つか種類があります。

TBATSモデルは、sinやcosなどの三角関数を利用し、季節性を表現します。このような三角関数による季節性はフーリエ級数に基づくものです（多くの人にとって、どうでもいいかも知れませんが……）。

例えば、時系列データy_tに対し、考慮したい季節性がM個、各季節性の周期がp_i、各季節性のフーリエ項がK_i個（i=1,2,\cdots,M）、N_tが季節性以外の時系列成分とします。このとき、次のように表現できます。

\displaystyle y_t = a + \sum_{i=1}^M \sum_{k=1}^{K_i} [ \alpha_{i_k} \sin (\frac{2 \pi k t}{p_i}) + \beta_{i_k} \cos (\frac{2 \pi k t}{p_i}) ] + N_t M=1かつK_1=1の場合、その季節性はsinとcosの2変数で表現されます。pは周期です。

\displaystyle y_t = a + \alpha \sin (\frac{2 \pi t}{p}) + \beta \cos (\frac{2 \pi t}{p}) + N_t M=1かつK_1=2の場合、sinとcosのセットが2つ（4変数）で表現されます。pは周期です。

\displaystyle y_t = a + \alpha_1 \sin (\frac{2 \pi t}{p}) + \beta_1 \cos (\frac{2 \pi t}{p}) + \alpha_2 \sin (\frac{2 \pi 2t}{p}) + \beta_2 \cos (\frac{2 \pi 2t}{p}) + N_t

sinとcosのセットが少ないと、季節性の表現が荒くなります。そう考えると、sinとcosのセットを増やせばいいのではとなりますが、変数が多くなります。

そこで、「sinとcosを何セット必要なのか」という問題がありますが、あまり多くないようにしましょう。

 

　小数点のある周期が扱える

今紹介した三角関数を利用した季節性表現は、複数の季節性を扱えるだけでなく、小数点のある周期が扱えます。

周期は通常は正の整数ですが、小数点のある周期にしたい場合もあります。

例えば、日単位の時系列データで週周期を考えたとき、週周期は「7」です。

では、年周期はどうでしょうか。通常は「365」になりますが、閏年を考慮すると年周期は「365.25」です。

三角関数による季節性は、このように整数の周期だけでなく、小数点のある周期も扱えます。

ちなみに、三角関数を使わずに季節性を表現したTABTSモデルを、BATSモデルといいます。古典的な方法で、季節性を表現します。

 

Pythonで実施しよう

　今回構築する4つのモデル

今回は、以下の4つのモデルを構築します。

  • TBATSモデル
  • SARIMAモデル
  • SARIMAX with Fourier Termsモデル
  • ARIMAX with Fourier Termsモデル

SARIMAモデルは、季節性を組み込んだ最も一般的な時系列モデルでしょう。ただ、季節成分が1つしか仮定できません。季節成分が2つ以上の場合、このSARIMAモデルで強引に時系列モデルをどうなるかを見てみます。

SARIMAモデルに説明変数Xを組み込んだのが、SARIMAX with Fourier Termsモデルです。説明変数Xで、SARIMAモデルに組み込めなかった季節成分を、Fourier級数をもとにした三角関数で季節性を表現し組み込みます。

ARIMAX with Fourier Termsモデルは、説明変数Xで複数の季節成分をFourier級数をもとにした三角関数で季節性を表現し組み込みます。TBATSモデルと近いものになります。

 

　tbats のインストール

TBATSモデルを構築するには、RのForecastというパッケージを利用することが多いです。

Python版もあります。tbatsというパッケージです。RのForecastのTBATSをもとに作成されたものです。

Tbatsは、以下のコードでインストールできます。

pip install tbats

 

Python版のtbatsが心配な方は、PythonからRのForecastのTBATSを呼び出し利用してください。

PythonからRの関数を利用したい方は、以下の記事を参考にしてください。

 

　必要なモジュールを読み込む

必要なモジュール一式を読み込みます。

以下、コードです。

import numpy as np
import pandas as pd

import statsmodels.api as sm

from tbats import TBATS, BATS
from pmdarima import auto_arima

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

　必要なデータを読み込む

Rで提供されているサンプルデータtaylor（30分ごとの電力需要の時系列データ）を利用します。

taylor は、2000年6月5日（月）から8月27日（日）までのイングランドとウェールズにおける30分ごとの電力需要（メガワット）の時系列データです。

Rで提供されている1,500以上のサンプルデータをPythonから利用できます。利用してみたい方は、以下の記事を参考にしていただければと思います。

 

では、このデータを読み込みます。

以下、コードです。

dataset = sm.datasets.get_rdataset("taylor", "forecast")
y = dataset.data['x']

y #確認

 

以下、実行結果です。

 

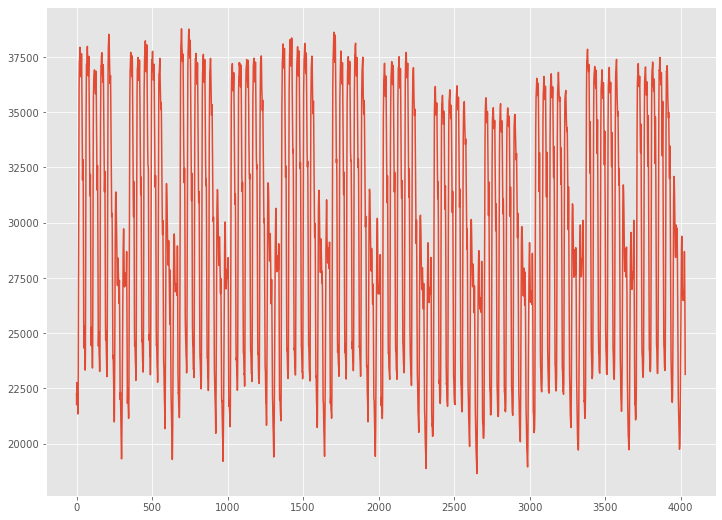
グラフ化し見てみます。

以下、コードです。

y.plot()
plt.show()

 

以下、実行結果です。

 

今回は、予測モデルを学習データで構築し、構築した予測モデルをテストデータ（後ろから7日間）で検証します。

学習データとテストデータを分解します。

以下、コードです。

y_train = y.iloc[:-336] #学習データ
y_test = y.iloc[-336:]  #テストデータ

 

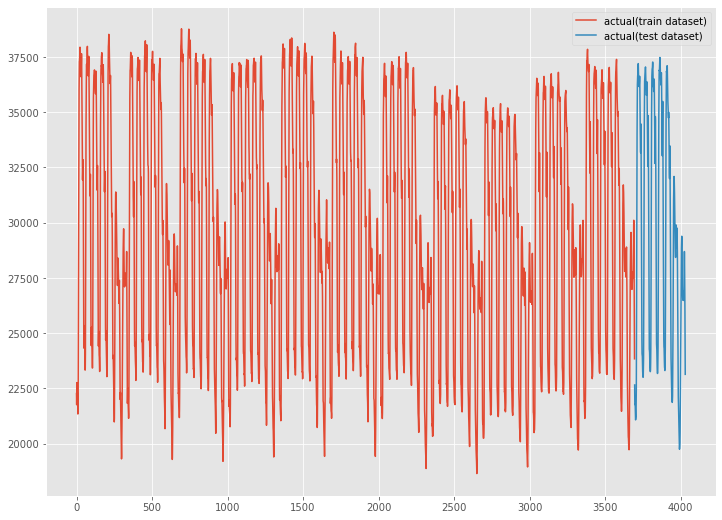
グラフ化し見てみます。

以下、コードです。

fig, ax = plt.subplots()
ax.plot(y_train.index, y_train.values, label="actual(train dataset)")
ax.plot(y_test.index, y_test.values, label="actual(test dataset)")
plt.legend()

 

以下、実行結果です。

 

構築した予測モデルは、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使い、予測精度の評価をしていきます。いずれの精度指標も値が小さいほど良いです。

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

　TBATSモデル

学習データで、TBATSモデルを構築します。季節性は、48周期と336周期の2つあります。

以下、コードです。

model = TBATS(seasonal_periods=(48, 336))
fitted_model = model.fit(y_train)

 

テストデータで、構築した予測モデルを評価します。

以下、コードです。

# 予測
train_pred = fitted_model.y_hat #学習データの期間
test_pred = fitted_model.forecast(steps=336) #テストデータの期間

# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

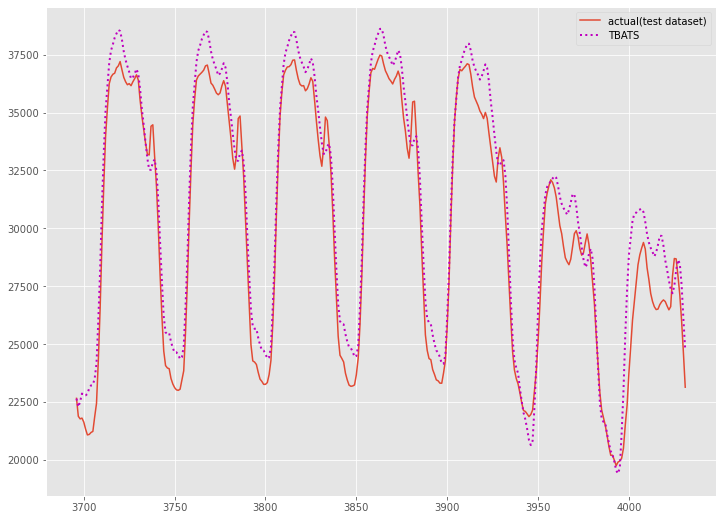
グラフ化し確認します。

以下、コードです。

# グラフ化（テストデータの期間）
fig, ax = plt.subplots()

ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_test.index, 
        test_pred, 
        label="TBATS", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

plt.legend()

 

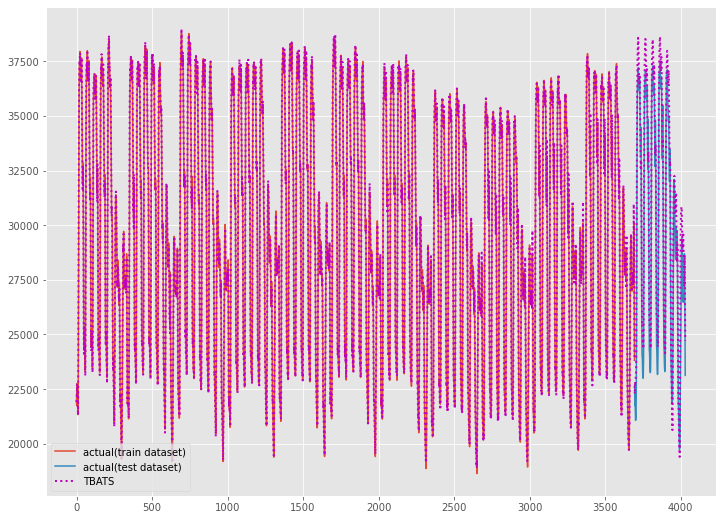
以下、実行結果です。

 

学習データを含めた全期間（学習データの期間＋テストデータの期間）をグラフ化し見てみます。

以下、コードです。

# グラフ化（全期間）
fig, ax = plt.subplots()

ax.plot(y_train.index, 
        y_train.values, 
        label="actual(train dataset)")
ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_train.index, 
        train_pred, 
        linestyle="dotted", 
        lw=2,
        color="m")
ax.plot(y_test.index, 
        test_pred, 
        label="TBATS", 
        linestyle="dotted", 
        lw=2, 
        color="m")

 

以下、実行結果です。

 

　SARIMAモデル
（季節性を1つだけ取り込む）

学習データで、SARIMAモデルを構築します。季節性は、48周期と336周期の2つありますが、48周期の方をSARIMAモデルで表現します。

以下、コードです。

arima_model = auto_arima(y=y_train,
                         seasonal=True,
                         m=48,
                         maxiter=10)

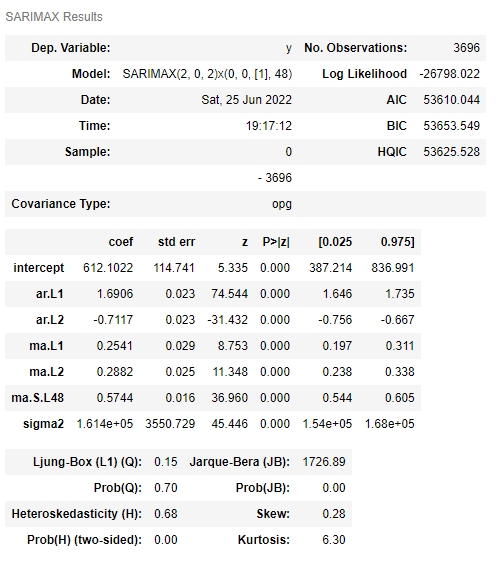
arima_model.summary() #確認

 

以下、実行結果です。

 

テストデータで、構築した予測モデルを評価します。

以下、コードです。

# 予測
train_pred = arima_model.predict_in_sample()   #学習データの期間
test_pred = arima_model.predict(n_periods=336) #テストデータの期間

# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

TBATSモデルに比べ、予測精度は悪化しています。

 

グラフ化し確認します。

以下、コードです。

# グラフ化（テストデータの期間）
fig, ax = plt.subplots()

ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_test.index, 
        test_pred, 
        label="SARIMA", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

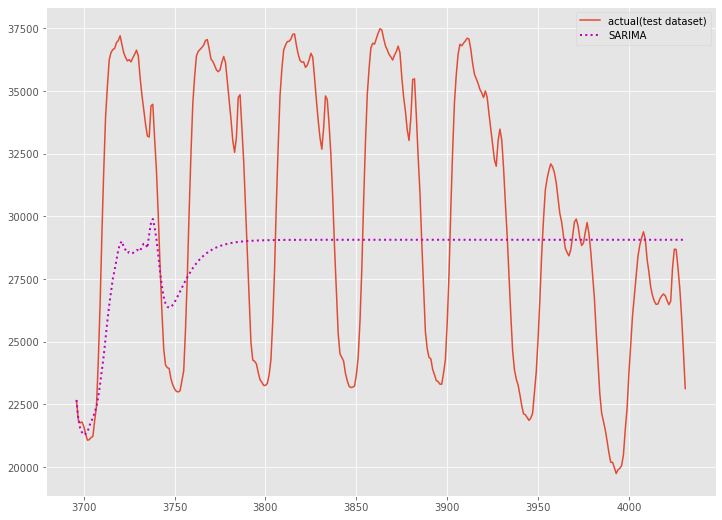
plt.legend()

 

以下、実行結果です。

 

学習データを含めた全期間（学習データの期間＋テストデータの期間）をグラフ化し見てみます。

以下、コードです。

# グラフ化（全期間）
fig, ax = plt.subplots()

ax.plot(y_train.index, 
        y_train.values, 
        label="actual(train dataset)")
ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_train.index, 
        train_pred, 
        linestyle="dotted", 
        lw=2,
        color="m")
ax.plot(y_test.index, 
        test_pred, 
        label="SARIMA", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

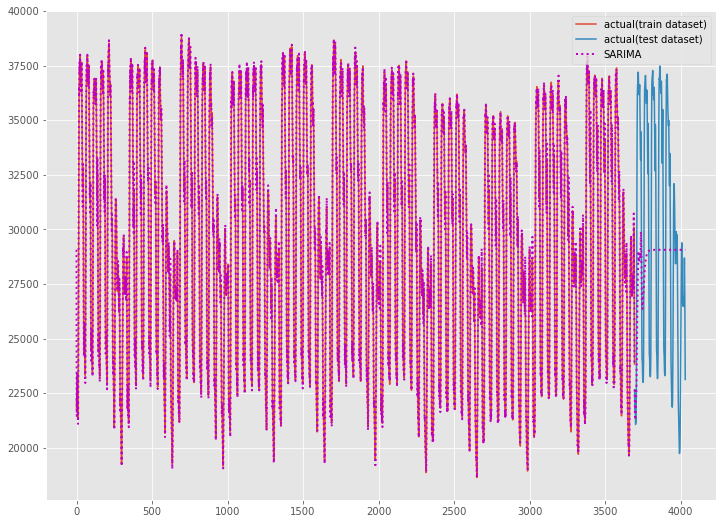
plt.legend()

 

以下、実行結果です。

 

　SARIMAX with Fourier Termsモデル
（説明変数Xで季節性を取り込む）

SARIMAX with Fourier Termsモデルを構築するには、季節成分を表現する説明変数Xを生成する必要があります。

季節性は、48周期と336周期の2つあります。48周期の方はSARIMAモデルの方で表現、336周期の方を三角関数で表現します。

 

今回は、336周期の季節性を表現するsinとcosの変数を2セット作ります。

以下、コードです。

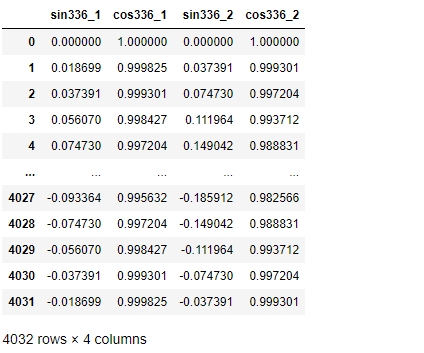
# 説明変数X（Fourier terms）の生成
seasonal = 336

## 空のデータフレーム生成
exog = pd.DataFrame()
exog.index = y.index

## 336周期のFourier terms
exog['sin336_1'] = np.sin(1 * 2 * np.pi * exog.index / seasonal)
exog['cos336_1'] = np.cos(1 * 2 * np.pi * exog.index / seasonal)
exog['sin336_2'] = np.sin(2 * 2 * np.pi * exog.index / seasonal)
exog['cos336_2'] = np.cos(2 * 2 * np.pi * exog.index / seasonal)

exog #確認

 

以下、実行結果です。

 

生成した説明変数を、学習データの説明変数とテストデータの説明変数に分割します。

以下、コードです。

exog_train = exog.iloc[:-336]
exog_test = exog.iloc[-336:]

 

学習データで、SARIMAXモデルを構築します。

以下、コードです。

arima_fourier_model = auto_arima(y=y_train,
                                 X=exog_train,
                                 seasonal=True,
                                 m=48,
                                 maxiter=10)

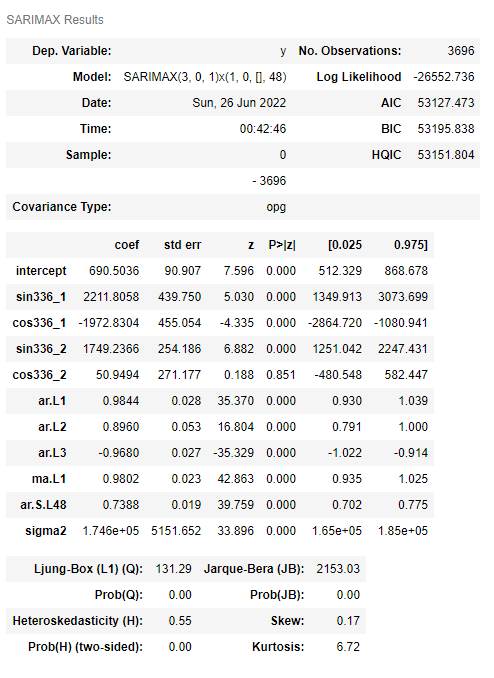
arima_fourier_model.summary() #確認

 

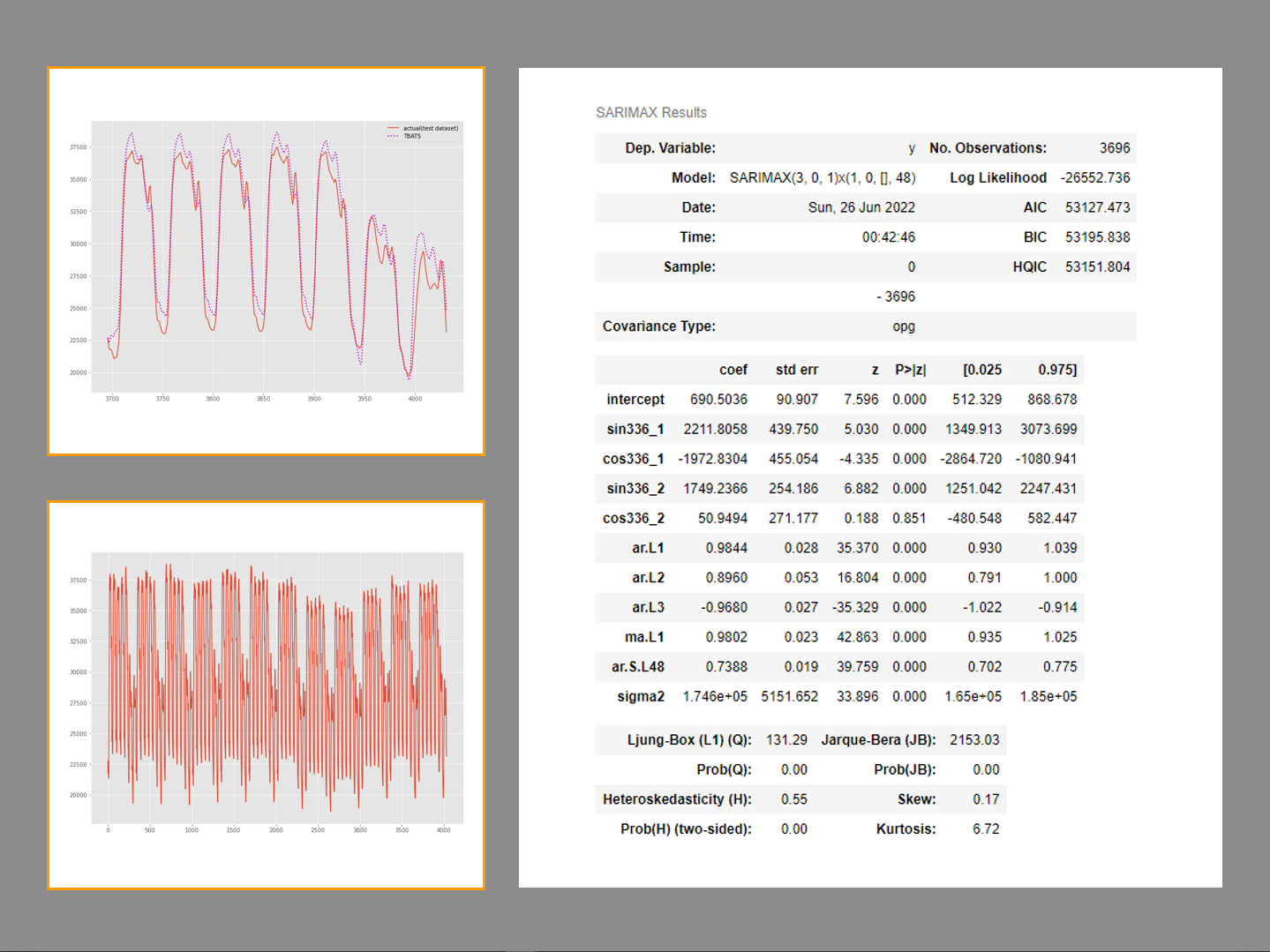
以下、実行結果です。

 

テストデータで、構築した予測モデルを評価します。

以下、コードです。

# 予測
## 学習データの期間
train_pred = arima_fourier_model.predict_in_sample(X=exog_train)
## テストデータの期間
test_pred = arima_fourier_model.predict(n_periods=336,
                                        X=exog_test)

# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

予測精度は、SARIMAモデルよりまし、という感じです。

 

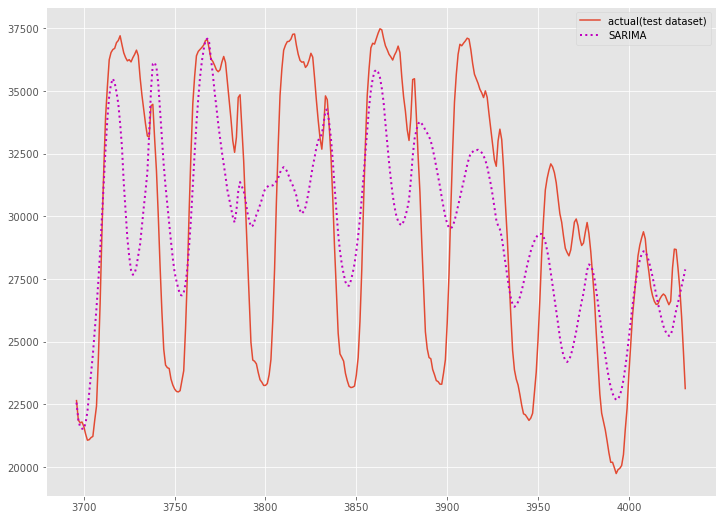
グラフ化し確認します。

以下、コードです。

# グラフ化（テストデータの期間）
fig, ax = plt.subplots()

ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_test.index, 
        test_pred, 
        label="SARIMA", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

plt.legend()

 

以下、実行結果です。

 

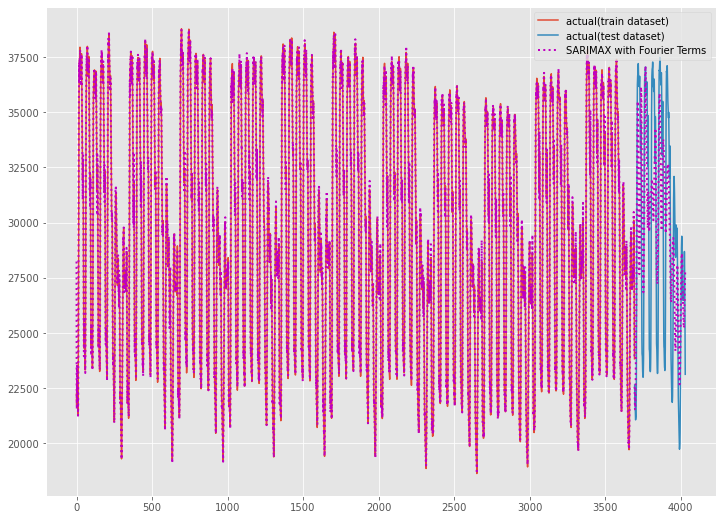
学習データを含めた全期間（学習データの期間＋テストデータの期間）をグラフ化し見てみます。

以下、コードです。

# グラフ化（全期間）
fig, ax = plt.subplots()

ax.plot(y_train.index, 
        y_train.values, 
        label="actual(train dataset)")
ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_train.index, 
        train_pred, 
        linestyle="dotted", 
        lw=2,
        color="m")
ax.plot(y_test.index, 
        test_pred, 
        label="SARIMAX with Fourier Terms", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

plt.legend()

 

以下、実行結果です。

 

　ARIMAX with Fourier Termsモデル
（説明変数Xで季節性を取り込む）

ARIMAX with Fourier Termsモデルを構築するには、季節成分を表現する説明変数Xを生成する必要があります。

季節性は、48周期と336周期の2つあります。それぞれ三角関数で表現します。

 

今回は、季節性ごとにsinとcosの変数を10セット作ります。

以下、コードです。

# 説明変数X（Fourier terms）の生成

## 空のデータフレーム生成
exog = pd.DataFrame()
exog.index = y.index

## Fourier termsの生成関数
def fourier_terms_gen(seasonal,terms_num):
    
    #seasonal:周期
    #terms_num:Fourier termの数（sinとcosのセット数）
    
    for num in range(terms_num):
        num = num + 1
        sin_colname = 'sin'+str(seasonal)+'_'+ str(num)
        cos_colname = 'cos'+str(seasonal)+'_'+ str(num)

        exog[sin_colname] = np.sin(num * 2 * np.pi * exog.index / seasonal)
        exog[cos_colname] = np.cos(num * 2 * np.pi * exog.index / seasonal)

## 336周期
fourier_terms_gen(seasonal=336,
                  terms_num=10)

## 48周期
fourier_terms_gen(seasonal=48,
                  terms_num=10)
    
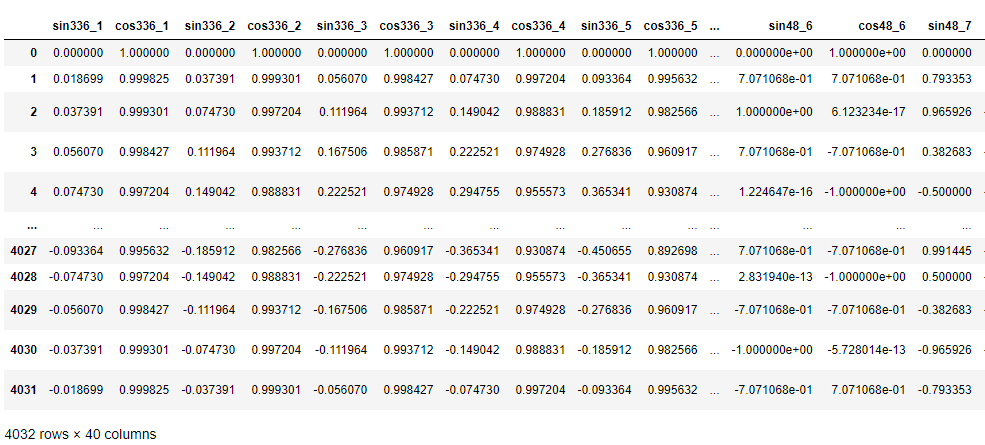
exog #確認

 

以下、実行結果です。

 

生成した説明変数を、学習データの説明変数とテストデータの説明変数に分割します。

以下、コードです。

exog_train = exog.iloc[:-336]
exog_test = exog.iloc[-336:]

 

学習データで、ARIMAXモデルを構築します。

以下、コードです。

# モデル構築
arima_fourier_model = auto_arima(y=y_train,
                                 X=exog_train,
                                 seasonal=False,
                                 maxiter=10)

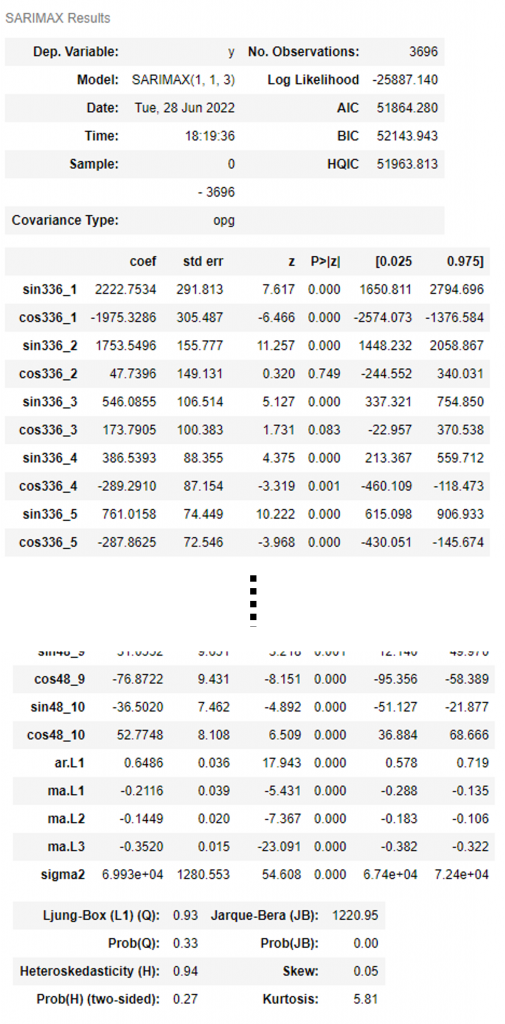
arima_fourier_model.summary() #確認

 

以下、実行結果です。

 

テストデータで、構築した予測モデルを評価します。

以下、コードです。

# 予測
## 学習データの期間
train_pred = arima_fourier_model.predict_in_sample(X=exog_train)
## テストデータの期間
test_pred = arima_fourier_model.predict(n_periods=336,
                                        X=exog_test)

# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

予測精度は、TBATSモデルと同等かそれ以上です。

 

グラフ化し確認します。

以下、コードです。

# グラフ化（テストデータの期間）
fig, ax = plt.subplots()

ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_test.index, 
        test_pred, 
        label="ARIMAX", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

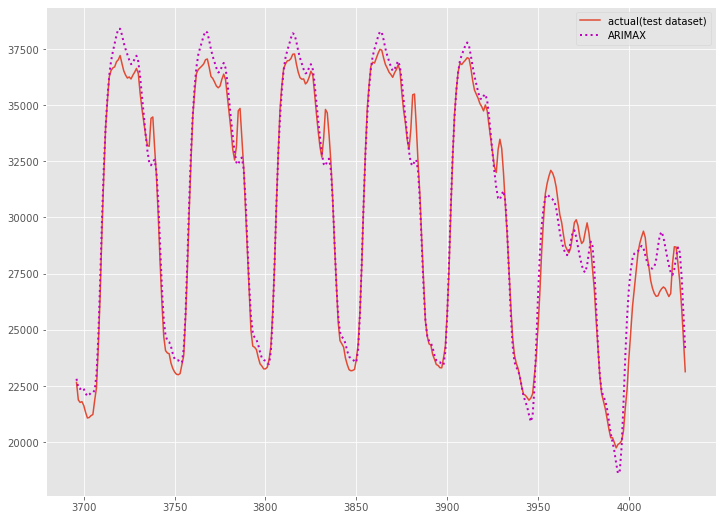
plt.legend()

 

以下、実行結果です。

 

学習データを含めた全期間（学習データの期間＋テストデータの期間）をグラフ化し見てみます。

以下、コードです。

# グラフ化（全期間）
fig, ax = plt.subplots()

ax.plot(y_train.index, 
        y_train.values, 
        label="actual(train dataset)")
ax.plot(y_test.index, 
        y_test.values, 
        label="actual(test dataset)")
ax.plot(y_train.index, 
        train_pred, 
        linestyle="dotted", 
        lw=2,
        color="m")
ax.plot(y_test.index, 
        test_pred, 
        label="ARIMAX with Fourier Terms", 
        linestyle="dotted", 
        lw=2, 
        color="m") 

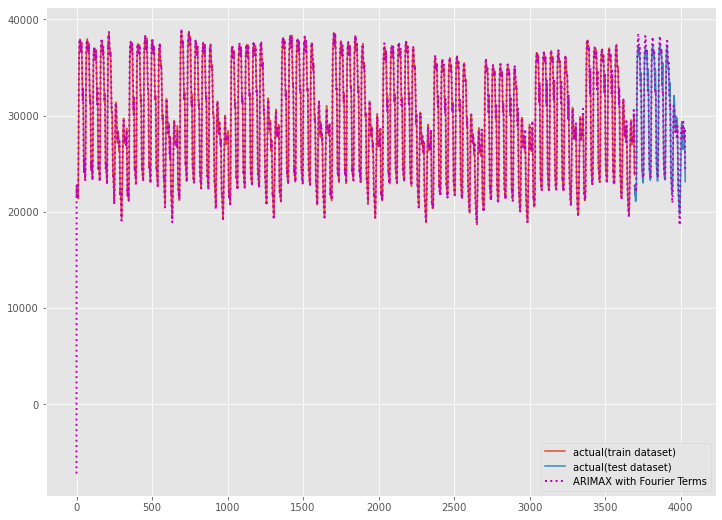
plt.legend()

 

以下、実行結果です。

 

まとめ

今回は、「複数季節性を持つ時系列データをモデル化する方法（TBATSモデルとARIMAモデル）」というお話しをしました。

フーリエ級数に基づく三角関数による季節性表現を採用することで、複数の季節性を表現することができます。

そのための時系列モデルとしてTBATSというモデルがあります。

時系列データでよく利用されるARIMA系のモデルでも、三角関数による季節性表現を説明変数に導入することで可能になります。

興味のある方は、試してみてください。

（Python版）複数季節性を持つ時系列データを線形回帰でモデル化する方法