説明変数Xを主成分分析(PCA)を行い、その主成分で回帰モデルを構築するのが、主成分回帰(PCR)です。
主成分は、主成分の分散が最大になるように作成され、できるだけ元の説明変数Xのもっている情報量を保持しようとします。
この主成分は、目的変数Yとは無関係に主成分分析で算出されます。
回帰モデルを構築するという視点で考えると、できれば目的変数Yと相関の高い主成分であると嬉しいでしょう。
それを実現するのが、部分的最小2乗回帰(PLS)です。
主成分は、目的変数Yと主成分の共分散が最大になるように作成され、目的変数Yを考慮したものになります。
今回は、「Pythonによる主成分回帰(PCR)と部分的最小2乗回帰(PLS)」というお話しをします。
Contents [hide]
なぜ、PCRとPLSを使うといいのか
回帰モデルを構築するとき、マルチコという推定した係数がおかしくなる現象が起こることがあります。その原因の1つが、相関の高い説明変数同士の存在です。
主成分分析は、相関の高い説明変数同士を取りまとめ主成分という新しい変数を生成します。その主成分同士の相関は低くなります。
要するには、マルチコ対策になるわけです。
さらに、主成分は、元の説明変数Xの情報量をある程度保持したまま、変数の数が少なくなります。
要するに、変数縮約という意味で非常に便利です。
主成分回帰(PCR)と部分的最小2乗回帰(PLS)は違いは……
- PCR:主成分が、主成分の分散が最大になるように作成
- PLS:主成分が、目的変数Yと主成分の共分散が最大になるように作成
ただ、主成分を幾つ作成すればいいのか? という問題があります。
今回は、ボストン住宅価格のサンプルデータを利用し、主成分回帰(PCR)と部分的最小2乗回帰(PLS)を使い、住宅価格を予測するモデルを構築していきます。説明変数の数は13個です。
今回構築する予測モデルは、以下の4つです。
- PCR(主成分回帰)
- 主成分の数を3としモデル構築
- 主成分の数をグリッドサーチで探索しモデル構築
- PLS(部分最小二乗回帰)
- 主成分の数を3としモデル構築
- 主成分の数をグリッドサーチで探索しモデル構築
- 主成分の数を3としモデル構築
ちなみに、scikit-learnを使いモデル構築していきます。まだ、scikit-learnをインストールされていない方は、scikit-learnをインストールして頂ければと思います。
pipでインストールする場合のコードは以下です。
pip install scikit-learn
condaでインストールする場合のコードは以下です。
conda install scikit-learn
必要なモジュールの読み込み
必要なモジュールを読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import PLSRegression
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
基本的なものばかりです。
必要なデータの読み込みとデータ分割
ボストン住宅価格のサンプルデータを読み込みます。
以下、コードです。
# データの読み込み(X:説明変数、y:目的変数) X,y = load_boston(return_X_y=True)
Xが説明変数で、yが目的変数です。
このデータを、学習データとテストデータに分割します。
学習データで予測モデルで構築し、構築した予測モデルを、テストデータで精度検証します。
以下、コードです。
# 学習データとテストデータへ分割
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.3,
random_state=123)
決定係数
PCR(主成分回帰)
PCR(主成分回帰)モデルは、次の手順で構築します。
- 説明変数を標準化し標準得点(平均0、標準偏差1)に変換する
- 標準得点で主成分分析を実施し主成分を抽出する
- 抽出した主成分で回帰モデルを構築する
次の3つの関数を使います。
- StandardScaler():標準化するための関数
- PCA():主成分分析をするための関数
- LinearRegression():回帰モデルを構築するための関数
この3つの関数を1つ1つ順番に使い、主成分回帰モデルを構築してもいいです。
面倒なので、今回はこの3つの関数をパイプラインでつなげ予測モデルを構築します。
主成分の数を3としモデル構築
パイプラインのインスタンス生成します。
以下、コードです。
# パイプラインのインスタンス生成
PCR_model = make_pipeline(StandardScaler(),
PCA(n_components=3),
LinearRegression())
学習データを使い、予測モデルを構築する。
以下、コードです。
# 学習 PCR_model.fit(X_train, y_train)
構築した予測モデルの予測精度を、学習データで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PCR_model.score(X_train, y_train),2)
# グラフ
plt.scatter(y_train, PCR_model.predict(X_train))
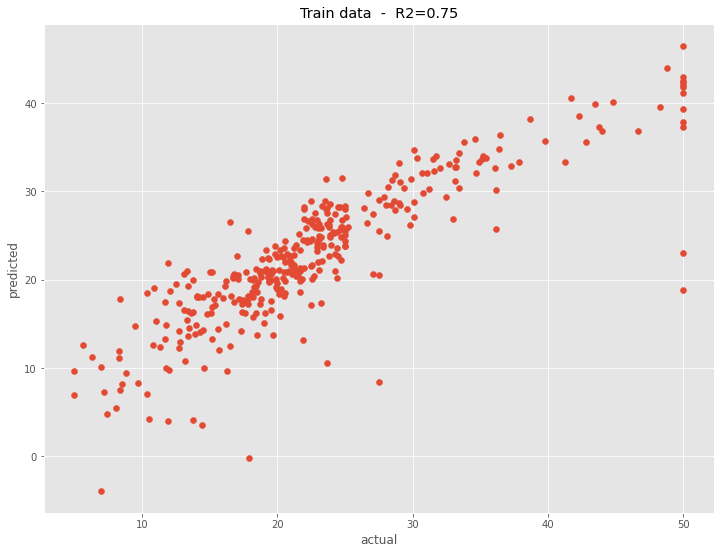
plt.title('Train data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
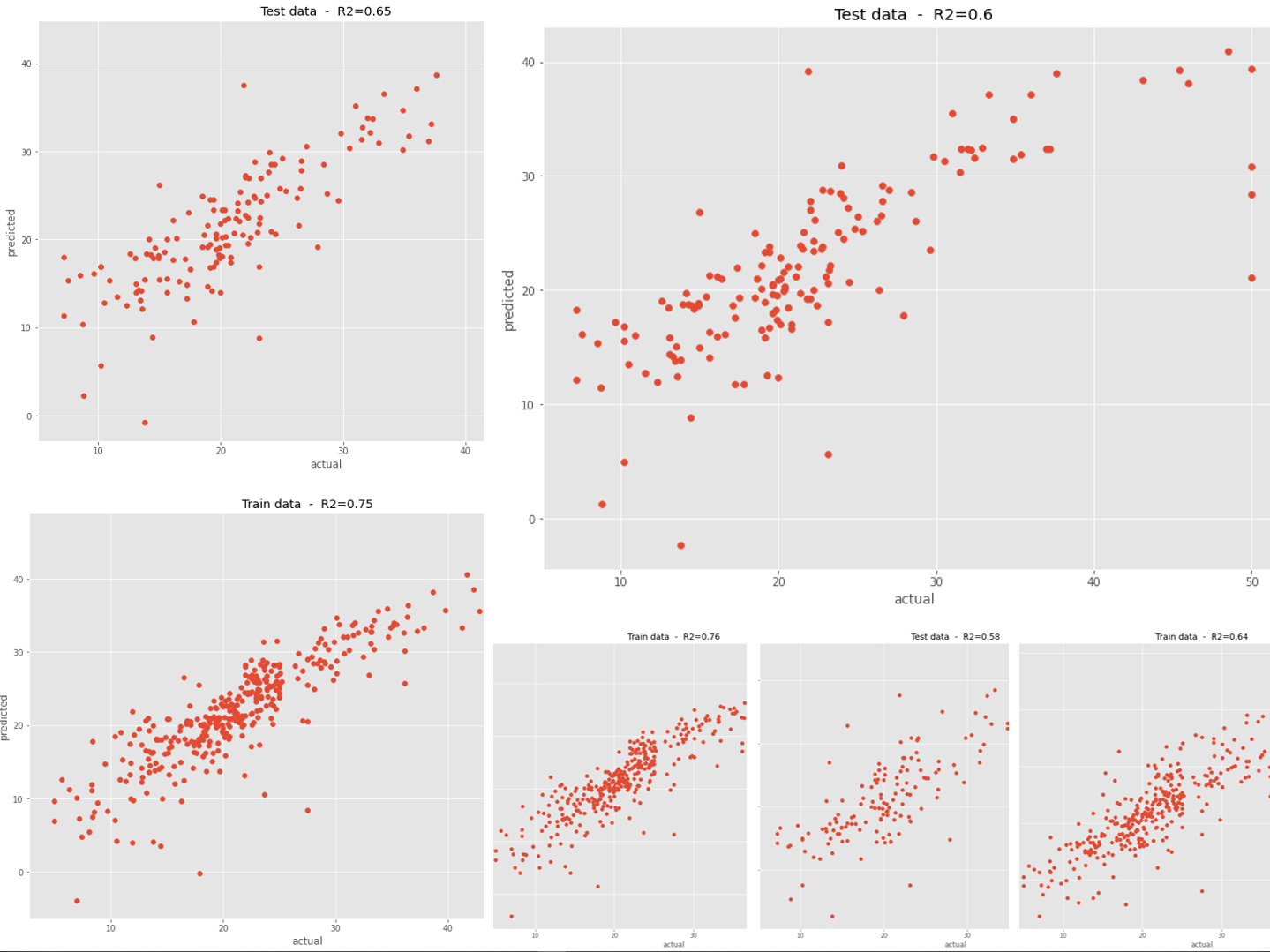
以下、実行結果です。
構築した予測モデルの予測精度を、テストデータで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PCR_model.score(X_test, y_test),2)
# グラフ
plt.scatter(y_test, PCR_model.predict(X_test))
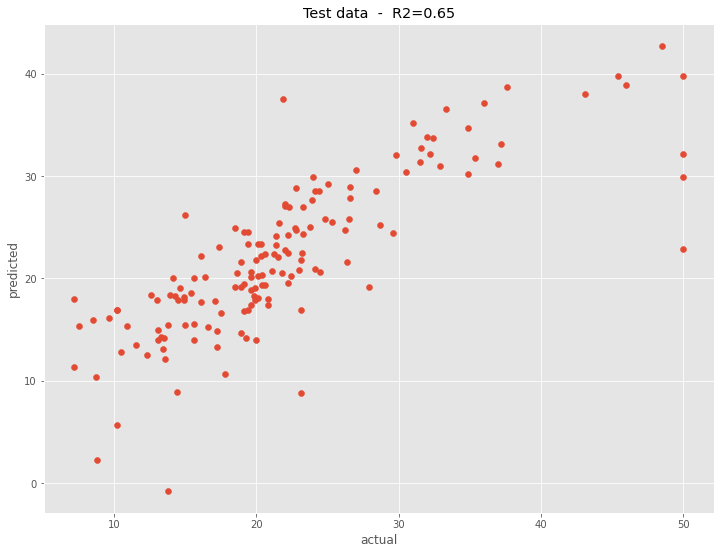
plt.title('Test data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
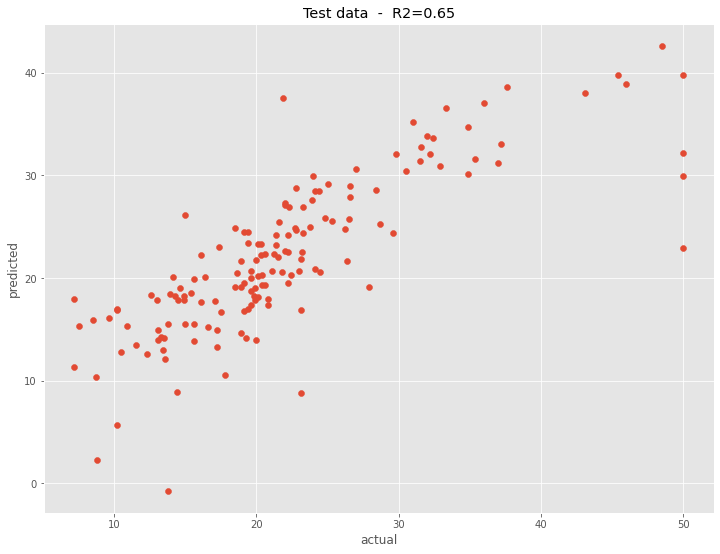
以下、実行結果です。
主成分の数をグリッドサーチで探索しモデル構築
主成分の数を、グリッドサーチ(候補すべてを探索)で探索し、モデル構築します。
以下、コードです。
# パイプライン定義
PCR_model = make_pipeline(StandardScaler(),
PCA(),
LinearRegression())
# 探索範囲
param = {
'pca__n_components' : np.arange(1, len(X[0])+1)
}
# グリッドサーチのインスタンス生成
PCR_grid = GridSearchCV(PCR_model,
param_grid=param,
cv=10
)
# グリッドサーチの実行
PCR_grid.fit(X_train, y_train)
# 最適パラメータ
PCR_grid.best_params_
構築した予測モデルの予測精度を、学習データで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PCR_grid.score(X_train, y_train),2)
# グラフ
plt.scatter(y_train, PCR_grid.predict(X_train))
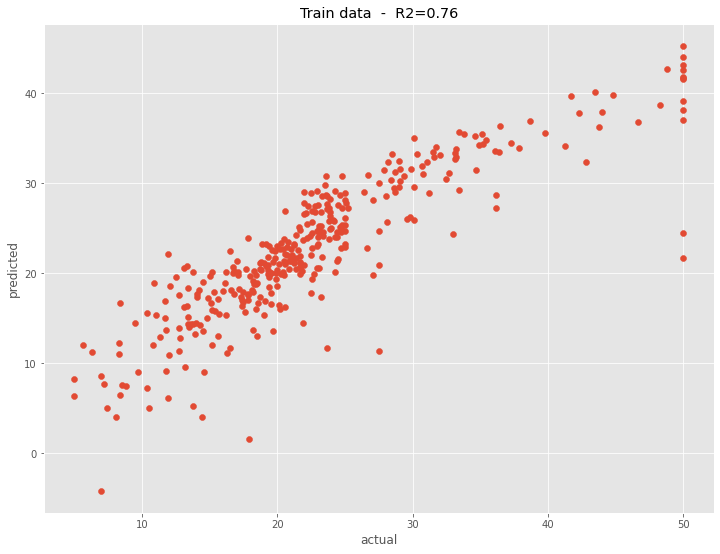
plt.title('Train data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
以下、実行結果です。
構築した予測モデルの予測精度を、テストデータで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PCR_grid.score(X_test, y_test),2)
# グラフ
plt.scatter(y_test, PCR_grid.predict(X_test))
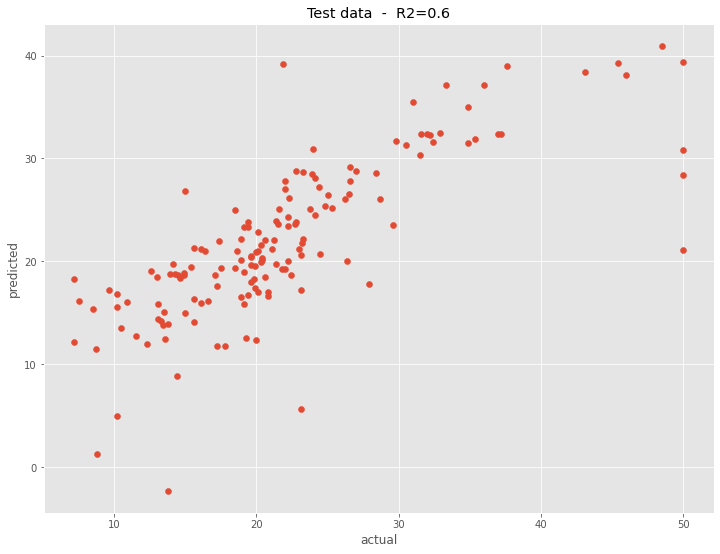
plt.title('Test data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
以下、実行結果です。
PLS(部分最小二乗回帰)
PCR(主成分回帰)モデルと異なり、PLS(部分最小二乗回帰)モデルのための関数があるので、それをそのまま利用します。
主成分の数を3としモデル構築
モデルのインスタンス生成します。
以下、コードです。
# モデルのインスタンス生成 PLS_model = PLSRegression(n_components=3)
学習データを使い、予測モデルを構築する。
以下、コードです。
# 学習 PLS_model.fit(X_train, y_train)
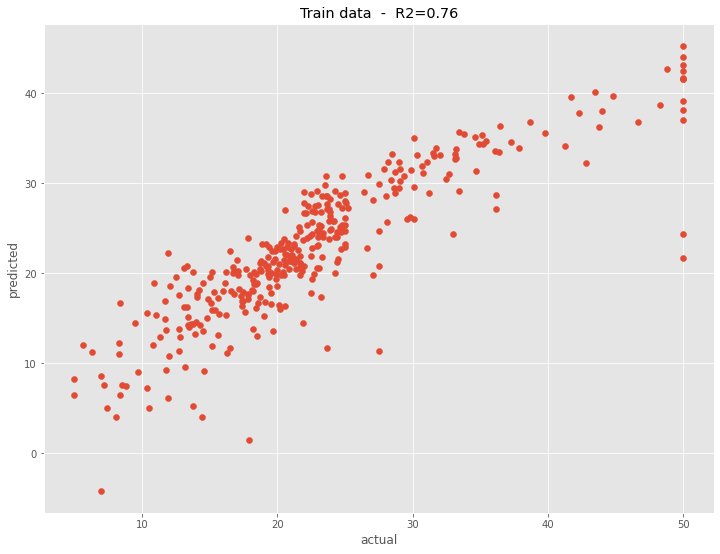
構築した予測モデルの予測精度を、学習データで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PLS_model.score(X_train, y_train),2)
# グラフ
plt.scatter(y_train, PLS_model.predict(X_train))
plt.title('Train data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
以下、実行結果です。
構築した予測モデルの予測精度を、テストデータで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PLS_model.score(X_test, y_test),2)
# グラフ
plt.scatter(y_test, PLS_model.predict(X_test))
plt.title('Test data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
以下、実行結果です。
主成分の数が同じ場合、このようにPCR(主成分回帰)よりも予測精度は高くなります。
主成分の数をグリッドサーチで探索しモデル構築
主成分の数を、グリッドサーチ(候補すべてを探索)で探索し、モデル構築します。
以下、コードです。
# モデルのインスタンス生成
PLS_model = PLSRegression()
# 探索範囲
param = {
'n_components' : np.arange(1, len(X[0])+1)
}
# グリッドサーチのインスタンス生成
PLS_grid = GridSearchCV(PLS_model,
param_grid=param,
cv=10
)
# グリッドサーチの実行
PLS_grid.fit(X_train, y_train)
# 最適パラメータ
PLS_grid.best_params_
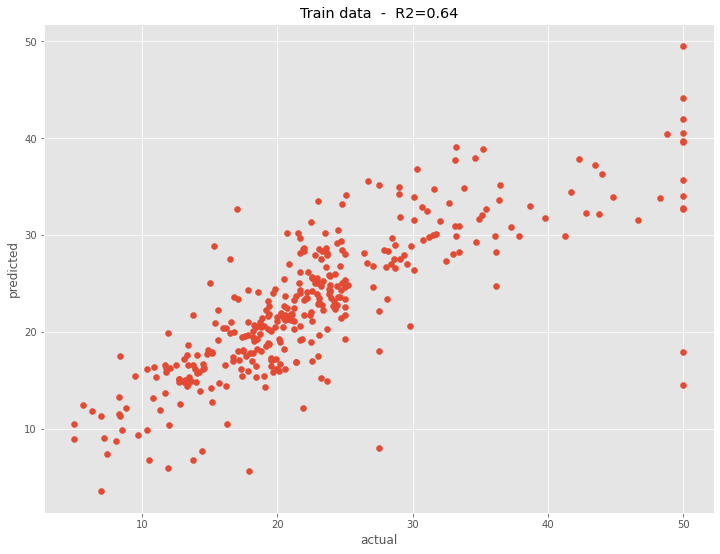
構築した予測モデルの予測精度を、学習データで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PLS_grid.score(X_train, y_train),2)
# グラフ
plt.scatter(y_train, PLS_grid.predict(X_train))
plt.title('Train data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
以下、実行結果です。
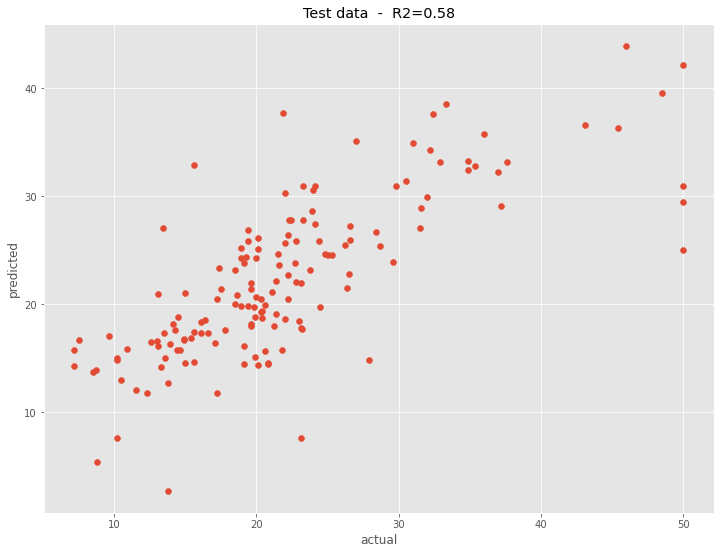
構築した予測モデルの予測精度を、テストデータで見てみます。
以下、コードです。
# R2(決定係数)
R2 = round(PLS_grid.score(X_test, y_test),2)
# グラフ
plt.scatter(y_test, PLS_grid.predict(X_test))
plt.title('Test data - R2='+str(R2))
plt.xlabel("actual")
plt.ylabel("predicted")
plt.show()
以下、実行結果です。
最適な主成分の数で予測モデルを構築すると、主成分回帰(PCR)と部分的最小2乗回帰(PLS)で、予測精度に大差はないようです。
まとめ
今回は、「Pythonによる主成分回帰(PCR)と部分的最小2乗回帰(PLS)」というお話ししました。
興味のある方は、試してみてください。