Pythonによるマーケティングミックスモデリング
（MMM：Marketing Mix Modeling）超入門 その5

Ridge回帰モデルでMMM①（AdStock非考慮）

3347
Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その5Ridge回帰モデルでMMM①（AdStock非考慮）

本当に売上に貢献している広告は、どの広告か？

売上と広告媒体等との関係性をモデリングし、どの広告媒体が売上にどれほど貢献していたのか分析することができます。

それが、マーケティングミックスモデリング（MMM：Marketing Mix Modeling）です。

前回までは、通常の線形回帰モデルでマーケティングミックスモデリング（MMM：Marketing Mix Modeling）を構築してきました。

その１　線形回帰モデルでMMMを作ろう！
https://www.salesanalytics.co.jp/datascience/datascience097/

その２　アドストック（Ad Stock）を考慮した線形回帰モデル
https://www.salesanalytics.co.jp/datascience/datascience098/

その３　ちょっと複雑なアドストック（Ad Stock）を考慮した線形回帰モデル
https://www.salesanalytics.co.jp/datascience/datascience099/

その４　最適なアドストック（Ad Stock）を探索しモデル構築
https://www.salesanalytics.co.jp/datascience/datascience100/

 

多くの広告・販促は似たような時期に集中し実施することが多く、結果的にマルチコという線形回帰モデルを構築しうる上で非常に良くない現象が起こる危険があります。

その対策の1つに、正則化項付き線形回帰モデルの1つである、Ridge回帰でモデルを構築する、という方法があります。モデルの説明力や予測精度は若干悪化しますが、非常に有効な方法です。

3回に分けてお話しします。

  • ① AdStock非考慮
  • ② シンプルなAdStock考慮
  • ③ 色々なAdStock考慮

 

ちなみに、アドストック（Ad Stock）を考慮するとは、飽和効果（収穫逓減）とキャリーオーバー（Carryover）効果を考慮するということです。具体的には、Pythonのscikit-learn（sklearn）のパイプラインを、以下のように構築しました。

 

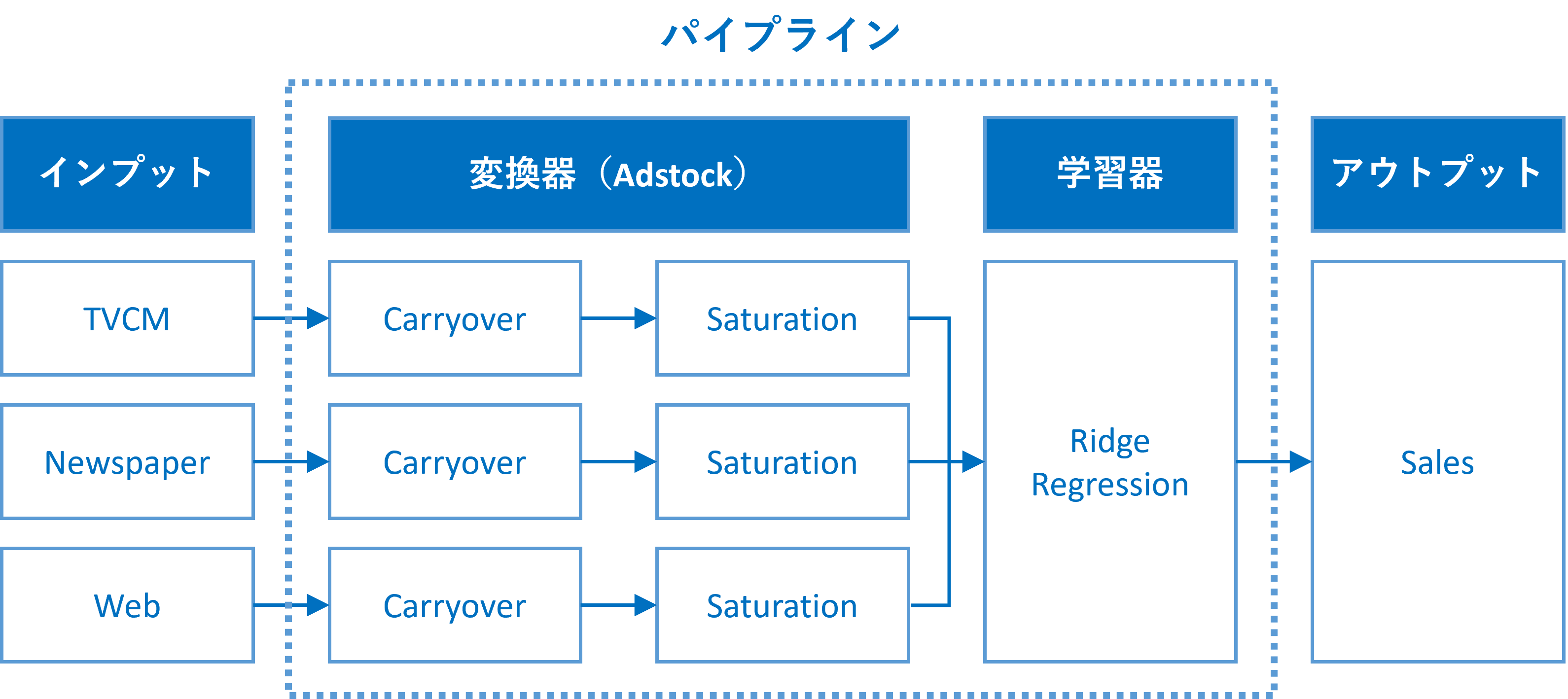
今回は、①のAdStockを考慮しないRidge回帰によるモデル構築です。Adstockを考慮しないため、パイプラインは構築しません。

正則化項付き線形回帰モデルとは

奇妙な数式など登場してきますので、興味のない方は読み飛ばして下さい。

 

通常の線形回帰モデルは、最小二乗法という方法で回帰式の回帰係数（定数含む）を求めます。

例えば、線形回帰式を以下のように表現したとします。

y_i = \beta_0 + \sum_{j=1}^p \beta_j x_{ij}

yが目的変数で、xが説明変数です。pが説明変数の数です。nがデータ数（データセットの行数）です。

何かしら回帰係数（定数含む）を設定すると、何かしらの線形回帰式が出来上がります。何かしらの線形回帰式が出来上がれば、yの予測値を求めることができます。

 

yの予測値は、yの実測値に近いほどいいでしょう。言い換えると、予測値と実測値の差は小さいほどいいでしょう。もう少し言うと、予測値と実測値の差を二乗した値は小さいほどいいでしょう。

予測値と実測値の差を二乗した値を最小化するような回帰係数（定数含む）を知ることができれば、でたらめに回帰係数（定数含む）を設定し線形回帰式を作るより、非常に嬉しいでしょう。

予測値と実測値の差を二乗した値を最小化するような回帰係数（定数含む）を求める方法が、最小二乗法です。

\hat{\beta} = \underset{\beta}{argmin} \{\sum_{i=1}^n (\beta_0 + \sum_{j=1}^p \beta_j x_{ij}-y_i)^2 \}

 

この最小二乗法にある制約（正則化項）を付け加えた、制約（正則化項）付き最小二乗法という方法で回帰式の回帰係数（定数含む）を求めるのが、正則化項付き線形回帰モデルです。

通常の線形回帰モデルと比べ、求めた回帰係数（定数含む）が0の方向に縮小（絶対値が小さくなる）します。

この制約（正則化項）により、マルチコ（説明変数同士の相関が高いために起こる不具合）や過学習などの影響を緩和してくれます。

 

どのような制約（正則化項）を加えるかで、名称が変わります。有名なのは、以下の3つです。

  • Ridge回帰
  • Lasso回帰
  • Elastic Net回帰

 

Ridge回帰は、線形回帰モデルの回帰係数の二乗和を正則化項として加えた推定法です。ハイパーパラメータとして、正則化項の重み（正則化パラメータ）を設定する必要があります。

\hat{\beta}_{ridge} = \underset{\beta}{argmin} \{\sum_{i=1}^n (\beta_0 + \sum_{j=1}^p \beta_j x_{ij}-y_i )^2 + \lambda \sum_{j=1}^p \beta_j^2 \}

 

Lasso回帰は、線形回帰モデルの回帰係数の絶対値の和を正則化項として加えた推定法です。ハイパーパラメータとして、正則化項の重み（正則化パラメータ）を設定する必要があります。

\hat{\beta}_{lasso} = \underset{\beta}{argmin} \{\sum_{i=1}^n (\beta_0 + \sum_{j=1}^p \beta_j x_{ij}-y_i )^2 + \lambda \sum_{j=1}^p |\beta_j| \}

Lasso回帰はRidge回帰と異なり、回帰係数を0にするため変数選択を自動で実施してくれます。

 

Elastic Net回帰は、Ridge回帰とLasso回帰のハイブリッドモデルです。ハイパーパラメータとして、その割合を設定する必要があります。もちろん、ハイパーパラメータとして、正則化項の重み（正則化パラメータ）を設定する必要があります。

\hat{\beta}_{elasticnet} = \underset{\beta}{argmin} \{\sum_{i=1}^n (\beta_0 + \sum_{j=1}^p \beta_j x_{ij}-y_i )^2 + \lambda \sum_{j=1}^p (\alpha |\beta_j| + (1-\alpha)\beta_j^2 ) \}

 

利用するデータセット（前回と同じ）

今回利用するデータセットの変数です。

  • Week：週
  • Sales：売上
  • TVCM：TV CMのコスト
  • Newspaper：新聞の折り込みチラシのコスト
  • Web：Web広告のコスト

 

以下からダウンロードできます。

MMM.csv
https://www.salesanalytics.co.jp/4zdt

 

線形回帰モデルと構築していたときの大きな違い

前回までの線形回帰モデルのケースとの大きな違いは、当然ですがRidge回帰で構築するというところです。

Ridge回帰には、ハイパーパラメータとして正則化パラメータというものがあり、モデル構築者が与える必要があります。今回は、ハイパーパラメータチューニング用のライブラリーであるOptunaを利用し、最適な正則化パラメータの値を探索し、その値を利用しMMMを構築します。

他は、線形回帰でMMMを構築したときと、ほぼ同じです。コードもほぼ同じです。

 

ライブラリーやデータセットなどの読み込み

先ずは、必要なライブラリーとデータセットを読み込みます。前回までと同じです。

 

　必要なライブラリーの読み込み

必要なライブラリーを読み込みます。

以下、コードです。

import numpy as np
import pandas as pd

from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import Ridge

from optuna.integration import OptunaSearchCV
from optuna.distributions import UniformDistribution

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ

 

　データセット（前回と同じ）の読み込み

前回と同じデータセットを読み込みます。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(url,
                 parse_dates=['Week'],
                 index_col='Week'
                )

# データ確認
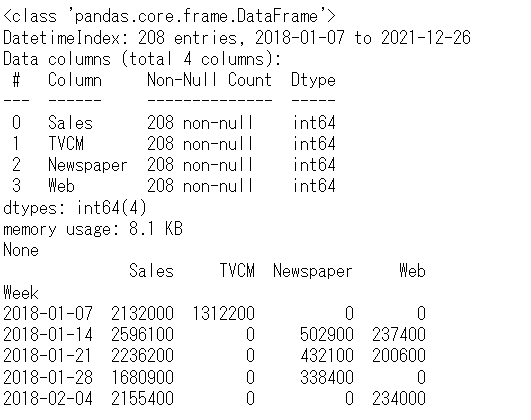
print(df.info()) #変数の情報
print(df.head()) #データの一部

# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']

 

以下、実行結果です。

 

ハイパーパラメータ探索

Ridge回帰の最適な正則化パラメータの値を探索します。

以下、コードです。

#
# ハイパーパラメータ探索
#

# Ridge回帰のインスタンス生成
MMM=Ridge()

# 探索するハイパーパラメータ範囲の設定
params = {
 'alpha': UniformDistribution(0.01, 1e10),
}

# ハイパーパラメータ探索の設定
optuna_search = OptunaSearchCV(
    estimator=MMM,
    param_distributions=params,
    n_trials=1000,
    cv=TimeSeriesSplit(),
    random_state=123,
)

# 探索実施
optuna_search.fit(X, y)

# 探索結果
optuna_search.best_params_

 

以下、実行結果です。最適な正則化パラメータの値です。

 

この値を正則化パラメータに設定し、MMMを全データで構築します。

 

モデルの構築と予測

　最適ハイパーパラメータで学習

以下、コードです。

#
# 最適ハイパーパラメータで学習
#

# パイプラインのインスタンス
MMM_best = MMM.set_params(**optuna_search.best_params_)

# 全データで学習
MMM_best.fit(X, y)

# R2（決定係数）
MMM_best.score(X, y)

 

以下、実行結果です。R2（決定係数）の値です。

 

　予測式の確認

以下、コードです。

# 
# 予測式の確認
# 

# 線形回帰モデルの切片と回帰係数
intercept = MMM_best.intercept_ #切片
coef = MMM_best.coef_           #回帰係数
alpha = MMM_best.alpha          #正則化パラメータ

# 回帰係数をSeries（シリーズ）化
weights = pd.Series(
    coef,
    index=X.columns
)

# 結果出力（切片と係数）
print('Intercept:\n', intercept, sep='')
print()
print('Coefficients:\n',weights, sep='')
print()
print('alpha:\n', alpha, sep='')

 

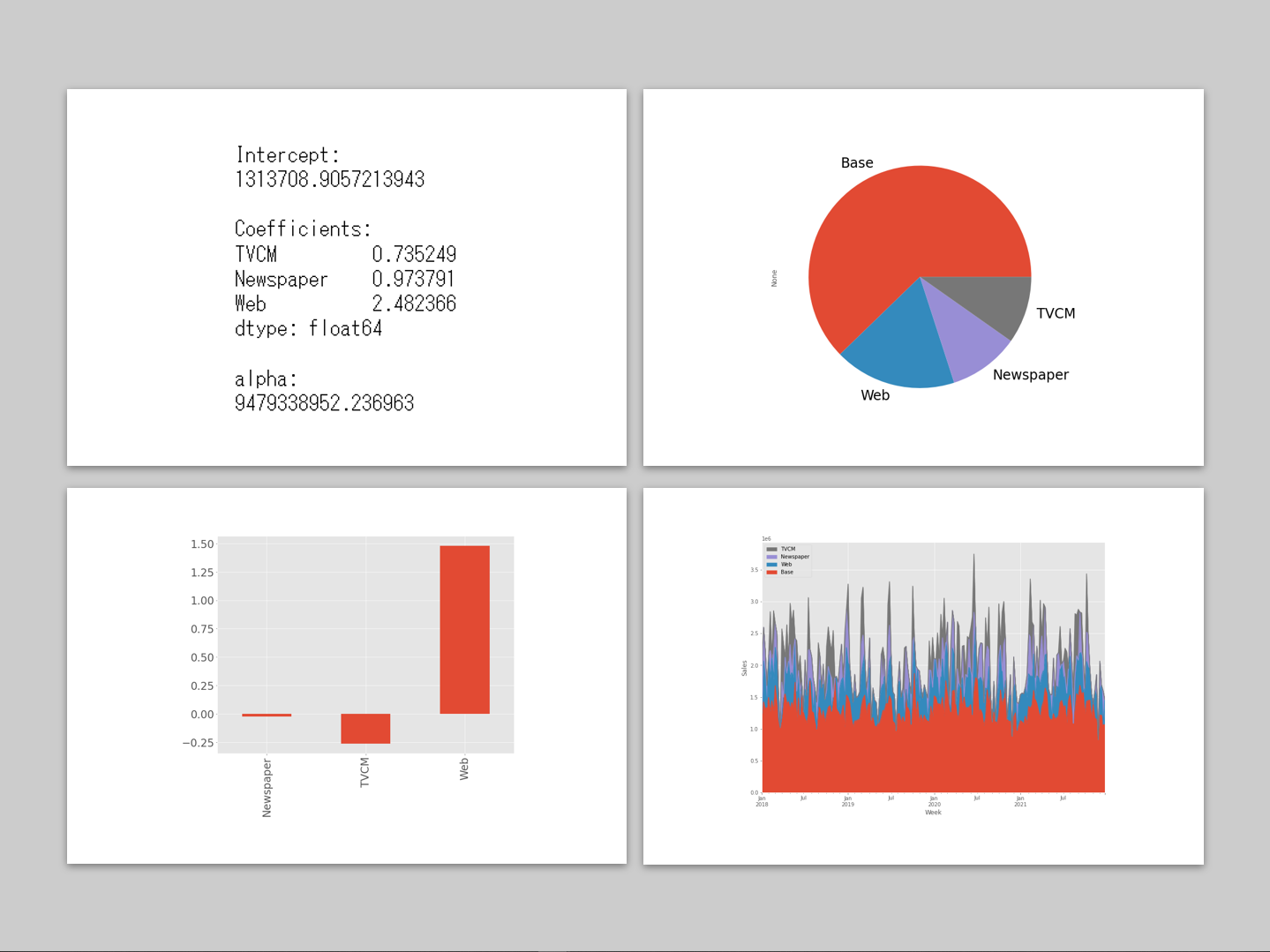
以下、実行結果です。

 

　予測の実施

以下、コードです。

#
# 予測の実施
# 

# 目的変数y（売上）の予測
pred = pd.DataFrame(MMM_best.predict(X),
                    index=X.index,
                    columns=['y'])

# 各媒体による売上の予測

## 値がすべて0の説明変数
X_ = X.copy()
X_.iloc[:,:]=0

## Base
pred['Base'] = MMM_best.predict(X_)

## 媒体
for i in range(len(X.columns)):
    X_.iloc[:,:]=0
    X_.iloc[:,i]=X.iloc[:,i]
    pred[X.columns[i]] = MMM_best.predict(X_) - pred['Base']
    
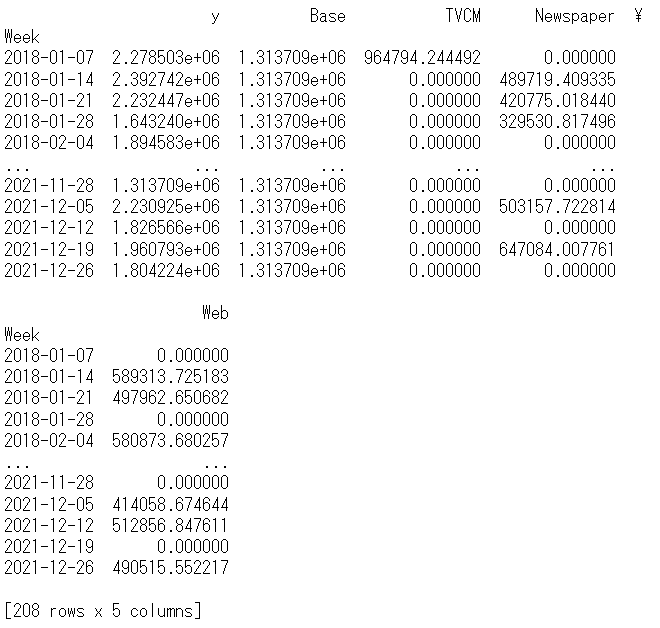
print(pred) #確認

 

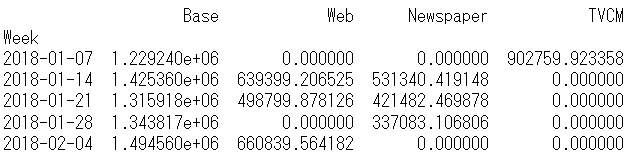
以下、実行結果です。y = Base + TVCM + Newspaper + Webです。

 

貢献度とマーケティングROIの算定

　貢献度の算定

以下、コードです。

#
# 貢献度の算定
#

# 予測値の補正
correction_factor = y.div(pred['y'], axis=0)   #補正係数
pred_adj = pred.mul(correction_factor, axis=0) #補正後の予測値

# 各媒体の貢献度だけ抽出
contribution = pred_adj[['Base', 'Web', 'Newspaper', 'TVCM']]

print(contribution.head()) #確認

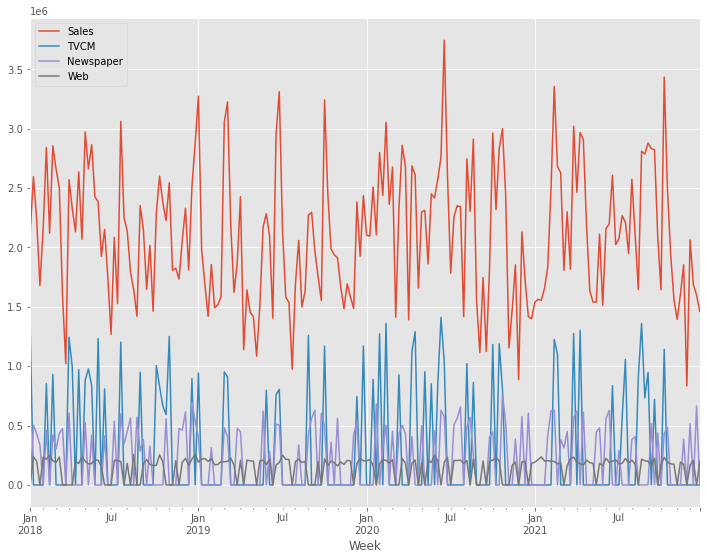
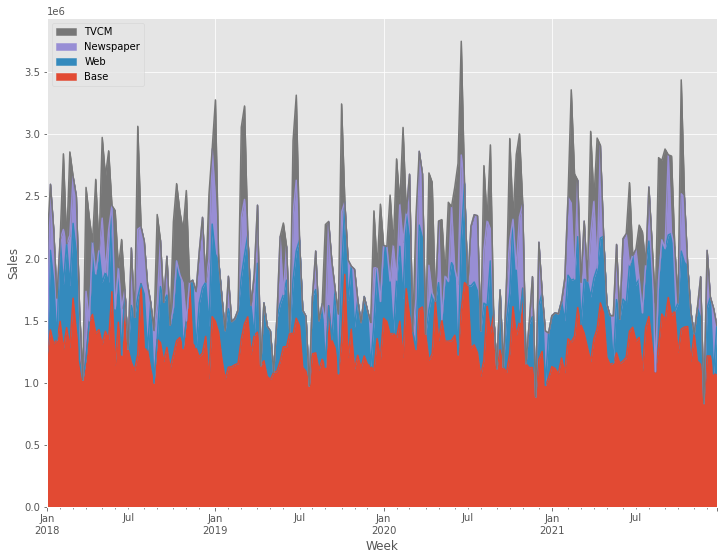
# グラフ化
ax = (contribution
      .plot.area(
          ylabel='Sales',
          xlabel='Week')
     )
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[::-1], labels[::-1])

 

以下、実行結果です。

 

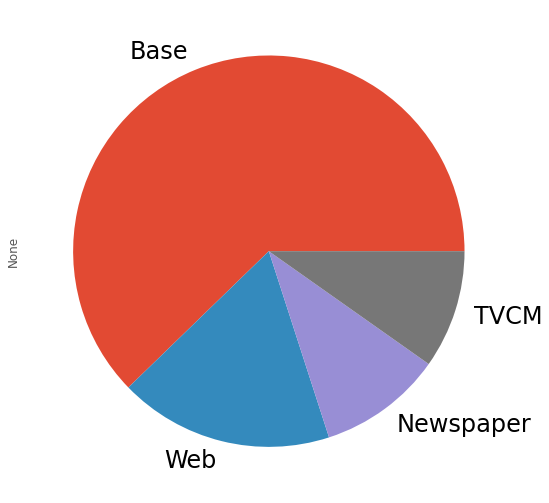
貢献度の構成比の算出します。

以下、コードです。

#
# 貢献度の構成比の算出
#

# 媒体別の貢献度の合計
contribution_sum = contribution.sum(axis=0)

# 集計結果の出力
print('売上貢献度（円）:\n', 
      contribution_sum, 
      sep=''
     )
print()
print('売上貢献度（構成比）:\n', 
      contribution_sum/contribution_sum.sum(), 
      sep=''
     )

# グラフ化
contribution_sum.plot.pie(fontsize=24)

 

以下、実行結果です。

 

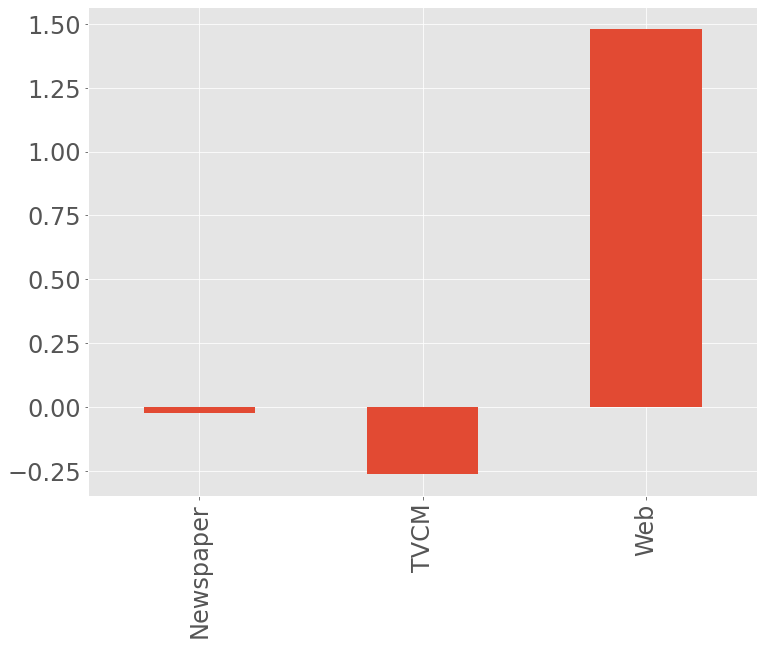
マーケティングROIの算定

以下、コードです。

#
# マーケティングROIの算定
#

# 各媒体のコストの合計
cost_sum = X.sum(axis=0)

# 各媒体のROIの計算
ROI = (contribution_sum.drop('Base', axis=0) - cost_sum)/cost_sum

print('ROI:\n', ROI, sep='') #確認

# グラフ化
ROI.plot.bar(fontsize=24)

 

以下、実行結果です。

 

まとめ

今回は、AdStockを考慮しないRidge回帰によるモデル構築についてお話ししました。

  • AdStock非考慮　→　今回
  • シンプルなAdStock考慮　→　次回
  • 色々なAdStock考慮

次回は、シンプルなAdStockを考慮したRidge回帰によるモデル構築についてお話しします。

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その6Ridge回帰モデルでMMM②（シンプルなAdStock考慮）