Pythonによるマーケティングミックスモデリング
（MMM：Marketing Mix Modeling）超入門 その8

主成分回帰モデル（PCR）でMMM①（AdStock非考慮）

2656
Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その8主成分回帰モデル（PCR）でMMM①（AdStock非考慮）

本当に売上に貢献している広告は、どの広告か？

売上と広告媒体等との関係性をモデリングし、どの広告媒体が売上にどれほど貢献していたのか分析することができます。

それが、マーケティングミックスモデリング（MMM：Marketing Mix Modeling）です。

ただ、多くの広告・販促は似たような時期に集中し実施することが多く、結果的にマルチコという線形回帰モデルを構築しうる上で非常に良くない現象が起こる危険があります。

Ridge回帰や主成分回帰（PCR）、PLS回帰などいつくか方法があります。

前回まで3回（その5～7）は、Ridge回帰の方法についてお話ししました。

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その5Ridge回帰モデルでMMM①（AdStock非考慮）

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その6Ridge回帰モデルでMMM②（シンプルなAdStock考慮）

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その7Ridge回帰モデルでMMM③（色々なAdStock考慮）

今回からは3回に分けて、主成分回帰（PCR）でモデルを構築する方法についてお話しします。

  • ① AdStock非考慮　→　今回
  • ② シンプルなAdStock考慮
  • ③ 色々なAdStock考慮

今回は、色々なAdStockを考慮した主成分回帰（PCR）によるモデル構築についてお話しします。

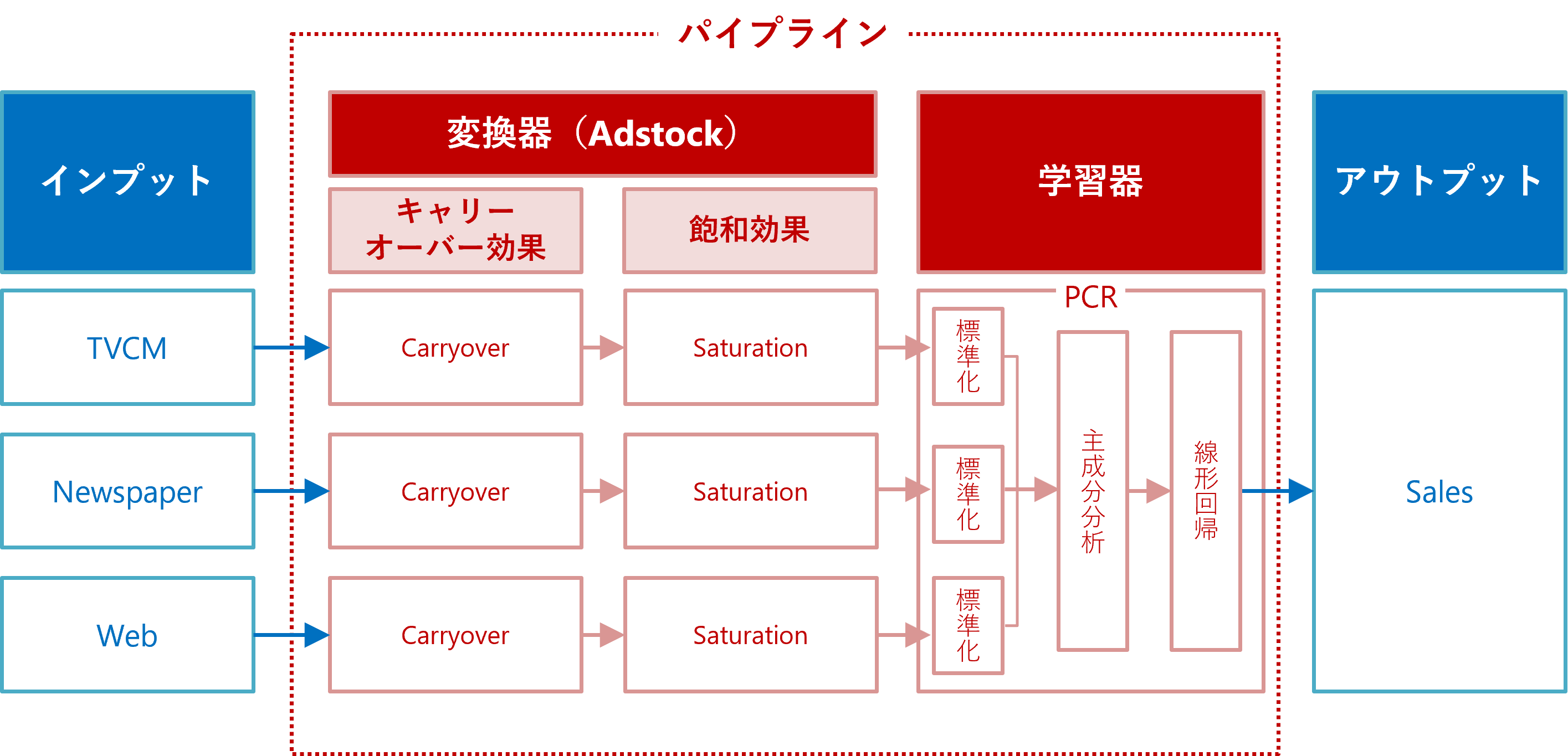
ちなみに、アドストック（Ad Stock）を考慮するとは、飽和効果（収穫逓減）とキャリーオーバー（Carryover）効果を考慮するということです。具体的には、Pythonのscikit-learn（sklearn）のパイプラインを、以下のように構築しました。

 

主成分回帰（PCR）とは？

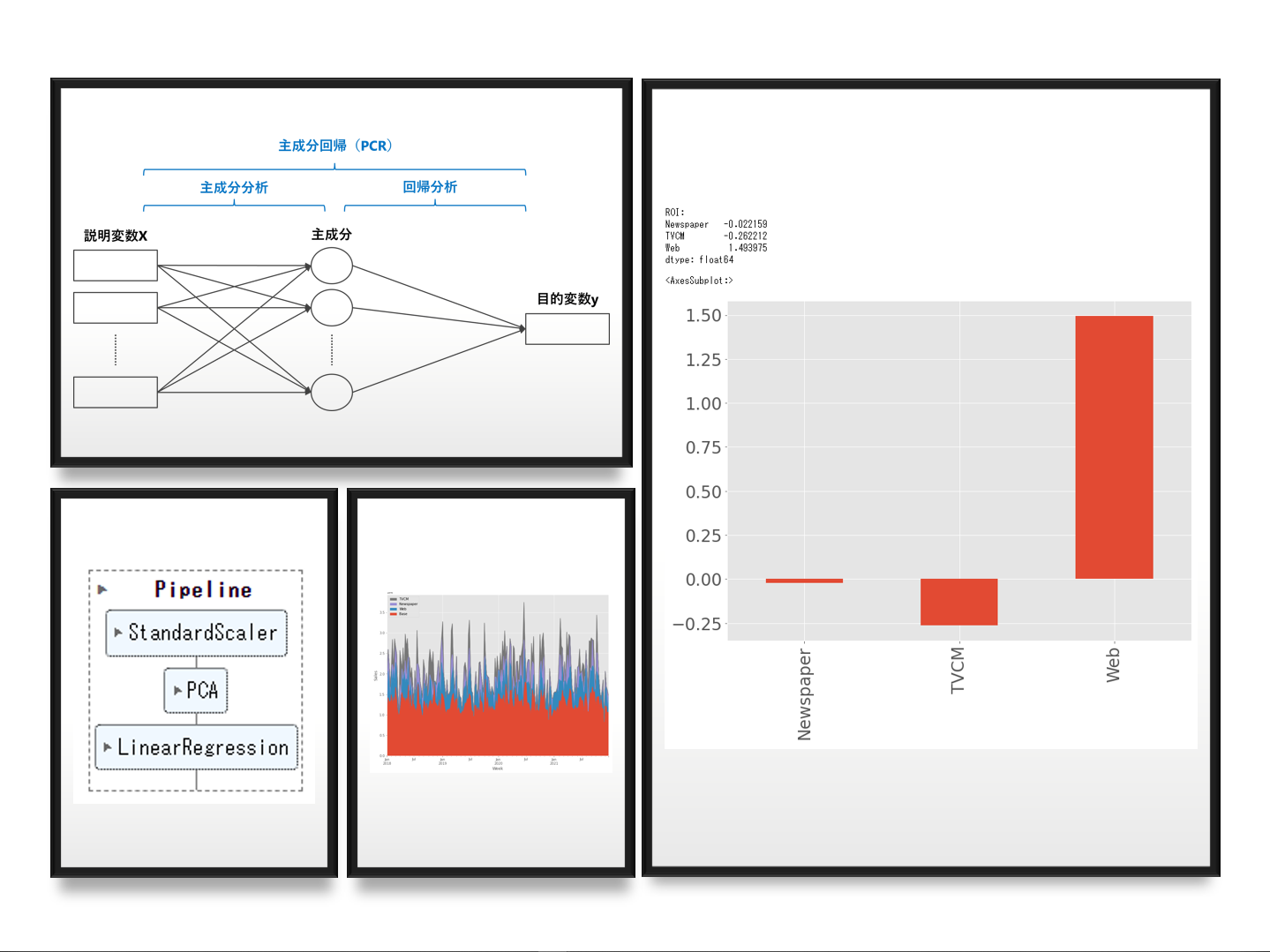
主成分回帰（PCR）とは、元の説明変数Xに対し主成分分析を実施し主成分得点（変換後のデータ）を求め、その主成分得点を使い線形回帰モデルを構築する手法です。要は、主成分分析×線形回帰という2つの数理モデルの組み合わせたものです。

 

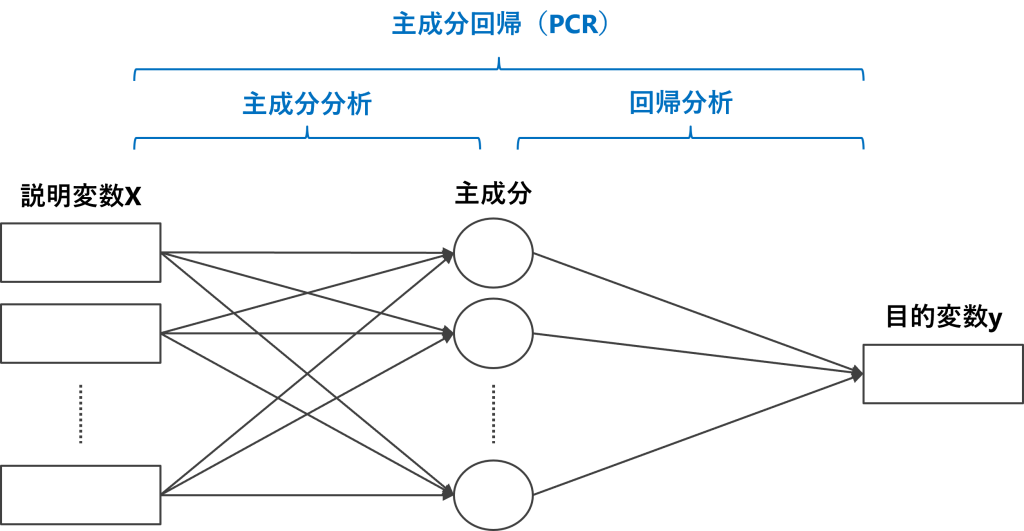
なぜ主成分分析を挟むかというと、いくつかの理由があります。

例えば……

  • データセットの次元を削減する
  • 主成分同士の相関が小さい

……などです。

主成分分析を実施することで、元の説明変数Xを主成分に変換します。主成分の変数の数は、説明変数Xの変数の数より少なくて済みます。それが次元削減です。例えば、100変数が10変数で十分、みたいなことになります。

この主成分分析によって生み出された主成分は、お互いの相関は非常に小さなものとなり、マルチコという現象が起こりにくくなります。

 

利用するデータセット（前回と同じ）

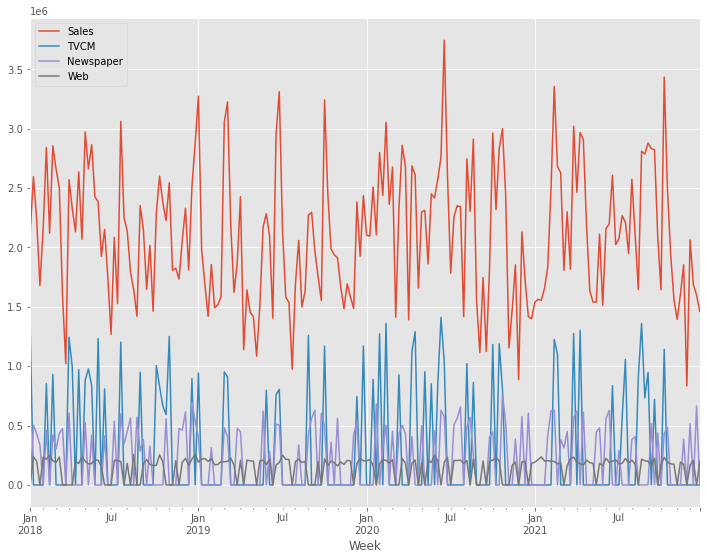
今回利用するデータセットの変数です。

  • Week：週
  • Sales：売上
  • TVCM：TV CMのコスト
  • Newspaper：新聞の折り込みチラシのコスト
  • Web：Web広告のコスト

以下からダウンロードできます。

MMM.csv
https://www.salesanalytics.co.jp/4zdt

 

線形回帰モデルと構築していたときの大きな違い

線形回帰モデルのケースとの大きな違いは、当然ですが主成分回帰（PCR）で構築するというところです。

主成分回帰（PCR）には、ハイパーパラメータとして主成分の数というものがあり、モデル構築者が与える必要があります。今回は、ハイパーパラメータチューニング用のライブラリーであるOptunaを利用し、最適な主成分の数を探索し、その値を利用しMMMを構築します。

他は、線形回帰でMMMを構築したときと、ほぼ同じです。コードもほぼ同じです。

 

ライブラリーやデータセットなどの読み込み

先ずは、必要なライブラリーとデータセットを読み込みます。前回までと同じです。

 

　必要なライブラリーの読み込み

必要なライブラリーを読み込みます。

以下、コードです。

import numpy as np
import pandas as pd

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression

from sklearn.pipeline import Pipeline
from sklearn.model_selection import TimeSeriesSplit
from optuna.distributions import IntUniformDistribution
from sklearn import set_config

from optuna.integration import OptunaSearchCV
from optuna.distributions import UniformDistribution

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ

 

　データセット（前回と同じ）の読み込み

前回と同じデータセットを読み込みます。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(url,
                 parse_dates=['Week'],
                 index_col='Week'
                )

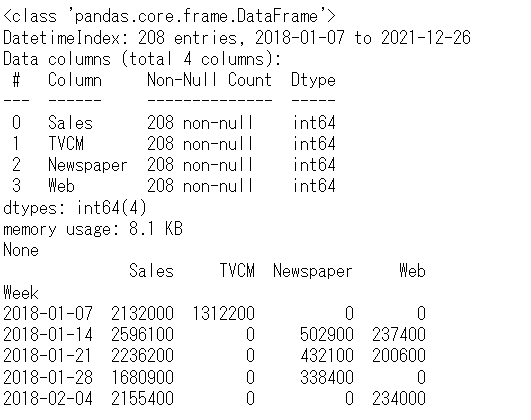
# データ確認
print(df.info()) #変数の情報
print(df.head()) #データの一部

# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']

 

以下、実行結果です。

 

パイプライン化

主成分回帰（PCR）は、元の説明変数Xを標準化し、標準化した値を利用し主成分分析し、主成分得点と目的変数yで線形回帰モデルを構築します。標準化とは、元のデータを平均で引き標準偏差で割ったものです。

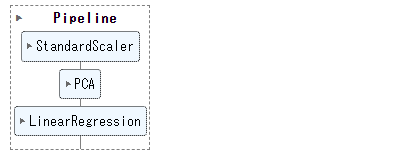
要するに、次のようなパイプラインを構築する必要があります。

  1. 標準化（StandardScaler）
  2. 主成分分析（PCA）
  3. 線形回帰（LinearRegression）

 

以下、コードです。

#
# Pipeline構築
#

# 標準化→主成分分析→線形回帰
MMM = Pipeline([
    ('SS', StandardScaler()),
    ('PCA', PCA()),
    ('regression', LinearRegression())
])

## パイプラインの確認
set_config(display='diagram')   
MMM

 

以下、実行結果です。

 

ハイパーパラメータ探索

主成分回帰（PCR）の最適な主成分の数の値を探索します。

以下、コードです。

#
# ハイパーパラメータ探索
#

# 探索するハイパーパラメータ範囲の設定
params = {
 'PCA__n_components':IntUniformDistribution(1, 3),
}

# ハイパーパラメータ探索の設定
optuna_search = OptunaSearchCV(
    estimator=MMM,
    param_distributions=params,
    n_trials=1000,
    cv=TimeSeriesSplit(),
    random_state=123,
)

# 探索実施
optuna_search.fit(X, y)

# 探索結果
optuna_search.best_params_

 

以下、実行結果です。最適な主成分の数です。

 

この値を主成分の数に設定し、MMMを全データで構築します。

 

モデルの構築と予測

　最適ハイパーパラメータで学習

以下、コードです。

#
# 最適ハイパーパラメータで学習
#

# パイプラインのインスタンス
MMM_best = MMM.set_params(**optuna_search.best_params_)

# 全データで学習
MMM_best.fit(X, y)

# R2（決定係数）
MMM_best.score(X, y)

 

以下、実行結果です。R2（決定係数）の値です。

 

　予測の実施

以下、コードです。

#
# 予測の実施
# 

# 目的変数y（売上）の予測
pred = pd.DataFrame(MMM_best.predict(X),
                    index=X.index,
                    columns=['y'])

# 各媒体による売上の予測

## 値がすべて0の説明変数
X_ = X.copy()
X_.iloc[:,:]=0

## Base
pred['Base'] = MMM_best.predict(X_)

## 媒体
for i in range(len(X.columns)):
    X_.iloc[:,:]=0
    X_.iloc[:,i]=X.iloc[:,i]
    pred[X.columns[i]] = MMM_best.predict(X_) - pred['Base']
    
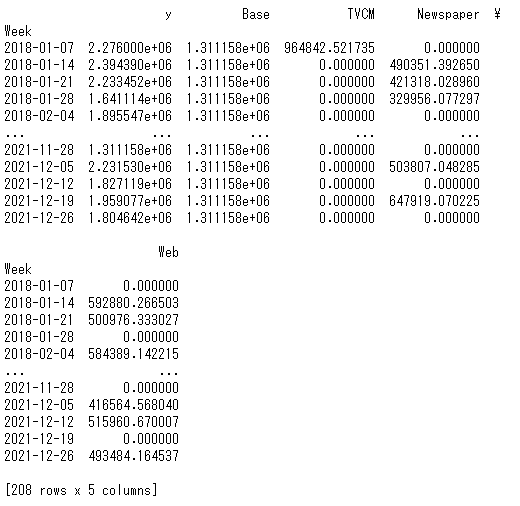
print(pred) #確認

 

以下、実行結果です。y = Base + TVCM + Newspaper + Webです。

 

貢献度とマーケティングROIの算定

　貢献度の算定

以下、コードです。

#
# 貢献度の算定
#

# 予測値の補正
correction_factor = y.div(pred['y'], axis=0)   #補正係数
pred_adj = pred.mul(correction_factor, axis=0) #補正後の予測値

# 各媒体の貢献度だけ抽出
contribution = pred_adj[['Base', 'Web', 'Newspaper', 'TVCM']]

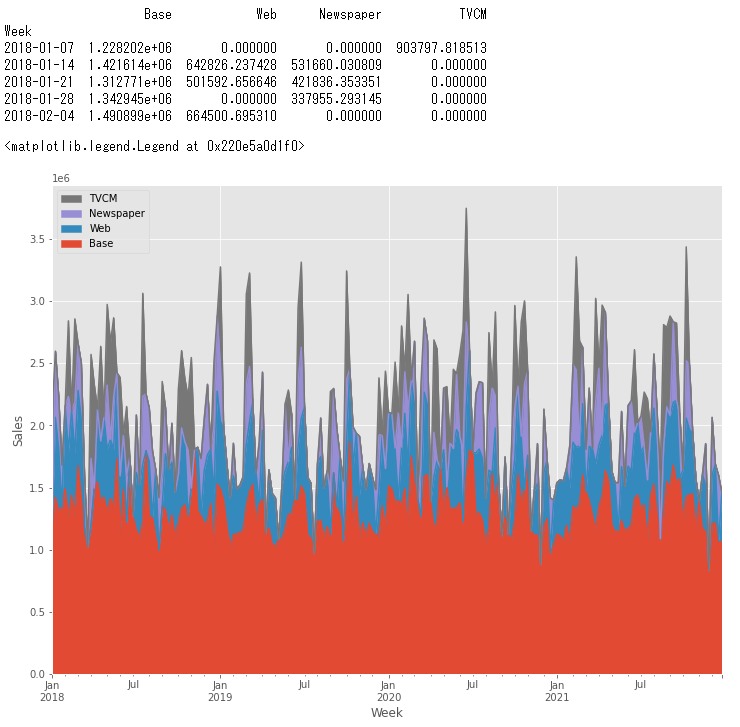
print(contribution.head()) #確認

# グラフ化
ax = (contribution
      .plot.area(
          ylabel='Sales',
          xlabel='Week')
     )
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[::-1], labels[::-1])

 

以下、実行結果です。

 

貢献度の構成比の算出します。

以下、コードです。

#
# 貢献度の構成比の算出
#

# 媒体別の貢献度の合計
contribution_sum = contribution.sum(axis=0)

# 集計結果の出力
print('売上貢献度（円）:\n', 
      contribution_sum, 
      sep=''
     )
print()
print('売上貢献度（構成比）:\n', 
      contribution_sum/contribution_sum.sum(), 
      sep=''
     )

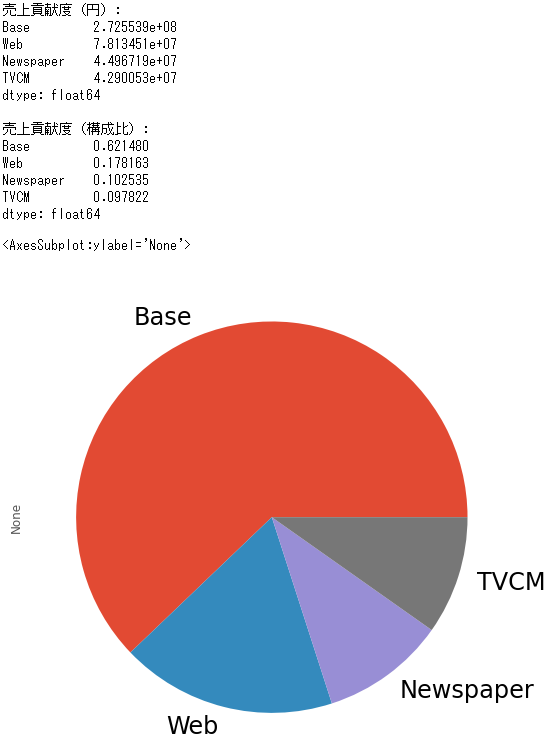
# グラフ化
contribution_sum.plot.pie(fontsize=24)

 

以下、実行結果です。

 

　マーケティングROIの算定

以下、コードです。

#
# マーケティングROIの算定
#

# 各媒体のコストの合計
cost_sum = X.sum(axis=0)

# 各媒体のROIの計算
ROI = (contribution_sum.drop('Base', axis=0) - cost_sum)/cost_sum

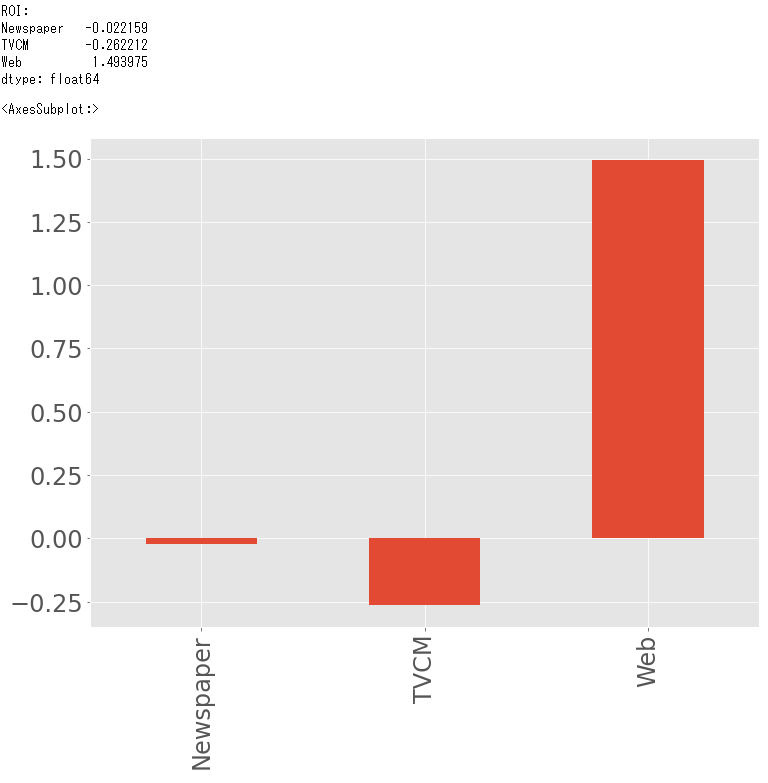
print('ROI:\n', ROI, sep='') #確認

# グラフ化
ROI.plot.bar(fontsize=24)

 

以下、実行結果です。

 

まとめ

今回は、AdStockを考慮しない主成分回帰（PCR）によるモデル構築についてお話ししました。

  • AdStock非考慮　→　今回
  • シンプルなAdStock考慮　→　次回
  • 色々なAdStock考慮

次回は、シンプルなAdStockを考慮した主成分回帰（PCR）によるモデル構築についてお話しします。

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その9主成分回帰モデル（PCR）でMMM②（シンプルなAdStock考慮）

初めての方へ
メルマガ
サービス
お問合せ