VAR（ベクトル自己回帰）モデルで描く時系列グラフィカルモデリング（Python版）

14193
VAR（ベクトル自己回帰）モデルで描く時系列グラフィカルモデリング（Python版）

グラフィカルモデリングとは、多変量データ（変数が複数あるデータセット）の変数間の構造を表す統計モデルをグラフによって表現したもので、小難しくいうと、確率変数間の依存関係をグラフ表現したものです。

変数間の関係を無向グラフや有向グラフなどで表現することで、視覚的に変数間の関係を把握することができます。

多変量時系列データに対するグラフィカルモデリングの1手法として、グレンジャー因果性に基づく方法があります。

グレンジャー因果性とは、ある時系列データAの過去の値が別の時系列データBの将来の値を予測する能力を有するというもので、予測的因果関係とも言われています。

先行指標の概念を持ち出せば、「Aの値の変化の後にBの値が変化している」というもので「Aは、Bの先行指標（先行系列）である」という感じです。

多変量時系列データに対するグラフィカルモデリングを作るとき、相互相関を利用するのが一番簡単です。

前回、「相互相関で描く時系列グラフィカルモデリング」というお話しをしました。

相互相関で描く時系列グラフィカルモデリング（Python版）

グレンジャー因果性と密接な関係にあるのがVAR（ベクトル自己回帰）モデルです。

今回は、もう1歩話しを進め、「VARモデルで描く時系列グラフィカルモデリング」というお話しをします。

VARモデルは、同時点における変数間の関係性は考慮されていません。同時点の関係性の検討に、通常の線形回帰モデルを活用します。

VAR（ベクトル自己回帰）モデル

多変量時系列データY_tに対し、自己回帰の次数がpのVARモデルは次のように表現されます。変数の数をKとします。

\displaystyle Y_t=ν+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t
  • ν：K次元の定数ベクトル
  • Y_{t-i}：目的変数ベクトルのラグi
  • A_i：ラグiのK \times K係数行列
  • U_t ：ホワイトノイズ

通常の1変量の時系列データのARモデルとの大きな違いは、過去の自分だけでなく、他の時系列データの過去も考慮されているところにあります。

欠点としては、同時点における変数間の関係性は考慮されていない、というところにあります。そのため、同時期の他の変数の影響を受けていたとしても、それは考慮されずモデル化されます。

解決策としては、例えば次の2つの方法があります。

  • VAR-LiNGAMを含めたSVAR（構造VAR）モデルを活用する
  • 同時点に関しては通常の線形回帰モデルを活用する

 

SVARモデルとは、次のようなモデルです。

\displaystyle Y_t=ν+A_0 Y_{t}+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

単に、A_0 Y_{t}が追加されただけです。行列A_0の対角成分は0です。

もしくは、次にようにも表現できます。

\displaystyle A_0  Y_t=ν+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

この場合には、行列A_0の対角成分は1です。

A_0の逆行列を求め、両辺に掛けると次のようになり、通常のVARモデルの式のような感じになります。

\displaystyle Y_t=A_0^{-1}ν+ A_0^{-1}A_1 Y_{t−1}+\dots+A_0^{-1}A_p Y_{t−p}+A_0^{-1}U_t

VAR-LiNGAMを含めたSVAR（構造VAR）モデルに関しては次回お話しします。

 

今回は、同時点に関しては通常の線形回帰モデルで検討します。

予測的因果関係という観点から考え、説明変数として追加することで目的変数の予測精度が上がるようであれば、その同時期の変数を説明変数として採用し、グレンジャー因果性がありそうだと考えるということです。

 

VARモデルとグレンジャー因果検定

VARモデルで多変量の時系列データをモデル化することで、グレンジャー因果性を検討することができます。

グレンジャー因果性があるかどうかは、そのための統計的仮説検定がありますので、それを活用してもいいでしょう。

  • 帰無仮説：グレンジャー因果性がない
  • 対立仮説：グレンジャー因果性がある

ただ、「見せかけの回帰」が生じるような場合、このグレンジャー因果性の検討ができません。

このあたりのお話しも含め、簡単に以下の記事で説明しています。興味のある方はご一読ください。

（Python版）VARモデルによるグレンジャー因果性とインパルス応答

 

簡単にいうと、時系列の変数Xと変数Yが単位根過程、つまり非定常な時系列データである場合、このグレンジャー因果性の検定は利用できません。

VARモデルでモデル化する前に、個々の時系列データが単位過程かどうかの検定（単位根検定）を実施し、定常と見なせるかどうか検討する必要があります。

非定常の場合には、定常になるような処置を施します。よくあるのは、その時系列データの差分（当期と前期の差）を計算し差分系列を作り、その差分系列を新たな時系列データとして利用する、という方法です。

 

必要なモジュールとデータの読み込み

では、必要なモジュールを読み込みます。

以下、コードです。

import pandas as pd
import numpy as np
from scipy import stats

import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.vector_ar.var_model import VAR

from graphviz import Digraph

from matplotlib import mlab
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

グラフは、前回同様graphvizライブラリーのモジュールで描きます。

statsmodelsライブラリーで、単位根検定やVARモデルの構築、グレンジャー因果性の検定などを実施します。

 

次に、今回利用するデータを読み込みます。前回と同じです。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/0olr'
df = pd.read_csv(url,
                 parse_dates=True,
                 index_col='day'
                )
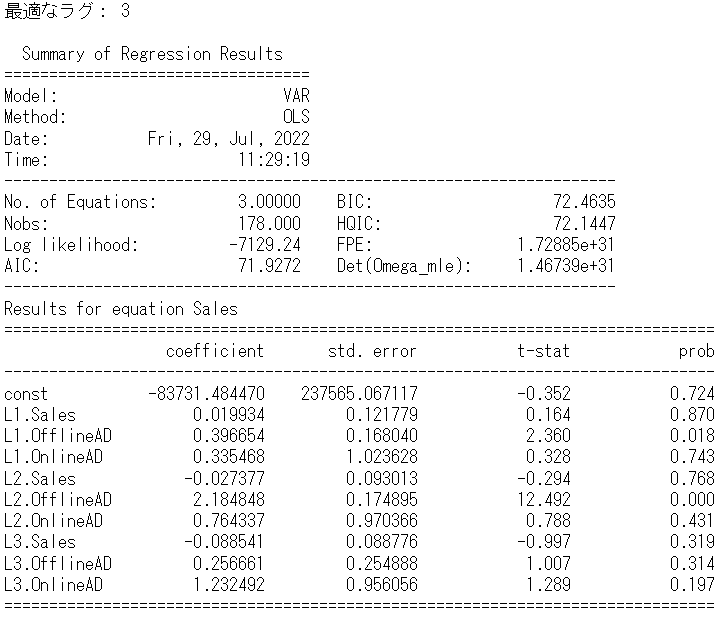
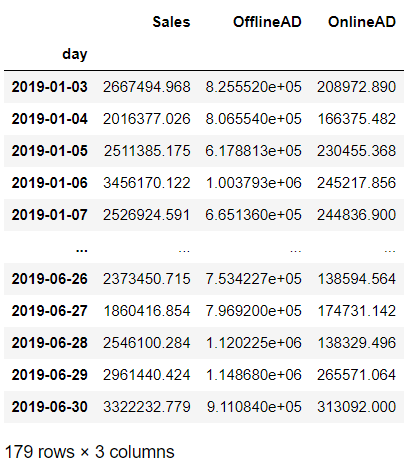
df #確認

 

以下、実行結果です。

 

日単位の3変量の時系列データです。

  • Sales：売上
  • OfflineAD：TVCMなどのオフライン広告のコスト
  • OnlineAD：Webなどのオンライン広告のコスト

 

目的変数が「Sales」で、残りの2つが説明変数です。

 

ADF単位根検定

3つの時系列データに対し、単位根検定をします。

今回は、以下の対立仮説のADF単位根検定（Augmented Dickey-Fuller 単位根検定）を実施します。

  • 帰無仮説：単位根がある（非定常）
  • 対立仮説：定数項＋定常過程

p値が0.05未満のとき帰無仮説が棄却されたと考え対立仮説を採択したいと思います。

 

ADF単位根検定を実施します。繰り返し文（for文）で順番に、各変数のp値を出力しています。

以下、コードです。

#
# Augmented Dickey-Fuller 単位根検定
#  帰無仮説：単位根がある
#  対立仮説：定数項＋定常過程
#

for i in range(len(df.columns)):
    #Augmented Dickey-Fuller 単位根検定
    c_results = adfuller(df.iloc[:,i],regression='c')  
    #p値出力
    print(df.columns[i],'\t',c_results[1])

 

以下、実行結果です。

 

いずれのp値も0.05未満のため、対立仮説を採択します。要は、定常な時系列と見なすということです。

 

グレンジャー因果を検定し有向グラフを作る

VARモデルを構築し、グレンジャー因果性を検討します。

 

　VARモデル構築

先ず、VARモデルを構築します。

以下、コードです。

# 最大のラグ数
maxlags = 10

# モデルのインスタンス生成
var_model = VAR(df)

# 最適なラグの探索
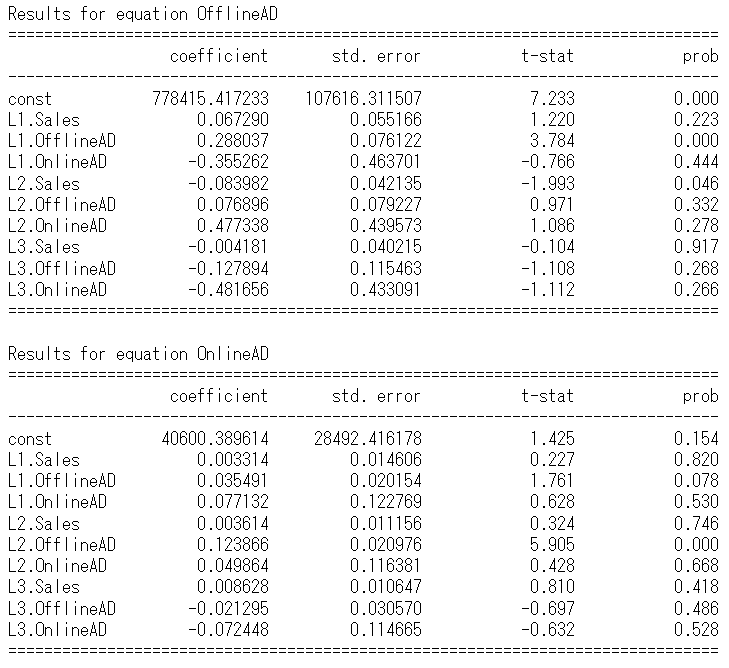
lag = var_model.select_order(maxlags).selected_orders
print('最適なラグ：',lag['aic'],'\n')

# モデルの学習
results = var_model.fit(lag['aic'])

print(results.summary())

 

以下、実行結果です。

 

　グレンジャー因果検定

次に、グレンジャー因果性を統計的仮説検定で検討していきます。

  • 帰無仮説：グレンジャー因果性がない
  • 対立仮説：グレンジャー因果性がある

p値が0.05未満のとき帰無仮説が棄却されたと考え対立仮説を採択します。

 

「Sales → OfflineAD 」のグレンジャー因果性の検定を実施します。

以下、コードです。p値を出力します。

# Sales -> OfflineAD の因果を検定
test_results = results.test_causality(causing=0, caused=1)  
test_results.pvalue #p値

 

以下、実行結果です。

 

ｐ値が、0,05未満ではないので、対立仮説は採択せず、グレンジャー因果性があるとはいえない、という結論になります。

もし、グレンジャー因果性があれば、graphvizの有向グラフの線を引きます。

 

　検定結果をもとに有向グラフを描く

すべての変数の組み合わせに対し、グレンジャー因果性の検定を実施しながら、グレンジャー因果性があるとなった場合に有向グラフの線を引く、という作業をする必要があります。

繰り返し文（for文）を使い、すべての変数の組み合わせに対しグレンジャー因果性の検定を実施しながら有向グラフの線を引く、という操作を実施したいと思います。

以下、コードです。p値と有向グラフを出力します。

#
# グレンジャー因果の検定と有向グラフの描写
#

# 有向グラフのインスタンスの生成
graph = Digraph()

# グラフにノードを追加
for i in range(len(df.columns)):
    graph.node(df.columns[i])

# 因果を検定し有意なとき線を引く
for i in range(len(df.columns)):
    for j in range(len(df.columns)):
        if i != j :
            #因果の検定
            test_results = results.test_causality(causing=i, caused=j) 
            #p値
            test_results.pvalue
            #検定結果の出力
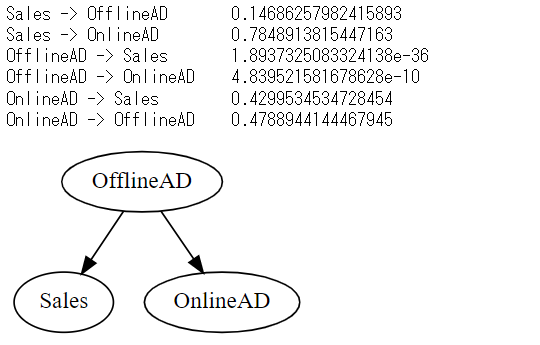
            print(df.columns[i],'->',df.columns[j],'\t',test_results.pvalue)
            #p値が0.05未満のとき線を追加
            if test_results.pvalue < 0.05:
                graph.edge(df.columns[i], df.columns[j])
            
# 有向グラフを表示
graph

 

以下、実行結果です。

 

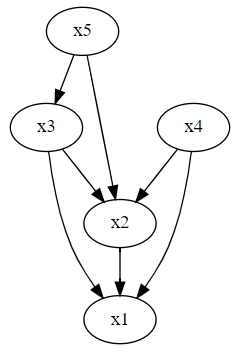
同時期が考慮されていないので、想定される有向グラフとちょっと違います。

同胎される有向グラフとは、次のようなグラフです。

 

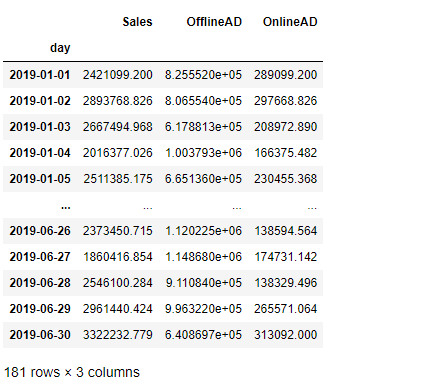
　インパルス応答

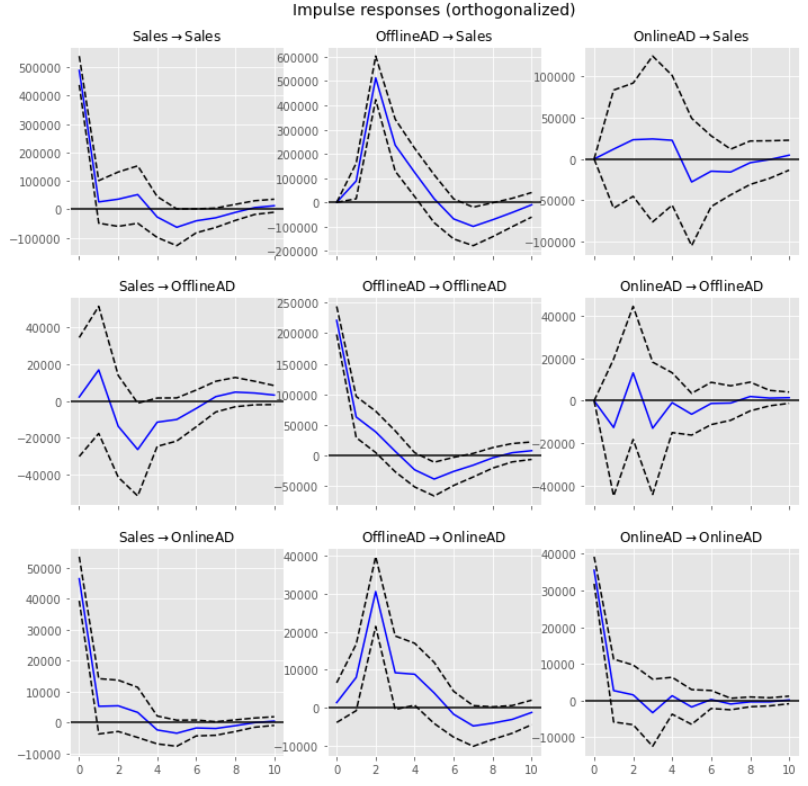
念のため、「ある時系列の変数Xに変動があったとき、他の時系列の変数Yにどう伝わっていくかをモデリング」した「直交化インパルス応答関数」を求めグラフ化し確認したいと思います。

以下、コードです。

# (直行化)インパルス応答関数
irf = results.irf()
irf.plot(orth=True)
plt.show()

 

以下、実行結果です。

 

見てわかる通り、変数間の同時点の影響が考慮されていません。次回のSVARモデルでインパルス応答関数を求め見てみると、同時点の影響が考慮されていることがわかります。

 

同時点は線形回帰モデルで検討

予測的因果関係という観点から考え、説明変数として追加することで目的変数の予測精度が上がるようであれば、その同時期の変数を説明変数として採用し、グレンジャー因果性がありそうだと考えます。

線形回帰モデル構築用のテーブルデータを、次の3変数で作ります。

  • Sales
  • OfflineADのラグ2
  • OnlineAD

以下。コードです。

df_AD = pd.concat([df['Sales'],
                   df['OfflineAD'].shift(2),
                   df['OnlineAD']
                  ],
                  axis=1).dropna()

 

以下、実行結果です。

 

次の2つの線形モデルを構築します

  • 説明変数パターン1：OfflineADのラグ2
  • 説明変数パターン2：OfflineADのラグ2、OnlineAD、OnlineAD×OfflineADのラグ2

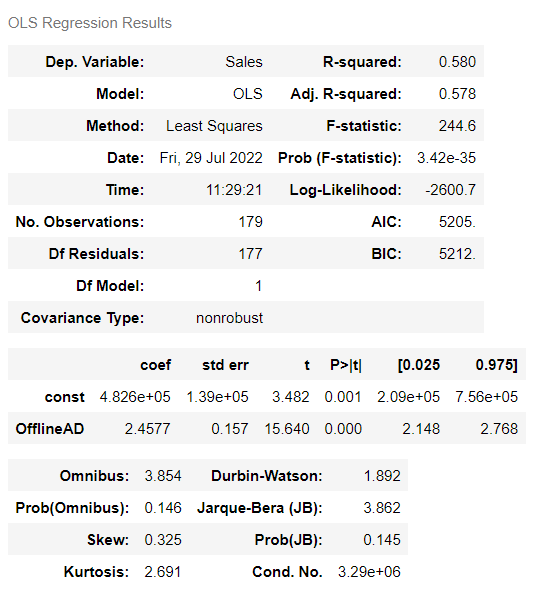
説明変数パターン1に比べ、説明変数パターン2が予測精度が非常に良ければ、OKという感じです。評価指標はR^2（決定係数）で判断します。R^2は最大1で値が大きい方が良いです。

　説明変数パターン1：OfflineADのラグ2

線形回帰モデル用ようのデータセット作ります。

以下、コードです。

#説明変数
X = df_AD.OfflineAD
X = sm.add_constant(X) #切片項追加

#目的変数
y = df_AD.Sales

X #確認

 

以下、実行結果です。

 

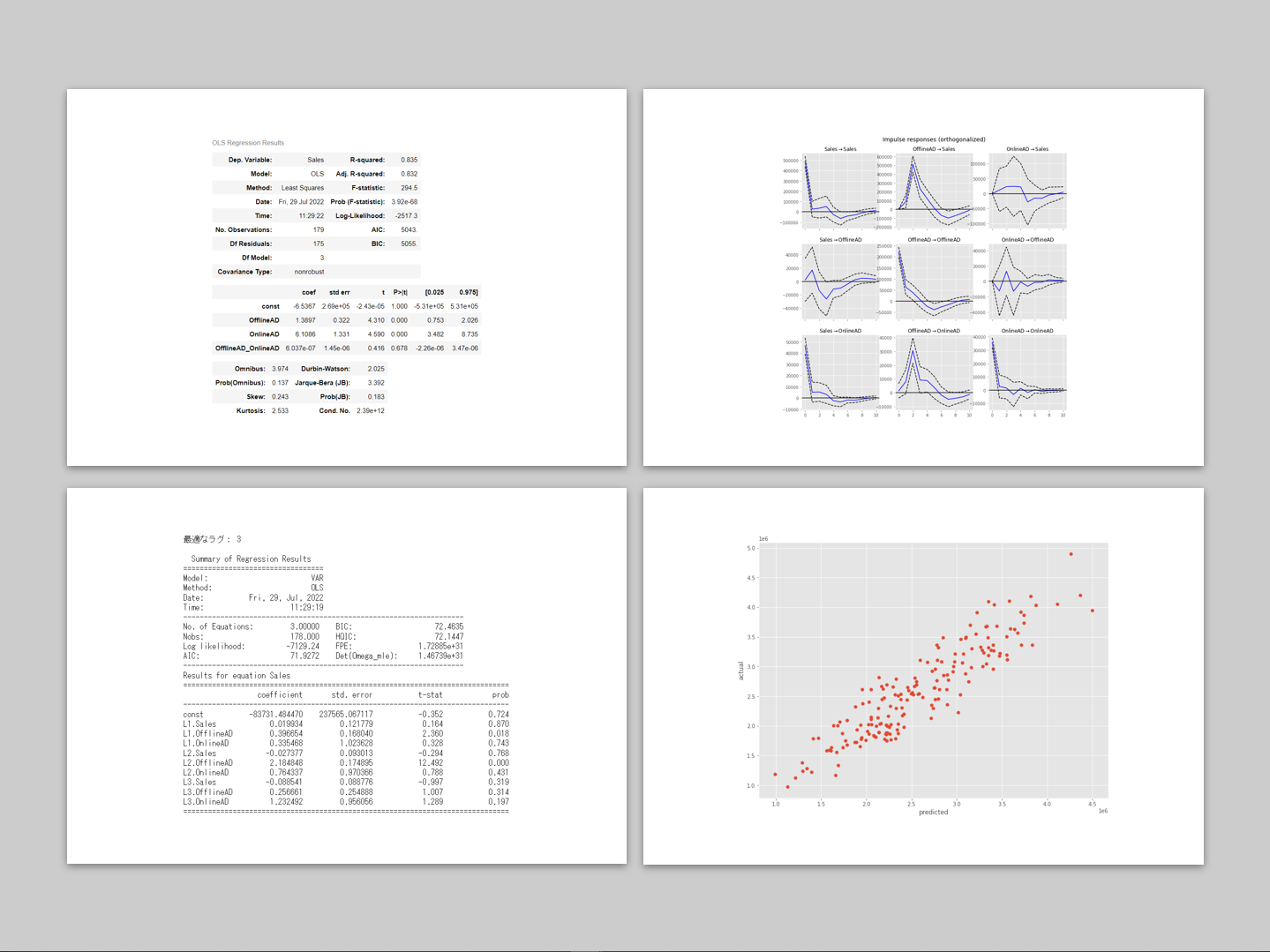
最小二乗法（OLS）で線形回帰モデルを学習します。

以下、コードです。

model = sm.OLS(y, X)
result = model.fit()
result.summary()

 

以下、実行結果です。

 

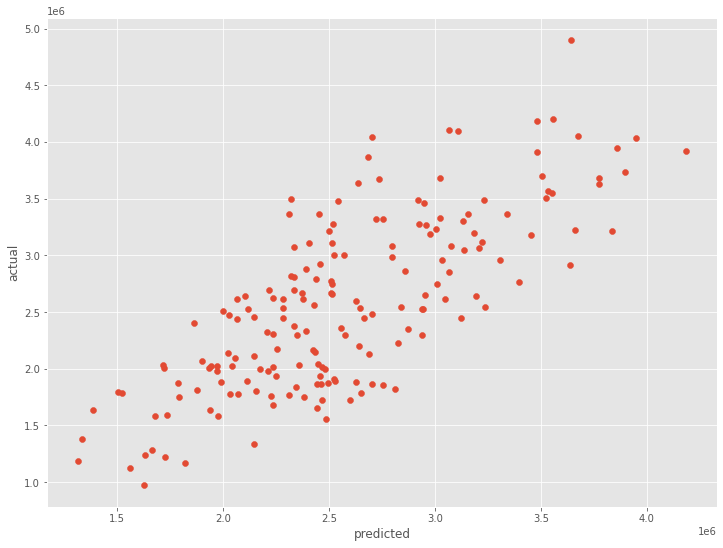
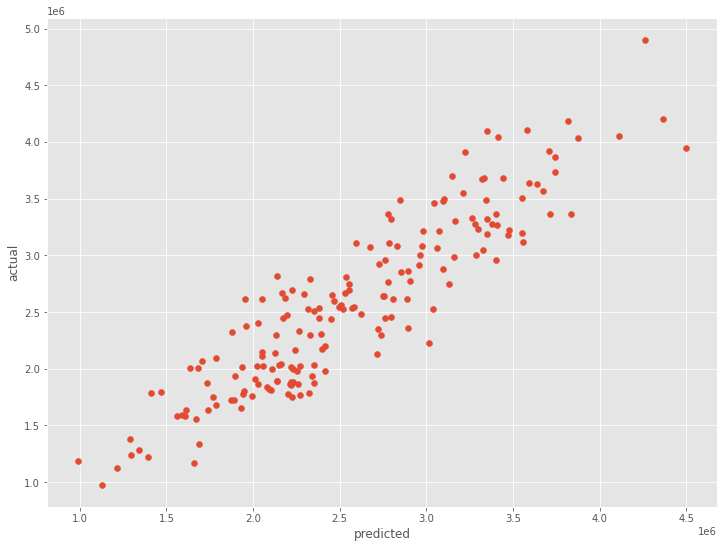
散布図（横軸：予測値、縦軸：実測値）を描き見てみます。

以下、コードです。

# 散布図（横軸：予測値、縦軸：実測値）

plt.scatter(result.fittedvalues,y)
plt.xlabel('predicted')
plt.ylabel('actual')

plt.show()

 

以下、実行結果です。

 

R^2（Adj. R-squared）は、0.578でした。

 

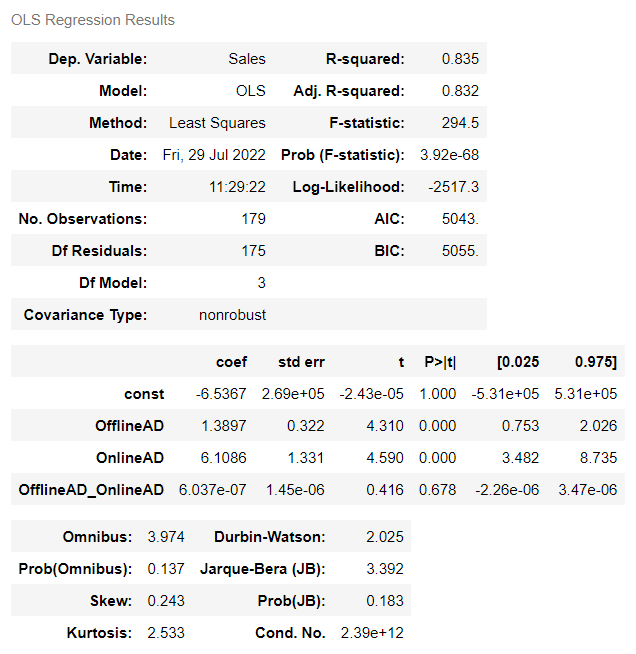
　説明変数パターン2：OfflineADのラグ2、OnlineAD、OnlineAD×OfflineADのラグ2

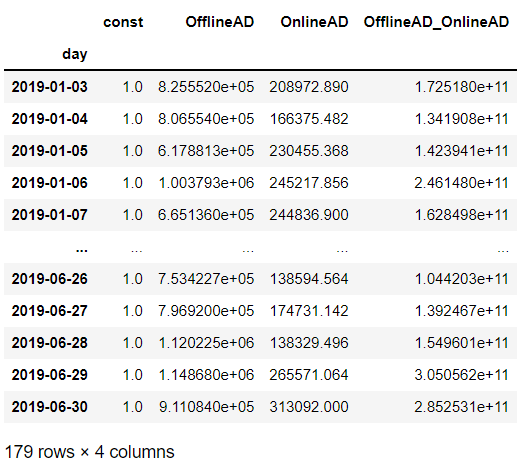
線形回帰モデル用ようのデータセット作ります。

以下、コードです。

#説明変数
X = df_AD.drop('Sales',axis=1)
X['OfflineAD_OnlineAD']=X.OfflineAD*X.OnlineAD
X = sm.add_constant(X) #切片項追加

#目的変数
y = df_AD.Sales

X #確認

 

以下、実行結果です。

 

最小二乗法（OLS）で線形回帰モデルを学習します。

以下、コードです。

model = sm.OLS(y,X)
result = model.fit()
result.summary()

 

以下、実行結果です。

＊散布図（横軸：予測値、縦軸：実測値）を描き見てみます。

以下、コードです。

# 散布図（横軸：予測値、縦軸：実測値）

plt.scatter(result.fittedvalues,y)
plt.xlabel('predicted')
plt.ylabel('actual')

plt.show()

 

以下、実行結果です。

 

R^2（Adj. R-squared）は、0.578から0.832へと大きく向上しました。

予測的因果関係という観点で考えると、同時点ではあるもののOnlineAD→Salesと考えられます。

 

有向グラフ

VARモデルと線形回帰モデルから、次のことが読み取れました。

  • OfflineAD→Sales
  • OnlineAD→Sales
  • OfflineAD→OnlineAD

 

この関係性を、有向グラフで描いて見ます。

以下、コードです。

#
# 有向グラフ（先行変数＋一致変数）
#

graph = Digraph()

# ノードを追加
for i in range(len(df.columns)):
    graph.node(df.columns[i])

# 辺を追加
graph.edge(df.columns[1], df.columns[0]) #OfflineAD -> Sales
graph.edge(df.columns[1], df.columns[2]) #OfflineAD -> OnlineAD
graph.edge(df.columns[2], df.columns[0]) #OnlineAD -> Sales

# 画像を表示
graph

 

以下、実行結果です。

 

まとめ

今回は、「VARモデルで描く時系列グラフィカルモデリング」というお話しをしました。

VARモデルは、同時点における変数間の関係性は考慮されていません。

解決策としては、例えば次の2つの方法があります。

  • VAR-LiNGAMを含めたSVAR（構造VAR）モデルを活用する
  • 同時点に関しては通常の線形回帰モデルを活用する

今回は、同時点に関しては通常の線形回帰モデルを活用する方法で実施しました。

もう一方の、VAR-LiNGAMを含めたSVAR（構造VAR）モデルを活用する方法も気になるところでしょう。

次回は、「SVAR（構造VAR）＆VAR-LiNGAMで描く時系列グラフィカルモデリング」というお話しをします。

非ガウスSVAR（VAR-LiNGAM）で描く時系列グラフィカルモデリング（Python版）