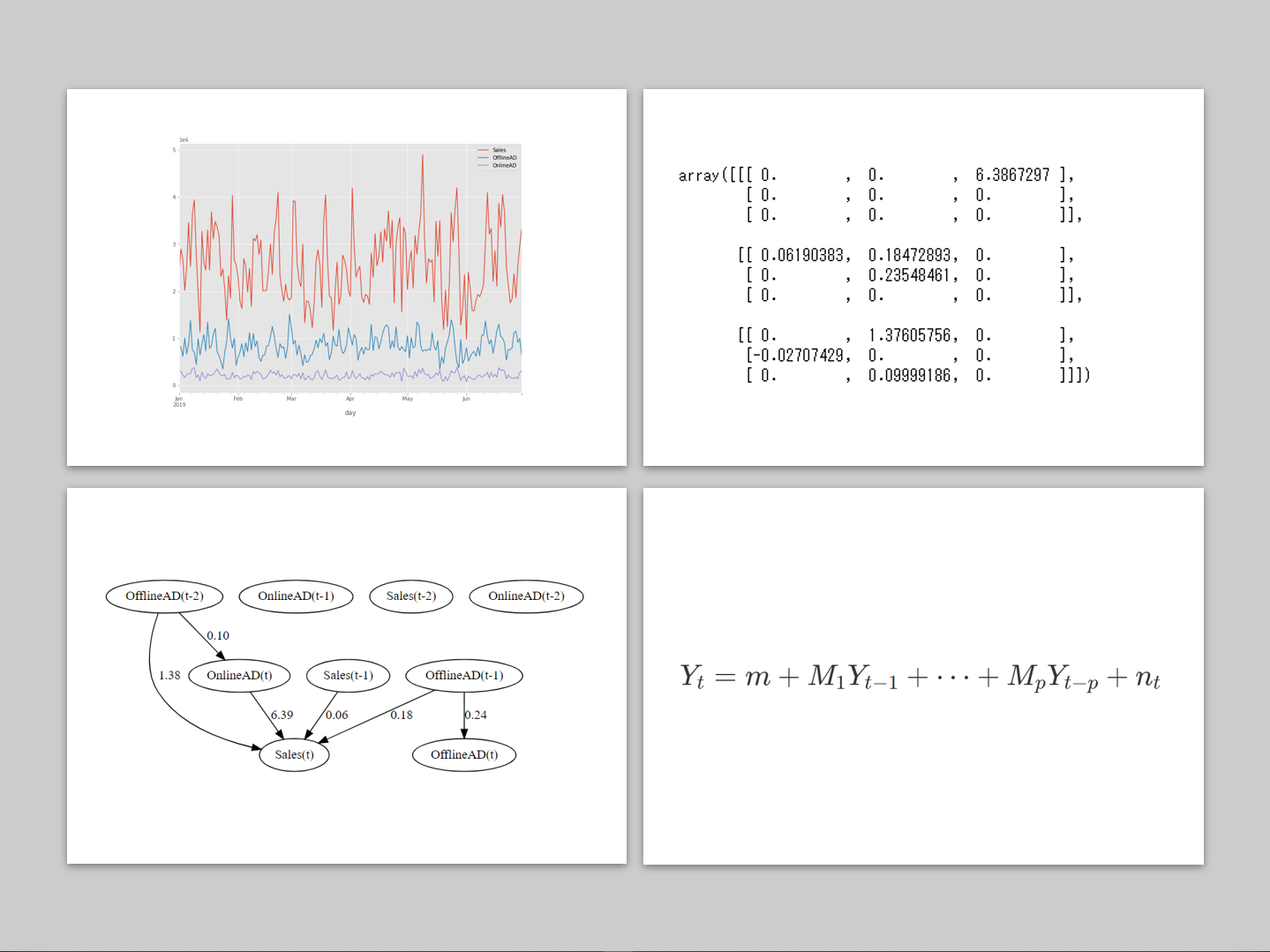
非ガウスSVAR（VAR-LiNGAM）で描く時系列グラフィカルモデリング（Python版）

グラフィカルモデリングとは、多変量データ（変数が複数あるデータセット）の変数間の構造を表す統計モデルをグラフによって表現したもので、小難しくいうと、確率変数間の依存関係をグラフ表現したものです。

変数間の関係を無向グラフや有向グラフなどで表現することで、視覚的に変数間の関係を把握することができます。

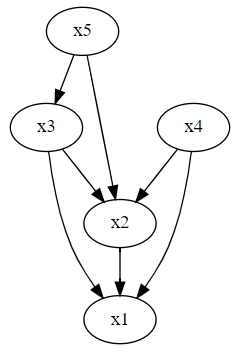
多変量時系列データに対するグラフィカルモデリングの1手法として、グレンジャー因果性に基づく方法があります。

グレンジャー因果性とは、ある時系列データAの過去の値が別の時系列データBの将来の値を予測する能力を有するというもので、予測的因果関係とも言われています。

多変量時系列データに対するグラフィカルモデリングを作るとき、相互相関を利用するのが一番簡単です。

前々回、「相互相関で描く時系列グラフィカルモデリング」というお話しをしました。

グレンジャー因果性と密接な関係にあるのがVAR（ベクトル自己回帰）モデルです。

前回、「VAR（ベクトル自己回帰）モデルで描く時系列グラフィカルモデリング」というお話をしました。

VARモデルは、同時点における変数間の関係性は考慮されていません。

解決策としては、例えば次の2つの方法があります。

VAR-LiNGAMを含めたSVAR（構造VAR）モデルを活用する
同時点に関しては通常の線形回帰モデルを活用する

前回は、同時点に関しては通常の線形回帰モデルを活用する方法で実施しました。

今回は、「非ガウスSVAR（VAR-LiNGAM）と時系列グラフィカルモデリング」というお話しをします。

VAR-LiNGAMとは、LiNGAMにVARモデルを取り入れ、時系列の因果も考慮した因果探索を行うものです。

Contents [hide]

SVAR（構造VAR）モデル
VAR-LiNGAM
　LiNGAMとは？
　非ガウスSVARモデル（VAR-LiNGAM）
　VARモデル → LiNGAM
LiNGAMのインストール
必要なモジュールとデータの読み込み
VAR-LiNGAMの構築
まとめ

SVAR（構造VAR）モデル

多変量時系列データ $Y_t$ に対し、自己回帰の次数が $p$ のSVARモデルは次のように表現されます。変数の数を $K$ とします。

\displaystyle Y_t=ν+A_0 Y_{t}+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

$ν$ ： $K$ 次元の定数ベクトル
$Y_{t-i}$ ：目的変数ベクトルのラグ $i$
$A_i$ ：ラグ $i$ の $K \times K$ 係数行列、 $A_0$ の対角成分は0
$U_t$ ：ホワイトノイズ

U_t

にホワイトノイズを仮定しています。時系列モデルではよくあることです。

ホワイトノイズとは、簡単にいうと次のように、変数間で相互に独立で、時間的にも独立な時系列データです。

平均：0
自己相関： $\sigma$
相互相関：０

この式から分かる通り、ホワイトノイズはガウスノイズ（正規分布を仮定）ではありません。

ガウス分布（正規分布）を仮定したホワイトノイズであるホワイトガウスノイズというものがありますが、ガウス分布（正規分布）の仮定は必須ではありません。

SVARモデルは次のようにも表現できます。

\displaystyle A_0  Y_t=ν+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

この場合には、行列 $A_0$ の対角成分は1です。

A_0

の逆行列を求め、両辺に掛けると次のようになります。

\displaystyle Y_t=A_0^{-1}ν+ A_0^{-1}A_1 Y_{t−1}+\dots+A_0^{-1}A_p Y_{t−p}+A_0^{-1}U_t

ちなみに、通常のVARモデルは次のようになります。

\displaystyle Y_t=ν+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

A_0 Y_{t}

があればSVARモデル、なければVARモデルという感じです。

VAR-LiNGAM

　LiNGAMとは？

LiNGAM（Linear Non-Gaussian Acyclic Model）とは、テーブルデータを対象にした因果探索アルゴリズムの一種です。時系列という観点で考えると、同時点の因果探索に利用できるかもしれない、となります。

多変量データ $X$ に対し、次のような式で表現されます。変数の数を $K$ とします。

\displaystyle X=ν+A X+e

LiNGAM（Linear Non-Gaussian Acyclic Model）の名称の一部に「Non-Gaussian」が付いてあるとおり、非ガウス（正規分布ではない分布）を仮定しています。そのことで、変数間の因果方向（例： $x_i \rightarrow x_j$ ）を識別することが可能になります。

VARモデルがグレンジャー因果性による時間的因果構造（先行と遅行）を探索するのに対し、時間情報のない中で行うLiNGAMは瞬間的因果構造を探索することになります。

　非ガウスSVARモデル（VAR-LiNGAM）

SVARモデルの数式を再度見てみましょう。

\displaystyle Y_t=ν+A_0 Y_{t}+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

$ν$ ： $K$ 次元の定数ベクトル
$Y_{t-i}$ ：目的変数ベクトルのラグ $i$
$A_i$ ：ラグ $i$ の $K \times K$ 係数行列、 $A_0$ の対角成分は0
$U_t$ ：ホワイトノイズ

LiNGAMの条件として非ガウス（正規分布ではない分布）を仮定しています。

そのため、LiNGAM（Linear Non-Gaussian Acyclic Model）は、非ガウスSVARモデルになります。

　VARモデル → LiNGAM

SVARモデルを次のように変形します。

\displaystyle (I - A_0)  Y_t=ν+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

行列 $I$ は単位行列（対角要素が1で、他の要素が0の行列）です。

I - A_0

の逆行列を求め、両辺に掛けると次のようになります。

\displaystyle Y_t=(I - A_0) ^{-1}ν+ (I - A_0) ^{-1}A_1 Y_{t−1}+\dots+(I - A_0) ^{-1}A_p Y_{t−p}+(I - A_0) ^{-1}U_t

ここで、表現をシンプルにするために、次のようにおきます。

$m = (I - A_0) ^{-1}ν$
$M_i = (I - A_0) ^{-1}A_i$
$n_t = (I - A_0) ^{-1}U_t$

そうすると、次のようになります。

\displaystyle Y_t=m+ M_1 Y_{t−1}+\dots+M_p Y_{t−p}+n_t

これは、VARモデルの式です。通常のVARモデルの学習方法で、 $m$ と $M_i$ を推定します。

n_t = (I - A_0) ^{-1}U_t

のノイズ部分は、次のように変形できます。

\displaystyle n_t = A_0 n_t +U_t

これは、LiNGAMの式です。通常のLiNGAMの学習方法で、 $A_0$ を推定します。

m

と

M_i

、

A_0

が推定されることで、

ν

と

A_i

を導き出すことができます。

要するに、次のSVARモデルの係数行列を得ることができます。

\displaystyle Y_t=ν+A_0 Y_{t}+A_1 Y_{t−1}+\dots+A_p Y_{t−p}+U_t

まとめると、先ずVARモデルとして学習を行い、次にLiNGAMモデルとして学習を行うことで、非ガウスSVARモデルを学習（係数行列を推定）することができます。

さらに、推定量に一致性という嬉しい性質もあります。一致性とは、データ量を増やすと正しい値に近づくという性質です。

より詳しく知りたい方は、以下の論文を一読ください。

Hyvärinen, A., Zhang, K., Shimizu, S., Hoyer, P. O., & Dayan, P. (Ed.). (2010). Estimation of a structural vector autoregression model using non-Gaussianity. Journal of Machine Learning Research, 11, Article 1709-1731.

LiNGAMのインストール

LiNGAMパッケージをインストールします。

以下、コードです。

pip install lingam

pip install lingam

他にも必要なパッケージがありますので、必要に応じでインストールして頂ければと思います。

numpy
scipy
scikit-learn
graphviz
statsmodels
factor_analyzer
python-igraph

必要なモジュールとデータの読み込み

では、必要なモジュールを読み込みます。

以下、コードです。

import pandas as pd

import numpy as np

import statsmodels.api as sm

import lingam

from lingam.utils import make_dot, print_causal_directions, print_dagc

from graphviz import Digraph

import matplotlib.pyplot as plt

plt.style.use('ggplot') #グラフのスタイル

plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

import pandas as pd import numpy as np import statsmodels.api as sm import lingam from lingam.utils import make_dot, print_causal_directions, print_dagc from graphviz import Digraph import matplotlib.pyplot as plt plt.style.use('ggplot') #グラフのスタイル plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

import pandas as pd
import numpy as np

import statsmodels.api as sm

import lingam
from lingam.utils import make_dot, print_causal_directions, print_dagc

from graphviz import Digraph

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

次に、今回利用するデータを読み込みます。前回と同じです。

以下、コードです。

# データセット読み込み

url = 'https://www.salesanalytics.co.jp/0olr'

df = pd.read_csv(url,

parse_dates=True,

index_col='day'

)

df #確認

# データセット読み込み url = 'https://www.salesanalytics.co.jp/0olr' df = pd.read_csv(url, parse_dates=True, index_col='day' ) df #確認

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/0olr'
df = pd.read_csv(url,
                 parse_dates=True,
                 index_col='day'
                )
df #確認

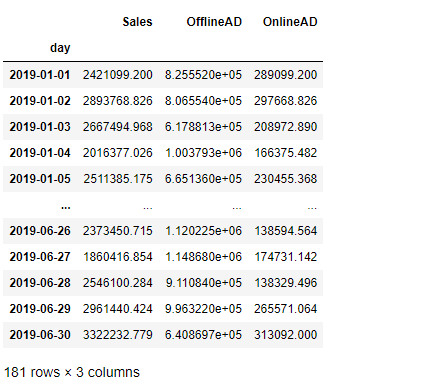
以下、実行結果です。

日単位の3変量の時系列データです。

Sales：売上
OfflineAD：TVCMなどのオフライン広告のコスト
OnlineAD：Webなどのオンライン広告のコスト

目的変数が「Sales」で、残りの2つが説明変数です。

VAR-LiNGAMの構築

では、VAR-LiNGAMで非ガウスSVARモデルを構築します。

以下、コードです。

# VAR-LiNGAMの構築

# インスタンス生成

model = lingam.VARLiNGAM(lags=2, prune=True)

# 学習

model.fit(df)

# # VAR-LiNGAMの構築 # # インスタンス生成 model = lingam.VARLiNGAM(lags=2, prune=True) # 学習 model.fit(df)

#
# VAR-LiNGAMの構築
#

# インスタンス生成
model = lingam.VARLiNGAM(lags=2, prune=True)

# 学習
model.fit(df)

学習し求めた、係数行列の推定値を見てみます。

以下、コードです。

# 係数行列の推定結果

model.adjacency_matrices_

# # 係数行列の推定結果 # model.adjacency_matrices_

#
# 係数行列の推定結果
#

model.adjacency_matrices_

以下、実行結果です。

3つの行列がありますが、順番に $A_0,A_1,A_2$ です。

この係数行列は、有向グラフの隣接行列です。ということは、有向グラフで表現することができます。

以下、コードです。

# 有向グラフ描写

# ノードのラベル

labels = ['Sales(t)', 'OfflineAD(t)', 'OnlineAD(t)',

'Sales(t-1)', 'OfflineAD(t-1)', 'OnlineAD(t-1)',

'Sales(t-2)', 'OfflineAD(t-2)', 'OnlineAD(t-2)']

# 有向グラフの描写

make_dot(np.hstack(model.adjacency_matrices_),

lower_limit=0.05,

ignore_shape=True,

labels=labels)

# # 有向グラフ描写 # # ノードのラベル labels = ['Sales(t)', 'OfflineAD(t)', 'OnlineAD(t)', 'Sales(t-1)', 'OfflineAD(t-1)', 'OnlineAD(t-1)', 'Sales(t-2)', 'OfflineAD(t-2)', 'OnlineAD(t-2)'] # 有向グラフの描写 make_dot(np.hstack(model.adjacency_matrices_), lower_limit=0.05, ignore_shape=True, labels=labels)

#
# 有向グラフ描写
#

# ノードのラベル
labels = ['Sales(t)', 'OfflineAD(t)', 'OnlineAD(t)', 
          'Sales(t-1)', 'OfflineAD(t-1)', 'OnlineAD(t-1)', 
          'Sales(t-2)', 'OfflineAD(t-2)', 'OnlineAD(t-2)']

# 有向グラフの描写
make_dot(np.hstack(model.adjacency_matrices_),
         lower_limit=0.05,
         ignore_shape=True,
         labels=labels)

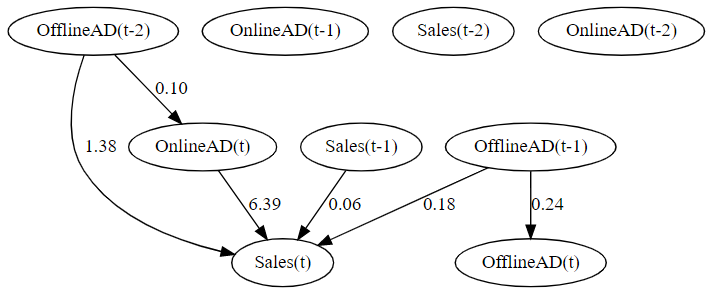
以下、実行結果です。