Pythonによるマーケティングミックスモデリング
（MMM：Marketing Mix Modeling）超入門 その13

PLS回帰モデルでMMM③（色々なAdStock考慮）

2265
Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その13PLS回帰モデルでMMM③（色々なAdStock考慮）

本当に売上に貢献している広告は、どの広告か？

売上と広告媒体等との関係性をモデリングし、どの広告媒体が売上にどれほど貢献していたのか分析することができます。

それが、マーケティングミックスモデリング（MMM：Marketing Mix Modeling）です。

ただ、多くの広告・販促は似たような時期に集中し実施することが多く、結果的にマルチコという線形回帰モデルを構築しうる上で非常に良くない現象が起こる危険があります。

その対策の1つに、PLS回帰でモデルを構築する、という方法があります。モデルの説明力や予測精度は若干悪化しますが、非常に有効な方法です。

3回に分けてお話しします。

  • ① AdStock非考慮
  • ② シンプルなAdStock考慮　→　前回
  • ③ 色々なAdStock考慮　→　今回

 

前回は、②のシンプルなAdStock考慮したPLS回帰によるモデル構築についてお話ししました。

Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その12PLS回帰モデルでMMM②（シンプルなAdStock考慮）

今回は、色々なAdStockを考慮したPLS回帰によるモデル構築についてお話しします。についてお話しします。

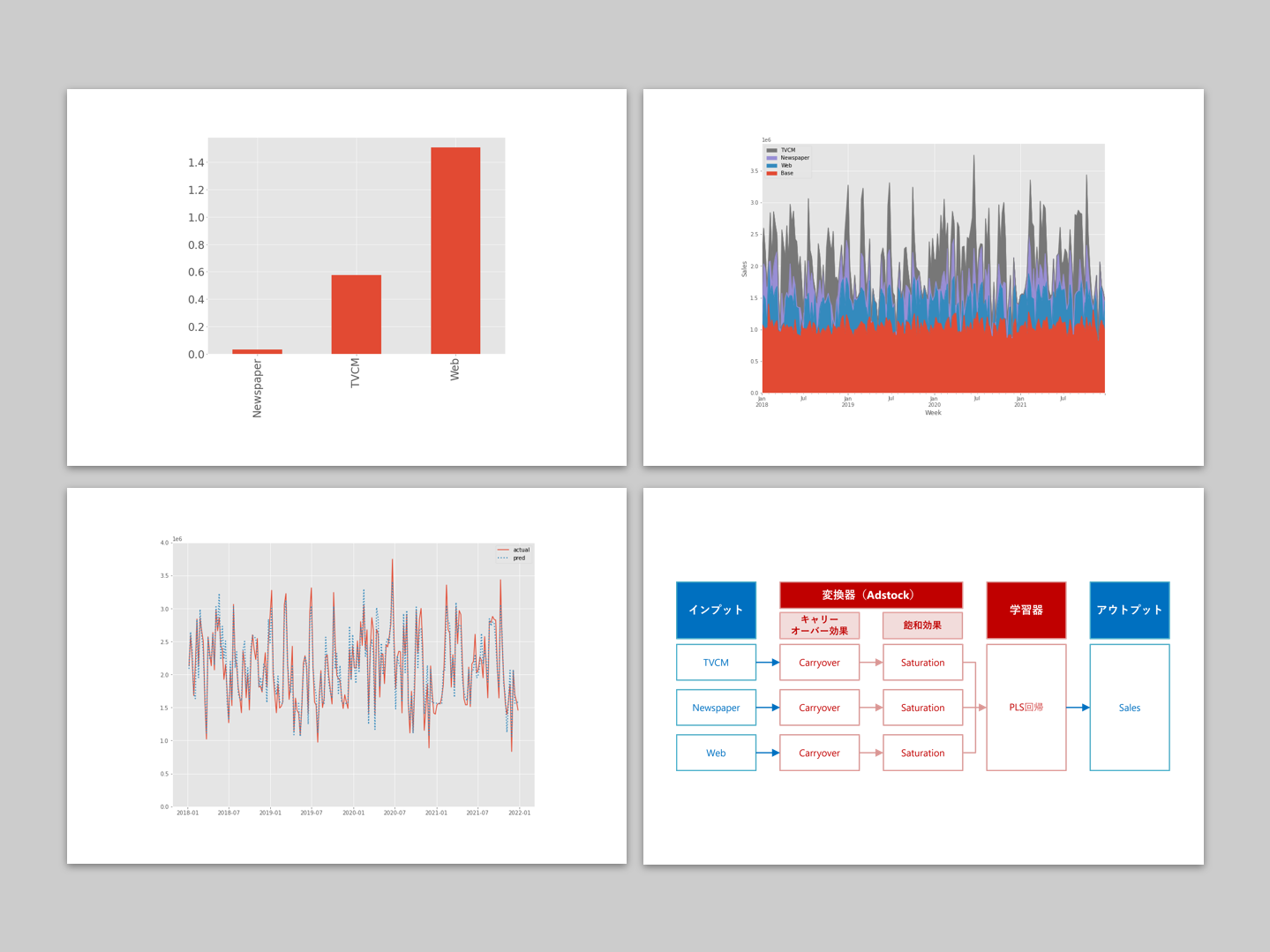
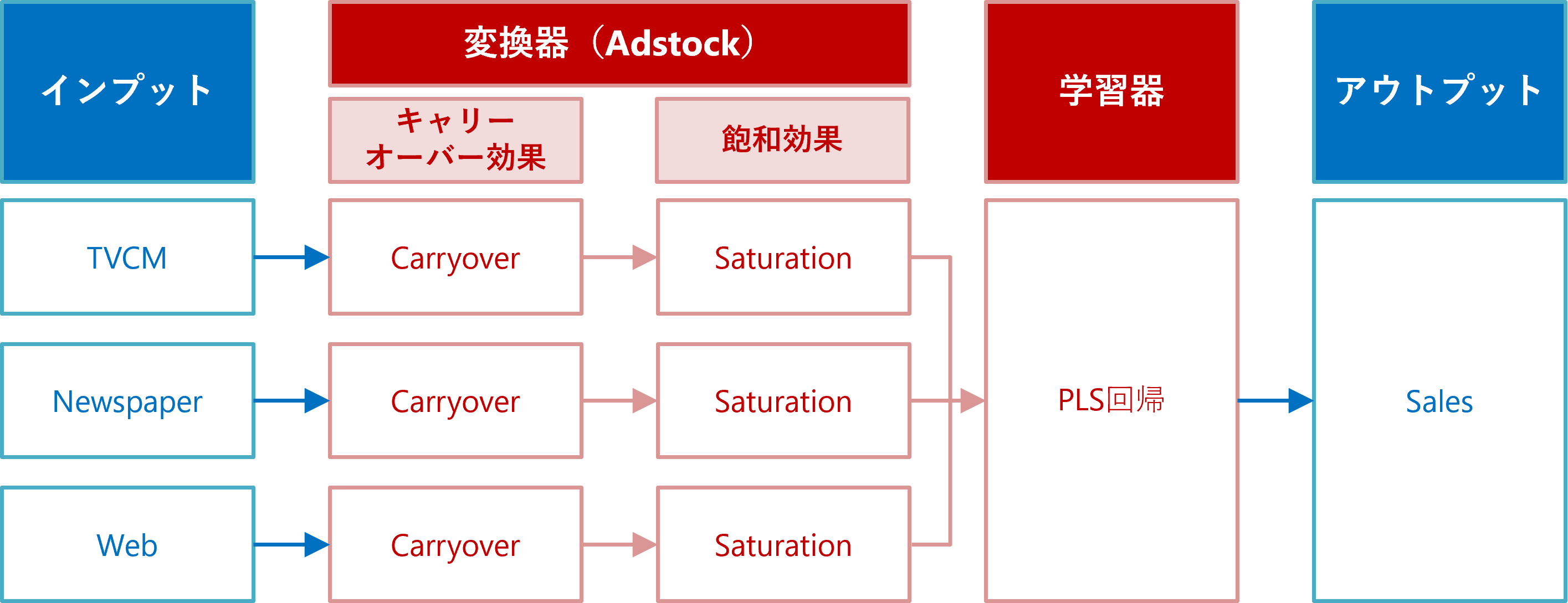
ちなみに、アドストック（Ad Stock）を考慮するとは、飽和効果（収穫逓減）とキャリーオーバー（Carryover）効果を考慮するということです。具体的には、Pythonのscikit-learn（sklearn）のパイプラインを、以下のように構築しました。

 

利用するデータセット（前回と同じ）

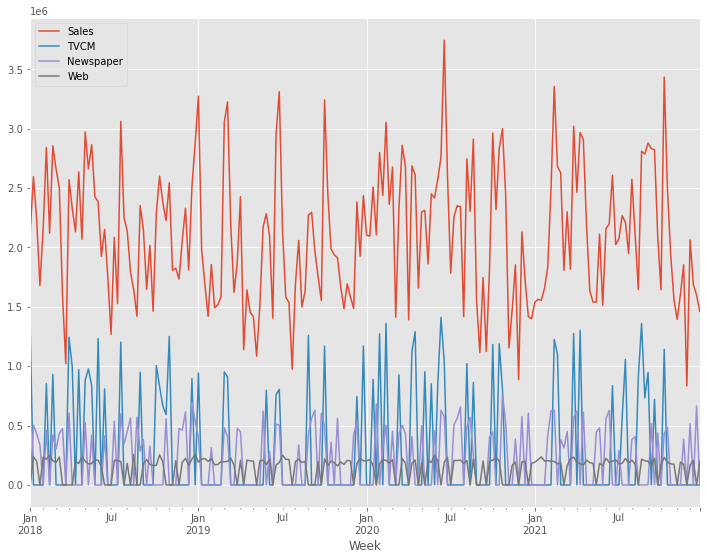
今回利用するデータセットの変数です。

  • Week：週
  • Sales：売上
  • TVCM：TV CMのコスト
  • Newspaper：新聞の折り込みチラシのコスト
  • Web：Web広告のコスト

以下からダウンロードできます。

MMM.csv
https://www.salesanalytics.co.jp/4zdt

 

アドストック（Ad Stock）

今回は、以下の関数の中から最適な組み合わせを探し、アドストック（Ad Stock）を表現し、モデル構築します。

  • キャリーオーバー効果モデル
    • 定率減少型キャリーオーバー効果モデル（simple_Carryover）
    • ピーク可変型キャリーオーバー効果モデル（peak_Carryover）
  • 飽和モデル
    • 指数型飽和モデル（exp_Saturation）
    • ロジスティック型飽和モデル（logit_Saturation）
    • ゴンペルツ型飽和モデル（gom_Saturation）

 

　キャリーオーバー効果モデル

　　定率減少型キャリーオーバー効果モデル

ピークが広告などの投入時で徐々に低減する「定率減少型キャリーオーバー効果モデル」を、数式で表現すると、次のようになります。

\displaystyle x_t^* = \displaystyle \sum_{l=0}^{L-1} w_{t-l} \cdot x_{t-l} , \quad w_{t-l} = R^{l} x_tはt期の広告などの投入量で、x_ t^*はt期とそれ以前までの広告などの効果の累積（残存効果を足したもの）です。

ハイパーパラメータは、次の2つです。

  • L(length)：効果の続く期間　※当期含む
  • R(rate)：減衰率

グラフで表現すると、次のようになります。横軸は、広告などを投入した後の経過時間（当期、1期後、2期後、・・・）を表し、縦軸は、効果の大きさを表します。

 

　　ピーク可変型キャリーオーバー効果モデル

広告などは、広告などを打ったときが効果のピークとは限りません。例えば、広告を打った数日後や数週間後に効果のピークが来ることもあります。

効果のピークが広告などを打ったときに限らない「ピーク可変型キャリーオーバー効果モデル」です。

数式で表現すると、次のようになります。

\displaystyle x_t^* = \frac{\displaystyle \sum_{l=0}^{L-1} w_{t-l} \cdot x_{t-l}}{\displaystyle \sum_{l=0}^{L-1} w_{t-l}} , \quad w_{t-l} = R^{(l-P)^2} x_tはt期の広告などの投入量で、x_ t^*はt期とそれ以前までの広告などの効果の累積（残存効果を足したもの）です。

ハイパーパラメータは、次の3つです。

  • L(length)：効果の続く期間　※当期含む
  • P(peak)：ピークの時期（広告などを打った日の場合は0、次期は1、など）
  • R(rate)：減衰率

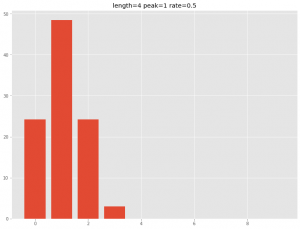
グラフで表現すると、次のようになります。横軸は、広告などを投入した後の経過時間（当期、1期後、2期後、・・・）を表し、縦軸は、効果の大きさを表します。

 

　飽和モデル

x_ t^*はt期とそれ以前までの広告などの効果の累積（残存効果を足したもの）で、x_ t^{**}は飽和モデルで変換した後のt期の値とします。

 

　　指数型飽和モデル

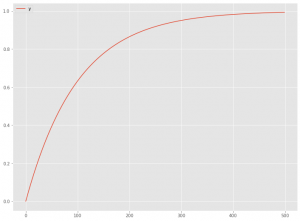
「指数型飽和モデル」を数式で表現すると、次のようになります。

x_ t^{**}=1-e^{-ax_ t^*}

グラフで表現すると、次のようになります。横軸はx_ t^*で、縦軸はx_ t^{**}です。

 

　　ロジスティック型飽和モデル

S字曲線を表現する関数でモデル化することもあります。代表的なのは、シグモイド関数やロジスティック曲線、ゴンペルツ曲線などです。

 

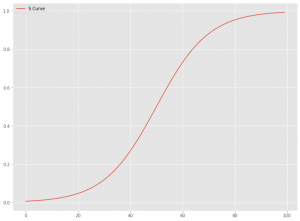
ロジスティック曲線による「ロジスティック型飽和モデル」を数式で表現すると、次のようになります。

\displaystyle x_ t^{**}= \frac{K}{1+b e^{c (x_ t^*-m)}}

ハイパーパラメータは、次の4つです。

  • K：上限パラメータ
  • b：形状パラメータ
  • c：形状パラメータ
  • m：位置パラメータ

 

　　ゴンペルツ型飽和モデル

ゴンペルツ曲線による「ゴンペルツ型飽和モデル」を数式で表現すると、次のようになります。

\displaystyle x_ t^{**}=Kb^{e^{-c(x_ t^*-m)}}

ハイパーパラメータは、次の4つです。

  • K：上限パラメータ
  • b：形状パラメータ
  • c：形状パラメータ
  • m：位置パラメータ

 

ライブラリーやデータセットなどの読み込み

先ずは、必要なライブラリーとデータセットを読み込みます。前回までと同じです。

 

　必要なライブラリーの読み込み

必要なライブラリーを読み込みます。

以下、コードです。

import numpy as np
import pandas as pd

from scipy.signal import convolve2d

from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score, TimeSeriesSplit
from sklearn import set_config

from sklearn.cross_decomposition import PLSRegression

import optuna
from optuna.integration import OptunaSearchCV
from optuna.distributions import UniformDistribution, IntUniformDistribution

import warnings
warnings.simplefilter('ignore')

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ

#指数表記しない設定
np.set_printoptions(precision=3,suppress=True)
pd.options.display.float_format = '{:.3f}'.format

 

　データセット（前回と同じ）の読み込み

前回と同じデータセットを読み込みます。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(url,
                 parse_dates=['Week'],
                 index_col='Week'
                )

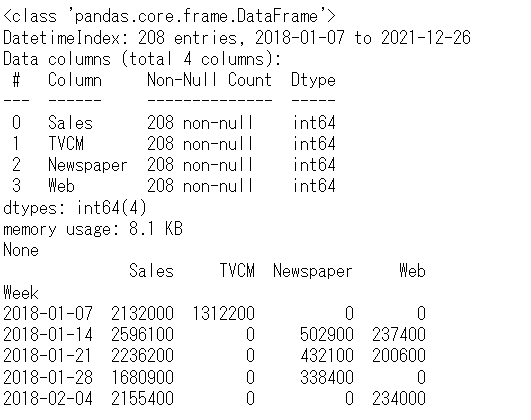
# データ確認
print(df.info()) #変数の情報
print(df.head()) #データの一部

# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']

 

以下、実行結果です。

 

ハイパーパラメータ探索

PLS回帰の最適な主成分の数と、キャリーオーバー効果や飽和効果のハイパーパラメータを探索します。

先ずは、Pipeline用変換器を定義します。

以下、コードです。

#
# Pipeline用変換器
#

# 飽和モデル

## 関数の定義

### 指数型飽和モデル（exp_Saturation）
def exp_Saturation(X: np.ndarray,a):
    return 1 - np.exp(-a*X)

### ロジスティック型飽和モデル（logit_Saturation）
def logit_Saturation(X: np.ndarray,K,b,c,m):
    return K/(1+b*np.exp(-c*(X-m)))

### ゴンペルツ型飽和モデル（gom_Saturation）
def gom_Saturation(X: np.ndarray,K,b,c,m):
    return K*(b**np.exp(-c*(X-m)))

## 変換器の定義

### 指数型飽和モデル（exp_Saturation）
class pipe_exp_Saturation(BaseEstimator, TransformerMixin):
    
    # 初期化
    def __init__(self,a=1.0):
        self.a = a
    
    # 学習
    def fit(self, X, y=None):
        return self
    
    # 処理（入力→出力）
    def transform(self, X):
        X_ = exp_Saturation(X,
                            self.a
                           ).reshape(-1,1)
        return X_
    
### ロジスティック型飽和モデル（logit_Saturation）
class pipe_logit_Saturation(BaseEstimator, TransformerMixin):
    
    # 初期化
    def __init__(self,K=1.0,m=100.0,b=1.0, c=0.1):
        self.K = K
        self.m = m
        self.b = b
        self.c = c
    
    # 学習
    def fit(self, X, y=None):
        return self
    
    # 処理（入力→出力）
    def transform(self, X):
        X_ = logit_Saturation(X,
                              self.K, 
                              self.b, 
                              self.c, 
                              self.m
                             ).reshape(-1,1)
        return X_

### ゴンペルツ型飽和モデル（gom_Saturation）
class pipe_gom_Saturation(BaseEstimator, TransformerMixin):
    
    # 初期化
    def __init__(self,K=1.0,m=100.0,b=1.0,c=0.1):
        self.K = K
        self.m = m
        self.b = b
        self.c = c
    
    # 学習
    def fit(self, X, y=None):
        return self
    
    # 処理（入力→出力）
    def transform(self, X):
        X_ = gom_Saturation(X,
                            self.K, 
                            self.b, 
                            self.c, 
                            self.m
                           ).reshape(-1,1)
        return X_

# キャリーオーバー効果モデル

## 関数の定義

### 定率減少型キャリーオーバー効果モデル（simple_Carryover）
def simple_Carryover(X: np.ndarray, rate, length):
    
    filter = (
        rate ** np.arange(length)
    ).reshape(-1, 1) 
    
    convolution = convolve2d(X, filter)
    
    if length > 1 : convolution = convolution[: -(length-1)]
        
    return convolution

### ピーク可変型キャリーオーバー効果モデル（peak_Carryover）
def peak_Carryover(X: np.ndarray, length, peak, rate):
    X = np.append(np.zeros(length-1), X)
    
    Ws = np.zeros(length)
    
    for l in range(length):
        W = rate**((l-peak)**2)
        Ws[length-1-l] = W
    
    carryover_X = []
    
    for i in range(length-1, len(X)):
        X_array = X[i-length+1:i+1]
        Xi = sum(X_array * Ws)/sum(Ws)
        carryover_X.append(Xi)
        
    return np.array(carryover_X)

## 変換器の定義

### 定率減少型キャリーオーバー効果モデル　※ピークが広告など投入時（simple_Carryover）
class pipe_simple_Carryover(BaseEstimator, TransformerMixin):
    # 初期化
    def __init__(self,length=4,rate=0.5):
        self.length = length
        self.rate = rate
        
    # 学習        
    def fit(self, X, y=None):
        return self
    # 処理（入力→出力）
    def transform(self, X):
        X_ = simple_Carryover(X, 
                              self.rate, 
                              self.length
                             )
        return X_
    
### Pipeline用変換器（キャリーオーバー効果モデル）
class pipe_peak_Carryover(BaseEstimator, TransformerMixin):
    # 初期化
    def __init__(self,length=4,peak=1,rate=0.5):
        self.length = length
        self.peak = peak
        self.rate = rate
        
    # 学習        
    def fit(self, X, y=None):
        return self
    # 処理（入力→出力）
    def transform(self, X):
        X_ = peak_Carryover(X, 
                            self.length, 
                            self.peak, 
                            self.rate
                           ) 
        return X_

 

次に、Optunaで利用する目的関数を定義します。

以下、コードです。

# 目的関数の設定
def objective(trial):
    
    #PCA
    n_components = trial.suggest_int(
        "n_components",
        1, 3
    )
    
    #TVCM
    
    ##TVCM Adstock func
    
    TVCM_Saturation_func = trial.suggest_categorical(
        "TVCM_Saturation_func",
        ["exp", "logit","gom"]
    )
    
    TVCM_Carryover_func = trial.suggest_categorical(
        "TVCM_Carryover_func",
        ["simple", "peak"]
    )
    
    ##TVCM_Saturation
    
    if TVCM_Saturation_func == 'exp':
        
        TVCM_a = trial.suggest_float(
            "TVCM_a", 
            0, 0.01
        )
        
        TVCM_Saturation = pipe_exp_Saturation(a=TVCM_a)
        
    elif TVCM_Saturation_func == 'logit':
        
        TVCM_K = trial.suggest_float(
            "TVCM_K", 
            np.min(X.TVCM), np.max(X.TVCM)*2
        )
        TVCM_m = trial.suggest_float(
            "TVCM_m",
            np.min(X.TVCM), np.max(X.TVCM)
        )
        TVCM_b = trial.suggest_float(
            "TVCM_b",
            0, 10
        )
        TVCM_c = trial.suggest_float(
            "TVCM_c",
            0, 1
        )
        
        TVCM_Saturation = pipe_logit_Saturation(
            K=TVCM_K,
            m=TVCM_m,
            b=TVCM_b,
            c=TVCM_c
        )
        
    else:
        
        TVCM_K = trial.suggest_float(
            "TVCM_K", 
            np.min(X.TVCM), 
            np.max(X.TVCM)*2
        )
        TVCM_m = trial.suggest_float(
            "TVCM_m", 
            np.min(X.TVCM), 
            np.max(X.TVCM)
        )
        TVCM_b = trial.suggest_float(
            "TVCM_b", 
            0, 1
        )
        TVCM_c = trial.suggest_float(
            "TVCM_c", 
            0, 1
        )     
        
        TVCM_Saturation = pipe_gom_Saturation(
            K=TVCM_K,
            m=TVCM_m,
            b=TVCM_b,
            c=TVCM_c
        )
        
    ##TVCM Carryover
    
    if TVCM_Carryover_func == 'simple':
        
        TVCM_rate = trial.suggest_float(
            "TVCM_rate", 
            0,1
        )
        TVCM_length = trial.suggest_int(
            "TVCM_length", 
            1,6
        )
        
        TVCM_Carryover = pipe_simple_Carryover(
            length=TVCM_length,
            rate=TVCM_rate
        )
        
    else:
        
        TVCM_rate = trial.suggest_float(
            "TVCM_rate", 
            0, 1
        )
        TVCM_length = trial.suggest_int(
            "TVCM_length",
            1,6
        )
        TVCM_peak = trial.suggest_int(
            "TVCM_peak",
            0,2
        )
        
        TVCM_Carryover = pipe_peak_Carryover(
            length=TVCM_length, 
            rate=TVCM_rate,
            peak=TVCM_peak
        )   
    #Newspaper
    
    ##Newspaper Adstock func
    
    Newspaper_Saturation_func = trial.suggest_categorical(
        "Newspaper_Saturation_func",
        ["exp", "logit","gom"]
    )
    
    Newspaper_Carryover_func = trial.suggest_categorical(
        "Newspaper_Carryover_func",
        ["simple", "peak"]
    )
    
    ##Newspaper_Saturation
    
    if Newspaper_Saturation_func == 'exp':
        
        Newspaper_a = trial.suggest_float(
            "Newspaper_a", 
            0, 0.01
        )
        
        Newspaper_Saturation = pipe_exp_Saturation(a=Newspaper_a)
        
    elif Newspaper_Saturation_func == 'logit':
        
        Newspaper_K = trial.suggest_float(
            "Newspaper_K",
            np.min(X.Newspaper), np.max(X.Newspaper)*2
        )
        Newspaper_m = trial.suggest_float(
            "Newspaper_m", 
            np.min(X.Newspaper), np.max(X.Newspaper)
        )
        Newspaper_b = trial.suggest_float(
            "Newspaper_b", 
            0, 10
        )
        Newspaper_c = trial.suggest_float(
            "Newspaper_c", 
            0, 1
        )
        
        Newspaper_Saturation = pipe_logit_Saturation(
            K=Newspaper_K,
            m=Newspaper_m,
            b=Newspaper_b,
            c=Newspaper_c
        )
        
    else:
        
        Newspaper_K = trial.suggest_float(
            "Newspaper_K", 
            np.min(X.Newspaper), np.max(X.Newspaper)*2
        )
        Newspaper_m = trial.suggest_float(
            "Newspaper_m", 
            np.min(X.Newspaper), np.max(X.Newspaper)
        )
        Newspaper_b = trial.suggest_float(
            "Newspaper_b", 
            0, 1
        )
        Newspaper_c = trial.suggest_float(
            "Newspaper_c", 
            0, 1
        )     
        
        Newspaper_Saturation = pipe_gom_Saturation(
            K=Newspaper_K,
            m=Newspaper_m,
            b=Newspaper_b,
            c=Newspaper_c
        )
        
    ##Newspaper Carryover
    
    if Newspaper_Carryover_func == 'simple':
        
        Newspaper_rate = trial.suggest_float(
            "Newspaper_rate", 
            0,1
        )
        Newspaper_length = trial.suggest_int(
            "Newspaper_length", 
            1,6
        )
        
        Newspaper_Carryover = pipe_simple_Carryover(
            length=Newspaper_length,
            rate=Newspaper_rate
        )
        
    else:
        
        Newspaper_rate = trial.suggest_float(
            "Newspaper_rate", 
            0, 1
        )
        Newspaper_length = trial.suggest_int(
            "Newspaper_length",
            1,6
        )
        Newspaper_peak = trial.suggest_int(
            "Newspaper_peak",
            0,2
        )
        
        Newspaper_Carryover = pipe_peak_Carryover(
            length=Newspaper_length,
            rate=Newspaper_rate,
            peak=Newspaper_peak
        )
            
    #Web
    
    ##Web Adstock func
    
    Web_Saturation_func = trial.suggest_categorical(
        "Web_Saturation_func",
        ["exp", "logit","gom"]
    )
    
    Web_Carryover_func = trial.suggest_categorical(
        "Web_Carryover_func",
        ["simple", "peak"]
    )
    
    ##Web_Saturation
    
    if Web_Saturation_func == 'exp':
        
        Web_a = trial.suggest_float(
            "Web_a", 
            0, 0.01
        )
        
        Web_Saturation = pipe_exp_Saturation(a=Web_a)
        
    elif Web_Saturation_func == 'logit':
        
        Web_K = trial.suggest_float(
            "Web_K", 
            np.min(X.Web), np.max(X.Web)*2
        )
        Web_m = trial.suggest_float(
            "Web_m", 
            np.min(X.Web), np.max(X.Web)
        )
        Web_b = trial.suggest_float(
            "Web_b", 
            0, 10
        )
        Web_c = trial.suggest_float(
            "Web_c", 
            0, 1
        )
        
        Web_Saturation = pipe_logit_Saturation(
            K=Web_K,
            m=Web_m,
            b=Web_b,
            c=Web_c
        )
        
    else:
        
        Web_K = trial.suggest_float(
            "Web_K", 
            np.min(X.Web), np.max(X.Web)*2
        )
        Web_m = trial.suggest_float(
            "Web_m", 
            np.min(X.Web), np.max(X.Web)
        )
        Web_b = trial.suggest_float(
            "Web_b", 
            0, 1
        )
        Web_c = trial.suggest_float(
            "Web_c", 
            0, 1
        )     
        
        Web_Saturation = pipe_gom_Saturation(
            K=Web_K,
            m=Web_m,
            b=Web_b,
            c=Web_c
        )
        
    ##Web Carryover
    
    if Web_Carryover_func == 'simple':
        
        Web_rate = trial.suggest_float(
            "Web_rate", 
            0,1
        )
        Web_length = trial.suggest_int(
            "Web_length", 
            1,6
        )
        
        Web_Carryover = pipe_simple_Carryover(
            length=Web_length,
            rate=Web_rate
        )
        
    else:
        
        Web_rate = trial.suggest_float(
            "Web_rate", 
            0, 1
        )
        Web_length = trial.suggest_int(
            "Web_length",
            1,6
        )
        Web_peak = trial.suggest_int(
            "Web_peak",
            0,2
        )
        
        Web_Carryover = pipe_peak_Carryover(
            length=Web_length,
            rate=Web_rate,
            peak=Web_peak
        )   
    
    # パイプライン化
    
    ## 変換器（Adstock）
    adstock = ColumnTransformer(
        [
         ('TVCM_pipe', Pipeline([
             ('TVCM_carryover', TVCM_Carryover),
             ('TVCM_saturation', TVCM_Saturation)
         ]), ['TVCM']),
         ('Newspaper_pipe', Pipeline([
             ('Newspaper_carryover', Newspaper_Carryover),
             ('Newspaper_saturation', Newspaper_Saturation)
         ]), ['Newspaper']),
         ('Web_pipe', Pipeline([
             ('Web_carryover', Web_Carryover),
             ('Web_saturation', Web_Saturation)
         ]), ['Web']),
        ],
        remainder='passthrough'
    )
    ## 説明変数の変換（adstock）→PLS回帰モデル
    MMM_pipe = Pipeline([
        ('adstock', adstock),
        ('PLS', PLSRegression(n_components))
    ])
        
    #CVによる評価
    score = cross_val_score(
        MMM_pipe,
        X,
        y,
        cv=TimeSeriesSplit()
    )
    accuracy = score.mean()
    return accuracy

 

Pipelineのハイパーパラメータを探索します。

以下、コードです。

# 目的関数の最適化を実行する
study = optuna.create_study(direction="maximize")
study.optimize(objective,
               n_trials=10000,
               show_progress_bar=True)

 

探索結果を見てみます。

以下、コードです。

# 探索結果
study.best_params

 

以下、実行結果です。

 

この値をハイパーパラメータに設定し、MMMを全データで構築します。

 

モデルの構築と予測

求めた最適なハイパーパラメータでモデルを学習します。

具体的には、先ずパイプラインの定義をします。次に、そのパイプラインに最適なハイパーパラメータを設定します。そのパイプラインを使い、精度検証をします。

 

　パイプライン構築

パイプライン用の、飽和モデルとキャリーオーバー効果の2つの変換器クラスを定義します。

以下、コードです。

# Pipeline用変換器
## 飽和モデル
class Saturation(BaseEstimator, TransformerMixin):
    
    # 初期化
    def __init__(self,func='exp',a=1.0,K=1.0,m=100.0,b=1.0, c=0.1):
        self.func = func
        self.a = a
        self.K = K
        self.m = m
        self.b = b
        self.c = c
    
    # 学習
    def fit(self, X, y=None):
        return self
    
    # 処理（入力→出力）
    def transform(self, X):
        if self.func == 'exp':
            X_ = exp_Saturation(X,
                                self.a
                               ).reshape(-1,1)
        elif self.func == "logit":
            X_ = logit_Saturation(X,
                                  self.K, 
                                  self.b,
                                  self.c, 
                                  self.m
                                 ).reshape(-1,1)
        else:
            X_ = gom_Saturation(X,
                                self.K, 
                                self.b, 
                                self.c, 
                                self.m
                               ).reshape(-1,1)
        return X_
    
## キャリーオーバー効果モデル
class Carryover(BaseEstimator, TransformerMixin):
    # 初期化
    def __init__(self,func='simple',length=4, peak=1, rate=0.5):
        self.func = func
        self.length = length
        self.peak = peak
        self.rate = rate
        
    # 学習        
    def fit(self, X, y=None):
        return self
    # 処理（入力→出力）
    def transform(self, X):
        if self.func == 'peak':
            X_ = peak_Carryover(X, 
                                self.length, 
                                self.peak, 
                                self.rate)  
        else:
            X_ = simple_Carryover(X, 
                                  self.rate, 
                                  self.length)
            
        return X_

 

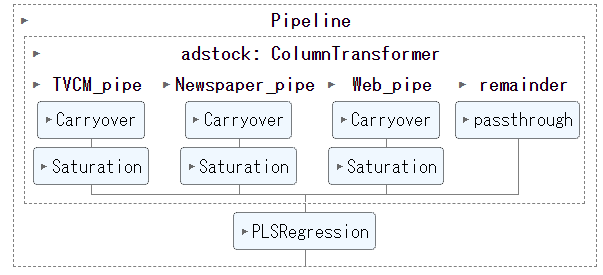
この2つの変換器でアドストック（Ad Stock）を表現します。これらの変換器と学習器（PLS回帰モデル）をつなげたパイプラインを構築します。

以下、コードです。

# Pipelineの設定
## 説明変数の変換部分（adstock）の定義
adstock = ColumnTransformer(
    [
     ('TVCM_pipe', Pipeline([
                           ('carryover', Carryover()),
                           ('saturation', Saturation())
     ]), ['TVCM']),
     ('Newspaper_pipe', Pipeline([
                           ('carryover', Carryover()),
                           ('saturation', Saturation())
     ]), ['Newspaper']),
     ('Web_pipe', Pipeline([
                           ('carryover', Carryover()),
                           ('saturation', Saturation())
     ]), ['Web']),
    ],
    remainder='passthrough'
)
## 説明変数の変換（adstock）→PLS回帰モデル（PLS）
MMM_pipe = Pipeline([
    ('adstock', adstock),
    ('PLS', PLSRegression())
])
## パイプラインの確認
set_config(display='diagram')   
MMM_pipe

 

以下、実行結果です。

 

　最適ハイパーパラメータで学習

以下、コードです。

# 最適ハイパーパラメータ
best_params={
 'PLS__n_components': 
    study.best_params.get('n_components'),
 'adstock__TVCM_pipe__carryover__func': 
    study.best_params.get('TVCM_Carryover_func'),
 'adstock__TVCM_pipe__carryover__length': 
    study.best_params.get('TVCM_length'),
 'adstock__TVCM_pipe__carryover__peak': 
    study.best_params.get('TVCM_peak'),
 'adstock__TVCM_pipe__carryover__rate': 
    study.best_params.get('TVCM_rate'),
 'adstock__TVCM_pipe__saturation__func': 
    study.best_params.get('TVCM_Saturation_func'),
 'adstock__TVCM_pipe__saturation__a': 
    study.best_params.get('TVCM_a'),
 'adstock__TVCM_pipe__saturation__K': 
    study.best_params.get('TVCM_K'),
 'adstock__TVCM_pipe__saturation__m': 
    study.best_params.get('TVCM_m'),
 'adstock__TVCM_pipe__saturation__b': 
    study.best_params.get('TVCM_b'),
 'adstock__TVCM_pipe__saturation__c': 
    study.best_params.get('TVCM_c'),
 'adstock__Newspaper_pipe__carryover__func': 
    study.best_params.get('Newspaper_Carryover_func'),
 'adstock__Newspaper_pipe__carryover__length': 
    study.best_params.get('Newspaper_length'),
 'adstock__Newspaper_pipe__carryover__peak': 
    study.best_params.get('Newspaper_peak'),
 'adstock__Newspaper_pipe__carryover__rate': 
    study.best_params.get('Newspaper_rate'),
 'adstock__Newspaper_pipe__saturation__func': 
    study.best_params.get('Newspaper_Saturation_func'),
 'adstock__Newspaper_pipe__saturation__a': 
    study.best_params.get('Newspaper_a'),
 'adstock__Newspaper_pipe__saturation__K': 
    study.best_params.get('Newspaper_K'),
 'adstock__Newspaper_pipe__saturation__m': 
    study.best_params.get('Newspaper_m'),
 'adstock__Newspaper_pipe__saturation__b': 
    study.best_params.get('Newspaper_b'),
 'adstock__Newspaper_pipe__saturation__c': 
    study.best_params.get('Newspaper_c'),
 'adstock__Web_pipe__carryover__func':
    study.best_params.get('Web_Carryover_func'),
 'adstock__Web_pipe__carryover__length': 
    study.best_params.get('Web_length'),
 'adstock__Web_pipe__carryover__peak': 
    study.best_params.get('Web_peak'),
 'adstock__Web_pipe__carryover__rate': 
    study.best_params.get('Web_rate'),
 'adstock__Web_pipe__saturation__func': 
    study.best_params.get('Web_Saturation_func'),
 'adstock__Web_pipe__saturation__a': 
    study.best_params.get('Web_a'),
 'adstock__Web_pipe__saturation__K': 
    study.best_params.get('Web_K'),
 'adstock__Web_pipe__saturation__m': 
    study.best_params.get('Web_m'),
 'adstock__Web_pipe__saturation__b': 
    study.best_params.get('Web_b'),
 'adstock__Web_pipe__saturation__c': 
    study.best_params.get('Web_c'),
}

# パイプラインのインスタンス
MMM_pipe_best = MMM_pipe.set_params(**best_params)

# 全データで学習
MMM_pipe_best.fit(X, y)

# R2（決定係数）
MMM_pipe_best.score(X, y)

 

以下、実行結果です。R2（決定係数）の値です。

 

　予測の実施

以下、コードです。

#
# 予測の実施
# 

# 目的変数y（売上）の予測
pred = pd.DataFrame(MMM_pipe_best.predict(X),
                    index=X.index,
                    columns=['y'])

# 各媒体による売上の予測

## 値がすべて0の説明変数
X_ = X.copy()
X_.iloc[:,:]=0

## Base
pred['Base'] = MMM_pipe_best.predict(X_)

## 媒体
for i in range(len(X.columns)):
    X_.iloc[:,:]=0
    X_.iloc[:,i]=X.iloc[:,i]
    pred[X.columns[i]] = MMM_pipe_best.predict(X_)[:,0]-pred['Base']
    
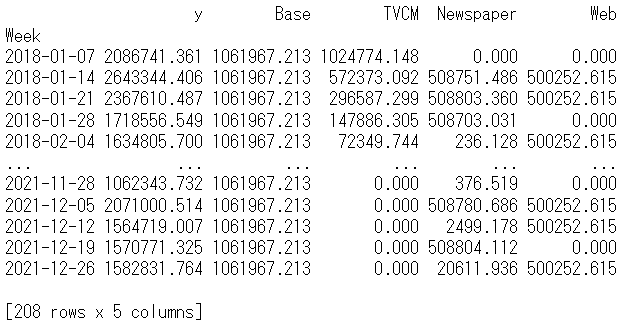
print(pred) #確認

# グラフ化（実測値と予測値）

## 散布図を描画
plt.scatter(y,pred['y'])
plt.title('R2:'+str(round(MMM_pipe_best.score(X, y),4)))
plt.ylabel('pred')
plt.xlabel('actual')
plt.show()

## 折れ線グラフ（時系列推移）
fig, ax = plt.subplots()
ax.plot(y.index, y.values, label="actual")
ax.plot(y.index, pred['y'].values, label="pred", linestyle="dotted", lw=2) 
ax.set_ylim(0, 4e6)
plt.legend()

 

以下、実行結果です。y = Base + TVCM + Newspaper + Webです。

 

貢献度とマーケティングROIの算定

　貢献度の算定

以下、コードです。

#
# 貢献度の算定
#

# 予測値の補正
correction_factor = y.div(pred['y'], axis=0)   #補正係数
pred_adj = pred.mul(correction_factor, axis=0) #補正後の予測値

# 各媒体の貢献度だけ抽出
contribution = pred_adj[['Base', 'Web', 'Newspaper', 'TVCM']]

print(contribution.head()) #確認

# グラフ化
ax = (contribution
      .plot.area(
          ylabel='Sales',
          xlabel='Week')
     )
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[::-1], labels[::-1])

 

以下、実行結果です。

 

貢献度の構成比の算出します。

以下、コードです。

#
# 貢献度の構成比の算出
#

# 媒体別の貢献度の合計
contribution_sum = contribution.sum(axis=0)

# 集計結果の出力
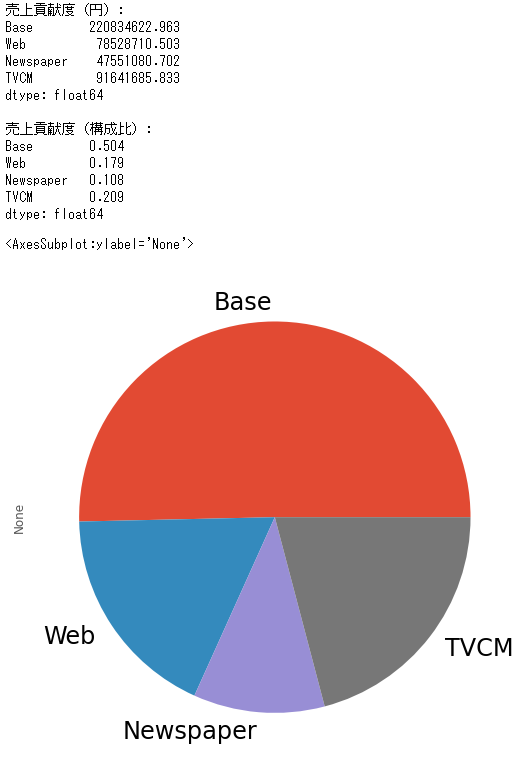
print('売上貢献度（円）:\n', 
      contribution_sum, 
      sep=''
     )
print()
print('売上貢献度（構成比）:\n', 
      contribution_sum/contribution_sum.sum(), 
      sep=''
     )

# グラフ化
contribution_sum.plot.pie(fontsize=24)

 

以下、実行結果です。

 

マーケティングROIの算定

以下、コードです。

#
# マーケティングROIの算定
#

# 各媒体のコストの合計
cost_sum = X.sum(axis=0)

# 各媒体のROIの計算
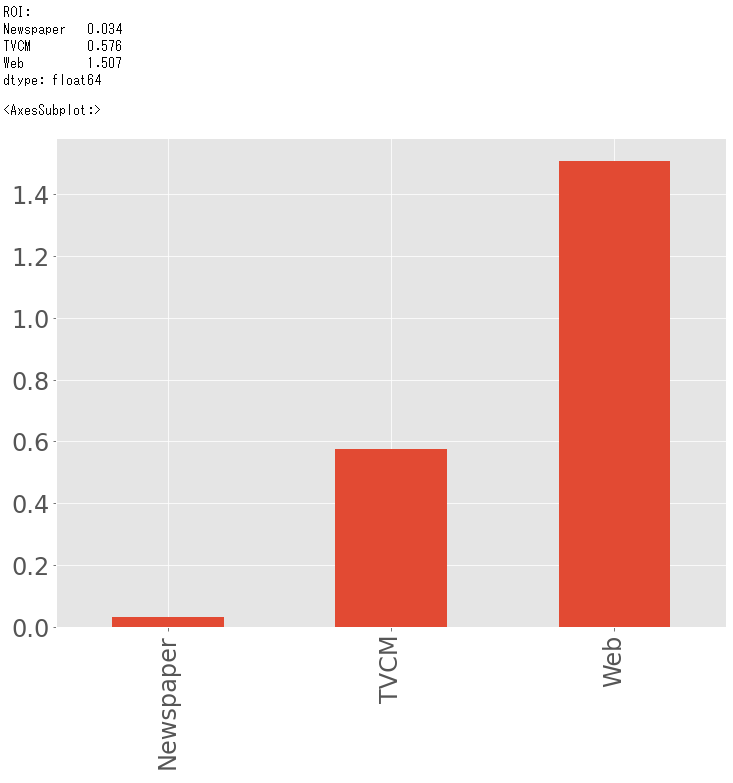
ROI = (contribution_sum.drop('Base', axis=0) - cost_sum)/cost_sum

print('ROI:\n', ROI, sep='') #確認

# グラフ化
ROI.plot.bar(fontsize=24)

 

以下、実行結果です。

 

まとめ

今回は、色々なAdStockを考慮したPLS回帰によるモデル構築についてお話ししました。

多くの広告・販促は似たような時期に集中し実施することが多く、結果的にマルチコという線形回帰モデルを構築しうる上で非常に良くない現象が起こる危険があります。

その対策の1つに、PLS（部分的最小二乗回帰、Partial Least Squares Regression）回帰モデルでモデルを構築する、という方法があります。

3回に分けてお話ししてきました。

  • ① AdStock非考慮　→　前々回
  • ② シンプルなAdStock考慮　→　前回
  • ③ 色々なAdStock考慮　→　今回

MMM（マーケティングミックスモデリング）で扱うデータの多くは、時系列データです。

ということは、時系列系のモデルを使えるのではないだろうか、となります。

次回は、「時系列ARIMAモデルでマーケティングミックスモデリング」というお話しをします。