Python Keras(TensorFlow)で作る
深層学習(Deep Learning)時系列予測モデル(その6)

時系列Encoder-Decoder(Seq2Seq)モデルで複数先予測（実践編）

6926
Python Keras(TensorFlow)で作る深層学習(Deep Learning)時系列予測モデル(その6) 時系列Encoder-Decoder(Seq2Seq)モデルで複数先予測（実践編）

売上などの時系列データを予測するモデルは、基本となるのは1期先予測（1-Step ahead prediction）ですが、実務では複数先予測（Multi-Step ahead prediction）が求められます。

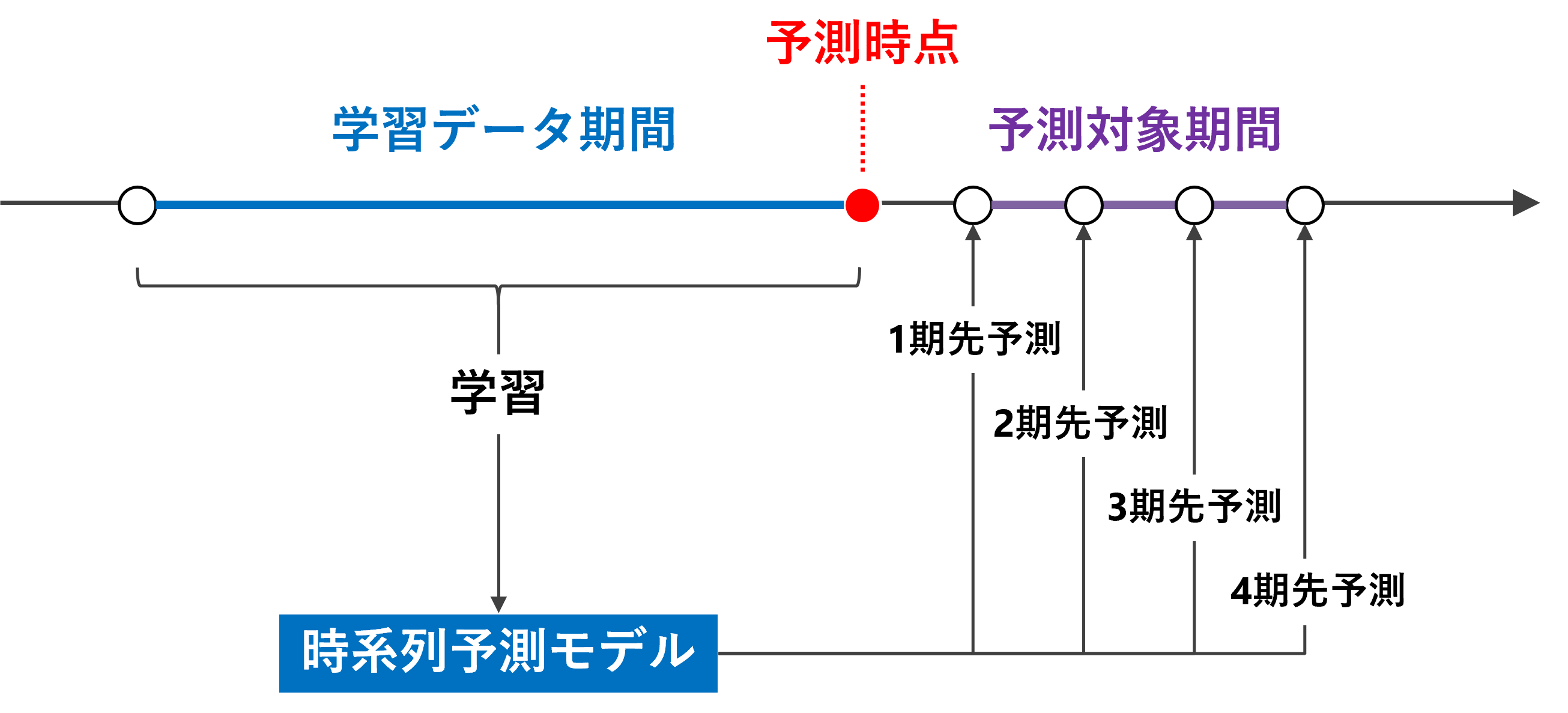
ニューラルネットワークの場合、どうなるのでしょうか？

幾つかやり方があります。

その1つが、Seq2Seq とも呼ばれるEncoder-Decoder型RNN（LSTMやGRUを含む）モデルを構築し複数先予測をするというものです。

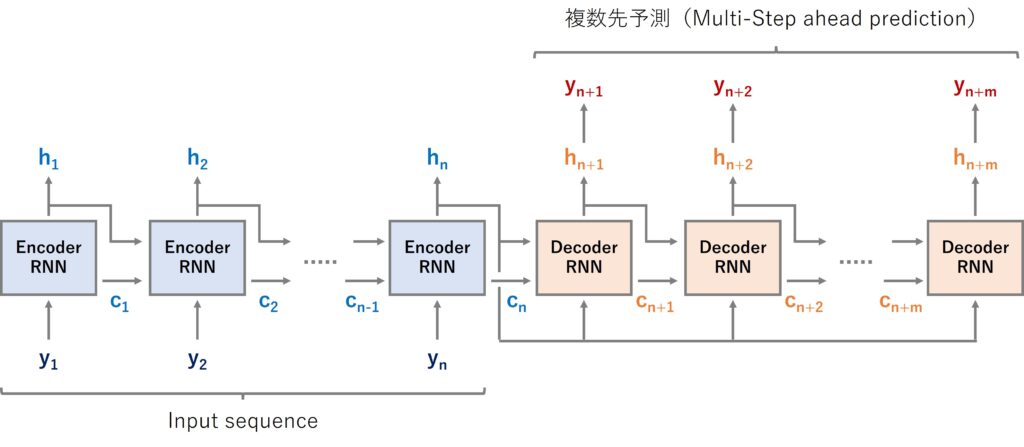
Encoder-Decoder型RNNは、Encoder層とDecoder層にRNNを組み込みます。Seq2Seqとも呼ばれます。

前回は、時系列データに対するEncoder-Decoder型RNN（LSTMやGRUを含む）モデルをKeras(TensorFlow)で作るときの作り方を、簡単に解説しました。

Python Keras(TensorFlow)で作る深層学習(Deep Learning)時系列予測モデル(その5) 時系列Encoder-Decoder(Seq2Seq)モデルで複数先予測（解説編）

今回は、Pythonによる実装例をお話しします。

サンプルデータ

サンプルデータは、次の2つです。

  • Peyton ManningのWikipediaのPV（ページビュー）
  • Airline Passengers（飛行機乗客数）

 

　Peyton ManningのWikipediaのPV（ページビュー）

Prophetで提供されているサンプルデータ（example_wp_log_peyton_manning.csv）です。

facebook/prophetのGitHubからダウンロードして使って頂くか、弊社のHPからダウンロードして使って頂ければと思います。

facebook/prophetのGitHub上のデータ
https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/bgr8

このデータセットは、説明変数のない目的変数が1変量の時系列データで、目的変数は日単位のPV（ページビュー数）です。

今回は、365日間の過去データから30日先を予測するモデルを構築します。

 

　Airline Passengers（飛行機乗客数）

Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h

このデータセットも、説明変数のない目的変数が1変量の時系列データで、目的変数は月単位の飛行機乗客数です。

 

データセットの形式のお話し

Keras（TensorFlow）のRNNのデータセットは、以下のような3元構造が基本になっています。

[サンプル（samples）,タイムステップ（time_steps）,特徴量（features）]

 

時系列データの特徴量の1つとして、ラグ変数というものがあります。

例えば、日販（1日の売上）であれば、「ラグ1の変数」とは「1日前の日販の変数」、「ラグ2の変数」とは「2日前の日販の変数」などです。

目的変数のラグ変数を作り、インプットデータXとアウトプットデータyを作っていきます。

 

例えば、以下のような日単位の時系列データがあったとします。

y(t=0),y(t=1),y(t=2),…

このとき、過去365日間のデータを使い、近未来30日間を予測するために、以下のようなデータセットを準備します。

インプットデータX アウトプットデータy
index x1 x2 … x365 y1 y2 … y30
0 y(t=394) y(t=393) … y(t=30) y(t=29) y(t=28) … y(t=0)
1 y(t=395) y(t=394) … y(t=31) y(t=30) y(t=29) … y(t=1)
2 y(t=396) y(t=395) … y(t=32) y(t=31) y(t=30) … y(t=2)
3 y(t=397) y(t=396) … y(t=33) y(t=32) y(t=31) … y(t=3)
4 y(t=398) y(t=397) … y(t=34) y(t=33) y(t=32) … y(t=4)
5 y(t=399) y(t=398) … y(t=35) y(t=34) y(t=33) … y(t=5)
6 y(t=400) y(t=399) … y(t=36) y(t=35) y(t=34) … y(t=6)
7 y(t=401) y(t=400) … y(t=37) y(t=36) y(t=35) … y(t=7)
8 y(t=402) y(t=401) … y(t=38) y(t=37) y(t=36) … y(t=8)
9 y(t=403) y(t=402) … y(t=39) y(t=38) y(t=37) … y(t=9)

 

予測精度の評価指標

今回の予測精度の評価指標も今までと同じで、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

 

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

準備

　必要なモジュールの読み込み

必要なモジュールを読み込みます。

以下、コードです。

#
# 必要なモジュールの読み込み
#

import numpy as np
import pandas as pd

from keras.models import Sequential
from keras.models import Model
from keras.layers import *
from keras.callbacks import EarlyStopping
from tensorflow.keras.utils import plot_model

from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

　説明変数と目的変数を生成する関数

時系列データからラグ特徴量を作り、説明変数と目的変数を生成する関数を作ります。

以下、コードです。

#
# データセット生成関数
#

def gen_dataset(dataset, input_sequence, output_sequence=1):
    
    X = []
    y = []
    
    for i in range(len(dataset) - input_sequence - output_sequence + 1):
        a = i + input_sequence
        b = a + output_sequence
        X.append(dataset[i:a, 0]) #ラグ特徴量
        y.append(dataset[a:b, 0]) #目的変数
        
    return np.array(X), np.array(y)

 

では、ここから以下のサンプルデータごとに説明していきます。

  • Peyton ManningのWikipediaのPV（ページビュー）
  • Airline Passengers（飛行機乗客数）

 

Peyton ManningのWikipediaのPV（ページビュー）

　データセットの読み込み

データセットを読み込みます。

以下、コードです。

#
# 必要なデータセット（時系列データ）の読み込み
#

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/bgr8'
df = pd.read_csv(url)

# データ確認
df.info() #変数の情報
df.head() #データの一部

 

以下、実行結果です。

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2905 entries, 0 to 2904
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   ds      2905 non-null   object 
 1   y       2905 non-null   float64
dtypes: float64(1), object(1)
memory usage: 45.5+ KB
None
           ds         y
0  2007-12-10  9.590761
1  2007-12-11  8.519590
2  2007-12-12  8.183677
3  2007-12-13  8.072467
4  2007-12-14  7.893572

 

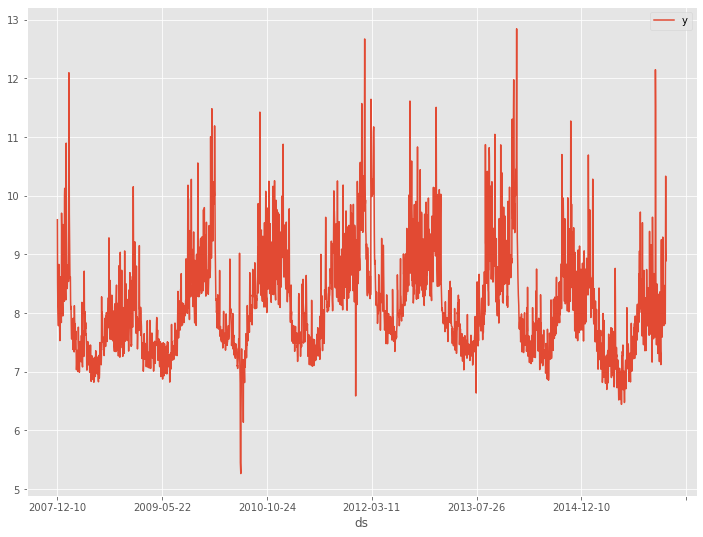
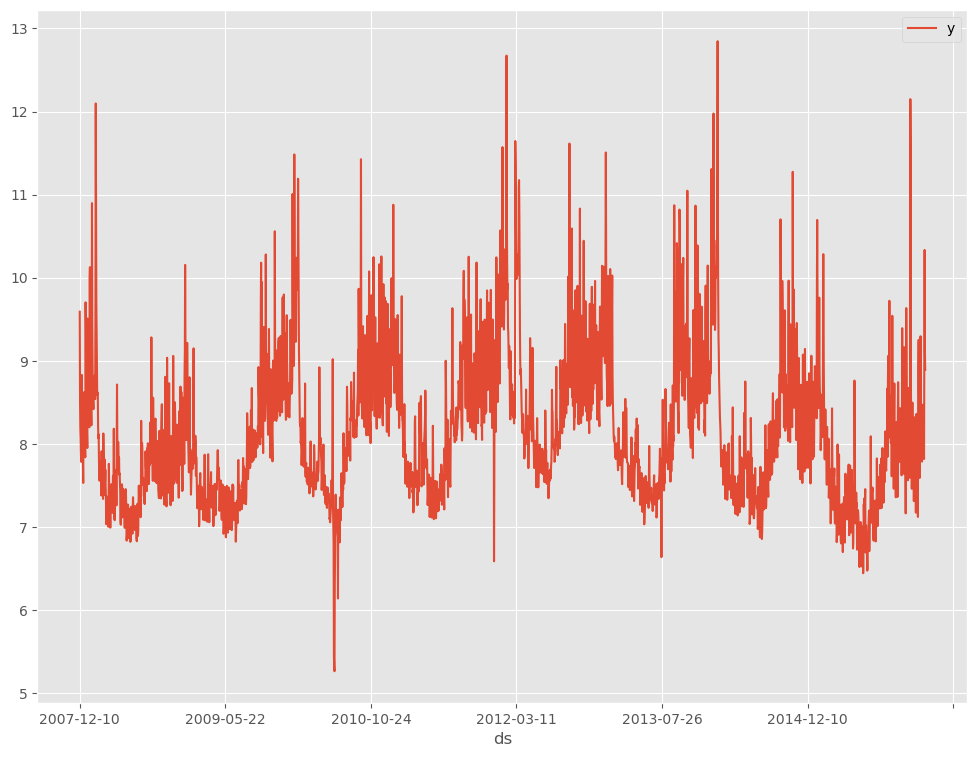
データを折れ線グラフで表現してみます。

以下、コードです。

#
# 時系列データのグラフ化（折れ線グラフ）
#

df.plot(kind='line',x='ds', y='y')

 

以下、実行結果です。

 

　Keras用データセットの準備

先程読み込んだデータセットはDataFrame形式です。NumPy配列へ変換します。

以下、コードです。

#
# 配列のデータセットに変換
#

dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32')    #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換

print(dataset) #確認

 

以下、実行結果です。

[[ 9.590761 ]
 [ 8.51959  ]
 [ 8.183677 ]
 ...
 [10.3337755]
 [ 9.125872 ]
 [ 8.891374 ]]

 

このNumPy配列へ変換したデータセット（1変量の時系列データ）から、説明変数と目的変数を生成します。

今回は、365日間の過去データから30日先を予測するモデルを構築することを想定しています。

以下、コードです。

#
# 説明変数Xと目的変数Yの生成
#

# Time Steps の長さ
input_sequence = 365

# 予測する長さ
output_sequence = 30

# データセット生成
X, Y = gen_dataset(dataset, input_sequence, output_sequence)

# 確認
print('X:',X.shape)
print(X)
print()
print('Y:',Y.shape)
print(Y)

 

以下、実行結果です。

X: (2511, 365)
[[ 9.590761   8.51959    8.183677  ... 10.153818   9.267855   8.434246 ]
 [ 8.51959    8.183677   8.072468  ...  9.267855   8.434246   8.137689 ]
 [ 8.183677   8.072468   7.893572  ...  8.434246   8.137689   8.044947 ]
 ...
 [ 8.1022835  7.8336     7.522941  ...  7.5918617  7.528869   7.1716566]
 [ 7.8336     7.522941   7.9102235 ...  7.528869   7.1716566  7.8913307]
 [ 7.522941   7.9102235  8.365439  ...  7.1716566  7.8913307  8.360071 ]]

Y: (2511, 30)
[[ 8.137689   8.044947   8.228977  ...  8.062118   8.066522   8.059592 ]
 [ 8.044947   8.228977   8.14119   ...  8.066522   8.059592   8.049427 ]
 [ 8.228977   8.14119    9.215627  ...  8.059592   8.049427   7.762171 ]
 ...
 [ 7.8913307  8.360071   8.110427  ...  7.8172226  9.273878  10.3337755]
 [ 8.360071   8.110427   7.7752757 ...  9.273878  10.3337755  9.125872 ]
 [ 8.110427   7.7752757  7.3472996 ... 10.3337755  9.125872   8.891374 ]]

 

次に、モデルの学習で利用する学習データと、そのモデルの検証で利用するテストデータに分割します。

今回は、直近30日間で予測モデルの検証していきます。要するに、テストデータは最後のレコード1行のみになります。

学習データは、直近30日間のデータが説明変数にも目的変数にも混じっていないデータ（最後の30レコードを除いたデータセット）を利用します。

以下、コードです。

#
# データセットを学習データとテストデータに分割
#

#テストデータのレコード数
test_length = 1

#学習データ（予測対象期間のデータが混じっていない期間）
X_train = X[:-output_sequence,:] 
Y_train = Y[:-output_sequence,:]

#テストデータ（予測対象期間のデータ※最終行）
X_test = X[-test_length:,:]  
Y_test = Y[-test_length:,:]

 

これらのデータセットを正規化（0-1の範囲にスケーリング）します。この正規化したデータセットを使いモデル構築を検討していきます。

以下、コードです。

#
# 正規化（0-1の範囲にスケーリング）
#

# 説明変数X
scaler_X = MinMaxScaler(feature_range=(0, 1))
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)

# 目的変数Y
scaler_Y = MinMaxScaler(feature_range=(0, 1))
Y_train = scaler_Y.fit_transform(Y_train)

 

　Keras用の学習用データセットの生成

Keras用の学習用データセットを作ります。

以下、コードです。

#
# 学習用データセット（サンプル数、タイムステップ, 特徴量数）の形に再構成
#

# 再構成
X_train = np.reshape(X_train, (X_train.shape[0],X_train.shape[1], 1))
X_test = np.reshape(X_test, (X_test.shape[0],X_test.shape[1], 1))

# 確認
print('X_train:',X_train.shape)
print('X_test:',X_test.shape)

 

以下、実行結果です。

X_train: (2481, 365, 1)
X_test: (1, 365, 1)

 

　予測モデルの学習（学習データ利用）

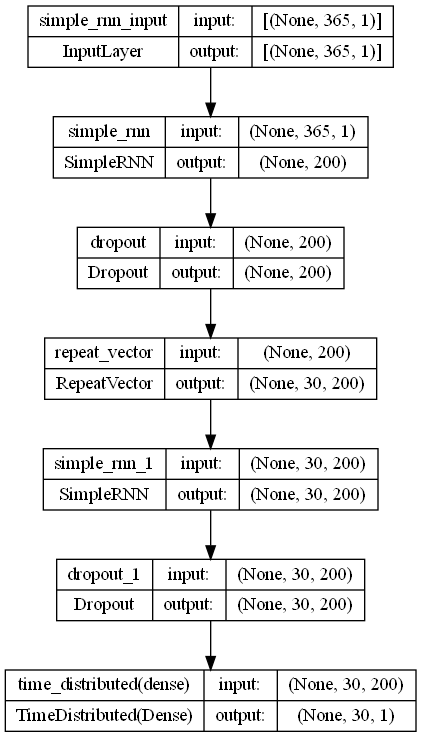
今回は、SimpleRNNでEncoder-Decoder型RNNを Sequential 形式で構築していきます。

モデルのインスタンスを作ります。

以下、コードです。

#
# インスタンスの生成
#

# モデル定義
model = Sequential()
model.add(SimpleRNN(200,input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(RepeatVector(output_sequence))
model.add(SimpleRNN(200, return_sequences=True))
model.add(Dropout(0.2))
model.add(TimeDistributed(Dense(1)))

# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mae'])

# モデルの視覚化
plot_model(model,show_shapes=True)

 

以下、実行結果です。

 

学習します。

以下、コードです。

# EaelyStoppingの設定
es = EarlyStopping(
    monitor='val_loss',
    mode='min',
    patience=20)

# 学習の実行
history = model.fit(
    X_train,
    Y_train,
    epochs=1000,
    batch_size=100,
    validation_split=0.2,
    callbacks=[es] ,
    verbose=1,
)

 

以下、実行結果です。

Epoch 1/1000
20/20 [==============================] - 7s 252ms/step - loss: 0.2723 - mae: 0.3702 - val_loss: 0.0141 - val_mae: 0.0915
Epoch 2/1000
20/20 [==============================] - 5s 232ms/step - loss: 0.0371 - mae: 0.1491 - val_loss: 0.0093 - val_mae: 0.0723
Epoch 3/1000
20/20 [==============================] - 5s 242ms/step - loss: 0.0228 - mae: 0.1160 - val_loss: 0.0074 - val_mae: 0.0630
.........
Epoch 146/1000
20/20 [==============================] - 6s 276ms/step - loss: 0.0075 - mae: 0.0616 - val_loss: 0.0058 - val_mae: 0.0568
Epoch 147/1000
20/20 [==============================] - 6s 280ms/step - loss: 0.0077 - mae: 0.0625 - val_loss: 0.0059 - val_mae: 0.0579
Epoch 148/1000
20/20 [==============================] - 5s 268ms/step - loss: 0.0077 - mae: 0.0629 - val_loss: 0.0056 - val_mae: 0.0552

 

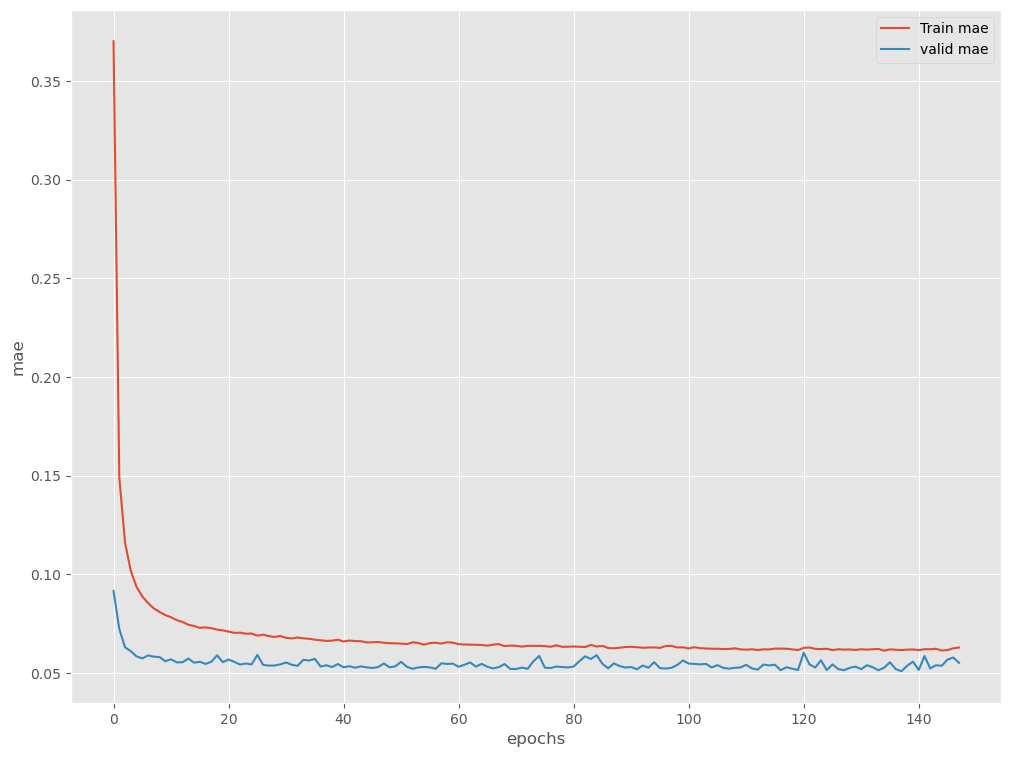
学習結果を出力します。

以下、コードです。

# 学習結果の出力
plt.plot(history.history['mae'], label='Train mae')
plt.plot(history.history['val_mae'], label='valid mae')
plt.ylabel('mae')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()

 

以下、実行結果です。

 

　予測モデルのテスト（テストデータ利用）

テストデータ期間を予測します。

以下、コードです。

#
# 予測の実施
#

# テストデータ期間
test_pred = model.predict(X_test)
test_pred = scaler_Y.inverse_transform(test_pred.reshape(1,-1)).T

print(test_pred) #確認

 

以下、実行結果です。

1/1 [==============================] - 0s 288ms/step
[[8.240319 ]
 [7.7578025]
 [7.662585 ]
.........
 [8.569353 ]
 [8.335754 ]
 [7.980287 ]]

 

精度指標を求めます。

以下、コードです。

#
# 予測モデルのテスト（テストデータ利用）
#

print('RMSE:\n', np.sqrt(mean_squared_error(df.y[-output_sequence:], test_pred)))
print('MAE:\n', mean_absolute_error(df.y[-output_sequence:], test_pred)) 
print('MAPE:\n', mean_absolute_percentage_error(df.y[-output_sequence:], test_pred))

 

以下、実行結果です。

RMSE:
 0.5777660772402515
MAE:
 0.42551014021589506
MAPE:
 0.048489167577992785

 

予測値をグラフ化します。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

ax.set_ylim([0, 15])

# 実測値の描写
ax.plot(df.index[-output_sequence:], df.y[-output_sequence:], label='actual(test)', color='gray')

# 予測値の描写
ax.plot(df.index[-output_sequence:], test_pred, label="predicted", color="c") 

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

Airline Passengers（飛行機乗客数）

　データセットの読み込み

データセットを読み込みます。

以下、コードです。

#
# 必要なデータセット（時系列データ）の読み込み
#

# データセット読み込み
url='https://www.salesanalytics.co.jp/591h'
df = pd.read_csv(url)
df.columns = ['ds','y']

# データ確認
print(df.info()) #変数の情報
print(df.head()) #データの一部

 

以下、実行結果です。

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 144 entries, 0 to 143
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype 
---  ------  --------------  ----- 
 0   ds      144 non-null    object
 1   y       144 non-null    int64 
dtypes: int64(1), object(1)
memory usage: 2.4+ KB
None
           ds    y
0  1949-01-01  112
1  1949-02-01  118
2  1949-03-01  132
3  1949-04-01  129
4  1949-05-01  121

 

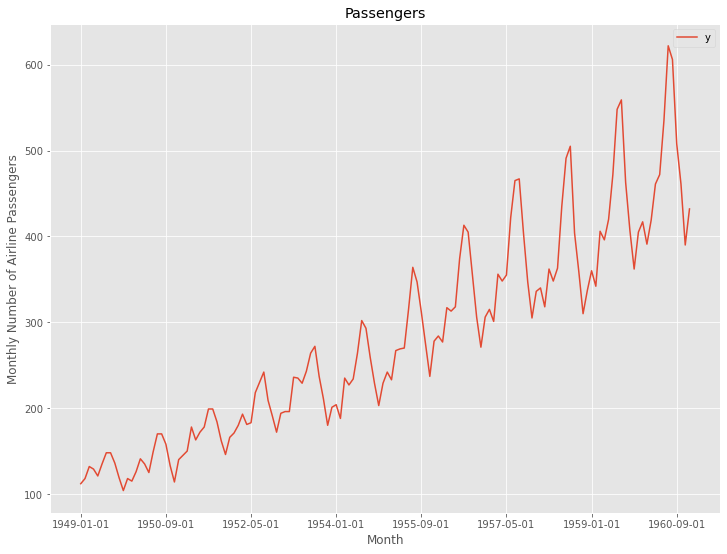
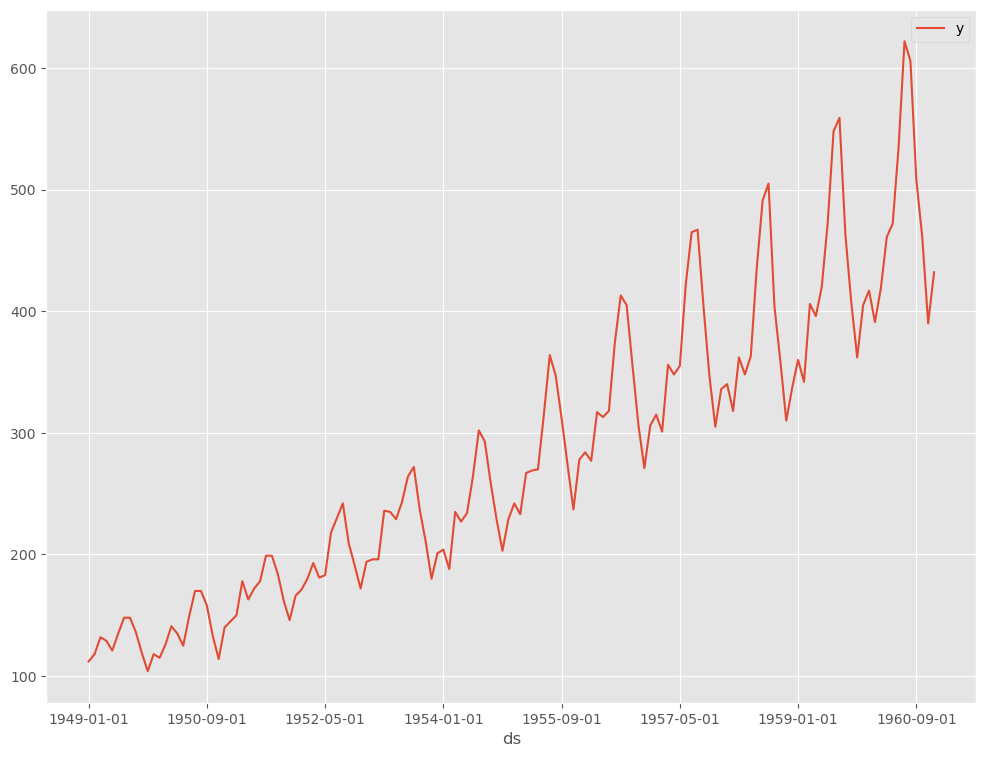
データを折れ線グラフで表現してみます。

以下、コードです。

#
# 時系列データのグラフ化（折れ線グラフ）
#

df.plot(kind='line',x='ds', y='y')

 

以下、実行結果です。

 

　Keras用データセットの準備

先程読み込んだデータセットはDataFrame形式です。NumPy配列へ変換します。

以下、コードです。

#
# 配列のデータセットに変換
#

dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32')    #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換

print(dataset) #確認

 

以下、実行結果です。

[[112.]
 [118.]
 [132.]
.........
 [461.]
 [390.]
 [432.]]

 

このNumPy配列へ変換したデータセット（1変量の時系列データ）から、説明変数と目的変数を生成します。

今回は、24ヶ月の過去データから12ヶ月先を予測するモデルを構築することを想定しています。

以下、コードです。

#
# 説明変数Xと目的変数Yの生成
#

# Time Steps の長さ
input_sequence = 24

# 予測する長さ
output_sequence = 12

# データセット生成
X, Y = gen_dataset(dataset, input_sequence, output_sequence)

# 確認
print('X:',X.shape)
print(X)
print()
print('Y:',Y.shape)
print(Y)

 

以下、実行結果です。

X: (109, 24)
[[112. 118. 132. ... 133. 114. 140.]
 [118. 132. 129. ... 114. 140. 145.]
 [132. 129. 121. ... 140. 145. 150.]
 ...
 [305. 336. 340. ... 559. 463. 407.]
 [336. 340. 318. ... 463. 407. 362.]
 [340. 318. 362. ... 407. 362. 405.]]

Y: (109, 12)
[[145. 150. 178. ... 162. 146. 166.]
 [150. 178. 163. ... 146. 166. 171.]
 [178. 163. 172. ... 166. 171. 180.]
 ...
 [362. 405. 417. ... 606. 508. 461.]
 [405. 417. 391. ... 508. 461. 390.]
 [417. 391. 419. ... 461. 390. 432.]]

 

次に、モデルの学習で利用する学習データと、そのモデルの検証で利用するテストデータに分割します。

今回は、直近12ヶ月間で予測モデルの検証していきます。要するに、テストデータは最後のレコード1行のみになります。

学習データは、直近12ヶ月間のデータが説明変数にも目的変数にも混じっていないデータ（最後の12レコードを除いたデータセット）を利用します。

以下、コードです。

#
# データセットを学習データとテストデータに分割
#

#テストデータのレコード数
test_length = 1

#学習データ（予測対象期間のデータが混じっていない期間）
X_train = X[:-output_sequence,:] 
Y_train = Y[:-output_sequence,:]

#テストデータ（予測対象期間のデータ※最終行）
X_test = X[-test_length:,:]  
Y_test = Y[-test_length:,:]

 

これらのデータセットを正規化（0-1の範囲にスケーリング）します。この正規化したデータセットを使いモデル構築を検討していきます。

以下、コードです。

#
# 正規化（0-1の範囲にスケーリング）
#

# 説明変数X
scaler_X = MinMaxScaler(feature_range=(0, 1))
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)

# 目的変数Y
scaler_Y = MinMaxScaler(feature_range=(0, 1))
Y_train = scaler_Y.fit_transform(Y_train)

 

　Keras用の学習用データセットの生成

Keras用の学習用データセットを作ります。

以下、コードです。

#
# 学習用データセット（サンプル数、タイムステップ, 特徴量数）の形に再構成
#

# 再構成
X_train = np.reshape(X_train, (X_train.shape[0],X_train.shape[1], 1))
X_test = np.reshape(X_test, (X_test.shape[0],X_test.shape[1], 1))

# 確認
print('X_train:',X_train.shape)
print('X_test:',X_test.shape)

 

以下、実行結果です。

X_train: (97, 24, 1)
X_test: (1, 24, 1)

 

　予測モデルの学習（学習データ利用）

今回は、SimpleRNNでEncoder-Decoder型RNNを Sequential 形式で構築していきます。

モデルのインスタンスを作ります。

以下、コードです。

#
# インスタンスの生成
#

# モデル定義
model = Sequential()
model.add(SimpleRNN(200,input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(RepeatVector(output_sequence))
model.add(SimpleRNN(200, return_sequences=True))
model.add(Dropout(0.2))
model.add(TimeDistributed(Dense(1)))

# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mae'])

# モデルの視覚化
plot_model(model,show_shapes=True)

 

以下、実行結果です。

 

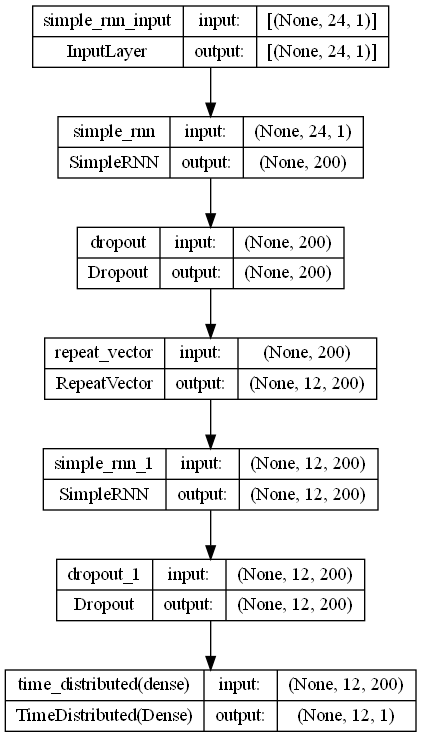
学習します。

以下、コードです。

# EaelyStoppingの設定
es = EarlyStopping(
    monitor='val_loss',
    mode='min',
    patience=20)

# 学習の実行
history = model.fit(
    X_train,
    Y_train,
    epochs=1000,
    batch_size=12,
    validation_split=0.2,
    callbacks=[es] ,
    verbose=1,
)

 

以下、実行結果です。

Epoch 1/1000
7/7 [==============================] - 2s 75ms/step - loss: 0.3509 - mae: 0.4140 - val_loss: 0.0730 - val_mae: 0.2254
Epoch 2/1000
7/7 [==============================] - 0s 21ms/step - loss: 0.0602 - mae: 0.1866 - val_loss: 0.0361 - val_mae: 0.1536
Epoch 3/1000
7/7 [==============================] - 0s 21ms/step - loss: 0.0330 - mae: 0.1352 - val_loss: 0.0421 - val_mae: 0.1634
......
Epoch 64/1000
7/7 [==============================] - 0s 18ms/step - loss: 0.0034 - mae: 0.0444 - val_loss: 0.0101 - val_mae: 0.0861
Epoch 65/1000
7/7 [==============================] - 0s 19ms/step - loss: 0.0034 - mae: 0.0448 - val_loss: 0.0055 - val_mae: 0.0610
Epoch 66/1000
7/7 [==============================] - 0s 20ms/step - loss: 0.0031 - mae: 0.0422 - val_loss: 0.0041 - val_mae: 0.0532

 

学習結果を出力します。

以下、コードです。

# 学習結果の出力
plt.plot(history.history['mae'], label='Train mae')
plt.plot(history.history['val_mae'], label='valid mae')
plt.ylabel('mae')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()

 

以下、実行結果です。

 

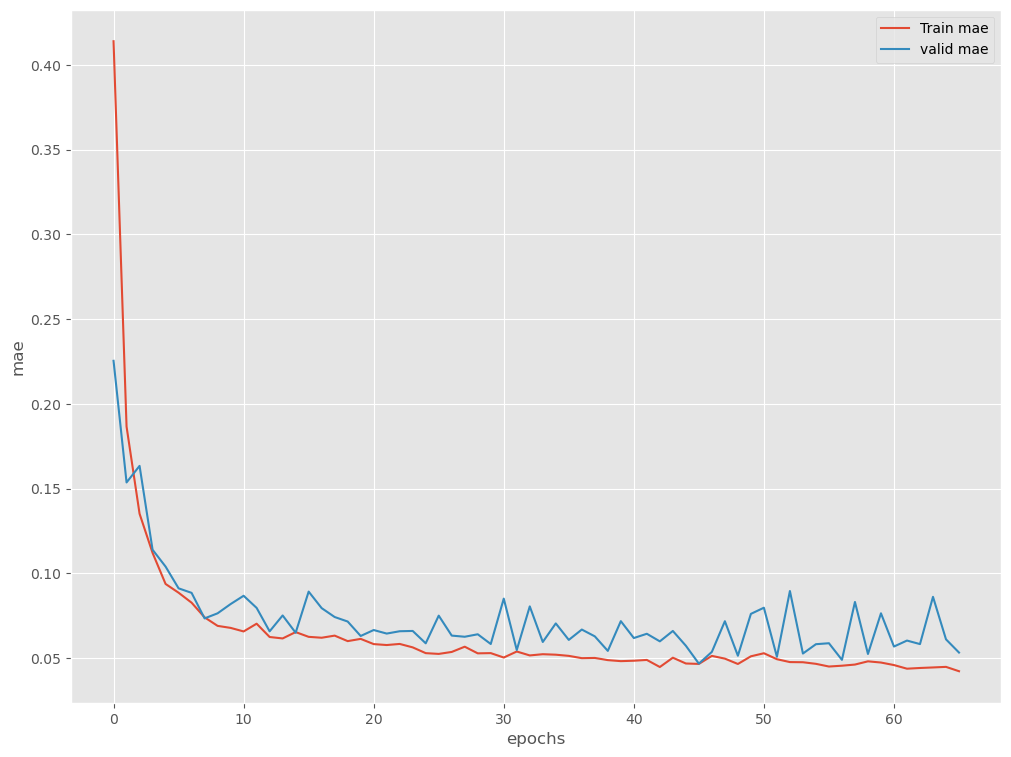
　予測モデルのテスト（テストデータ利用）

テストデータ期間を予測します。

以下、コードです。

#
# 予測の実施
#

# テストデータ期間
test_pred = model.predict(X_test)
test_pred = scaler_Y.inverse_transform(test_pred.reshape(1,-1)).T

print(test_pred) #確認

 

以下、実行結果です。

1/1 [==============================] - 0s 288ms/step
[[406.472  ]
 [420.2418 ]
 [427.3197 ]
 [430.76535]
 [459.9534 ]
 [528.2502 ]
 [598.82245]
 [595.47327]
 [536.1719 ]
 [455.53894]
 [411.09216]
 [435.0235 ]]

 

精度指標を求めます。

以下、コードです。

#
# 予測モデルのテスト（テストデータ利用）
#

print('RMSE:\n', np.sqrt(mean_squared_error(df.y[-output_sequence:], test_pred)))
print('MAE:\n', mean_absolute_error(df.y[-output_sequence:], test_pred)) 
print('MAPE:\n', mean_absolute_percentage_error(df.y[-output_sequence:], test_pred))

 

以下、実行結果です。

RMSE:
 18.406210728346238
MAE:
 15.714454650878906
MAPE:
 0.033885986945439865

 

予測値をグラフ化します。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

ax.set_ylim([0, 800])

# 実測値の描写
ax.plot(df.index[-output_sequence:], df.y[-output_sequence:], label='actual(test)', color='gray')

# 予測値の描写
ax.plot(df.index[-output_sequence:], test_pred, label="predicted", color="c") 

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

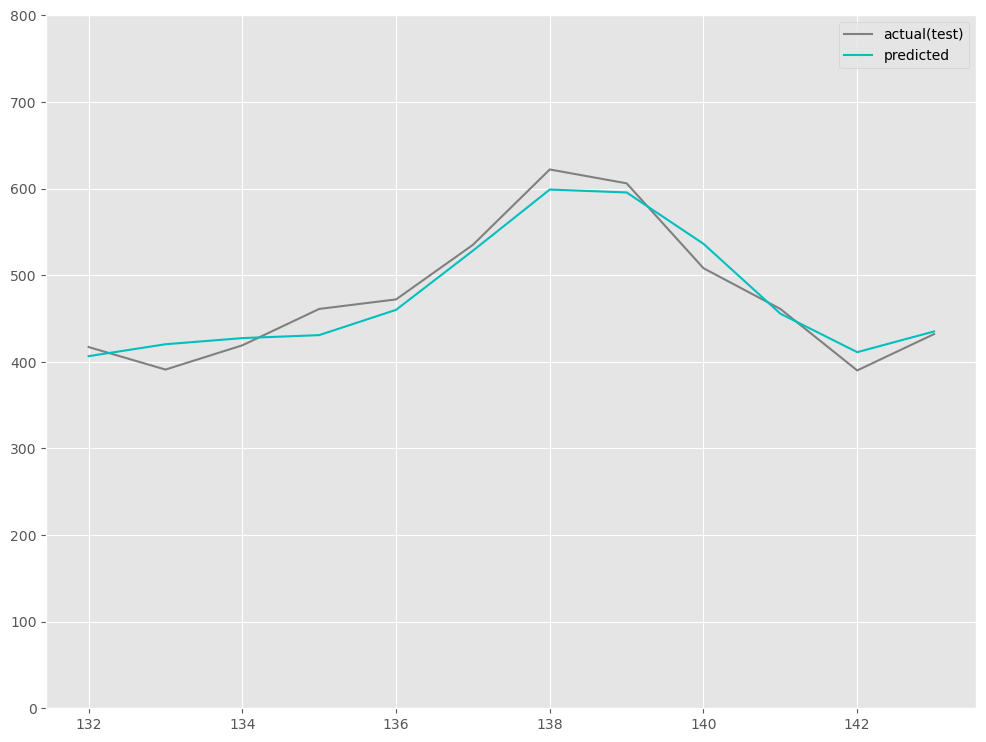
より高精度な時系列予測モデル構築に向けて

より高精度な予測モデルを目指すのなら、幾つか方法論があります。

  • 時系列データを定常化して構築する
  • トレンド・季節性などを分解し構築する
  • 双方向LSTM（Bidirectional LSTM）を取り入れる
  • Time2Vec層を取り入れる
  • Attentionを上手く使い構築する

などなど色々あります。

AttentionはTransformerの流行の影響で注目されていますが、Attentionを組み込んだからと言って必ず精度が向上するわけではありません。

 

まとめ

今回は、時系列データに対するEncoder-Decoder型RNN（LSTMやGRUを含む）モデルをKeras(TensorFlow)で作りました。

次回は、双方向LSTM（Bidirectional LSTM）で実施する場合について説明します。

Python Keras(TensorFlow)で作る深層学習(Deep Learning)時系列予測モデル(その7) Bidirectional RNN（双方向RNN）モデルで複数先予測