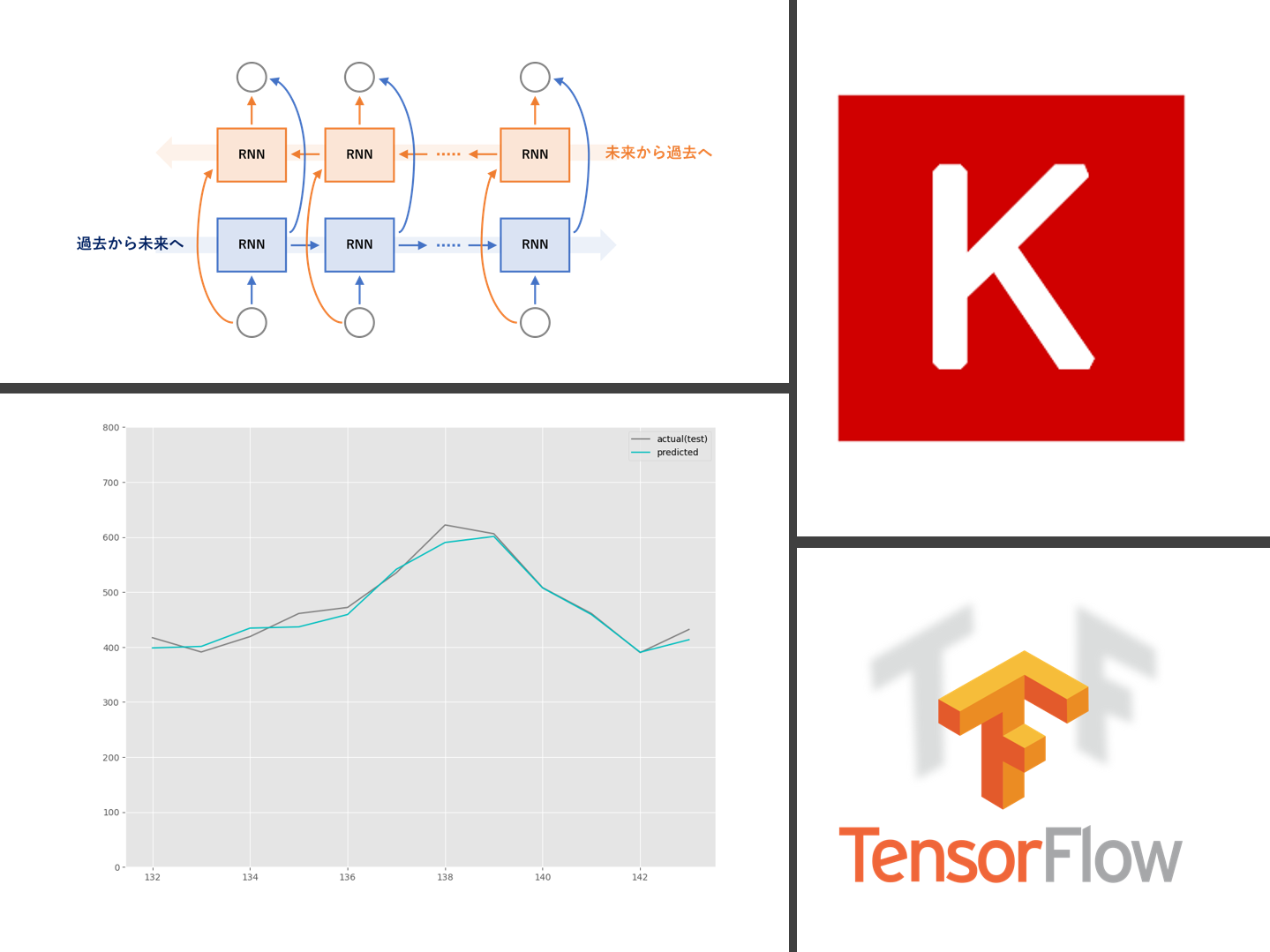
Python Keras(TensorFlow)で作る
深層学習(Deep Learning)時系列予測モデル(その7)

Bidirectional RNN（双方向RNN）モデルで複数先予測

2942
Python Keras(TensorFlow)で作る深層学習(Deep Learning)時系列予測モデル(その7) Bidirectional RNN（双方向RNN）モデルで複数先予測

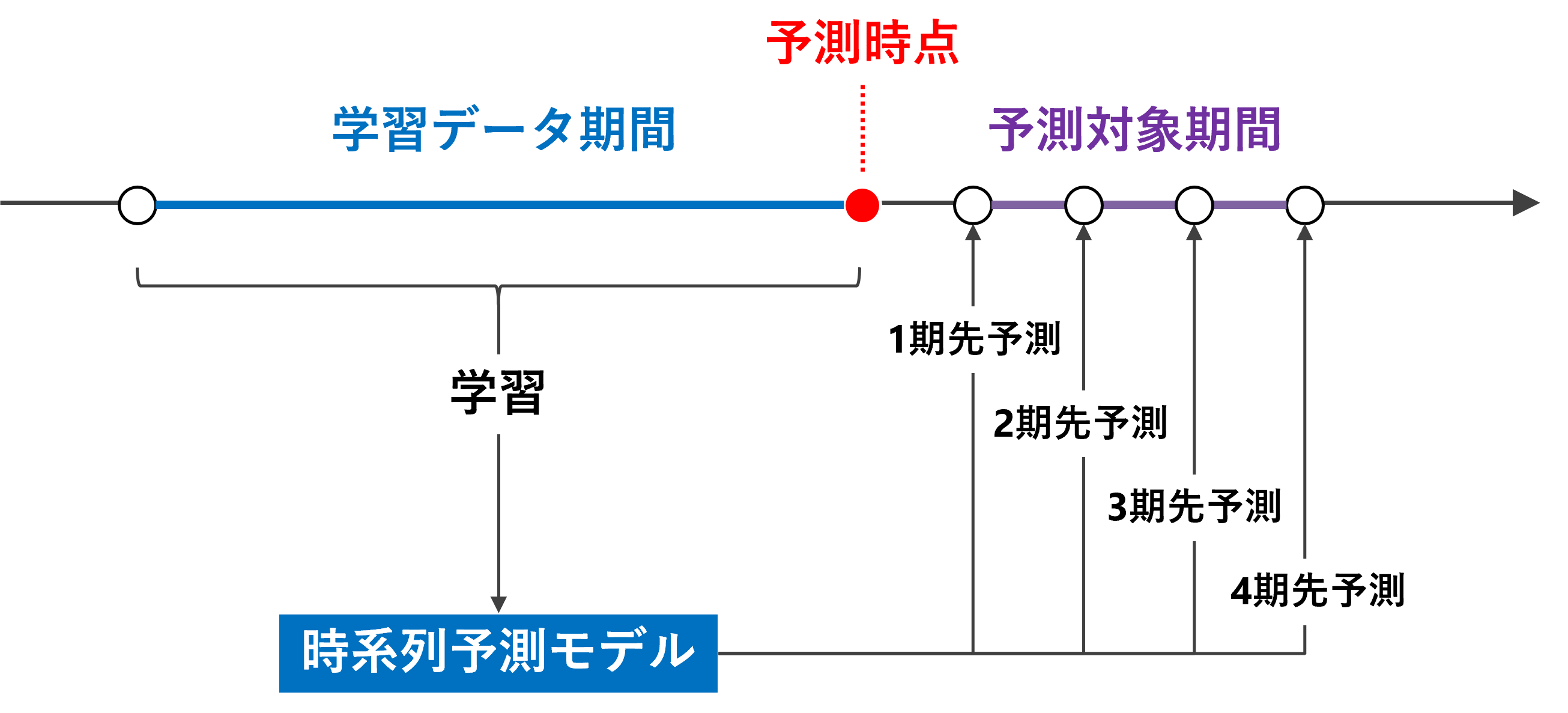
売上などの時系列データを予測するモデルは、基本となるのは1期先予測（1-Step ahead prediction）ですが、実務では複数先予測（Multi-Step ahead prediction）が求められます。

ニューラルネットワークの場合、どうなるのでしょうか？

幾つかやり方があります。

その中の1つに、時系列の多変量予測モデルを1つ作る方法があります。言い換えると、目的変数yを多変量化（ベクトル化）し予測モデルを1つ作るということです。

RNN（SimpleRNNやLSTM、GRU）をそのまま利用する方法を、以前お話ししました。正直、高精度な予測モデルができる可能性はありますが、多くの場合そうでもありません。

RNN（SimpleRNNやLSTM、GRU）を発展したものにBidirectional RNN（双方向RNN）というものがあります。

ちなみに、LSTMの場合はBidirectional LSTM（双方向LSTM）、GRUの場合はBidirectional GRU（双方向GRU）と呼ばれます。

今回は、Bidirectional Simple RNN（双方向Simple RNN）を利用し、目的変数yを多変量化（ベクトル化）し予測モデルを1つ作る場合についてお話しします。

Bidirectional RNN（双方向RNN）

RNN（SimpleRNNやLSTM、GRU）は、通常は過去から未来へ向かい順伝播していきます。

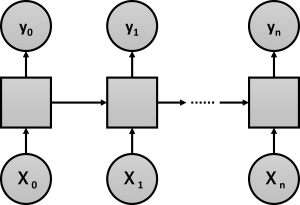
このRNN（SimpleRNNやLSTM、GRU）は一層である必要はなく、多層化することがあります。多層化する方法は、簡単なものでは主に3つあります。

  • 順伝播するRNN（通常のRNN）を単純に積み重ね多層化する
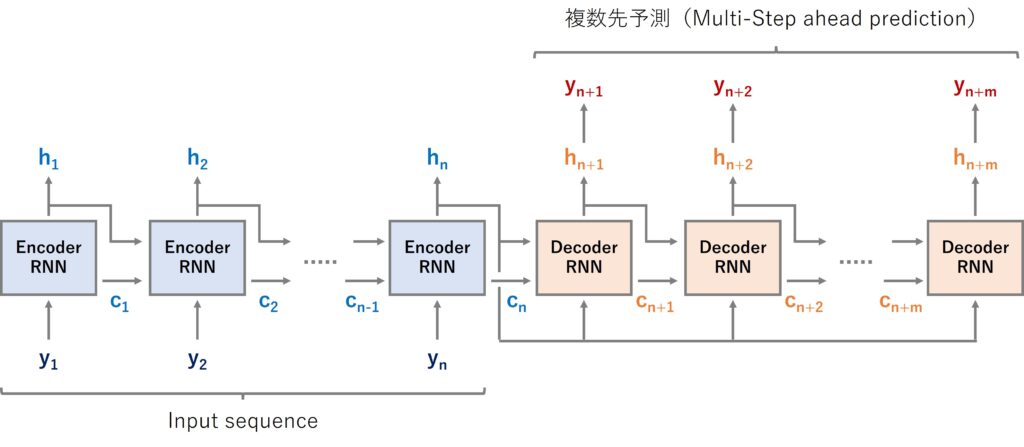
  • 順伝播するRNNでEncoder層（RNN）とDecoder層（RNN）を構築し多層化する
  • 順伝播するRNN（通常のRNN）と逆伝播するRNNで多層化する

2番目のものが前回扱った時系列Encoder-Decoder(Seq2Seq)モデルです。

今回扱うのが、3番目の「順伝播するRNN（通常のRNN）と逆伝播するRNNで多層化」で、SimpleRNNで双方向（順伝播と逆伝播）化したモデルです。

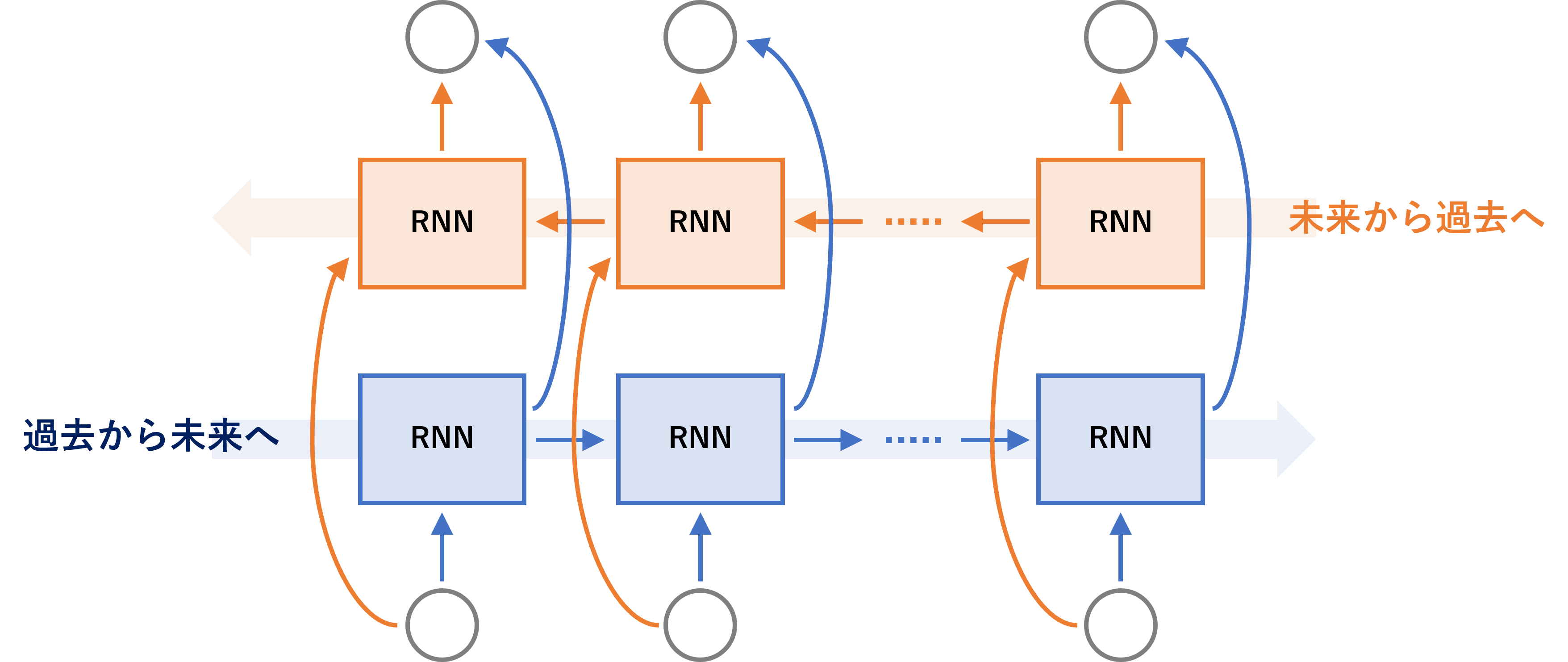
Bidirectional RNN（双方向RNN）モデルと言います。

モデル構築は非常に簡単で、Keras(TensorFlow)の場合、例えばSimpleRNN(…)と記述していた箇所をBidirectional(SimpleRNN(…))とするだけです。

 

サンプルデータ　※前回と同じ

サンプルデータは、次の2つです。

  • Peyton ManningのWikipediaのPV（ページビュー）
  • Airline Passengers（飛行機乗客数）

 

　Peyton ManningのWikipediaのPV（ページビュー）

Prophetで提供されているサンプルデータ（example_wp_log_peyton_manning.csv）です。

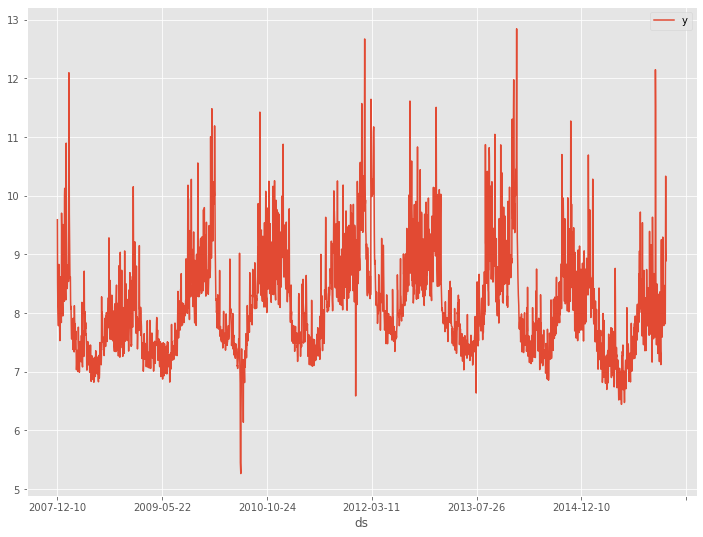
facebook/prophetのGitHubからダウンロードして使って頂くか、弊社のHPからダウンロードして使って頂ければと思います。

facebook/prophetのGitHub上のデータ
https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/bgr8

このデータセットは、説明変数のない目的変数が1変量の時系列データで、目的変数は日単位のPV（ページビュー数）です。

今回は、365日間の過去データから30日先を予測するモデルを構築します。

 

　Airline Passengers（飛行機乗客数）

Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

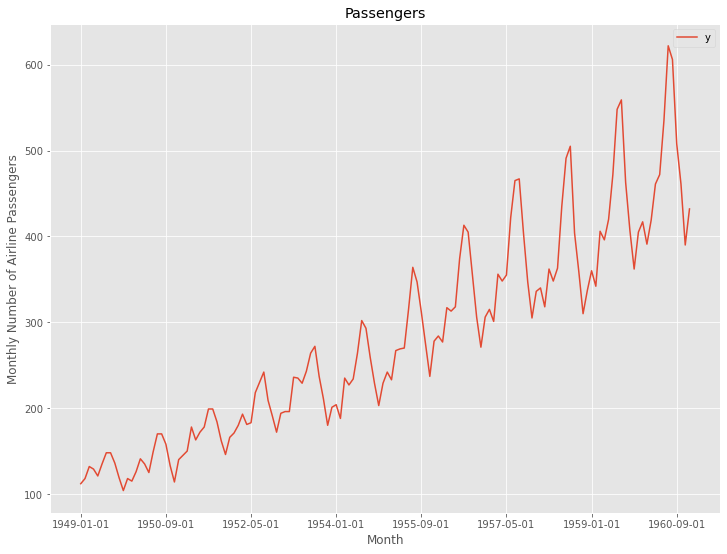
弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h

このデータセットも、説明変数のない目的変数が1変量の時系列データで、目的変数は月単位の飛行機乗客数です。

 

データセットの形式のお話し　※前回と同じ

Keras（TensorFlow）のRNNのデータセットは、以下のような3元構造が基本になっています。

[サンプル（samples）,タイムステップ（time_steps）,特徴量（features）]

 

時系列データの特徴量の1つとして、ラグ変数というものがあります。

例えば、日販（1日の売上）であれば、「ラグ1の変数」とは「1日前の日販の変数」、「ラグ2の変数」とは「2日前の日販の変数」などです。

目的変数のラグ変数を作り、インプットデータXとアウトプットデータyを作っていきます。

 

例えば、以下のような日単位の時系列データがあったとします。

y(t=0),y(t=1),y(t=2),…

このとき、過去365日間のデータを使い、近未来30日間を予測するために、以下のようなデータセットを準備します。

インプットデータX アウトプットデータy
index x1 x2 … x365 y1 y2 … y30
0 y(t=394) y(t=393) … y(t=30) y(t=29) y(t=28) … y(t=0)
1 y(t=395) y(t=394) … y(t=31) y(t=30) y(t=29) … y(t=1)
2 y(t=396) y(t=395) … y(t=32) y(t=31) y(t=30) … y(t=2)
3 y(t=397) y(t=396) … y(t=33) y(t=32) y(t=31) … y(t=3)
4 y(t=398) y(t=397) … y(t=34) y(t=33) y(t=32) … y(t=4)
5 y(t=399) y(t=398) … y(t=35) y(t=34) y(t=33) … y(t=5)
6 y(t=400) y(t=399) … y(t=36) y(t=35) y(t=34) … y(t=6)
7 y(t=401) y(t=400) … y(t=37) y(t=36) y(t=35) … y(t=7)
8 y(t=402) y(t=401) … y(t=38) y(t=37) y(t=36) … y(t=8)
9 y(t=403) y(t=402) … y(t=39) y(t=38) y(t=37) … y(t=9)

 

予測精度の評価指標　※前回と同じ

今回の予測精度の評価指標も今までと同じで、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

 

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

準備

　必要なモジュールの読み込み

必要なモジュールを読み込みます。

以下、コードです。

#
# 必要なモジュールの読み込み
#

import numpy as np
import pandas as pd

from keras.models import Sequential
from keras.models import Model
from keras.layers import *
from keras.callbacks import EarlyStopping
from tensorflow.keras.utils import plot_model

from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

　説明変数と目的変数を生成する関数

時系列データからラグ特徴量を作り、説明変数と目的変数を生成する関数を作ります。

以下、コードです。

#
# データセット生成関数
#

def gen_dataset(dataset, input_sequence, output_sequence=1):
    
    X = []
    y = []
    
    for i in range(len(dataset) - input_sequence - output_sequence + 1):
        a = i + input_sequence
        b = a + output_sequence
        X.append(dataset[i:a, 0]) #ラグ特徴量
        y.append(dataset[a:b, 0]) #目的変数
        
    return np.array(X), np.array(y)

 

では、ここから以下のサンプルデータごとに説明していきます。

  • Peyton ManningのWikipediaのPV（ページビュー）
  • Airline Passengers（飛行機乗客数）

 

Peyton ManningのWikipediaのPV（ページビュー）

　データセットの読み込み

データセットを読み込みます。

以下、コードです。

#
# 必要なデータセット（時系列データ）の読み込み
#

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/bgr8'
df = pd.read_csv(url)

# データ確認
df.info() #変数の情報
df.head() #データの一部

 

以下、実行結果です。

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2905 entries, 0 to 2904
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   ds      2905 non-null   object 
 1   y       2905 non-null   float64
dtypes: float64(1), object(1)
memory usage: 45.5+ KB
None
           ds         y
0  2007-12-10  9.590761
1  2007-12-11  8.519590
2  2007-12-12  8.183677
3  2007-12-13  8.072467
4  2007-12-14  7.893572

 

データを折れ線グラフで表現してみます。

以下、コードです。

#
# 時系列データのグラフ化（折れ線グラフ）
#

df.plot(kind='line',x='ds', y='y')

 

以下、実行結果です。

 

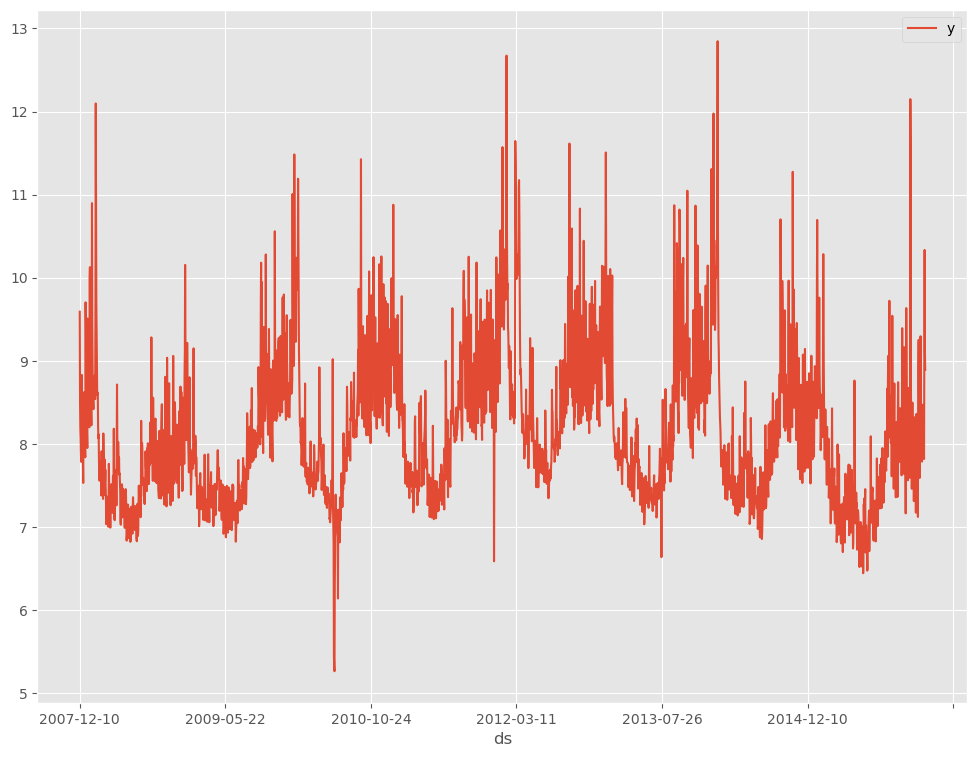
　Keras用データセットの準備

先程読み込んだデータセットはDataFrame形式です。NumPy配列へ変換します。

以下、コードです。

#
# 配列のデータセットに変換
#

dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32')    #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換

print(dataset) #確認

 

以下、実行結果です。

[[ 9.590761 ]
 [ 8.51959  ]
 [ 8.183677 ]
 ...
 [10.3337755]
 [ 9.125872 ]
 [ 8.891374 ]]

 

このNumPy配列へ変換したデータセット（1変量の時系列データ）から、説明変数と目的変数を生成します。

今回は、365日間の過去データから30日先を予測するモデルを構築することを想定しています。

以下、コードです。

#
# 説明変数Xと目的変数Yの生成
#

# Time Steps の長さ
input_sequence = 365

# 予測する長さ
output_sequence = 30

# データセット生成
X, Y = gen_dataset(dataset, input_sequence, output_sequence)

# 確認
print('X:',X.shape)
print(X)
print()
print('Y:',Y.shape)
print(Y)

 

以下、実行結果です。

X: (2511, 365)
[[ 9.590761   8.51959    8.183677  ... 10.153818   9.267855   8.434246 ]
 [ 8.51959    8.183677   8.072468  ...  9.267855   8.434246   8.137689 ]
 [ 8.183677   8.072468   7.893572  ...  8.434246   8.137689   8.044947 ]
 ...
 [ 8.1022835  7.8336     7.522941  ...  7.5918617  7.528869   7.1716566]
 [ 7.8336     7.522941   7.9102235 ...  7.528869   7.1716566  7.8913307]
 [ 7.522941   7.9102235  8.365439  ...  7.1716566  7.8913307  8.360071 ]]

Y: (2511, 30)
[[ 8.137689   8.044947   8.228977  ...  8.062118   8.066522   8.059592 ]
 [ 8.044947   8.228977   8.14119   ...  8.066522   8.059592   8.049427 ]
 [ 8.228977   8.14119    9.215627  ...  8.059592   8.049427   7.762171 ]
 ...
 [ 7.8913307  8.360071   8.110427  ...  7.8172226  9.273878  10.3337755]
 [ 8.360071   8.110427   7.7752757 ...  9.273878  10.3337755  9.125872 ]
 [ 8.110427   7.7752757  7.3472996 ... 10.3337755  9.125872   8.891374 ]]

 

次に、モデルの学習で利用する学習データと、そのモデルの検証で利用するテストデータに分割します。

今回は、直近30日間で予測モデルの検証していきます。要するに、テストデータは最後のレコード1行のみになります。

学習データは、直近30日間のデータが説明変数にも目的変数にも混じっていないデータ（最後の30レコードを除いたデータセット）を利用します。

以下、コードです。

#
# データセットを学習データとテストデータに分割
#

#テストデータのレコード数
test_length = 1

#学習データ（予測対象期間のデータが混じっていない期間）
X_train = X[:-output_sequence,:] 
Y_train = Y[:-output_sequence,:]

#テストデータ（予測対象期間のデータ※最終行）
X_test = X[-test_length:,:]  
Y_test = Y[-test_length:,:]

 

これらのデータセットを正規化（0-1の範囲にスケーリング）します。この正規化したデータセットを使いモデル構築を検討していきます。

以下、コードです。

#
# 正規化（0-1の範囲にスケーリング）
#

# 説明変数X
scaler_X = MinMaxScaler(feature_range=(0, 1))
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)

# 目的変数Y
scaler_Y = MinMaxScaler(feature_range=(0, 1))
Y_train = scaler_Y.fit_transform(Y_train)

 

　Keras用の学習用データセットの生成

Keras用の学習用データセットを作ります。

以下、コードです。

#
# 学習用データセット（サンプル数、タイムステップ, 特徴量数）の形に再構成
#

# 再構成
X_train = np.reshape(X_train, (X_train.shape[0],X_train.shape[1], 1))
X_test = np.reshape(X_test, (X_test.shape[0],X_test.shape[1], 1))

# 確認
print('X_train:',X_train.shape)
print('X_test:',X_test.shape)

 

以下、実行結果です。

X_train: (2481, 365, 1)
X_test: (1, 365, 1)

 

　予測モデルの学習（学習データ利用）

今回は、SimpleRNNでBidirectional RNN（双方向RNN）を Sequential 形式で構築していきます。単に、RNNを追加するコードに「Bidirectional」が付け加わっただけです。

モデルのインスタンスを作ります。

以下、コードです。

#
# インスタンスの生成
#

# モデル定義
model = Sequential()
model.add(Bidirectional(SimpleRNN(200),
                        input_shape=(X_train.shape[1], X_train.shape[2])))          
model.add(Dropout(0.2))
model.add(Dense(units=output_sequence))

# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mae'])

# モデルの視覚化
plot_model(model,show_shapes=True)

 

以下、実行結果です。

 

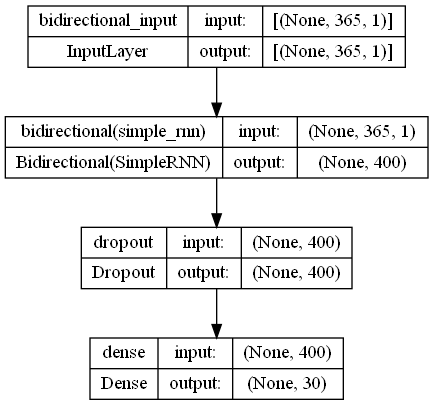
学習します。

以下、コードです。

# EaelyStoppingの設定
es = EarlyStopping(
    monitor='val_loss',
    mode='min',
    patience=20)

# 学習の実行
history = model.fit(
    X_train,
    Y_train,
    epochs=1000,
    batch_size=100,
    validation_split=0.2,
    callbacks=[es] ,
    verbose=0,
)

 

　予測モデルのテスト（テストデータ利用）

テストデータ期間を予測します。

以下、コードです。

#
# 予測の実施
#

# テストデータ期間
test_pred = model.predict(X_test)
test_pred = scaler_Y.inverse_transform(test_pred.reshape(1,-1)).T

print(test_pred) #確認

 

以下、実行結果です。

[[8.572349 ]
 [7.9938493]
 [7.7313504]
 [7.714966 ]
 [7.72323  ]
 [7.953319 ]
 [8.68514  ]
 [8.58083  ]
 [8.176232 ]
 [8.073722 ]
 [7.959346 ]
 [7.852381 ]
 [8.252636 ]
 [8.865088 ]
 [8.677817 ]
 [8.336045 ]
 [8.223161 ]
 [8.188505 ]
 [8.107517 ]
 [8.727009 ]
 [9.134221 ]
 [8.958569 ]
 [8.456622 ]
 [8.410385 ]
 [8.279283 ]
 [8.308097 ]
 [8.670389 ]
 [9.156925 ]
 [8.955848 ]
 [8.676446 ]]

 

精度指標を求めます。

以下、コードです。

#
# 予測モデルのテスト（テストデータ利用）
#

print('RMSE:\n', np.sqrt(mean_squared_error(df.y[-output_sequence:], test_pred)))
print('MAE:\n', mean_absolute_error(df.y[-output_sequence:], test_pred)) 
print('MAPE:\n', mean_absolute_percentage_error(df.y[-output_sequence:], test_pred))

 

以下、実行結果です。

RMSE:
 0.4767436707744991
MAE:
 0.38658771403138986
MAPE:
 0.0457602160835292

 

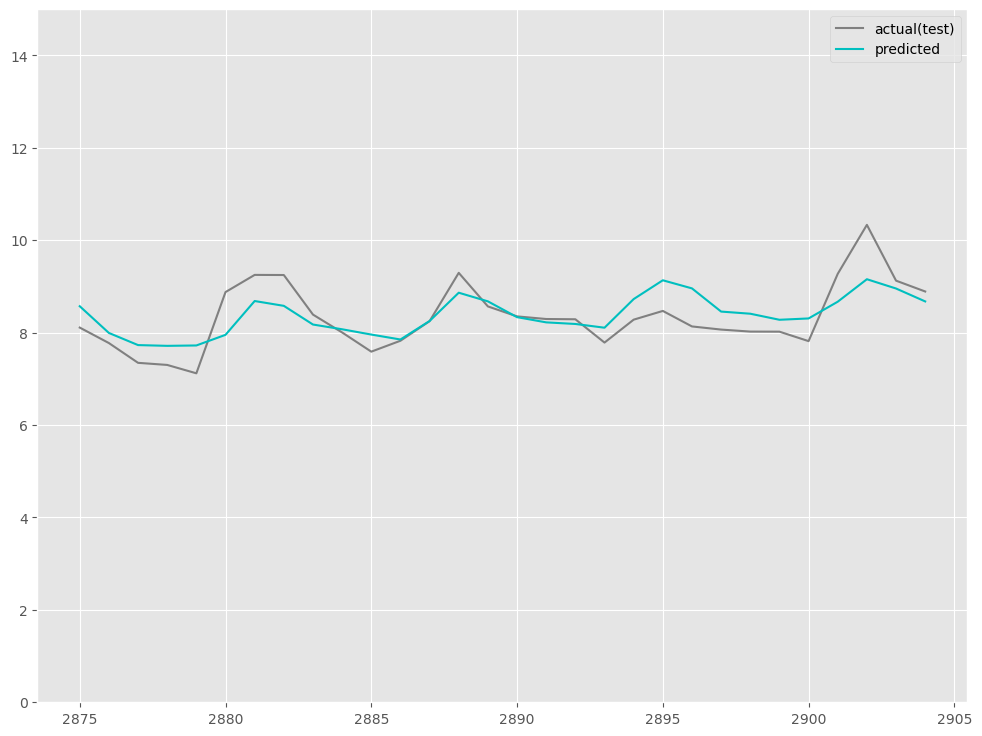
予測値をグラフ化します。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

ax.set_ylim([0, 15])

# 実測値の描写
ax.plot(df.index[-output_sequence:], df.y[-output_sequence:], label='actual(test)', color='gray')

# 予測値の描写
ax.plot(df.index[-output_sequence:], test_pred, label="predicted", color="c") 

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

ちなみに、前回の時系列Encoder-Decoder(Seq2Seq)モデルの場合の精度は以下です。

RMSE:
 0.5777660772402515
MAE:
 0.42551014021589506
MAPE:
 0.048489167577992785

 

Airline Passengers（飛行機乗客数）

　データセットの読み込み

データセットを読み込みます。

以下、コードです。

#
# 必要なデータセット（時系列データ）の読み込み
#

# データセット読み込み
url='https://www.salesanalytics.co.jp/591h'
df = pd.read_csv(url)
df.columns = ['ds','y']

# データ確認
print(df.info()) #変数の情報
print(df.head()) #データの一部

 

以下、実行結果です。

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 144 entries, 0 to 143
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype 
---  ------  --------------  ----- 
 0   ds      144 non-null    object
 1   y       144 non-null    int64 
dtypes: int64(1), object(1)
memory usage: 2.4+ KB
None
           ds    y
0  1949-01-01  112
1  1949-02-01  118
2  1949-03-01  132
3  1949-04-01  129
4  1949-05-01  121

 

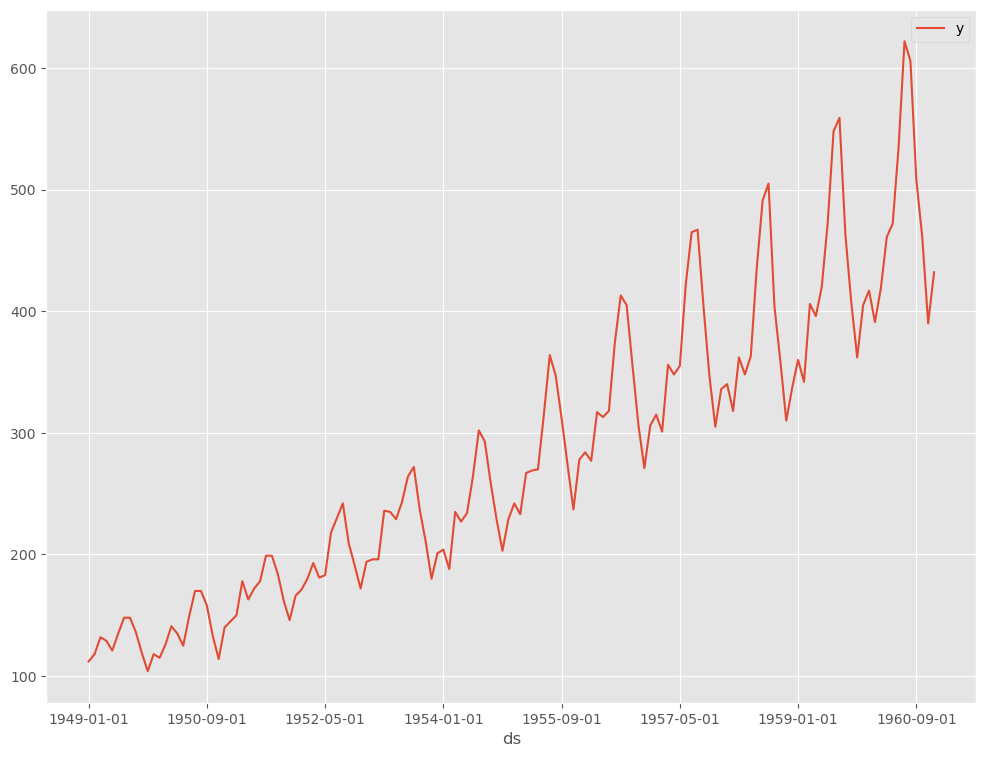
データを折れ線グラフで表現してみます。

以下、コードです。

#
# 時系列データのグラフ化（折れ線グラフ）
#

df.plot(kind='line',x='ds', y='y')

 

以下、実行結果です。

 

　Keras用データセットの準備

先程読み込んだデータセットはDataFrame形式です。NumPy配列へ変換します。

以下、コードです。

#
# 配列のデータセットに変換
#

dataset = df.y.values #NumPy配列へ変換
dataset = dataset.astype('float32')    #実数型へ変換
dataset = np.reshape(dataset, (-1, 1)) #1次元配列を2次元配列へ変換

print(dataset) #確認

 

以下、実行結果です。

[[112.]
 [118.]
 [132.]
.........
 [461.]
 [390.]
 [432.]]

 

このNumPy配列へ変換したデータセット（1変量の時系列データ）から、説明変数と目的変数を生成します。

今回は、24ヶ月の過去データから12ヶ月先を予測するモデルを構築することを想定しています。

以下、コードです。

#
# 説明変数Xと目的変数Yの生成
#

# Time Steps の長さ
input_sequence = 24

# 予測する長さ
output_sequence = 12

# データセット生成
X, Y = gen_dataset(dataset, input_sequence, output_sequence)

# 確認
print('X:',X.shape)
print(X)
print()
print('Y:',Y.shape)
print(Y)

 

以下、実行結果です。

X: (109, 24)
[[112. 118. 132. ... 133. 114. 140.]
 [118. 132. 129. ... 114. 140. 145.]
 [132. 129. 121. ... 140. 145. 150.]
 ...
 [305. 336. 340. ... 559. 463. 407.]
 [336. 340. 318. ... 463. 407. 362.]
 [340. 318. 362. ... 407. 362. 405.]]

Y: (109, 12)
[[145. 150. 178. ... 162. 146. 166.]
 [150. 178. 163. ... 146. 166. 171.]
 [178. 163. 172. ... 166. 171. 180.]
 ...
 [362. 405. 417. ... 606. 508. 461.]
 [405. 417. 391. ... 508. 461. 390.]
 [417. 391. 419. ... 461. 390. 432.]]

 

次に、モデルの学習で利用する学習データと、そのモデルの検証で利用するテストデータに分割します。

今回は、直近12ヶ月間で予測モデルの検証していきます。要するに、テストデータは最後のレコード1行のみになります。

学習データは、直近12ヶ月間のデータが説明変数にも目的変数にも混じっていないデータ（最後の12レコードを除いたデータセット）を利用します。

以下、コードです。

#
# データセットを学習データとテストデータに分割
#

#テストデータのレコード数
test_length = 1

#学習データ（予測対象期間のデータが混じっていない期間）
X_train = X[:-output_sequence,:] 
Y_train = Y[:-output_sequence,:]

#テストデータ（予測対象期間のデータ※最終行）
X_test = X[-test_length:,:]  
Y_test = Y[-test_length:,:]

 

これらのデータセットを正規化（0-1の範囲にスケーリング）します。この正規化したデータセットを使いモデル構築を検討していきます。

以下、コードです。

#
# 正規化（0-1の範囲にスケーリング）
#

# 説明変数X
scaler_X = MinMaxScaler(feature_range=(0, 1))
X_train = scaler_X.fit_transform(X_train)
X_test = scaler_X.transform(X_test)

# 目的変数Y
scaler_Y = MinMaxScaler(feature_range=(0, 1))
Y_train = scaler_Y.fit_transform(Y_train)

 

　Keras用の学習用データセットの生成

Keras用の学習用データセットを作ります。

以下、コードです。

#
# 学習用データセット（サンプル数、タイムステップ, 特徴量数）の形に再構成
#

# 再構成
X_train = np.reshape(X_train, (X_train.shape[0],X_train.shape[1], 1))
X_test = np.reshape(X_test, (X_test.shape[0],X_test.shape[1], 1))

# 確認
print('X_train:',X_train.shape)
print('X_test:',X_test.shape)

 

以下、実行結果です。

X_train: (97, 24, 1)
X_test: (1, 24, 1)

 

　予測モデルの学習（学習データ利用）

今回は、SimpleRNNでBidirectional RNN（双方向RNN）を Sequential 形式で構築していきます。単に、RNNを追加するコードに「Bidirectional」が付け加わっただけです。

モデルのインスタンスを作ります。

以下、コードです。

#
# インスタンスの生成
#

# モデル定義
model = Sequential()
model.add(Bidirectional(SimpleRNN(200),
                        input_shape=(X_train.shape[1], X_train.shape[2])))          
model.add(Dropout(0.2))
model.add(Dense(units=output_sequence))

# コンパイル
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mae'])

# モデルの視覚化
plot_model(model,show_shapes=True)

 

以下、実行結果です。

 

学習します。

以下、コードです。

# EaelyStoppingの設定
es = EarlyStopping(
    monitor='val_loss',
    mode='min',
    patience=20)

# 学習の実行
history = model.fit(
    X_train,
    Y_train,
    epochs=1000,
    batch_size=12,
    validation_split=0.2,
    callbacks=[es] ,
    verbose=1,
)

 

　予測モデルのテスト（テストデータ利用）

テストデータ期間を予測します。

以下、コードです。

#
# 予測の実施
#

# テストデータ期間
test_pred = model.predict(X_test)
test_pred = scaler_Y.inverse_transform(test_pred.reshape(1,-1)).T

print(test_pred) #確認

 

以下、実行結果です。

[[398.39584]
 [401.12122]
 [434.41354]
 [436.69836]
 [459.1149 ]
 [541.40045]
 [590.14105]
 [601.0653 ]
 [507.39395]
 [459.07745]
 [390.5549 ]
 [413.36823]]

 

精度指標を求めます。

以下、コードです。

#
# 予測モデルのテスト（テストデータ利用）
#

print('RMSE:\n', np.sqrt(mean_squared_error(df.y[-output_sequence:], test_pred)))
print('MAE:\n', mean_absolute_error(df.y[-output_sequence:], test_pred)) 
print('MAPE:\n', mean_absolute_percentage_error(df.y[-output_sequence:], test_pred))

 

以下、実行結果です。

RMSE:
 15.477268995784373
MAE:
 12.186251322428385
MAPE:
 0.02571185418214778

 

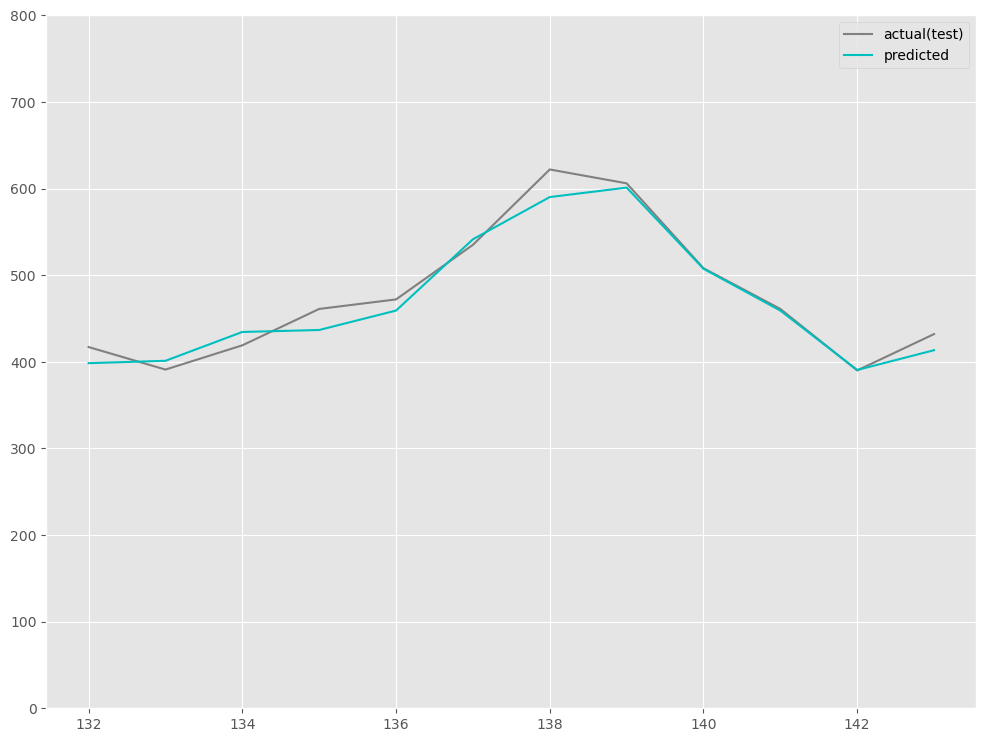
予測値をグラフ化します。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

ax.set_ylim([0, 800])

# 実測値の描写
ax.plot(df.index[-output_sequence:], df.y[-output_sequence:], label='actual(test)', color='gray')

# 予測値の描写
ax.plot(df.index[-output_sequence:], test_pred, label="predicted", color="c") 

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

ちなみに、前回の時系列Encoder-Decoder(Seq2Seq)モデルの場合の精度は以下です。

RMSE:
 18.406210728346238
MAE:
 15.714454650878906
MAPE:
 0.033885986945439865

 

まとめ

今回は、Bidirectional Simple RNN（双方向Simple RNN）を利用し、目的変数yを多変量化（ベクトル化）し予測モデルを1つ作る場合についてお話ししました。

次回は、時系列データを定常化して構築する方法について説明します。