基本となる3つの特徴選択手法とPythonでの実装

25558
基本となる3つの特徴選択手法とPythonでの実装

特徴量選択（変数選択）は、機械学習系の予測モデルなどを構築するとき、最初に行う重要なステップの1つです。

予測に寄与しない特徴量（説明変数）を取り除くことで、よりシンプルな予測モデルを構築を目指します。

色々な考え方や手法、アプローチ方法があります。

今回は、「基本となる3つの特徴選択手法とPythonでの実装」というお話しです。

基本となる3つの考え方

幾つかやり方がありますが、基本となるのは次の3つ考え方です。

  • フィルター法（Filter Method）
  • ラッパー法（Wrapper Method）
  • 埋め込み法（Embedded Method）

 

　フィルター法（Filter Method）

フィルター法は最もシンプルなアプローチです。

ある基準をもとに、必要な特徴量選択（変数選択）していくからです。

最も簡単なのは、相関係数を利用した方法です。

各特徴量（説明変数）に対し目的変数との相関係数を求め、その相関係数の絶対値が、ある値以上の場合に選択するというものです。

相関係数は、-1から+1の間の値をとり、0に近いほど相関が無い状態となります。

これだけでは終わりません。

相関係数の絶対値がある基準以上であるということで選択された特徴量（説明変数）に対し、さらにある検討を行います。

それは、選択された特徴量（説明変数）同士の相関係数はどうなっているか、という検討です。

もし、ある特徴量（説明変数）同士の相関係数の絶対値が1に近しい場合、どちらか一方の特徴量（説明変数）だけ選択すれば十分です。

整理すると……

  1. 目的変数その相関係数を求め、その絶対値が、ある値以上の特徴量（説明変数）を選択候補とする
  2. 選択候補となった、特徴量（説明変数）同士の相関を求め、その絶対値が、ある値以上の場合、一方のみを選択する

今回は相関係数で説明しましたが、相関係数である必要はありません。

 

　ラッパー法（Wrapper Method）

ラッパー法は、モデルを構築しながらある指標を見て特徴量選択（変数選択）するアプローチです。

よく利用されるものに、変数減少法（Backward Elimination）や変数増加法（Forward Selection）というものがあります。

統計的検定でよく利用されるp値をもとに、変数減少法（Backward Elimination）を簡単に説明します。

  1. 先ず、全ての特徴量（説明変数）を使いモデル構築します
  2. 最もp値の大きな係数を持つ特徴量（説明変数）を探します
  3. p値が0.05よりも大きい場合、その特徴量（説明変数）を除去します
  4. 残りの特徴量（説明変数）を使いモデル構築します
  5. 最もp値の大きな係数を持つ特徴量（説明変数）を探します
  6. p値が0.05よりも大きい場合、その特徴量（説明変数）を除去します
  7. 以後、最もp値の大きな係数のp値が、0.05よりも小さくなるまで続けます

今回はp値で説明しましたが、p値である必要はありません。

最近では、RFE（Recursive Feature Elimination）法がよく利用されます。RFE法は、予測モデルのパフォーマンス（予測精度など）を見ながら特徴量選択（変数選択）します。

 

　埋め込み法（Embedded Method）

埋め込み法は、構築するモデルそのものに、特徴量選択（変数選択）のメカニズムが組み込まれているもので、代表的なものはLasso系のモデルです。

例えば、Lasso回帰モデルは、予測に不必要と思われる特徴量（説明変数）の係数を0にすることで、結果的に特徴量選択（変数選択）を実施します。

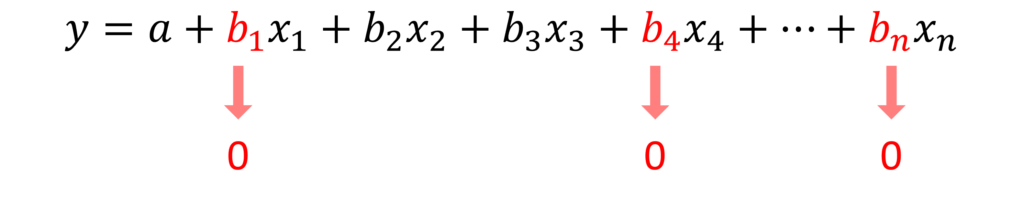
Lasso回帰は、重回帰のようなものですが、この点が通常の重回帰との大きな違いです。

ただ、Lasso回帰のハイパーパラメータであるλ（Complexity Parameter）によって、選択される特徴量（説明変数）が変わります。scikit-learnではαという記号で表現されています。

  • λ（Complexity Parameter）が0の場合、通常の重回帰と同じになります
  • λ（Complexity Parameter）の値が大きいほど、選択される特徴量（説明変数）の数は減少します

 

構築する予測モデルのアルゴリズム

構築する予測モデルのアルゴリズムは、次の2つです。

  • 重回帰モデル（線形回帰モデル）もしくはLasso回帰モデル
  • ランダムフォレスト

基本は、重回帰モデルをベースに特徴量選択（変数選択）を行い、選択された特徴量選択（変数選択）を使い重回帰とランダムフォレストで予測モデルを構築していきます。

 

実施する特徴量選択（変数選択）

特徴量選択（変数選択）は、次の7つを行い、それぞれ2つの予測モデル（重回帰とランダムフォレスト）を構築していきます。

フィルター法：

  • 相関係数を利用する方法

ラッパー法：

  • p値を利用した変数減少法
  • RFE法による変数選択
  • RFE法による変数選択（CV実施）

埋め込み法：

  • Lasso回帰（ラムダを小さな値にした場合）
  • Lasso回帰（ラムダを大きな値にした場合）
  • Lasso回帰（CVによるラムダの自動選択）

CVとは交差検証（cross-validation）のことです。

今回はあまり言及しませんが、CVは過学習（オーバーフィッティング）を防ぎ予測の汎化性能を向上させるために行います。予測系のモデルを構築するとき、実施することが多いです。

簡単に言うと、CVを実施することで、実務で使えるモデルになる可能性が高まります。

もう1点補足事項があります。

RFE法による特徴量選択（変数選択）そのものを重回帰（線形回帰）ではなく、ランダムフォレストでも行えます。RFE法による特徴量選択（変数選択）をランダムフォレストで行い、予測モデルの構築もランダムフォレストで行う方法も、おまけで言及します。

 

サンプルデータ

今回はPythonのscikit-learnで提供されている、California Housing(カリフォルニアの住宅価格)のデータセットを利用します。

目的変数yであるtargetは、住宅価格です。

説明変数Xは、以下の8変数です。

変数 説明
Medlnc 世帯所得
HouseAge 築年数
AveRooms 部屋数
AveBedrms 寝室数
Population 居住人数
AveOcuup 世帯人数
Latitude 緯度
Longitude 経度

このデータセットを、学習データとテストデータに分割し、学習データで特徴量選択（変数選択）をし予測モデルの学習を行い、テストデータで精度検証します。

精度検証で利用する指標は、決定係数R^2を用います。R^2は、0以上1以下の値をとり、値が1に近いほど良いとされています。

 

Pythonの実行例

　準備（モジュールやデータセット）

では先ず、必要なモジュールを読み込みます。

以下、コードです。

#
# モジュールの読み込み
#

import numpy as np
import pandas as pd

import statsmodels.api as sm
from sklearn.feature_selection import RFE
from sklearn.feature_selection import RFECV
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import Lasso
from sklearn.linear_model import LassoCV
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_california_housing

import seaborn as sns
import matplotlib.pyplot as plt

 

次にデータセットを読み込みます。

以下、コードです。

#
# データセットの読み込み
#

# データセット
dataset = fetch_california_housing()

# 説明変数
X = pd.DataFrame(dataset.data, columns=dataset.feature_names)

# 目的変数（住宅価格の中央値）
y = pd.Series(dataset.target, name='target')

# 目的変数+説明変数
df = pd.concat([y,X], axis=1)

print(df)

 

以下、実行結果です。

       target  MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  \
0       4.526  8.3252      41.0  6.984127   1.023810       322.0  2.555556   
1       3.585  8.3014      21.0  6.238137   0.971880      2401.0  2.109842   
2       3.521  7.2574      52.0  8.288136   1.073446       496.0  2.802260   
3       3.413  5.6431      52.0  5.817352   1.073059       558.0  2.547945   
4       3.422  3.8462      52.0  6.281853   1.081081       565.0  2.181467   
...       ...     ...       ...       ...        ...         ...       ...   
20635   0.781  1.5603      25.0  5.045455   1.133333       845.0  2.560606   
20636   0.771  2.5568      18.0  6.114035   1.315789       356.0  3.122807   
20637   0.923  1.7000      17.0  5.205543   1.120092      1007.0  2.325635   
20638   0.847  1.8672      18.0  5.329513   1.171920       741.0  2.123209   
20639   0.894  2.3886      16.0  5.254717   1.162264      1387.0  2.616981   

       Latitude  Longitude  
0         37.88    -122.23  
1         37.86    -122.22  
2         37.85    -122.24  
3         37.85    -122.25  
4         37.85    -122.25  
...         ...        ...  
20635     39.48    -121.09  
20636     39.49    -121.21  
20637     39.43    -121.22  
20638     39.43    -121.32  
20639     39.37    -121.24  

[20640 rows x 9 columns]

 

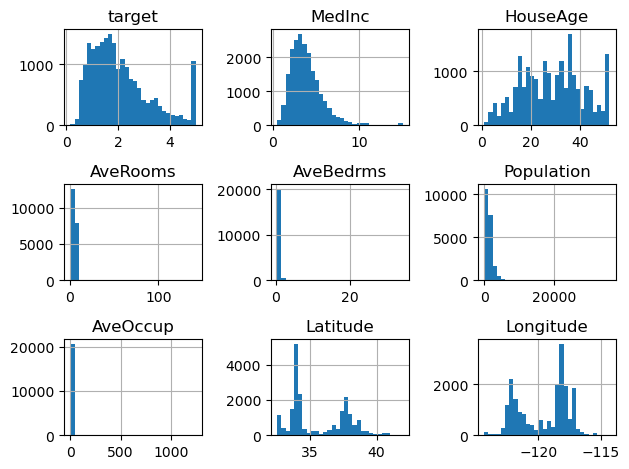
各変数のヒストグラムを作成し分布状況を見てみます。

以下、コードです。

#
# ヒストグラム
#

df.hist(bins=30)
plt.tight_layout()

 

 

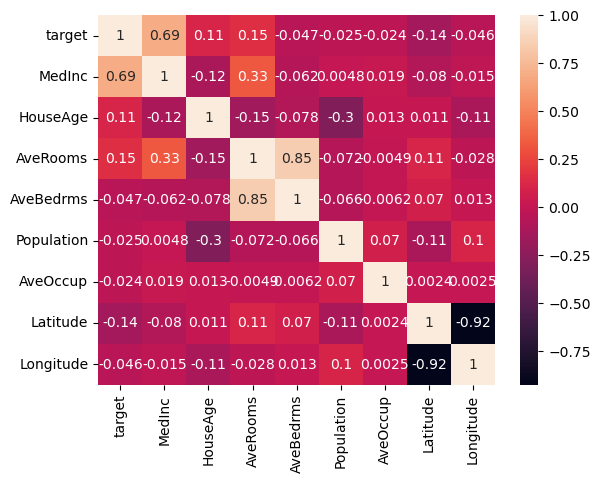
変数間の相関状況を、相関係数とヒートマップで見てみます。

以下、コードです。

#
# 相関関係+ヒートマップ
#

# 相関係数
cor = df.corr()

# ヒートマップ
sns.heatmap(cor, annot=True)
plt.show()

 

以下、実行結果です。

 

このデータセットを学習用とテスト用に2分割します。

以下、コードです。

#
# データセットを学習用とテスト用に分割
#

X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    train_size=0.7,
    test_size=0.3,
    random_state=123
)

 

学習用データでモデル構築し、構築したモデルはテストデータで検証します。

ここで、説明変数すべてを使い、重回帰とランダムフォレストのモデルを学習し、それぞれ精度検証してみます。精度指標は、決定係数R^2です。

まずは、重回帰です。

以下、コードです。

#
# モデル構築（重回帰）と精度検証（R2）
#

# インスタンス
model = LinearRegression()

# 学習（学習データ利用）
model.fit(X_train, y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train, y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test, y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.6046764934772872
決定係数R2（テストデータ）: 0.6093453526850203

 

次は、ランダムフォレストです。

以下、コードです。

#
# モデル構築（ランダムフォレスト）と精度検証（R2）
#

# インスタンス
model_rf = RandomForestRegressor()

# 学習（学習データ利用）
model_rf.fit(X_train, y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train, y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test, y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.972538155925435
決定係数R2（テストデータ）: 0.8116753365405092

 

通常は、説明変数を減らすと学習データに対する精度は悪化します。適切に特徴量選択（変数選択）されると、それほど悪化することなくモデル構築することができます。

また、適切な特徴量選択（変数選択）はテストデータに対する精度もそれほど悪化させません。悪化どころか、精度向上することすらあります。

以下の2つのモデルの精度をベースに、それぞれの特徴量選択（変数選択）によって、決定係数R^2がどうなるのかを見ていきます。

 

　フィルター法（Filter Method）で特徴量選択（変数選択）

相関係数を利用する方法で、特徴量選択（変数選択）を実施します。

目的変数targetと、説明変数の相関係数を求めます。

以下、コードです。

# 相関係数（学習データ）
cor = pd.concat([X_train, y_train], axis=1).corr()

# 目的変数との相関係数の絶対値
target_cor = abs(cor['target'])

print(target_cor)

 

以下、実行結果です。

MedInc        0.688627
HouseAge      0.099537
AveRooms      0.148227
AveBedrms     0.044280
Population    0.020798
AveOccup      0.018481
Latitude      0.145068
Longitude     0.043840
target        1.000000
Name: target, dtype: float64

 

ある基準を設定し、特徴量選択（変数選択）を実施します。今回は、相関係数の絶対値が0.1より大きい、という基準を設けます。

以下、コードです。

#
# 特徴量選択（変数選択）
#

# 基準
c = 0.1

# 選択の実施
X_selected = target_cor[target_cor>c]
X_selected = X_selected.drop('target').index

# 選択した特徴量（説明変数）
print(X_selected)

 

以下、実行結果です。

Index(['MedInc', 'AveRooms', 'Latitude'], dtype='object')

 

3つの説明変数が選択されました。

選択された説明変数同士の相関を見てみます。

以下、コードです。

# 選択した特徴量（説明変数）同士の相関

print(X_train[X_selected].corr())

 

以下、実行結果です。

            MedInc  AveRooms  Latitude
MedInc    1.000000  0.314345 -0.080874
AveRooms  0.314345  1.000000  0.097190
Latitude -0.080874  0.097190  1.000000

 

選択された説明変数同士の相関は、それほど高くはありません。

 

この選択された説明変数を使いモデル構築し精度検証します。

まずは、重回帰です。

以下、コードです。

#
# 重回帰
#

# 学習（学習データ利用）
model.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train[X_selected],y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test[X_selected],y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.48594110598767914
決定係数R2（テストデータ）: 0.4848108949227409

 

次は、ランダムフォレストです。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9442492219203433
決定係数R2（テストデータ）: 0.5839031822876586

 

3変数にしては、まずまずの精度だと思います。

ただ、ランダムフォレストに関しては、学習データに対する精度に対し、テストデータに対する精度が非常に悪いです。

 

以下、ここまでのまとめです。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58

 

　ラッパー法（Wrapper Method）で特徴量選択（変数選択）

　　p値を利用した変数減少法

p値を利用した変数減少法で、特徴量選択（変数選択）を実施します。

学習データで重回帰モデルを構築し、各説明変数の係数のp値を求めます。

以下、コードです。

#
# 重回帰の学習とその結果（係数のp値の出力）
#

# 切片追加
X_ = sm.add_constant(X)

# 重回帰学習
lr = sm.OLS(y,X_).fit()

# 各係数のp値
lr.pvalues

 

以下、実行結果です。

const          0.000000e+00
MedInc         0.000000e+00
HouseAge       3.505485e-98
AveRooms       1.026311e-73
AveBedrms     6.725726e-115
Population     4.024472e-01
AveOccup       8.303694e-15
Latitude       0.000000e+00
Longitude      0.000000e+00
dtype: float64

 

例えば、p値が0.05より大きい説明変数を一気に削除してもいいですが、p値は説明変数の組み合わせなどで値が変わるので、今回は1つ1つステップワイズに削除していきます。

具体的には、p値が0.05より大きい説明変数を1つ1つ削除していきます。

以下、コードです。

#
# 特徴量選択（変数選択）
#

# 関数定義（変数減少法）
## 引数colsは特徴量、引数cは基準
def backward_elimination(cols,c):
    
    while (len(cols)>0):
        
        # p値を格納するハコ
        p = []
        
        # モデル構築（重回帰）
        X_ = sm.add_constant(X_train[cols])
        lr = sm.OLS(y_train,X_).fit()
        
        # p値の抽出
        p = pd.Series(lr.pvalues.values[1:],index = cols)      
        
        # ｐ値が最大の特徴量がc以上の場合に除外
        if(max(p)>c):  
            cols.remove(p.idxmax())
        else:
            break

    return cols

# 特徴量選択（変数選択）の実施
X_selected = backward_elimination(cols=list(X.columns),c=0.05)

print(X_selected)

 

以下、実行結果です。

['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'AveOccup', 'Latitude', 'Longitude']

 

7つの説明変数が選択されました。

この選択された説明変数を使いモデル構築し精度検証します。

まずは、重回帰です。

以下、コードです。

#
# 重回帰
#

# 学習（学習データ利用）
model.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train[X_selected],y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test[X_selected],y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.6046674337823821
決定係数R2（テストデータ）: 0.609322150512182

 

次は、ランダムフォレストです。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9725120763604077
決定係数R2（テストデータ）: 0.8127617664607761

 

８変数ある中で7変数を選択したということもあり、精度は非常にいいです。

特徴量選択（変数選択）という観点から見ると、もう少し減らしてほしいところです。

 

以下、ここまでのまとめです。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58
Wrapper
Method		 p値を利用した変数減少法 7 0.61 0.81

 

　　RFE法（重回帰）による変数選択

RFE法で、特徴量選択（変数選択）を実施します。RFE法の中で変数選択で利用するモデルは重回帰モデル（線形回帰モデル）です。

以下、コードです。

#
# 特徴量選択（変数選択）
#

# インスタンス
rfe = RFE(LinearRegression())

# 特徴量選定（変数選択）の実施
X_rfe = rfe.fit(X_train,y_train)  
X_selected = X.columns[X_rfe.support_]

# 選択した特徴量
print(X_selected)

 

以下、実行結果です。

Index(['MedInc', 'AveBedrms', 'Latitude', 'Longitude'], dtype='object')

 

4つの説明変数が選択されました。

この選択された説明変数を使いモデル構築し精度検証します。

まずは、重回帰です。

以下、コードです。

#
# 重回帰
#

# 学習（学習データ利用）
model.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train[X_selected],y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test[X_selected],y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.5880850343452326
決定係数R2（テストデータ）: 0.5896749274366709

 

次は、ランダムフォレストです。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9746225904826062
決定係数R2（テストデータ）: 0.8312069494252233

 

4変数で、ここまでの精度は非常にスゴイことです。

 

おまけです。

RFE法の中で利用するモデルは重回帰モデル（線形回帰モデル）である必要がありません。例えば、ランダムフォレストでも構いません。

そこで、RFE法の中でランダムフォレストを利用し特徴量選択（変数選択）し、さらにその選択された変数でランダムフォレストでモデル構築してみます。

以下、コードです。

#
# ランダムフォレストで特徴量選択（変数選択）
#

# インスタンス
rfe = RFE(RandomForestRegressor())

# 特徴量選定（変数選択）の実施
X_rfe = rfe.fit(X_train,y_train)  
X_selected = X.columns[X_rfe.support_]

#
# ランダムフォレストで学習
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9729618621961282
決定係数R2（テストデータ）: 0.8197392134436304

 

以下、ここまでのまとめです。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58
Wrapper
Method		 p値を利用した変数減少法 7 0.61 0.81
RFE法による変数選択 4 0.59 0.83

 

　　RFE法（重回帰）による変数選択（CV実施）

RFE法でCV（クロスバリデーション）を使いながら、特徴量選択（変数選択）を実施します。RFE法の中で変数選択で利用するモデルは重回帰モデル（線形回帰モデル）です。

以下、コードです。

#
# 特徴量選択（変数選択）
#

# インスタンス
rfecv = RFECV(LinearRegression())

# 特徴量選定（変数選択）の実施
X_rfecv = rfecv.fit(X_train,y_train)  
X_selected = X.columns[X_rfecv.support_]

# 選択した特徴量
print(X_selected)

 

以下、実行結果です。

Index(['MedInc', 'AveRooms', 'AveBedrms', 'Latitude', 'Longitude'], dtype='object')

 

5つの説明変数が選択されました。

この選択された説明変数を使いモデル構築し精度検証します。

まずは、重回帰です。

以下、コードです。

#
# 重回帰
#

# 学習（学習データ利用）
model.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train[X_selected],y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test[X_selected],y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.5943479777721856
決定係数R2（テストデータ）: 0.5974605369859933

 

次は、ランダムフォレストです。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9741901484120278
決定係数R2（テストデータ）: 0.8262748730379657

 

先程のRFE法も含め、RFE法を使うことでより少ない変数でそれなりの精度のモデルを構築できることが分かります。

以下、ここまでのまとめです。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58
Wrapper
Method		 p値を利用した変数減少法 7 0.61 0.81
RFE法による変数選択 4 0.59 0.83
RFE法による変数選択
（CV実施）		 5 0.60 0.83

 

おまけです。

RFE法の中で利用するモデルは重回帰モデル（線形回帰モデル）である必要がありません。例えば、ランダムフォレストでも構いません。

そこで、RFE法の中でランダムフォレストを利用し特徴量選択（変数選択）し、さらにその選択された変数でランダムフォレストでモデル構築してみます。

以下、コードです。

#
# ランダムフォレストで特徴量選択（変数選択）
#

# インスタンス
rfecv = RFECV(RandomForestRegressor())

# 特徴量選定（変数選択）の実施
X_rfecv = rfecv.fit(X_train,y_train)  
X_selected = X.columns[X_rfecv.support_]

#
# ランダムフォレストで学習
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9730009124636899
決定係数R2（テストデータ）: 0.817970011100611

 

　埋め込み法（Embedded Method）で特徴量選択（変数選択）

　　準備

Lasso回帰用に、説明変数を標準化します。標準化は、平均値で引き標準偏差で割ることで行います。

以下、コードです。

#
# 説明変数の標準化（Lassoで利用）
#

# インスタンス
ss = StandardScaler()

# 学習データの標準化
X_train_std = ss.fit_transform(X_train)

# テストデータの標準化
X_test_std = ss.transform(X_test)

 

　　Lasso回帰（ラムダを小さな値にした場合）

Lasso回帰で、特徴量選択（変数選択）を実施します。

ハイパーパラメータであるλ（Complexity Parameter）によって、選択される特徴量（説明変数）が変わります。scikit-learnではαという記号で表現されています。

このαを小さくしてLasso回帰でモデル構築します。

以下、コードです。

# インスタンス ※alphaがラムダに相当
model = Lasso(alpha=0.01)

# 特徴量選定（変数選択）の実施
model.fit(X_train_std,y_train)  

# 選択した特徴量
X_selected = X.columns[model.coef_!=0]
print(X_selected)

 

以下、実行結果です。

Index(['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'AveOccup', 'Latitude','Longitude'],dtype='object')

 

7つの説明変数が選択されました。

Lasso回帰で構築したモデルを精度検証します。Lasso回帰は、重回帰のようなものです。

以下、コードです。

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train_std,y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test_std,y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.6003857868395432
決定係数R2（テストデータ）: 0.603833785086933

 

選択された説明変数を使い、ランダムフォレストでモデル構築し精度検証します。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9723557545398214
決定係数R2（テストデータ）: 0.8129145376342433

 

以下、ここまでのまとめです。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58
Wrapper
Method		 p値を利用した変数減少法 7 0.61 0.81
RFE法による変数選択 4 0.59 0.83
RFE法による変数選択
(CV実施)		 5 0.60 0.83
Embedded
Method		 Lasso回帰
(ラムダを小さな値にした場合)		 7 0.60 0.82

 

　　Lasso回帰（ラムダを大きな値にした場合）

先程よりもαを大きくしてLasso回帰でモデル構築します。

以下、コードです。

# インスタンス ※alphaがラムダに相当
model = Lasso(alpha=0.1)

# 特徴量選定（変数選択）の実施
model.fit(X_train_std,y_train)  

# 選択した特徴量
X_selected = X.columns[model.coef_!=0]
print(X_selected)

 

以下、実行結果です。

Index(['MedInc', 'HouseAge', 'Latitude'], dtype='object')

 

3つの説明変数が選択されました。

Lasso回帰で構築したモデルを精度検証します。

以下、コードです。

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train_std,y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test_std,y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.4931538083109166
決定係数R2（テストデータ）: 0.49335445780577014

 

選択された説明変数を使い、ランダムフォレストでモデル構築し精度検証します。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9453254132138406
決定係数R2（テストデータ）: 0.6038472613787464

 

Lasso回帰のハイパーパラメータαの値によって、選択される説明変数も変化しモデルの精度が大きく変化することが見て取れます。

 

以下、ここまでのまとめです。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58
Wrapper
Method		 p値を利用した変数減少法 7 0.61 0.81
RFE法による変数選択 4 0.59 0.83
RFE法による変数選択
(CV実施)		 5 0.60 0.83
Embedded
Method		 Lasso回帰
(ラムダを小さな値にした場合)		 7 0.60 0.82
Lasso回帰
(ラムダを大きな値にした場合)		 3 0.49 0.60

 

　　Lasso回帰（CVによるラムダの自動選択）

Lasso回帰でCV（クロスバリデーション）を使いながら、ハイパーパラメータの値の自動選択と特徴量選択（変数選択）を実施します。

ちなみに、scikit-learnではαという記号で表現されていますが、λ（Complexity Parameter）と表現されることが多いです。

以下、コードです。

# インスタンス ※alphaがラムダに相当
model = LassoCV()

# 特徴量選定（変数選択）の実施
model.fit(X_train_std,y_train)  

# 選択した特徴量
X_selected = X.columns[model.coef_!=0]
print(X_selected)

 

以下、実行結果です。

Index(['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'AveOccup', 'Latitude', 'Longitude'],dtype='object')

 

7つの説明変数が選択されました。

Lasso回帰で構築したモデルを精度検証します。

以下、コードです。

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model.score(X_train_std,y_train))
print('決定係数R2（テストデータ）:', 
      model.score(X_test_std,y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.593720103285507
決定係数R2（テストデータ）: 0.5965197581774595

 

選択された説明変数を使い、ランダムフォレストでモデル構築し精度検証します。

以下、コードです。

#
# ランダムフォレスト
#

# 学習（学習データ利用）
model_rf.fit(X_train[X_selected], y_train)

# 精度検証（決定係数R2）
print('決定係数R2（学習データ）:', 
      model_rf.score(X_train[X_selected], y_train))
print('決定係数R2（テストデータ）:', 
      model_rf.score(X_test[X_selected], y_test))

 

以下、実行結果です。

決定係数R2（学習データ）: 0.9722117553608073
決定係数R2（テストデータ）: 0.8108357681057874

 

Lasso回帰による特徴量選択（変数選択）も、そこそこの精度がでることが分かります。

特に、Lasso回帰で特徴量選択（変数選択）し、その選択された説明変数でランダムフォレストで構築すると、精度的には非常に良いことが分かります。

この点は、RFE法のときと同じです。

要は、特徴量選択（変数選択）は線形系のシンプルなモデルで行った方が良く、その選択された説明変数で構築するのは、線形系よりも複雑な数理モデル（アルゴリズム）がいいことが、何となく垣間見れます。

アプローチ 変数選択アルゴリズム 変数の数 テストデータ 決定係数R^2
重回帰 ランダム
フォレスト
未実施 全変数を利用 8 0.61 0.81
Filter
Method		 相関係数を利用する方法 3 0.48 0.58
Wrapper
Method		 p値を利用した変数減少法 7 0.61 0.81
RFE法による変数選択 4 0.59 0.83
RFE法による変数選択
（CV実施）		 5 0.60 0.83
Embedded
Method		 Lasso回帰
(ラムダを小さな値にした場合)		 7 0.60 0.82
Lasso回帰
(ラムダを大きな値にした場合)		 3 0.49 0.60
Lasso回帰
(CVによるラムダの自動選択)		 7 0.60 0.81

 

まとめ

今回は、「基本となる3つの特徴選択手法とPythonでの実装」というお話しをしました。

基本となるのは次の3つのアプローチです。

  • フィルター法（Filter Method）
  • ラッパー法（Wrapper Method）
  • 埋め込み法（Embedded Method）

その中で、よりシンプルな以下の方法を紹介しました。

フィルター法：

  • 相関係数を利用する方法

ラッパー法：

  • p値を利用した変数減少法
  • RFE法による変数選択
  • RFE法による変数選択（CV実施）

埋め込み法：

  • Lasso回帰（ラムダを小さな値にした場合）
  • Lasso回帰（ラムダを大きな値にした場合）
  • Lasso回帰（CVによるラムダの自動選択）

相関係数やp値を利用する方法は、昔から行われてきました。

ここ、10年～20年でRFE法をLasso回帰などを利用した、より機械学習っぽい手法が使われるようになりました。

ただ、データ理解などを念頭においた場合、相関係数やp値を利用する方法を実施しておいたほうがいいでしょう。