Jupyter AI は、JupyterLab の拡張機能で、色々なAI機能が提供されています。
その中で、データサイエンティストとして嬉しいのが、コード生成機能です。
会話しながら、Pythonコーディングを実施できます。
今現在(2023年6月29日現在)、Jupyter AI はまだ開発中ですが、使いやすく有望なツールになることでしょう。
前回、Jupyter AI のインストールと簡単な使い方について説明しました。
既にJupyter AI(jupyter_ai)がインストールされ使える状態という前提で、今回はお話しを進めます。まだJupyter AI(jupyter_ai)がインストールなどの設定をされていない方は、前回の記事を参考にしてください。
今回は、「回帰問題の予測モデルをJupyter AIで作ろう!」というお話しをします。
回帰問題とは、連続的な数値を予測する問題で、構築する予測モデルの目的変数が量的変数となります。
Contents [hide]
今回利用するJupyter AIの構文
今回利用する構文は以下です。【プロンプト】と記載されているところに、ChatGPTに与える質問や指示などを記載します。
%%ai chatgpt -f code 【プロンプト】
プロンプトに記載されている質問や指示などに応じて、Pythonコードがセルごと生成されます。
そのPythonコードの記載されたセルを実行することで、データ分析を進めることができます。
データセットの説明
今回はscikit-learnから提供されているカリフォルニアの住宅価格データセットを使います。
【今回使用】
scikit-learnから提供されているサンプルデータセット
https://scikit-learn.org/stable/datasets/index.html#california-housing-dataset
データ数は20640件です。
目的変数は、カリフォルニアの区画ごとの住宅価格の中央値です。
特徴量(説明変数)は、以下の8個です。
| 項目名 | 詳細 |
| MedInc | 区画の収入の中央値 |
| HouseAge | 区画の築年数 |
| AveRoom | 区画の家の部屋数の平均値 |
| AveBedrms | 区画の寝室の平均値 |
| Population | 区画の人口 |
| AveOccup | 区画の平均入居率 |
| Latitude | 区画の緯度 |
| Longitude | 区画の経度 |
準備
では、準備をします。
以下のコードをJupyter Labに記述し実行するだけです。
import os os.environ["OPENAI_API_KEY"]="あなたのOpenAI API Key" %load_ext jupyter_ai
回帰問題
データ読み込みと探索的データ分析
データ読み込みと、最初の探索的データ分析
先ず、以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code scikit-learnから提供されているカリフォルニアの住宅価格データセット(fetch_california_housing)を使います。 目的変数はyに、特徴量はXに格納して下さい。 データ理解のために、データの可視化と探索的データ分析をして下さい。
次のような回答(Pythonコード)を得ました。
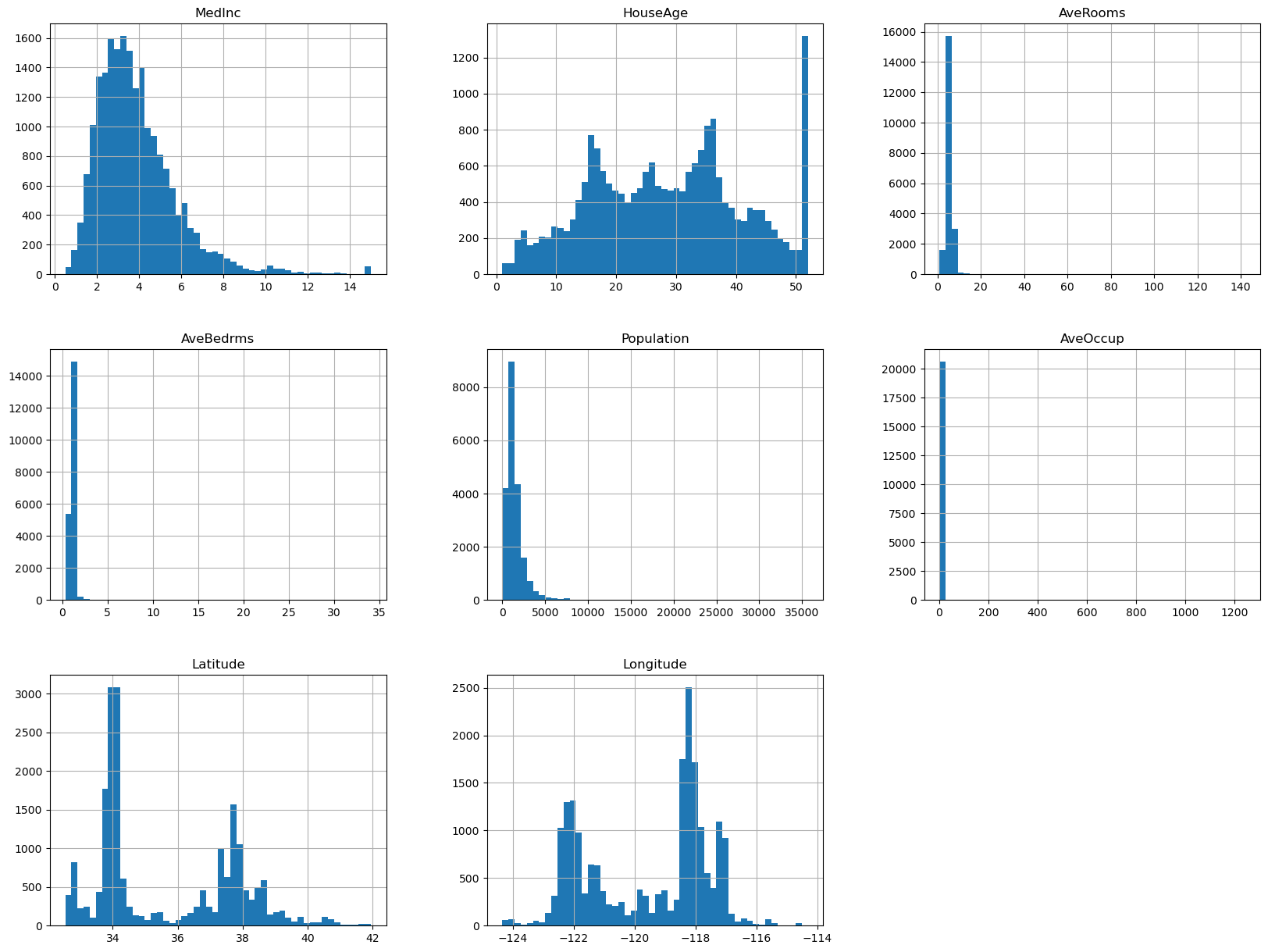
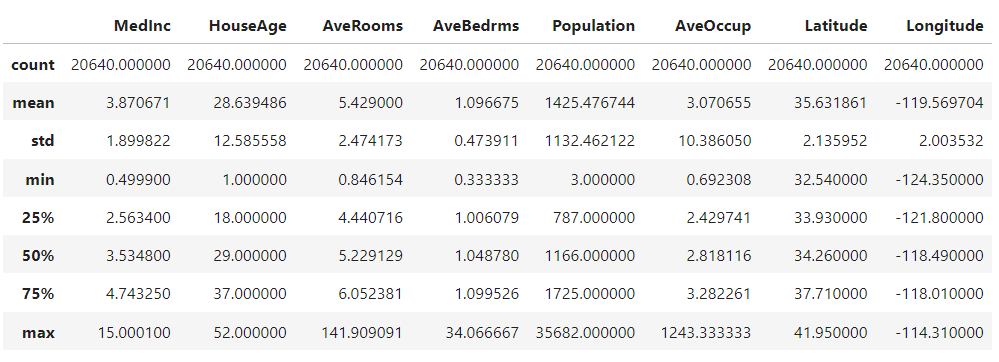
from sklearn.datasets import fetch_california_housing import pandas as pd import matplotlib.pyplot as plt # データセットの読み込み dataset = fetch_california_housing() # 目的変数と特徴量の格納 X = pd.DataFrame(dataset.data, columns=dataset.feature_names) y = pd.Series(dataset.target) # データの可視化 X.hist(bins=50, figsize=(20,15)) plt.show() X.describe(include='all')
このPythonコードをそのまま実行します。
以下、実行結果です。
さらなる探索的データ分析
探索的データ分析としては不十分な気がしますので、以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code 続けてください。
次のような回答(Pythonコード)を得ました。
import seaborn as sns
# 目的変数と特徴量の結合
df = pd.concat([X, y], axis=1)
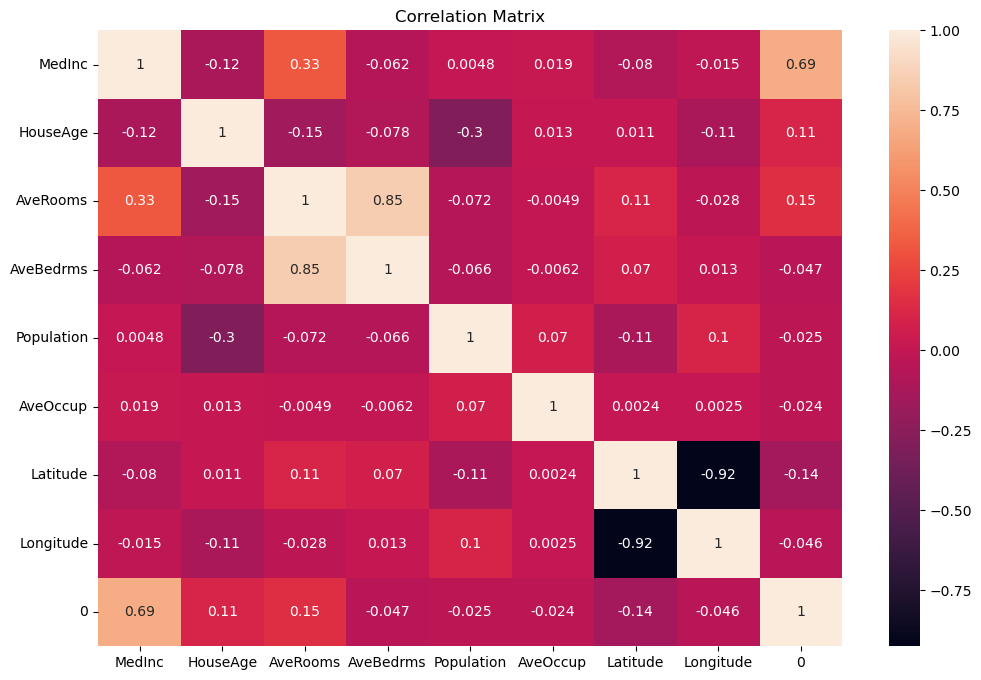
# 目的変数と特徴量の相関行列の可視化
corr_matrix = df.corr()
plt.figure(figsize=(12, 8))
sns.heatmap(corr_matrix, annot=True)
plt.title('Correlation Matrix')
plt.show()
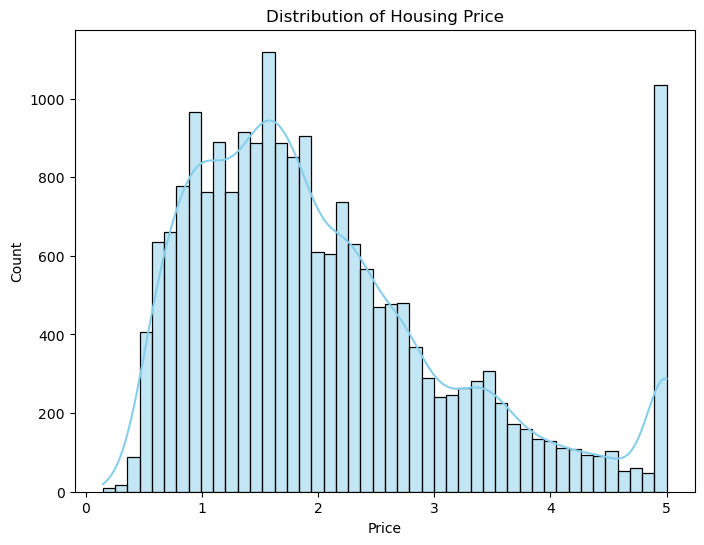
# 目的変数の分布の可視化
plt.figure(figsize=(8, 6))
sns.histplot(y, kde=True, color='skyblue')
plt.title('Distribution of Housing Price')
plt.xlabel('Price')
plt.ylabel('Count')
plt.show()
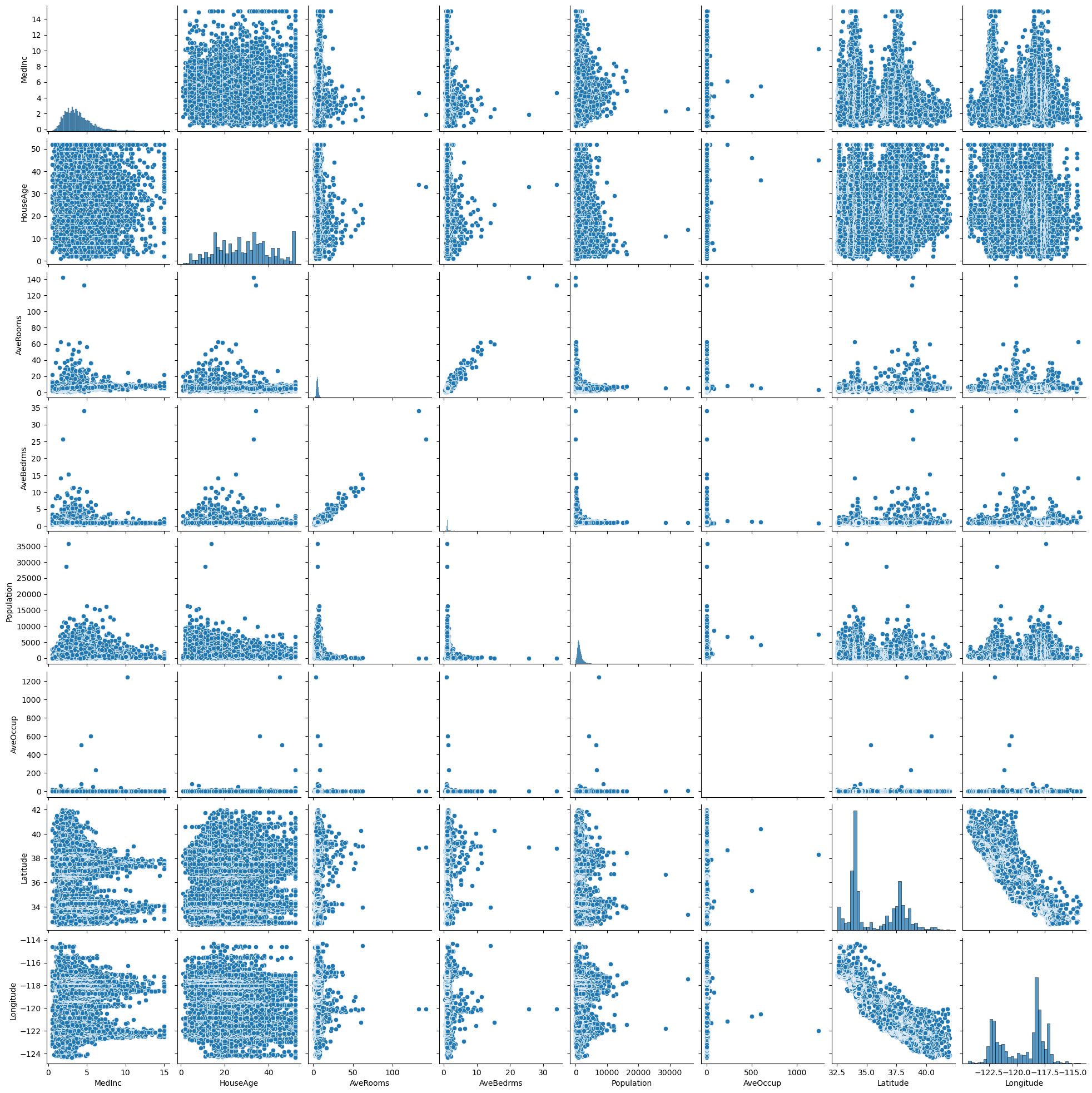
# 特徴量の間の散布図行列の可視化
sns.pairplot(df, vars=dataset.feature_names, kind='scatter')
plt.show()
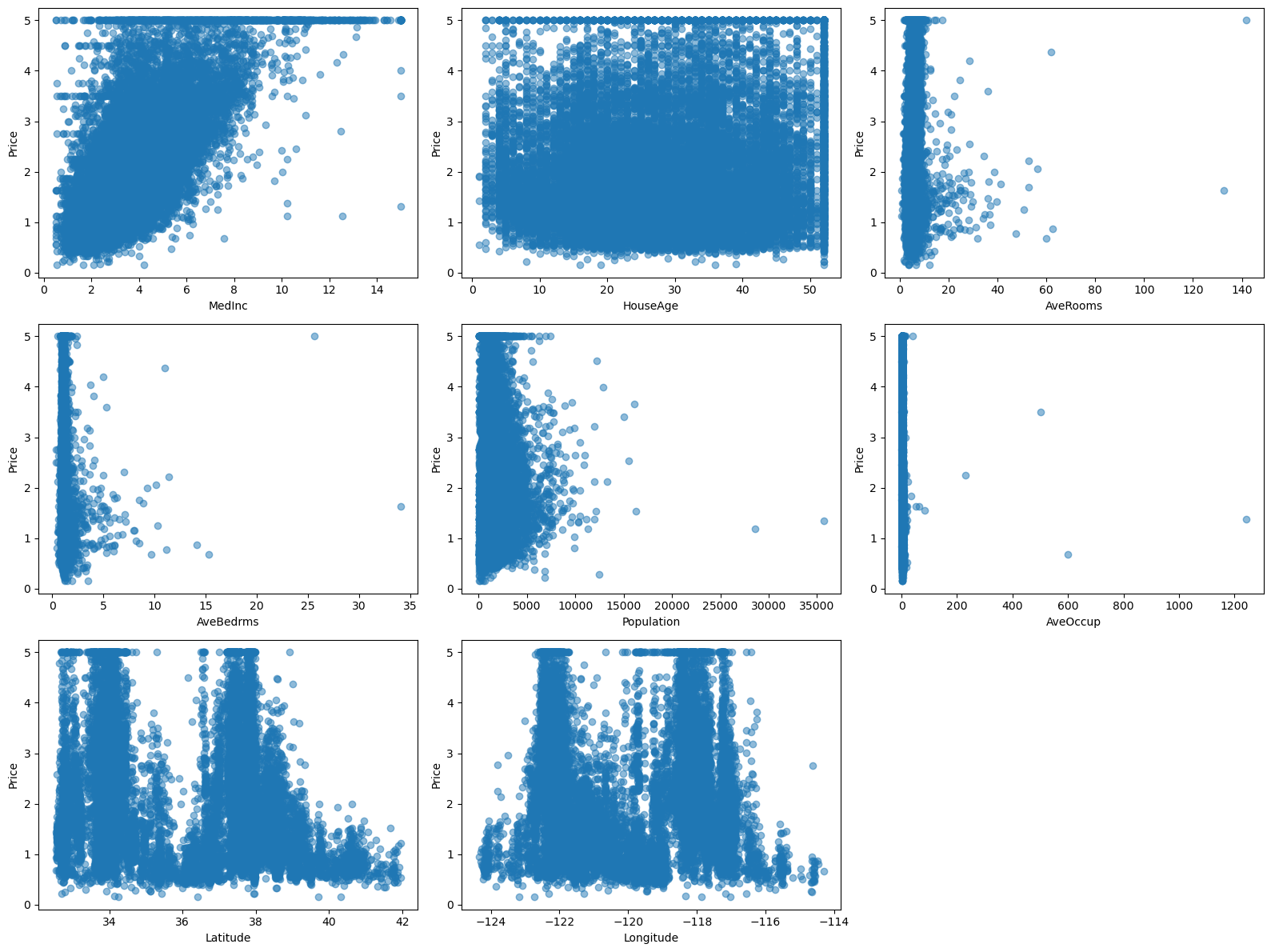
# 目的変数と特徴量の散布図の可視化
plt.figure(figsize=(16, 12))
for i, feature in enumerate(dataset.feature_names):
plt.subplot(3, 3, i+1)
plt.scatter(X[feature], y, alpha=0.5)
plt.xlabel(feature)
plt.ylabel('Price')
plt.tight_layout()
plt.show()
このPythonコードをそのまま実行します。
以下、実行結果です。
特徴量重要度も知りたい
特徴量重要度も知りたいので、名指しで指示を出してみます。
以下のようなコード(プロンプト付きコード)を記載しました。
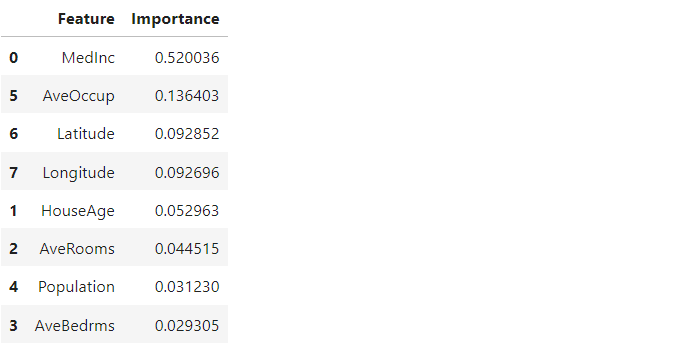
%%ai chatgpt -f code 住宅価格にとって重要な特徴量を見つけるため 特徴量重要度のランキングを作って下さい。
次のような回答(Pythonコード)を得ました。
from sklearn.ensemble import RandomForestRegressor
# ランダムフォレストモデルの作成
model = RandomForestRegressor(random_state=42)
model.fit(X, y)
# 特徴量重要度の取得
importance = model.feature_importances_
# 特徴量重要度のランキングの作成
feature_importance = pd.DataFrame({'Feature': dataset.feature_names, 'Importance': importance})
feature_importance_ranked = feature_importance.sort_values('Importance', ascending=False)
feature_importance_ranked
このPythonコードをそのまま実行します。
以下、実行結果です。
探索的データ分析はこのあたりで終えます。
次は予測モデルの構築です。
予測モデルの構築
とりあえず作ってみて
先ず、以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code scikit-learnから提供されているカリフォルニアの住宅価格データセット(fetch_california_housing)を使います。 住宅価格を予測するモデルを構築して下さい。 テストデータの決定係数を出力してください。
次のような回答(Pythonコード)を得ました。
from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import r2_score # データセットの読み込み dataset = fetch_california_housing() # 目的変数と特徴量の格納 X = dataset.data y = dataset.target # 訓練データとテストデータへの分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 線形回帰モデルの作成と訓練 model = LinearRegression() model.fit(X_train, y_train) # テストデータに対する予測 y_pred = model.predict(X_test) # テストデータの決定係数の出力 r2_score(y_test, y_pred)
このPythonコードをそのまま実行します。
以下、実行結果です。出力されているのはテストデータの決定係数
0.5757877060324521
微妙な結果ですね。
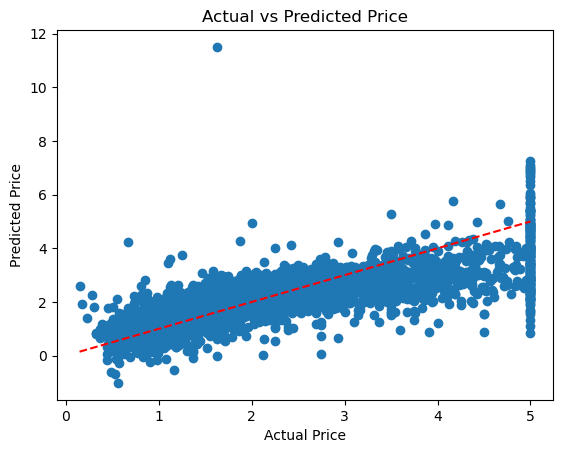
テストデータの予測値と実測値の散布図を見たいところです。
以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code 予測値と実測値の散布図を描いてください。
次のような回答(Pythonコード)を得ました。
import matplotlib.pyplot as plt
# 予測値と実測値の散布図の描画
plt.scatter(y_test, y_pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.xlabel('Actual Price')
plt.ylabel('Predicted Price')
plt.title('Actual vs Predicted Price')
plt.show()
このPythonコードをそのまま実行します。
以下、実行結果です。
予測精度が微妙そうなので、予測モデルの改良をします。
取り急ぎ改良して!
以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code 工夫して予測モデルの精度を上げてください。
次のような回答(Pythonコード)を得ました。
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
# ランダムフォレストモデルのパラメータグリッド
param_grid = {
'n_estimators': [100, 200, 300],
'max_depth': [None, 5, 10],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4]
}
# グリッドサーチを使用して最適なパラメータを探索
grid_search = GridSearchCV(RandomForestRegressor(random_state=42), param_grid, cv=5, scoring='r2')
grid_search.fit(X_train, y_train)
# 最適なモデルを取得
best_model = grid_search.best_estimator_
# テストデータに対する予測
y_pred = best_model.predict(X_test)
# テストデータの決定係数の出力
r2_score(y_test, y_pred)
このPythonコードをそのまま実行します。
以下、実行結果です。出力されているのはテストデータの決定係数
0.8061927273680218
びっくりするぐらい、数値が改善されています。
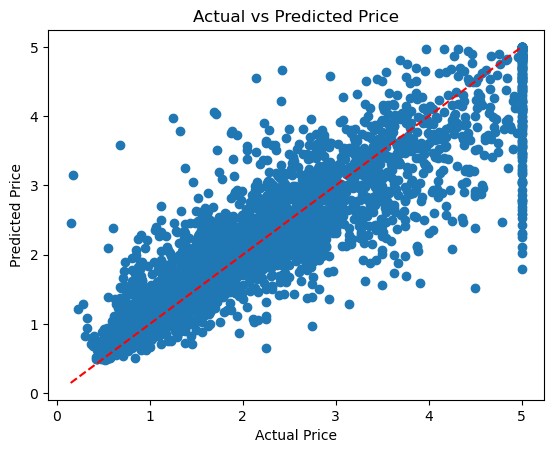
テストデータの予測値と実測値の散布図を見たいところです。
以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code 予測値と実測値の散布図を描いてください
次のような回答(Pythonコード)を得ました。
# 予測値と実測値の散布図の描画
plt.scatter(y_test, y_pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.xlabel('Actual Price')
plt.ylabel('Predicted Price')
plt.title('Actual vs Predicted Price')
plt.show()
このPythonコードをそのまま実行します。
以下、実行結果です。
さらなる予測モデルの改良に挑みます。
AutoML(自動機械学習)で改良して!
ただ、手作業で右往左往してもつまらないので、AutoML(自動機械学習)で予測モデルの改良に挑みます。今回は、TPOTというPythonのAutoML(自動機械学習)ライブラリーを使います。
以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code TPOTを使い予測モデルの精度を上げてください。
次のような回答(Pythonコード)を得ました。
from tpot import TPOTRegressor # TPOTによるモデルの自動最適化 tpot = TPOTRegressor(generations=5, population_size=50, random_state=42, verbosity=2) tpot.fit(X_train, y_train) # 最適なモデルを取得 best_model = tpot.fitted_pipeline_ # テストデータに対する予測 y_pred = best_model.predict(X_test) # テストデータの決定係数の出力 r2_score(y_test, y_pred)
このPythonコードをそのまま実行します。
以下、実行結果です。
Best pipeline: GradientBoostingRegressor(input_matrix, alpha=0.75, learning_rate=0.1, loss=huber, max_depth=8, max_features=0.45, min_samples_leaf=1, min_samples_split=9, n_estimators=100, subsample=0.8500000000000001) 0.8270281238593913
さらなる改善に成功したようです。
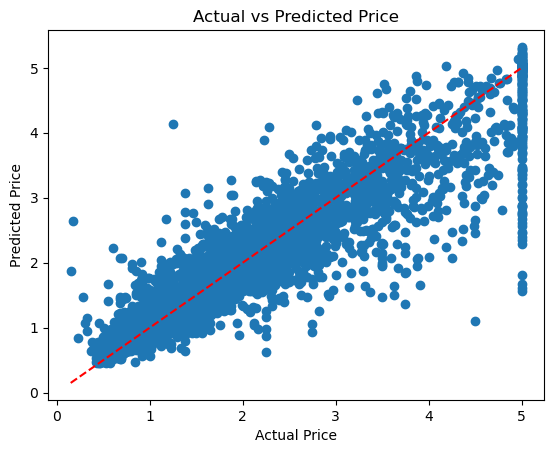
テストデータの予測値と実測値の散布図を見たいところです。
以下のようなコード(プロンプト付きコード)を記載しました。
%%ai chatgpt -f code 予測値と実測値の散布図を描いてください。
次のような回答(Pythonコード)を得ました。
# 予測値と実測値の散布図の描画
plt.scatter(y_test, y_pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')
plt.xlabel('Actual Price')
plt.ylabel('Predicted Price')
plt.title('Actual vs Predicted Price')
plt.show()
このPythonコードをそのまま実行します。
以下、実行結果です。
どのような予測モデルつまりパイプライン(変換器と予測器の組み合わせ)を構築したのか、知りたいところです。
サイドパネルにあるチャットインターフェイス(プロンプトを入力する部分)で、Best pipelineがどのようなものなのかを聞いてみましょう。
チャットインターフェイス(プロンプトを入力する部分)に以下をインプットし、ChatGPTに聞いてみました。
以下のような回答を得ました。
このパイプラインは、GradientBoostingRegressorアルゴリズムを使用して回帰モデルを構築するための最適な手順を示しています。以下にパイプラインの各ステップを説明します。
GradientBoostingRegressor(input_matrix):GradientBoostingRegressorは、勾配ブースティングアンサンブルモデルを使用して回帰タスクを行うためのクラスです。input_matrixは、回帰に使用される入力データの行列です。
alpha=0.75, learning_rate=0.1, loss='huber', max_depth=8, max_features=0.45, min_samples_leaf=1, min_samples_split=9, n_estimators=100, subsample=0.8500000000000001:GradientBoostingRegressorのインスタンス化とパラメータの設定を行います。alpha=0.75は、ハブロス関数のスケーリングパラメータを設定します。この値は、外れ値の影響を制御します。learning_rate=0.1は、学習率を設定します。学習率は、各弱学習器の予測結果を反映させるための重みの大きさを制御します。loss='huber'は、損失関数を指定します。ここではハブロス関数が使用されています。ハブロス関数は、外れ値に対して頑健な回帰を行います。max_depth=8は、各弱学習器(決定木)の最大深度を制限します。深い木はより複雑なモデルを表現できますが、過学習のリスクも増えます。max_features=0.45は、各弱学習器の特徴量の最大数を制限します。特徴量のランダムなサブセットが使用されます。min_samples_leaf=1は、葉ノード(終端ノード)に含まれる最小サンプル数を指定します。この値が小さいほど、モデルはより複雑になります。min_samples_split=9は、ノードを分割するために必要な最小サンプル数を指定します。この値が小さいほど、モデルはより複雑になります。n_estimators=100は、使用する弱学習器の数を指定します。ブースティングは、複数の弱学習器を組み合わせることで性能を向上させます。subsample=0.8500000000000001は、各弱学習器に使用するトレーニングサンプルの割合を指定します。ランダムなサンプリングが行われます。
- このパイプラインでは、
GradientBoostingRegressorによって回帰モデルが構築されます。- パラメータに基づいて、指定された数の弱学習器がトレーニングされ、予測結果が組み合わされます。
- モデルは入力データに適合し、目標値を予測するために使用されます。
このパイプラインは、GradientBoostingRegressorを使用して回帰モデルを構築するための最適な手順を提供しています。ただし、データセットや問題によって最適なパラメータや前処理手法が異なる場合があります。
まとめ
今回は、「回帰問題の予測モデルをJupyter AIで作ろう!」というお話しをしました。
プロンプト(テキストによる質問や指示など)だけで、Pythonコーディングしながら、回帰問題の予測モデルを構築できました。
ただ、最低限のデータサイエンスの知識がないと、プロンプト(テキストによる質問や指示など)すらかけないので、そこのお勉強はなくならないかもしれません。
今回は回帰問題を扱ったので、次回は分類問題を扱います。