時系列モデルを構築するとき、季節成分をモデルに組み込むことが多いです。
季節成分をモデルに組み込むには、その周期期間を知らなくてはなりません。

季節成分の周期期間の見つけ方は幾つかあります。
前回、自己相関分析による周期の長さの見つけ方を説明しました。
今回は、スペクトル分析による周期の長さの見つけ方を説明します。
Contents [hide]
スペクトル分析とは?
スペクトル分析とは、信号の特徴を周波数領域で解析する手法で、時系列データを異なる周期的な波の和に変換しその特徴を分析する手法です。
要は、季節成分の周期性を分析することができます。
よく使われるスペクトル分析の手法には、フーリエ変換(特に高速フーリエ変換、FFT)やウェーブレット変換などがあります。
今回は、フーリエ変換(高速フーリエ変換FFT)を使います。
フーリエ変換(高速フーリエ変換FFT)って何だよ! と困惑された方もいるかも知れませんが、深く考えなくても大丈夫です。そのようなものがある、というぐらいで大丈夫です。

とはいえ気持ち悪いので何となく知りたい…… という方は、あまり深入りはしませんが、以下で少し捕捉説明をします。興味のある方のみ一読下さい。
高速フーリエ変換(FFT: Fast Fourier Transform)は、離散フーリエ変換(DFT: Discrete Fourier Transform)を高速に行うアルゴリズムの一つです。
フーリエ変換は、時系列データ解析などの信号解析において非常に重要な手法であり、周期的なパターンの発見、ノイズのフィルタリング、信号の圧縮など、さまざまな用途に使用されます。
ちなみに、時系列データは一般的には信号(時間とともに変化する特性)と見なすことができます。時系列データ以外の信号には、音声、画像、温度、株価、心電図などがあります。
離散フーリエ変換(DFT: Discrete Fourier Transform)は、時系列データなどの連続的な信号(波形)を一連の離散的なサンプルに分解し、そのサンプルがどの周波数成分から成り立っているかを分析するための数学的な手法です。
具体的には、任意の離散的な時間領域の信号を、その信号の周波数領域へと変換します。この変換により、時間領域での波形(信号)を、それがどのような周波数と振幅を持つ成分から構成されているかを示す周波数スペクトルに変換することができます。
どのように周期性を見つけるのか?
高速フーリエ変換で、時間領域の時系列データを周波数成分に分解することができます。
そのとき、分解した周波数成分ごとにパワースペクトルという値を得ることができ、それを見ることでどの程度影響を与えているかが分かります。
要は、パワースペクトルの高い周波数が、見つけたい季節成分の周期の長さです。

下の図は、ある時系列データに対し高速フーリエ変換を実行した結果です。
横軸が周波数、縦軸がパワースペクトルです。
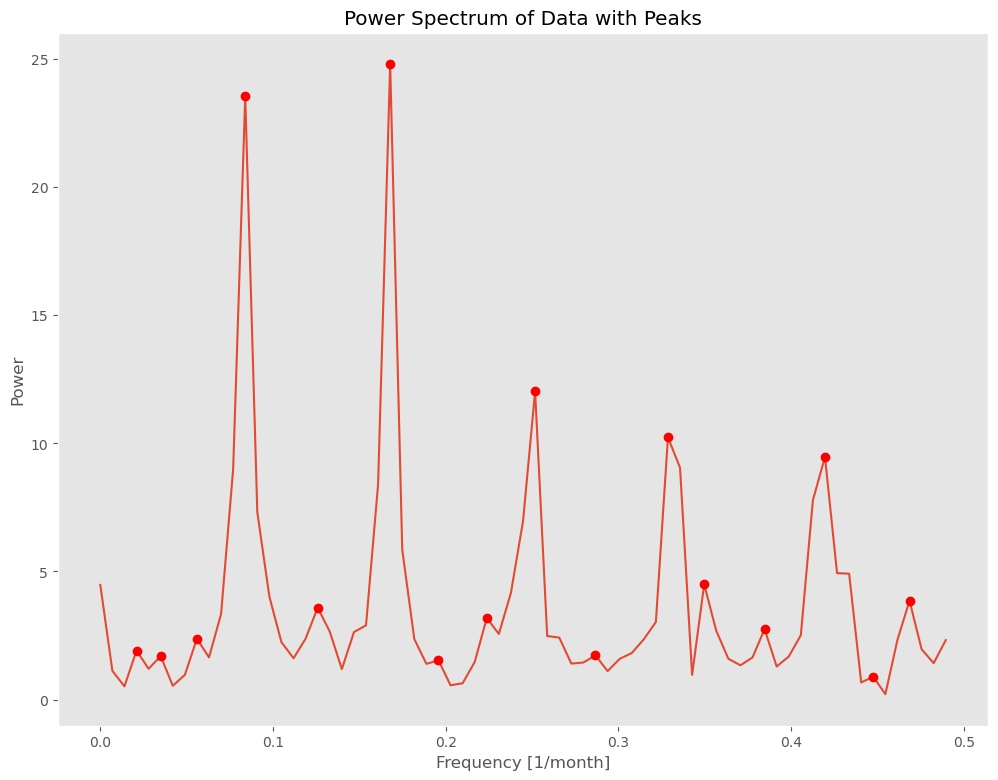
この図を見ていただくと分かるかと思いますが、パワースペクトルがピークとなる周波数が幾つかあります。ピークとなる箇所(local maximum)に●をつけています。
この図の場合、ピークとなる周波数の中で、特に高い(パワースペクトルが大きい)ピークが2つあります。
要は、主な季節成分が2つあることが分かります。
ちなみに、周波数は周期期間の逆数ですから、周波数から周期期間(=1÷周波数)は簡単に求まります。

ということで、以下に具体的な手順を示します。
- データの準備: 分析したい時系列データを用意します。
- フーリエ変換の実行: 時系列データに対して高速フーリエ変換(FFT)を実行します。
- パワースペクトルの計算: フーリエ変換の結果を用いてパワースペクトルを計算します。パワースペクトルは各周波数成分がデータにどれだけの影響を与えているかを示します。
- パワースペクトルの解析: パワースペクトルを解析して、最も強い影響を持つ周波数(つまり、最も強いピークを持つ周波数)を見つけます。この周波数はデータの主要な周期性を示します。
このように、スペクトル分析を用いて時系列データの周期性を抽出することができます。
ただし、この手法はデータがトレンド非定常ではないときに最も効果的です。非定常なデータに対しては、ウェーブレット変換などの方がいいでしょう。
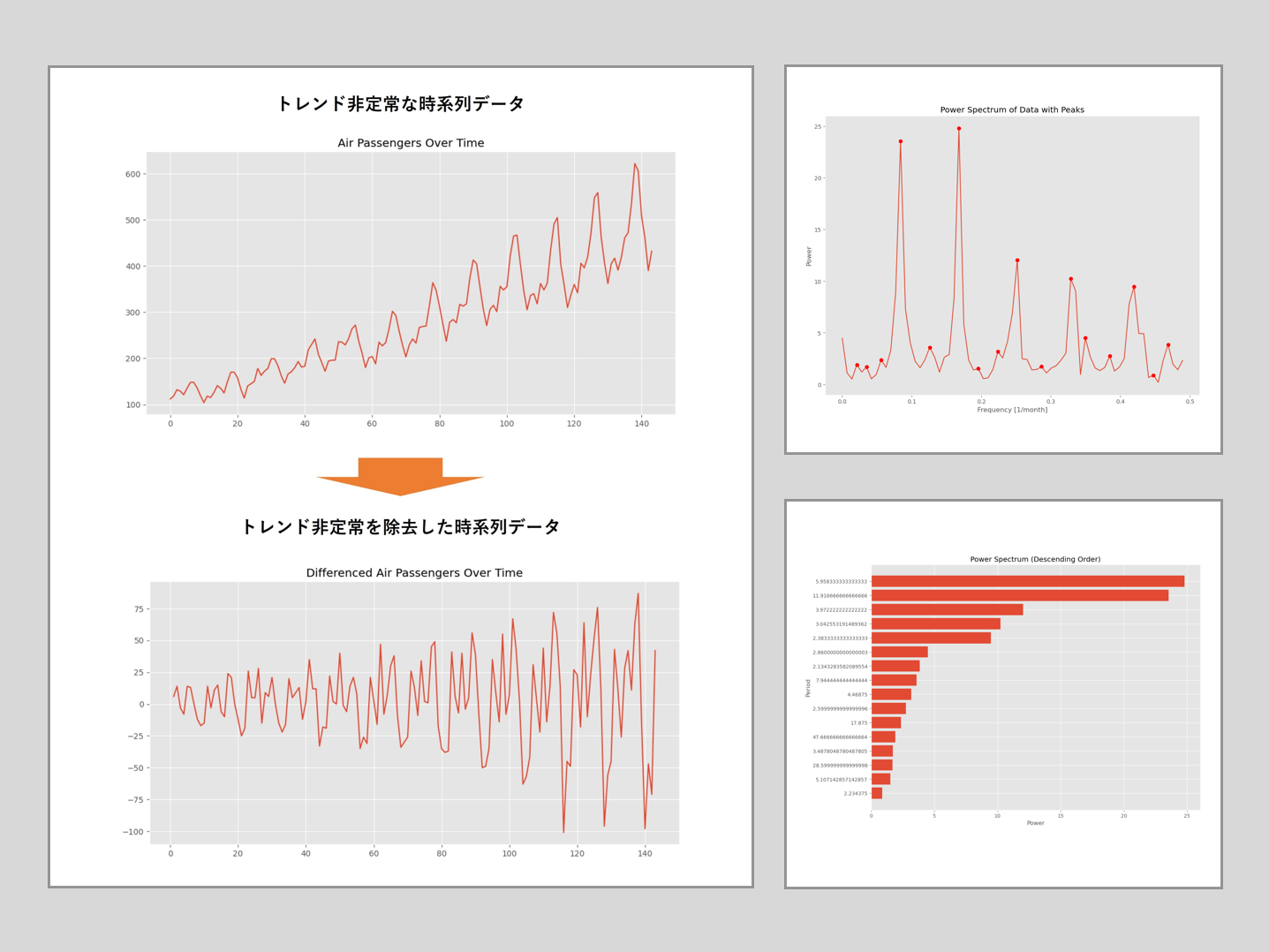
トレンド非定常を除去すると見つけやすくなる
自己相関分析で時系列データの季節成分の周期期間を検討するとき、トレンド非定常性を除去してあると見つけやすくなるというお話しを以下の記事でしました。
同じような理由で、スペクトル分析分析で時系列データの季節成分の周期期間を検討するとき、トレンド非定常性を除去してあると見つけやすくなります。
トレンド非定常性とは何? そもそも非定常って何? と思われた方は以下の記事を参考にしてください。
ということで、次の2パターンで時系列データの季節成分の周期期間を検討していきます。
- トレンド非定常性を除去しない場合
- トレンド非定常性を除去した場合
「トレンド非定常性を除去しない場合」とは、トレンド非定常性の除去をせず、元の時系列データのままスペクトル分析を実施する場合です。
「トレンド非定常性を除去した場合」とは、トレンド非定常性の除去をした時系列データに対し、スペクトル分析を実施する場合です。
サンプルデータ
時系列データの分析例でよく登場する「航空旅客データ」(AirPassengers)を使います。
航空旅客データは、国際航空旅客の月次データを指します。具体的には、1949年から1960年までの12年間の国際航空旅客数(単位: 1000人)を含む時系列データです。各データポイントは、その月の旅客数を示しています。
このデータセットは周期性(季節性)とトレンド(一般的に増加しています)の両方を含んでいます。特に、旅行の高シーズンやオフシーズンに対応する明確な季節的なパターンが見られます。このような特性から、航空旅客データは時系列分析の手法を学習したり、試したりするためのクラシックなデータセットとして広く使われています。
Pythonのstatsmodelsライブラリでは、このデータセットを’AirPassengers’という名前で取得することができます。このデータセットを使って、時系列分析の各種手法(例えば、移動平均、指数平滑、ARIMA、季節調整など)を試すことができます。
周期期間の検出例
準備(モジュールとデータの読み込み)
先ず、必要なモジュールを読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
import statsmodels.api as sm
from scipy.signal import argrelextrema
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]
このコードはいくつかのPythonのパッケージをインポートし、グラフのスタイルとサイズを設定しています。それぞれのパッケージとコード行の役割について以下に説明します。
import numpy as np:NumPyは数値計算を効率的に行うためのPythonライブラリです。配列や行列の演算、線形代数、フーリエ変換などの機能を提供します。このコードでは、npという短縮名を使ってNumPyを参照します。
import pandas as pd:pandasはデータ分析と操作を行うためのPythonライブラリです。表形式のデータを効率的に扱うことができ、欠損値の処理、データのフィルタリングや変換、統計量の計算などが可能です。このコードでは、pdという短縮名を使ってpandasを参照します。
import statsmodels.api as sm:Statsmodelsは統計的モデルの推定、検定、予測、データ探索などを行うためのPythonライブラリです。線形モデル、一般化線形モデル、ロバスト線形モデル、線形混合効果モデルなど多くの統計的モデルをサポートしています。このコードでは、smという短縮名を使ってStatsmodelsを参照します。
from scipy.signal import argrelextrema:SciPyは科学技術計算を行うためのPythonライブラリで、scipy.signalは信号処理用のモジュールです。argrelextremaは、配列の相対的な極大値(すなわち、その両隣よりも値が大きい位置)のインデックスを計算する関数です。
import matplotlib.pyplot as plt:Matplotlibはグラフ描画のためのPythonライブラリで、pyplotはその中でも特に便利な機能をまとめたモジュールです。このコードでは、pltという短縮名を使ってpyplotを参照します。
plt.style.use('ggplot'):Matplotlibのstyleモジュールを使って、グラフの全体的なスタイル(色、線の種類、背景色など)を設定します。ggplotは、R言語のデータ可視化パッケージであるggplot2のスタイルを模したものです。
plt.rcParams['figure.figsize'] = [12, 9]:rcParamsは、Matplotlibのグラフのデフォルト設定を管理する辞書型オブジェクトです。この行では、新たに作成するグラフのフィギュア(全体の描画領域)のサイズを12×9(単位はインチ)に設定しています。
以上がこのコードの説明となります。
次に、データセットを読み込みます。
以下、コードです。
# StatsmodelsからAirPassengersデータセットをロード
dataset = sm.datasets.get_rdataset('AirPassengers')
# 時系列データを抽出
data = dataset.data['value']
# 時系列データをプロット
plt.figure(figsize=(12, 6))
plt.plot(data)
plt.title('Air Passengers Over Time')
plt.grid(True)
plt.show()
このコードは、Statsmodelsパッケージの一部として提供されているAirPassengersというデータセットを読み込み、そのデータをグラフにプロットして表示するものです。具体的には、以下の処理を行っています。
dataset = sm.datasets.get_rdataset('AirPassengers'):get_rdataset関数を使って、Rの統計データセットからAirPassengersというデータセットを読み込んでいます。AirPassengersデータセットは、月ごとの国際航空旅客数を記録した時系列データです。
data = dataset.data['value']:get_rdataset関数によって返されるオブジェクトは、データセットの本体であるデータフレームとメタデータ(データセットの説明、情報など)を含んでいます。この行では、データフレームから’value’という列を抽出し、それをdataという変数に代入しています。この’value’列が、時間経過に伴う航空旅客数を表しています。
plt.figure(figsize=(12, 6)):Matplotlibのfigure関数を使って、新たに描画領域(フィギュア)を作成しています。figsize=(12, 6)という引数で、フィギュアのサイズを12×6インチに設定しています。
plt.plot(data):plot関数を使って、時系列データdataをグラフにプロットしています。
plt.title('Air Passengers Over Time'):title関数を使って、グラフのタイトルを設定しています。
plt.grid(True):grid関数を使って、グラフにグリッド線を表示しています。
plt.show():show関数を使って、作成したグラフを画面に表示しています。
以上がこのコードの説明となります。
以下、実行結果です。
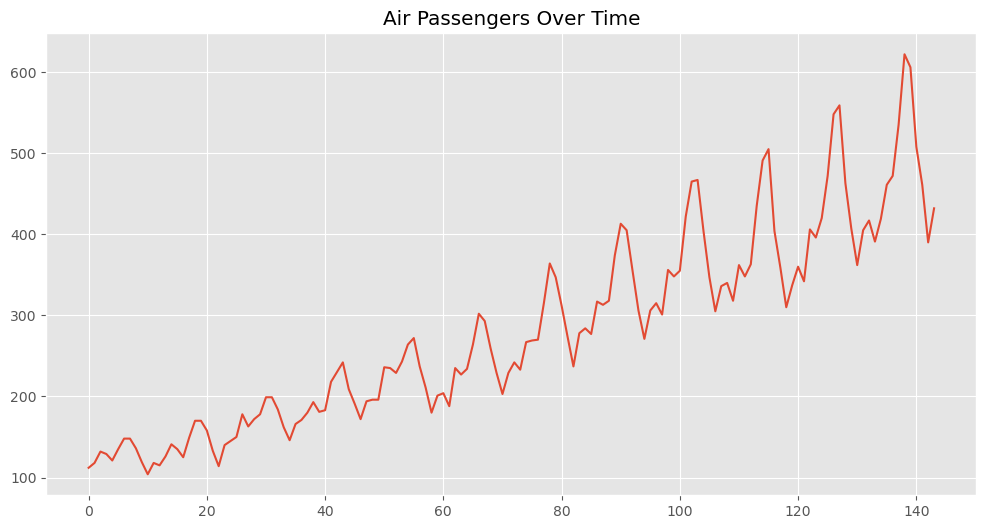
トレンド非定常性を除去しない場合
では、トレンド非定常性の除去をせず、元の時系列データのままスペクトル分析を実施していきます。
高速フーリエ変換 (FFT)を実行しパワースペクトルを計算、そしてパワースペクトルのピークの周波数を探します。そのとき、その周波数の周期期間も求めます。
以下、コードです。
# データセットの値を取得
y = dataset.data['value'].values
# データのサイズとサンプリング間隔を設定
N = y.size
T = 1.0
# 高速フーリエ変換 (FFT)を実行
yf = np.fft.fft(y)
xf = np.fft.fftfreq(N, d=T)[:N//2]
# パワースペクトルを計算
power_spectrum = 2.0/N * np.abs(yf[0:N//2])
# パワースペクトルのピークを探す
peaks = argrelextrema(power_spectrum, np.greater)
# ピークの周波数とパワーを取得
peak_freqs = xf[peaks]
peak_powers = power_spectrum[peaks]
# ピークの周期を計算
peak_periods = 1 / peak_freqs
# パワースペクトルとピークをプロット
plt.plot(xf, power_spectrum)
plt.plot(peak_freqs, peak_powers, 'ro')
plt.grid()
plt.title('Power Spectrum of AirPassengers Data with Peaks')
plt.xlabel('Frequency [1/month]')
plt.ylabel('Power')
plt.show()
このコードは、航空旅客数の時系列データからパワースペクトルを計算し、そのピーク(主要な周期性を示す部分)を見つけてグラフにプロットするものです。具体的には以下の処理を行っています。
y = dataset.data['value'].values:データセットから’value’列を取得し、その値をnumpy配列としてyに格納しています。これが航空旅客数の時系列データです。
N = y.size; T = 1.0:データのサイズ(点の数)をNに、サンプリング間隔をTに設定しています。このデータセットは月ごとのデータなので、サンプリング間隔Tは1.0(1ヵ月)です。
yf = np.fft.fft(y); xf = np.fft.fftfreq(N, d=T)[:N//2]:numpyのfft.fft関数で高速フーリエ変換(FFT)を行い、fft.fftfreq関数で対応する周波数を計算しています。ここで、N//2までの部分を取っているのは、FFTの結果が対称性を持つためで、実際には半分のデータだけで全情報が得られます。
power_spectrum = 2.0/N * np.abs(yf[0:N//2]):FFTの結果からパワースペクトルを計算しています。パワースペクトルは、各周波数成分が信号の全体に占めるパワー(強さ)の割合を示します。
peaks = argrelextrema(power_spectrum, np.greater):scipyのargrelextrema関数を使って、パワースペクトルのピーク(相対的な最大値)を探しています。
peak_freqs = xf[peaks]; peak_powers = power_spectrum[peaks]:ピークの周波数とパワーを取得しています。
peak_periods = 1 / peak_freqs:ピークの周期を計算しています。周期は周波数の逆数で、このデータセットでは月単位の値となります。
plt.plot(xf, power_spectrum); plt.plot(peak_freqs, peak_powers, 'ro'):パワースペクトルとそのピークをグラフにプロットしています。ピークは赤色の円で表示しています。
plt.grid(); plt.title('Power Spectrum of AirPassengers Data with Peaks'); plt.xlabel('Frequency [1/month]'); plt.ylabel('Power'); plt.show():グラフにタイトルと軸ラベルを設定し、グリッド線を表示し、最後にshow関数でグラフを画面に表示しています。
以上がこのコードの説明となります。
以下、実行結果です。横軸が周波数、縦軸がパワースペクトルです。
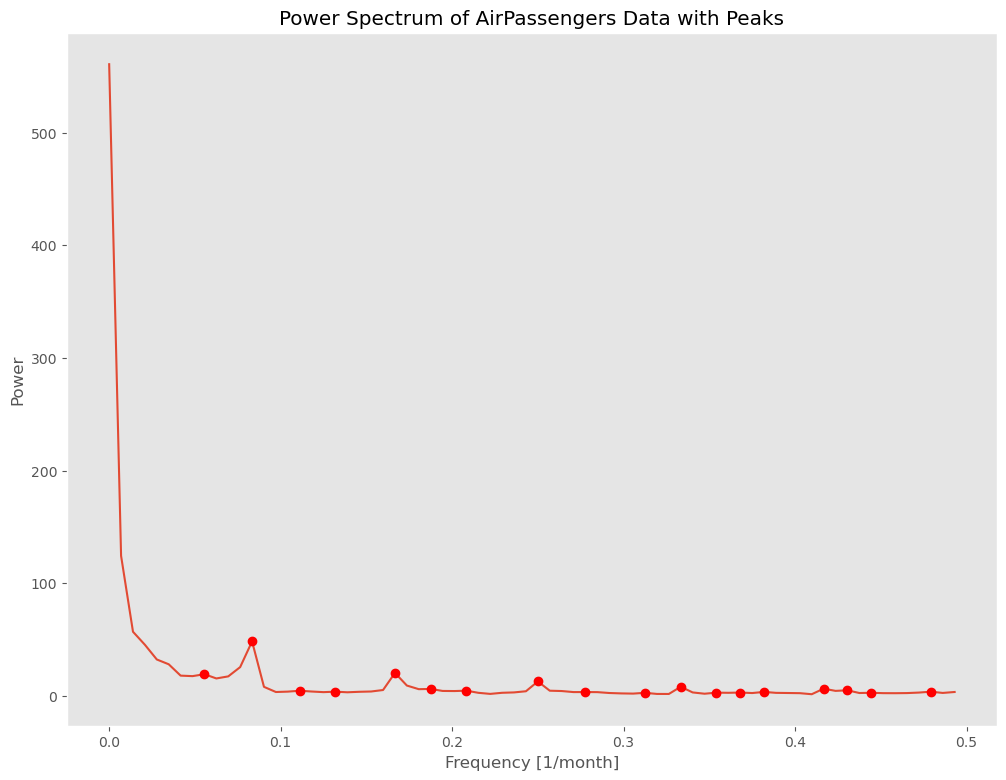
パワースペクトルがピークとなる周波数が幾つかあります。ピークとなる箇所(local maximum)に●をつけています。
周波数が0.0と0.1の間に、気になるピークの箇所が1つあります。
グラフだけだと、具体的な周波数や周期期間が分からないので、ピークの情報(周波数、パワー、周期)をデータフレームにまとめ出力します。
以下、コードです。
# ピークの情報(周波数、パワー、周期)をデータフレームにまとめる
peak_df = pd.DataFrame({
'Frequency': peak_freqs,
'Power': peak_powers,
'Period': peak_periods,
})
peak_df = peak_df.sort_values('Power', ascending=False)
print(peak_df)
このコードは、先程計算したピークの情報(周波数、パワー、周期)をpandasのデータフレームにまとめ、パワーの降順にソートして表示するものです。
具体的には以下の処理を行っています。
peak_df = pd.DataFrame({'Frequency': peak_freqs, 'Power': peak_powers, 'Period': peak_periods}):pandasのDataFrame関数を使って、ピークの情報をデータフレームにまとめています。データフレームは表形式のデータを効率的に扱うためのデータ構造で、各列には任意の名前を付けることができます。ここでは、ピークの周波数を’Frequency’、パワーを’Power’、周期を’Period’という名前の列に格納しています。
peak_df = peak_df.sort_values('Power', ascending=False):sort_values関数を使って、’Power’列の値に基づいてデータフレームをソートしています。ascending=Falseという引数で、降順(大きい値から小さい値の順)にソートすることを指定しています。
print(peak_df):最後に、ソートした結果を表示しています。
以上がこのコードの説明となります。
以下、実行結果です。
Frequency Power Period 1 0.083333 48.355814 12.000000 4 0.166667 20.396891 6.000000 0 0.055556 19.248942 18.000000 7 0.250000 12.829011 4.000000 10 0.333333 8.106544 3.000000 14 0.416667 6.416783 2.400000 5 0.187500 6.188780 5.333333 15 0.430556 4.968030 2.322581 6 0.208333 4.643156 4.800000 2 0.111111 4.581388 9.000000 3 0.131944 3.762903 7.578947 17 0.479167 3.750227 2.086957 13 0.381944 3.539359 2.618182 8 0.277778 3.413807 3.600000 12 0.368056 2.982421 2.716981 11 0.354167 2.890600 2.823529 16 0.444444 2.783163 2.250000 9 0.312500 2.741477 3.200000
- Frequency:周波数
- Power:パワースペクトル
- Period:周期期間
周波数が0.0と0.1の間にあった一番大きなピークの周波数は0.08333で、その周期期間は12ヶ月です。
このことから、12ヶ月周期がありそうなことが分かります。
パワースペクトルのピークの周期期間を、パワースペクトル降順でグラフ化してみました。
以下、コードです。
# パワーの降順でソートし、横棒グラフをプロット
peak_df = peak_df.sort_values('Power', ascending=True)
plt.barh(list(range(1, len(peak_df)+1)), peak_df['Power'], tick_label=peak_df['Period'])
plt.xlabel('Power')
plt.ylabel('Period')
plt.title('Power Spectrum (Descending Order)')
plt.show()
このコードは、先程作成したピークのデータフレームをパワーの昇順にソートし、その結果を横棒グラフとしてプロットするものです。
具体的には以下の処理を行っています。
peak_df = peak_df.sort_values('Power', ascending=True):sort_values関数を使って、データフレームを’Power’列の値に基づいて昇順(小さい値から大きい値の順)にソートしています。
plt.barh(list(range(1, len(peak_df)+1)), peak_df['Power'], tick_label=peak_df['Period']):Matplotlibのbarh関数を使って横棒グラフをプロットしています。1つ目の引数は棒の位置(ここでは1からデータフレームの長さまでの整数列)、2つ目の引数は棒の長さ(ここではパワーの値)、3つ目の引数は各棒に対応するラベル(ここでは周期の値)です。
plt.xlabel('Power'); plt.ylabel('Period'); plt.title('Power Spectrum (Descending Order)'):グラフのx軸ラベル、y軸ラベル、タイトルを設定しています。
plt.show():最後に、show関数でグラフを画面に表示しています。
以上がこのコードの説明となります。
以下、実行結果です。
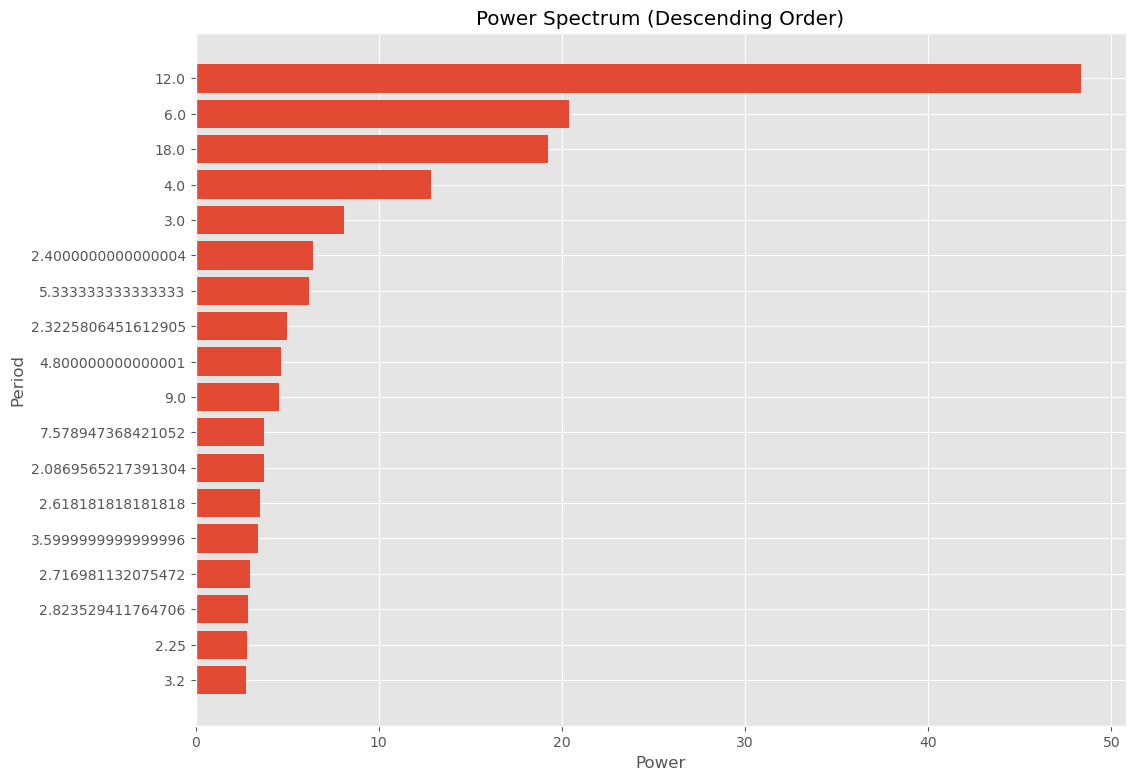
スペクトル分析による周期の長さの見つけ方としては、以上で終了しても構いません。
12ヶ月周期がありそうな気配ということが分かります。
発展した話題として、パワースペクトルのピークの有意性の検討を次からしていきます。
【発展した話題】ピークの有意性検討
このパートはやや難しくなります。飛ばしても問題ございません。

パワースペクトルのピークが「有意」であると判断するための統計的な方法があります。
その一つとして、ブートストラップ法を使った方法があります。
ここでは、ブートストラップ法そのものの説明や、時系列データに対するブートストラップ法の説明は割愛します。別の機会に、取り上げます。
今回は、幾つかある時系列データに対するブートストラップ法の中の、移動ブロックブートストラップ法(Moving Block Bootstrap, MBB)を使います。
以下に概要だけ説明を加えます。興味のある方は一読下さい。
移動ブロックブートストラップ (Moving Block Bootstrap, MBB) は、時系列データを処理するための統計的手法の一つです。時系列データは、時間的な依存関係をもつため、通常のブートストラップ手法をそのまま適用することができません。ブートストラップは一般的に観測値が独立であるという仮定のもとで動作しますが、時系列データは通常、時間的に連続した観測値が互いに関連しているため、この仮定は成り立ちません。
MBBは、これに対する解決策の一つです。この手法は、時系列データから「ブロック」と呼ばれる連続した観測値のセットをランダムに選び出し、これらを組み合わせて新たな時系列データを生成します。これにより、元の時系列データの時間的な依存関係を維持しつつ、新たなデータセットを生成することが可能となります。
MBBの主な手順は以下の通りです:
- まず、ブロックの長さ
- 次に、元の時系列データからランダムに位置を選び、その位置から
- このブロックをブートストラップサンプルとして保存します。
- 2と3の手順を繰り返し、必要な数のブロックを取得します。
- 取得したブロックを順番に連結して、新たなブートストラップサンプルを生成します。
この手法は、元の時系列データの時間的な依存関係を反映したブートストラップサンプルを生成するため、元のデータの統計的特性をより正確に推定することが可能となります。
ただし、適切なブロックの長さ
上記の最後に記載されていますが、ブロックの長さは、移動ブロックブートストラップ法(Moving Block Bootstrap, MBB)の結果に大きな影響を与えます。
ブロックの長さが長い場合:
- メリット:時間的な依存性をよりよく保持することができます。これは、長い時間スケールでの依存性や、長期的なトレンドを反映するために重要です。また、元のデータの分布をより忠実に再現する可能性があります。
- デメリット:ブロックの数が少なくなるため、ブートストラップサンプルの多様性が減少します。これにより、ブートストラップサンプルの統計的な特性が元のデータのそれと大きく異なる可能性があります。さらに、特にデータの数が少ない場合、適切なブートストラップサンプルを生成することが難しくなる可能性があります。
ブロックの長さが短い場合:
- メリット:ブロックの数が多くなるため、ブートストラップサンプルの多様性が増します。これにより、様々なパターンのブートストラップサンプルを生成することが可能になり、結果として推定値の不確かさをより正確に評価することができる可能性があります。
- デメリット:時間的な依存性を十分に保持することができない可能性があります。これは、短い時間スケールでの依存性しか反映できないため、元のデータの長期的なトレンドや周期性をうまく捉えることができないかもしれません。
ブロックの長さを選ぶ際には、これらのメリットとデメリットを考慮に入れる必要があります。
では、どのようにしてブロックサイズを選べばいいのでしょうか?
ブロックの長さを選ぶための方法は存在します。
例えば、信頼区間の幅が最も小さくなるブロックサイズを最適なブロックサイズとして選択する、というものです。
具体的には次のような手順で行われます。
- 異なるブロックサイズ(例えば、ブロックサイズ1, 2, 3, …, n)を用いて、それぞれブートストラップサンプルを生成します。
- 各ブロックサイズについて、ブートストラップサンプルから統計的推定値(例えば、平均や分散)を計算し、その信頼区間を求めます。
- それぞれのブロックサイズについて計算した信頼区間の幅(信頼区間の上限値と下限値の差)を比較します。
- 信頼区間の幅が最も小さいブロックサイズを選択します。
幾つか注意点があります。
- 計算量が大きくなる
- 信頼区間の幅が最小となるブロックサイズが必ずしも「最適」であるとは限らない
この方法は、信頼区間の幅が小さいほど、推定値の不確かさが小さいと考えられるため、最も精確な推定を行うことができるであろうという思想が前提になります。
要するに……
- 移動ブロックブートストラップ法(Moving Block Bootstrap, MBB)を使うことで元のデータの時間的な依存性を維持したまま、時系列データに対する統計的な推定を行うことが可能となります。
- ただし、適切なブロックのサイズを選ぶのが難しいなどの問題点があります。
そこで、今回は適切なブロックのサイズを選ぶために、グリッドサーチ(総当り法)を実施します。要は、ブロッグサイズを色々変化(2,3,4…)しながら、一番良さそうなブロックサイズ(信頼区間の幅が最も小さなブロックサイズ)を選びます。
先ず、最適なブロックサイズを選ぶ関数を定義します。
以下、コードです。
def optimal_block_size(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE):
# ブロックサイズの範囲を設定
block_size_range = list(range(2, 24)) # Adjust this to your preferred range
# 各ブロックサイズでブートストラップを実行し、信頼区間の幅の平均を記録
average_interval_widths = []
for block_size in block_size_range:
bootstrap_powers = np.zeros((N_BOOTSTRAP, len(y)//2))
for i in range(N_BOOTSTRAP):
bootstrap_sample = []
while len(bootstrap_sample) < len(y):
start_index = np.random.randint(0, len(y) - block_size + 1)
bootstrap_sample += list(y[start_index: start_index + block_size])
bootstrap_sample = bootstrap_sample[:len(y)] # Adjust the length of bootstrap_sample to N
bootstrap_yf = np.fft.fft(bootstrap_sample)
bootstrap_powers[i, :] = 2.0/len(y) * np.abs(bootstrap_yf[0:len(y)//2])
lower_bound = np.percentile(bootstrap_powers, LOWER_PERCENTILE, axis=0)
upper_bound = np.percentile(bootstrap_powers, UPPER_PERCENTILE, axis=0)
average_interval_width = np.mean(upper_bound - lower_bound)
average_interval_widths.append(average_interval_width)
# 最適なブロックサイズを選択
optimal_block_size = block_size_range[np.argmin(average_interval_widths)]
return optimal_block_size
この関数では、ブロックサイズの範囲(2から24まで)を設定し、各ブロックサイズについて移動ブロックブートストラップ法(Moving Block Bootstrap, MBB)を適用して信頼区間の幅の平均を計算します。その結果、信頼区間の幅が最も小さくなるブロックサイズを最適なブロックサイズとして選択します。
具体的には以下の処理を行っています。
- ブロックサイズの範囲を設定します。
- 各ブロックサイズについて、以下の操作を行います。
- ブートストラップサンプルを作成します。この際、元のデータからランダムに選んだ位置からブロックサイズ分のデータを抽出し、これを連結して新たなデータセットを作ります。
- ブートストラップサンプルからパワースペクトルを計算します。
- 上記の操作を指定された回数(ブートストラップサンプルの数)だけ繰り返し、各ブートストラップサンプルのパワースペクトルを記録します。
- ブートストラップサンプルのパワースペクトルから、指定されたパーセンタイルに基づく信頼区間の下限と上限を計算します。
- 信頼区間の幅の平均を計算します。
- 信頼区間の幅の平均が最小となるブロックサイズを最適なブロックサイズとして選択します。
以上がこのコードの説明となります。
先程の「トレンド非定常性の除去していない元の時系列データ」に対し、試しに使ってみます。
以下、コードです。
# 使用例
N_BOOTSTRAP = 1000
LOWER_PERCENTILE = 0.5
UPPER_PERCENTILE = 99.5
block_size = optimal_block_size(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE)
print("Optimal block size: ", block_size)
N_BOOTSTRAP = 1000; LOWER_PERCENTILE = 0.5; UPPER_PERCENTILE = 99.5:ブートストラップ法のための定数(ブートストラップサンプルの数、信頼区間の下限と上限のパーセンタイル)を設定しています。信頼区間の下限が0.5%、上限が99.5%なので99%信頼区間ということです。
block_size = optimal_block_size(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE):先程定義したoptimal_block_size関数を呼び出し、最適なブロックサイズを計算しています。この関数はブロックブートストラップ法を用いて、各ブロックサイズでブートストラップサンプルを生成し、信頼区間の幅の平均を計算し、その最小値を持つブロックサイズを最適なブロックサイズとして選択します。
print("Optimal block size: ", block_size):最適なブロックサイズを表示しています。
以下、実行結果です。
Optimal block size: 23
最適なブロックサイズは、23という結果になりました。
この結果を反映した移動ブロックブートストラップ法(Moving Block Bootstrap, MBB)を用いて、パワースペクトルのピークの有意性の検討をしていきます。
以下、コードです。
# ブートストラップサンプルの数とパーセンタイルを設定
N_BOOTSTRAP = 10000
LOWER_PERCENTILE = 0.5
UPPER_PERCENTILE = 99.5
# ブートストラップ法を用いて信頼区間を計算
n_bootstrap = N_BOOTSTRAP
bootstrap_powers = np.zeros((n_bootstrap, N//2))
# ブロックブートストラップのブロックサイズを設定
block_size = optimal_block_size(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE)
# ブートストラップ法を用いて信頼区間を計算
n_bootstrap = N_BOOTSTRAP
bootstrap_powers = np.zeros((n_bootstrap, N//2))
for i in range(n_bootstrap):
bootstrap_sample = []
while len(bootstrap_sample) < N:
start_index = np.random.randint(0, N - block_size + 1)
bootstrap_sample += list(y[start_index: start_index + block_size])
bootstrap_sample = bootstrap_sample[:N] # Adjust the length of bootstrap_sample to N
bootstrap_yf = np.fft.fft(bootstrap_sample)
bootstrap_powers[i, :] = 2.0/N * np.abs(bootstrap_yf[0:N//2])
# ブートストラップパワーの下位と上位パーセンタイルを計算
lower_bound = np.percentile(bootstrap_powers, LOWER_PERCENTILE, axis=0)
upper_bound = np.percentile(bootstrap_powers, UPPER_PERCENTILE, axis=0)
# ピークが有意かどうかを判断(ピークパワーが信頼区間外であるか)
significant = np.logical_and(peak_powers > lower_bound[peaks], peak_powers > upper_bound[peaks])
# ピークの情報データフレームに有意情報を追加
peak_df = peak_df.sort_index()
peak_df['Significant'] = significant
# パワーの降順でピーク情報のデータフレームをソートして表示
peak_df = peak_df.sort_values('Power', ascending=False)
print(peak_df)
N_BOOTSTRAP = 10000; LOWER_PERCENTILE = 0.5; UPPER_PERCENTILE = 99.5: ブートストラップ法に用いるパラメータ(ブートストラップサンプルの数、信頼区間の下位と上位パーセンタイル)を設定しています。信頼区間の下限が0.5%、上限が99.5%なので99%信頼区間ということです。block_size = optimal_block_size(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE):optimal_block_size関数を用いて最適なブロックサイズを計算しています。- ブートストラップ法を用いて信頼区間を計算します。
- まず
n_bootstrapとbootstrap_powersを初期化し、ブートストラップサンプルを生成してそのパワースペクトルを計算します。 - ブートストラップサンプルはランダムに選ばれた開始インデックスから
block_sizeの長さだけデータを抽出し、それを繰り返して生成します。 - 各ブートストラップサンプルに対して高速フーリエ変換(FFT)を行い、その絶対値の二乗を計算してパワースペクトルを求めます。
- まず
lower_bound = np.percentile(bootstrap_powers, LOWER_PERCENTILE, axis=0); upper_bound = np.percentile(bootstrap_powers, UPPER_PERCENTILE, axis=0): ブートストラップパワーの下位と上位パーセンタイルを計算し、それぞれ信頼区間の下限と上限としています。significant = np.logical_and(peak_powers > lower_bound[peaks], peak_powers > upper_bound[peaks]): ピークのパワーが信頼区間外にあるかどうかを判断し、その結果をsignificantに格納しています。peak_df = peak_df.sort_index(); peak_df['Significant'] = significant: ピークの情報を持つデータフレームpeak_dfにsignificantを新しい列として追加します。peak_df = peak_df.sort_values('Power', ascending=False); print(peak_df): データフレームをパワーの降順にソートし、その結果を表示しています。
以下、実行結果です。
Frequency Power Period Significant 1 0.083333 48.355814 12.000000 False 4 0.166667 20.396891 6.000000 False 0 0.055556 19.248942 18.000000 False 7 0.250000 12.829011 4.000000 False 10 0.333333 8.106544 3.000000 False 14 0.416667 6.416783 2.400000 False 5 0.187500 6.188780 5.333333 False 15 0.430556 4.968030 2.322581 False 6 0.208333 4.643156 4.800000 False 2 0.111111 4.581388 9.000000 False 3 0.131944 3.762903 7.578947 False 17 0.479167 3.750227 2.086957 False 13 0.381944 3.539359 2.618182 False 8 0.277778 3.413807 3.600000 False 12 0.368056 2.982421 2.716981 False 11 0.354167 2.890600 2.823529 False 16 0.444444 2.783163 2.250000 False 9 0.312500 2.741477 3.200000 False
Significantが有意かどうかを表しています。
- True:有意である
- False:有意でない
要は、どれも有意ではない、という結果になりました。99%信頼区間でしたので、有意水準は1%です。
つまり、12ヶ月周期があるように見えたが、それはそう見えただけの可能性がある、ということです。
ただ、トレンド非定常な時系列データで実施しているので、トレンド成分の影響で季節成分が見えにくくなった可能性があります。
といういことで、トレンド非定常性の除去をした時系列データに対し、スペクトル分析を実施しましょうとなります。
ただ、トレンド非定常性を除去しない場合の処理が長くなったので、ここまでの一連の処理を関数化します。
要するに、その関数を使い、サクッとトレンド非定常性の除去をした時系列データに対しスペクトル分析を実施する、ということです。
ここまでの処理を関数化
以下、コードです。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import argrelextrema
import pandas as pd
def detect_period(y):
# 定数の設定(フーリエ変換)
N = y.size
T = 1.0
# 定数の設定(ブートストラップ)
N_BOOTSTRAP = 10000
LOWER_PERCENTILE = 0.5
UPPER_PERCENTILE = 99.5
# 高速フーリエ変換 (FFT)を実行
yf = np.fft.fft(y)
xf = np.fft.fftfreq(N, d=T)[:N//2]
# パワースペクトルを計算
power_spectrum = 2.0/N * np.abs(yf[0:N//2])
# パワースペクトルのピーク(ローカルマキシマ)を探す
peaks = argrelextrema(power_spectrum, np.greater)
# ピークの周波数とパワーを取得
peak_freqs = xf[peaks]
peak_powers = power_spectrum[peaks]
# ピークの周期を計算
peak_periods = 1 / peak_freqs
# パワースペクトルとピークをプロット
plt.plot(xf, power_spectrum)
plt.plot(peak_freqs, peak_powers, 'ro')
plt.grid()
plt.title('Power Spectrum of Data with Peaks')
plt.xlabel('Frequency [1/month]')
plt.ylabel('Power')
plt.show()
# ブロックブートストラップのブロックサイズを設定
block_size = optimal_block_size(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE)
# ブートストラップ法を用いて信頼区間を計算
n_bootstrap = N_BOOTSTRAP
bootstrap_powers = np.zeros((n_bootstrap, N//2))
for i in range(n_bootstrap):
bootstrap_sample = []
while len(bootstrap_sample) < N:
start_index = np.random.randint(0, N - block_size + 1)
bootstrap_sample += list(y[start_index: start_index + block_size])
bootstrap_sample = bootstrap_sample[:N] # Adjust the length of bootstrap_sample to N
bootstrap_yf = np.fft.fft(bootstrap_sample)
bootstrap_powers[i, :] = 2.0/N * np.abs(bootstrap_yf[0:N//2])
lower_bound = np.percentile(bootstrap_powers, LOWER_PERCENTILE, axis=0)
upper_bound = np.percentile(bootstrap_powers, UPPER_PERCENTILE, axis=0)
# ピークが有意かどうかを判断
significant = np.logical_and(peak_powers > lower_bound[peaks], peak_powers > upper_bound[peaks])
# ピークの情報をデータフレームにまとめる
peak_df = pd.DataFrame({
'Frequency': peak_freqs,
'Power': peak_powers,
'Period': peak_periods,
'Significant': significant,
})
# 横棒グラフをプロット(降順)
peak_df = peak_df.sort_values('Power', ascending=True)
plt.barh(list(range(1, len(peak_df)+1)), peak_df['Power'], tick_label=peak_df['Period'])
plt.xlabel('Power')
plt.ylabel('Period')
plt.title('Power Spectrum (Descending Order)')
plt.show()
# パワーの降順に並び替えて表示
peak_df = peak_df.sort_values('Power', ascending=False)
print(peak_df)
先程の「トレンド非定常性の除去していない元の時系列データ」に対し、試しに使ってみます。
以下、コードです。
# データセットのロードと解析
dataset = sm.datasets.get_rdataset('AirPassengers')
y = dataset.data['value'].values
detect_period(y)
以下、実行結果です。


Frequency Power Period Significant 1 0.083333 48.355814 12.000000 False 4 0.166667 20.396891 6.000000 False 0 0.055556 19.248942 18.000000 False 7 0.250000 12.829011 4.000000 False 10 0.333333 8.106544 3.000000 False 14 0.416667 6.416783 2.400000 False 5 0.187500 6.188780 5.333333 False 15 0.430556 4.968030 2.322581 False 6 0.208333 4.643156 4.800000 False 2 0.111111 4.581388 9.000000 False 3 0.131944 3.762903 7.578947 False 17 0.479167 3.750227 2.086957 False 13 0.381944 3.539359 2.618182 False 8 0.277778 3.413807 3.600000 False 12 0.368056 2.982421 2.716981 False 11 0.354167 2.890600 2.823529 False 16 0.444444 2.783163 2.250000 False 9 0.312500 2.741477 3.200000 False
先程と同じ結果が出力されたかと思います。
トレンド非定常性を除去した場合
トレンド非定常性の除去をした時系列データに対し、スペクトル分析を実施する場合です。
先ず、トレンド非定常性の除去をします。
以下、コードです。
# データのトレンド非定常性を除去するために、最初の差分を取る
data_diff = data.diff().dropna()
# 差分を取った時系列データをプロット
plt.figure(figsize=(12, 6))
plt.plot(data_diff)
plt.title('Differenced Air Passengers Over Time') # タイトルを設定
plt.grid(True) # グリッド線を表示
plt.show() # プロットを表示
このコードは、元の時系列データからトレンドの非定常性を除去するために最初の差分を取り、その結果をプロットするものです。
具体的には、以下の処理を行っています。
data_diff = data.diff().dropna():pandasのdiff関数を使って、元の時系列データの最初の差分を計算しています。差分を取ることで、時系列データのトレンドの非定常性を除去することができます。dropna関数は、差分を取った結果生じる最初の欠損値を除去します。
plt.figure(figsize=(12, 6)); plt.plot(data_diff); plt.title('Differenced Air Passengers Over Time'); plt.grid(True); plt.show():matplotlibの関数を使って、差分を取った時系列データをプロットしています。タイトルとグリッド線を設定し、show関数でグラフを画面に表示しています。
以上がこのコードの説明となります。
以下、実行結果です。
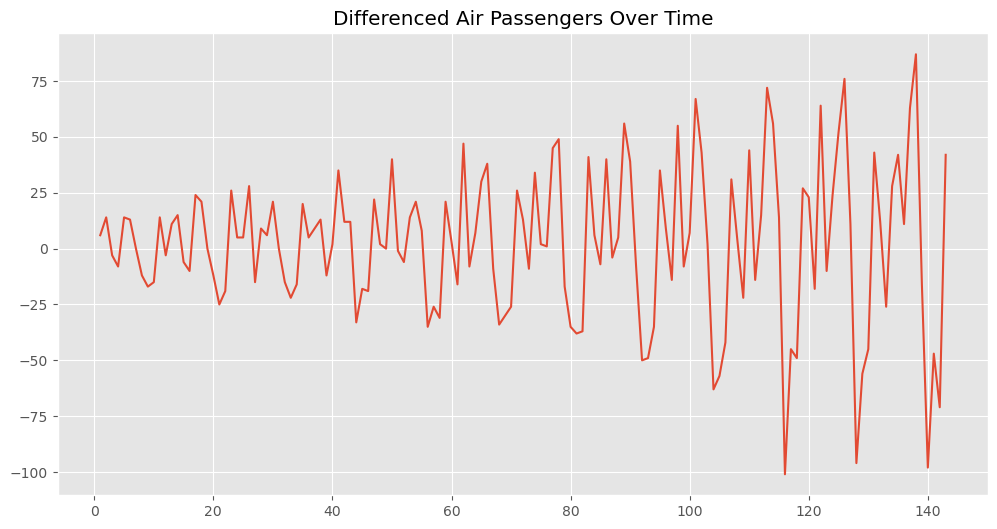
元の時系列データからトレンドが除去された新しい時系列データが得られました。これにより、データの季節性や他のパターンをより明確にできます。
このトレンド非定常性の除去をした時系列データに対し、高速フーリエ変換 (FFT)を実行しパワースペクトルを計算、そしてパワースペクトルのピークの周波数を探します。そのとき、その周波数の周期期間も求めます。
先程定義した関数を使います。
以下、コードです。
y = data_diff.values detect_period(y)
以下、実行結果です。
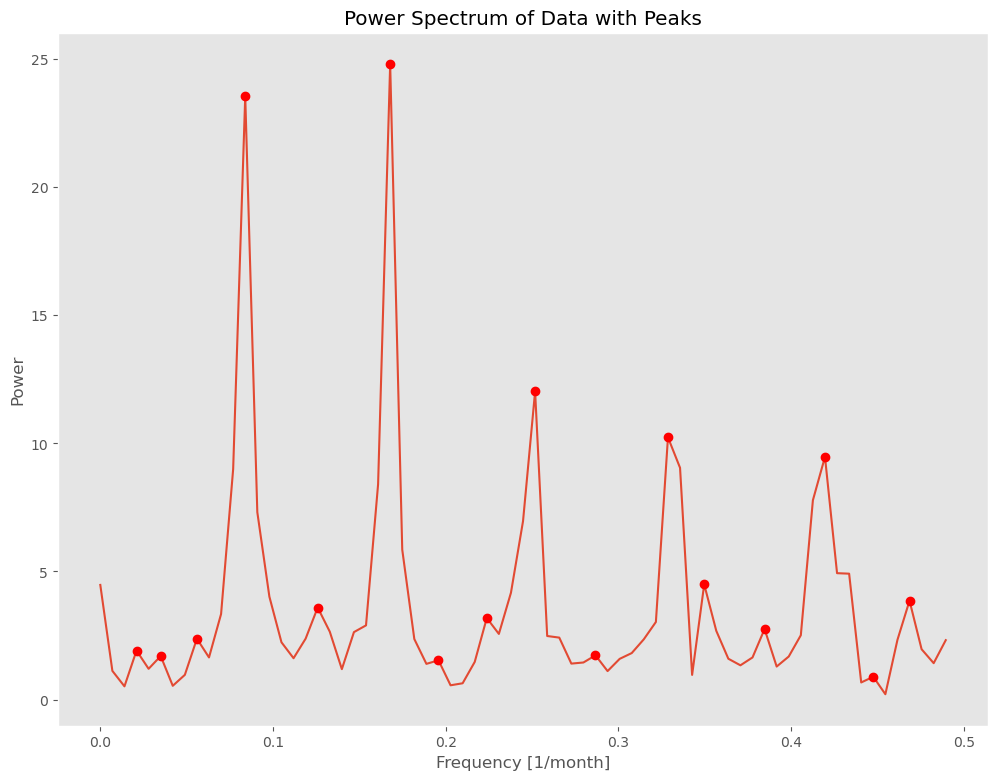
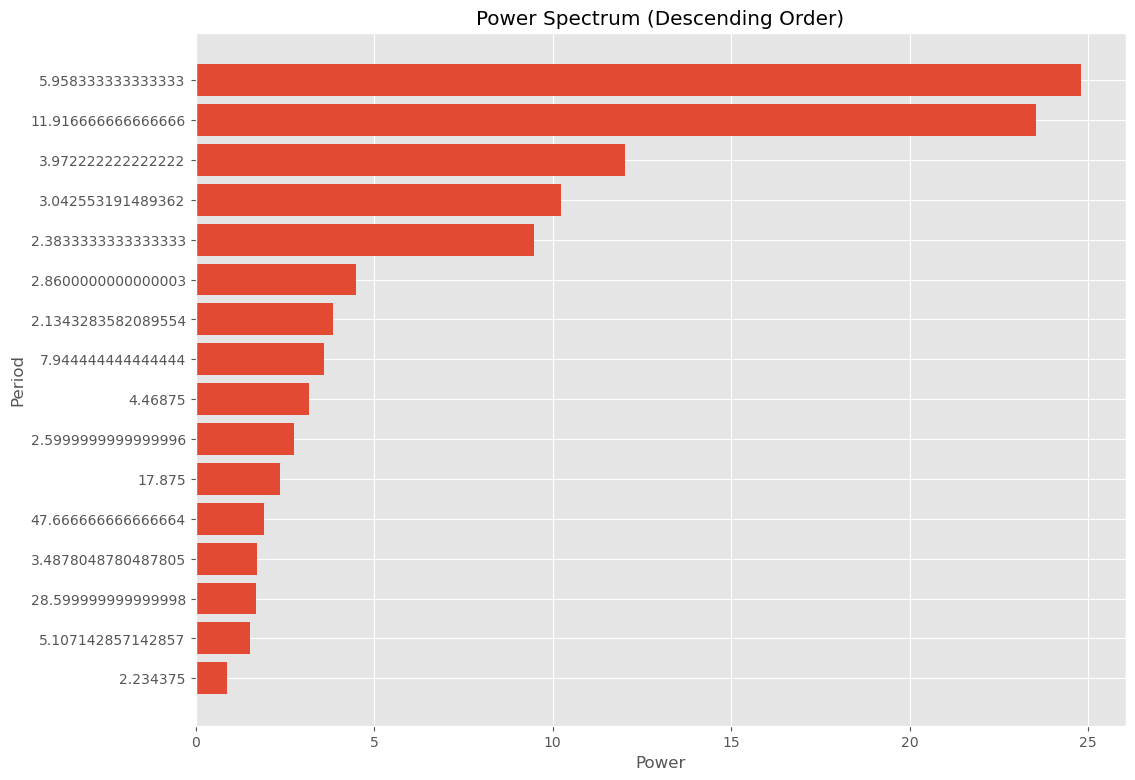
Frequency Power Period Significant 5 0.167832 24.805383 5.958333 True 3 0.083916 23.550430 11.916667 True 8 0.251748 12.034165 3.972222 False 10 0.328671 10.236364 3.042553 False 13 0.419580 9.475237 2.383333 False 11 0.349650 4.496870 2.860000 False 15 0.468531 3.859098 2.134328 False 4 0.125874 3.592507 7.944444 False 7 0.223776 3.183167 4.468750 False 12 0.384615 2.753009 2.600000 False 2 0.055944 2.375038 17.875000 False 0 0.020979 1.911933 47.666667 False 9 0.286713 1.726903 3.487805 False 1 0.034965 1.699250 28.600000 False 6 0.195804 1.533140 5.107143 False 14 0.447552 0.890691 2.234375 False
この結果から、季節性の周期期間は2つあり、6ヶ月周期(6≒5.95833)と12ヶ月周期(12≒11.916667)です。
自己相関分析の場合と「周期の長さが違うぞ問題」が勃発!
トレンド非定常性の除去をした時系列データに対し、スペクトル分析を実施することで、周期期間が明確になりましたが、前回の自己相関分析による方法と一部異なります。
- 自己相関分析の結果:12ヶ月周期
- スペクトル分析の結果:6ヶ月周期と12ヶ月周期
どう解釈すればいいでしょうか?
整理しながら解釈していきます。
自己相関分析とスペクトル分析から得られた結果は、データに存在する周期性を示しています。
自己相関分析の結果、12ヶ月周期が検出されました。これは一年間の旅客数の動向(つまり季節性)を反映していると考えられます。航空旅客数は、休暇シーズンや特定の祝日など、年間を通じて定期的に変動する傾向があります。
一方で、スペクトル分析の結果はより微妙な情報を提供しています。スペクトル分析は、データの周期性を時間領域から周波数領域に変換することで、データに含まれる異なる周波数成分を検出します。この場合、スペクトル分析は6ヶ月と12ヶ月の周期性を示しています。
これは、年間を通じての主な季節変動(12ヶ月周期)に加えて、半年ごとの何らかの変動(6ヶ月周期)もデータに存在する可能性を示しています。たとえば、夏と冬の旅行シーズンが明確に区別され、それぞれが年間旅客数に大きな影響を与えている可能性があります。または、特定のプロモーション活動やイベントが半年ごとに行われている可能性もあります。
重要な点は、これらの周期性が統計的に有意であり、かつビジネスの観点から意味をなすかどうかを評価することです。結果の解釈は、具体的なビジネスドメインや他の外部情報を考慮に入れる必要があります。
要するに、12ヶ月周期に関しては疑う余地はなさそうです。感覚的にも問題なさそうな気がします。
6ヶ月周期はどうでしょうか?
データからはありそうだ、と導かれたので、検討する余地がありそうです。
他のデータを交えながらデータ分析をするのもいいですが、例えばその業界や業務に詳しい人などにヒアリングなどを実施したりするのもいいでしょう。

データは、社会現象の一面の一部しか捉えていません。
そのことを踏まえ補うのは、人の経験や記憶、知恵などです。その人智をデータに融合すると、素敵なことが起こることでしょう。
コード整理
以上で記載したコード(モジュールのインポート部分と、2つの関数optimal_block_sizeとdetect_periodの定義)さえすれば、使え回しできます。
ただ、ちょっとごちゃごちゃしているので、以下のようにコードを整理しました。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.signal import argrelextrema
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]
# ブートストラップサンプルを生成する関数
def generate_bootstrap_sample(y, block_size):
bootstrap_sample = []
while len(bootstrap_sample) < len(y):
start_index = np.random.randint(0, len(y) - block_size + 1)
bootstrap_sample += list(y[start_index: start_index + block_size])
return bootstrap_sample[:len(y)] # ブートストラップサンプルの長さをNに調整
# ブートストラップ法を用いた信頼区間の計算を行う関数
def bootstrap_method(y, block_size, n_bootstrap, lower_percentile, upper_percentile):
bootstrap_powers = np.zeros((n_bootstrap, len(y)//2))
for i in range(n_bootstrap):
bootstrap_sample = generate_bootstrap_sample(y, block_size)
bootstrap_yf = np.fft.fft(bootstrap_sample)
bootstrap_powers[i, :] = 2.0/len(y) * np.abs(bootstrap_yf[0:len(y)//2])
lower_bound = np.percentile(bootstrap_powers, lower_percentile, axis=0)
upper_bound = np.percentile(bootstrap_powers, upper_percentile, axis=0)
return lower_bound, upper_bound
# パワースペクトルとピークをプロットする関数
def plot_power_spectrum(xf, power_spectrum, peak_freqs, peak_powers):
plt.plot(xf, power_spectrum)
plt.plot(peak_freqs, peak_powers, 'ro')
plt.grid()
plt.title('Power Spectrum of Data with Peaks')
plt.xlabel('Frequency [1/month]')
plt.ylabel('Power')
plt.show()
# パワースペクトルをパワーの降順にプロットする関数
def plot_power_spectrum_descending(peak_df):
peak_df = peak_df.sort_values('Power', ascending=True)
plt.barh(list(range(1, len(peak_df)+1)), peak_df['Power'], tick_label=peak_df['Period'])
plt.xlabel('Power')
plt.ylabel('Period')
plt.title('Power Spectrum (Descending Order)')
plt.show()
# 最適なブロックサイズを計算する関数
def optimal_block_size(y, n_bootstrap, lower_percentile, upper_percentile, block_size_range):
average_interval_widths = []
for block_size in block_size_range:
lower_bound, upper_bound = bootstrap_method(y, block_size, n_bootstrap, lower_percentile, upper_percentile)
average_interval_width = np.mean(upper_bound - lower_bound)
average_interval_widths.append(average_interval_width)
optimal_block_size = block_size_range[np.argmin(average_interval_widths)]
return optimal_block_size
# 周期を検出する関数
def detect_period(y, n_bootstrap, lower_percentile, upper_percentile, block_size_range):
N = y.size
T = 1.0
yf = np.fft.fft(y)
xf = np.fft.fftfreq(N, d=T)[:N//2]
power_spectrum = 2.0/N * np.abs(yf[0:N//2])
peaks = argrelextrema(power_spectrum, np.greater)
peak_freqs = xf[peaks]
peak_powers = power_spectrum[peaks]
peak_periods = 1 / peak_freqs
plot_power_spectrum(xf, power_spectrum, peak_freqs, peak_powers)
block_size = optimal_block_size(y, n_bootstrap, lower_percentile, upper_percentile, block_size_range)
lower_bound, upper_bound = bootstrap_method(y, block_size, n_bootstrap, lower_percentile, upper_percentile)
significant = np.logical_and(peak_powers > lower_bound[peaks], peak_powers > upper_bound[peaks])
peak_df = pd.DataFrame({
'Frequency': peak_freqs,
'Power': peak_powers,
'Period': peak_periods,
'Significant': significant,
})
plot_power_spectrum_descending(peak_df)
peak_df = peak_df.sort_values('Power', ascending=False)
print(peak_df)
使用例です。
トレンド非定常性を除去しない場合です。
以下、コードです。
import statsmodels.api as sm
# データセットの読み込み
data = sm.datasets.get_rdataset('AirPassengers').data['value']
y = data.values
# 定数の設定
N_BOOTSTRAP = 10000
LOWER_PERCENTILE = 0.5
UPPER_PERCENTILE = 99.5
BLOCK_SIZE_RANGE = list(range(2, 24)) # ブロックサイズの範囲
# detect_period関数の実行
detect_period(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE, BLOCK_SIZE_RANGE)
実行結果は、先程と同じものが出力されるので割愛します。
トレンド非定常性を除去した場合です。
以下、コードです。
import statsmodels.api as sm
# データセットの読み込み
data = sm.datasets.get_rdataset('AirPassengers').data['value']
# データのトレンド非定常性を除去するために、最初の差分を取る
data_diff = data.diff().dropna()
y = data_diff.values
# 定数の設定
N_BOOTSTRAP = 10000
LOWER_PERCENTILE = 0.5
UPPER_PERCENTILE = 99.5
BLOCK_SIZE_RANGE = list(range(2, 24)) # ブロックサイズの範囲
# detect_period関数の実行
detect_period(y, N_BOOTSTRAP, LOWER_PERCENTILE, UPPER_PERCENTILE, BLOCK_SIZE_RANGE)
実行結果は、先程と同じものが出力されるので割愛します。
まとめ
今回は、スペクトル分析による周期の長さの見つけ方を説明しました。
前回の自己相関分析による方法と、今回のスペクトル分析による方法が、2大手法です。
ただし、この2つの手法はデータがトレンド非定常ではないときに最も効果的です。
要は、トレンド成分を除去した時系列データに対し実施する、ということです。
非定常なデータに対して実施できる、ウェーブレット変換による方法もあります。別の機会にお話しします。