ビジネスの世界のデータの多くは、時間軸のあるデータである時系列データです。
時系列データを手に入れたら、どのようなデータかなんとなく知りたくなります。
時系列データの多くは色々な変化をしながら推移していきます。
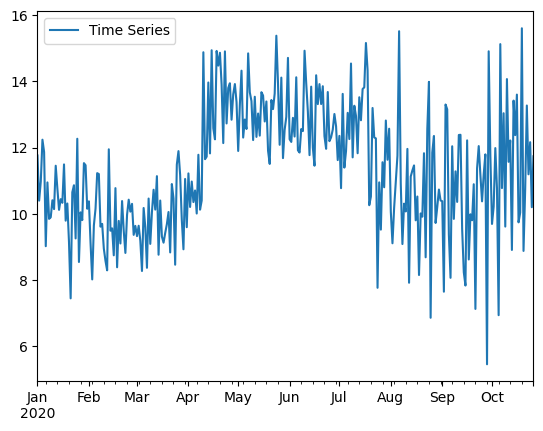
例えば……
- 全体の水準が大きくなったと思えば、水準が急激に落ちたり
- 上昇トレンドがあったかと思えば、下降トレンドになったり
- 振幅の幅が急激に大きくなったり、小さくなったり
……などなど。
時系列データは一定ではなく、このような変化をすることも少なくありません
そこで知りたくなるのが、このような変化をする時期、つまり変化点です。
変化点を検出する技術は色々とあります。
幸いにも、Pythonのライブラリーの中に時系列データの変化点を見つけるためのパッケージがいくつかあります。
今回は、「Python ruptures でサクッと時系列データの変化点を見つける方法」というお話しをします。
Contents [hide]
今回扱う変化点
時系列データには色々な種類の変化があります。
この中で今回は、1変量時系列データの次の3つの変化を扱います。
- 水準変化(レベルシフト)
- トレンド変化
- 分散変化
水準変化(レベルシフト)とは、平均の変化のことです。
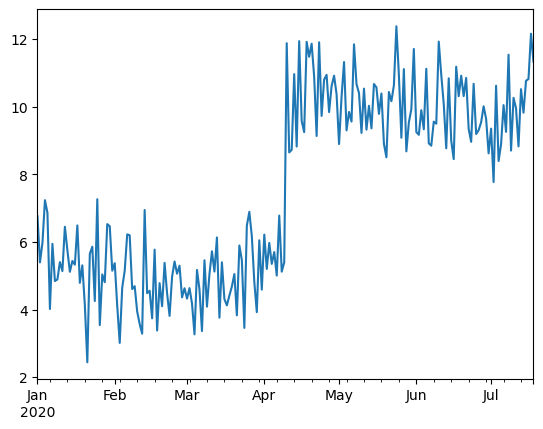
トレンド変化とは、例えば上昇トレンドから下降トレンドになるといった変化です。
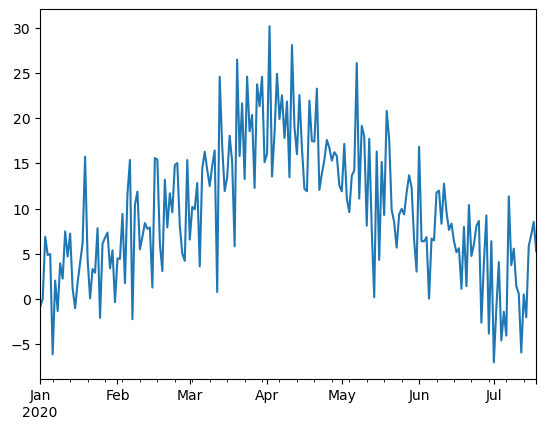
分散変化とは、データの振幅の幅の大きさの変化です。
他にも、季節成分の周期変化や、多変量時系列データの水準変化や分散・共分散変化などもありますが、今回は扱いません。
rupturesライブラリーの概要
今回利用するPythonライブラリーは、rupturesです。
ちなみに、変化点を検出するには、以下の2つを検討する必要があります。
- どの変化点検出アルゴリズムを使うのか?
- どのコスト関数を使うのか?
この組み合わせによって、検出できる変化点が変わってきます。
rupturesは、3つの変化点(水準変化・トレンド変化・分散変化)を検出するための多様なアルゴリズムとそのためのコスト関数が実装されています。
変化点検出アルゴリズム
rupturesライブラリには、多くの変化点検出アルゴリズムが実装されています。主なアルゴリズムには以下のものがあります。
- Pelt search method (Pelt): PELTは”Pruned Exact Linear Time”の略で、与えられたコスト関数に対して、リニアな計算時間で最適な変化点のセットを見つけることができます。
- Binary segmentation (Binseg): データを二つに分割し、それぞれの部分が異なる統計的特性を持つかどうかを評価します。これを再帰的に適用して、複数の変化点を検出します。
- Window-based change point detection (Window): このアルゴリズムは、データの窓をスライドさせながら、窓内のデータが一定の統計的特性から逸脱しているかどうかを評価します。
- Dynamic programming (Dynp): このアルゴリズムは、コスト関数の最小化問題を解くために動的計画法を使用します。このアプローチは通常、最適な変化点のセットを見つけることができますが、計算時間が長くなる可能性があります。
- Bottom-up segmentation (BottomUp): このアルゴリズムは、初めにすべての観測を個々のセグメントとして扱い、次に最もコストが低い2つの隣接するセグメントをマージしていきます。これを繰り返して、最終的に指定した数のセグメントになるまでマージします。
具体的な問題やデータに最も適したアルゴリズムを選択することが重要です。
ただ、どうやって選べばいいの? という疑問もあるかと思います。
| アルゴリズム | 精度 | ロバスト性 | スピード |
|---|---|---|---|
| Pelt | 高精度 | 中 | 高速 |
| Binseg | 高精度 | 早期の変化に敏感 | データが大きいと遅くなる |
| Window | 中精度 | 適切な窓サイズが選ばれた場合に高い | 中程度 |
| Dynp | 高精度 | 高い | データ量が多いと遅い |
| BottomUp | 中精度 | 高い | データ量が多いと遅い |
- 精度: この項目は、アルゴリズムがどの程度正確にデータの変化点を特定できるかを表しています。高精度のアルゴリズムは、真の変化点をより正確に特定する傾向があります。
- ロバスト性: データの異常値やノイズに対するアルゴリズムの耐性を示します。高いロバスト性を持つアルゴリズムは、異常値やノイズが含まれるデータでも、正確に変化点を特定できる傾向があります。
- スピード: アルゴリズムがデータを処理し、変化点を検出するのにどの程度の時間がかかるかを示します。高速なアルゴリズムは、より大きなデータセットでも短時間で結果を返すことができます。
要するに……
- データの量が非常に大きい場合には、PeltやWindowが適しています。
- ノイズが多い場合には、DynpやBottomUpが適しています。
- 精度が重要な場合には、PeltやDynpが適しています。
可能であれば、複数のアルゴリズムを試し、その結果を比較するというアプローチも有効です。
以下、やや詳細説明です。
| アルゴリズム | 特徴 | メリット | デメリット |
|---|---|---|---|
| Pelt search method (Pelt) | データ内の変化点を効率的に検出します。与えられたコスト関数に対して、リニアな計算時間で最適な変化点のセットを見つけることができます。 | 効率的で、大規模なデータセットでも高速に動作します。また、最適な変化点のセットを見つけることができます。 | コスト関数を適切に設定する必要があります。また、一部の複雑な変化パターンを見逃す可能性があります。 |
| Binary segmentation (Binseg) | データを二つに分割し、それぞれの部分が異なる統計的特性を持つかどうかを評価します。これを再帰的に適用して、複数の変化点を検出します。 | シンプルで直感的なアルゴリズムであり、複数の変化点を検出することが可能です。 | データが大きい場合や、変化点が密集している場合には計算時間が増大します。また、必ずしも最適な変化点のセットを見つけられるわけではありません。 |
| Window-based change point detection (Window) | データの窓をスライドさせながら、窓内のデータが一定の統計的特性から逸脱しているかどうかを評価します。 | 計算が効率的で、リアルタイムのデータストリームに対する変化点検出に適しています。 | 窓のサイズを適切に選択する必要があります。窓のサイズが大きすぎると小さな変化を見逃し、小さすぎるとノイズに影響されやすくなります。 |
| Dynamic programming (Dynp) | コスト関数の最小化問題を解くために動的計画法を使用します。このアプローチは通常、最適な変化点のセットを見つけることができます。 | 最適な変化点のセットを見つけることができます。 | 計算時間が長くなる可能性があります。特にデータ量が大きい場合や、変化点が多い場合には計算時間が著しく増えます。 |
| Bottom-up segmentation (BottomUp) | 初めにすべての観測を個々のセグメントとして扱い、次に最もコストが低い2つの隣接するセグメントをマージしていきます。これを繰り返して、最終的に指定した数のセグメントになるまでマージします。 | 変化点の数を指定することで、見つけたい変化点の数に応じた結果を得ることができます。 | 最適な変化点のセットを見つけられるわけではありません。 |
コスト関数
変化点検出アルゴリズムは、コスト関数を最小化するような変化点のセットを探します。
コスト関数は、「セグメント内のデータが一貫した統計的特性を持つという仮定」のもとで、データとの間の「適合度」を測定したものです。
- セグメント内のデータが一貫した統計的特性を持つという仮定:「水準が同じ」「トレンドが同じ」「分散が同じ」
- データとの間の「適合度」:この仮定と実際のデータとの間の差異
ちなみに、セグメントとは、変化点で分割されたデータセットです。
コスト関数の選び方が非常に重要であることが分かります。
主なコスト関数には以下のものがあります。
| コスト関数 | 特徴 | メリット | デメリット | 得意な変化点 |
|---|---|---|---|---|
| l1 | 一次ノルム(絶対値)を用いる | 外れ値に強い | 高次のトレンドや非線形性を捉えにくい | 水準変化 |
| l2 | 二次ノルム(ユークリッドノルム)を用いる | データの平均をうまく捉える | 外れ値に弱い | 水準変化 |
| rbf | ラジアル基底関数カーネルを用いる | 非線形な変化を捉える | パラメータ選択が難しい | 非線形な変化 |
| linear | ピースワイズ線形回帰に基づく | 線形トレンドをうまく捉える | 非線形なトレンドを捉えにくい | トレンド変化 |
| clinear | 線形スプラインで近似 | 連続的な線形変化を捉える | 非線形なトレンドを捉えにくい | 連続性を保つ線形トレンド変化 |
| normal | 正規分布に基づく | 平均と分散の変化を同時に捉える | 正規性の仮定が必要 | 水準変化、分散変化 |
| ar | 自己回帰モデルに基づく | 時間依存性を捉える | パラメータ選択が難しい | 時間依存性の変化 |
| rank | 順位に基づく | 非パラメトリックな変化を捉える | データの分布を考慮しない | 順序の変化 |
| mahalanobis | マハラノビス距離に基づく | 多変量データを考慮する | データの分布が多変量正規分布と仮定される | 多変量データの変化 |
| cosine | コサイン距離に基づく | データの向きの変化を捉える | データの大きさを考慮しない | データの向きの変化 |
ライブラリーのインストール
rupturesもインストールしなければPython上で使えません。
まだインストールされていない方は、インストールしましょう。
以下、condaでインストールするときのコードです。
conda install ruptures
以下、pipでインストールするときのコードです。
pip install ruptures
変化点を検知しよう! – その1 –
(アルゴとコスト関数をユーザが設定)
先ずは、どの変化点検知アルゴリズムとコスト関数を使うのかを、事前に決めて変化点の検知をしていきます。
もっともオーソドックスなやり方です。
今回利用する時系列データは、乱数などを利用し以下の3種類のサンプルデータを作ります。
- signal_l:水準変化のサンプルデータ
- signal_t:トレンド変化のサンプルデータ
- signal_v:分散変化のサンプルデータ
必要なモジュールの読み込み
では、必要なモジュールを読み込みます。
以下、コードです。
import numpy as np
import ruptures as rpt
from ruptures.metrics import precision_recall
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]
水準変化(レベルシフト)検知
先ず、サンプルデータを作ります。
- 水準数:4
- 変化点:200,400,600
- レコード数:800
以下、コードです。
# 各水準のデータ数 n = 200 # 変化点 bkps = [200,400,600,800] # 水準変化のデータを生成 level1 = np.random.normal(10, 10, n) + np.ones(n) * 50 level2 = np.random.normal(10, 20, n) + np.ones(n) * 100 level3 = np.random.normal(10, 10, n) + np.ones(n) * 75 level4 = np.random.normal(10, 20, n) + np.ones(n) * 125 # 全ての水準を結合 data = np.concatenate([level1, level2, level3, level4]) signal_l = data.reshape(-1, 1) # プロット plt.plot(signal_l) plt.show()
以下、実行結果です。
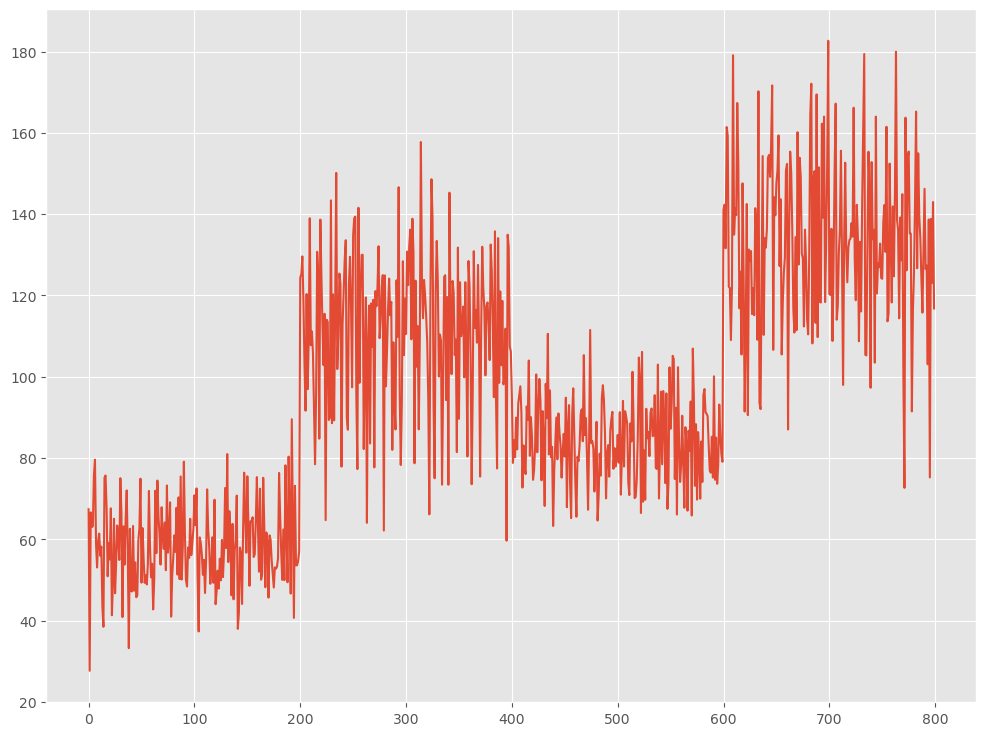
このサンプルデータから変化点を検出します。
- コスト関数:l2
- アルゴリズム:Dynp
以下、コードです。
# コスト関数の設定 model = "l2" # アルゴの設定と学習 algo = rpt.Dynp(model=model).fit(signal_l) # 変化点の検出 my_bkps = algo.predict(n_bkps=3) # 結果のプロット rpt.show.display(signal_l, bkps, my_bkps, figsize=(12, 9)) plt.show() # 検出された変化点 my_bkps
以下、実行結果です。出力されている数字は、検知した変化点です。
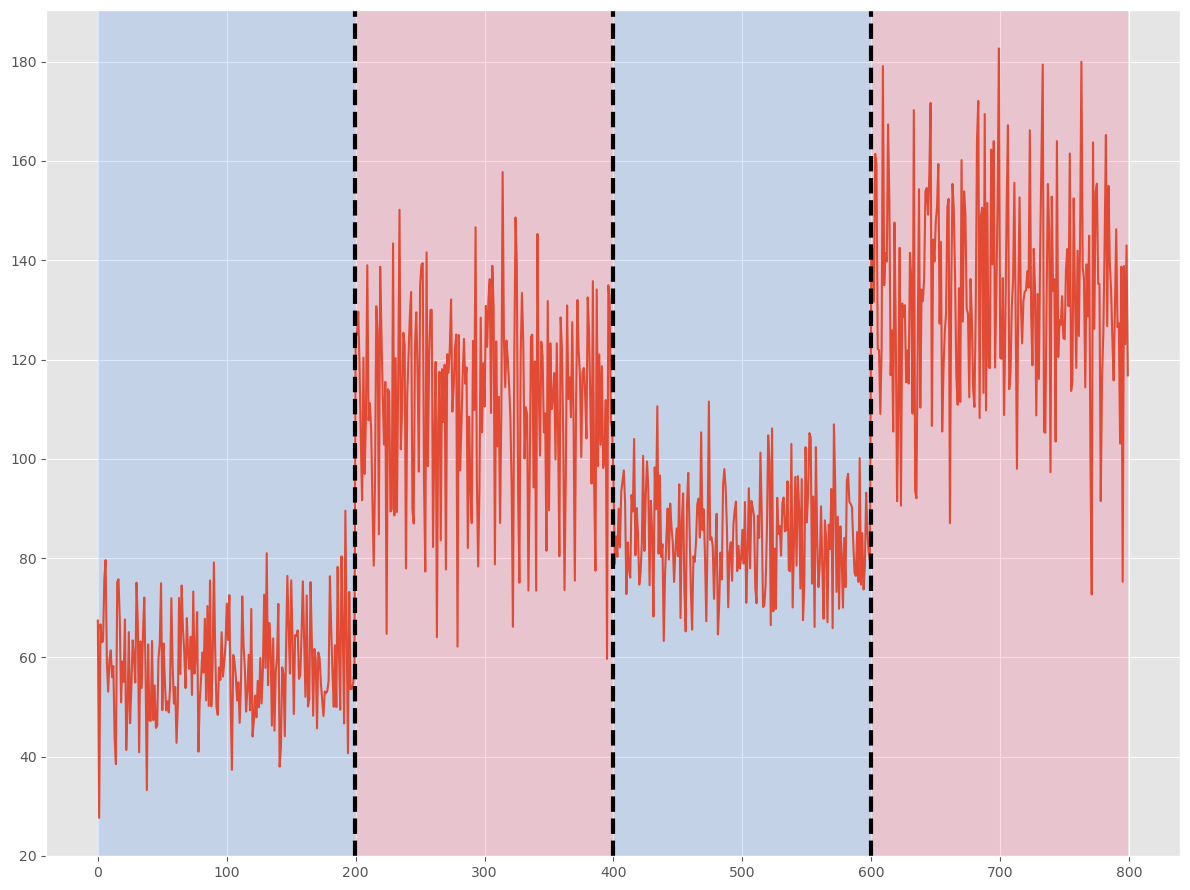
[200, 400, 600, 800]
黒い縦の点線が検知した変化点です。真の変化点は、青と赤の背景の境になります。
検知した変化点と真の変化点が、一致していることが分かります。
トレンド変化検知
先ず、サンプルデータを作ります。
- 水準数:4
- 変化点:200,400,600
- レコード数:800
以下、コードです。
# 各トレンドのデータ数
n = 200
# 変化点
bkps = [200,400,600,800]
# 各トレンドのデータを生成
data1 = np.linspace(1, 20, n)+np.random.normal(0, 3, n)
data2 = np.linspace(20, 20, n)+np.random.normal(0, 3, n)
data3 = np.linspace(20, 50, n)+np.random.normal(0, 3, n)
data4 = np.linspace(50, 30, n)+np.random.normal(0, 3, n)
# 連番(説明変数)
x = np.arange(800)
# サンプルデータ
data = np.concatenate([data1,data2,data3,data4])
signal_t = np.stack([data, x], 1)
# プロット
for i in range(signal_t.shape[1]):
plt.plot(signal_t[:,i])
plt.show()
以下、実行結果です。
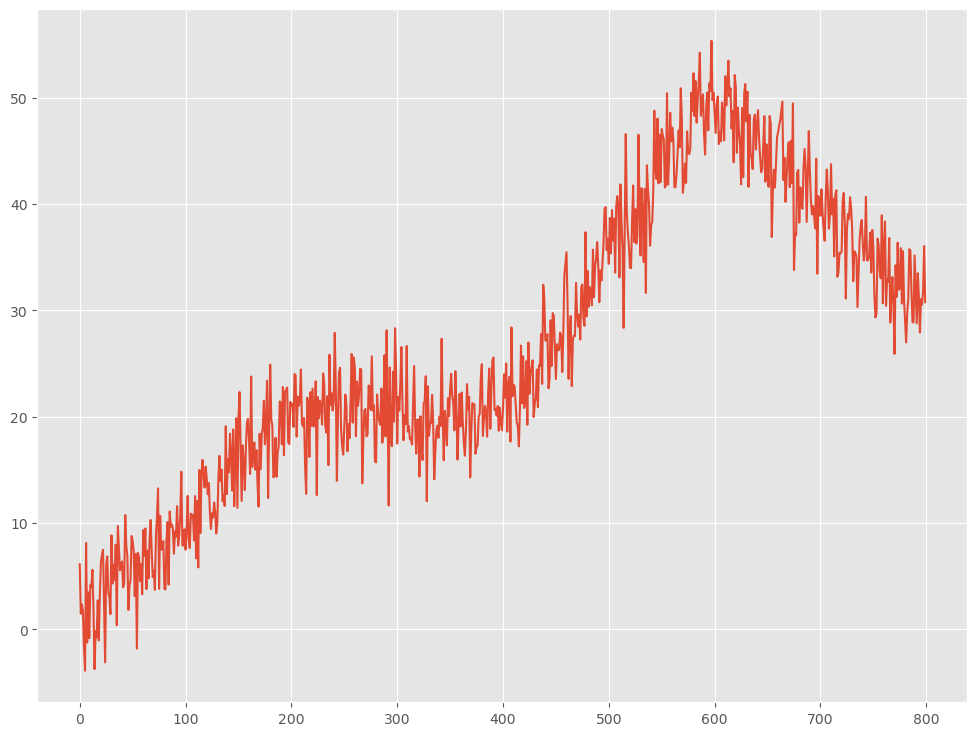
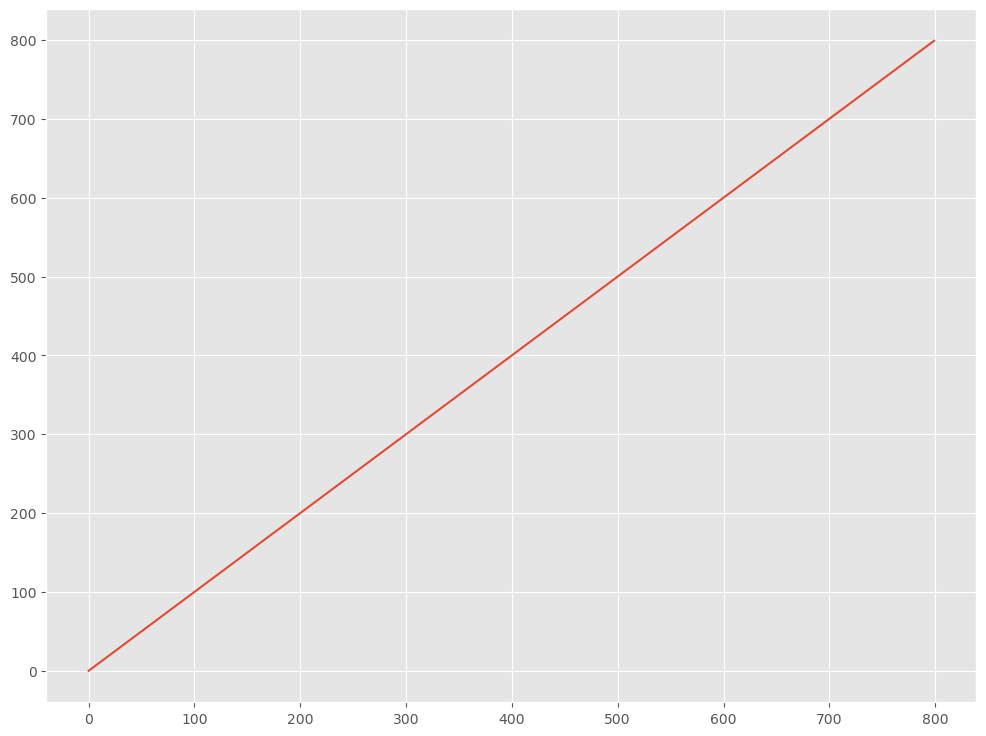
1つ目の折れ線グラフが対象となる時系列データ(目的変数)で、2つ目の折れ線グラフが説明変数として利用する連番(0,1,2,…)です。
このサンプルデータから変化点を検出します。
- コスト関数:clinear
- アルゴリズム:Dynp
以下、コードです。
# コスト関数の設定 model = "clinear" # アルゴの設定と学習 algo = rpt.Dynp(model=model).fit(signal_t) # 変化点の検出 my_bkps = algo.predict(n_bkps=3) # 結果のプロット rpt.show.display(signal_t, bkps, my_bkps, figsize=(12, 9)) plt.show() # 検出された変化点 my_bkps
以下、実行結果です。出力されている数字は、検知した変化点です。
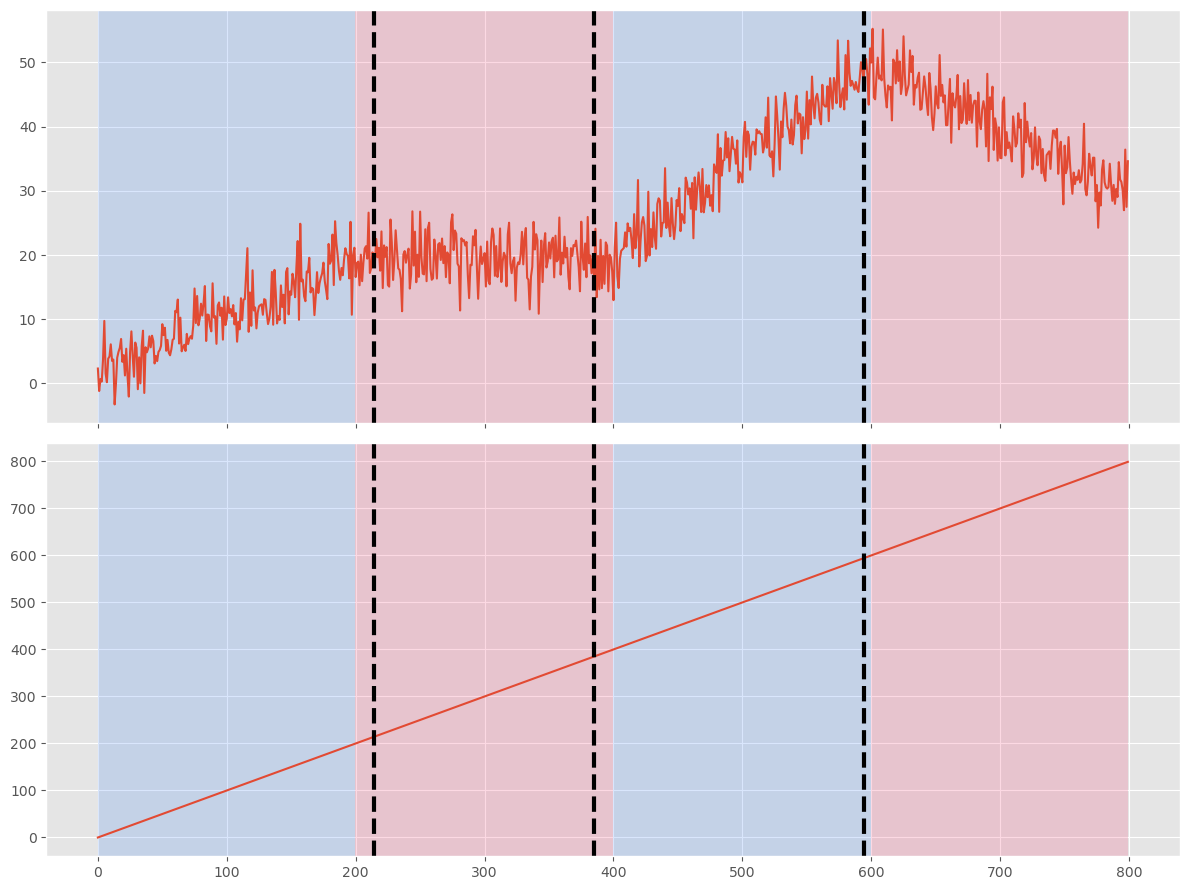
[215, 385, 595, 800]
検知した変化点と真の変化点が、大まかには一致していることが分かります。
分散変化検知
先ず、サンプルデータを作ります。
- 水準数:4
- 変化点:200,400,600
- レコード数:800
以下、コードです。
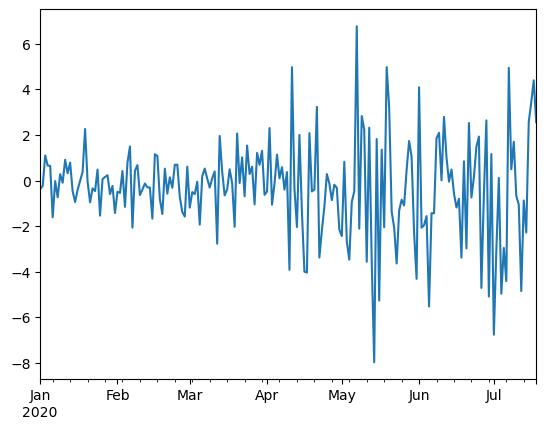
# 各トレンドのデータ数 n = 200 # 変化点 bkps = [200,400,600,800] # 各トレンドのデータを生成 data1 = np.random.normal(0, 1, n) data2 = np.random.normal(0, 5, n) data3 = np.random.normal(0, 10, n) data4 = np.random.normal(0, 3, n) # サンプルデータ data = np.concatenate([data1,data2,data3,data4]) signal_v = data.reshape(-1, 1) # プロット plt.plot(signal_v) plt.show()
以下、実行結果です。
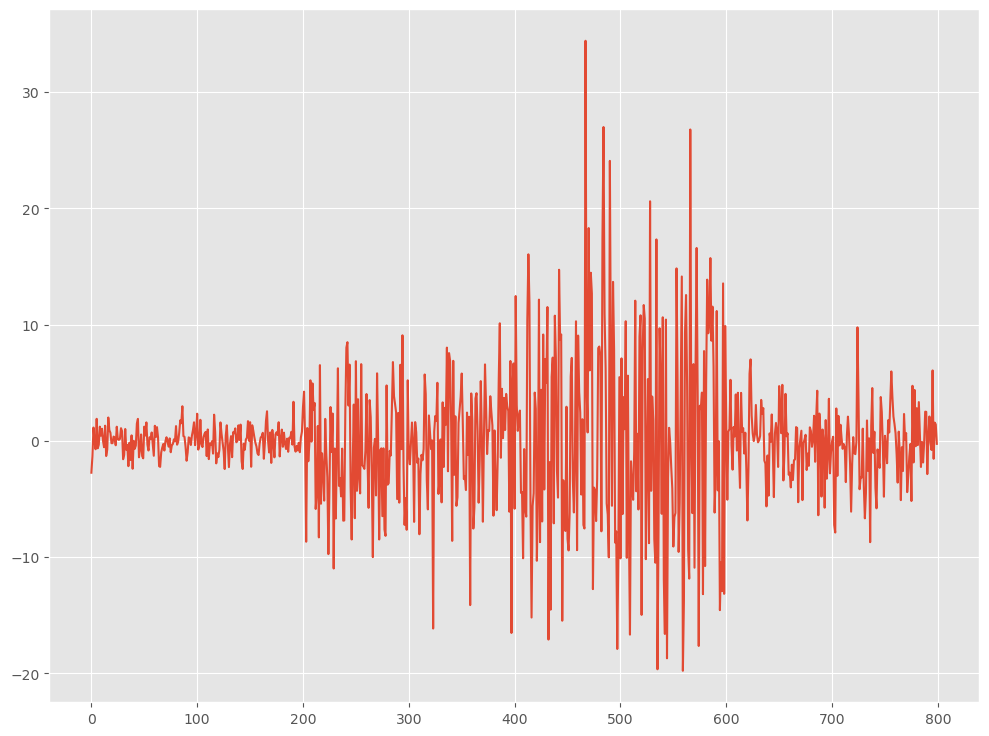
このサンプルデータから変化点を検出します。
- コスト関数:normal
- アルゴリズム:Dynp
以下、コードです。
# コスト関数の設定 model = "normal" # アルゴの設定と学習 algo = rpt.Dynp(model=model).fit(signal_v) # 変化点の検出 my_bkps = algo.predict(n_bkps=3) # plot rpt.display(signal_v, bkps, my_bkps, figsize=(12, 9)) plt.show() # 検出された変化点 my_bkps
以下、実行結果です。出力されている数字は、検知した変化点です。
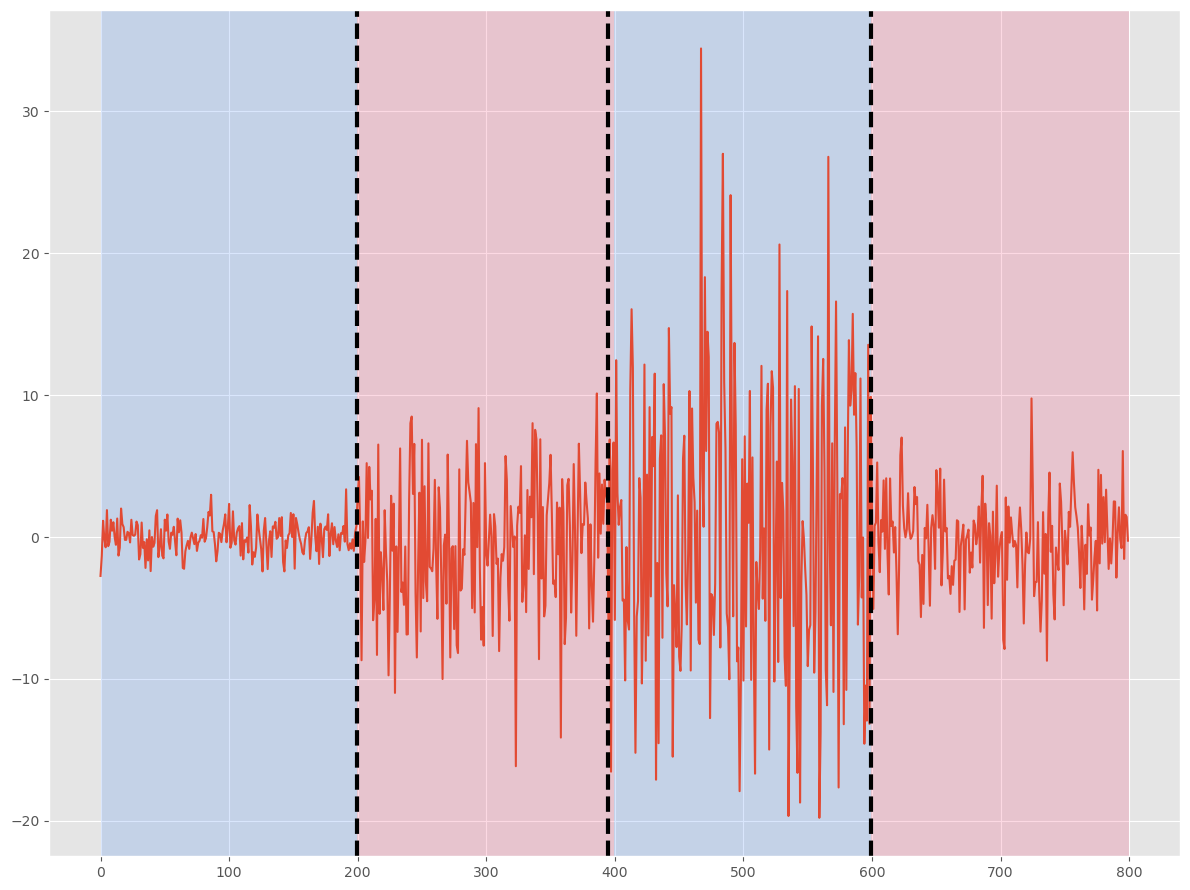
[200, 395, 600, 800]
検知した変化点と真の変化点が、ほぼ一致していることが分かります。
変化点を検知しよう! – その2 –
(アルゴとコスト関数の組み合わせを自動探索)
適切に変化点を検知するには、対象となる時系列データに応じて、変化点検知アルゴリズムとコスト関数の組み合わせを適切に選ぶ必要があります。
そのため、実務で利用するときには、過去データもしくは学習データなどを利用し、どの変化点検知アルゴリズムとコスト関数の組み合わせが適切か、検討する必要があります。
ただ、変化点検知アルゴリズムとコスト関数が多数あるため、機械的に検討するプログラムを作った方がいいでしょう。
このとき、どの組み合わせがいいのかを評価する指標が必要です。
今回は、分類問題でよく利用されるF1スコアを使います。
つまり、F1スコアを最大化する組み合わせが最適であると判断する、ということです。
以下は、F1スコアの簡単な解説です。
F1スコアは、分類問題においてモデルの性能を評価するための指標の1つで、適合率(Precision)と再現率(Recall)の調和平均をとることで計算されます。
具体的には、以下のように定義されます。
F1 = 2 * (Precision * Recall) / (Precision + Recall)
ここで、
- 適合率(Precision)は、モデルが正と予測した変化点の中で実際に正であったものの割合を示します。つまり、正しく検出された変化点数を、予測した変化点数で割った値です。
- 再現率(Recall)は、実際の正の変化点のうちモデルが正と予測したものの割合を示します。つまり、正しく検出された変化点数を、真の変化点数で割った値です。
F1スコアは適合率と再現率のバランスを取るための指標で、どちらか一方だけが高いと全体のスコアは下がります。このため、適合率と再現率の両方を重視したい場合に使用されます。
変化点検出の問題においては、F1スコアは検出した変化点(正)が実際の変化点とどの程度一致しているかを評価するために用いられます。この評価には適合率(検出した変化点のうち正解の割合)と再現率(全ての正解の変化点のうち、どの程度を検出できたかの割合)の両方が必要となります。このため、F1スコアは変化点検出問題において非常に有用な評価指標となります。
では、アルゴとコスト関数の組み合わせを自動探索する関数を定義します。
以下、コードです。
# 必要なモジュールを読み込みます
import matplotlib.pyplot as plt
import ruptures as rpt
import numpy as np
from ruptures.metrics import precision_recall
# アルゴリズムと対応するrupturesのクラスを辞書で定義します
ALGORITHMS = {
'pelt': rpt.Pelt,
'binseg': rpt.Binseg,
'bottomup': rpt.BottomUp,
'window': rpt.Window,
'dynp': rpt.Dynp
}
# コスト関数のリストを定義します
COSTS = ['l1', 'l2', 'normal', 'ar', 'linear', 'normal', 'mahalanobis', 'rbf', 'rank', 'cosine', 'clinear']
# PELTアルゴリズム用のpenalty値の範囲を定義します
PEN_RANGE = [1, 10, 100, 500, 1000, 5000, 10000]
# 他のアルゴリズム用の分割点数の範囲を定義します。
N_BKPS_RANGE = range(1, 5)
# 適合率と再現率からF1スコアを計算する関数を定義します
def compute_f1_score(precision, recall):
return 2 * (precision * recall) / (precision + recall) if precision + recall != 0 else 0
# 変化点検出の結果をプロットする関数を定義します
def plot_results(signal, bkps, bkps_detected, algo, cost):
rpt.show.display(signal, bkps, bkps_detected, figsize=(10, 6))
plt.title(f"Best combination: Algorithm - {algo}, Cost - {cost}")
plt.show()
# 指定したデータに対して、すべてのアルゴリズムとコスト関数の組み合わせで変化点検出を行い、最良の結果を返す関数を定義します
def detect_change_points(signal):
results = []
# すべてのコスト関数に対してループを回します
for cost in COSTS:
# すべてのアルゴリズムに対してループを回します。
for algo, Algo in ALGORITHMS.items():
# PELTアルゴリズム用のpenalty値または他のアルゴリズム用の分割点数の範囲に対してループを回します
for pen in PEN_RANGE if algo == 'pelt' else N_BKPS_RANGE:
try:
# 指定したアルゴリズムとコスト関数で変化点検出器を作成し、データをフィットします
detector = Algo(model=cost).fit(signal)
# PELTアルゴリズムの場合はpenalty値、それ以外の場合は分割点数を指定して変化点を予測します
bkps_detected = detector.predict(pen=pen) if algo == 'pelt' else detector.predict(n_bkps=pen)
# 適合率と再現率を計算します
precision, recall = precision_recall(bkps, bkps_detected)
# F1スコアを計算します
f1_score = compute_f1_score(precision, recall)
# 結果をリストに追加します。
results.append((f1_score, precision, recall, algo, cost, pen, bkps_detected))
except Exception as e:
# エラーが発生した場合は、その情報を表示します
print(f"Combination of Algorithm: {algo}, Cost: {cost}, Pen/N_bkps: {pen} failed with error: {e}")
# 最良の結果を取得します
best_result = max(results)
best_f1_score, best_precision, best_recall, best_algo, best_cost, best_pen, best_bkps_detected = best_result
# 最良の結果を表示します
print(f"Best combination is Algorithm: {best_algo}, Cost: {best_cost}, Pen/N_bkps: {best_pen} with F1 score: {best_f1_score}, Precision: {best_precision}, Recall: {best_recall}")
print(f"Detected change points: {best_bkps_detected[:-1]}")
# 最良の結果をプロットします
plot_results(signal, bkps, best_bkps_detected, best_algo, best_cost)
このコードは、ざっくり以下の4つのパートで構成されています。
- 設定値の定義:変化点検出アルゴリズム(PELT, Binary Segmentation, Bottom-Up, Window-Based, Dynp)とコスト関数(l1, l2, normal, ar, linear, normal, mahalanobis, rbf, rank, cosine, clinear)を定義しています。また、PELTアルゴリズムのペナルティ値と、他のアルゴリズムの分割点数の範囲も設定しています。
- F1スコアの計算:F1スコアは、検出結果の精度を測るための指標で、適合率(precision)と再現率(recall)の調和平均です。このスコアが大きいほど検出結果の精度が高いと言えます。
- 変化点検出の実行:各アルゴリズムとコスト関数の組み合わせで変化点検出を行い、その結果をF1スコアで評価しています。その中で最もスコアが高かった組み合わせとその時の変化点の位置を出力しています。
- 結果の可視化:最も良かった組み合わせで検出した変化点を、元の時系列データ上にプロットしています。
実行例を示します。サンプルデータは先ほど作った以下のものをそのまま使います。
- signal_l:水準変化のサンプルデータ
- signal_t:トレンド変化のサンプルデータ
- signal_v:分散変化のサンプルデータ
先ず、水準変化のサンプルデータに対する変化点検知です。
以下、コードです。
detect_change_points(signal_l)
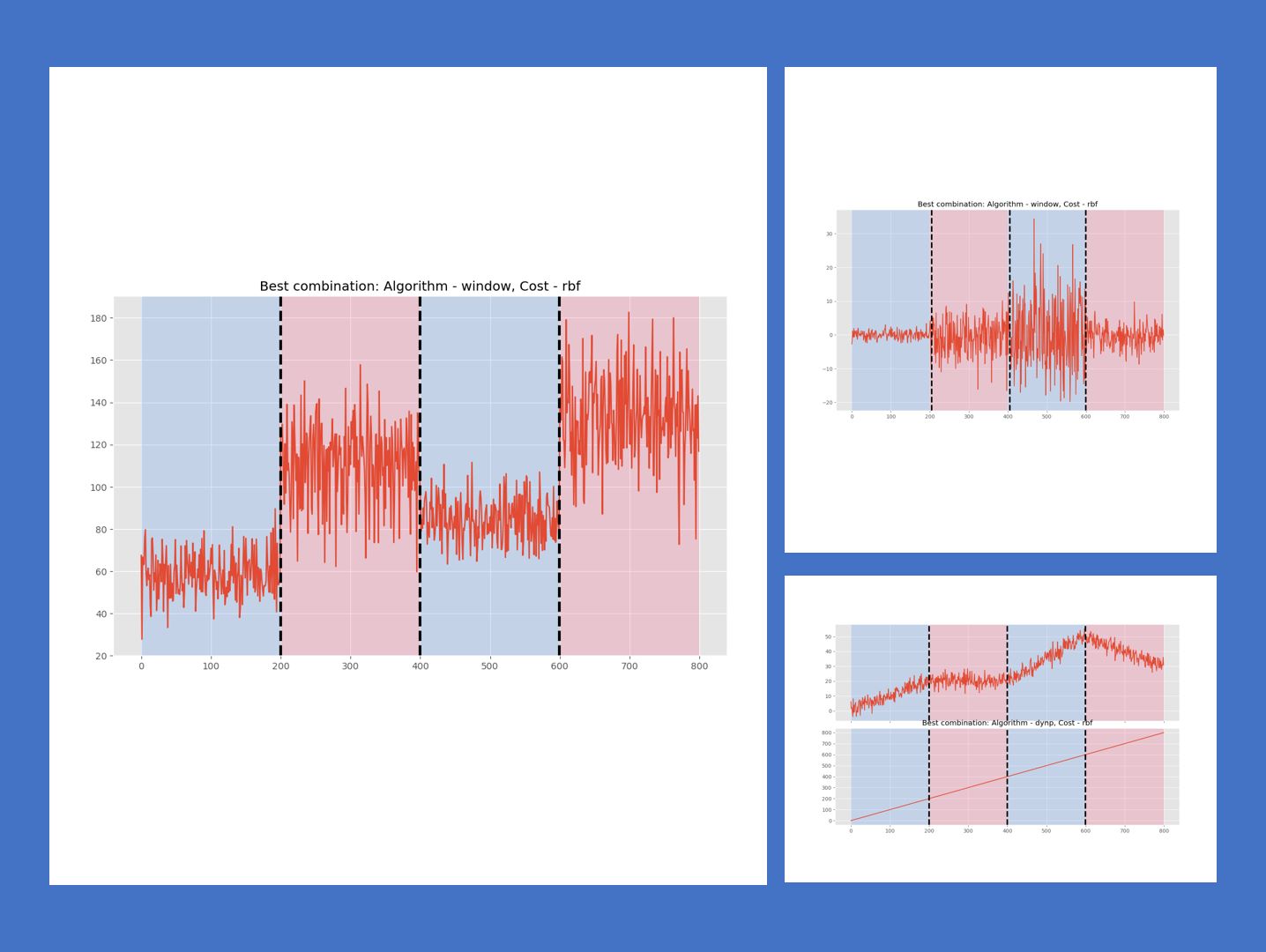
以下、実行結果です。
Best combination is Algorithm: window, Cost: rbf, Pen/N_bkps: 3 with F1 score: 1.0, Precision: 1.0, Recall: 1.0 Detected change points: [200, 400, 600]
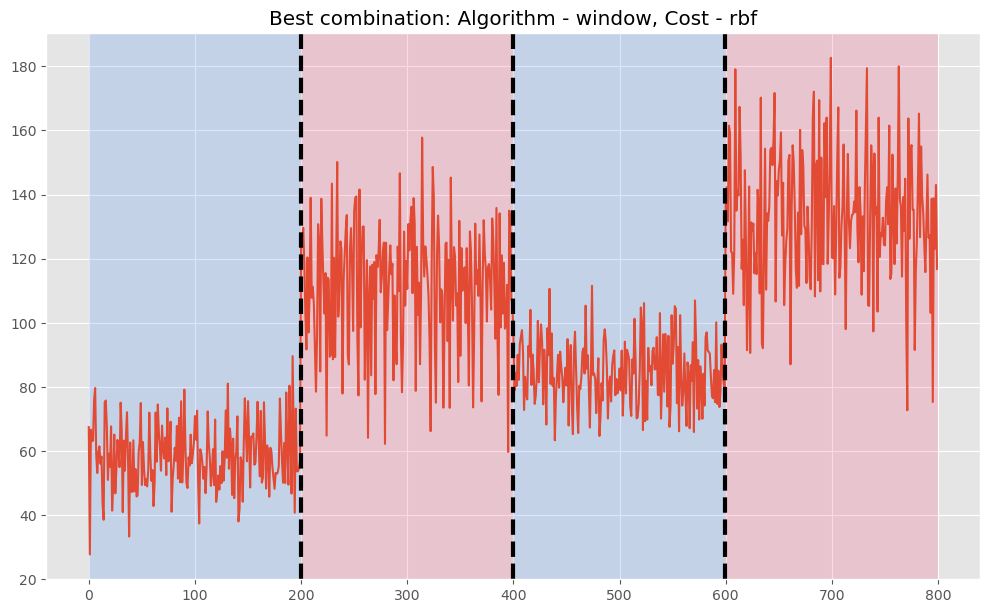
- コスト関数:rbf
- アルゴリズム:Window
- 検知した変化点:[200, 400, 600]の3つ
次に、トレンド変化のサンプルデータに対する変化点の検知です。
以下、コードです。
detect_change_points(signal_t)
以下、実行結果です。
Best combination is Algorithm: dynp, Cost: rbf, Pen/N_bkps: 3 with F1 score: 1.0, Precision: 1.0, Recall: 1.0 Detected change points: [200, 400, 600]
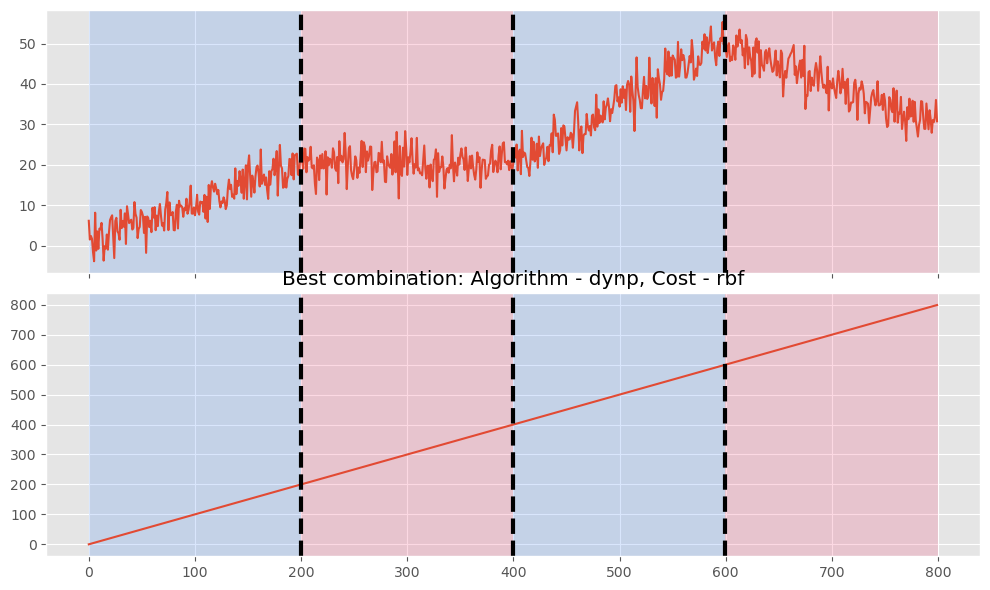
- コスト関数:rbf
- アルゴリズム:Dynp
- 検知した変化点:[200, 400, 600]の3つ
最後に、分散変化のサンプルデータに対する変化点の検知です。
以下、コードです。
detect_change_points(signal_v)
以下、実行結果です。
Best combination is Algorithm: window, Cost: rbf, Pen/N_bkps: 3 with F1 score: 1.0, Precision: 1.0, Recall: 1.0 Detected change points: [205, 405, 600]
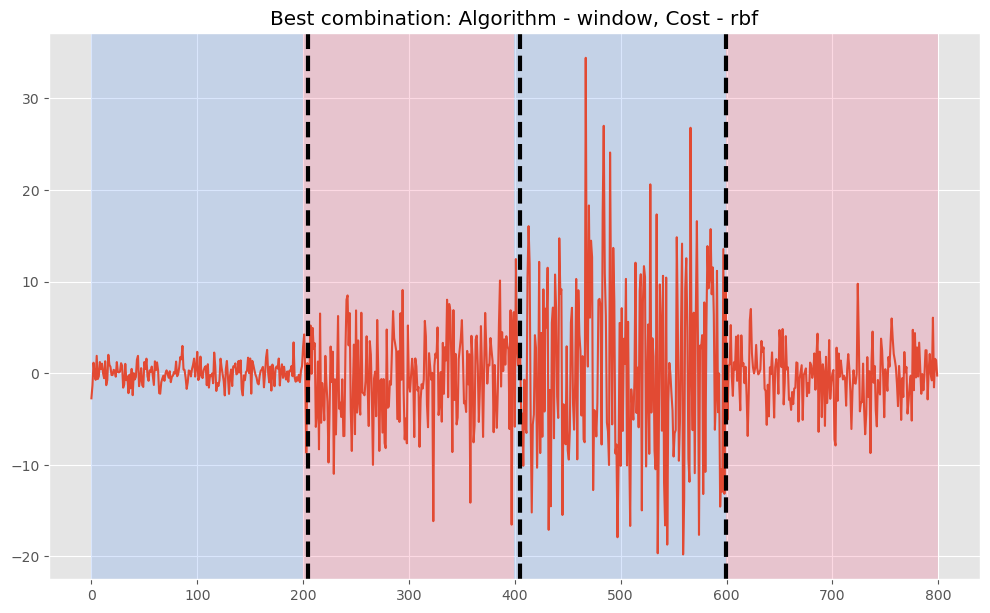
- コスト関数:rbf
- アルゴリズム:Window
- 検知した変化点:[205, 405, 600]の3つ
以上から分かる通り、適切にアルゴリズムとコスト関数の組み合わせを選ぶと、とってもいい感じで変化点を見つけてくれます。
まとめ
今回は、「Python ruptures でサクッと時系列データの変化点を見つける方法」というお話しをしました。
時系列データには色々な種類の変化があります。
この中で今回は、1変量時系列データの次の3つの変化を扱いました。
- 水準変化(レベルシフト)
- トレンド変化
- 分散変化
時系列データを手にしたとき、データ理解のためにも、モデル構築のためにも、ぜひ試してみてください。