Python SciPyで手を動かしながら学ぶ数理最適化
– 第4回: 整数最適化と組合せ最適化 –

4086
Python SciPyで手を動かしながら学ぶ数理最適化– 第4回: 整数最適化と組合せ最適化 –

今回は、数理最適化のさらに高度な領域である「整数最適化」と「組合せ最適化」に焦点を当てます。

これらの最適化手法は、現実の複雑な問題を解決するために広く用いられています。

有名なところでは、巡回セールスマン問題やナップサック問題、スケジューリング問題などです。

以下は、最適ルートを求める巡回セールスマン問題の結果例です。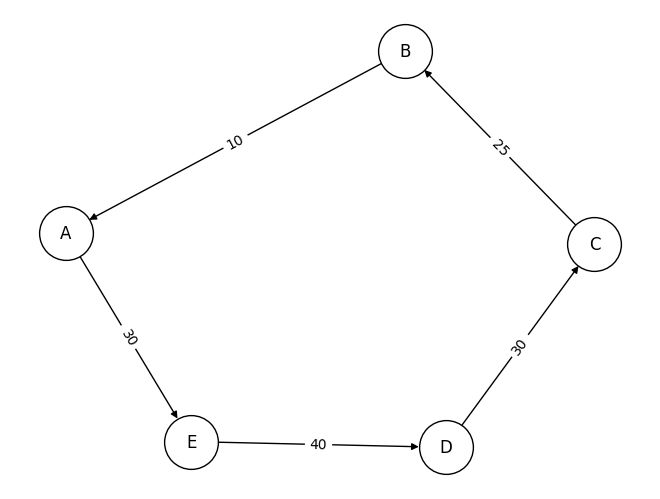

これらの概念の基本的な理解を深め、それぞれの手法がどのように異なる問題に適用されるか、そしてその解法について簡単に解説していきます。

SciPyでは限界があるため、PuLPを使います。

整数最適化の基本理論

　整数最適化とは何か

整数最適化は、変数が整数のみを取る制約を持つ最適化問題です。

これは、分割不可能な資源や、はっきりと区分される選択肢（例えば工場でのシフト数や製品の製造個数）を扱う際に特に重要になります。

変数が全て整数である場合を「純整数最適化問題」と呼び、一部の変数のみが整数である場合を「混合整数最適化問題」と呼びます。

 

　整数線形最適化と整数非線形最適化の違い

整数最適化問題は、目的関数や制約条件が線形か非線形かによってさらに分類されます。

「整数線形最適化」では、目的関数と制約条件が共に線形関数です。これに対し、「整数非線形最適化」では、少なくとも一つの目的関数または制約条件が非線形関数です。

整数線形最適化は理論的には比較的扱いやすいが、実世界の複雑な問題はしばしば非線形要素を含むため、非線形最適化が必要になることがあります。

 

　整数最適化の特徴と難易度

整数最適化は、その性質上、一般の線形最適化問題に比べて計算が困難です。

整数制約があるために、解の空間が離散的になり、連続的な手法では効率的に解を求められないことが多いです。

特に、整数非線形最適化問題は、非線形性と整数制約の両方が複雑さを増大させるため、非常に難易度が高いと言えます。

 

組合せ最適化の基礎

　組合せ最適化とは何か

組合せ最適化は、有限な要素の集合から特定の基準に基づいて最適な部分集合を選ぶ問題です。

これは、順列、組み合わせ、サブセット、グラフといった組合せ数学に根ざした問題に焦点を当てています。

組合せ最適化問題はしばしば整数最適化問題と重なります。

 

　組合せ最適化の応用分野

組合せ最適化は様々な分野で応用されています。

具体的な例は以下の通りです。

  • 物流と配送: 配送ルートの最適化や車両のスケジューリング。
  • 製造業: 製造ラインの効率化や資源配分。
  • ネットワークデザイン: 通信ネットワークやコンピュータネットワークの最適設計。
  • 金融: ポートフォリオ最適化やリスク管理。

組合せ最適化は、整数最適化と密接に関連しており、実際には多くの問題が両者を併用して解かれます。

 

　組合せ最適化の代表的な問題と例

組合せ最適化の代表的な問題には以下のようなものがあります。

巡回セールスマン問題 (TSP)
最も有名な組合せ最適化問題の一つで、セールスマンが各都市を一度だけ訪れて出発点に戻る最短ルートを見つける問題です。

ナップサック問題
限られた容量のナップサックに、異なる価値と重さを持つアイテムを詰め込む最適な組み合わせを見つける問題です。

施設配置問題 (Facility Location Problem)
顧客に最適な場所に施設（例えば倉庫や店舗）を配置する問題です。

 

代表的な問題の定式化

　巡回セールスマン問題 (TSP)

都市の集合を C=\{1,2,...,n\} 、都市間の距離を d_{i\,i} とした場合、以下のように表現できます。

  • x_{ij}：移動ルートに、都市iから都市jのルートが含まれる場合は1、そうでなければ0。
  • u_i：都市iに割り当てられる順序を表す補助変数。

目的関数：

\displaystyle \text{minimize } \sum_{i=1}^{n}\sum_{j\neq i,j=1}^{n}d_{i j}x_{i j}

制約条件：

各都市iから、ただ一つの都市jへ移動

\displaystyle \sum_{j=1,j\neq i}^{n}\,x_{i j}=1 \quad\forall i\in\{1,\cdot\cdot\cdot,n\}

各都市jへ、ただ一つの都市iから移動

\displaystyle \sum_{i=1,i\neq j}^{n}\,x_{i j}=1 \quad\forall j\in\{1,\cdot\cdot\cdot,n\}

サブツアー除去の制約（解が小さなループにならないようにする）

\displaystyle u_{i}-u_{j}+n\cdot x_{i j}\leq n-1\quad\forall i,j\in\{1,\cdot\cdot\cdot,n\},i\neq j

 

サブツアー除去の制約に、MTZ制約（Miller-Tucker-Zemlin制約、部分巡回路排除制約）を用いています。

この制約は、巡回セールスマン問題(TSP)のようなグラフ上での経路問題を扱う際に、解が１つの連続するルートになることを保証するためのものです。つまり、部分巡回路（すべての都市を通らないルート）を排除する役割を果たします。

MTZ制約では、各都市（頂点）に順序を割り当てる変数が導入されます。この変数は、経路がある都市から別の都市へと進むたびに増加します。このようにして、部分巡回路が作られることを防ぎます。

この制約は、問題の規模が大きい場合には計算時間が大幅に増加する欠点があります。そのため、他の部分巡回路を排除するための手法（例えば、制約付き最適化やカットを用いたヒューリスティックな探索手法など）と組み合わせて用いられることが多いです。

 

　ナップサック問題

アイテムの集合 I=\{1,2,...,n\} 、各アイテム i \in I には価値 v_i と重さ w_i が割り当てられ、ナップサックの最大容量を W とした場合、問題は以下のように表現できます。

  • x_{i}：アイテムiがナップサップに含まれる場合は1、そうでなければ0。

目的関数：

\displaystyle \text{maximize } \sum_{i=1}^{n}v_{i}x_{i}

制約条件：

\displaystyle \sum_{i=1}^{n}w_{i}x_{i}\leq W

 

　施設配置問題 (Facility Location Problem)

施設の集合 F=\{1,2,...,m\} と顧客の集合 D=\{1,2,...,n\} 、施設から顧客までのコストが c_{ij} 、施設 j \in F の開設コスト f_i とした場合、問題は以下のように表現できます。

  • x_{i j}：施設iから顧客jへサービスが提供される場合は1、そうでなければ0。
  • y_i：施設iが開設される場合は1、そうでなければ0。

目的関数：

\displaystyle \text{minimize } \sum_{i=1}^{m}\sum_{j=1}^{n}c_{i j}x_{i j}+\sum_{i=1}^{m}f_{i}y_{i}

制約条件：

各顧客はただ一つの施設からサービスを受ける

\displaystyle \sum_{i=1}^{m} x_{i j}=1 \quad\forall j\in D

施設が開設されていない場合、そこからサービスを提供できない

\displaystyle x_{i j} \le y_i \quad\forall i\in F, \forall j\in D

 

整数最適化と組合せ最適化の解法

　ScyPyを使った整数最適化のアプローチ

ScyPy（サイパイ）は科学技術計算のためのPythonライブラリで、線形計画問題をはじめとした最適化問題に対応しています。整数最適化については直接的なサポートはありませんが、線形計画問題における制約条件や目的関数を適切に設定することで、一部の整数最適化問題を解くことが可能です。

例えば、ScyPyのlinprog関数を使用して、線形計画問題を解くことができます。しかし、これは変数が連続値であることを前提としており、変数が整数でなければならない場合には適用できません。このような場合、結果を丸めることで近似的な解を得るか、他のライブラリを使用することを検討する必要があります。

 

　整数最適化に特化した他のライブラリ（PuLP, Gurobi等）

整数最適化に特化したライブラリとしては、PuLPやGurobiがあります。

  • PuLP: PuLPはPythonで書かれたオープンソースのライブラリで、線形計画問題および整数線形計画問題に対応しています。簡単なインターフェースを持ち、様々なソルバー（CBC、GLPKなど）と統合されているため、幅広い問題に対応可能です。
  • Gurobi: Gurobiは高性能な数理最適化ソルバーで、線形計画問題、整数線形計画問題、二次計画問題などを解くことができます。商用ソフトウェアですが、非営利目的であれば無料ライセンスも提供されています。Gurobiは高度なアルゴリズムと最適化技術を採用しており、特に大規模かつ複雑な問題に対して高速に解を求めることが可能です。

 

　整数最適化問題の実装例とコードの解説

PulpはPythonのパッケージであり、pipを使用してインストールできます。ターミナルまたはコマンドプロンプトを開き、次のコマンドを入力します。

pip install pulp

 

ここではPuLPを使用して、簡単なナップサック問題を解くコードの例を示します。

import pulp

# 問題の定義
problem = pulp.LpProblem('KnapsackProblem', pulp.LpMaximize)

# 変数の定義（0か1の値を取る変数）
x1 = pulp.LpVariable('x1', lowBound=0, upBound=1, cat='Integer')
x2 = pulp.LpVariable('x2', lowBound=0, upBound=1, cat='Integer')
x3 = pulp.LpVariable('x3', lowBound=0, upBound=1, cat='Integer')

# 目的関数
problem += 15*x1 + 10*x2 + 10*x3

# 制約条件
problem += 2*x1 + 3*x2 + 4*x3 <= 5

# 問題の解決
status = problem.solve()
print(pulp.LpStatus[status])

# 結果の表示
print(f"x1 = {x1.value()}, x2 = {x2.value()}, x3 = {x3.value()}")

 

上記のコードは、ナップザック問題（Knapsack Problem）の一種で、最適化（Optimization）問題を解いています。

  • まず`import pulp`で、`pulp`というPythonのパッケージをインポートします。
  • 問題の定義：`pulp.LpProblem`クラスを使って、「ナップザック問題」を定義します。ここで、`’KnapsackProblem’`が問題の名前、`pulp.LpMaximize`が最大化問題であることを示しています。
  • 変数の定義：`pulp.LpVariable`関数を用いて、3つの0か1の値を取る整数変数x1, x2, x3を定義します。
    • 変数名（`name`）: これはPythonでの変数名とは異なり、問題を解くために使用される数学的な表現や出力に使用される名前です。ただ、例のようにPythonの変数名と同じにすることが多いです。
    • 下限（`lowBound`）: これは変数が取り得る最小値を設定します。デフォルトでは、この値は`None`で、変数はマイナス無限大を取り得ることを意味します。
    • 上限（`upBound`）: これは変数が取り得る最大値を設定します。デフォルトでは、この値は`None`で、変数はプラス無限大を取り得ることを意味します。
    • カテゴリ（`cat`）: これは変数のタイプを設定します。主に`’Continuous’`（連続変数）または`’Integer’`（整数変数）が使用され、更に`’Binary’`（バイナリ変数、0または1の値を取る）も選択可能です。デフォルトでは変数は連続となります。
  • 目的関数：目的関数を定義します。ここでは、`15*x1 + 10*x2 + 10*x3`が問題の目的関数であり、この関数を最大化することが目的となっています。
  • 制約条件：制約条件を設定します。この問題では、`2*x1 + 3*x2 + 4*x3 <= 5`が制約条件となります。これは、各変数に各重みをかけた合計が5以下でなければならないことを示しています。
  • 問題の解決：`problem.solve()`を実行して問題を解きます。この関数は最適解を見つけ出し、解の状態を返します。解の状態は`pulp.LpStatus[status]`で確認できます。これは、「Optimal」、「Infeasible」、「Unbounded」、「Undefined」などの値を持ちます。
    • Optimal: ソルバーが最適な解を見つけ出しました。
    • Infeasible: 問題は解けません、つまり制約を満たす解が存在しません。
    • Unbounded: 問題の解は無制限です、つまり目的関数が無限に大きくなる方向に進むことができます。
    • Undefined: ソルバーは問題の解を見つけられませんでした、あるいは見つけることが不確かであると判断しました。
  • 結果の表示：最後に、各変数の最適値を出力します。

このコードはPulpパッケージを使用して、ナップザック問題を解くためのもので、問題は個々のアイテム（各x）をナップザック（制約）に詰めるかどうかを決定し、ナップザック内のアイテムの価値（目的関数）を最大化するようなアイテムの選び方を見つけるものです。

 

実世界での応用例

　工業スケジューリングにおける整数最適化

「ABC製造株式会社」は自動車部品を生産する企業で、複数の製品を限られた数の生産ラインで効率良く生産する課題を抱えていました。特に、異なる製品に対する生産時間と納期の違いにより、最適な生産スケジュールの作成が困難でした。整数最適化を用いることで、生産ラインの利用を最適化することで納期短縮し、全体的な効率を改善することができました。

最適化問題を定式化します。

  • 製品 i の生産に必要な時間を t_i
  • 機械 j が使用可能かどうかを変数 x_{ij} で表現（x_{ij}=1 の場合は機械 j が製品 i の生産に使用）
  • 目標は、各製品の生産を最適に割り当て、納期最小化

目的関数

\displaystyle \text{minimize } Z=\sum_{i=1}^{n} \sum_{j=1}^{m}x_{ij}t_i

制約条件

各製品 i は一つの生産ライン j でのみ生産される。

\displaystyle \sum_{j=1}^{m}x_{i j}=1\quad\forall i\in\{1,\cdot\cdot\cdot,n\}

各生産ライン j は一度に一つの製品 i しか生産できない。

\displaystyle \sum_{i=1}^{n}x_{i j}\leq1\quad\forall j\in\{1,\cdot\cdot\cdot,m\}

二値変数の制約。

\displaystyle x_{i j}\in\{0,1\}\quad\forall i,j

 

以下、コードです。

from pulp import *

# 問題の設定
prob = LpProblem("Scheduling_Problem", LpMinimize)

# 製品と生産ライン
products = ['A', 'B', 'C', 'D']
lines = [1, 2]

# 生産時間
production_time = {'A': 2, 'B': 3, 'C': 4, 'D': 5}

# 変数の設定
x = LpVariable.dicts(
    "x", 
    [(i, j) 
        for i in products 
        for j in lines
    ], 
    0, 
    1, 
    LpBinary
    )

# 目的関数の設定
prob += lpSum(
    [x[i, j] * production_time[i] 
        for i in products 
        for j in lines
    ]
    )

# 制約条件の追加
for i in products:
    prob += lpSum([x[i, j] for j in lines]) == 1

for j in lines:
    prob += lpSum([x[i, j] for i in products]) <= 1

# 問題の解決
prob.solve()

# 結果の出力
for v in prob.variables():
    print(f"{v.name} = {v.varValue}")

print(f"Total Production Time: {value(prob.objective)}")

 

上記のコードはPuLPを使用して、ABC製造株式会社の生産スケジューリング問題を解決するためのものです。目的は製品を生産ラインに割り当て、生産時間の合計を最小化することです。コードは目的関数と制約条件を定義し、解を求めます。実行すると、どの製品がどの生産ラインで生産されるべきかが決定され、生産時間の合計が出力されます。

  • 問題の設定：`pulp.LpProblem`を使って問題を定義します。この問題は最小化問題であり、’Scheduling_Problem’と名付けられています
  • 製品と生産ライン：四つの製品（’A’,’B’,’C’,’D’）と二つの生産ライン（1,2）が定義されています
  • 生産時間：各製品についての生産時間が辞書`production_time`に格納されています
  • 変数の設定：`pulp.LpVariable.dicts`を用いて、製品と生産ラインに対する二次元のバイナリ変数`x`を定義します。`x[i,j]`は製品`i`が生産ライン`j`を使用するか否か（0:使用しない,1:使用する）を示す変数です
  • 目的関数の設定：`lpSum`を用いて目的関数を設定します。目的関数は全ての製品と生産ラインの組についての`x[i, j] * production_time[i]`の合計で、これは全ての製品の生産時間の総和を表します
  • 制約条件の追加：制約条件を定義しています。最初の制約条件は、各製品がちょうど一つの生産ラインで生産されることを保証します。次の制約は、それぞれの生産ラインで生産できる製品は一つだけという制約です
  • 問題の解決：`prob.solve()`を実行して問題を解きます
  • 結果の出力：各変数の値と目的関数の値（総生産時間）を出力しています

 

以下、実行結果です。

x_('A',_1) = 1.0
x_('A',_2) = 0.0
x_('B',_1) = 1.0
x_('B',_2) = 0.0
x_('C',_1) = 1.0
x_('C',_2) = 0.0
x_('D',_1) = 0.0
x_('D',_2) = 1.0
Total Production Time: 14.0

 

この結果は、製品AとB、Cは生産ライン1で、製品Dは生産ライン2で生産すべきであることを示しています。合計生産時間が14時間となり、これが可能な最小の生産時間です。

 

　ロジスティクスと経路最適化

物流業界では、商品を効率的に配送するために経路最適化が欠かせません。整数最適化は、配送車両の数、配送先、道路の状況などを考慮して、最もコスト効率の良いルートを計算します。これにより、燃料費の削減、配送時間の短縮、顧客満足度の向上が期待できます。

最適化問題を定式化します。

  • d_{i\,i} ：都市iと都市jの距離
  • x_{ij}：移動ルートに、都市iから都市jのルートが含まれる場合は1、そうでなければ0。
  • u_i：都市iに割り当てられる順序を表す補助変数。

目的関数：

\displaystyle \text{minimize } \sum_{i=1}^{n}\sum_{j\neq i,j=1}^{n}d_{i j}x_{i j}

制約条件：

各都市iから、ただ一つの都市jへ移動

\displaystyle \sum_{j=1,j\neq i}^{n}\,x_{i j}=1 \quad\forall i\in\{1,\cdot\cdot\cdot,n\}

各都市jへ、ただ一つの都市iから移動

\displaystyle \sum_{i=1,i\neq j}^{n}\,x_{i j}=1 \quad\forall j\in\{1,\cdot\cdot\cdot,n\}

サブツアー除去の制約（解が小さなループにならないようにする）

\displaystyle u_{i}-u_{j}+n\cdot x_{i j}\leq n-1\quad\forall i,j\in\{1,\cdot\cdot\cdot,n\},i\neq j

二値変数の制約。

\displaystyle x_{i j}\in\{0,1\}\quad\forall i,j

 

以下、コードです。

from pulp import *

# 問題の設定
prob = LpProblem("Route_Optimization", LpMinimize)

# 都市
cities = ['A', 'B', 'C', 'D', 'E']

# 距離データ
distances = {
    ('A', 'B'): 10, 
    ('B', 'A'): 10,
    ('A', 'C'): 20, 
    ('C', 'A'): 20,
    ('A', 'D'): 15, 
    ('D', 'A'): 15,
    ('A', 'E'): 30,
    ('E', 'A'): 30,
    ('B', 'C'): 25, 
    ('C', 'B'): 25,
    ('B', 'D'): 35, 
    ('D', 'B'): 35,
    ('B', 'E'): 20,
    ('E', 'B'): 20,
    ('C', 'D'): 30, 
    ('D', 'C'): 30, 
    ('C', 'E'): 15,
    ('E', 'C'): 15,
    ('D', 'E'): 40,
    ('E', 'D'): 40
    }

# 変数の設定（xとu）
x = LpVariable.dicts(
    "x", 
    [(i, j) for i in cities for j in cities if i != j], 
    lowBound=0, 
    upBound=1, 
    cat='Integer'
    )

u = LpVariable.dicts(
    "u", 
    [i for i in cities], 
    lowBound=0, 
    upBound=len(cities)-1, 
    cat='Integer'
    )

# 目的関数の設定
prob += lpSum([
    x[i, j] * distances[(i, j)]
        for i in cities 
        for j in cities if i != j and (i, j) in distances
    ])

# 制約条件の追加
for i in cities:
    prob += lpSum([x[i, j] for j in cities if i != j]) == 1
    prob += lpSum([x[j, i] for j in cities if i != j]) == 1

# MTZ制約（部分巡回路排除制約）の追加
for i in cities[1:]:
    for j in cities[1:]:
        if i != j:
            prob += u[i] - u[j] + (len(cities) * x[i, j]) <= len(cities) - 1

# 問題の解決
prob.solve()

# 結果の出力
for v in prob.variables():
    print(f"{v.name} = {v.varValue}")

print("Correct Total Distance: ", value(prob.objective))

 

上記のコードはPuLPを使用して、XYZ物流株式会社の経路最適化問題を解決するためのものです。目的は都市間の距離の合計を最小化することです。コードは目的関数と制約条件を定義し、解を求めます。実行すると、最適なルートが決定され、全体の移動距離が出力されます。

  • 問題の設定：最小化問題オブジェクトを定義します。この問題の名前は “Route_Optimization” です
  • 距離データ：都市間の距離を定義します。鍵と値のペアが都市のペアとその間の距離です
  • 変数の設定：変数を定義します。各(i, j)ペアについて、x[i, j] = 1 は都市 i から都市 j に辺（経路）があることを示し、x[i, j] = 0 は辺がないことを示します
  • 目的関数の設定：選択されたすべての経路の距離の合計を最小化することを目指しています
  • 制約条件の追加：各都市について、その都市から出ていく辺と入ってくる辺がちょうど1つずつであるという制約を追加します
  • MTZ制約の追加：この制約は、解が1つの連続するルートになることを保証するサブツアー除去の制約です
  • 問題の解決：`prob.solve()` 関数を呼び出すことで、最適化問題を解きます
  • 結果の出力：最後に、全ての変数とその最適値、さらに総距離（目的関数の値）を出力します

 

以下、実行結果です。

u_B = 0.0
u_C = 2.0
u_D = 3.0
u_E = 1.0
x_('A',_'B') = 1.0
x_('A',_'C') = 0.0
x_('A',_'D') = 0.0
x_('A',_'E') = 0.0
x_('B',_'A') = 0.0
x_('B',_'C') = 0.0
x_('B',_'D') = 0.0
x_('B',_'E') = 1.0
x_('C',_'A') = 0.0
x_('C',_'B') = 0.0
x_('C',_'D') = 1.0
x_('C',_'E') = 0.0
x_('D',_'A') = 1.0
x_('D',_'B') = 0.0
x_('D',_'C') = 0.0
x_('D',_'E') = 0.0
x_('E',_'A') = 0.0
x_('E',_'B') = 0.0
x_('E',_'C') = 1.0
x_('E',_'D') = 0.0
Correct Total Distance:  90.0

 

変数 u は訪問順番（Aから開始）です。

  • u_B = 0.0 : 都市Bの訪問順位は1
  • u_C = 2.0 : 都市Cの訪問順位は3
  • u_D = 3.0 : 都市Dの訪問順位は4
  • u_E = 1.0 : 都市Eの訪問順位は2

変数 x は移動ルートです。

  • x_(A, B) = 1.0 : 都市Aから都市Bへと直接移動する
  • x_(B, E) = 1.0 : 都市Bから都市Eへと直接移動する
  • x_(C, D) = 1.0 : 都市Cから都市Dへと直接移動する
  • x_(D, A) = 1.0 : 都市Dから都市Aへと直接移動する
  • x_(E, C) = 1.0 : 都市Eから都市Cへと直接移動する

以上から、最短ルートは A → B → E → C → D → A で、その合計距離は 90 となります。]

 

最後に、グラフィカルにグラフ（アークとノード）で描いてみます。

ライブラリーnetworkxを使いますので、インストールされていない場合は、pip install networkxでインストールしてください。

では描きます。以下、コードです。

import networkx as nx
import matplotlib.pyplot as plt

# 新しいグラフを作成
G = nx.DiGraph()

# エッジとその重みを定義
edges = [
    ('A', 'B', 10), 
    ('B', 'E', 20), 
    ('E', 'C', 15), 
    ('C', 'D', 30), 
    ('D', 'A', 15)
]

# グラフにエッジを追加
G.add_weighted_edges_from(edges)

# グラフを描画
pos = nx.spring_layout(G)  # ノードの位置を計算
nx.draw(
    G, 
    pos, 
    with_labels=True, 
    node_color='white', 
    edgecolors='black', 
    node_size=1500
    )  # ノードを描画（黒の枠線付き）
nx.draw_networkx_edge_labels(
    G, 
    pos, 
    edge_labels=nx.get_edge_attributes(G, 'weight')
    )  # エッジのラベル（重み）を描画

plt.savefig("graph.png")
plt.show()

 

以下、実行結果です。

 

まとめ

今回は、「整数最適化と組合せ最適化」についてお話ししました。

  • 整数最適化と組合せ最適化は、実世界の問題を数学的にモデル化し、最適な解を見つけ出す強力な手段
  • 多くのビジネス上の課題に適用可能で、コスト削減や効率向上、意思決定の質向上に貢献可能
  • 問題の定式化と適切なソルバーの選択が成功の鍵

SciPyでは限界があるため、PuLPを使いました。

次回は、Scikit-learnで構築した数理モデルを目的変数に利用する方法を紹介します。次回もぜひご期待ください。

Python SciPyで手を動かしながら学ぶ数理最適化– 第5回: Scikit-learnモデルとSciPy最適化の統合 –