Python SciPyで手を動かしながら学ぶ数理最適化– 第5回: Scikit-learnモデルとSciPy最適化の統合 –

数理最適化と機械学習の融合は、ビジネスの意思決定に革命をもたらす可能性を秘めています。

具体的には、Scikit-learnで数理モデルを構築し、その数理モデルを目的変数としたSciPyを用い最適化問題を解きます。

例えば、マーケティング変数Xによって売上yを予測する数理モデルを、Scikit-learnで構築したとします。この売上yを予測する数理モデルを最大化する、マーケティング変数Xの組み合わせを求めることができます。

ただ、大きな問題が1つあり、求めたい大域的最適解ではなく局所的最適解に陥ることがあります。後で説明します。

Contents

Scikit-learnの基本
　Scikit-learnとは？
　ビジネスでよく登場する予測モデル例の一覧
　予測モデルの構築手順
【復習】Python SciPyを使用した最適化
　SciPyの最適化ツールの紹介
　実際のコード例と解説
Scikit-learnモデルとSciPy最適化の統合
　構築した予測モデルを目的変数として使用する方法
　Basinhoppingによる大域的最適解
ケーススタディ（Scikit-learnモデル×SciPy最適化）
　サンプルデータ
　予測モデル構築
　最適化問題を解く
まとめ

Scikit-learnの基本

　Scikit-learnとは？

Scikit-learnとは、Pythonのオープンソースの機械学習ライブラリです。

様々な分類、回帰、クラスタリングなどの機械学習アルゴリズムを提供し、NumPyやSciPyなどの数値計算ライブラリと連携できます。

scikit-learnは、データの前処理、学習、予測、評価などの機能を備えており、初学者から上級者まで幅広く利用されています。

　ビジネスでよく登場する予測モデル例の一覧

モデルの種類	ビジネス応用例	使用可能なアルゴリズム
顧客離反予測	顧客がサービスをやめる確率の予測	ロジスティック回帰、ランダムフォレスト、SVMなど
購買予測	顧客の製品購入の予測	ロジスティック回帰、ランダムフォレスト、SVMなど
販売予測	将来の売上の予測	線形回帰、ランダムフォレストなど
広告効果予測	広告キャンペーンの効果の予測	線形回帰、ランダムフォレスト、時系列予測モデルなど
品質管理予測	製品の品質が基準を満たしているかの予測	ロジスティック回帰、ランダムフォレスト、SVMなど
需要予測	製品の需要の予測	時系列予測モデルなど
クレジットスコア予測	個人のクレジットリスクの予測	ロジスティック回帰など
株価予測	株価の動きの予測	回帰分析、時系列分析など
不正検出	取引の不正行為の検出	ロジスティック回帰、ランダムフォレスト、SVMなど

　予測モデルの構築手順

Scikit-learnを使用する際の、数理モデルの基本的なステップは以下の通りです。

データの読み込みと前処理：初めに、分析に適したデータセットを選択し、必要に応じて前処理を行います。これには、欠損値の処理、変数のスケーリング、カテゴリ変数のエンコーディングなどが含まれます。また、データセットを学習データとテストデータに分割します。
モデルの選択：次に、問題の種類（分類、回帰など）に応じて適切なモデルを選択します。Scikit-learnは多くの組み込みモデルを提供しており、線形モデル、サポートベクターマシン、決定木などがあります。
学習データでモデル構築：選択したモデルにトレーニングデータをフィットさせ、パラメータを調整します。この段階では、クロスバリデーションやグリッドサーチを用いて最適なパラメータを見つけることも重要です。
テストデータによる評価：モデルのパフォーマンスをテストデータで評価し、必要に応じてパラメータを調整します。
予測モデルの完成：実務で利用する予測モデルを完成させます。多くの場合、分割前のデータセットすべてを使い構築します。

【復習】Python SciPyを使用した最適化

SciPyライブラリは、科学計算に特化したPythonのライブラリの一つであり、特に最適化問題に対して豊富なツールと関数を提供しています。

これらのツールを活用することで、様々な最適化問題に対して効率的かつ効果的な解を見つけることができます。

　SciPyの最適化ツールの紹介

SciPyの最適化モジュールには、以下のような多様な関数が含まれています。

最適化アルゴリズム：SciPyは、minimize関数を通じて、様々な最適化アルゴリズム（例：Nelder-Mead法、BFGS法、CG法）を提供します。これらは、特定の関数の最小値を見つけるために使用されます。
制約付き最適化：等式または不等式の制約条件を持つ最適化問題を解くための関数も提供されています。
大域的最適化：複数の局所最適解が存在する問題に対して、大域的な最適解を見つけるためのツールも含まれています。

　実際のコード例と解説

以下に、SciPyを使用して簡単な最適化問題を解く一例を示します。

ここでは、二次関数 $x^2+5x+8$ の最小値を見つけるシンプルなケースを考えます。

import scipy.optimize as opt
import numpy as np

# 最適化する目的関数の定義
def objective_function(x):
    return x**2 + 5*x + 8

# 初期値
initial_guess = 0

# 最適化実行
result = opt.minimize(objective_function, initial_guess)

# 結果の表示
print("最適解:", result.x)
print("関数の最小値:", result.fun)

モジュールのインポート:
- scipy.optimize モジュールを opt としてインポートします。これは、最適化アルゴリズムを提供するSciPyのサブモジュールです。
- numpy モジュールを np としてインポートします。これは、数値計算に広く用いられるPythonライブラリです。
目的関数の定義:
- objective_function という名前の関数を定義します。この関数は、与えられた入力 x に対して x**2 + 5*x + 8 の値を計算し、返します。
初期値の設定:
- 最適化プロセスの初期値として initial_guess に 0 を設定します。
最適化の実行:
- opt.minimize 関数を用いて objective_function を最小化します。この関数は、与えられた初期値 initial_guess から開始して、関数が最小となる点を探索します。
結果の表示:
- result.x で最適化によって得られた解（最適解）を取得し、表示します。
- result.fun で最適化によって得られた関数の最小値を取得し、表示します。

以下、実行結果です。

最適解: [-2.50000002]
関数の最小値: 1.7500000000000009

Scikit-learnモデルとSciPy最適化の統合

機械学習モデルと最適化理論の融合は、ビジネス上の意思決定をデータ駆動で進化させる鍵です。

特に、Scikit-learnで構築された機械学習モデルとSciPyの最適化アルゴリズムを統合することで、複雑な問題解決に新たなアプローチを提供します。

　構築した予測モデルを目的変数として使用する方法

Scikit-learnで構築したモデルの出力を、SciPy最適化アルゴリズムの目的変数として活用することで、実際のビジネス問題に応じた最適な解を導き出すことができます。

例えば、製品の価格設定、生産プロセスの最適化、サプライチェーン管理など、多岐にわたる問題に対応可能です。

以下、構築した予測モデルを目的変数として利用するときの手順です。

【１】モデルの構築：Scikit-learnを用いて、特定のビジネス問題に適した予測モデルを構築します。
【２】目的関数の定義：モデルの出力を利用して、特定の目的（例：利益の最大化、コストの最小化）に合わせた目的関数を定義します。
【３】最適化の実行：SciPyの最適化アルゴリズムを使用して、目的関数を最大化または最小化します。

　Basinhoppingによる大域的最適解

Scikit-learnの機械学習アプローチで構築した予測モデルの多くは、非線形な複雑なモデルになることが多いです。

このとき大きな問題が1つあり、求めたい大域的最適解ではなく局所的最適解に陥ることがあります。

大域的最適解（Global Optimum）
大域的最適解は、最適化されるべき関数において、全ての可能な解の中で最も良い解です。これは、問題全体の範囲にわたって最良の解を意味し、その関数の最小値または最大値に相当します。大域的最適解は、全ての局所的最適解の中でも最良の解です。

局所的最適解（Local Optimum）
局所的最適解は、最適化されるべき関数において、その近傍内で最も良い解ですが、必ずしも全体の最適解ではありません。局所的最適解は、その近くの解よりも優れているが、別の領域により良い解が存在する可能性があります。

そこで登場するのが、SciPyの basinhopping アルゴリズムです。

basinhopping は、ランダムなステップを使用して複数の局所的最適解から脱出し、大域的な視点から最適解を見つけ出す手法です。これにより、より複雑で実践的なビジネス問題に対しても、効果的な最適化解を得ることが可能になります。

ここで、先ほどの二次関数 $x^2+5x+8$ の最小値を見つける例を使い、basinhopping のコーディング例を示します。

import scipy.optimize as opt
import numpy as np

# 最適化する関数の定義
def objective_function(x):
    return x**2 + 5*x + 8

# 初期値
initial_guess = 0

# 最適化の実行
result = opt.basinhopping(objective_function, initial_guess)

# 結果の表示
print("最適解:", result.x)
print("関数の最小値:", result.fun)

minimize がbasinhopping に代わっただけで、あまり大きな変化がなさそうに見えます。

basinhopping には、大域的最適化を求めるために設定する引数があり、その引数を適切に設定する必要があります。

以下、その引数です。

`func`: 最適化を求める目的となる関数です。この関数は一部または全てのパラメータをベクトルとして受け取り、スカラー値を返さなければなりません。
`x0`: 最適化の初期推定値です。このパラメータは配列で、目的関数が受け取るパラメータの数と同じ長さであるべきです。
`niter`: バシンホッピングの反復回数。デフォルトは100。
`T`: Acceptance testのための温度パラメータ（気温）。高い温度は、目的関数の値がより大きくなるようなステップも受け入れやすくします。デフォルトは1.0。
`stepsize`: ランダムなステップの大きさ。デフォルトは1.0。
`minimizer_kwargs`: ローカル最適化手法をカスタマイズするためのキーワード引数。例えば、制約や境界などを定義できます。
`take_step`: ステップを取るためのオプショナルな呼び出し可能オブジェクト。この引数を指定するとデフォルトの方法を置き換えます。
`accept_test`: 別のオプショナルな呼び出し可能オブジェクト。これを使って、ステップが受け入れできるかどうかの評価の方法やその他のチェックなどをカスタマイズできます。
`callback`: 結果が最適化されるたびに呼び出されるオプショナルな呼び出し可能オブジェクト。
`interval`: メトロポリスacceptanceをどれくらいの頻度で試すか。
`disp`: メッセージがターミナルに表示されるかどうか。デフォルトはFalse。
`niter_success`: 目的関数が改善しなくなったときに終了するための反復回数。デフォルトは3回。

設定が必須なのは、目的変数を設定する`func`と初期値である`x0`です。

他には、最適化手法を設定するための`minimizer_kwargs`や、反復回数である`niter`、探索終了に関わる`niter_success`、温度パラメータ（気温）`T`、ランダムなステップサイズである`stepsize`を設定することが多いです。

ちなみに、反復回数などを増やすと非常に時間が掛かりますが、より良い解に近づく可能性が高まります。

ケーススタディ（Scikit-learnモデル×SciPy最適化）

ここでは、製品の価格設定最適化を例に取り上げます。

ビジネス問題：ある企業がある製品を販売しており、売上を最大化するための最適な価格設定を求めたい
データ：過去の販売データと価格データなど
目的：売上に直結する価格設定の最適化

　サンプルデータ

まず、サンプルデータ（価格：price、売上：sales）を作ります。

以下、コードです。

import numpy as np
import pandas as pd

import warnings
warnings.filterwarnings("ignore", category=UserWarning)

# サンプルデータ生成
np.random.seed(0)
prices = np.random.normal(150, 20, 100) 
sales = 5000 - (prices - 150)**2  + np.random.normal(0, 100, 100)
data = pd.DataFrame({'Price': prices, 'Sales': sales})

print(data)

以下、実行結果です。乱数でサンプルデータを作っているので、人によって若干ことなります。

         Price        Sales
0   185.281047  3943.562798
1   158.003144  4801.173777
2   169.574760  4489.780284
3   194.817864  3088.298739
4   187.351160  3487.578521
..         ...          ...
95  164.131463  4783.147110
96  150.210000  5077.134955
97  185.717410  3806.617047
98  152.538242  5209.880923
99  158.039787  5069.014616

[100 rows x 2 columns]

このサンプルデータをプロットします。

以下、コードです。

import matplotlib.pyplot as plt
import seaborn as sns

# 散布図と近似線を作成
plt.figure(figsize=(7,5))
sns.regplot(
    data=data,
    x='Price', y='Sales', 
    scatter_kws={'color':'blue'}, 
    line_kws={'color':'red', 'ls': '--'}, 
    order=2) 

plt.title('Price vs Sales with non-linear fit')
plt.show()

以下、実行結果です。

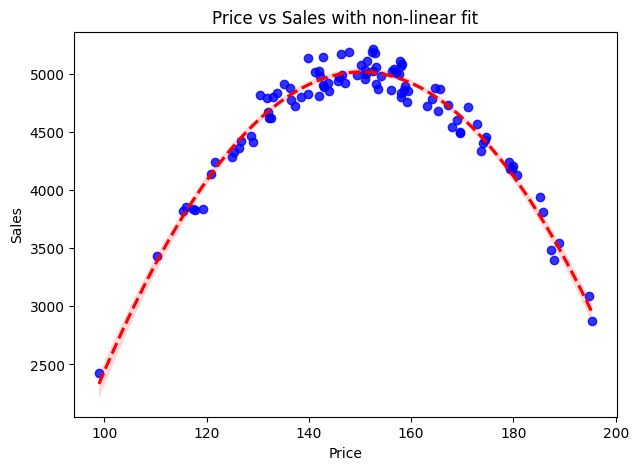
価格（price）を150円近くに設定すると、売上（sales）が最大化しそうです。

では、売上が最大化する価格設定を探求していきます。

　予測モデル構築

まずは、価格（price）Xで売上（sales）yを予測するモデルを、ランダムフォレストで構築しても問題なさそうかを検討します。

データセットを学習データとテストデータに分割し、学習データで構築した予測モデルが、テストデータでも十分に高精度であれば、問題ないと判断します。

以下、コードです。

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error

# 説明変数Xと目的変数yに分ける
X = data[['Price']]
y = data['Sales']

# データを学習用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(
    X, 
    y, 
    test_size=0.3, 
    random_state=42)

# ランダムフォレストモデルの学習
model = RandomForestRegressor()
model.fit(X_train, y_train)

# テストデータでの予測
preds = model.predict(X_test)

# 精度評価
r2 = r2_score(y_test, preds)   # R^2スコア
mae = mean_absolute_error(y_test, preds)  # 平均絶対誤差(MAE)

print('R^2 score:', r2)
print('MAE:', mae)

以下、実行結果です。

R^2 score: 0.8844782415478085
MAE: 125.17625325601507

問題なさそうですが、念のため散布図でも確認します。

以下、コードです。

# 予測値と実測値の散布図
plt.scatter(y_test, preds)
plt.plot([min(y_test),max(y_test)], [min(y_test),max(y_test)],'r')
plt.xlabel("True Values")
plt.ylabel("Predictions")
plt.title("True vs Predicted Values")
plt.grid(True)
plt.show()

以下、実行結果です。

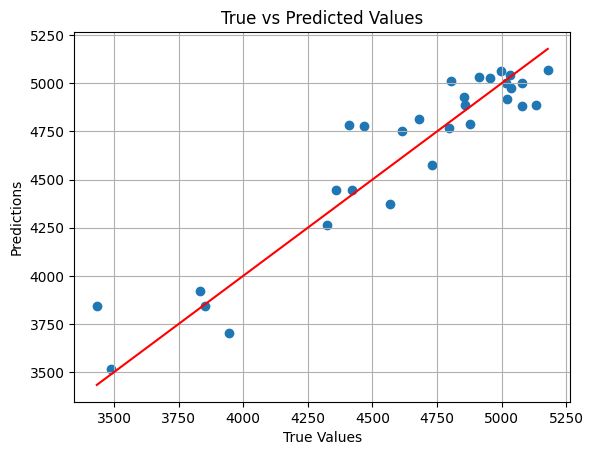
問題なさそうなので、すべてのデータを使い予測モデルを構築します。

以下、コードです。

from sklearn.ensemble import RandomForestRegressor

# 説明変数Xと目的変数yに分ける
X=data[['Price']]
y=data['Sales']

# ランダムフォレストモデルの構築
model = RandomForestRegressor()
model.fit(X, y)

　最適化問題を解く

この構築した予測モデルを使い、最適化問題を解きます。

以下、コードです。

from scipy.optimize import basinhopping

# 目的関数の定義（モデルの予測を利用）
def objective_function(price):
    price_=price.reshape(-1, 1)
    predicted_sales = model.predict(price_)
    return -predicted_sales[0]

# 最適化の実行（結果は保存されますが、出力されません）
result = basinhopping(
    func=objective_function, 
    x0=[100.0], 
    niter=10000,
    T=10,
    stepsize=10,
    niter_success=10,
    minimizer_kwargs={
        "method": "L-BFGS-B", 
        "bounds": [(100, 500)],
    },
)

# 結果の表示
optimal_price = result.x[0]
predicted_sales = -result.fun
optimal_price, predicted_sales

モジュールのインポート:
- scipy.optimize モジュールから basinhopping 関数をインポートします。これは、大域的最適化問題のためのアルゴリズムです。
目的関数の定義:
- objective_function という関数を定義します。この関数は価格（price）を引数として受け取り、予測された売上（predicted_sales）を計算して返します。
- 価格は reshape メソッドを用いて、モデル予測に適した形式に変換されます。
- 予測された売上は model.predict メソッドによって計算され、その負の値が返されます（最小化問題に変換するため）。
最適化の実行:
- basinhopping 関数を使用して、目的関数 objective_function の大域的最適解を探索します。
- 初期値 x0 は [100.0] と設定されています。
- niter はアルゴリズムの反復回数で、ここでは 10000 に設定されています。
- T は温度パラメータで、ここでは 10 に設定されています。
- stepsize はステップサイズで、ここでは 10 に設定されています。
- niter_success は連続する成功の最大回数で、ここでは 10 に設定されています。
- minimizer_kwargs は内部の最小化関数に渡されるキーワード引数で、ここでは L-BFGS-B 法を使用し、価格の範囲を 100 から 500 に制限しています。
結果の表示:
- result.x[0] から最適解（optimal_price）を取得します。
- result.fun から関数の最小値（predicted_sales）を取得し、その負の値を表示します。

以下、実行結果です。

最適解: 148.59912716165437
関数の最大値: 5112.3455223976725

まとめ

今回は、「Scikit-learnモデルとSciPy最適化の統合」についてお話ししました。

数理最適化と機械学習の組み合わせは、ビジネスの意思決定において大きな可能性を秘めています。

機械学習による予測は、複雑な市場の動向や消費者行動の理解を深めることができ、これを数理最適化に統合することで、より具体的で効果的な戦略を導き出すことが可能になります。