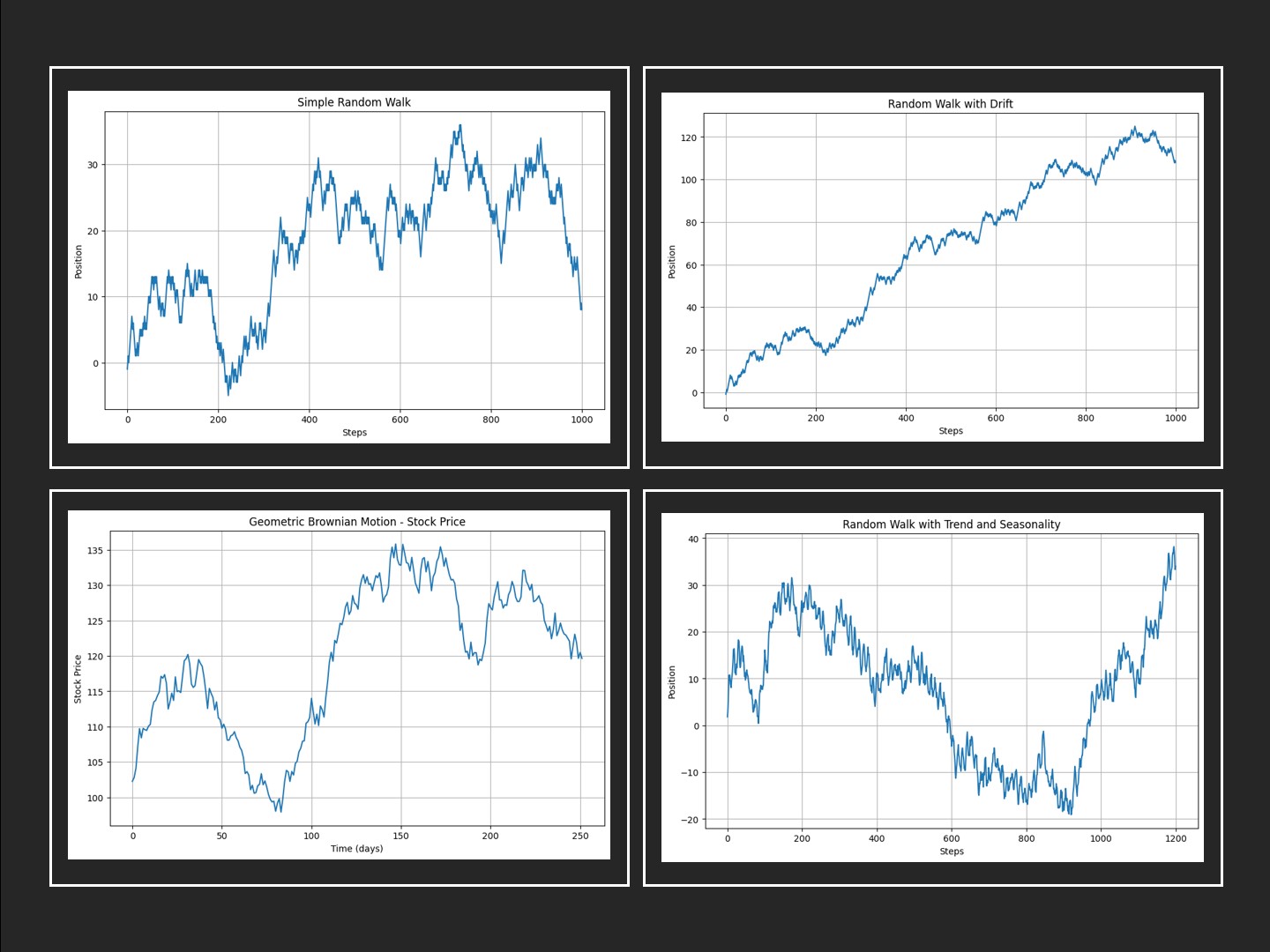
様々な時系列ランダムウォークと近未来分析

ビジネスの現場では時系列データは当然のごとく登場します。売上や販売データ、在庫データ、センサーデータなどすべて時系列データです。

そのような時系列データの中に、ランダムウォークと呼ばれる時系列データが登場することがあります。

株価の変動から消費者行動のパターン、製品の需要予測に至るまで、ビジネスにおける様々な現象に、この予測不可能なランダムウォークの要素が顔を出すことがあります。

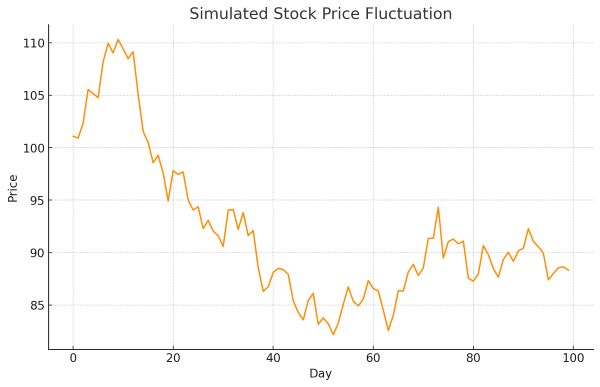
そもそも、ランダムウォークには色々なものがありますし、時系列データを予測可能な部分と予測不可能なランダムウォークの部分、定常な部分（ホワイトノイズ）などに分離することもあります。

今回は、Pythonで具体的なランダムウォークデータを再現しながら、データの背後にあるパターンを明らかにしていきます。

より精度の高い近未来分析の一助となればと思います。

Contents

はじめに
　ランダムウォークの基本概念
　時系列データ分析におけるランダムウォークの重要性
　ランダムウォークモデルの役割
　ランダムウォークモデルと近未来分析
　ランダムウォークモデルの種類
主なランダムウォークの描写
　シンプルランダムウォーク
　ドリフト付きランダムウォーク
　トレンドと季節性を持つランダムウォーク
　幾何ブラウン運動と金融データ
ランダムウォークの同定方法
　同定の流れ
　　Step 1. データの観察と前処理
　　Step 2. ランダムウォークかどうかの判断（定常性の検定）
　　Step 3. ランダムウォークの種類の同定（定常性・トレンド・正規性の検定）
　幾何ブラウン運動の例
　おまけ（VaRとBlack-Scholesモデル）
まとめ

はじめに

　ランダムウォークの基本概念

ランダムウォークとは、次の位置がランダムに決定される時系列データのことです。

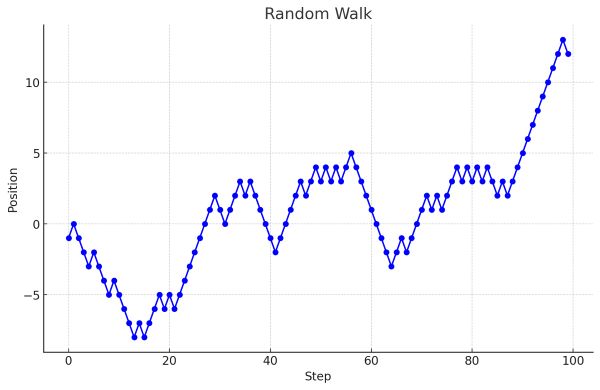
各ステップでランダムに決定される方向に進む過程を数学的にモデル化したもので、シンプルなランダムウォークの数式は次のように表現されます。

\displaystyle X_{n+1} = X_n + \epsilon_{n+1}

ここで、 $X_n$ はステップ $n$ での位置を表し、 $\epsilon_{n+1}$ は時間 $n+1$ で取られるランダムなステップです。

また、ランダムウォークが0から始まる場合、次のようにも書けます。

\displaystyle X_n = X_0 + \sum_{i=1}^{n} \epsilon_i

ここで、 $X_0$ は開始位置（しばしば0）を表し、 $\sum_{i=1}^{n} \epsilon_i$ はステップ $n$ までのランダムステップの累積和を表します。この式は、開始点から $n$ ステップ目までにどのように位置がランダムに変動するかを示しています。

このようなランダムウォークは、金融市場の株価変動、物理学における粒子の動き、生物の移動パターンなど、多岐にわたる現象をモデル化するのに使われます。

ランダムウォークは、その予測不可能性から「酔っ払いの歩行」と例えられることもあります。

　時系列データ分析におけるランダムウォークの重要性

時系列データ分析では、過去のデータから未来を予測することが一つの大きな目標です。

ランダムウォークは、未来の価値が過去の価値から独立しており予測不可能です。

しかし、実際には多くの時系列データがランダムウォークに似た振る舞いを示すため、このモデルはデータの特性を理解し、より複雑な予測モデルを構築するための基礎となります。

　ランダムウォークモデルの役割

ランダムウォークの代表例として、例えば金融市場の株価変動があります。

実際、目の前の株価変動がランダムウォークであると同定されてしまったら、その株価変動は予測不可能であることを意味します。

であるならば、なぜ予測不可能な株価変動を、ランダムウォークモデルを使用して分析するのでしょうか。

ランダムウォークモデルは、市場の将来の価格を具体的に予測するためではなく、例えば以下のような市場の振る舞いやリスクの性質を理解するために用いられます。

市場の効率性の理解
ランダムウォークモデルは、効率的市場仮説を支持するためによく引用されます。この仮説は、全ての既知の情報がすでに価格に反映されているため、将来の価格変動を予測することは不可能であると主張します。

リスクの定量化
モデルを使用して、市場のボラティリティ（価格の変動幅）を定量化することができます。これにより、投資家はポートフォリオのリスクをよりよく理解し、管理することができます。

シミュレーションとシナリオ分析
ランダムウォークモデルを利用して、様々な市場条件下での価格変動のシミュレーションを行い、投資戦略のストレステストを実施することが可能です。これは、予測ではなく、可能性の探索に役立ちます。

　ランダムウォークモデルと近未来分析

ランダムウォークモデルに基づくシミュレーションは、将来の市場を「予測」するのではなく、価格変動のランダムな性質とその結果として生じうるリスクを分析するために利用します。

これは、市場がどのように動くかについての確定的な予測をするものではありませんが、投資家がリスクを評価し、そのリスクに対してどのようにポジションを取るかを決定する上で重要な洞察を与えてくれます。

したがって、ランダムウォークモデルを使用する際の主な目的は、市場の動きを「正確に予測する」ことではなく、市場の振る舞いのランダム性を理解し、そのランダム性を通じてリスクを管理し、投資戦略を形成することにあります。

そのためには、実際の市場の動きを反映したランダムウォークモデルを探し出す必要があります。

　ランダムウォークモデルの種類

目の前の時系列データが、どの種類のランダムウォークなのかを同定するには、ランダムウォークにどのようなものがあるのを知らないことには始まりません。

実際、ランダムウォークモデルには色々なバリエーションがあります。以下は主なものです。

ランダムウォークの種類	概要	例
シンプルランダムウォーク(Simple Random Walk)	最も基本的な形式で、各ステップは同じ確率で上または下に移動	株価が一定確率で上下するモデル
ドリフト付きランダムウォーク(Random Walk with Drift)	各ステップに一定の傾向(ドリフト)があり、長期的なトレンドを模倣	経済成長
トレンド付きランダムウォーク(Random Walk with a Trend)	ドリフト付きに似るが、より明確な上昇下降トレンド	経済の長期トレンド
幾何ブラウン運動(Geometric Brownian Motion)	株価などで使われ、価格が連続的に変動し、正規分布に従うと仮定	金融市場の株価や為替レート
レヴィフライト(Lévy Flight)	ステップ長がレヴィ分布に従う。小さなステップと大きなステップが混在し不規則なパスを生成	動物の餌探し行動
多重ランダムウォーク(Multi-dimensional Random Walk)	2次元や3次元など、複数の独立した次元でのランダムウォーク	分子のブラウン運動
反射原理を持つランダムウォーク(Random Walk with Reflection)	ある閾値に達すると反対方向に「反射」する	株価が特定水準を上回らない場合
制約付きランダムウォーク(Constrained Random Walk)	特定条件下でのみ許されるランダムウォーク	迷路内を動くランダムウォーク
自己回避ランダムウォーク(Self-avoiding Random Walk)	過去の位置を再訪問しない	高分子ポリマー鎖の形状
分岐ランダムウォーク(Branching Random Walk)	各ステップで新しい「枝」がランダム生成	感染者が接触により新たに他者を感染させていく様子
加速度ランダムウォーク(Accelerated Random Walk)	各ステップで速度がランダム変化	粒子加速器での粒子運動
ランダムウォークのスケール不変性(Scale Invariant Random Walk)	時間・距離のスケールを変えても統計的性質が不変	流体乱流の解析

テキストで説明されてもわけわからん！という方もいると思いますので、次から主要なランダムウォークを、Pythonコードでサンプルデータを作りグラフ化し示していきます。

主なランダムウォークの描写

　シンプルランダムウォーク

シンプルランダムウォークは、最も基本的なランダムウォークの形式で、各ステップで等しい確率で上または下に進むモデルです。金融で言えば、株価が次の時点で上がるか下がるかが完全にランダムであると仮定した場合のモデルに相当します。

Pythonを使用してシンプルランダムウォークをシミュレーションしてみましょう。ここでは、NumPyライブラリを使用します。NumPyは、Pythonで科学計算を行うための基本的なパッケージの一つです。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt

# シード値を設定して再現性を保証
np.random.seed(0)

# ステップ数
n_steps = 1000

# 各ステップでの変化: -1 または 1
steps = np.random.choice([-1, 1], size=n_steps)

# ランダムウォークのパスを計算
position = np.cumsum(steps)

# プロット
plt.figure(figsize=(10, 6))
plt.plot(position)
plt.title('Simple Random Walk')
plt.xlabel('Steps')
plt.ylabel('Position')
plt.grid(True)
plt.show()

このコードは、1000ステップのシンプルランダムウォークを生成し、その経路をプロットします。np.random.choice関数は各ステップで-1または1をランダムに選択し、np.cumsum関数はこれらの変化を累積してパスを計算します。

以下、実行結果です。

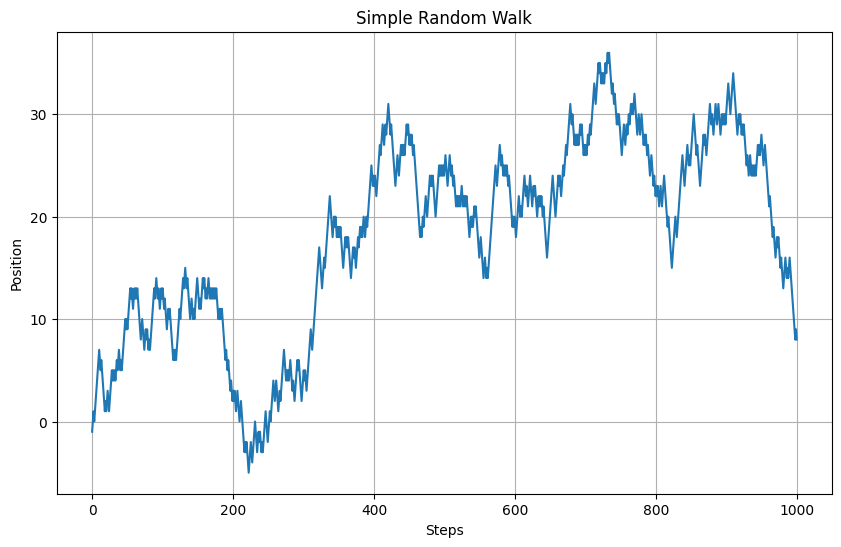
生成されたグラフは、シンプルランダムウォークの特徴を示しています。パスは無作為に上下し、特定の方向性を持たず、時間が経つにつれて変動の幅が広がります。

これは、シンプルランダムウォークが予測不可能な過程であることを示しています。

　ドリフト付きランダムウォーク

ドリフト付きランダムウォークは、各ステップでのランダムな変動に加えて、一定の方向への傾向（ドリフト）が存在するモデルです。金融市場での株価や為替レートの動きをモデル化する際に特に有用であり、長期的な成長トレンドやインフレーションの影響を表現するのに使われます。

ドリフト付きランダムウォークをシミュレートするために、先ほどのシンプルランダムウォークのコードに少し変更を加えます。ドリフト項を追加することで、各ステップに一定の傾向を持たせることができます。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt

# シード値を設定
np.random.seed(0)

# ステップ数
n_steps = 1000
# ドリフト項
drift = 0.1

# 各ステップでの変化: -1 または 1 にドリフトを加える
steps = np.random.choice([-1, 1], size=n_steps) + drift

# ランダムウォークのパスを計算
position = np.cumsum(steps)

# プロット
plt.figure(figsize=(10, 6))
plt.plot(position)
plt.title('Random Walk with Drift')
plt.xlabel('Steps')
plt.ylabel('Position')
plt.grid(True)
plt.show()

このコードでは、drift変数を導入し、各ステップでの変動に一定の値を加えています。これにより、ランダムウォークに一定の傾向が加わり、結果のパスが時間とともに上昇または下降していく様子が観察できます。

以下、実行結果です。

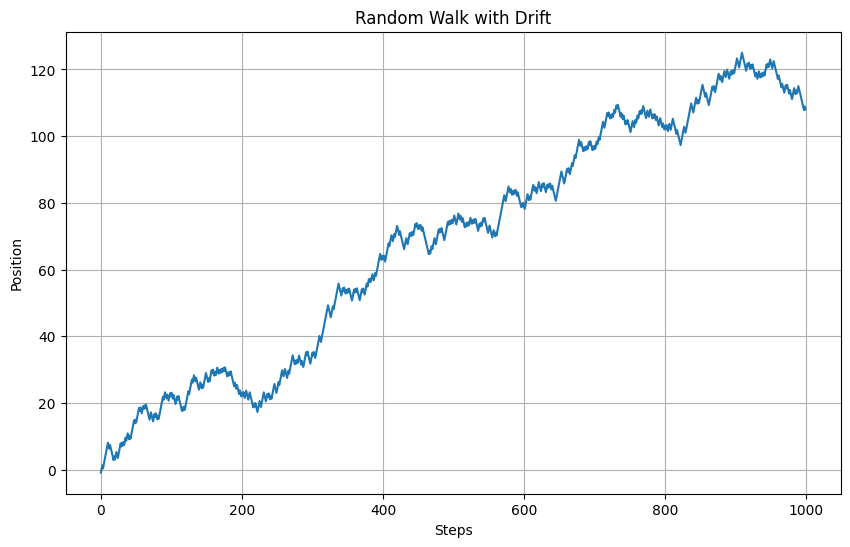
ドリフトの大きさを変えることで、モデルの長期的な傾向を調整することができます。ドリフトが正の値の場合、ランダムウォークは長期的に上昇傾向を示し、負の値の場合は下降傾向を示します。

経済データをモデル化する際には、実際のデータの長期的なトレンドを分析し、適切なドリフト値を設定することが重要です。

　トレンドと季節性を持つランダムウォーク

トレンド付きランダムウォークでは、ランダムウォークに加えて、明確な上昇または下降のトレンドが存在します。このトレンドは、経済の成長や、ある期間にわたる消費者行動の変化など、長期にわたる一定の傾向を表しています。

季節性を持つデータでは、年間や四半期ごとの周期的な変動が見られ、これらは季節による消費パターンの変化、気候の影響などによるものです。

季節性を含むトレンド付きランダムウォークモデルを構築するには、季節性の周期を考慮した上で、各周期における平均的な変動を加える必要があります。これにより、実際のデータに近い時系列データのシミュレーションが可能になります。

以下は、トレンドと季節性を含むランダムウォークのPythonによる簡単な実装例です。この例では、年間の季節性を模擬するために、特定の周期で変動する成分を追加しています。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)  # シード値を設定

n_steps = 1200  # ステップ数（例えば、100年分の月次データ）
trend = 0.05  # トレンドの強さ
seasonality = np.sin(np.linspace(0, 2 * np.pi, 12))  # 12ヶ月の季節性パターン
seasonal_effect = np.tile(seasonality, n_steps // 12)  # 季節性効果をデータ全体に適用

steps = np.random.normal(loc=trend, scale=1, size=n_steps)  # トレンドとランダムネスを含むステップ
steps += seasonal_effect[:n_steps]  # 季節性効果を加える

position = np.cumsum(steps)  # ランダムウォークのパスを計算

plt.figure(figsize=(10, 6))
plt.plot(position)
plt.title('Random Walk with Trend and Seasonality')
plt.xlabel('Steps')
plt.ylabel('Position')
plt.grid(True)
plt.show()

このコードでは、np.random.normalを使用して、各ステップにトレンドと正規分布によるランダムな変動を加えています。さらに、seasonal_effectを加えることで、周期的な季節性の効果を模擬しています。

以下、実行結果です。

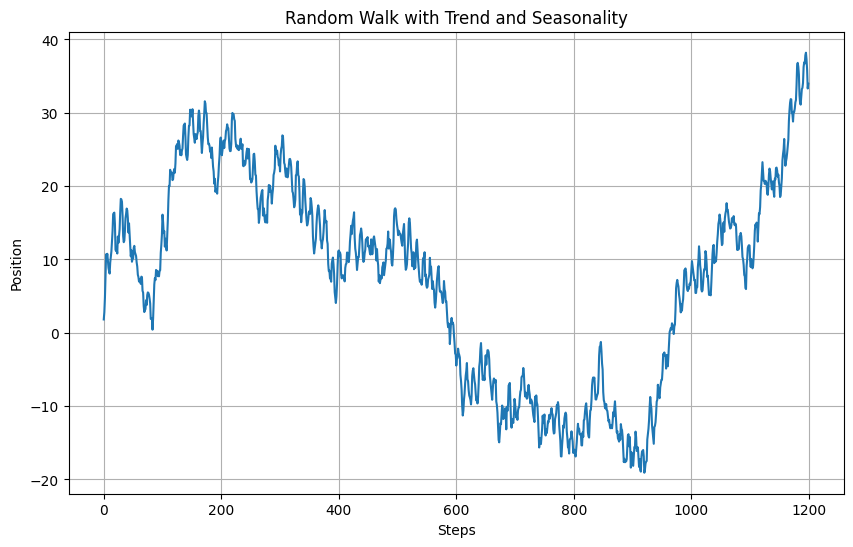
このモデルは、季節性の影響を受ける経済データや消費者行動の時系列分析に特に有効です。トレンドと季節性を考慮することで、より現実に近いデータの挙動を捉え、予測の精度を高めることが可能になります。

　幾何ブラウン運動と金融データ

幾何ブラウン運動（Geometric Brownian Motion, GBM）は、連続時間でのランダムウォークの一形式で、金融市場での株価や商品価格のモデリングに広く使用されます。

このモデルは、価格の対数が時間と共に正規分布に従うランダムウォークをすると仮定します。GBMは、価格が負になることがなく、時間の経過とともに価格の変動率が一定であることを特徴としています。

幾何ブラウン運動を用いて株価の時系列データをモデル化するPythonコードの例を示します。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)  # シード値を設定

# パラメータ設定
n_steps = 252  # 1年間の取引日数
dt = 1/n_steps  # 時間の刻み幅
mu = 0.1  # 年間の平均リターン
sigma = 0.2  # 年間のボラティリティ
S0 = 100  # 初期株価

# GBMのシミュレーション
t = np.linspace(0, 1, n_steps)  # 時間
W = np.random.standard_normal(size = n_steps)  # 標準正規分布に従う乱数
W = np.cumsum(W)*np.sqrt(dt)  # ブラウン運動
X = (mu - 0.5 * sigma**2) * t + sigma * W  # 対数リターン
S = S0 * np.exp(X)  # 株価

# プロット
plt.figure(figsize=(10, 6))
plt.plot(S)
plt.title('Geometric Brownian Motion - Stock Price')
plt.xlabel('Time (days)')
plt.ylabel('Stock Price')
plt.grid(True)
plt.show()

このコードは、初期株価を基に、1年間の株価変動を幾何ブラウン運動を使ってシミュレーションします。muは期待リターン率を、sigmaは株価のボラティリティ（リスク）を表します。

以下、実行結果です。

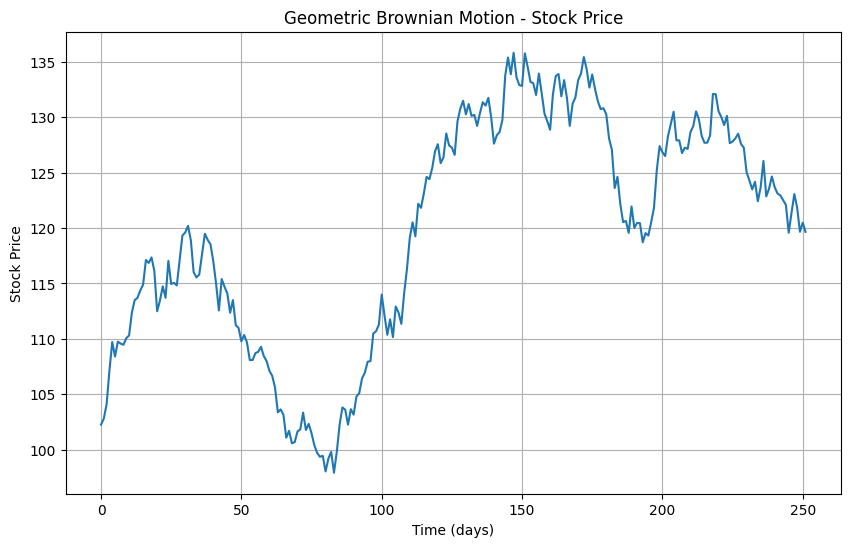
幾何ブラウン運動モデルを使用することで、様々なリスクシナリオをシミュレーションし、株価や投資ポートフォリオの将来価値の分布を評価することが可能です。このモデルは、オプション価格評価やリスク管理戦略の策定においても重要な役割を果たします。

ランダムウォークの同定方法

手元の時系列データがランダムウォークであるかどうか、そしてどの種類のランダムウォークであるかを同定するには、例えば以下の統計的仮説検定を駆使した流れで分析を進めます。

Step 1. データの観察と前処理
Step 2. ランダムウォークかどうかの判断（定常性の検定）
Step 3. ランダムウォークの種類の同定（定常性・トレンド・正規性の検定）

あくまでも一例ですのでご参考まで。

　同定の流れ

　　Step 1. データの観察と前処理

データの可視化: 時系列データをプロットして、パターンやトレンド、季節性などの初期の観察を行います。

前処理: 欠損値の処理、データの正規化や変換（対数変換など）を検討します。

　　Step 2. ランダムウォークかどうかの判断（定常性の検定）

時系列データがランダムウォーク（非定常性）を示すかどうかを判断するために、ADF検定（Augmented Dickey-Fuller test）やKPSS検定（Kwiatkowski-Phillips-Schmidt-Shin test）などの単位根検定を実施します。

ADF検定
– 帰無仮説（H0）: データは非定常性（いわゆる単位根を含む）を示す
– 対立仮説（H1）: データは定常性を示す（非定常ではない）

KPSS検定
– 帰無仮説（H0）: データは定常性を示す
– 対立仮説（H1）: データは非定常性を示す

非定常であると判定された場合、ランダムウォークの可能性がでてきます。

なぜならば、ランダムウォークが非定常だからです。もちろん、ランダムウォーク以外の非定常な時系列データはたくさんあります。

　　Step 3. ランダムウォークの種類の同定（定常性・トレンド・正規性の検定）

各種統計的検定を用いて、前述の特性を持つランダムウォークの種類を同定します。

今回は、以下のようにして同定していきます。この考え方は必ずしも十分なわけではありません（3種類のランダムウォークしか登場していない、など）ので、参考までにしてください。

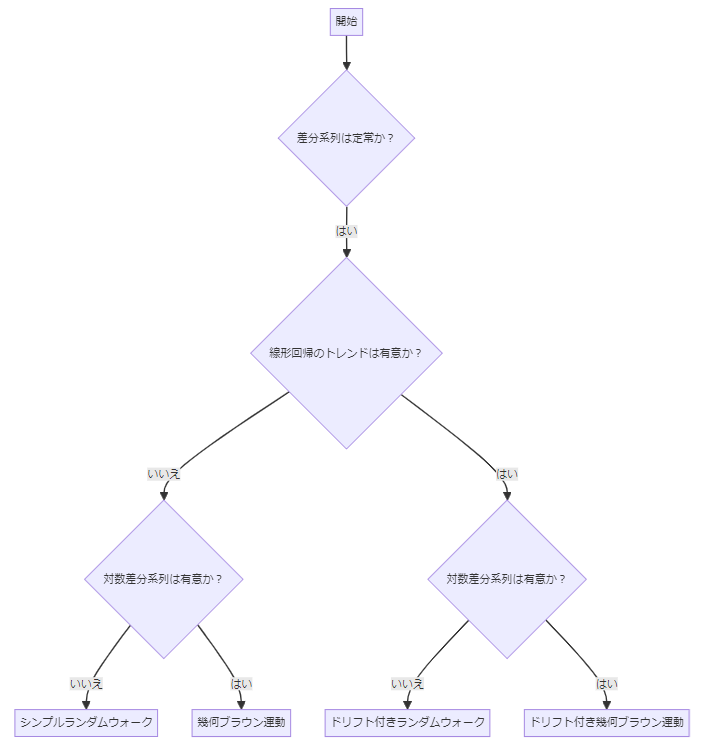
先ず、時系列の差分を取って、それが定常であるかを確認します。

差分系列が定常である場合、シンプルランダムウォークやドリフト付きランダムウォーク、幾何ブラウン運動などの可能性がでてきます。

次に、元の時系列データに対し線形回帰分析（説明変数は時間）などを実施し、トレンド成分の可能性を検討します。

もし、トレンド成分（切片）が有意である場合、それはドリフト付きランダムウォークかドリフト付き幾何ブラウン運動の可能性がでてきます。

さらに、対数変換した時系列データの差分を取り、それが正規分布に従っているかどうかを検討します。

正規分布でないという確証が得られなければ、幾何ブラウン運動としましょう。

ちなみに、幾何ブラウン運動にはドリフト（平均収益率）が付いているものが多いですが、稀にボラティリティ（変動）のみを考慮したドラフト無し幾何ブラウン運動を扱うことがあります。

　幾何ブラウン運動の例

今回利用する幾何ブラウン運動のサンプルデータを作ります。このサンプルデータは金融データ（株価など）をイメージしています。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
S0 = 100  # 初期株価
mu = 0.05  # 平均リターン
sigma = 0.2  # ボラティリティ
T = 1.0  # 時間（年単位）
dt = 0.01  # 時間の刻み幅
N = int(T / dt)  # ステップ数

# ウィーナー過程の生成
np.random.seed(42)
W = np.random.standard_normal(size=N)
W = np.cumsum(W)*np.sqrt(dt)  # スケールに合わせる

# 幾何ブラウン運動の計算
time = np.linspace(0, T, N)
S = S0 * np.exp((mu - 0.5 * sigma**2) * time + sigma * W)

このサンプルデータを用い、先ほどの5ステップを実施していきます。

Step 1. データの観察と前処理

先ず、データを観察します。

以下、コードです。

# データのプロット
plt.figure(figsize=(10, 6))
plt.plot(time, S)
plt.title('Geometric Brownian Motion')
plt.xlabel('Time')
plt.ylabel('Price')
plt.show()

以下、実行結果です。

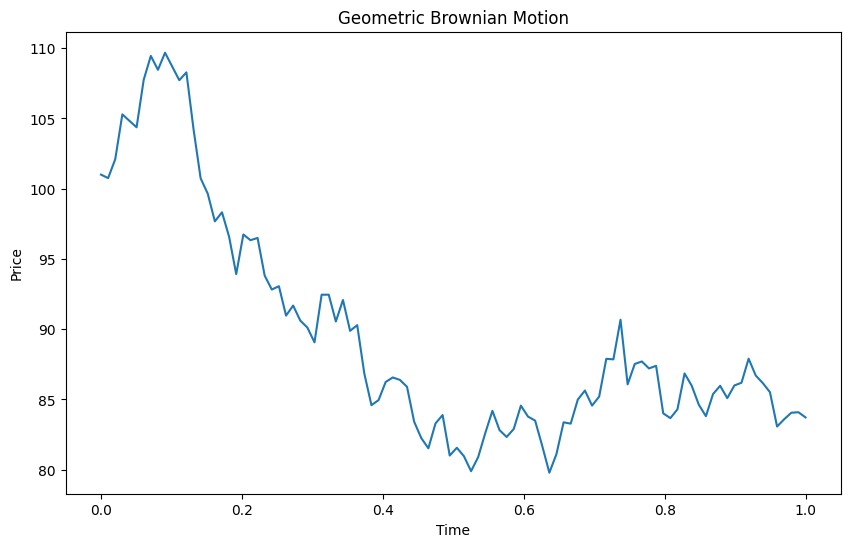
Step 2. ランダムウォークかどうかの判断（定常性の検定）

次に、定常性の検定を実施し、ランダムウォークである可能性を探ります。

以下の2つの検定を実施します。

ADF検定
KPSS検定

ADF検定をします。

以下、コードです。

'''
ADF検定
- 帰無仮説（H0）: データは非定常性（いわゆる単位根を含む）を示す
- 対立仮説（H1）: データは定常性を示す（非定常ではない）
'''

from statsmodels.tsa.stattools import adfuller

adf_result = adfuller(S) 

print('ADF Statistic: %f' % adf_result[0])
print('p-value: %f' % adf_result[1])
print('Critical Values:')
for key, value in adf_result[4].items():
    print('\t%s: %.3f' % (key, value))

以下、実行結果です。

ADF Statistic: -1.378565
p-value: 0.592508
Critical Values:
    1%: -3.498
    5%: -2.891
    10%: -2.583

ADF統計値は-1.378565であり、これは全ての臨界値（1%、5%、10%）よりも大きいです。さらに、p値は0.592508であり、これは一般に使用される有意水準0.05よりもはるかに大きいです。これらの結果から、ADF検定の帰無仮説（つまり、系列がいわゆる単位根を持つ、即ち非定常である）を棄却することはできません。

したがって、この時系列データは非定常であると結論付けることができます。

KPSS検定を実施します。

以下、コードです。

'''
KPSS検定
- 帰無仮説（H0）: データは定常性を示す
- 対立仮説（H1）: データは非定常性を示す
'''

from statsmodels.tsa.stattools import kpss

kpss_test = kpss(S)
kpss_test

以下、実行結果です。

(1.167869745885551,
 0.01,
 5,
 {'10%': 0.347, '5%': 0.463, '2.5%': 0.574, '1%': 0.739})

KPSS統計値は1.167869745885551であり、この値は全ての臨界値（1%、5%、10%）よりも大きいです。p値0.01は有意水準0.05より小さいため、KPSS検定では帰無仮説を棄却し、つまりデータが定常ではないことを示す結果が得られました。

これらADF検定とKPSS検定の結果から、この時系列データは非定常であると結論付けることができます。

これはデータが時間経過とともにその統計的特性（平均や分散など）が変化していることを示しています。したがって、このデータを分析するときは、その非定常性を考慮に入れる必要があります。

非定常性は、ランダムウォークなど、時間経過とともにその統計的特性（平均や分散など）が変化するような時系列データに特有の性質です。

したがって、検定結果から、これらのデータがランダムウォークである可能性があります。ただし、非定常性はランダムウォークだけでなく、トレンドありや季節性を持つ時系列、分散が時間依存性を持つ（例えば、ボラティリティクラスタリング）時系列にも見られます。

さらなる統計的検定を実施し、どのランダムウォークなのかを確かめます。

Step 3. ランダムウォークの種類の同定（定常性・トレンド・正規性の検定）

差分系列が定常かどうかを検定します。ADF検定とKPSS検定の両方を実施します。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.stattools import kpss

# データの差分を取る
S_diff = np.diff(S)

# ADF検定の実行
adf_test = adfuller(S_diff)
print('ADF p-value: %f' % adf_test[1])

# KPSS検定の実行
kpss_result_diff = kpss(S_diff)
print('KPSS p-value: %f' % kpss_result_diff[1])

以下、実行結果です。

ADF p-value: 0.000000
KPSS p-value: 0.100000

ADF検定の結果、p値は0.0です。これは0.05よりも小さく、私たちが帰無仮説（つまり、データは非定常である）を棄却できることを意味します。したがって、差分系列は定常であると考えられます。

一方、KPSS検定では、p値は0.1であり、これは0.05よりも大きいです。したがって、帰無仮説（データは定常である）を棄却することはありません。

これらのADFとKPSSの両方の検定から、差分系列が定常であると結論付けることができます。

ただ、シンプルなランダムウォークなのか、ドリフト付きなのか、どのようなランダムウォークなのかまでは不明です。

時系列データに対して線形回帰分析を行い、トレンド（ドリフト）成分の存在を確認します。

以下、コードです。

from statsmodels.regression.linear_model import OLS
import statsmodels.api as sm

# 時系列の差分データに対する線形回帰
t = np.arange(len(S))
X = sm.add_constant(t)  # 定数項（バイアス）を追加
model = OLS(S, X).fit()

# 回帰結果の要約を表示
print(model.summary())

以下、実行結果です。

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.580
Model:                            OLS   Adj. R-squared:                  0.576
Method:                 Least Squares   F-statistic:                     135.5
Date:                Sun, 10 Mar 2024   Prob (F-statistic):           3.50e-20
Time:                        11:42:38   Log-Likelihood:                -306.55
No. Observations:                 100   AIC:                             617.1
Df Residuals:                      98   BIC:                             622.3
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const        100.1063      1.041     96.203      0.000      98.041     102.171
x1            -0.2114      0.018    -11.640      0.000      -0.247      -0.175
==============================================================================
Omnibus:                        5.129   Durbin-Watson:                   0.099
Prob(Omnibus):                  0.077   Jarque-Bera (JB):                2.826
Skew:                           0.173   Prob(JB):                        0.243
Kurtosis:                       2.253   Cond. No.                         114.
==============================================================================

この回帰分析の結果から、以下の結論を導き出すことができます。

「R-squared」(決定係数)の値が0.580であることから、選択した1つの独立変数（時間）が従属変数（価格）の変動の58%を説明していることを意味します。これは、一方の変数が他方の変数とどの程度の関係を持っているかを定量化します。

「coef」（係数）が-0.2114であることから、時間の単位増加ごとに、価格が平均で-0.2114減少することを示しています。これは、データにネガティブなトレンド（つまり価格の低下）が存在することを示しています。

「p-value: 0.000」は価格と時間の間に強い統計的関連性があることを示しています。つまり、有意水準0.05以下であるため、帰無仮説（時間と価格の間に関連性はない）を棄却し、価格が時間とマイナスの相関があると結論付けることができます。

以上より、この時系列データは時間とともに減少するトレンドを持つことが確認できます。

ここまでの結果から、ドリフト付きランダムウォーク、もしくは、ドリフト付き幾何ブラウン運動の可能性がでてきました。

幾何ブラウン運動データの対数変換された時系列データの差分（対数リターン）は正規分布に従います。

ということで、対数変換した時系列データの差分を取り、それが正規分布に従っているかの検定（今回はシャピロ・ウィルク検定）を行います。

ちなみに、シャピロ・ウィルク検定は、データが正規分布に従っているかどうかを検定する際に使用される統計的手法です。

帰無仮説(H0)と対立仮説(H1)は以下のように設定されます。

帰無仮説(H0): データは正規分布に従っている
対立仮説(H1): データは正規分布に従っていない

p値が有意水準(通常5%や1%など)より小さい場合、帰無仮説は棄却され、対立仮説「データは正規分布に従っていない」を採択します。

一方、p値が有意水準以上であれば、帰無仮説を棄却できず、正規分布からの逸れは有意ではないと判断されます。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import shapiro

# 対数変換された時系列データの差分を計算
log_returns = np.diff(np.log(S))

# 正規性検定（シャピロ・ウィルク検定）
shapiro_test = shapiro(log_returns)

print(f'Shapiro-Wilk test statistic = {shapiro_test[0]}, p-value = {shapiro_test[1]}')

以下、実行結果です。

Shapiro-Wilk test statistic = 0.9897328019142151, p-value = 0.6498544216156006

ここでのシャピロ・ウィルク検定の統計量は0.9897328019142151で、対応するp値は0.6498544216156006です。

通常、p値が0.05より小さい場合、我々は帰無仮説を棄却し、代わりに対立仮説（即ち、データは正規分布から得られていない）を受け入れます。

帰無仮説(H0): データは正規分布に従っている
対立仮説(H1): データは正規分布に従っていない

しかし、この場合、p値は0.05よりも大きいため、帰無仮説を棄却することはありません。

従って、この検定結果は、対数変換した時系列データの差分が正規分布に従う可能性が高いことを示しています。

この結果から、幾何ブラウン運動データであると判断します。

幾何ブラウン運動のパラメータを推定するために、まず対数リターンの計算を行います。その後、それぞれ時間経過に対する平均リターンとボラティリティを推定します。これらの推定値は、それぞれログリターンの平均値と標準偏差に相当します。

この推定値と共にデータをモデリングするためのモンテカルロシミュレーションも行います。最後に、実際のデータとモデリングした推定値を比較します。

先ず、パラメータの推定を行います。

以下、コードです。

# 対数リターンの計算
log_returns = np.log(S[1:]) - np.log(S[:-1])

# ドリフト（mu）と拡散（sigma）の推定
mu = log_returns.mean()
sigma = log_returns.std()

# パラメータの表示
mu, sigma

以下、実行結果です。

(-0.0018952254328122383, 0.018122802555777143)

推定された平均リターン（μ）は -0.001895で、ボラティリティ（σ）は 0.01812です。

　おまけ（VaRとBlack-Scholesモデル）

幾何ブラウン運動と言えば株価などの金融データです。

ということで、おまけとして株価などの価格データとして想定して近未来分析を進めていきます。

先ほど推定した平均リターンとボラティリティを用いて、複数の将来の価格パスを生成することで、リスク管理のためのシミュレーションを行い、将来の価格分布を推定することが可能です。

具体的には、幾何ブラウン運動に基づくランダムウォークを生成し、各期間における分布をシミュレーションします。

これからVaRとBlack-Scholesモデルという金融工学の概念が登場しますが、詳しい説明は割愛します。

先ず、VaR（Value at Risk）やCVaR（Conditional Value at Risk）などの価格下落リスク指標を評価します。

ちなみに、VaRはある確信水準での最大損失を、CVaRはVaRを超える損失の平均値を示す指標であり、どちらも金融リスク管理において広く利用されています。

以下、コードです。10000回のモンテカルロシミュレーションを実施し、リスク評価しています。

# ランダムシードの設定
np.random.seed(42)

# シミュレートするパスの数
num_paths = 10000

# 時間ステップ
dt = T/N
t = np.linspace(0, T, N)

# パスを格納するための配列の初期化
S_sim = np.zeros((num_paths, N))

# 初期価格の設定
S_sim[:, 0] = S0

# モンテカルロシミュレーション
for path in range(num_paths):
    W = np.random.standard_normal(size=N)
    W = np.cumsum(W)*np.sqrt(dt)  # スケールされたウィーナープロセス
    S_sim[path] = S0 * np.exp((mu - 0.5 * sigma**2) * t + sigma * W)  # 幾何ブラウン運動

# 最終価格の配列
final_prices = S_sim[:, -1]

# Value-at-Risk (VaR) at 95% confidence level
var_95 = np.percentile(final_prices, 5)

# Conditional Value-at-Risk (CVaR) at 95% confidence level
cvar_95 = final_prices[final_prices <= var_95].mean()

var_95, cvar_95

以下、実行結果です。

(96.83931530686587, 96.09071227415316)

VaRの値96.84は、価格が96.84以下になる確率が5%であることを示しています。5%の確率で価格が96.84以下に下落するリスクがあると解釈されます。

CVaRの値96.09は、価格がVaRの96.84よりも低い場合の平均的な価格（つまり96.09）を示しています。価格が96.84以下になる場合の平均的な価格は96.09であると解釈されます。

さらに、Black-Scholesモデル（オプション価格評価モデルの1つ）を用いて、オプションの公正価値を計算します。

今回はパラメータを以下のように設定しました。

S = S0: 現在の資産価格。ここでは、S0は解析データ中における資産の初期価格です。
K = 100: オプションのストライク価格を示します。この価格がオプションを行使する際の価格となります。
T = 1: オプションが満期になるまでの期間を年単位で表します。ここでは1年と設定されています。
r = 0.01:リスクフリーレートです。ここでは年利1%が設定されています。
sigma : 資産のボラティリティ。この値は、以前の計算で求めたsigmaの値を設定します。

以下、コードです。

import numpy as np
from scipy.stats import norm

# Black-Scholesの公式をオプション価格算定用に
def black_scholes(S, K, T, r, sigma):
    """
    Parameters:
        S: Current price of the underlying asset
        K: Strike price of the option
        T: Time until option maturity (in years)
        r: Risk-free interest rate
        sigma: Volatility of the underlying asset
    Returns: Option price
    """
    # d1とd2パラメータの計算
    d1 = (np.log(S / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
    d2 = (np.log(S / K) + (r - 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
    
    # オプション価格の計算
    option_price = (S * norm.cdf(d1, 0, 1) - K * np.exp(-r * T) * norm.cdf(d2, 0, 1))

    return option_price

# パラメータ設定
S = S0          # 現在の資産価格
K = 100         # ストライク価格
T = 1           # 満期までの期間（年）
r = 0.01        # リスクフリーレート
sigma = sigma   # 基礎資産のボラティリティ

# オプション価格の計算
option_price = black_scholes(S, K, T, r, sigma)
option_price

以下、実行結果です。

1.3237135913184233

Black-Scholesモデルを用いて計算したオプション（ヨーロピアンコールオプション）の公正価格は約1.32です。

市場でのオプションの実際の価格が1.32よりも低い場合、オプションは理論価格よりも割安とみなすことができます。そのため、投資機会として購入を検討するかもしれません。

逆に、1.32よりも高い場合は、オプションが過大評価されている可能性があり、購入を避けるか、売却を検討するかもしれません。

ちなみに、オプション取引とは、特定の資産（株式、債券、商品、指数など）を将来の特定の日（満期日）にあらかじめ定められた価格（ストライク価格）で購入または売却する権利を取引する金融取引です。

まとめ

今回は、「様々な時系列ランダムウォークと近未来分析」というお話しをしました。

ランダムウォークは、株価変動、消費者行動のパターン、製品の需要予測など、ビジネスに関連する多様な現象をモデル化するのに使用される時系列データです。

シンプルなランダムウォークから、ドリフトやトレンド、季節性を取り入れたより複雑なモデルに至るまで、さまざまなランダムウォークモデルの種類を紹介しました。

ランダムウォークモデルを理解し適用することで、ビジネスリーダーやデータサイエンティストは、市場の不確実性の中でより情報に基づいた戦略的な決定を行うことができることでしょう。