【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第4回】Pythonによる大域的最適化のハイブリッド手法 –

本連載では、Pythonを用いた非線形計画問題の大域的最適化手法について、これまで3回にわたって解説してきました。

第1回では非線形計画問題と大域的最適化の基礎的な概念を取り上げました。

第2回ではメタヒューリスティクスを中心とした確率的手法を取り上げました。

第3回では区間分割法や分枝限定法などの決定論的手法を取り上げました。

しかし、実際の問題に対して単一の手法を適用するだけでは、効率的に高品質な解を得ることが難しい場合があります。

そこで、今回は、複数の手法を組み合わせたハイブリッド手法に着目します。

ハイブリッド手法は、メタヒューリスティクスと決定論的手法の長所を活かし、短所を補い合うことで、より効果的に大域的最適解を求めることができます。

Contents

ハイブリッド手法とは
　決定論的手法とメタヒューリスティクスの分類
　ハイブリッド手法の組み合わせ方
　ハイブリッド手法のメリットとデメリット
ハイブリッド最適化アルゴリズムの設計
　メタヒューリスティクスとローカルサーチの組み合わせ
　　制約なし非線形計画問題
　　制約付き非線形計画問題
　グローバルサーチとローカルサーチの組み合わせ
　　制約なし非線形計画問題
　　制約付き非線形計画問題
　メタヒューリスティクス、グローバルサーチ、ローカルサーチの組み合わせ
　　制約なし非線形計画問題
　　制約付き非線形計画問題
　ハイブリッド最適化の実装上の留意点とテクニック
ハイブリッド手法の性能評価と考察
　ハイブリッド手法の評価方法
　各手法の選択とパラメータ設定の影響
　ハイブリッド手法の性能比較と考察
　ハイブリッド手法の適用上の留意点
まとめ

ハイブリッド手法とは

ハイブリッド手法は、複数の最適化手法を組み合わせることで、それぞれの手法の長所を活かし、短所を補い合う最適化手法です。

ここでは、ハイブリッド手法の概要、決定論的手法とメタヒューリスティクスの分類、ハイブリッド手法の組み合わせ方、メリットとデメリット、適用領域について説明します。

　決定論的手法とメタヒューリスティクスの分類

最適化手法は、決定論的手法とメタヒューリスティクス（グローバルサーチ）に大別されます。決定論的手法には、ローカルサーチとグローバルサーチがあります。

手法	特徴	大域的最適解の保証	解を得るまでの時間
決定論的手法ローカルサーチ	与えられた初期点から始めて、近傍の点を探索しながら最適解を求める SciPyの最適化手法、CyIPOPT	×	比較的短い
決定論的手法グローバルサーチ	探索空間全体を対象とし、大域的最適解を求める区間分割法、分枝限定法、リプシッツ最適化	○	膨大な時間が必要になることがある
メタヒューリスティクス（グローバルサーチ）	自然現象や生物の行動を模倣した確率的な探索手法大域的最適解の発見に優れている	△	決定論的手法のグローバルサーチに比べ短い

決定論的手法のローカルサーチは、与えられた初期点から始めて、近傍の点を探索しながら最適解を求める手法です。大域的最適解ではなく局所的最適解を求めるアルゴリズムです。第1回で紹介したSciPyを利用したやり方や、次回紹介するCyIPOPTを利用したやり方などがあります。

一方、決定論的手法のグローバルサーチは、探索空間全体を対象とし、大域的最適解を求める手法で、区間分割法、分枝限定法、リプシッツ最適化などがこれに当たります。大域的最適解を求めることができますが、解を得るまでに膨大な時間が必要になることがあります。第3回に紹介しました。

メタヒューリスティクス（グローバルサーチ）は、自然現象や生物の行動を模倣した確率的な探索手法で、大域的最適解の発見に優れており、グローバルサーチの一種とみなすことができます。大域的最適解であることを保証しませんが、決定論手法のグローバルサーチに比べ解を得るまでの時間が短くなります。

　ハイブリッド手法の組み合わせ方

ハイブリッド手法では、以下のような組み合わせ方が考えられます。

組み合わせ方	手順
メタヒューリスティクス + ローカルサーチ	メタヒューリスティクスで大域的な探索を行い、良好な解の候補を見つけるローカルサーチで局所的な探索を行う
グローバルサーチ + ローカルサーチ	区間分割法、分枝限定法、リプシッツ最適化などのグローバルサーチで大域的な探索を行い、良好な解の候補を見つけるローカルサーチで局所的な探索を行う
メタヒューリスティクス + グローバルサーチ + ローカルサーチ	メタヒューリスティクスで大域的な探索を行い、良好な解の候補を見つけるグローバルサーチでさらに探索を行うローカルサーチで解を洗練する

　ハイブリッド手法のメリットとデメリット

ハイブリッド手法のメリットは以下の通りです。

大域的探索能力と局所的探索能力を併せ持つことで、より効率的に高品質な解を求められる。
単一の手法よりもロバスト性が高く、様々な問題に適用可能。

一方、デメリットは以下の通りです。

アルゴリズムの設計や実装が複雑になる。
各手法のパラメータ調整が難しい場合がある。
問題によっては、単独手法よりも計算時間がかかる場合がある。

ハイブリッド手法は、以下のような問題に適しています。

大域的最適解の発見が難しい問題
局所的最適解が多数存在する問題
高品質な解が求められる問題
計算時間に余裕がある問題

ハイブリッド最適化アルゴリズムの設計

ハイブリッド最適化アルゴリズムを設計する際は、問題の特性や要求される解の品質、計算時間の制約などを考慮して、適切な手法の組み合わせを選択する必要があります。

ここでは、代表的な組み合わせ方とその実装例について説明します。

　メタヒューリスティクスとローカルサーチの組み合わせ

メタヒューリスティクスとローカルサーチを組み合わせることで、大域的探索能力と局所的探索能力を併せ持つアルゴリズムを設計できます。

アルゴリズムの設計方針

グローバル探索の実施: メタヒューリスティックスを使用して、探索空間全体から良好な解の候補を見つけ出します。
ローカルサーチの適用: メタヒューリスティックスで見つけた解を初期点として、ローカルサーチを適用し解の質をさらに向上させます。
結果の比較と更新: ローカルサーチ後の解が以前の解よりも良い場合、最良解を更新します。
反復処理: 上記のプロセスを繰り返し、改善が見られなくなるまで、または特定の反復回数に達するまで実行します。

　　制約なし非線形計画問題

前回同様、多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は $(x_0,x_1)=(-3,4)$ で、最適値は 0 です。

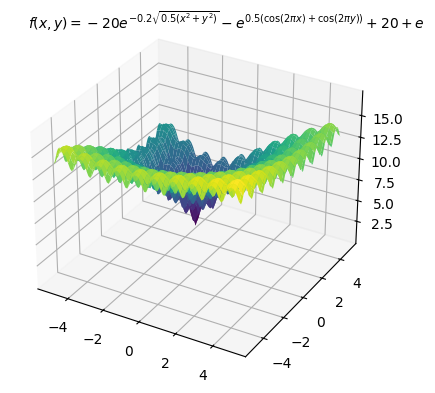
以下、コードです。変数の上下限制約のみ入れています。

import numpy as np
import pygmo as pg
from scipy.optimize import minimize

#
# 目的関数などの定義
#

# 目的関数
def objective(x):
    a = 20  # 定数a
    b = 0.2  # 定数b
    c = 2 * np.pi  # 定数c
    n = len(x)  # 入力xの要素数
    x_offset = np.array([x[0] + 3, x[1] - 4])  # xのオフセット調整
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))  # 二乗の合計項
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))  # cos項
    return sum_sq_term + cos_term + a + np.e  # 関数の合計値を返す

# 最適化する変数の下限と上限
bounds = ((-5, 5), (-5, 5))

#
# メタヒューリスティクスの設定
#

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        return [objective(x)]  # 評価関数
    
    def get_bounds(self):
        return ([-100, -100], [100, 100])  # xの上下界を設定

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# アルゴリズムを設定
algo = pg.algorithm(pg.de(gen=100))

# 初期個体群を生成
pop = pg.population(prob, 20)

#
# 最適解を探索
#

for i in range(10):
    pop = algo.evolve(pop)  # メタヒューリスティック
    best_x = pop.champion_x  # 最良解
    best_f = pop.champion_f[0]  # 最良評価値
    
    # ローカルサーチ
    result = minimize(
        objective, 
        best_x, 
        bounds=bounds,
        method='SLSQP')

    # 最適解の更新  
    if result.fun < best_f:  # もし改善されたら、
        best_x = result.x  # 最良解を更新
        best_f = result.fun  # 最良評価値を更新

# 結果を表示
print(f"Best solution: {best_x}")
print(f"Best objective value: {best_f}")

このコードを説明します。

目的関数などの定義

目的関数(objective): この関数は最小化したい対象で、入力xに対してスカラー値を返します。
変数の範囲(bounds)：変数の上下界を指定。

メタヒューリスティクスの設定

カスタム問題クラス(CustomProblem): PyGMOで最適化を行うために、最適化する問題を定義するクラスです。fitnessメソッドは目的関数の値を計算し、get_boundsメソッドで変数の上下界を指定します。
PyGMO問題オブジェクトとアルゴリズム: ここではCustomProblemをPyGMOの問題オブジェクトに変換し、差分進化アルゴリズム(DE)を用いて最適化を行います。DEは進化的アルゴリズムの一種で、特に連続値最適化問題において効果的です。
初期個体群の生成: 初期個体群を20個生成し、これを最適化の出発点とします。

最適解の探索

メタヒューリスティクスとローカルサーチ: メインループ内で、まずDEによるグローバルサーチを行い、得られた最良解に対してSciPyのminimize関数（SLSQP法）を用いたローカルサーチを実施します。これにより、グローバルサーチによる探索とローカルサーチによる精密化を組み合わせた最適化戦略を実現しています。
結果の更新と表示: 各イテレーションで、最良解とその目的関数値を更新し、最終的に最適な解とその評価値を出力します。

以下、実行結果です。

Best solution: [<span>-2.99999997 4.00000002</span>]
Best objective value: <span>9.064115902290837e-08</span>

以下は小数点2桁目を四捨五入した結果です。

最適解（Optimal solution）： $(x_0,x_1)=(-3.0,4.0)$
最適値（Optimal value）：0.0

　　制約付き非線形計画問題

前回同様、以下の非線形計画問題を扱います。最適解は $(x_0,x_1)=(1,1)$ で、最適値は $0$ です。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

制約条件はペナルティとして目的関数に組み込み最適化します。

以下、コードです。

import numpy as np
import pygmo as pg
from scipy.optimize import minimize

#
# 目的関数などの定義
#

# 目的関数
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] - 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

cons = ({'type': 'ineq', 'fun': constraint1},
        {'type': 'ineq', 'fun': constraint2},
        {'type': 'ineq', 'fun': constraint3})

# 最適化する変数の下限と上限
bounds = ((-5, 5), (-5, 5))

# 制約違反のペナルティを計算する関数
def calculate_penalty(x):
    c1 = constraint1(x)
    c2 = constraint2(x)
    c3 = constraint3(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

#
# メタヒューリスティクスの設定
#

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値とペナルティを合計
        obj = objective(x)
        penalty = calculate_penalty(x)
        return [obj + penalty * 1e10]  # ペナルティの重みを調整

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# アルゴリズムを設定
algo = pg.algorithm(pg.de(gen=100))

# 初期個体群を生成
pop = pg.population(prob, 20)

#
# 最適解を探索
#

for i in range(10):
    pop = algo.evolve(pop)  # メタヒューリスティック
    best_x = pop.champion_x  # 最良解
    best_f = pop.champion_f[0]  # 最良評価値
    
    # ローカルサーチ
    result = minimize(
        objective, 
        best_x,
        bounds=bounds,
        constraints=cons, 
        method='SLSQP')

    # 最適解の更新  
    if result.fun < best_f:  # もし改善されたら、
        best_x = result.x  # 最良解を更新
        best_f = result.fun  # 最良評価値を更新

# 結果を表示
print(f"Best solution: {best_x}")
print(f"Best objective value: {best_f}")

以下、実行結果です。

Best solution: [<span>0.9999861 0.99997051</span>]
Best objective value: <span>4.762737533284361e-10</span>

以下は小数点2桁目を四捨五入した結果です。

最適解（Optimal solution）： $(x_0,x_1)=(1.0,1.0)$
最適値（Optimal value）：0.0

　グローバルサーチとローカルサーチの組み合わせ

グローバルサーチとローカルサーチを組み合わせることで、より効率的に大域的最適解を求めることができます。今回は、グローバルサーチとして分枝限定法を使ったやり方でいきます。

アルゴリズムの設計方針

サブ問題の生成: 分岐限定法で問題空間を小さなサブ問題に分割します。
サブ問題の解析: ローカルサーチで各サブ問題の局所最適解を高速に求めます。
優先度付きキュー: 最も有望なサブ問題を優先的に解くために優先度付きキューを使用します。
最良解の更新: 新たな解が現在の最良解より良い場合、最良解を更新します。
終了条件: サブ問題の探索範囲が許容誤差以下になったら探索を終了します。

　　制約なし非線形計画問題

先ほどと同様、多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は $(x_0,x_1)=(-3,4)$ で、最適値は 0 です。

以下、コードです。変数の上下限制約のみ入れています。

from typing import Tuple, Callable
import numpy as np
import heapq
from scipy.optimize import minimize

# 目的関数の定義
def objective(x):
    a = 20  # 定数a
    b = 0.2  # 定数b
    c = 2 * np.pi  # 定数c
    n = len(x)  # 入力xの要素数
    x_offset = np.array([x[0] + 3, x[1] - 4])  # xのオフセット調整
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))  # 二乗の合計項
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))  # cos項
    return sum_sq_term + cos_term + a + np.e  # 関数の合計値を返す

# 分岐限定法の関数を定義（中でローカルサーチを実施）
def branch_and_bound(f: Callable[[np.ndarray], float], x_range: Tuple[Tuple[float, float], Tuple[float, float]], eps: float) -> Tuple[np.ndarray, float]:
    best_solution = None
    best_value = float('inf')
    
    # 初期区間での最適化を行い、キューに追加
    initial_guess = np.array([(a + b) / 2 for a, b in x_range])
    res = minimize(
        f, 
        initial_guess, 
        bounds=x_range, 
        method='L-BFGS-B')
    if res.success:
        mid = res.x
        f_mid = res.fun
        queue = [(-f_mid, x_range)]
    else:
        return None, None  # 初期最適化が失敗した場合

    while queue:
        _, current_range = heapq.heappop(queue)

        # 分割した区間で最適化を行い、評価
        for i in range(len(current_range)):
            a, b = current_range[i]
            if b - a > eps:
                left_range = list(current_range)
                right_range = list(current_range)
                
                # 区間を半分に分割
                mid_point = (a + b) / 2
                left_range[i] = (a, mid_point)
                right_range[i] = (mid_point, b)
                
                # 左側の区間で最適化
                res_left = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in left_range]), 
                    bounds=left_range, 
                    method='L-BFGS-B')
                if res_left.success:
                    heapq.heappush(queue, (-res_left.fun, tuple(left_range)))
                    if res_left.fun < best_value:
                        best_solution = res_left.x
                        best_value = res_left.fun
                
                # 右側の区間で最適化
                res_right = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in right_range]), 
                    bounds=right_range, 
                    method='L-BFGS-B')
                if res_right.success:
                    heapq.heappush(queue, (-res_right.fun, tuple(right_range)))
                    if res_right.fun < best_value:
                        best_solution = res_right.x
                        best_value = res_right.fun

    return best_solution, best_value

#
# 最適解を探索
#

# 探索範囲とパラメータの定義
x_range = ((-5, 5), (-5, 5)) # 探索範囲を設定
eps = 0.1  # 許容誤差を設定

# 分岐限定法を実行（中でローカルサーチを実施）
result, value = branch_and_bound(objective, x_range, eps)

# 結果を表示
print(f"Best solution: {result}")
print(f"Best objective value: {value}")

このコードを説明します。

目的関数の定義

目的関数(objective): この関数は最小化したい対象で、入力xに対してスカラー値を返します。

分岐限定法の関数の定義

関数branch_and_bound: この関数は、分岐限定法を用いて与えられた目的関数fの最小値を見つける主要なアルゴリズムです。関数は目的関数f、探索範囲x_range、そして許容誤差epsを引数に取ります。
- 初期化: 初期区間における最適化問題を解き、その解を優先度付きキュー（最小ヒープ）に追加します。この時、SciPyのminimize関数を用いており、方法としてL-BFGS-Bを選択しています。
- 探索ループ: キューが空になるまで、最適化問題のサブセットを取り出し、それをさらに細分化して新たなサブ問題を生成し、解きます。各ステップで、探索範囲を半分に分割して新たなサブ問題を作り、それぞれに対して最適化を実施します。このプロセスを繰り返すことで、最適解に近づきます。
- 更新と終了: 各サブ問題に対する最適化が成功した場合、その解と目的関数値を評価し、現在の最良解よりも良い場合は更新します。また、新たなサブ問題が許容誤差epsよりも大きい場合にのみ、さらに分割して探索を続けます。

最適解の探索

探索範囲とパラメータの定義：x_range = ((-5, 5), (-5, 5)): 探索範囲をxとyの両方で-5から5に設定。eps = 1: 許容誤差を1に設定。
分岐限定法の実行：result, value = branch_and_bound(objective, x_range, eps): 分岐限定法を用いてobjective関数の最小値を探索。
結果の表示：print(f"Best solution: {result}"): 最適解（変数の値）を表示。print(f"Best objective value: {value}"): 最適解の目的関数値を表示。

以下、実行結果です。

Best solution: [-3.  4.]
Best objective value: 1.847312081082464e-09

以下は小数点2桁目を四捨五入した結果です。

最適解（Optimal solution）： $(x_0,x_1)=(-3.0,4.0)$
最適値（Optimal value）：0.0

　　制約付き非線形計画問題

先ほどと同様、以下の非線形計画問題を扱います。最適解は $(x_0,x_1)=(1,1)$ で、最適値は $0$ です。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

制約条件はペナルティとして目的関数に組み込み最適化します。

以下、コードです。

from typing import Tuple, Callable
import numpy as np
import heapq
from scipy.optimize import minimize

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] - 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

cons = ({'type': 'ineq', 'fun': constraint1},
        {'type': 'ineq', 'fun': constraint2},
        {'type': 'ineq', 'fun': constraint3})

# 制約違反のペナルティを計算する関数
def calculate_penalty(x):
    c1 = constraint1(x)
    c2 = constraint2(x)
    c3 = constraint3(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

# ペナルティを加えた目的関数を再定義
def objective_with_penalty(x):
    obj = objective(x)
    penalty = calculate_penalty(x)
    return obj + penalty * 1e10

# 分岐限定法の関数を定義（中でローカルサーチを実施）
def branch_and_bound(f: Callable[[np.ndarray], float], x_range: Tuple[Tuple[float, float], Tuple[float, float]], eps: float) -> Tuple[np.ndarray, float]:
    best_solution = None
    best_value = float('inf')
    
    # 初期区間での最適化を行い、キューに追加
    initial_guess = np.array([(a + b) / 2 for a, b in x_range])
    res = minimize(
        f, 
        initial_guess, 
        bounds=x_range, 
        method='L-BFGS-B')
    if res.success:
        mid = res.x
        f_mid = res.fun
        queue = [(-f_mid, x_range)]
    else:
        return None, None  # 初期最適化が失敗した場合

    while queue:
        _, current_range = heapq.heappop(queue)

        # 分割した区間で最適化を行い、評価
        for i in range(len(current_range)):
            a, b = current_range[i]
            if b - a > eps:
                left_range = list(current_range)
                right_range = list(current_range)
                
                # 区間を半分に分割
                mid_point = (a + b) / 2
                left_range[i] = (a, mid_point)
                right_range[i] = (mid_point, b)
                
                # 左側の区間で最適化
                res_left = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in left_range]), 
                    bounds=left_range, 
                    method='L-BFGS-B')
                if res_left.success:
                    heapq.heappush(queue, (-res_left.fun, tuple(left_range)))
                    if res_left.fun < best_value:
                        best_solution = res_left.x
                        best_value = res_left.fun
                
                # 右側の区間で最適化
                res_right = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in right_range]), 
                    bounds=right_range, 
                    method='L-BFGS-B')
                if res_right.success:
                    heapq.heappush(queue, (-res_right.fun, tuple(right_range)))
                    if res_right.fun < best_value:
                        best_solution = res_right.x
                        best_value = res_right.fun

    return best_solution, best_value

#
# 最適解を探索
#

# 探索範囲とパラメータの定義
x_range = ((-5, 5), (-5, 5)) # 探索範囲を設定
eps = 1  # 許容誤差を設定

# 分岐限定法を実行（中でローカルサーチを実施）
result, value = branch_and_bound(objective_with_penalty, x_range, eps)

# 結果を表示
print(f"Best solution: {result}")
print(f"Best objective value: {value}")

以下、実行結果です。

Best solution: [<span>0.99999738 0.99999477</span>]
Best objective value: <span>6.8841060803455755e-12</span>

以下は小数点2桁目を四捨五入した結果です。

最適解（Optimal solution）： $(x_0,x_1)=(1.0,1.0)$
最適値（Optimal value）：0.0

　メタヒューリスティクス、グローバルサーチ、ローカルサーチの組み合わせ

メタヒューリスティクス、グローバルサーチ、ローカルサーチを組み合わせることで、より高度なハイブリッド最適化アルゴリズムを設計できます。

アルゴリズムの設計方針

解の候補を探索: メタヒューリスティクスを使用して、広範囲から良好な解の候補を見つけます。
サブ問題の生成: メタヒューリスティックスで見つけた解を初期点として、分岐限定法で問題空間を小さなサブ問題に分割します
サブ問題の解析: ローカルサーチで各サブ問題の局所最適解を高速に求めます。
優先度付きキュー: 最も有望なサブ問題を優先的に解くために優先度付きキューを使用します。
最良解の更新: 新たな解が現在の最良解より良い場合、最良解を更新します。
終了条件: サブ問題の探索範囲が許容誤差以下になったら探索を終了します。

　　制約なし非線形計画問題

以下、コードです。変数の上下限制約のみ入れています。

import numpy as np
import pygmo as pg
import heapq
from scipy.optimize import minimize
from typing import Tuple, Callable

#
# 分岐限定法の関数を定義（ローカルサーチを中で実施）
#
def branch_and_bound(f: Callable[[np.ndarray], float], x_range: Tuple[Tuple[float, float], Tuple[float, float]], eps: float) -> Tuple[np.ndarray, float]:
    best_solution = None
    best_value = float('inf')
    
    # 初期区間での最適化を行い、キューに追加
    initial_guess = np.array([(a + b) / 2 for a, b in x_range])
    res = minimize(
        f, 
        initial_guess, 
        bounds=x_range, 
        method='L-BFGS-B')
    if res.success:
        mid = res.x
        f_mid = res.fun
        queue = [(-f_mid, x_range)]
    else:
        return None, float('inf')  # 初期最適化が失敗した場合

    while queue:
        _, current_range = heapq.heappop(queue)

        # 分割した区間で最適化を行い、評価
        for i in range(len(current_range)):
            a, b = current_range[i]
            if b - a > eps:
                left_range = list(current_range)
                right_range = list(current_range)
                
                # 区間を半分に分割
                mid_point = (a + b) / 2
                left_range[i] = (a, mid_point)
                right_range[i] = (mid_point, b)
                
                # 左側の区間で最適化
                res_left = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in left_range]), 
                    bounds=left_range, 
                    method='L-BFGS-B')
                if res_left.success:
                    heapq.heappush(queue, (-res_left.fun, tuple(left_range)))
                    if res_left.fun < best_value:
                        best_solution = res_left.x
                        best_value = res_left.fun
                
                # 右側の区間で最適化
                res_right = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in right_range]), 
                    bounds=right_range, 
                    method='L-BFGS-B')
                if res_right.success:
                    heapq.heappush(queue, (-res_right.fun, tuple(right_range)))
                    if res_right.fun < best_value:
                        best_solution = res_right.x
                        best_value = res_right.fun

    return best_solution, best_value

#
# 目的関数などの定義
#
def objective(x):
    a = 20  # 定数a
    b = 0.2  # 定数b
    c = 2 * np.pi  # 定数c
    n = len(x)  # 入力xの要素数
    x_offset = np.array([x[0] + 3, x[1] - 4])  # xのオフセット調整
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))  # 二乗の合計項
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))  # cos項
    return sum_sq_term + cos_term + a + np.e  # 関数の合計値を返す

#
# メタヒューリスティクスの設定
#
# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        return [objective(x)]  # 評価関数
    
    def get_bounds(self):
        return ([-100, -100], [100, 100])  # xの上下界を設定

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# アルゴリズムを設定
algo = pg.algorithm(pg.de(gen=100))

# 初期個体群を生成
pop = pg.population(prob, 20)

#
# 最適解を探索
#
for i in range(10):
    # メタヒューリスティクス
    pop = algo.evolve(pop)  
    best_x = pop.champion_x  # 最良解
    best_f = pop.champion_f[0]  # 最良評価値
    eps = 1  # 許容誤差を設定
    x_range = tuple((x - eps*5, x + eps*5) for x in best_x) # 探索範囲

    # グローバルサーチ：分岐限定法を実施（ローカルサーチを中で実施）
    result_info = branch_and_bound(objective, x_range, eps)

    if result_info is not None:
        result, value = result_info
        # 最適解の更新 
        if value < best_f:  # もし改善されたら、
            best_x = result  # 最良解を更新
            best_f = value   # 最良評価値を更新

# 結果を表示
print(f"Best solution: {best_x}")
print(f"Best objective value: {best_f}")

分岐限定法の関数の定義

関数branch_and_bound: この関数は、分岐限定法を用いて与えられた目的関数fの最小値を見つける主要なアルゴリズムです。関数は目的関数f、探索範囲x_range、そして許容誤差epsを引数に取ります。
- 初期化: 初期区間における最適化問題を解き、その解を優先度付きキュー（最小ヒープ）に追加します。この時、SciPyのminimize関数を用いており、方法としてL-BFGS-Bを選択しています。
- 探索ループ: キューが空になるまで、最適化問題のサブセットを取り出し、それをさらに細分化して新たなサブ問題を生成し、解きます。各ステップで、探索範囲を半分に分割して新たなサブ問題を作り、それぞれに対して最適化を実施します。このプロセスを繰り返すことで、最適解に近づきます。
- 更新と終了: 各サブ問題に対する最適化が成功した場合、その解と目的関数値を評価し、現在の最良解よりも良い場合は更新します。また、新たなサブ問題が許容誤差epsよりも大きい場合にのみ、さらに分割して探索を続けます。

目的関数の定義

目的関数(objective): この関数は最小化したい対象で、入力xに対してスカラー値を返します。

メタヒューリスティクスの設定

CustomProblemクラス
- 最適化問題を定義するカスタムクラス。
- fitness(self, x): 目的関数を定義。引数xに対する評価値をリストで返す。
- get_bounds(self): 変数の上下界を定義。この例では[-100, 100]。
PyGMO問題オブジェクトの作成：prob = pg.problem(CustomProblem()): CustomProblemクラスのインスタンスをPyGMOの問題オブジェクトに変換。
アルゴリズムの設定：algo = pg.algorithm(pg.de(gen=100)): 差分進化アルゴリズムを設定。世代数は100。
初期個体群の生成：pop = pg.population(prob, 20): 最適化問題に対して初期個体数20の個体群を生成。

最適解を探索

メタヒューリスティクスによる探索
- for i in range(10):：このループは、最適化プロセスを10回繰り返します。各繰り返しで、メタヒューリスティクスに基づく最適化と、分岐限定法によるさらなる探索を行います。
- pop = algo.evolve(pop): PyGMOの進化的アルゴリズムを使用して、個体群popを進化させます。このステップでは、最適化問題の潜在的な解が生成され、評価されます。
- best_x = pop.champion_x: 進化後の個体群から、最良の解（最適解）を取得します。
- best_f = pop.champion_f[0]: 最良解に対応する目的関数の値（評価値）を取得します。
分岐限定法によるグローバルサーチ
- eps = 1: この値は、分岐限定法で使用する探索範囲の分割精度を定義します。
- x_range = tuple((x - eps*5, x + eps*5) for x in best_x): メタヒューリスティクスで得られた最良解を中心に、探索範囲を定義します。ここでは、各次元についてeps*5だけ範囲を広げた区間を探索範囲としています。
- result_info = branch_and_bound(objective, x_range, eps): 分岐限定法を使用して、上で定義した探索範囲内で目的関数objectiveの最小値を探索します。
最適解の更新
- 分岐限定法からの戻り値result_infoがNoneでない場合、すなわち探索が成功した場合、最適解とその評価値が返されます。
- if value < best_f:: 分岐限定法によって得られた解の評価値が、現在の最良評価値よりも小さい場合、つまり改善されている場合、最良解とその評価値を更新します。
結果の表示：最適化プロセスで見つかった最良の解（best_x）とその目的関数値（best_f）を出力します。

以下、実行結果です。

Best solution: [<span>-3. 4.</span>]
Best objective value: <span>1.3938113330169699e-08</span>

以下は小数点2桁目を四捨五入した結果です。

最適解（Optimal solution）： $(x_0,x_1)=(-3.0,4.0)$
最適値（Optimal value）：0.0

　　制約付き非線形計画問題

先ほどと同様、以下の非線形計画問題を扱います。最適解は $(x_0,x_1)=(1,1)$ で、最適値は $0$ です。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

メタヒューリスティックおよびグローバルサーチ時は制約条件はペナルティとして目的関数に組み込み最適化します。

以下、コードです。

import numpy as np
import pygmo as pg
import heapq
from scipy.optimize import minimize
from typing import Tuple, Callable

#
# 分岐限定法の関数を定義（ローカルサーチを中で実施）
#
def branch_and_bound(f: Callable[[np.ndarray], float], x_range: Tuple[Tuple[float, float], Tuple[float, float]], eps: float) -> Tuple[np.ndarray, float]:
    best_solution = None
    best_value = float('inf')
    
    # 初期区間での最適化を行い、キューに追加
    initial_guess = np.array([(a + b) / 2 for a, b in x_range])
    res = minimize(
        f, 
        initial_guess, 
        bounds=x_range, 
        method='L-BFGS-B')
    if res.success:
        mid = res.x
        f_mid = res.fun
        queue = [(-f_mid, x_range)]
    else:
        return None, float('inf')  # 初期最適化が失敗した場合

    while queue:
        _, current_range = heapq.heappop(queue)

        # 分割した区間で最適化を行い、評価
        for i in range(len(current_range)):
            a, b = current_range[i]
            if b - a > eps:
                left_range = list(current_range)
                right_range = list(current_range)
                
                # 区間を半分に分割
                mid_point = (a + b) / 2
                left_range[i] = (a, mid_point)
                right_range[i] = (mid_point, b)
                
                # 左側の区間で最適化
                res_left = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in left_range]), 
                    bounds=left_range, 
                    method='L-BFGS-B')
                if res_left.success:
                    heapq.heappush(queue, (-res_left.fun, tuple(left_range)))
                    if res_left.fun < best_value:
                        best_solution = res_left.x
                        best_value = res_left.fun
                
                # 右側の区間で最適化
                res_right = minimize(
                    f, 
                    np.array([(a + b) / 2 for a, b in right_range]), 
                    bounds=right_range, 
                    method='L-BFGS-B')
                if res_right.success:
                    heapq.heappush(queue, (-res_right.fun, tuple(right_range)))
                    if res_right.fun < best_value:
                        best_solution = res_right.x
                        best_value = res_right.fun

    return best_solution, best_value

#
# 目的関数などの定義
#

# 目的関数
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] - 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

# 制約違反のペナルティを計算する関数
def calculate_penalty(x):
    c1 = constraint1(x)
    c2 = constraint2(x)
    c3 = constraint3(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

# 分岐限定法で利用するペナルティを加えた目的関数
def objective_with_penalty(x):
    obj = objective(x)
    penalty = calculate_penalty(x)
    return obj + penalty * 1e10

#
# メタヒューリスティクスの設定
#

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値とペナルティを合計
        obj = objective(x)
        penalty = calculate_penalty(x)
        return [obj + penalty * 1e10]  # ペナルティの重みを調整

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# アルゴリズムを設定
algo = pg.algorithm(pg.de(gen=100))

# 初期個体群を生成
pop = pg.population(prob, 20)

#
# 最適解を探索
#

for i in range(10):
    # メタヒューリスティクス
    pop = algo.evolve(pop)  
    best_x = pop.champion_x  # 最良解
    best_f = pop.champion_f[0]  # 最良評価値
    eps = 1  # 許容誤差を設定
    x_range = tuple((x - eps*5, x + eps*5) for x in best_x) # 探索範囲

    # グローバルサーチ：分岐限定法を実施（ローカルサーチを中で実施）
    result_info = branch_and_bound(objective_with_penalty, x_range, eps)

    if result_info is not None:
        result, value = result_info
        # 最適解の更新 
        if value < best_f:  # もし改善されたら、
            best_x = result  # 最良解を更新
            best_f = value   # 最良評価値を更新

# 結果を表示
print(f"Best solution: {best_x}")
print(f"Best objective value: {best_f}")

以下、実行結果です。

Best solution: [<span>0.99999777 0.99999554</span>]
Best objective value: <span>4.971818839392247e-12</span>

以下は小数点2桁目を四捨五入した結果です。

最適解（Optimal solution）： $(x_0,x_1)=(1.0,1.0)$
最適値（Optimal value）：0.0

　ハイブリッド最適化の実装上の留意点とテクニック

ハイブリッド最適化を実装する際は、以下のような点に留意する必要があります。

各手法のパラメータ設定

メタヒューリスティクスの個体数、世代数、交叉率、突然変異率など
グローバルサーチの探索範囲、分割数、終了条件など
ローカルサーチの初期値、終了条件など

手法間の情報の受け渡し方法

メタヒューリスティクスからグローバルサーチへの初期値の引き継ぎ方法
グローバルサーチからローカルサーチへの初期値の引き継ぎ方法

計算時間の配分

各手法にどれだけの計算時間を割り当てるか
問題の特性や要求される解の品質に応じて、適切に配分する必要がある

ハイブリッド最適化の設計には、問題に関する深い理解と、各手法の特性に関する知識が必要です。さらに、数値実験を通じて、各手法の効果を検証し、最適な組み合わせを見つけることが重要です。

ハイブリッド手法の性能評価と考察

ハイブリッド手法の性能を評価するためには、適切な評価指標を設定し、ベンチマーク問題を用いて性能を比較する必要があります。

また、各手法の選択やパラメータ設定が性能に与える影響についても考察が必要です。ここでは、ハイブリッド手法の評価方法と考察について説明します。

　ハイブリッド手法の評価方法

ハイブリッド手法の性能を評価するための指標には、以下のようなものがあります。

収束速度：最適解への収束の速さを評価する指標。反復回数や計算時間などで測定する。
解の精度：得られた解の最適性を評価する指標。最適値からの誤差や、制約条件の違反度などで測定する。
計算時間：アルゴリズムの実行に要する時間を評価する指標。

これらの指標を用いて、ハイブリッド手法の性能を評価します。ただし、問題によって適切な指標は異なるため、問題の特性を考慮して指標を選択する必要があります。

また、ハイブリッド手法の性能を評価するためには、ベンチマーク問題を用いて性能を比較することが重要です。

ベンチマーク問題には、以下のような特徴があります。

最適解が既知である
問題の規模や難易度が異なる
様々な特性（非線形性、多峰性など）を持つ

代表的なベンチマーク問題の目的関数として用いるものに、Ackley関数、Rastrigin関数、Rosenbrock関数などがあります。今回いくつか利用しました。

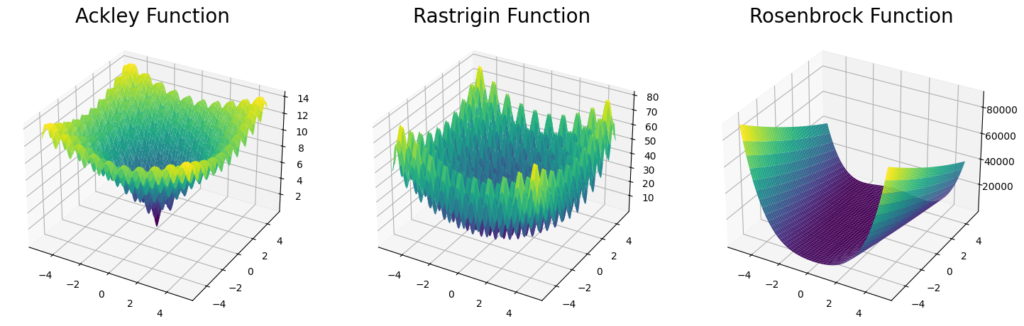
これらの問題を用いて、ハイブリッド手法の性能を評価し、比較します。

また、最適化ソフトウェアテストCUTEstのPythonインターフェースが提供されています。これにより、PythonユーザーがCUTEstのテスト問題コレクションに簡単にアクセスできるようになります。

　各手法の選択とパラメータ設定の影響

ハイブリッド手法の性能は、各手法の選択やパラメータ設定に大きく影響されます。

メタヒューリスティクスの選択
問題の特性に応じて、遺伝的アルゴリズム（GA）、粒子群最適化（PSO）、差分進化（DE）などを選択する必要があります。また、各手法のパラメータ（個体数、世代数、交叉率、突然変異率など）の設定も重要です。

グローバルサーチの選択
区間分割法、分枝限定法、リプシッツ最適化などの中から、問題の特性に応じて適切な手法を選択する必要があります。また、各手法のパラメータ（分割数、終了条件など）の設定も重要です。

ローカルサーチの選択
勾配法、ニュートン法、準ニュートン法などの中から、問題の特性に応じて適切な手法を選択する必要があります。また、各手法のパラメータ（ステップサイズ、終了条件など）の設定も重要です。

これらの選択やパラメータ設定が、ハイブリッド手法の性能に大きく影響するため、適切な選択とチューニングが必要です。

　ハイブリッド手法の性能比較と考察

ハイブリッド手法の性能を評価するためには、単独の手法との比較や、異なるハイブリッド手法との比較が重要です。

単独手法との比較
メタヒューリスティクス、グローバルサーチ、ローカルサーチをそれぞれ単独で用いた場合の性能と、ハイブリッド手法の性能を比較します。これにより、ハイブリッド化による性能の向上を確認することができます。

異なるハイブリッド手法との比較
メタヒューリスティクスとローカルサーチの組み合わせ、グローバルサーチとローカルサーチの組み合わせ、メタヒューリスティクスとグローバルサーチとローカルサーチの組み合わせなど、異なる組み合わせ方の性能を比較します。これにより、問題に適した組み合わせ方を検討することができます。

性能比較の結果から、以下のような考察が得られます。

ハイブリッド化による性能の向上の度合い
問題の特性に応じた適切な手法の組み合わせ方
各手法の選択やパラメータ設定の影響の大きさ
ハイブリッド手法の適用可能性と限界

これらの考察を踏まえて、ハイブリッド手法の設計や適用を行うことが重要です。

　ハイブリッド手法の適用上の留意点

ハイブリッド手法を実際の問題に適用する際には、以下のような点に留意する必要があります。

問題の定式化
ハイブリッド手法を適用するためには、問題を適切に定式化する必要があります。目的関数や制約条件の設定が不適切だと、良い解が得られない可能性があります。

手法の選択
問題の特性に応じて、適切な手法を選択する必要があります。不適切な手法を選択すると、性能が十分に発揮されない可能性があります。

パラメータのチューニング
各手法のパラメータは、問題ごとに適切にチューニングする必要があります。パラメータの設定が不適切だと、性能が大きく低下する可能性があります。

計算コストとのトレードオフ
ハイブリッド手法は、単独の手法よりも計算コストが高くなる傾向があります。計算コストと解の品質のトレードオフを考慮して、適用する必要があります。

これらの点に留意しながら、ハイブリッド手法を適用することが重要です。

まとめ

本シリーズ「【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！」では、Pythonを用いた非線形計画問題の大域的最適化手法について、4回にわたって解説してきました。

第1回では、非線形計画問題と大域的最適化の基礎的な概念を紹介し、Pythonを用いた問題の定式化方法や最適化ライブラリについて説明しました。

第2回では、メタヒューリスティクスを中心とした確率的手法について解説し、遺伝的アルゴリズムや粒子群最適化のPythonでの実装例を示しました。

第3回では、区間分割法や分枝限定法などの決定論的手法について解説し、それぞれの手法のPythonでの実装例を示しました。

第4回では、メタヒューリスティクスと決定論的手法を組み合わせたハイブリッド手法について解説し、PyGMOやSciPyを用いた実装例を示しました。

非線形計画問題の大域的最適化に対する様々なアプローチを紹介し、それぞれの手法のメリットとデメリット、適用上の留意点などについて説明してきました。問題の特性に応じて適切な手法を選択し、パラメータをチューニングすることの重要性を理解していただけたのではないでしょうか。

次回は最終回です。第1回で紹介したSciPyを使った最適化（ローカルサーチ）を、 最適化ライブラリーCyIPOPTで実施する方法をお話しします。CyIPOPTは大規模問題に対応した素晴らしいライブラリーです。

【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第5回】SciPyからCyIPOPTへ: 大規模非線形最適化への移行 –