ビジネスデータを解き明かす！ Python STL分解で時系列データを理解しよう

ビジネス環境は常に変化しています。

市場の動向、消費者行動の変化、季節的な要因、経済の波など、多くの要素が企業の成長と収益性に影響を与えています。

これらの変化を理解し、将来のトレンドを予測するためには、時系列分析が不可欠です。時系列分析を通じて、企業は過去のデータから洞察を得ることができ、より情報に基づいた意思決定が可能になります。

時系列分析は、ビジネスにおいて次のような価値を提供します。

トレンドの特定: 長期的な売上の増減や市場の成長など、ビジネスの動向を把握できます。
季節性の把握: 年間を通じてビジネスのパフォーマンスに影響を与える季節的なパターンを特定します。
異常値の検出: 予期しないスパイクやドロップが発生した場合に警告し、原因を調査することができます。
将来予測: 過去のデータを基にして、将来の売上、在庫需要、その他の重要なビジネス指標を予測します。

時系列分析は、ビジネス戦略を立案し、リスクを管理し、競争優位性を維持するための強力なツールです。

そのツールの中の1つに、STL分解という時系列分析手法があります。

トレンドや季節性などを分解し、手元の時系列データの特徴を炙り出し、その分解結果をもとにビジネス上の意思決定に反映させたり、その分解結果をもとに時系列予測や異常検知などのモデル構築に役立たせることができます。

Contents

時系列分析の基礎
　時系列データとは何か
　時系列分析の主要な用途
　時系列分析の課題と解決策の概要
STL分解とは
　STL分解の概念
　STL分解のメリットとビジネスへの応用例
　STL分解の基本的な考え方
　　アルゴリズムのステップ
　　Loess平滑化
　他の時系列分析手法との比較
Pythonで時系列データを扱う準備
　必要なPythonライブラリの紹介
　時系列データの読み込みと前処理
　STL分解の実装例
STL分解の実施とその解釈例
　トレンドの理解
　季節性の把握
　残差の分析
　ケーススタディ
STL分解を用いた時系列予測
　時系列予測の基本概念
　STL分解後のデータで予測モデルを構築する方法
　ケーススタディ
STL分解を活用したビジネスの戦略立案と変革
　トレンド分析からの戦略立案
　季節変動を利用したプロモーション戦略
　不確実性の管理とリスク評価
　ビジネス変革
まとめ

時系列分析の基礎

　時系列データとは何か

時系列データは、一定期間にわたって定期的に収集されるデータであり、時間の経過と共に変化する値を記録したものです。

これは、毎日の気温、月間売上高、年間降水量など、さまざまな形態で存在します。

時系列データの根本的な特徴は、その時点の観測値が前後の観測値に依存していることにあります。

この時間的依存性が時系列分析の中心的な課題であり、また魅力でもあります。

　時系列分析の主要な用途

時系列分析はビジネス、経済、科学、工学など、幅広い分野で使用されています。

その主要な用途には以下のようなものがあります。

予測
最も一般的な用途の一つで、将来の値を予測します。例えば、次の四半期の売上、次週の株価、明日の気温などです。

季節性の特定
年間、月間、週間、日間の周期で発生するパターンを特定します。これにより、ビジネスは需要の変動をよりよく理解し、計画することができます。

トレンド分析
長期的な増加または減少の傾向を識別します。トレンド分析により、ビジネスは市場の変化に対応し、戦略を調整することができます。

異常検出
データの中で通常とは異なるパターンを検出します。異常検出は、フラウド（不正）検出、品質管理、環境モニタリングなどで使用されます。

　時系列分析の課題と解決策の概要

時系列分析は、その時点依存性や、データ内のトレンド、季節性、ノイズなど、複数の要素を考慮する必要があるため、一般的なデータ分析とは異なる課題を抱えています。

主な課題には以下のようなものがあります。

非定常性
時系列データの統計的性質が時間と共に変化する場合があります。これに対処する一つの方法として、データの差分を取ることで、データをより定常的にすることです。

季節性とトレンド
データからトレンドや季節性を識別し、除去する必要があります。ちなみに、トレンドや季節性は非定常です。これには、STL分解のような手法が有効です。

予測の不確実性
予測は常にある程度の不確実性を伴います。なぜならば、予測対象が未来のことだからです。この不確実性を定量化し、モデルの精度を評価する方法を理解することが重要です。

時系列分析のこれらの課題に対処するためには、適切なモデル選択、データの前処理、予測手法の選択が不可欠です。

STL分解とは

　STL分解の概念

STL分解は、「Seasonal and Trend decomposition using Loess」の略で、時系列データを季節性（seasonal）、トレンド（trend）、そして残差（remainder）の成分に分解する手法です。

この手法は、1990年にRobert B. Clevelandらによって開発されました。

Cleveland, Robert B, William S Cleveland, Jean E McRae, and Irma J Terpenning. 1990. “STL: A Seasonal-Trend Decomposition Procedure Based on Loess.” Journal of Official Statistics 6 (1): 3–73.
https://www.salesanalytics.co.jp/l5bq

STL分解の主な特徴は、柔軟性が高く、任意の周期性を持つデータに対して適用可能である点です。また、トレンドや季節性の形状が時間とともに変化するデータに対しても強力です。

　STL分解のメリットとビジネスへの応用例

STL分解には以下のようなメリットがあります。

柔軟性: 任意の季節周期に対応でき、季節成分の変化に柔軟に対応できます。
ロバスト性: 外れ値の影響を受けにくいです。
解釈性: 分解された成分（トレンド、季節性、残差）は、ビジネスの意思決定に有用な洞察を提供します。

ビジネスへの応用例としては、以下のようなものがあります。

売上予測: 売上データを季節性とトレンドに分解することで、将来の売上のより高精度な予測を実現します。
在庫管理: 季節性を考慮した、より精密な在庫管理を実現します。
市場分析: トレンド分析を通じて、市場の成長や縮小の今後の傾向を理解し対処できるようにします。

　STL分解の基本的な考え方

STL分解では、時系列データ $Y_t$ を、トレンド成分 $T_t$ 、季節成分 $S_t$ 、そして残差成分 $R_t$ に分解します。ここで、 $t$ は時間を表します。

$\displaystyle Y_t=T_t+S_t+R_t$

　　アルゴリズムのステップ

ステップ 1 (初期トレンドの推定): まず、時系列データから初期トレンド成分を推定します。Loess平滑化が用いられます。
ステップ 2 (季節成分の推定): 初期トレンドをデータから除去した後、季節成分を推定します。これは、データから初期トレンド成分を差し引いた残差に対して、季節周期ごとにLoess平滑化を適用することで行います。
ステップ 3 (トレンド成分の再推定): 季節成分をデータから除去した後、トレンド成分を再推定します。季節調整されたデータに対して再びLoess平滑化が適用されます。
ステップ 4 (残差成分の計算): トレンド成分と季節成分を元の時系列データから差し引くことで、残差成分が計算されます。
ステップ 5 (繰り返し処理): 上記のステップ2から4を繰り返し処理します。各繰り返しで、季節成分とトレンド成分の推定が更新され、精度が向上します。

　　Loess平滑化

Loess平滑化は、局所的な回帰を利用した非線形の平滑化技術です。

データ点の小さな近傍に対して線形回帰を行い、各近傍で計算された回帰曲線の値を使用して平滑化された値を得ます。

STL分解においては、このLoess平滑化がキーとなる技術であり、トレンドと季節成分の柔軟な推定を可能にします。

Loess平滑化においては、以下のような重み付き最小二乗法を用います。

$\displaystyle \min_{\alpha,\beta}\sum_{i} \omega_i \left( y_i - \left( \alpha+\beta x_i \right) \right)$

ここで、 $y_i$ はデータ点、 $x_i$ は独立変数（この場合は時間）、 $\omega_i$ は重み（データ点が予測点に近いほど大きくなります）、 $\alpha$ と $\beta$ は線形回帰モデルのモデルパラメータ（切片と係数）です。

STL分解はこのLoess平滑化を用いて、時系列データのトレンド成分と季節成分を柔軟に抽出し、データを分析しやすくします。

　他の時系列分析手法との比較

STL分解は他の時系列分析手法、例えばARIMA（自己回帰積分移動平均モデル）や指数平滑化と比較して、特に季節性の分析とトレンド抽出において優れた柔軟性と解釈性を持ちます。

ARIMAモデルは時系列データの予測に強力ですが、季節性やトレンドの明確な分解には不向きな場合があります。

指数平滑化は計算が簡単で予済みが容易ですが、STLのようにデータを明確に分解することはできません。

STL分解はこれらの手法と組み合わせて使用することで、時系列分析の精度を高めることが可能です。

例えば、STL分解でトレンドと季節性を取り除いた後、残差に対してARIMAモデルを適用することで、より精密な予測が行えます。

Pythonで時系列データを扱う準備

時系列分析を行う前に、適切なPython環境のセットアップと、時系列データを扱うためのライブラリに慣れることが重要です。

　必要なPythonライブラリの紹介

時系列分析においては、以下のPythonライブラリが特に有用です。

NumPy: 数値計算を効率的に行うためのライブラリ。配列操作や数学関数などの基本的な機能を提供します。
Pandas: データ分析と操作のためのライブラリ。時系列データを含むさまざまな形式のデータを扱うための強力な機能を持っています。
MatplotlibおよびSeaborn: データの可視化を行うためのライブラリ。時系列データのトレンドや季節性を視覚的に分析するのに役立ちます。
Statsmodels: 統計的モデリングと時系列分析のためのライブラリ。STL分解を含む多くの時系列分析手法を提供しています。

多くの環境では、最初からデフォルトでインストールされている可能性が高いです。pip listなどでインストールされているか確認しておきましょう。

ちなみに、これらのライブラリをインストールするには、例えばpipであれば以下のコマンドでまとめて行えます。

pip install numpy pandas matplotlib seaborn statsmodels

Pythonの環境をセットアップするには、Anacondaなどのconda系やPythonの公式配布版など、さまざまな方法があります。

conda環境の場合も最初からデフォルトでインストールされている可能性が高いです。conda listなどでインストールされているか確認しておきましょう。

conda環境であれば、以下でまとめてインストールできます。

conda install numpy pandas matplotlib seaborn statsmodels

　時系列データの読み込みと前処理

以下のサンプルデータを利用します。ダウンロードできます。

sample1.csv
https://www.salesanalytics.co.jp/r7xe

Pandasライブラリを使用して、時系列データを読み込み、前処理を行います。

以下に、CSVファイルから時系列データを読み込む基本的な例を示します。

import pandas as pd

# CSVファイルからデータを読み込む
df = pd.read_csv('sample1.csv', index_col='Date', parse_dates=True)

# 最初の5行を表示
print(df.head())

このコードは、Date列をインデックスとして使用し、日付を適切に解析することで時系列データを読み込みます。

以下、実行結果です。

             Sales
Date              
2023-01-01  100.00
2023-01-02  101.36
2023-01-03     NaN
2023-01-04  104.08
2023-01-05  105.44

データの前処理には、欠損値（NaN）の処理、不要な列の削除、データの正規化などが含まれる場合があります。

以下は、欠損値（NaN）の確認をし、その後補完処理を実施しているコード例です。

# 欠損値の確認
print(df.isnull().sum())

# 欠損値を前の値で埋める
df.fillna(method='ffill', inplace=True)

# 最初の5行を表示
print(df.head())

以下、実行結果です。

Sales    21
dtype: int64
             Sales
Date              
2023-01-01  100.00
2023-01-02  101.36
2023-01-03  101.36
2023-01-04  104.08
2023-01-05  105.44

変数Salesの欠損値（NaN）のあるレコードは 21 あります。

df.fillnaで欠損値（NaN）を補完処理を実施しています。

　STL分解の実装例

PythonでSTL分解を行うには、statsmodelsライブラリを使用します。

以下に、STL分解を実行し、結果を可視化するためのPythonコードです。

import pandas as pd
from statsmodels.tsa.seasonal import STL
import matplotlib.pyplot as plt

# CSVファイルからデータを読み込む
df = pd.read_csv('sample1.csv', index_col='Date', parse_dates=True)

# 欠損値を前の値で埋める
df.fillna(method='ffill', inplace=True)

# STL分解の実行
stl = STL(df['Sales'], period=365)
result = stl.fit()

# 分解された成分の取得
trend = result.trend
seasonal = result.seasonal
resid = result.resid

# 結果の可視化
plt.figure(figsize=(10, 8))

plt.subplot(411)
plt.plot(df['Sales'], label='Original')
plt.legend(loc='best')
plt.title('Original Data')

plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.title('Trend Component')

plt.subplot(413)
plt.plot(seasonal, label='Seasonality')
plt.legend(loc='best')
plt.title('Seasonal Component')

plt.subplot(414)
plt.plot(resid, label='Residual')
plt.legend(loc='best')
plt.title('Residual Component')

plt.tight_layout()
plt.show()

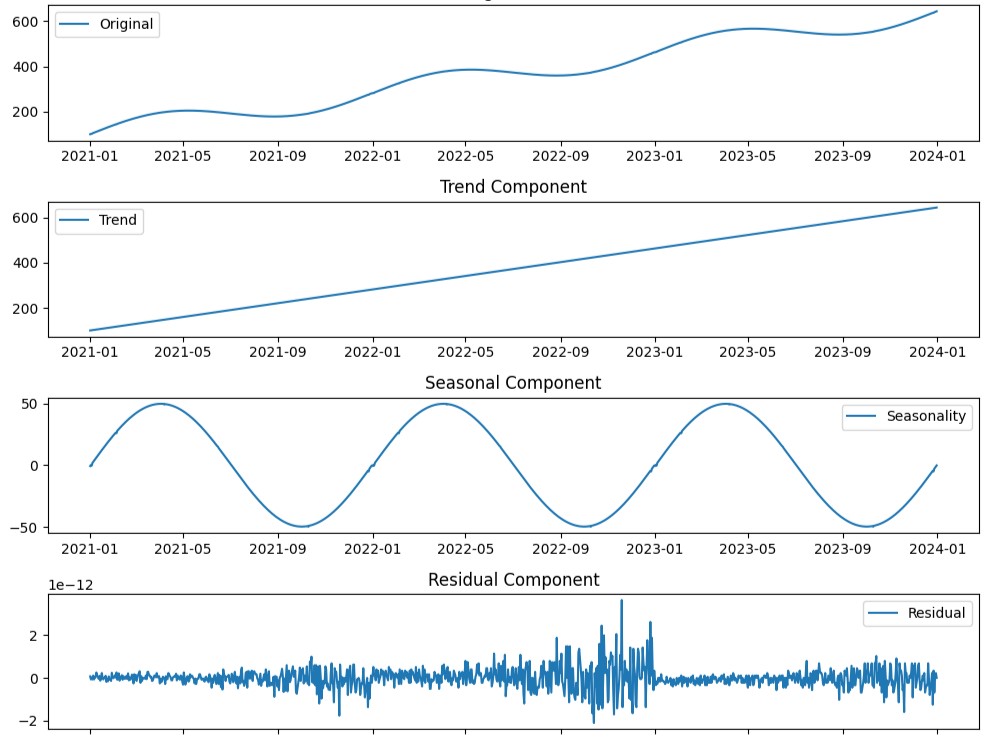
このコードは、時系列データを読み込み、STL分解を行い、オリジナルのデータ（Original Data）、トレンド成分（Trend Component）、季節成分（Seasonal Component）、残差成分（Residual Component）をそれぞれプロットします。

必要なライブラリのインポート
- pandas: データ分析を支援する機能を提供するライブラリ。CSVファイルの読み込みやデータの前処理に使用します。
- statsmodels.tsa.seasonal.STL: 時系列データをトレンド、季節性、残差成分に分解するSTL分解を行うクラス。
- matplotlib.pyplot: データの可視化を行うためのライブラリ。
CSVファイルからデータの読み込み
- 'sample1.csv'からデータを読み込み、日付がインデックスとして設定され、日付の解析が行われるようにします。
欠損値の処理
- .fillna(method='ffill', inplace=True)を用いて、データ内の欠損値を前の値で埋めます。
STL分解の実行
- STL(df['Sales'], period=365)でSTL分解を初期化し、sales列のデータに対して365日の周期で分解を行います。
- .fit()メソッドを使用して分解を実行し、結果をresultに格納します。
分解された成分の取得
- result.trend, result.seasonal, result.residを使用して、トレンド成分、季節性成分、残差成分をそれぞれ取得します。
結果の可視化
- matplotlib.pyplotの機能を使用して、オリジナルのデータとSTL分解によって得られた各成分（トレンド、季節性、残差）を4つのサブプロットにプロットします。
- 各サブプロットには、成分の種類に応じたタイトルが付けられ、凡例が表示されます。
- .tight_layout()でプロット間の重なりを防ぎ、見やすく整理します。

以下、実行結果です。

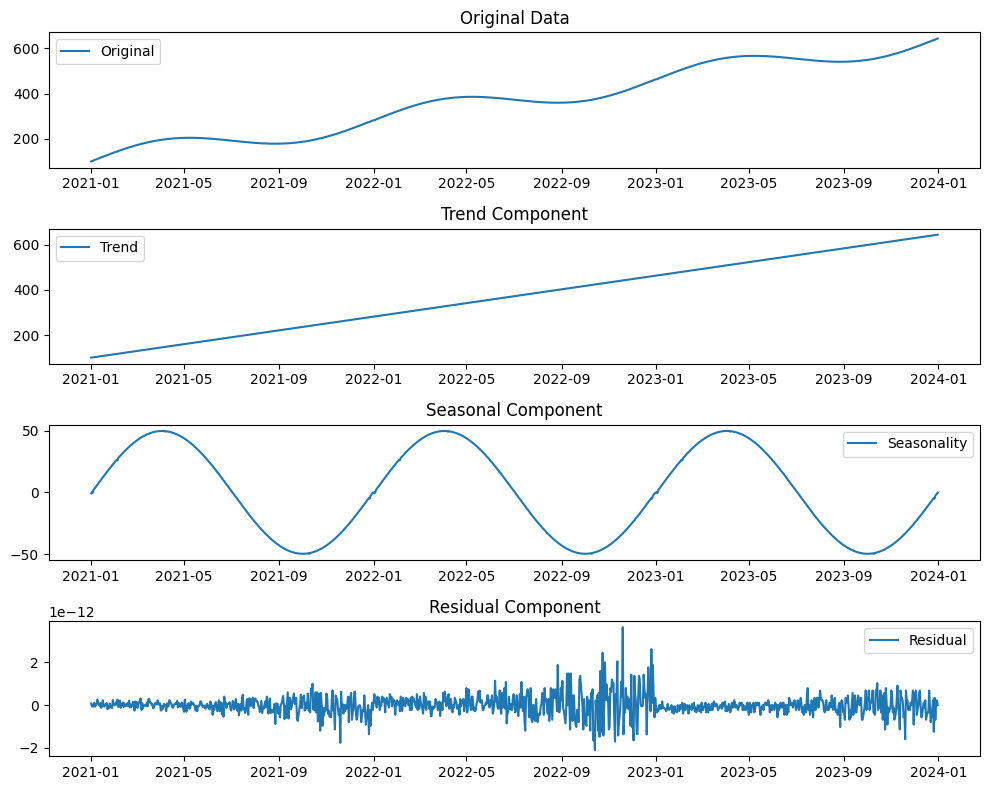
STL分解の実施とその解釈例

STL分解を使用する主な目的の一つは、時系列データをより理解しやすい形に分解し、その背後にあるパターンや動向を明らかにすることです。

STL分解によって得られるトレンド、季節性、残差の各成分を解釈することで、ビジネス上の意思決定に役立つ洞察を得ることができます。

　トレンドの理解

トレンド成分は時系列データの長期的な変化を示します。

この成分を分析することで、ビジネスが成長しているのか、あるいは衰退しているのかといった全体的な方向性を把握できます。

トレンドが上昇または下降している場合、市場の需要が増加または減少していることを示す可能性があります。

また、新しい競争者の登場や技術の変化など、外部からの影響を反映している場合もあります。

　季節性の把握

季節成分は、周期的なパターンや季節ごとの変動を示します。

この成分から、特定の時期に需要が高まる商品やサービスがあるかどうかを識別できます。

季節性の分析を通じて、ビジネスは在庫管理、プロモーション活動、価格設定戦略を最適化することができます。

例えば、季節的な需要のピークに合わせて在庫を増やしたり、オフシーズンに割引を提供したりすることが可能です。

　残差の分析

残差成分は、トレンドや季節性によって説明されないデータの変動を示します。

この成分は、モデルがデータの特定の動きを捉えきれていないことを示す可能性があります。

残差を分析することで、データに含まれる予期しないイベントや異常値を特定できます。

これは、フラウド（不正）の検出、品質管理の問題、あるいはデータ収集プロセスにおけるエラーの特定に役立つことがあります。

　ケーススタディ

実際のビジネスシナリオでSTL分解を使用する例として、小売業の月間売上データを考えてみましょう。

STL分解により、年間を通じての売上のトレンド、夏休みや年末年始などの季節的な販売ピーク、および特定のプロモーションやイベントが売上に与える影響を分析できます。

これらの情報を基に、小売業者は在庫管理を改善し、将来の売上予測をより正確に行うことができます。

以下のサンプルデータを利用します。ダウンロードできます。

sample2.csv
https://www.salesanalytics.co.jp/yil9

時系列データを読み、STL分解でトレンドと季節性の抽出をします。

以下、コードです。

import numpy as np
import pandas as pd
from statsmodels.tsa.seasonal import STL
import matplotlib.pyplot as plt

# STL分解の実行
df = pd.read_csv('sample2.csv', index_col='Date', parse_dates=True)

stl_new = STL(df['Sales'], period=12)
result_new = stl_new.fit()

# 分解された成分の取得
trend_new_example = result_new.trend
seasonal_new_example = result_new.seasonal
resid_new_example = result_new.resid

# 結果の可視化
plt.figure(figsize=(14, 10))

plt.subplot(411)
plt.plot(df['Sales'], label='Original Sales')
plt.legend(loc='best')
plt.title('Original Data')

plt.subplot(412)
plt.plot(trend_new_example, label='Trend')
plt.legend(loc='best')
plt.title('Trend Component')

plt.subplot(413)
plt.plot(seasonal_new_example, label='Seasonality')
plt.legend(loc='best')
plt.title('Seasonal Component')

plt.subplot(414)
plt.plot(resid_new_example, label='Residual')
plt.legend(loc='best')
plt.title('Residual Component')

plt.tight_layout()
plt.show()

以下、実行結果です。

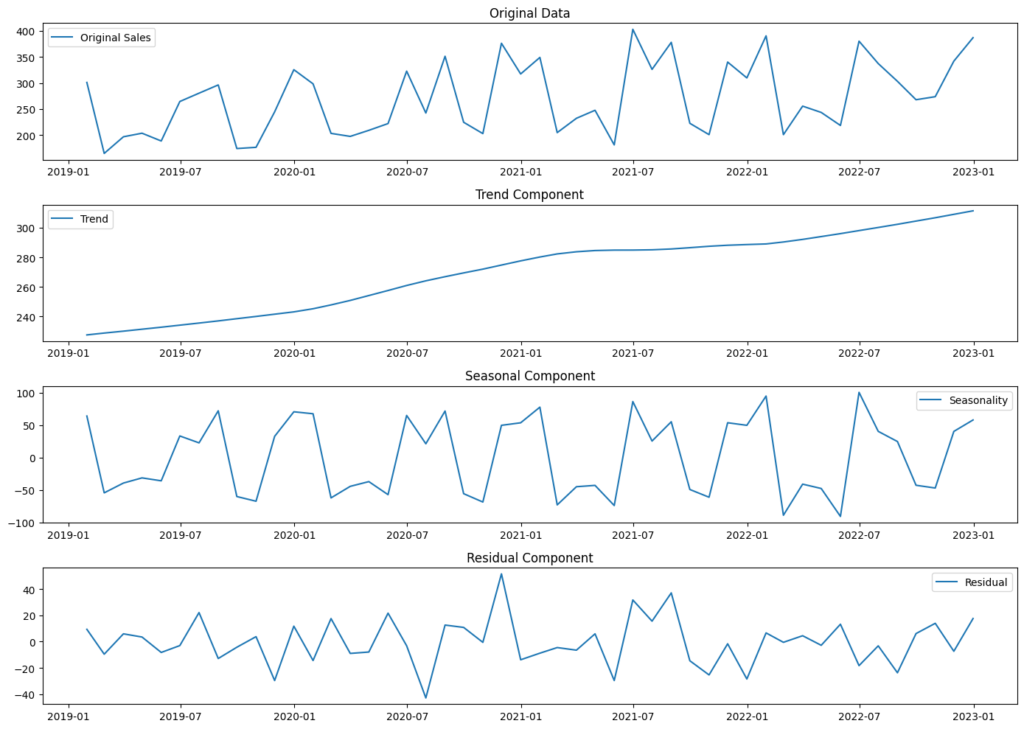
以下、解釈例です。

トレンド成分
トレンドのグラフは、データの長期的な変化を示しており、このケースでは売上が徐々に増加していることが示されています。このトレンドから、ビジネスが成長していることが読み取れます。

季節成分
季節性のグラフは、特定の時期に繰り返されるパターンを示しており、夏と冬の売上が他の季節に比べて高いことが示されています。これは、夏休みや年末年始のような特定の季節に需要が高まる商品やサービスがあることを意味します。

残差成分
残差のグラフは、トレンドや季節性によって説明されないデータの変動を示しています。この成分は、データのノイズや未捉えられたパターン、特定のプロモーションやイベントによる影響を示している可能性があります。

このSTL分解の結果を利用して、この小売業者は次の意思決定に活かしました。

在庫管理の最適化
季節成分から明らかになった売上のピーク時に合わせて、適切な量の在庫を確保することで、過剰在庫や在庫不足のリスクを軽減することができました。

プロモーション計画
売上が自然に増加する季節にプロモーション活動を行うことで、さらなる売上の増加を実現しました。また、トレンド成分が示す全体的な成長軌道に基づいて、長期的なマーケティング戦略を策定しました。

将来の売上予測の精度向上
STL分解によって抽出されたトレンドと季節性のパターンを活用し、より正確な将来の売上予測を実現し、ビジネス計画の立案に活かしました。

このように、STL分解は時系列データの背後にある複雑なパターンを理解し、ビジネス上の意思決定を支援するための強力なツールです。

正確なデータ分析に基づく戦略的な計画は、ビジネスの成長を促進し、競争優位性を確立するために不可欠です。

STL分解を用いた時系列予測

STL分解は、時系列データをトレンド、季節性、残差成分に分解する強力なツールですが、その真価は分解された成分を用いた予測にあります。

予測モデルを構築する際にSTL分解を使用することで、季節性やトレンドの影響をより正確にモデル化し、将来の値を予測することが可能になります。

　時系列予測の基本概念

時系列予測では、過去のデータに基づいて未来の値を予測します。

これには多くの手法が存在し、ARIMA、指数平滑化、機械学習モデルなどが有名です。

STL分解を予測プロセスに組み込むことで、これらのモデルがデータの季節性やトレンドをより効果的に捉えることができます。

　STL分解後のデータで予測モデルを構築する方法

STL分解を行った後、通常のアプローチは、トレンド成分と残差成分に対して予測モデルを構築することです。

以下は、STL分解後のトレンド成分に対して予測モデルを適用するプロセス例です。

データの分割: トレンド成分を訓練セットとテストセットに分割します。
モデルの選択: 線形回帰など、トレンド成分を表現できる適切なモデルを選択します。
モデルの訓練: トレンド成分に対してモデルを訓練します。
予測の実行: モデルを使用して将来のトレンド成分の値を予測します。
予測の調整: 季節性を予測値に加えて、最終的な予測値を得ます。

　ケーススタディ

小売業者が、STL分解を使用して将来の売上を予測する場合、季節性の明瞭なパターンとトレンドの増加を反映したモデルを構築できます。

これにより、プロモーション活動のタイミングや在庫レベルの調整など、より効果的なビジネス戦略を立案することが可能になります。

以下のサンプルデータを利用します。ダウンロードできます。

sample3.csv
https://www.salesanalytics.co.jp/txbm

先ず、時系列データを読み、STL分解でトレンドと季節性の抽出をします。

以下、コードです。

import numpy as np
import pandas as pd
from statsmodels.tsa.seasonal import STL
import matplotlib.pyplot as plt

# sample3.csvを読み込む
df_sales = pd.read_csv('sample3.csv', index_col='Date', parse_dates=True)

stl = STL(df_sales['Sales'], period=12)
result = stl.fit()

trend = result.trend
seasonal = result.seasonal
resid = result.resid

# 分解結果の可視化
plt.figure(figsize=(14, 8))
plt.subplot(411)
plt.plot(df_sales['Sales'], label='Original')
plt.title('Original Data')
plt.legend()

plt.subplot(412)
plt.plot(trend, label='Trend')
plt.title('Trend')
plt.legend()

plt.subplot(413)
plt.plot(seasonal, label='Seasonality')
plt.title('Seasonal')
plt.legend()

plt.subplot(414)
plt.plot(resid, label='Residual')
plt.title('Residual')
plt.legend()

plt.tight_layout()
plt.show()

以下、実行結果です。

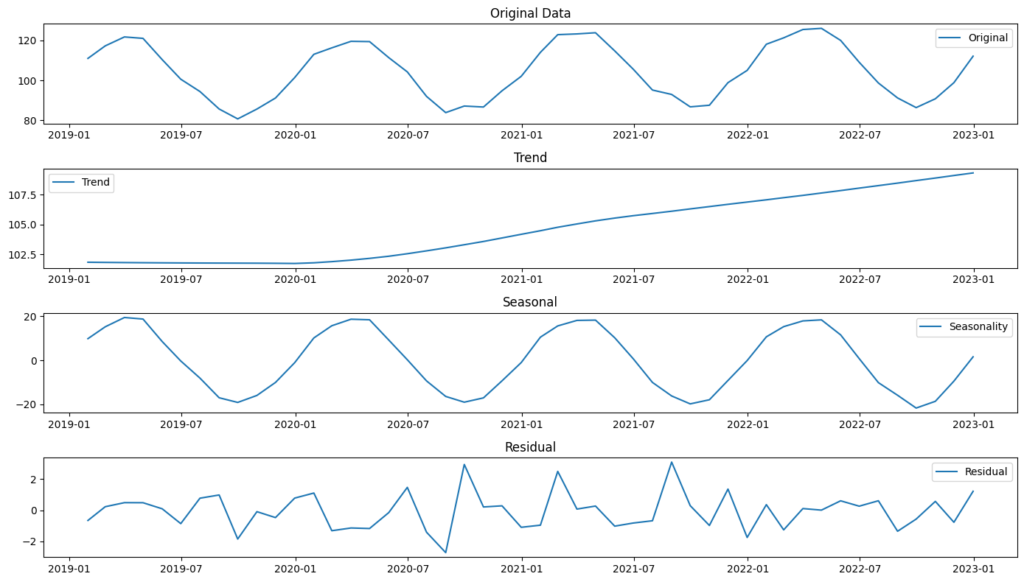
トレンド成分に基づいて将来の売上を予測します。

今回は説明を簡単にするため、線形回帰を使用します。

以下、コードです。

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# トレンド成分でモデルを訓練
X = np.arange(len(trend)).reshape(-1, 1)  # 時間を説明変数として使用
y = trend
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = LinearRegression()
model.fit(X_train, y_train)

# 未来の時間点での売上を予測
future_X = np.arange(len(trend), len(trend) + 12).reshape(-1, 1)  # 次の1年間を予測
future_sales = model.predict(future_X)

# 予測結果の可視化
plt.figure(figsize=(10, 6))
plt.plot(X, y, label='Actual Trend')
plt.plot(future_X, future_sales, label='Predicted Sales', linestyle='--')
plt.ylim(0,150) 
plt.legend()
plt.show()

このコードは、線形回帰モデルを使用して時系列データのトレンド成分に基づく将来の売上を予測し、その結果を可視化するプロセスを示しています。

必要なライブラリのインポート
- sklearn.linear_model.LinearRegression: 線形回帰モデルを提供するクラス。
- sklearn.model_selection.train_test_split: データを訓練セットとテストセットに分割する関数。
トレンド成分でモデルを訓練
- np.arange(len(trend)).reshape(-1, 1): トレンド成分の長さに等しい連続する整数の配列を作成し、それを時間として説明変数Xとして使用します。
- y = trend: トレンド成分を目的変数として使用します。
- train_test_split: データセットを訓練セットとテストセットに分割します。この例では、テストセットのサイズを全データの20%に設定しています。
線形回帰モデルの初期化と訓練
- model = LinearRegression(): 線形回帰モデルのインスタンスを作成します。
- model.fit(X_train, y_train): 訓練セットを使用して線形回帰モデルを訓練します。
未来の売上の予測
- np.arange(len(trend), len(trend) + 12).reshape(-1, 1): トレンド成分の末尾からさらに12時点分（通常は1年間を想定）の未来の時間点を生成します。
- future_sales = model.predict(future_X): 生成した未来の時間点に対して売上を予測します。
予測結果の可視化
- plt.figure(figsize=(10, 6)): 可視化する図のサイズを指定します。
- plt.plot(X, y, label='Actual Trend'): 実際のトレンド成分をプロットします。
- plt.plot(future_X, future_sales, label='Predicted Sales', linestyle='--'): 予測された売上を点線でプロットします。
- plt.ylim(0,150): y軸の範囲を指定します（必要に応じて調整）。
- plt.legend(): 凡例を表示します。
- plt.show(): 図を表示します。

以下、実行結果です。

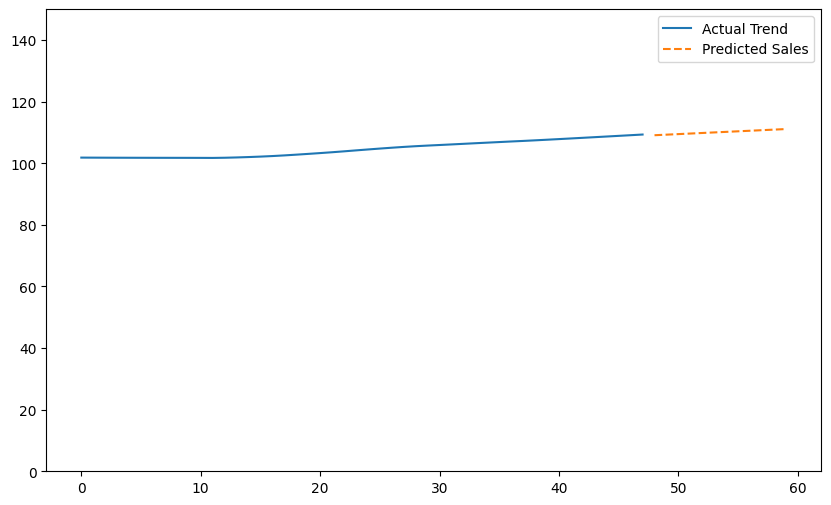
季節成分を予測したトレンド成分に追加しプロットします。

今回は、季節成分そのものはモデル化しませんが、状況によっては季節成分そのものをモデル化することもあります。

以下、コードです。

# トレンド予測に季節成分を追加
# まずは季節成分の最後の12ヶ月（1年間）のデータを取得します。
last_year_seasonal = seasonal[-12:]

# 実際のトレンドにも季節成分を加えてプロットするため、元のデータの季節成分を取得します。
actual_sales_with_seasonality = df_sales['Sales'][-len(X):]

# 予測されたトレンドに季節成分を加算して最終的な売上予測を行います。
final_sales_prediction = future_sales + last_year_seasonal.values

# 予測結果の可視化
plt.figure(figsize=(10, 6))
plt.plot(X, actual_sales_with_seasonality, label='Actual Sales')
plt.plot(future_X, future_sales, label='Predicted Trend', linestyle='--')
plt.plot(future_X, final_sales_prediction, label='Predicted Sales with Seasonality', linestyle='--')
plt.ylim(0,150) 
plt.legend()
plt.show()

このコードは、線形回帰によるトレンド予測に季節成分を追加し、最終的な売上予測に季節性を考慮するプロセスを実装しています。

季節成分の取得:
- last_year_seasonal = seasonal[-12:]で季節成分の最後の12ヶ月分のデータを取得します。
- これは、予測期間に相当する季節性パターンを反映するために使用されます。
実際の売上データに季節成分を加える:
- actual_sales_with_seasonality = df_sales['Sales'][-len(X):]で、分析対象の期間における実際の売上データ（トレンドと季節性が含まれる）を取得します。
最終的な売上予測の計算:
- final_sales_prediction = future_sales + last_year_seasonal.valuesで、予測されたトレンドに先ほど取得した季節成分を加算し、最終的な売上予測を行います。
- これにより、季節性を考慮した予測値が得られます。
予測結果の可視化:
- plt.figure(figsize=(10, 6))で可視化する図のサイズを指定します。
- plt.plot(X, actual_sales_with_seasonality, label='Actual Sales')で、実際の売上データ（トレンドと季節性を含む）をプロットします。
- plt.plot(future_X, future_sales, label='Predicted Trend', linestyle='--')で、予測されたトレンド（季節性を除く）を点線でプロットします。
- plt.plot(future_X, final_sales_prediction, label='Predicted Sales with Seasonality', linestyle='--')で、季節性を考慮した最終的な売上予測を点線でプロットします。
- plt.ylim(0,150)でy軸の範囲を指定します（必要に応じて調整）。
- plt.legend()で凡例を表示します。
- plt.show()で図を表示します。

以下、実行結果です。

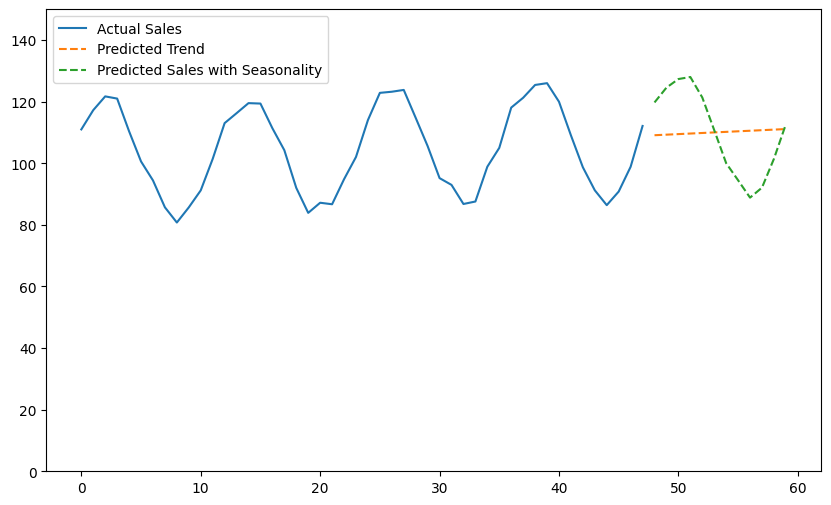
このケーススタディでは、STL分解を用いて季節性とトレンドを抽出し、そのトレンド成分に基づいて線形回帰モデルで将来の売上を予測しました。

このアプローチにより、小売業者はプロモーション活動の計画や在庫レベルの調整に有用な情報を得ることができます。

実際のビジネスでは、モデルの選択やパラメータの調整により、さらに精度の高い予測が可能になります。

STL分解を活用したビジネスの戦略立案と変革

STL分解による時系列分析を活用し、より情報に基づいた戦略的意思決定を行うことが可能になります。

　トレンド分析からの戦略立案

市場成長の機会の特定
トレンド成分の上昇は市場拡大や需要増加を示しています。この情報を基に、新しい市場セグメントの開拓や、製品ラインの拡張などの成長戦略を検討できます。

将来のリスクの予測
トレンド成分の減少は、市場の縮小や競争の激化を示唆している可能性があります。これに対しては、コスト削減、効率化、あるいは差別化戦略の強化が考えられます。

　季節変動を利用したプロモーション戦略

ピーク時期の利益最大化
季節成分の分析により、特定の時期に需要が高まることが明らかになった場合、その期間に合わせてプロモーション活動や在庫調整を行うことで、利益を最大化できます。

オフシーズンの売上促進
需要が低下する時期には、割引キャンペーンや限定オファーを通じて顧客の関心を喚起し、売上を促進することが可能です。

　不確実性の管理とリスク評価

異常値の監視と対応
残差成分の分析により、通常のトレンドや季節性から逸脱する異常なデータポイントを特定できます。これらは、外部イベントや市場の変動などの影響によるものである可能性があり、迅速な対応が求められることがあります。

リスクマネジメント
残差成分の変動幅を分析することで、ビジネスが直面する可能性のあるリスクレベルを評価し、それに応じた対策を講じることができます。

　ビジネス変革

STL分解をはじめとする時系列分析は、ビジネスにおけるデータ駆動型意思決定を支援し、組織の戦略的方向性を大きく変える可能性を秘めています。

STL分解を利用することで、ビジネスは以下のような多様な領域でプロセスを最適化し、効率を向上させることができます。

在庫管理: 季節性とトレンドの予測に基づいて、在庫レベルを最適化し、過剰在庫や品切れを防ぎます。
価格戦略: 市場の需要動向を反映した柔軟な価格戦略を立案し、収益性を最大化します。
プロモーションとマーケティング: 季節性の分析に基づき、プロモーションのタイミングを計画し、マーケティング効果を高めます。

時系列分析を通じて得られる未来の市場動向の予測は、組織の長期的な戦略立案に不可欠です。STL分解による分析結果は、新規事業の機会評価、リスク管理、資源配分の最適化など、戦略的な意思決定に活用されます。

まとめ

今回は、ビジネスデータを解き明かすための強力なツールであるSTL分解と時系列分析の基本を説明しました。

STL分解を活用することで、ビジネスは時系列データの背後にあるトレンド、季節性、そして残差成分を明らかにし、これらの洞察を基により精度の高い予測を行う可能性が広がります。

小売業者のケーススタディを例に挙げ、STL分解がいかにビジネスプロセスの最適化、在庫管理、プロモーション戦略、そして戦略的意思決定に貢献するかを取り上げました。

また、季節性やトレンドを正確に捉えることの重要性と、それらを予測モデルに統合する方法についても簡単に解説しました。

STL分解をはじめとする時系列分析技術は、データに基づいた洞察を提供し、ビジネスの意思決定プロセスを大きく変革する力を持っています。

データのトレンドを理解し、未来を予測する能力は、競争が激化する市場において組織が成功を収めるための鍵となります。