時系列分析は、過去のデータから未来を予測する重要な手段です。経済、金融、気象予報など多岐にわたる分野で用いられ、データの時間的な変動を捉えることで、より正確な意思決定をサポートします。

説明変数を時系列モデルに組み込むことで、モデルの予測精度を向上させることができます。

これらの変数はモデルに追加情報を提供し、単に過去のデータパターンだけではなく、外部からの影響を反映させることが可能になります。

説明変数を組み込んだ時系列モデルの1つが、RegARIMAモデルです。

今回は、「説明変数を組み込んだ時系列モデル『RegARIMA』のPython実装」というお話しをします。

時系列データとは何か

時系列データとは、一定の時間間隔で順に記録されたデータのことです。

例えば、毎日の気温、毎月の売上などがこれにあたります。

各データ点はその時点の情報を含み、これにより時間に関連したトレンドや繰り返しパターンを分析することができます。

このようなデータの分析を通じて、未来の動向を予測したり、過去のパターンを理解することが可能です。

 

ARIMAモデルとその拡張

RegARIMAの説明の前に、ARIMA系のモデルを幾つか紹介します。

　ARモデル（自己回帰モデル、Autoregressive）

自己回帰モデルは、過去の値が未来の値に影響を与えるという考えに基づいています。次の値 y_t は、過去の p 期間の値の線形結合として表現されます。

以下、コード例です。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX

# モデルパラメータを設定
order = (1, 0, 0)  # ARIMA(p, d, q)のパラメータ

# ARモデルの定義
model = SARIMAX(
    endog=np.array([]), 
    order=order, 
    seasonal=False)

# モデルパラメーターのダミー値を設定
np.random.seed(123)
params = np.random.rand(model.k_params)

# データのシミュレーション
simulated_data = model.simulate(params, nsimulations=100)

# シミュレーションデータのプロット
plt.figure(figsize=(10, 6))
plt.plot(simulated_data)
plt.title('AR(1) Process Simulation')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

 

以下、実行結果です。

 

　MAモデル（移動平均モデル、Moving Average）

移動平均モデルでは、過去の予測誤差が現在の値に影響を与えると考えます。
次の値 y_t は、過去 q 期間の予測誤差の線形結合として表現されます。

以下、コード例です。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX

# モデルパラメータを設定
order = (0, 0, 1)  # ARIMA(p, d, q)のパラメータ

# MAモデルの定義
model = SARIMAX(
    endog=np.array([]), 
    order=order, 
    seasonal=False)

# モデルパラメーターのダミー値を設定
np.random.seed(123)
params = np.random.rand(model.k_params)

# データのシミュレーション
simulated_data = model.simulate(params, nsimulations=100)

# シミュレーションデータのプロット
plt.figure(figsize=(10, 6))
plt.plot(simulated_data)
plt.title('MA(1) Process Simulation')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

 

以下、実行結果です。

 

　ARMAモデル

ARMAモデルはARとMAモデルを組み合わせたもので、過去の値と過去の誤差が現在の値に影響を与えます。

以下、コード例です。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX

# モデルパラメータを設定
order = (0, 0, 1)  # ARIMA(p, d, q)のパラメータ

# MAモデルの定義
model = SARIMAX(
    endog=np.array([]), 
    order=order, 
    seasonal=False)

# モデルパラメーターのダミー値を設定
np.random.seed(123)
params = np.random.rand(model.k_params)

# データのシミュレーション
simulated_data = model.simulate(params, nsimulations=100)

# シミュレーションデータのプロット
plt.figure(figsize=(10, 6))
plt.plot(simulated_data)
plt.title('MA(1) Process Simulation')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

 

以下、実行結果です。

 

　ARIMAモデル

ARIMAモデル（自己回帰和分移動平均モデル）は、非定常時系列データに対して効果的な予測モデルです。

ARIMAは「和分（Integrated）」の概念を取り入れたARMAモデルの一般化形式であり、データを定常化するために差分を取るプロセスを含んでいます。

以下、コード例です。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX

# モデルパラメータを設定
order = (1, 1, 1)  # ARIMA(p, d, q)のパラメータ

# SARIMAXモデルの定義
model = SARIMAX(
    endog=np.array([]), 
    order=order, 
    seasonal=False)

# モデルパラメーターのダミー値を設定
np.random.seed(123)
params = np.random.rand(model.k_params)

# データのシミュレーション
simulated_data = model.simulate(params, nsimulations=100)

# シミュレーションデータのプロット
plt.figure(figsize=(10, 6))
plt.plot(simulated_data_arima, label='ARIMA(1,1,1) Process Simulation')
plt.title('ARIMA(1,1,1) Process Simulation')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()

 

以下、実行結果です。

 

　季節性ARIMA（SARIMA）

SARIMAモデルは季節変動を考慮したARIMAモデルで、季節的なパターンを持つデータに適しています。

SARIMAモデルでは、非季節的なパラメータ（p, d, q）と季節的なパラメータ（P, D, Q, m）の両方を指定します。

以下、コード例です。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX

# モデルパラメータを設定
order = (1, 1, 1)  # ARIMA(p, d, q)のパラメータ
seasonal_order = (1, 1, 1, 12)  # 季節成分(S, D, Q, s)のパラメータ

# SARIMAXモデルの定義
model = SARIMAX(
    endog=np.array([]), 
    order=order, 
    seasonal_order=seasonal_order)

# モデルパラメーターのダミー値を設定
np.random.seed(123)
params = np.random.rand(model.k_params)

# データのシミュレーション
simulated_data = model.simulate(params, nsimulations=100)

# シミュレーションデータのプロット
plt.figure(figsize=(10, 6))
plt.plot(simulated_data)
plt.title('SARIMA(1,1,1)(1,1,1,12) Process Simulation')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

 

以下、実行結果です。

 

　ARIMAXモデル（外生変数付きARIMA）

ARIMAXモデルは、外生変数（説明変数）を組み込んだARIMAモデルです。このモデルは、外部からの影響を反映したい場合に適しています。

以下、コード例です。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX

# モデルパラメータを設定
order = (1, 1, 1)  # ARIMA(p, d, q)のパラメータ

# ダミーデータを設定し、一時的なレベルシフトを表現
endog_data = np.zeros(100)  # Xに相当するダミーデータ
endog_data[40:60] = 1  # 40から59までの値に対して一時的にレベルを上げる

# SARIMAXモデルの定義
model = SARIMAX(
    endog=endog_data, 
    order=order, 
    seasona=False)

# モデルパラメーターのダミー値を設定
np.random.seed(123)
params = np.random.rand(model.k_params)

# データのシミュレーション
simulated_data = model.simulate(params, nsimulations=100)-endog_data*10

# シミュレーションデータのプロット
plt.figure(figsize=(10, 6))
plt.plot(simulated_data)
plt.title('ARIMAX(1,1,1) Process Simulation')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

 

以下、実行結果です。

 

RegARIMAモデルの紹介

　RegARIMAモデルの概念と構造

RegARIMA（Regression with ARIMA errors）モデルは、時系列データの予測を改善するために、線形回帰モデルとARIMAモデリングを組み合わせたアプローチです。

このモデルは、まず外生変数（説明変数）を使用して線形回帰モデルの構築を行い、その後、回帰モデルの残差に対してARIMAモデルを適用します。

この手法は、回帰分析から得られる誤差の構造をモデル化し、より正確な予測を行うことを可能にします。

 

　RegARIMAとARIMAXの比較

RegARIMAとARIMAXは共に外生変数（説明変数）を取り入れる点で共通していますが、アプローチには重要な違いがあります。

 

　　ARIMAX モデルのメリットとデメリット

ARIMAXは、外生変数を直接時系列モデルの一部として組み込み、時系列データと外生変数の間の直接的な相互作用をモデル化したものです。

以下は、このモデルのメリットです。

直接的な統合
ARIMAXモデルは時系列データのダイナミクス（自己回帰部分と移動平均部分）と外生変数の影響を直接的に一つのモデルで統合します。これにより、外生変数と目的変数の間の相互作用をモデル内で直接捉えることができます。

単一モデル
パラメータの推定や予測が一つの統合モデル内で完結するため、モデルの扱いや解釈が直接的である。

以下、デメリットです。

パラメータの推定が困難
複数のパラメータ（自己回帰、移動平均、外生変数の係数）を同時に推定する必要があるため、データが十分でない場合やモデルが複雑な場合、過剰適合や推定の不安定さが生じやすい。

モデルの複雑性
外生変数の影響が時間ダイナミクスと混在するため、その効果を分離して解釈することが難しい場合があります。

 

　　RegARIMA モデルのメリットとデメリット

RegARIMAでは、外生変数に基づいた線形回帰を先に実施し、その残差を用いてARIMAモデルを構築します。

以下は、このモデルのメリットです。

明確な影響分離
線形回帰で外生変数の影響を先にモデル化し、その残差に対してARIMAモデルを適用するため、各変数の影響をより明確に分離して理解できます。

柔軟性
初めに回帰モデルを用いることで、非時系列のデータやカテゴリカルなデータを容易に取り入れることができる。また、残差に対するモデルが適切であれば、より良い予測精度を達成することが可能です。

以下、デメリットです。

二段階の手続き
モデルの構築が二段階に分かれるため、全体としてのモデル構築や診断が複雑になることがあります。

独立性の仮定
回帰分析の残差が独立であるという仮定に基づいていますが、この仮定が崩れると残差のARIMAモデルが不適切な結果をもたらす可能性があります。

 

　　注意点

データの構造の理解
どちらのモデルもデータの構造や変数間の関係を正しく理解し、適切なモデルを選択することが重要です。

パラメータの適切な推定
外生変数（説明変数）の数やモデルの複雑さが推定を困難にする場合、情報量規準などを用いてモデルの選択を行うことが必要です。

モデルの診断と評価
どちらのモデルも残差の分析や予測精度の評価が重要であり、適切な診断手法を用いることが必要です。

選択するモデルは、データの性質、目的、そして解釈の容易さなどに基づいて慎重に行うべきです。

どちらのアプローチもそれぞれの場面で有効ですが、具体的な状況やデータの特性に最も適合するものを選ぶことが肝心です。

 

　RegARIMA モデルの構築手順

RegARIMA（回帰分析による残差のARIMAモデリング）モデルの構築は、いくつかのステップに分けられます。

以下は、このモデルを構築するための一般的な手順です。

ステップ 1: データの準備

• データ収集: 対象となる時系列データおよび外生変数を収集します。
• データのクレンジング: 欠損値の処理や異常値の検討を行います。
• 変数の変換: 必要に応じて、ログ変換や差分取りなどの変換を外生変数に対して行います。

ステップ 2: 回帰モデルの構築

• 変数の選択: 目的変数に影響を与える可能性のある外生変数を選択します。
• モデルの推定: 線形回帰モデルを用いて、外生変数と目的変数との関係をモデル化します。
• モデルの診断: 推定した回帰モデルの診断を行い、モデルがデータに適合しているか評価します（例えば、残差のプロット、F統計量、R^2値など）。

ステップ 3: 残差の時系列分析

• 残差の抽出: ステップ2で構築したモデルの残差を計算します。
• 残差の定常性チェック: 残差が定常であるかどうかを確認します（ADF検定など）。
• ARIMAモデルの選定と推定: 残差に対して適切なARIMAモデル（パラメータのp, d, qの選択）を選び、パラメータを推定します。

ステップ 4: モデルの検証

• 残差の診断: ARIMAモデルの残差が白色雑音になっているかどうかをチェックします。
• 予測性能の評価: 時系列のクロスバリデーションや保留サンプルによるモデルの予測性能を評価します。
• モデルの比較: 必要に応じて他のモデルとの比較を行い、最も適したモデルを選択します。

ステップ 5: モデルの適用

• 予測の実施: 最終的なモデルを使用して未来の値の予測を行います。
• モデルの更新: 新たなデータが利用可能になった場合、モデルを再推定し、パラメータを更新します。

 

　RegARIMAモデルのPython実装

PythonでRegARIMAモデルを実装する例を示します。

ここでは、statsmodelsとscikit-learnの機能を利用してモデルを組み立てます。

以下、コードです。

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error

# データ生成
np.random.seed(0)
dates = pd.date_range(start='2020-01-01', periods=100)
X = np.random.normal(size=(100, 1))  # 外生変数
y = 2.5 * X.squeeze() + np.random.normal(size=100)  # 時系列データ

# 線形回帰モデル
reg = LinearRegression().fit(X, y)
y_pred = reg.predict(X)
residuals = y - y_pred

# ARIMAモデルを残差に適用
arima_model = ARIMA(residuals, order=(3,0,1))
arima_result = arima_model.fit() 

# 残差の予測
residuals_pred = arima_result.predict(start=1, end=100)

# 最終予測
final_pred = y_pred + residuals_pred

# 評価
mse = mean_squared_error(y, final_pred)
print("MSE:", mse)

 

このコードを簡単に説明します。

• ライブラリのインポート:
  • numpyとpandasをインポートしてデータ操作と数学的処理を行います。
  • LinearRegressionをsklearnからインポートして線形回帰分析を行います。
  • ARIMAをstatsmodelsからインポートして時系列予測を行います。
  • mean_squared_errorをsklearnからインポートして予測の精度を評価します。
• データ生成:
  • numpyの乱数シードを固定します。
  • pd.date_rangeを用いて100日間の日付データを生成します。
  • 正規分布からランダムな外生変数Xを生成します。
  • Xを使って線形関係に従いつつノイズが加えられた目的変数yを生成します。
• 線形回帰モデルの適用:
  • LinearRegressionを使用してXからyを予測するモデルを構築します。
  • 予測値y_predを計算します。
  • 実際のyと予測値y_predの差（残差）を計算します。
• ARIMAモデルの適用:
  • 残差データに対してARIMAモデルを適用します。
  • この例では、自己回帰の次数を3、差分の次数を0、移動平均の次数を1としています。
  • ARIMAモデルをフィットさせます。
• 残差の予測:
  • フィットしたARIMAモデルを使用して、学習データ範囲内での残差の予測値を計算します。
• 最終予測の計算:
  • 線形回帰の予測値とARIMAモデルによる残差の予測値を合算して、最終的な予測値を得ます。
• モデル評価:
  • mean_squared_errorを使用して、実際のy値と最終予測値との間の平均二乗誤差（MSE）を計算し、出力します。
  • これによりモデルの予測精度が評価されます。

 

以下、実行結果です。

MSE: 1.1759591143464996

 

　RegARIMAクラスの作成

Pythonには、現在（2024/04/17）ではRegARIMAクラスが実装されているライブラリがないようです。

そのため、先ほど示した通り、回帰分析を実施し、その後にARIMAモデルを適用するという手間が発生しました。

毎度毎度このコードを繰り返すのは面倒なのです。

 

そこで、ここでは、scikit-learn（sklearn）ベースのRegARIMAクラスを定義します。後で、このクラスを使った分析例を提示します。

今回は、純粋な線形回帰モデルではなく、正則項付きの線形回帰モデルの一種である、Ridge回帰モデルを組み込んだRegARIMAモデルのクラスになります。

Ridge回帰にした理由は、正則項のより過学習やマルチコなどの良くない減少を緩和させるためです。

 

以下、コードです。

#
# RegARIMAモデルのクラスの定義
#

class RegARIMAModel:
    def __init__(self, ridge_alpha=1.0):
        """
        RegARIMAモデルクラスを初期化
        :param ridge_alpha: Ridge回帰の正則化パラメータ
        """
        self.ridge_alpha = ridge_alpha
        self.ridge_model = Ridge(alpha=ridge_alpha)
        self.arima_model = None
        self.residuals = None

    def fit(self, X, y):
        """
        モデルをデータにフィットさせる
        :param X: 説明変数のndarray
        :param y: 目的変数のndarray
        """
        # Ridge回帰でフィット
        self.ridge_model.fit(X, y)
        
        # Ridge回帰の残差を計算
        predictions = self.ridge_model.predict(X)
        self.residuals = y - predictions
        
        # 残差に対してauto_arimaを実行
        self.arima_model = auto_arima(self.residuals, seasonal=False, stepwise=False,
                                      suppress_warnings=True, error_action="ignore", trace=False)

    def predict_in_sample(self, X):
        """
        学習データに対する予測値を出力する
        :param X: 説明変数のndarray
        :return: 予測された値
        """
        # Ridge回帰からの予測
        ridge_predictions = self.ridge_model.predict(X)
        
        # ARIMAモデルからの学習データの予測値
        arima_predictions = self.arima_model.predict_in_sample()
        
        # Ridgeの予測とARIMAの予測の和を返す
        return ridge_predictions + arima_predictions

    def predict(self, X, n_periods=1):
        """
        モデルを使って予測する
        :param X: 説明変数のndarray
        :param n_periods: 予測する期間の数
        :return: 予測された値
        """
        # Ridge回帰からの予測
        ridge_predictions = self.ridge_model.predict(X)
        
        # ARIMAモデルからの未来予測
        arima_predictions = self.arima_model.predict(n_periods=n_periods)
        
        # Ridgeの予測とARIMAの予測の和を返す
        return ridge_predictions + arima_predictions[0]

 

このクラスは、線形回帰（リッジ回帰）とARIMAを組み合わせた時系列モデル、すなわちRegARIMAモデルを実装しています。

• クラスの初期化 (__init__ メソッド)
  • ridge_alpha: リッジ回帰の正則化パラメータを指定します。デフォルトは1.0です。
  • self.ridge_model: Ridge オブジェクトを作成し、正則化パラメータ alpha に ridge_alpha を設定します。
  • self.arima_model: 初期状態ではNoneで、後にARIMAモデルがここに格納されます。
  • self.residuals: リッジ回帰後の残差を格納するための変数で、初期状態ではNoneです。
• モデルのフィット (fit メソッド)
  • X: 説明変数の配列（ndarray形式）。
  • y: 目的変数の配列（ndarray形式）。
  • リッジ回帰モデルにXとyをフィットさせ、予測値を計算します。
  • self.residuals: 実際の値 y とリッジ回帰による予測値の差（残差）を計算し保存します。
  • self.arima_model: 残差に対して auto_arima を実行し、最適なパラメータを持つARIMAモデルを自動的に選択します。
• 学習データに対する予測 (predict_in_sample メソッド)
  • リッジ回帰モデルからの予測値とARIMAモデルからの学習データの予測値を合算して最終的な予測値を生成します。
• 新しいデータに対する予測 (predict メソッド)
  • n_periods: 未来予測する期間の数を指定します。
  • リッジ回帰モデルとARIMAモデルの両方から予測値を生成し、それらを合算して最終的な予測結果を提供します。

一様、scikit-learn（sklearn）ベースのパイプラインなどでも使えるかと思います。

今回は、Ridge回帰でしたが、他の回帰系のモデルで置き換えても問題ございません。

 

RegARIMAの実行例

　準備

今回利用するモジュールを読み込みます。

よくあるものが多いですが、optuna や pmdarima などをインストールされていない方は、pip や conda などでインストールしておいてください。

以下、コードです。

#
# 必要なモジュールの読み込み
#

import pandas as pd
import numpy as np
import datetime
import optuna

from functools import partial

from pmdarima import auto_arima
from sklearn.linear_model import Ridge

from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error

from pmdarima import model_selection

import warnings
warnings.simplefilter('ignore')

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

RegARIMAモデルのクラスの定義をします。先ほど説明したものと同じものです。

以下、コードです。

#
# RegARIMAモデルのクラスの定義
#

class RegARIMAModel:
    def __init__(self, ridge_alpha=1.0):
        """
        RegARIMAモデルクラスを初期化
        :param ridge_alpha: Ridge回帰の正則化パラメータ
        """
        self.ridge_alpha = ridge_alpha
        self.ridge_model = Ridge(alpha=ridge_alpha)
        self.arima_model = None
        self.residuals = None

    def fit(self, X, y):
        """
        モデルをデータにフィットさせる
        :param X: 説明変数のndarray
        :param y: 目的変数のndarray
        """
        # Ridge回帰でフィット
        self.ridge_model.fit(X, y)
        
        # Ridge回帰の残差を計算
        predictions = self.ridge_model.predict(X)
        self.residuals = y - predictions
        
        # 残差に対してauto_arimaを実行
        self.arima_model = auto_arima(self.residuals, seasonal=False, stepwise=False,
                                      suppress_warnings=True, error_action="ignore", trace=False)

    def predict_in_sample(self, X):
        """
        学習データに対する予測値を出力する
        :param X: 説明変数のndarray
        :return: 予測された値
        """
        # Ridge回帰からの予測
        ridge_predictions = self.ridge_model.predict(X)
        
        # ARIMAモデルからの学習データの予測値
        arima_predictions = self.arima_model.predict_in_sample()
        
        # Ridgeの予測とARIMAの予測の和を返す
        return ridge_predictions + arima_predictions

    def predict(self, X, n_periods=1):
        """
        モデルを使って予測する
        :param X: 説明変数のndarray
        :param n_periods: 予測する期間の数
        :return: 予測された値
        """
        # Ridge回帰からの予測
        ridge_predictions = self.ridge_model.predict(X)
        
        # ARIMAモデルからの未来予測
        arima_predictions = self.arima_model.predict(n_periods=n_periods)
        
        # Ridgeの予測とARIMAの予測の和を返す
        return ridge_predictions + arima_predictions[0]

 

データセットを読み込みます。

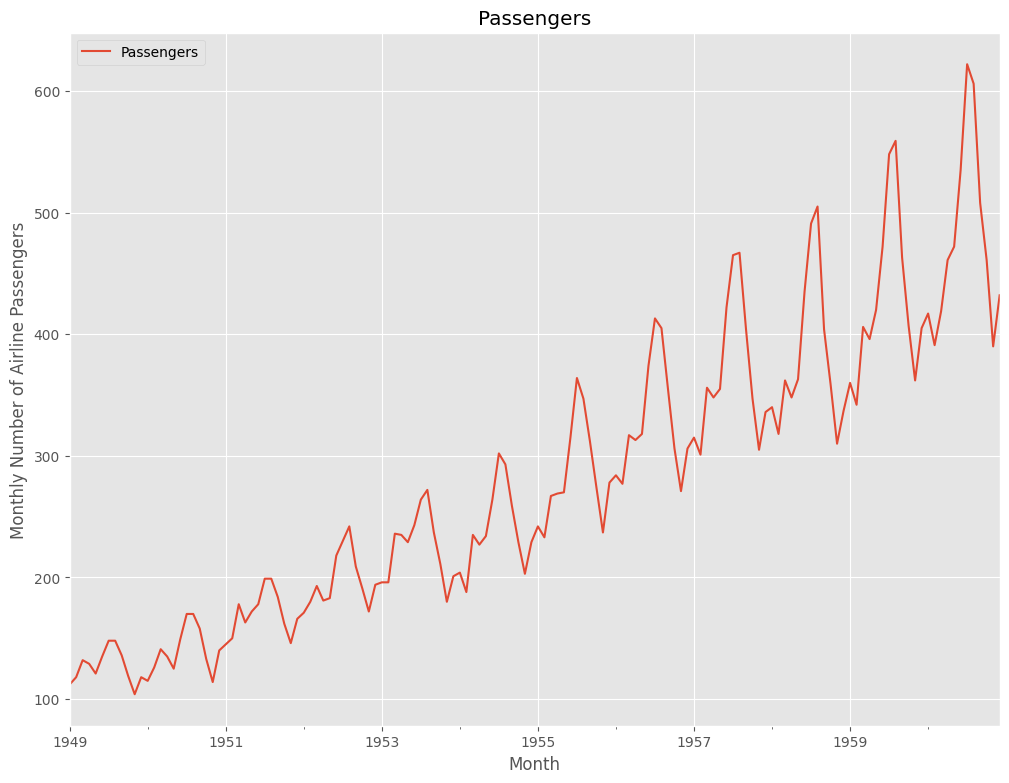
今回利用する時系列データのデータセットは、Airline Passengers（飛行機乗客数）です。Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

以下、コードです。

#
# Airline passenger データセットの読み込み
#

dataset = 'https://www.salesanalytics.co.jp/2024_ts_df1'  #データセットのあるURL
df = pd.read_csv(dataset,                    #読み込むデータセット
                index_col='Month',           #変数「Month」をインデックスに設定
                parse_dates=True)            #インデックスを日付型に設定

print(df) #確認

 

以下、実行結果です。

            Passengers
Month                 
1949-01-01         112
1949-02-01         118
1949-03-01         132
1949-04-01         129
1949-05-01         121
...                ...
1960-08-01         606
1960-09-01         508
1960-10-01         461
1960-11-01         390
1960-12-01         432

[144 rows x 1 columns]

 

どのようなデータなのか、プロットし確認します。

以下、コードです。

# プロット
df.plot()
plt.title('Passengers')                               #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers')    #タテ軸のラベル
plt.xlabel('Month')                                   #ヨコ軸のラベル
plt.show()

 

以下、実行結果です。

 

季節性を表現する特徴量を、三角関数（Sin , Cos）で生成します。

SinとCosのセットであるフーリエ項（基底）をその程度作るのかで、季節性の表現の柔軟性が変わります。多ければ多いほど柔軟な表現になります。フーリエ項（基底）の係数は、データで後で学習し求めます。

まず、フーリエ項（基底）を生成し元のデータセットに付け加える関数を定義します。

以下、コードです。

#
# 三角関数特徴量の生成関数を定義
#

def add_fourier_terms(df, num, seasonal):
    '''
    引数df: 元のデータフレーム
    引数num: フーリエ項の数（基底の数）、sinとcosのセット数
    引数seasonal: フーリエ変換の周期
    戻り値: フーリエ項を追加後のデータフレーム
    '''
    # t列がdfにない場合、t列を0からdfの長さまでの連番で作成
    if 't' not in df.columns:
        df['t'] = pd.RangeIndex(start=0, stop=len(df))

    # 三角関数特徴量(フーリエ項)を追加
    for i in range(1, num + 1):
        # sin項を追加
        df['sin_' + str(i)] = np.sin(i * 2 * np.pi * df.t / seasonal)
        # cos項を追加
        df['cos_' + str(i)] = np.cos(i * 2 * np.pi * df.t / seasonal)

    return df

#
# 三角関数特徴量とトレンド項の交互作用項の生成関数を定義
#

def add_interaction_terms(df, num):
    """
    DataFrameの't'列とsin, cos変数の積を新たな変数として追加する関数
    """
    for i in range(1, num+1):
        df[f't_sin_{i}'] = df['t'] * df[f'sin_{i}']
        df[f't_cos_{i}'] = df['t'] * df[f'cos_{i}']
    
    return df

 

この関数を使い、季節成分を生成しデータセットに加えます。

以下、コードです。

# 三角関数特徴量を追加したデータフレームを表示して確認
df = add_fourier_terms(df, num=5, seasonal=12)

print(df) #確認

 

以下、実行結果です。

            Passengers    t     sin_1         cos_1         sin_2  cos_2  \
Month                                                                      
1949-01-01         112    0  0.000000  1.000000e+00  0.000000e+00    1.0   
1949-02-01         118    1  0.500000  8.660254e-01  8.660254e-01    0.5   
1949-03-01         132    2  0.866025  5.000000e-01  8.660254e-01   -0.5   
1949-04-01         129    3  1.000000  6.123234e-17  1.224647e-16   -1.0   
1949-05-01         121    4  0.866025 -5.000000e-01 -8.660254e-01   -0.5   
...                ...  ...       ...           ...           ...    ...   
1960-08-01         606  139 -0.500000 -8.660254e-01  8.660254e-01    0.5   
1960-09-01         508  140 -0.866025 -5.000000e-01  8.660254e-01   -0.5   
1960-10-01         461  141 -1.000000 -1.175970e-14  2.351941e-14   -1.0   
1960-11-01         390  142 -0.866025  5.000000e-01 -8.660254e-01   -0.5   
1960-12-01         432  143 -0.500000  8.660254e-01 -8.660254e-01    0.5   

                   sin_3         cos_3         sin_4  cos_4     sin_5  \
Month                                                                   
1949-01-01  0.000000e+00  1.000000e+00  0.000000e+00    1.0  0.000000   
1949-02-01  1.000000e+00  6.123234e-17  8.660254e-01   -0.5  0.500000   
1949-03-01  1.224647e-16 -1.000000e+00 -8.660254e-01   -0.5 -0.866025   
1949-04-01 -1.000000e+00 -1.836970e-16 -2.449294e-16    1.0  1.000000   
1949-05-01 -2.449294e-16  1.000000e+00  8.660254e-01   -0.5 -0.866025   
...                  ...           ...           ...    ...       ...   
1960-08-01 -1.000000e+00 -1.028765e-14  8.660254e-01   -0.5 -0.500000   
1960-09-01  1.274375e-14  1.000000e+00 -8.660254e-01   -0.5  0.866025   
1960-10-01  1.000000e+00  2.106826e-14 -4.703882e-14    1.0 -1.000000   
1960-11-01 -1.963149e-15 -1.000000e+00  8.660254e-01   -0.5  0.866025   
1960-12-01 -1.000000e+00 -3.427154e-15 -8.660254e-01   -0.5 -0.500000   

                   cos_5  
Month                     
1949-01-01  1.000000e+00  
1949-02-01 -8.660254e-01  
1949-03-01  5.000000e-01  
1949-04-01  1.194340e-15  
1949-05-01 -5.000000e-01  
...                  ...  
1960-08-01  8.660254e-01  
1960-09-01 -5.000000e-01  
1960-10-01 -1.616596e-14  
1960-11-01  5.000000e-01  
1960-12-01 -8.660254e-01  

[144 rows x 12 columns]

 

さらに、季節成分とトレンドの交互作用項を付け加えます。

以下、コードです。

# 関数を呼び出して、dfに交互作用項を追加
df = add_interaction_terms(df, num=5)

print(df) #確認

 

以下、実行結果です。

            Passengers    t     sin_1         cos_1         sin_2  cos_2  \
Month                                                                      
1949-01-01         112    0  0.000000  1.000000e+00  0.000000e+00    1.0   
1949-02-01         118    1  0.500000  8.660254e-01  8.660254e-01    0.5   
1949-03-01         132    2  0.866025  5.000000e-01  8.660254e-01   -0.5   
1949-04-01         129    3  1.000000  6.123234e-17  1.224647e-16   -1.0   
1949-05-01         121    4  0.866025 -5.000000e-01 -8.660254e-01   -0.5   
...                ...  ...       ...           ...           ...    ...   
1960-08-01         606  139 -0.500000 -8.660254e-01  8.660254e-01    0.5   
1960-09-01         508  140 -0.866025 -5.000000e-01  8.660254e-01   -0.5   
1960-10-01         461  141 -1.000000 -1.175970e-14  2.351941e-14   -1.0   
1960-11-01         390  142 -0.866025  5.000000e-01 -8.660254e-01   -0.5   
1960-12-01         432  143 -0.500000  8.660254e-01 -8.660254e-01    0.5   

                   sin_3         cos_3         sin_4  cos_4  ...     t_sin_1  \
Month                                                        ...               
1949-01-01  0.000000e+00  1.000000e+00  0.000000e+00    1.0  ...    0.000000   
1949-02-01  1.000000e+00  6.123234e-17  8.660254e-01   -0.5  ...    0.500000   
1949-03-01  1.224647e-16 -1.000000e+00 -8.660254e-01   -0.5  ...    1.732051   
1949-04-01 -1.000000e+00 -1.836970e-16 -2.449294e-16    1.0  ...    3.000000   
1949-05-01 -2.449294e-16  1.000000e+00  8.660254e-01   -0.5  ...    3.464102   
...                  ...           ...           ...    ...  ...         ...   
1960-08-01 -1.000000e+00 -1.028765e-14  8.660254e-01   -0.5  ...  -69.500000   
1960-09-01  1.274375e-14  1.000000e+00 -8.660254e-01   -0.5  ... -121.243557   
1960-10-01  1.000000e+00  2.106826e-14 -4.703882e-14    1.0  ... -141.000000   
1960-11-01 -1.963149e-15 -1.000000e+00  8.660254e-01   -0.5  ... -122.975607   
1960-12-01 -1.000000e+00 -3.427154e-15 -8.660254e-01   -0.5  ...  -71.500000   

                 t_cos_1       t_sin_2  t_cos_2       t_sin_3       t_cos_3  \
Month                                                                         
1949-01-01  0.000000e+00  0.000000e+00      0.0  0.000000e+00  0.000000e+00   
1949-02-01  8.660254e-01  8.660254e-01      0.5  1.000000e+00  6.123234e-17   
1949-03-01  1.000000e+00  1.732051e+00     -1.0  2.449294e-16 -2.000000e+00   
1949-04-01  1.836970e-16  3.673940e-16     -3.0 -3.000000e+00 -5.510911e-16   
1949-05-01 -2.000000e+00 -3.464102e+00     -2.0 -9.797174e-16  4.000000e+00   
...                  ...           ...      ...           ...           ...   
1960-08-01 -1.203775e+02  1.203775e+02     69.5 -1.390000e+02 -1.429984e-12   
1960-09-01 -7.000000e+01  1.212436e+02    -70.0  1.784126e-12  1.400000e+02   
1960-10-01 -1.658118e-12  3.316237e-12   -141.0  1.410000e+02  2.970624e-12   
1960-11-01  7.100000e+01 -1.229756e+02    -71.0 -2.787671e-13 -1.420000e+02   
1960-12-01  1.238416e+02 -1.238416e+02     71.5 -1.430000e+02 -4.900830e-13   

                 t_sin_4  t_cos_4     t_sin_5       t_cos_5  
Month                                                        
1949-01-01  0.000000e+00      0.0    0.000000  0.000000e+00  
1949-02-01  8.660254e-01     -0.5    0.500000 -8.660254e-01  
1949-03-01 -1.732051e+00     -1.0   -1.732051  1.000000e+00  
1949-04-01 -7.347881e-16      3.0    3.000000  3.583020e-15  
1949-05-01  3.464102e+00     -2.0   -3.464102 -2.000000e+00  
...                  ...      ...         ...           ...  
1960-08-01  1.203775e+02    -69.5  -69.500000  1.203775e+02  
1960-09-01 -1.212436e+02    -70.0  121.243557 -7.000000e+01  
1960-10-01 -6.632473e-12    141.0 -141.000000 -2.279400e-12  
1960-11-01  1.229756e+02    -71.0  122.975607  7.100000e+01  
1960-12-01 -1.238416e+02    -71.5  -71.500000 -1.238416e+02  

[144 rows x 22 columns]

 

学習データとテストデータ（直近12ヶ月間）に分割します。

予測モデルを作ってテストをしていきますので、データセットを学習データとテストデータに分割します。テストデータの期間は直近12ヶ月間で、それより前の期間が学習データです。

以下、コードです。

#
# データセットを学習データとテストデータ（直近12ヶ月間）に分割
#

# データ分割
train, test = model_selection.train_test_split(df, test_size=12)

# 学習データ
y_train = train['Passengers']              #目的変数y
X_train = train.drop('Passengers', axis=1) #説明変数X

# テストデータ
y_test = test['Passengers']              #目的変数y
X_test = test.drop('Passengers', axis=1) #説明変数X

 

目的変数をプロットし、確認します。

以下、コードです。

#
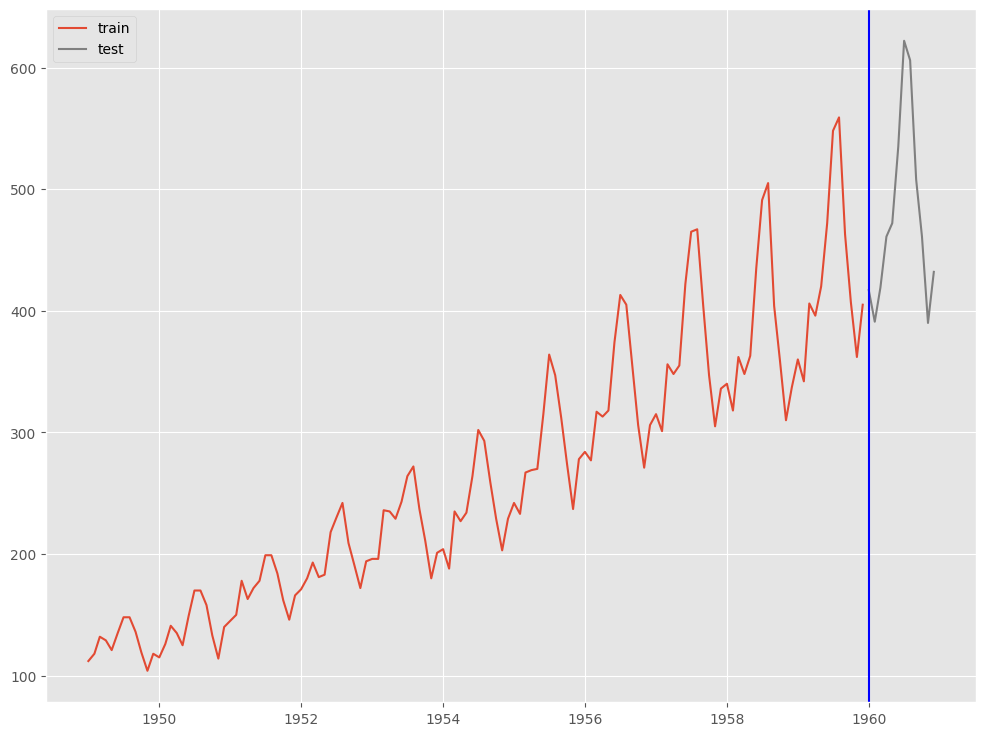
# グラフ（学習データとテストデータ）
#

fig, ax = plt.subplots()

# 学習データの描写
ax.plot(train.index.values, train.Passengers.values, label='train')

# テストデータの描写
ax.plot(test.index.values, test.Passengers.values, label='test', color='gray') 

# 学習データとテスデータの間の縦線の描写
ax.axvline(datetime.datetime(1960,1,1),color='blue') 

# 凡例表示
ax.legend() 

plt.show()

 

以下、実行結果です。

 

　RegARIMA

Ride回帰にはハイパーパラメータが1つ（正則項の重み）ありますが、デフォルトの設定のままモデル構築していきます。

予測モデルの学習（学習データ利用）をします。

以下、コードです。

# インスタンス作成
model = RegARIMAModel()

# 学習
model.fit(X_train, y_train)

 

予測モデルのテスト（テストデータ利用）をします。

以下、コードです。

#
# 予測の実施
#

# 学習データ期間の予測
train_pred = model.predict_in_sample(X = X_train)

# テストデータ期間の予測
test_pred = model.predict(n_periods=12,X = X_test)

 

予測精度を評価します。

以下、コードです。

#
# 予測精度（テストデータ）
#

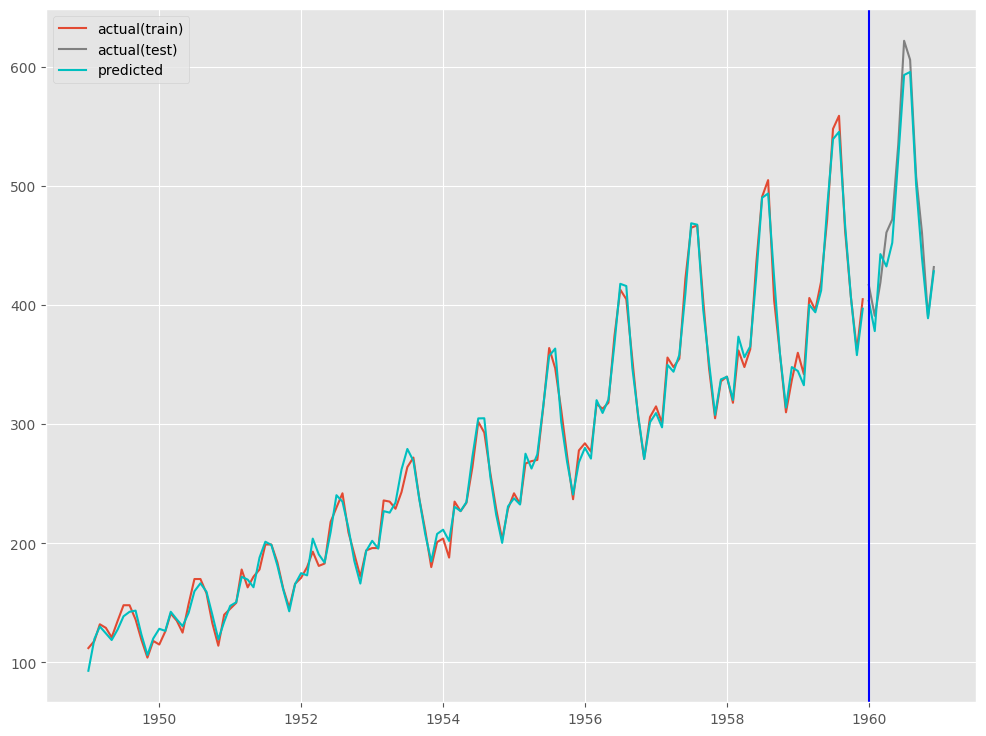
print('RMSE:\n',np.sqrt(mean_squared_error(test.Passengers, test_pred)))
print('MAE:\n',mean_absolute_error(test.Passengers, test_pred)) 
print('MAPE:\n',mean_absolute_percentage_error(test.Passengers, test_pred))

 

以下、実行結果です。

RMSE:
 17.537664126786577
MAE:
 15.125211964123471
MAPE:
 0.03171637185795654

 

プロットし確認してみます。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

# 実測値の描写
## 学習データ
ax.plot(train.index.values, train.Passengers.values, label='actual(train)')
## テストデータ
ax.plot(test.index.values, test.Passengers.values, label='actual(test)', color='gray')

# 予測値の描写
## 学習データ
ax.plot(train.index.values, train_pred, color='c')
## テストデータ
ax.plot(test.index.values, test_pred, label="predicted", color="c") 

# 学習データとテスデータの間の縦線の描写
ax.axvline(datetime.datetime(1960,1,1),color='blue')

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

　RegARIMA（Optunaによるハイパーパラメータ調整込み）

Ride回帰の最適なハイパーパラメータ（正則項の重み）をOptunaで探索し、その結果を使いモデル構築していきます。

まず、Optunaで最適なハイパーパラメータを探索します。

Optunaによるハイパーパラメータ探索（ベイズ最適化アプローチ）について、知りたい方は以下を参考にしてください。

では、Ride回帰の最適なハイパーパラメータ（正則項の重み）をOptunaで探索します。

以下、コードです。

# Optunaでの目的関数
def objective(trial, X, y):
    ridge_alpha = trial.suggest_float('ridge_alpha', 0.01, 10.0)
    model = RegARIMAModel(ridge_alpha=ridge_alpha)
    model.fit(X, y)  

    # 予測値を計算
    predictions = model.predict_in_sample(X)  

    # 平均二乗誤差(MSE)を計算
    mse = mean_squared_error(y, predictions)
    return mse

# ログ非出力
optuna.logging.set_verbosity(optuna.logging.WARNING)
optuna.logging.disable_default_handler()

# Optunaのスタディを作成し、最適化を実行
study = optuna.create_study(direction='minimize')
objective_partial = partial(objective, X=X_train, y=y_train)
study.optimize(objective_partial, n_trials=100, show_progress_bar=True)

# 最適なパラメータを出力
ridge_alpha = study.best_trial.params['ridge_alpha']
print('Best ridge_alpha:', ridge_alpha)

 

以下、実行結果です。

Best trial: 95. Best value: 50.9335: 100%|██████████| 100/100 [01:33<00:00,  1.07it/s]Best ridge_alpha: 2.632486616806249

 

予測モデルの学習（学習データ利用）をします。

以下、コードです。

# インスタンス作成
model = RegARIMAModel(
    ridge_alpha=study.best_trial.params['ridge_alpha'])

# 学習
model.fit(X_train, y_train)

 

予測モデルのテスト（テストデータ利用）をします。

以下、コードです。

#
# 予測の実施
#

# 学習データ期間の予測
train_pred = model.predict_in_sample(X = X_train)

# テストデータ期間の予測
test_pred = model.predict(n_periods=12,X = X_test)

 

予測精度を評価します。

以下、コードです。

#
# 予測精度（テストデータ）
#

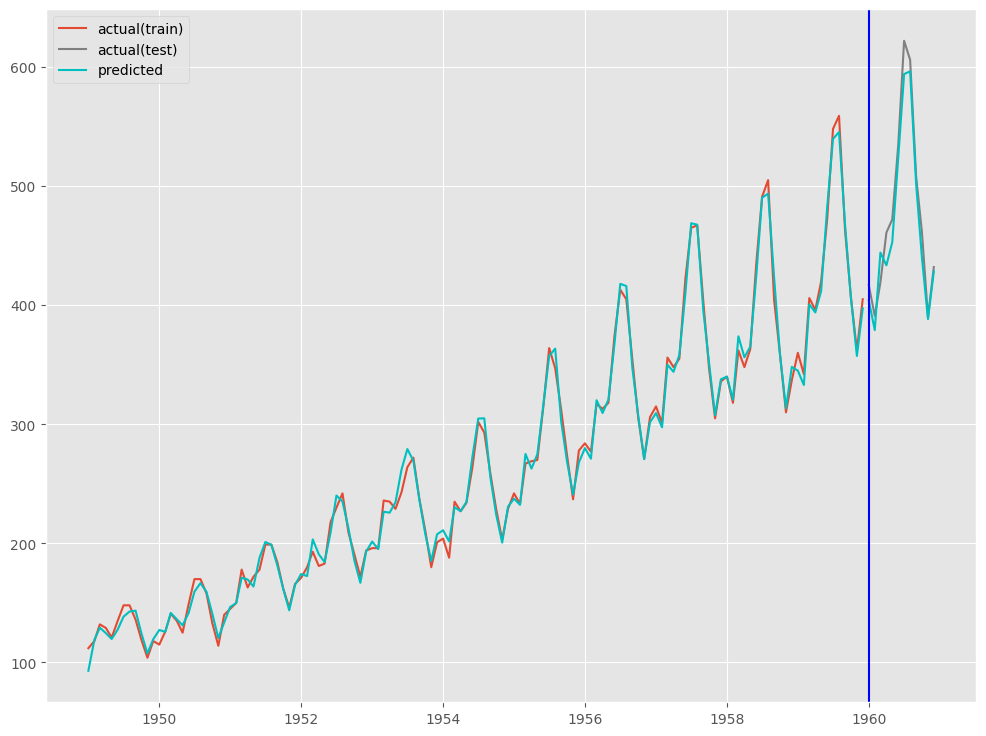
print('RMSE:\n',np.sqrt(mean_squared_error(test.Passengers, test_pred)))
print('MAE:\n',mean_absolute_error(test.Passengers, test_pred)) 
print('MAPE:\n',mean_absolute_percentage_error(test.Passengers, test_pred))

 

以下、実行結果です。

RMSE:
 17.266868087186207
MAE:
 14.857222711918183
MAPE:
 0.031231899293579727

 

プロットし確認してみます。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

# 実測値の描写
## 学習データ
ax.plot(train.index.values, train.Passengers.values, label='actual(train)')
## テストデータ
ax.plot(test.index.values, test.Passengers.values, label='actual(test)', color='gray')

# 予測値の描写
## 学習データ
ax.plot(train.index.values, train_pred, color='c')
## テストデータ
ax.plot(test.index.values, test_pred, label="predicted", color="c") 

# 学習データとテスデータの間の縦線の描写
ax.axvline(datetime.datetime(1960,1,1),color='blue')

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

 （おまけ）ARIMAXの場合

予測モデルの学習（学習データ利用）をします。

以下、コードです。

# 学習
model = auto_arima(
    y=y_train,
    X=X_train,
    seasonal=False

 

予測モデルのテスト（テストデータ利用）をします。

以下、コードです。

#
# 予測の実施
#

# 学習データ期間の予測
train_pred = model.predict_in_sample(X = X_train)

# テストデータ期間の予測
test_pred = model.predict(n_periods=12,X = X_test)

 

予測精度を評価します。

以下、コードです。

#
# 予測精度（テストデータ）
#

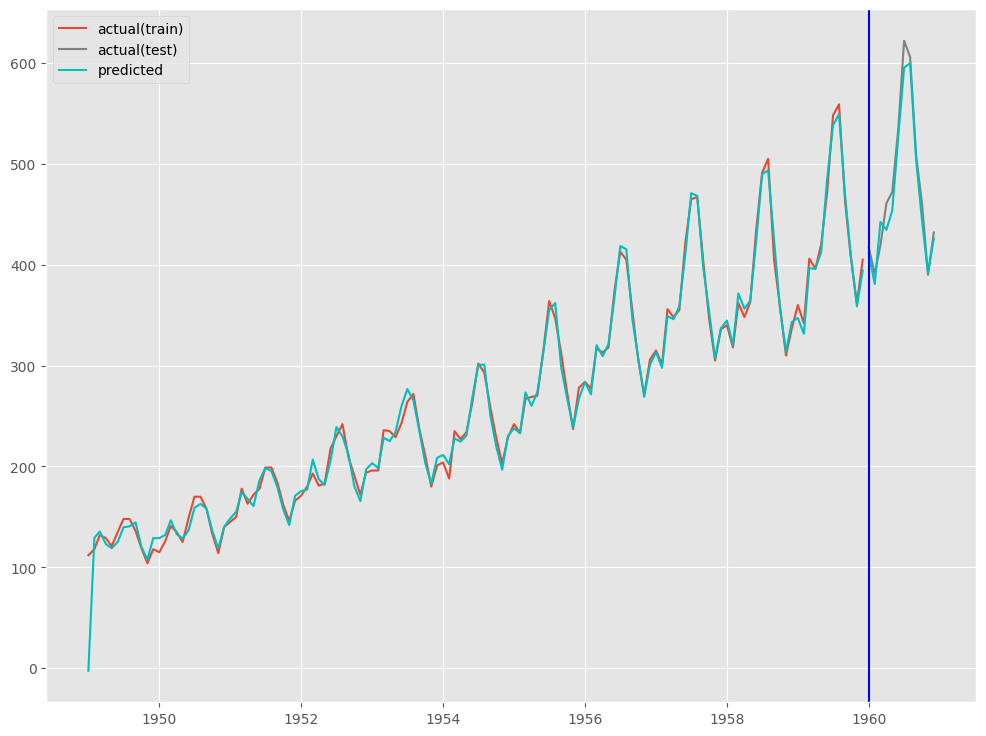
print('RMSE:\n',np.sqrt(mean_squared_error(test.Passengers, test_pred)))
print('MAE:\n',mean_absolute_error(test.Passengers, test_pred)) 
print('MAPE:\n',mean_absolute_percentage_error(test.Passengers, test_pred))

 

以下、実行結果です。

RMSE:
 15.45431236493971
MAE:
 12.81081511929107
MAPE:
 0.026927716633301572

 

プロットし確認してみます。

以下、コードです。

#
# グラフ（予測値と実測値）
#

fig, ax = plt.subplots()

# 実測値の描写
## 学習データ
ax.plot(train.index.values, train.Passengers.values, label='actual(train)')
## テストデータ
ax.plot(test.index.values, test.Passengers.values, label='actual(test)', color='gray')

# 予測値の描写
## 学習データ
ax.plot(train.index.values, train_pred, color='c')
## テストデータ
ax.plot(test.index.values, test_pred, label="predicted", color="c") 

# 学習データとテスデータの間の縦線の描写
ax.axvline(datetime.datetime(1960,1,1),color='blue')

# 凡例表示
ax.legend()

plt.show()

 

以下、実行結果です。

 

実世界の応用事例

RegARIMAモデルはその柔軟性と外生変数の効果を分析する能力により、多様な分野で有効なツールとして利用されています。

 

　ビジネス事例

ある大規模な小売チェーンで、販売促進キャンペーンや季節イベントの影響を予測するためにRegARIMAモデルを使用しました。

このモデルで、特定のプロモーションや季節変動が消費者の購買行動にどのように影響するかを把握しました。

その結果、在庫管理やマーケティング戦略を最適化するのに役立ちました。

 

　経済事例

RegARIMAモデルを使用して、政策変更や国際市場の変動などの外生的要因が経済指標に与える影響を分析することがあります。

例えば、政府の財政政策や金融政策の変更が国内総生産（GDP）成長にどのような影響を与えるかをモデル化することが可能です。

これにより、政策立案者はより情報に基づいた意思決定を行うことができます。

 

　金融事例

RegARIMAモデルを用いて株価や金利の変動を予測することがあります。

外生変数として、政治的なイベントや経済報告などが考慮されます。

これにより、市場の不確実性を評価し、リスク管理や投資戦略の調整を行うことができます。

 

　気象学事例

RegARIMAモデルを使用して気温や降水量の予測を行うこともあります。

外生変数として気圧、湿度、風向きなどの気象条件を考慮します。

これは特に農業計画の立案や災害対策の準備に活用したり、店舗ビジネスで活用したりします。

 

　製造業事例

RegARIMAモデルを利用して生産プロセスの最適化を行っている製造業もいます。

この企業では、外生変数として市場の需要変動や供給チェーンの状態を考慮することで、生産量の調整や在庫レベルの最適化が可能となりました。

これにより、製造コストの削減や供給過多による損失の低減が図られます。

 

まとめ

今回は、説明変数を組み込んだ時系列モデル、特にRegARIMAモデルの概念、構造、およびPythonでの実装について取り上げました。

• 時系列モデルの基礎：自己回帰（AR）、移動平均（MA）、自己回帰移動平均（ARMA）およびその拡張であるARIMAとSARIMAモデル。
• 説明変数の組み込み：ARIMAXとRegARIMAモデルを通じて外生変数の組み込み方法とその影響を理解しました。
• RegARIMAモデルの実装と応用：Pythonを用いたRegARIMAモデルの実装例と、実際のデータに基づくケーススタディを紹介しました。

今後、説明変数付きのARIMAモデルは、より進化を遂げることでしょう。

例えば、モデルの改善と新技術の統合です。

機械学習やディープラーニングの進化により、時系列モデルの予測精度をさらに高める新しいアプローチが開発されています。これらの技術を組み合わせることで、より複雑なデータ構造やパターンを捉えることが期待されます。

他には、リアルタイムデータ対応です。

IoTデバイスやオンラインプラットフォームからのリアルタイムデータを活用することで、時系列モデルはさらに動的な意思決定ツールとしての機能を強化できます。

今後も、データ駆動の意思決定が重要性を増す中で、RegARIMAのような高度な時系列分析ツールが、さまざまな業界での挑戦を解決する鍵となるでしょう。

あなたがこの記事を通じて、実務や研究において有益な洞察を得られることを願っています。