機械学習やAIが私たちの生活やビジネスにますます浸透している一方で、それらの技術がどのように判断や予測を行っているのかを理解することが求められています。
この理解が不十分だと、AIの予測や判断がブラックボックスのように感じられ、信頼性が低下してしまいます。特に、ビジネスでAIを利用する場合、その判断の根拠を明確にすることが非常に重要です。
以下のブログでは、説明可能AI(XAI)の重要性についてお話ししました。
AIがどのようにして判断を下しているのかを理解できないと、その結果に対して不安や疑念が生じます。
例えば、顧客のクレジットリスクをAIが高いと判断した場合、その根拠を明確に説明できなければ、審査担当者や顧客に納得してもらうのが難しくなります。
XAIの目的は、AIの判断の根拠を明らかにし、透明性を提供することにあります。これにより、AIの結果を信頼し、ビジネスの重要な意思決定をAIに基づいて行うことができるようになります。
ここで紹介するDALEXは、機械学習モデルの予測結果を解釈し、理解しやすい形で可視化するためのツールです。
DALEXは、Diverse And eXplainable(多様で説明可能な)という名前の通り、さまざまなモデルや手法に適用でき、モデルの振る舞いや予測の根拠を明らかにします。
これにより、AIの予測に対する信頼性が向上し、ビジネスの意思決定がより確かなものとなります。
Contents [hide]
DALEXのインストール
DALEXはPythonのライブラリで、簡単にインストールして使用することができます。
インストールは以下のコマンドで行います。
pip install dalex
このコマンドをターミナルやコマンドプロンプトで実行すると、DALEXとその依存関係がインストールされます。
DALEXの中でLIME (Local Interpretable Model-agnostic Explanations)というをローカル解釈手法を利用するときは、あらかじめインストールしておきます。
インストールは以下のコマンドで行います。
pip install lime
また、DALEXはモデルの解釈に加えて、データの処理や可視化にも関与するため、scikit-learnやpandasといったライブラリも必要です。
これらのライブラリはすでにインストールされていることが多いですが、もしなければ同様にインストールしておきましょう。
シンプルな使用例を用いた説明
それでは、DALEXを使ってシンプルなモデルを解釈する例を見ていきましょう。
ここでは、ランダムフォレストという機械学習モデルを使って、顧客のクレジットリスクを予測し、その予測結果をDALEXで解釈してみます。
準備
まず、モデルを作成し、データを準備します。
以下、コードです。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
# シンプルなデータセットを作成
data = pd.DataFrame({
'age': [25, 45, 35, 50, 23, 33, 48, 28, 24, 40, 55, 26, 38, 62, 31, 46, 60, 22, 37, 29],
'income': [50000, 100000, 75000, 120000, 45000, 60000, 110000, 58000, 52000, 95000,
70000, 49000, 64000, 130000, 57000, 115000, 125000, 38000, 69000, 62000],
'purchase_history': [1, 0, 0, 1, 1, 0, 1, 0, 1, 1,
0, 1, 0, 1, 0, 1, 1, 1, 0, 1],
'buy': [1, 0, 0, 1, 0, 0, 1, 0, 0, 1,
0, 1, 0, 1, 0, 1, 1, 0, 0, 1] # ターゲット変数
})
# 特徴量とターゲットに分ける
X = data[['age', 'income', 'purchase_history']]
y = data['buy']
# データをトレーニングセットとテストセットに分ける
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42)
# ランダムフォレストモデルの作成とトレーニング
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)
このシンプルなデータセットは、顧客の年齢、収入、購入履歴に基づいて、商品を購入するかどうかを予測するためのものです。
以下、データセットの変数です。
age: 顧客の年齢income: 顧客の収入purchase_history: 過去の購入履歴(1は購入したことがある、0は購入したことがない)buy: 目的変数で、顧客が商品を購入するかどうか(1は購入する、0は購入しない)
このデータセットをトレーニングセットとテストセットに分け、トレーニングセットを使ってランダムフォレストモデルをトレーニングしました。
次に、このモデルの予測を解釈するために、DALEXのエクスプレイナーオブジェクトを、テストセットを使って作成します。
以下、コードです。
import dalex as dx # DALEXのエクスプレイナーオブジェクトを作成 explainer = dx.Explainer(model, X_test, y_test, label="Random Forest Model")
このエクスプレイナーオブジェクトは、モデルの解釈に必要な情報を保持し、様々な分析を行うときに利用します。
モデルのグローバル解釈
変数重要度
変数重要度は、機械学習モデルが予測を行う際に、どの特徴量(変数)が最も重要であるかを定量化する手法です。
この情報を基に、ビジネスにおける重要な意思決定をサポートすることができます。
例えば、クレジットリスクを評価するモデルでは、年収や過去の借入履歴などが重要な特徴量として特定されるかもしれません。
重要度の高い特徴量は、モデルの決定に大きく寄与していることを示します。
では、変数重要度をプロットします。
以下、コードです。
# 変数重要度をプロット importance = explainer.model_parts() importance.plot()
このプロットには、各特徴量の重要度が視覚的に示されます。
縦軸には特徴量が表示され、横軸にはそれぞれの重要度が示されます。
棒グラフの長さが長いほど、その特徴量がモデルの予測に対して重要であることを示します。
以下、実行結果です。
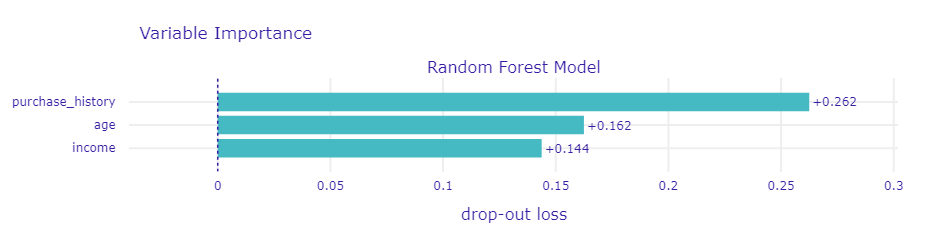
Variable Importanceの結果を解釈すると、以下のようになります。
purchase_history(購入履歴) は最も重要な変数であり、Variable Importanceは0.262です。age(年齢) が次に重要な変数であり、Variable Importanceは0.162です。これは、収入がモデルの予測に最も大きな影響を与えていることを示しています。income(収入) は最も影響が少ない変数であり、Variable Importanceは0.144です。
Variable Importanceが高いほど、その変数がモデルの予測に与える影響が大きいことを意味します。
したがって、購入履歴が顧客が商品を購入するかどうかを予測する上で最も重要な要素であることがわかります。
部分依存プロット(PDP)
部分依存プロット(PDP)は、特定の特徴量がモデルの予測に与える影響を視覚化するための手法です。
PDPは、他の全ての特徴量が一定と仮定した上で、特定の特徴量が予測値にどのような影響を与えるかを示します。
この手法は、特徴量が非線形に作用する場合や、相互作用がある場合に特に有用です。
では、DALEXを使ってPDPを作成します。
以下、コードです。
# 部分依存プロットの作成 pdp_age = explainer.model_profile(variables=["age"]) pdp_age.plot()
このプロットでは、縦軸が予測値、横軸が特徴量の値を示しています。
横軸の値が変化するにつれて、予測値がどのように変動するかを視覚的に確認できます。
例えば、ageが増加すると予測値が上昇する場合、この特徴量が正の影響を与えていることを意味します。
以下、実行結果です。
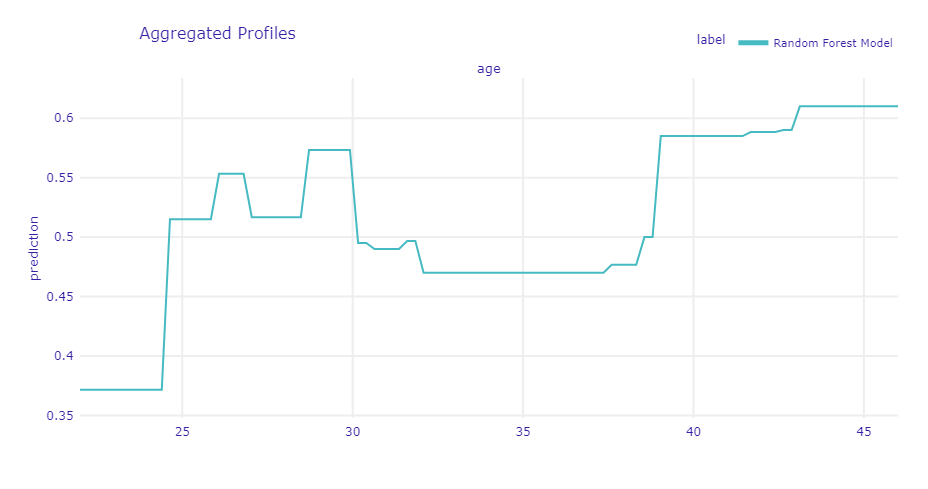
年齢がどのようにモデルの予測に影響を与えているかが分かります。
以下の3点で解釈します。
- 傾向: 年齢が増加するにつれて、モデルの予測値が上昇しています。これは、年齢が高いほど商品を購入する可能性が高いことを示しています。
- 変化の大きさ: 予測値の変化は比較的大きく、特に37歳から45歳の範囲で顕著です。これは、この年齢範囲がモデルの予測に大きな影響を与えていることを示しています。
- 非線形性: 予測値の変化はざっくりみると年齢とともに大きくなりますが、特定の年齢範囲で急激な変化が見られます。これは、年齢が複雑な影響を与えていることを示しています。
このプロットから、年齢がモデルの予測にどのような役割を果たしていることがわかります。
モデルのローカル解釈
SHAP値
SHAP値(Shapley Additive Explanations)は、個々の予測に対して各特徴量がどの程度影響を与えたかを定量的に示す手法です。
ローカル解釈を行う際に、特定のデータポイントに対するモデルの予測がどのように形成されたのかを理解するために非常に有効です。
これにより、なぜそのような予測が行われたのかを説明することができ、AIの透明性を向上させます。
では、DALEXを使ってSHAP値を計算し視覚化します。
以下、コードです。
# テストデータから特定の顧客を選ぶ selected_customer = X_test.iloc[[3]] # 選ばれた顧客のデータを表示 print(selected_customer) # ローカル解釈を行う shap_values = explainer.predict_parts(selected_customer) shap_values.plot()
このプロットには、各特徴量がどのように予測に影響を与えたかが視覚的に示されます。
SHAP値は、正または負の値として表示され、予測に対してどの程度プラスまたはマイナスの影響を与えたかが分かります。
以下、実行結果です。
age income purchase_history 1 45 100000 0
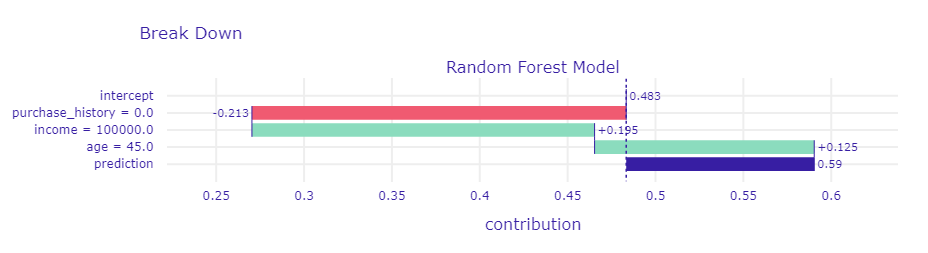
ローカル解釈の結果を解釈します。
選ばれた顧客のデータは以下の通りです。
- 購入履歴: 0 (購入したことがない)
- 収入: 100000
- 年齢: 45歳
ローカル解釈のプロットから、各特徴量がモデルの予測にどのように影響を与えているかがわかります。
purchase_history (購入履歴)
- 購入履歴が0であることが、モデルの予測に対してどのように影響しているかを示しています。
- 過去に購入したことがない顧客は、新たに購入する可能性が低いことを示しています。
- 今回は、購入履歴が0であることが、予測値を0.213だけ減少させ、累積予測値は-0.213になります。
income (収入)
- 収入が100000であることが、モデルの予測に対してどのように影響しているかを示しています。
- 収入が高いほど、購入する可能性が高くなる傾向があることがわかります。
- 今回は、収入が100000であることが、予測値を0.195だけ増加させ、累積予測値は-0.018になります。
age (年齢)
- 年齢が45歳であることが、モデルの予測に対してどのように影響しているかを示しています。
- プロットのバーの長さと方向から、年齢が予測値をどの程度押し上げるか、または押し下げるかがわかります。
- 今回は、年齢が45歳であることが、予測値を0.125だけ減少させ、最終的な予測値は0.59になります。
このローカル解釈の結果から、特定の顧客が商品を購入するかどうかの予測に対して、各特徴量がどのように影響を与えているかを理解することができます。
Ceteris Paribusプロファイル
Ceteris Paribusプロファイルは、特定のデータポイントにおける予測が、各特徴量の値が変化した場合にどのように変動するかを視覚化する手法です。
これは、他の全ての条件を一定に保ちながら、1つの特徴量だけを変化させたときに予測結果がどのように変わるかを示します。
これにより、個々の予測における特徴量の影響を詳細に分析することができます。
では、DALEXを使ってCeteris Paribusプロファイルを作成します。
以下、コードです。
# Ceteris Paribus プロファイルの作成 cp_profile = explainer.predict_profile(selected_customer) cp_profile.plot()
Ceteris Paribus プロファイルは、特定の顧客に対して、他の変数を一定に保ちながら、ある変数がどのようにモデルの予測に影響を与えるかを示します。以下の点に注目して解釈します。
- 縦軸(y軸): モデルの予測値(確率)
- 横軸(x軸): 特定の変数の値
以下、実行結果です。
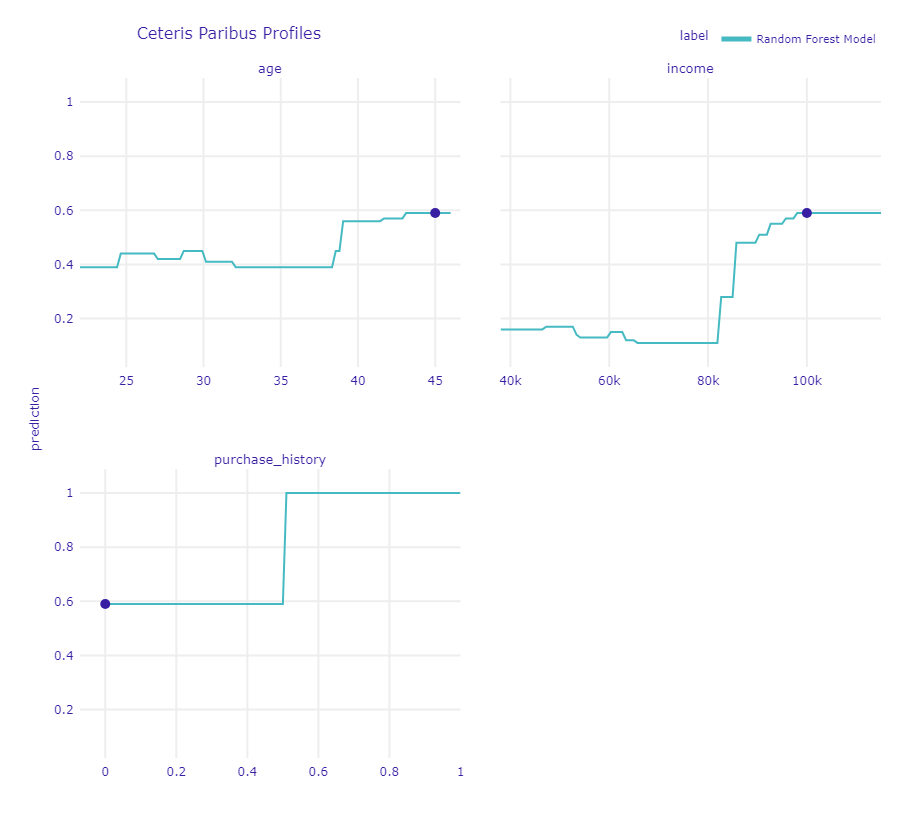
Ceteris Paribus プロファイルの結果を基に、特定の顧客に対して各変数がどのようにモデルの予測に影響を与えるかを確認します。
- age (年齢): 年齢が増加するにつれて、モデルの予測値がどのように変化するかを示しています。年齢が高くなるほど、予測値が上昇する傾向が見られます。
- income (収入): 収入が増加するにつれて、モデルの予測値がどのように変化するかを示しています。収入が高いほど、予測値が上昇する傾向が見られます。
- purchase_history (購入履歴): 購入履歴が変化することで、モデルの予測値がどのように変化するかを示しています。購入履歴が1である場合、予測値が高くなる傾向が見られます。
このプロファイルから、特定の顧客に対して各変数がどのように影響を与えているかを理解することができます。
LIME
LIME (Local Interpretable Model-agnostic Explanations) とは、機械学習モデルの予測をローカルに解釈するための手法で、選択された顧客に対するモデルの予測のローカル解釈を示します。
LIMEプロットの各バーは、特徴とその予測への寄与を表します。
- 横軸 (x軸): 特徴量の影響度 (影響の大きさ)
- 縦軸 (y軸): 特徴量の名前
- バーの長さ: 特徴量の影響度の大きさ
- バーの方向: 予測値に対する影響の方向(正または負)
バーの長さと方向は、予測に対する特徴の影響の大きさと方向を示します。
正の寄与は予測確率を増加させ、負の寄与は予測確率を減少させる。
これは、どの特徴がこの特定の予測に最も影響を与えたかを理解するのに役立ちます。
- 各特徴量が予測にどの程度影響を与えているかを確認します。
- 影響度が大きい特徴量は、予測に対して重要な役割を果たしていることを示します。
- 影響の方向を確認し、特徴量が予測値を増加させるか減少させるかを理解します。
LIMEは、特定の予測に対して、その予測に最も影響を与えた特徴量を特定し、その影響度を示します。
では、LIMEプロットを出力します。
以下、コードです。
lime = explainer.predict_surrogate(selected_customer) lime.plot()
以下、実行結果です。
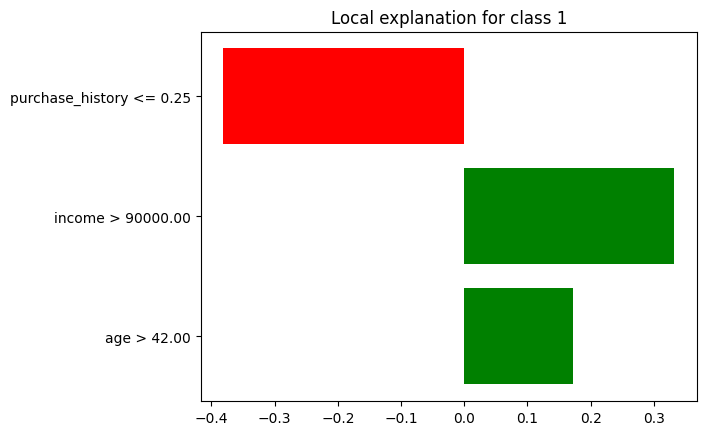
出力を見てみると、SHAP値とほぼ同じのようにも見えます。必ずしも一致するわけではありません。ちょっとした違いがあります。
理論的背景の違い
- SHAP: ゲーム理論に基づいており、各特徴量の寄与を公平に分配するためのShapley値を計算します。これにより、各特徴量が予測にどの程度寄与しているかを正確に評価できます。
- LIME: ローカルな線形モデルを用いて、特定の予測に対する特徴量の影響を評価します。LIMEは、モデルの周辺での予測を近似するために、局所的な線形モデルをフィッティングします。
計算方法の違い
- SHAP: 全ての特徴量の組み合わせを考慮してShapley値を計算するため、計算コストが高くなることがあります。ただし、近似アルゴリズムも存在します。
- LIME: 特定の予測に対して局所的な線形モデルをフィッティングするため、計算コストは比較的低いです。
解釈の一貫性の違い
- SHAP: グローバルな一貫性を持ち、全ての予測に対して一貫した解釈を提供します。つまり、特徴量の寄与は全ての予測に対して同じ方法で計算されます。
- LIME: ローカルな解釈に焦点を当てているため、異なる予測に対して異なる線形モデルがフィッティングされることがあります。これにより、一貫性が欠ける場合があります。
出力の形式の違い
- SHAP: 各特徴量の寄与を示すShapley値を出力し、これを用いて予測の解釈を行います。
- LIME: ローカルな線形モデルの係数を出力し、これを用いて予測の解釈を行います。
これらの違いにより、SHAPは理論的により厳密で一貫性のある解釈を提供しますが、計算コストが高くなることがあります。一方、LIMEは計算コストが低く、特定の予測に対する迅速な解釈を提供しますが、一貫性が欠ける場合があります。
モデルの選択と比較
DALEXを使って、複数のモデルを比較します。
ランダムフォレストとロジスティック回帰の2つのモデルを比較する例を示します。
モデルのトレーニング
まず、ランダムフォレストとロジスティック回帰のモデルをトレーニングします。
from sklearn.linear_model import LogisticRegression from sklearn.ensemble import RandomForestClassifier # ランダムフォレストモデル rf_model = RandomForestClassifier(random_state=42) rf_model.fit(X_train, y_train) # ロジスティック回帰モデル logistic_model = LogisticRegression(random_state=42) logistic_model.fit(X_train, y_train)
エクスプレイナーオブジェクトの作成
次に、このモデルの予測を解釈するために、DALEXのエクスプレイナーオブジェクトを、テストセットを使って作成します。
# ランダムフォレストのエクスプレイナー
rf_explainer = dx.Explainer(
rf_model,
X_test,
y_test,
label="Random Forest Model")
# ロジスティック回帰のエクスプレイナー
logistic_explainer = dx.Explainer(
logistic_model,
X_test,
y_test,
label="Logistic Regression Model")
パフォーマンス比較
今回の分類問題の予測パフォーマンスを評価します。
以下、コードです。
rf_performance = rf_explainer.model_performance("classification")
logistic_performance = logistic_explainer.model_performance("classification")
print(pd.concat((rf_performance.result, logistic_performance.result)))
以下、実行結果です。
recall precision f1 accuracy auc Random Forest Model 1.0 0.666667 0.8 0.833333 1.00 Logistic Regression Model 0.5 0.333333 0.4 0.500000 0.75
以下のように解釈できます。
ランダムフォレストモデル
- Accuracy (0.833): 全体の予測精度が83.3%であり、モデルが正しく予測した割合が高いことを示しています。
- Precision (0.667): 正と予測した中で実際に正であった割合が66.7%であり、誤検出が少ないことを示しています。
- Recall (1.0): 実際に正であったものを全て正しく予測しており、見逃しがないことを示しています。
- F1 Score (0.8): PrecisionとRecallの調和平均が0.8であり、バランスの取れた性能を示しています。
ロジスティック回帰モデル
- Accuracy (0.5): 全体の予測精度が50%であり、モデルの予測がランダムな予測と同程度であることを示しています。
- Precision (0.333): 正と予測した中で実際に正であった割合が33.3%であり、誤検出が多いことを示しています。
- Recall (0.5): 実際に正であったものの半分しか正しく予測できておらず、見逃しが多いことを示しています。
- F1 Score (0.4): PrecisionとRecallの調和平均が0.4であり、全体的な性能が低いことを示しています。
総合的に見ると、ランダムフォレストモデルの方がロジスティック回帰モデルよりも優れた予測性能を持っていることがわかります。
残差の逆累積分布
残差の逆累積分布(Reverse cumulative distribution of residuals)をプロットします。
以下、コードです。
rf_performance = rf_explainer.model_performance() logistic_performance = logistic_explainer.model_performance() rf_performance.plot(logistic_performance)
このプロットの見方です。
- 横軸(∣residual∣|\text{residual}|∣residual∣)**: 残差の絶対値(予測値と実際の値の差の絶対値)を示しています。
- 縦軸(%): データの逆累積割合を示します。この値は「残差の絶対値」(横軸の値)が特定の値より大きいデータポイントが占める割合を示します。
通常、グラフの左下にあるモデルが良いとされています。
以下、実行結果です。
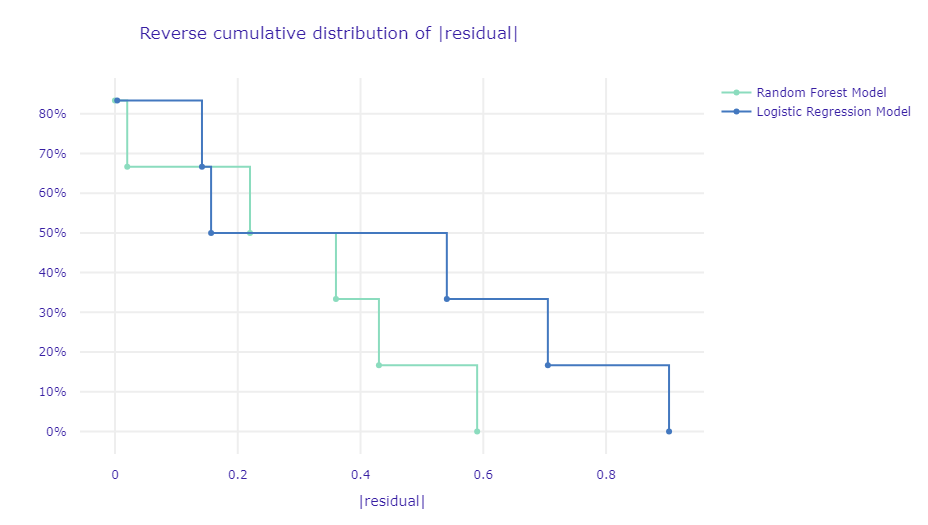
ランダムフォレストモデル(緑の線)とロジスティック回帰モデル(青い線)の両方がプロットされています。
左側に近い線ほど、モデルの残差が小さいことを示しており、そのモデルの予測がより正確であることを意味します。
ランダムフォレストモデルの残差が小さい範囲に多くのデータが集中しており、このモデルが全体としてより精度の高い予測を行っていると解釈できます。
このグラフから、どちらのモデルがより正確な予測を行っているかを評価できます。
他のモデルパフォーマンス指標と合わせて、この情報を使用して、どのモデルがビジネスニーズに最も適しているかを判断します。
グルーバル解釈の比較
変数重要度の違いも見てみます。
以下、コードです。
rf_importance = rf_explainer.model_parts() logistic_importance = logistic_explainer.model_parts() rf_importance.plot(logistic_importance)
以下、実行結果です。
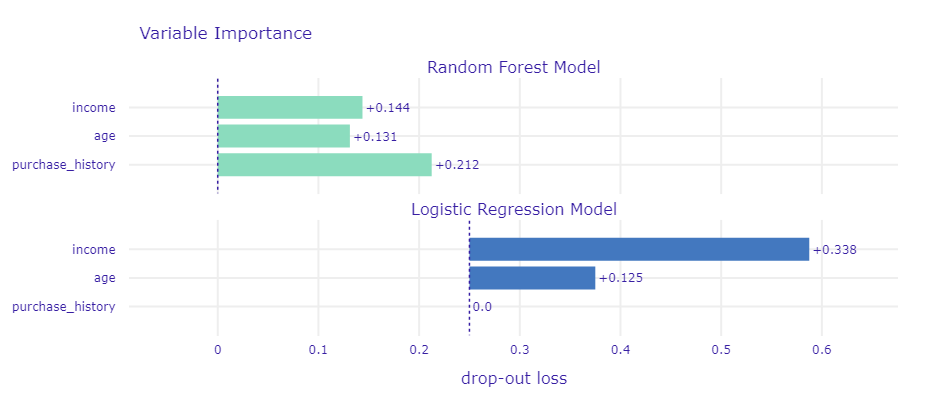
部分依存プロット(PDP)の違いも見てみます。
以下、コードです。
rf_pdp = rf_explainer.model_profile() logistic_pdp = logistic_explainer.model_profile() rf_pdp.plot(logistic_pdp)
以下、実行結果です。
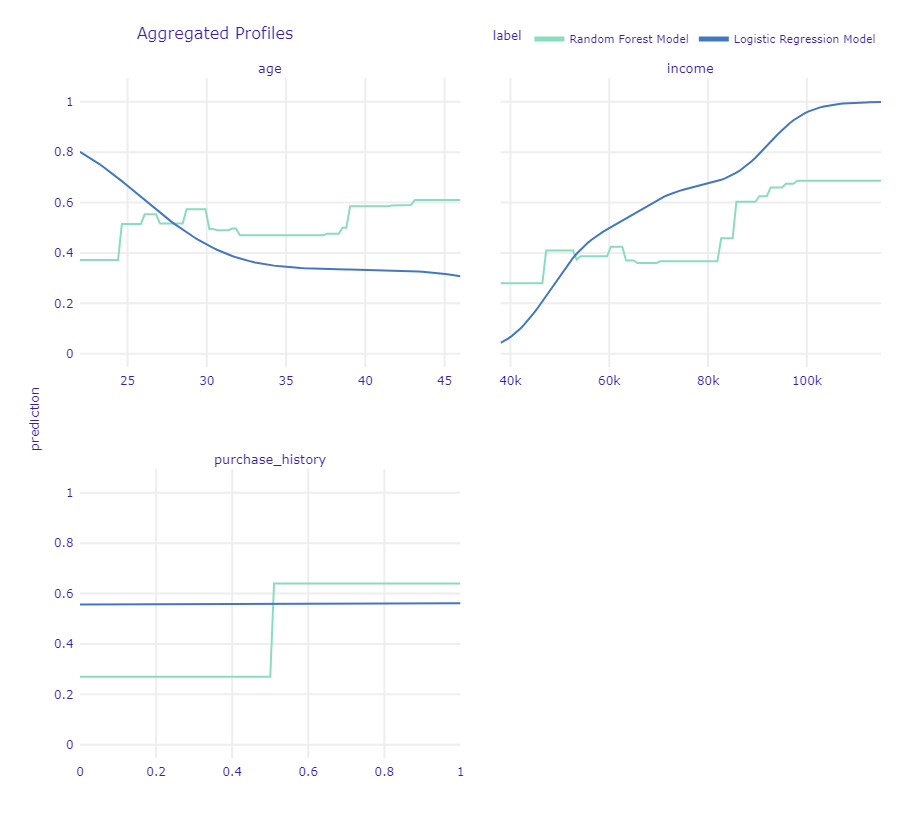
ROC曲線の比較
ROC曲線の比較もします。
以下、コードです。
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
# ランダムフォレストの予測確率
rf_y_prob = rf_model.predict_proba(X_test)[:, 1]
# ロジスティック回帰の予測確率
logistic_y_prob = logistic_model.predict_proba(X_test)[:, 1]
# ROC曲線の計算
rf_fpr, rf_tpr, _ = roc_curve(y_test, rf_y_prob)
logistic_fpr, logistic_tpr, _ = roc_curve(y_test, logistic_y_prob)
# AUCスコアの計算
rf_auc = roc_auc_score(y_test, rf_y_prob)
logistic_auc = roc_auc_score(y_test, logistic_y_prob)
# ROC曲線のプロット
plt.figure(figsize=(10, 6))
plt.plot(rf_fpr, rf_tpr, label=f'Random Forest (AUC = {rf_auc:.2f})')
plt.plot(logistic_fpr, logistic_tpr, label=f'Logistic Regression (AUC = {logistic_auc:.2f})')
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()
ROC曲線(Receiver Operating Characteristic Curve)は、分類モデルの性能を評価するためのグラフで、異なる閾値でのモデルの真陽性率(True Positive Rate, TPR)と偽陽性率(False Positive Rate, FPR)をプロットしたものです。
以下はROC曲線の主要なポイントです。
- 真陽性率(TPR): 実際に正例であるデータのうち、モデルが正例と予測した割合。これは感度(Sensitivity)とも呼ばれます。
- 偽陽性率(FPR): 実際には負例であるデータのうち、モデルが正例と予測した割合。これは1 – 特異度(Specificity)です。
- 対角線: ROC曲線上の対角線(y = x)は、ランダムな予測を示します。モデルの性能がこの線に近いほど、予測がランダムであることを意味します。
- AUC(Area Under the Curve): ROC曲線の下の面積を表します。AUCが1に近いほど、モデルの性能が高いことを示します。AUCが0.5の場合、モデルの性能はランダムな予測と同等です。
ROC曲線の解釈例です。
- 左上に近い曲線: モデルの性能が高いことを示します。真陽性率が高く、偽陽性率が低いことを意味します。
- 対角線に近い曲線: モデルの性能が低いことを示します。予測がランダムであることを意味します。
以下、実行結果です。
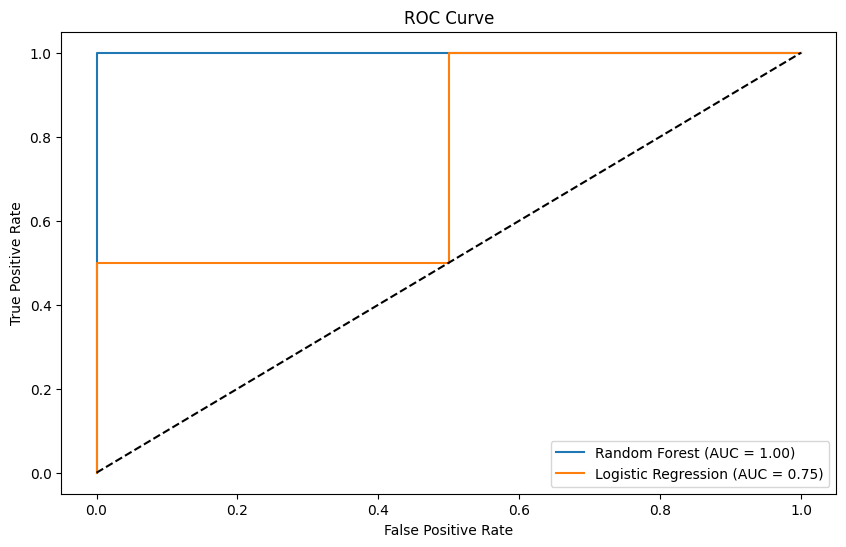
今回のROC曲線のプロット結果から、ランダムフォレストモデルとロジスティック回帰モデルの性能を比較すると、ランダムフォレストモデルのAUCが1.00であり、ロジスティック回帰モデルのAUCが0.75です。
これは、ランダムフォレストモデルの方がロジスティック回帰モデルよりも優れた識別能力を持っていることを示しています。
DALEXで説明可能AIを実現する
DALEXを活用してAIモデルの予測結果を解釈し、ビジネスのさまざまな場面で活用する方法について解説しました。
ここで、これまでの内容をまとめ、DALEXがどのように説明可能AI(XAI)の実現に役立つかを整理します。
モデルの透明性を提供
- ビジネスの意思決定において、AIの予測がどのようにして行われたのかを理解することが不可欠です。
- DALEXを使うことで、モデルの決定要因を視覚的に把握でき、ビジネス担当者や顧客に対してその根拠を明確に説明できます。
複雑なモデルの解釈を簡単に
- ランダムフォレストや勾配ブースティングのような複雑なモデルは、高い予測精度を持つ一方で、その内部の動作が理解しづらいという課題があります。
- DALEXは、こうした複雑なモデルでも、変数重要度や部分依存プロット、SHAP値を使って、どの変数がどのように予測に寄与しているかをわかりやすく示すことができます。
ビジネスの意思決定をサポート
- DALEXを活用することで、AIの予測結果に対する理解が深まり、ビジネス上の意思決定がよりデータに基づいたものになります。
- 例えば、クレジットリスクの評価、マーケティングキャンペーンの最適化、製造業における予知保全など、さまざまなケースでAIの予測を効果的に活用し、リスク管理や収益の最大化を図ることができます。
まとめ
DALEXは、AIモデルの予測を解釈し、その根拠を明確にするための強力なツールです。
ビジネスシーンにおいて、複雑なモデルの「ブラックボックス」問題を解決し、透明性と信頼性を提供することができます。
モデルの予測結果を理解しやすくし、ビジネスの意思決定をサポートするために不可欠な役割を果たします。
これからのビジネスの成功に向けて、DALEXを使った説明可能AIの実践をぜひ進めてみてください。