状態空間モデルは、観測できない状態を時系列データの背後にある要素として捉え、データからその状態を推定する強力なツールです。
今回は、ローカルレベルモデルや季節性を含むモデルなど、具体的なビジネスシナリオを通じて、Pythonを用いた実装例を簡単に解説します。
データの変動要因を正確に捉え、より精度の高い将来予測を実現するための方法を習得しましょう。
Contents
状態空間モデルの概要
状態空間モデルとは？
状態空間モデルは、時系列データを分析する強力なツールです。このモデルは、直接観測できない「状態」が時間とともに変化し、その状態が観測可能なデータに影響を与えると考えます。
ビジネスの文脈で考えてみましょう。例えば、あなたが小売店の経営者だとします。毎日の売上（観測可能なデータ）は、その日の店の魅力（直接観測できない状態）に影響を受けます。この魅力は日々少しずつ変化し、それが売上に反映されると考えられます。
例えば、線形状態空間モデルは、以下の2つの方程式で表現されます。
観測方程式：観測値と状態の関係を表す
状態方程式：状態が時間とともにどう変化するかを表す
ここで、
：時刻tにおける観測値（例：日次売上） ：時刻tにおける状態（例：店の人気度） ：観測行列 ：遷移行列 ：観測ノイズ ：状態ノイズ
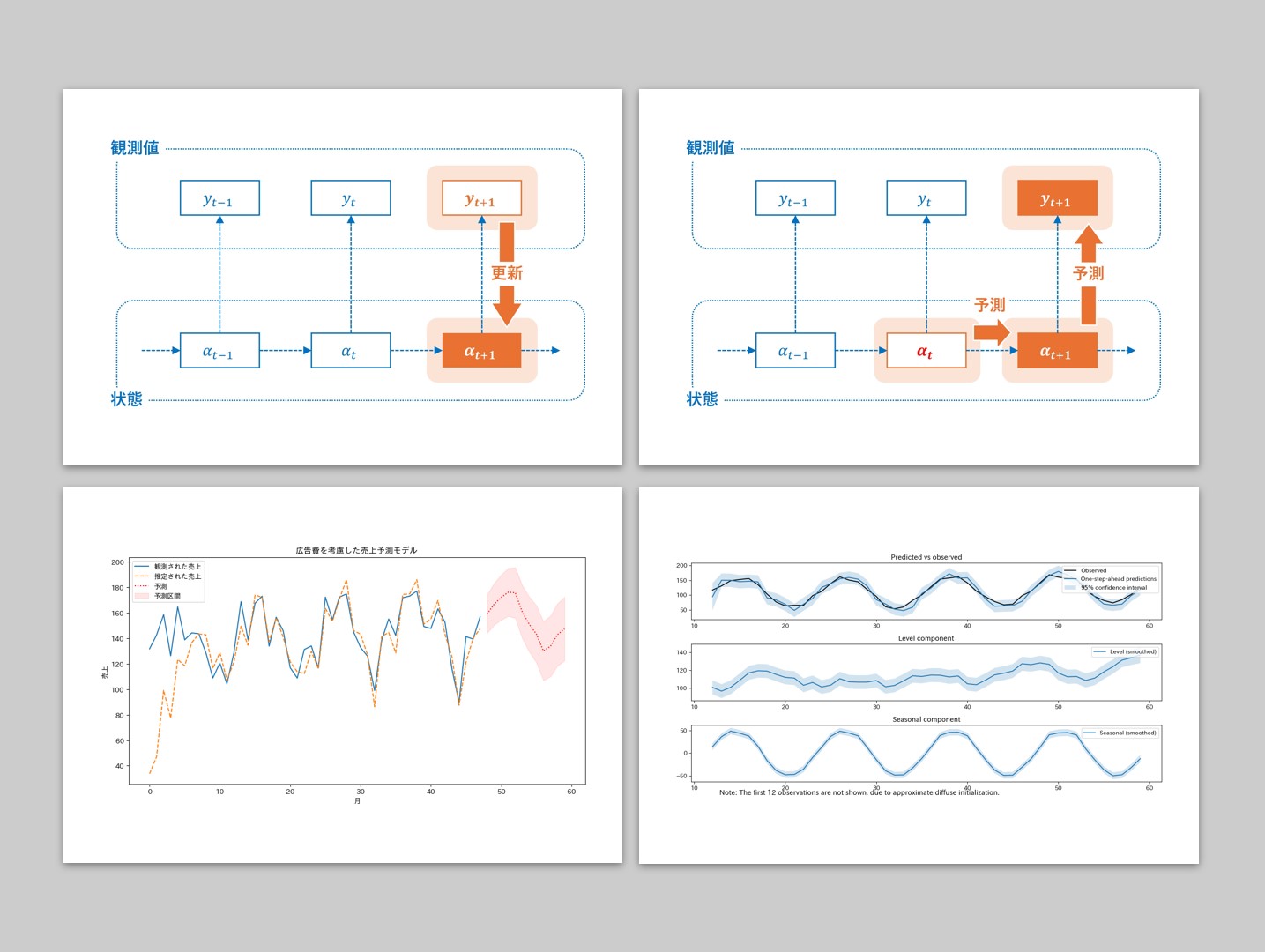
状態空間モデルを図で表すと以下のようになります。
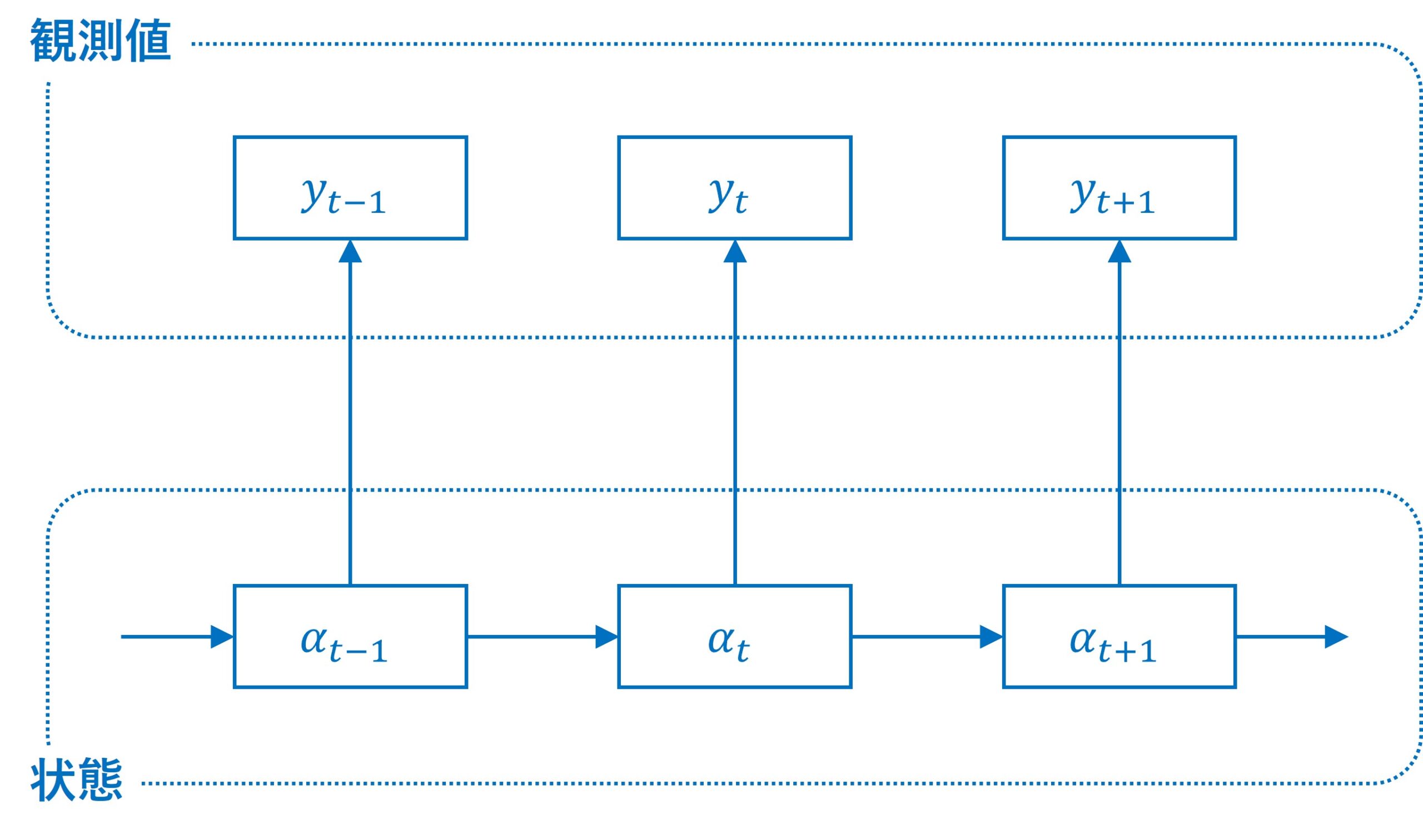
状態の推定と予測
状態空間モデルの目的の1つが、観測されたデータ
主なものに、以下の4種類があります。
- フィルタリング（Filtering）
- 平滑化（Smoothing）
- 1期先予測（One-step-ahead prediction）
- 将来予測（Forecasting）
フィルタリング（Filtering）
フィルタリングの目的は、現在の観測データを使ってノイズを除去し、現在の隠れた状態を推定することです。後ほど説明するカルマンフィルタなどを用いる場合、観測データに含まれるノイズを取り除き、隠れた状態を推定するプロセスがフィルタリングです。ここで重要なのは、過去と現在のデータを使って現在の状態を推定するという点です。リアルタイムに隠れた状態を推定できるため、リアルタイムでの推定が必要な場面に有効です。
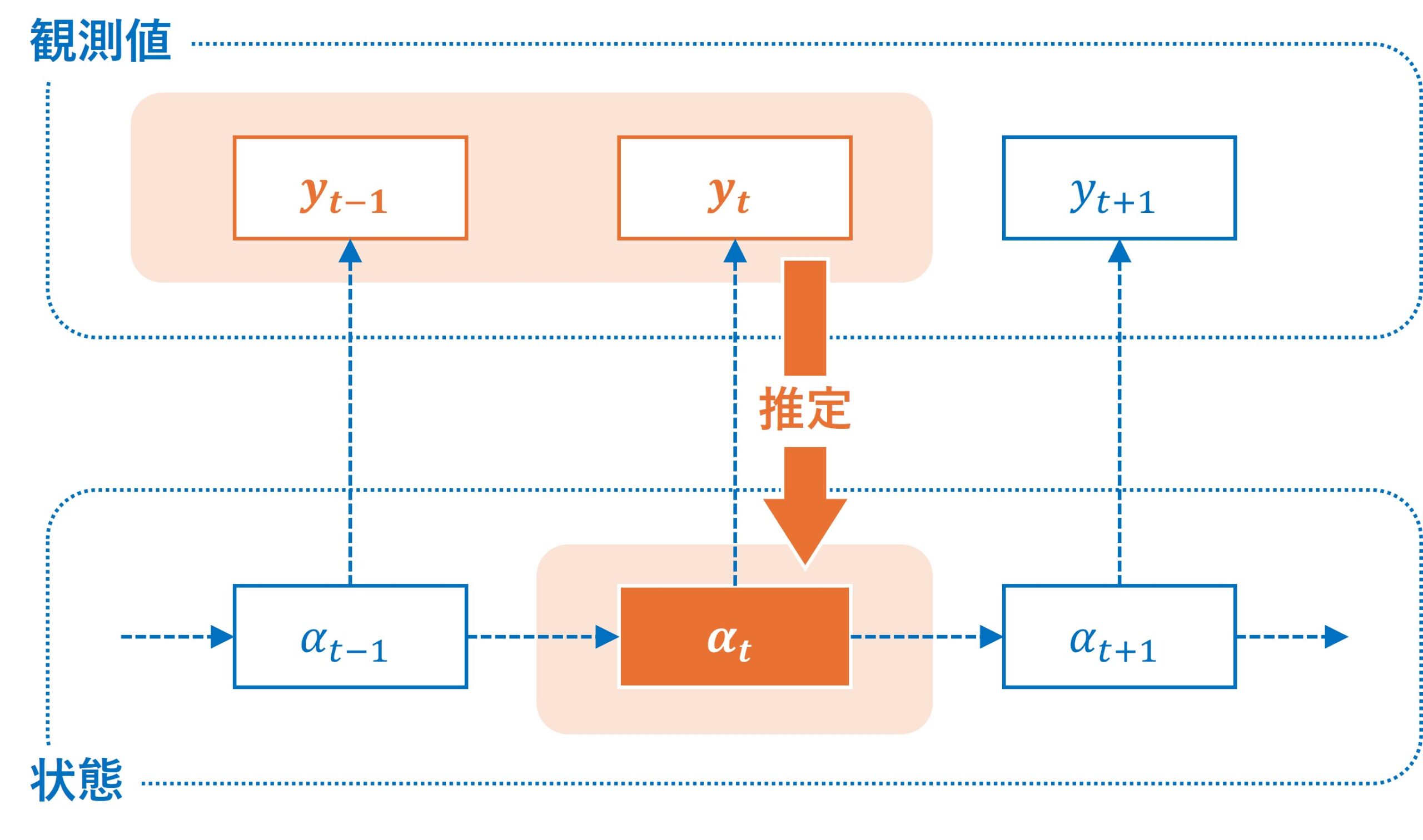
平滑化（Smoothing）
平滑化の目的は、過去から現在までの観測データをすべて利用して、過去の隠れた状態をより正確に推定することです。フィルタリングが現在のデータに基づいてリアルタイムで推定を行うのに対し、平滑化は推定する状態から見て過去のデータと未来のデータの両方を使って、隠れた状態の再計算を行います。
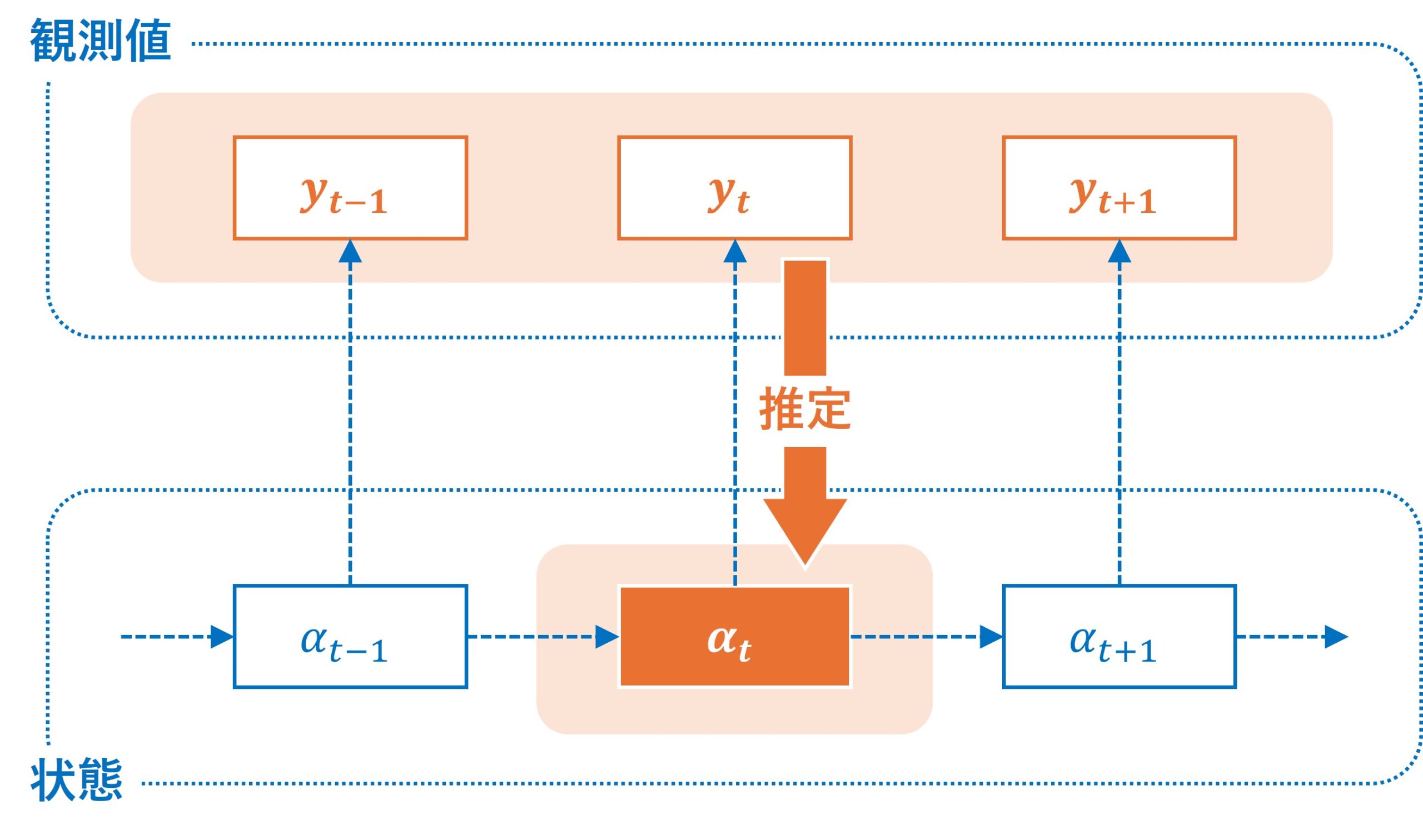
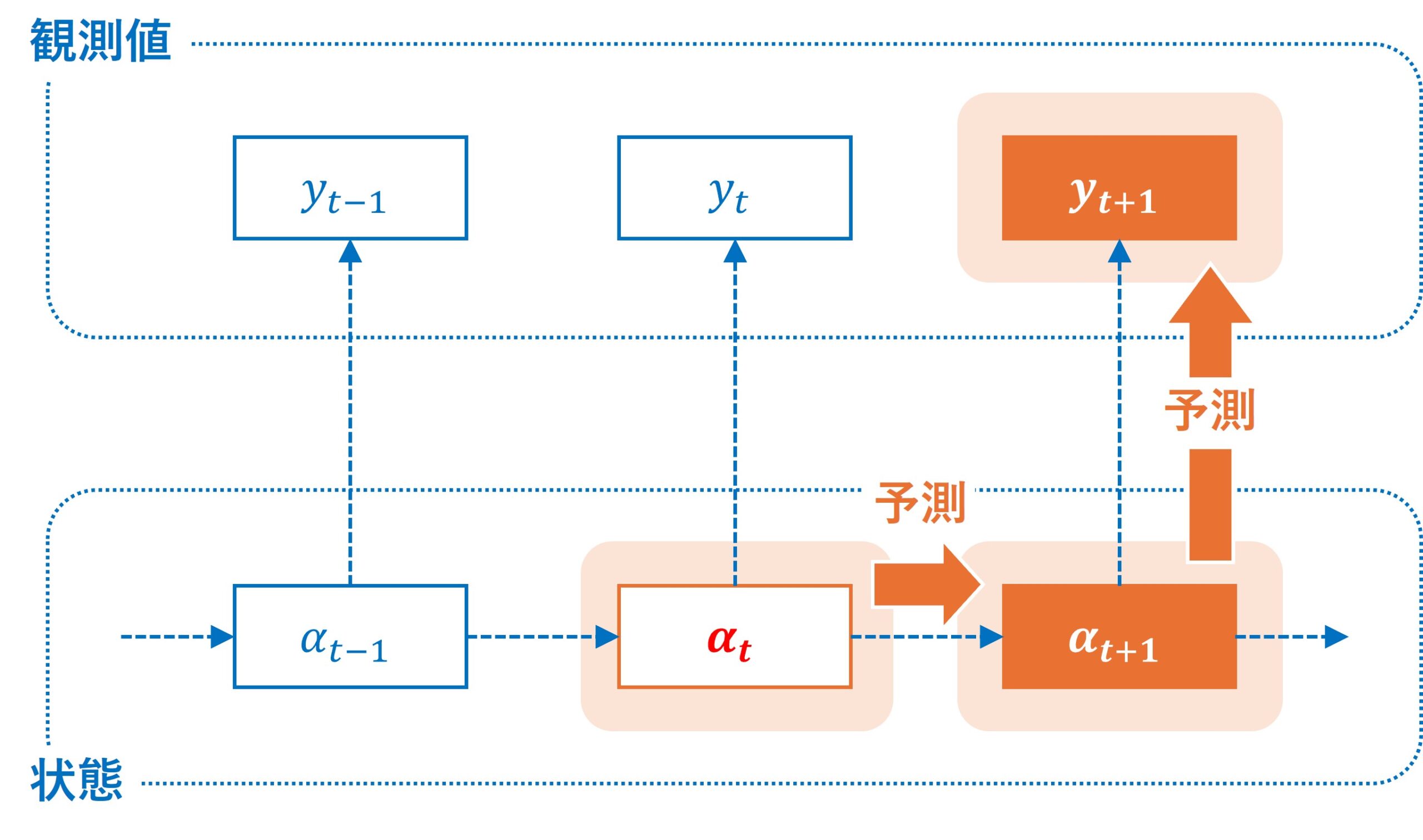
1期先予測（One-step-ahead prediction）
1期先予測は、直前の状態に基づいて、次の時点の状態や観測値を推定するプロセスです。。これは、次に説明する将来予測の一種ですが、特に時間が経過するごとに逐次的に予測を更新する場合に使用されます。1期先予測は、例えば短期的な売上予測や在庫管理など、即座に意思決定が必要なシナリオで非常に有効です。時間の経過とともにデータが更新されるたびに、予測も更新されるため、動的なシステムでのリアルタイム予測が可能になります。
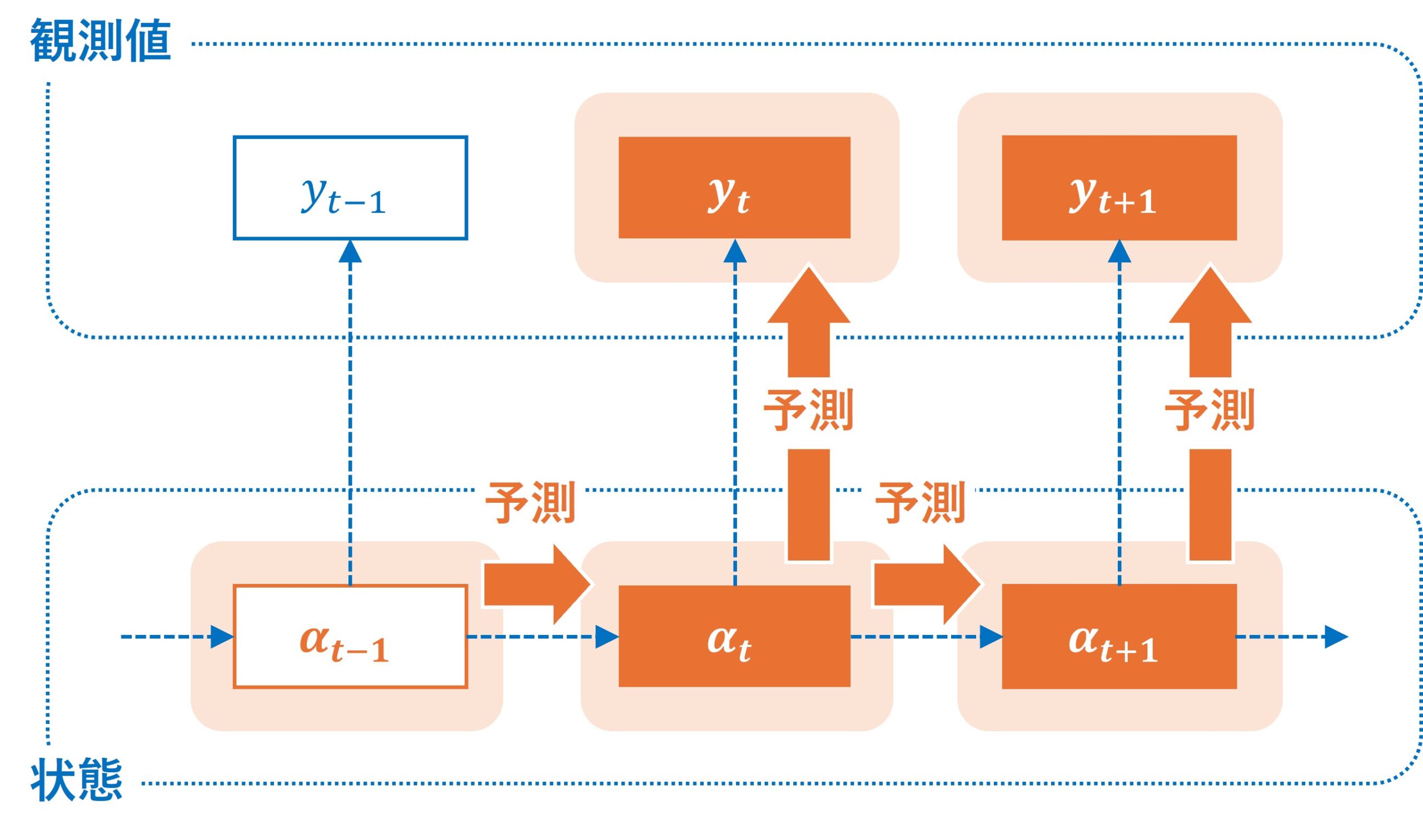
将来予測（Forecasting）
将来予測の目的は、過去のデータに基づいて未来の隠れた状態や観測値を予測することです。カルマンフィルタなどを使う場合、現在の時点での状態を基に、次の時点以降の状態をモデル化し、将来の状態を推定します。予測は、観測データが存在しない未来の値を推定するため、今後の売上の予測などのケースでよく利用されます。多くの場合、複数先予測になります。
カルマンフィルタ (Kalman filter)とは？
状態の推定方法には幾つか方法があります。
先ほどから説明に登場しているカルマンフィルタ (Kalman filter)とは、観測ノイズ
観測方程式
\displaystyle y_t = Z_t \alpha_t + \epsilon_t- y_t ：時刻 t における観測値（例：日次売上）
- Z_t ：観測行列
- \alpha_t ：時刻 t における状態（例：店の人気度）
- \epsilon_t ：観測ノイズ
状態方程式
状態方程式は、状態が時間とともにどのように変化するかを表します。
\displaystyle \alpha_t = T_t \alpha_{t-1} + \eta_t- \alpha_t ：時刻 t における状態
- T_t ：遷移行列
- \eta_t ：状態ノイズ
カルマンフィルタのアルゴリズム
ここで簡単に、カルマンフィルタのアルゴリズムの流れについて説明します。
カルマンフィルタには2つのステップがあり、このステップを交互に繰り返すことで、状態を推定します。
- 予測ステップ
- 更新ステップ
予測ステップ（1期前予測）
まず、状態の予測です。
- 直前の状態推定値 \alpha_{t-1} に基づいて、次の時刻 t の状態 \alpha_t を予測します。\displaystyle \hat{\alpha}_{t|t-1} = T_t \hat{\alpha}_{t-1|t-1} + \eta_t
次は、誤差共分散の予測です。
- 予測された状態の誤差共分散行列を計算します。\displaystyle P_{t|t-1} = T_t P_{t-1|t-1} T_t^T + Q_t
- ここで、 P_{t|t-1} は予測誤差共分散行列、 Q_t は状態ノイズの共分散行列です。
このステップの最後は、観測値の予測です。
- 予測された状態 \hat{\alpha}_{t|t-1} に基づいて、次の観測値を予測します。\displaystyle \hat{y}_{t|t-1} = Z_t \hat{\alpha}_{t|t-1}
更新ステップ（フィルタリング）
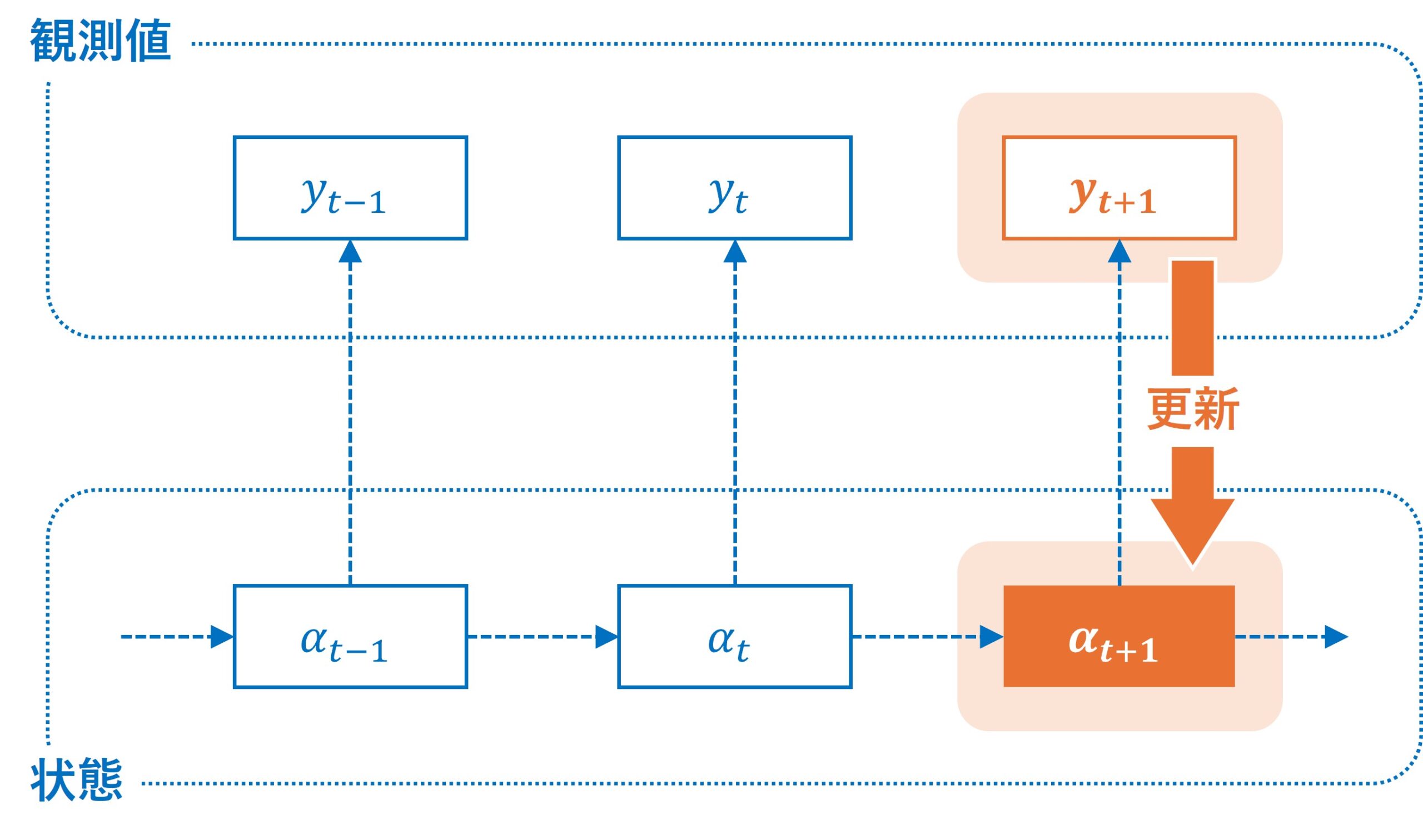
更新の前に、残差とカルマインゲインというものを計算します。
まず、残差（イノベーション）の計算です。
- 実際の観測値 y_t と予測値 \hat{y}_{t|t-1} の差（残差）を計算します。
- \displaystyle v_t = y_t - \hat{y}_{t|t-1}
次は、カルマンゲインの計算です。
- 残差に基づいて予測を修正するためのカルマンゲイン K_t を計算します。\displaystyle K_t = P_{t|t-1} Z_t^T (Z_t P_{t|t-1} Z_t^T + R_t)^{-1}
- ここで、 R_t は観測ノイズの共分散行列です。
ここから、更新していきます。
まず、状態の更新です。
- カルマンゲインを用いて状態推定を更新します。\displaystyle \hat{\alpha}_{t|t} = \hat{\alpha}_{t|t-1} + K_t v_t
次に、誤差共分散行列の更新です。
\displaystyle P_{t|t} = (I - K_t Z_t) P_{t|t-1}
カルマンフィルタは、予測ステップと更新ステップを繰り返すことで、状態を逐次的に推定します。
このプロセスは、例えば売上の予測や位置の追跡など、リアルタイムなシステムにおいて非常に有効です。
複数先予測
カルマンフィルタを用いた複数先予測では、予測ステップを繰り返し適用し、更新ステップを行わずに状態の予測を進めます。
以下、複数先予測の流れです。
- 状態の予測を繰り返す：観測データがないため、更新ステップを行わずに予測ステップを繰り返します。
- 観測値の予測：各ステップで予測された状態に基づいて観測値を推定します。
数式を使って、どのような感じになるのかを説明します。
まず、1期先予測（通常の予測ステップ）です。
- 状態の予測：\displaystyle \hat{\alpha}_{t+1|t} = T_t \hat{\alpha}_{t|t} + \eta_{t+1}
- 観測値の予測：\displaystyle \hat{y}_{t+1|t} = Z_{t+1} \hat{\alpha}_{t+1|t}
次に、2期先予測です。
- 状態の予測：\displaystyle \hat{\alpha}_{t+2|t} = T_{t+1} \hat{\alpha}_{t+1|t} + \eta_{t+2}
- 観測値の予測：\displaystyle \hat{y}_{t+2|t} = Z_{t+2} \hat{\alpha}_{t+2|t}
さらに、3期先予測です。
- 状態の予測：\displaystyle \hat{\alpha}_{t+3|t} = T_{t+2} \hat{\alpha}_{t+2|t} + \eta_{t+3}
- 観測値の予測：\displaystyle \hat{y}_{t+3|t} = Z_{t+3} \hat{\alpha}_{t+3|t}
複数先予測のポイントを整理すると……
- 予測ステップの繰り返し：複数期先の予測では観測値が得られないため、更新ステップを行わずに状態遷移モデルを繰り返し適用します。
- 不確実性の増加：ステップを進めるごとに予測誤差共分散が増加し、予測の不確実性も増します。\displaystyle P_{t+2|t} = T_{t+1} P_{t+1|t} T_{t+1}^T + Q_{t+2}
カルマンフィルタを使った複数先予測では、予測ステップが進むごとに不確実性が増大しますが、短期間の予測においては十分な精度を期待できます。
その他の推定方法
カルマンフィルタのような正規性と線型性を仮定しない方法に、粒子フィルタ (Particle filter)というものがあります。カルマンフィルタよりも計算量が多くなるものの、非正規性と非線型性を許すことで、複雑な予測や推定をすることができます。
粒子フィルタもカルマンフィルタと同様に予測とフィルタリングを繰り返す逐次的なアルゴリズムですが、複雑な分布を重み付きの乱数（粒子）で近似します。このような近似をモンテカルロ近似といいます。
他には、マルコフ連鎖モンテカルロ法 (Markov Chain Monte Carlo methods: MCMC)というものもあります。MCMCは、時系列モデルに限らず、複雑な統計モデルのパラメータ推定に用いられます。
粒子フィルタと同様、分布をたくさんの乱数で近似しますが、粒子フィルタが逐次的に予測 とフィルタリング を繰り返すのに対し、MCMCは初めから全時点のデータを使って分布を近似します。そのため平滑化分布のみが計算され、予測分布を得るには追加の計算が必要になります。
Pythonでの実装例
これから、いくつかの基本的な状態空間モデルをビジネス事例とPythonの実装例とともに見ていきましょう。
ローカルレベルモデル
あなたの会社が新商品を発売したとします。発売直後の売上は日々大きく変動しますが、その背後には「真の人気度」があると考えられます。ローカルレベルモデルは、この状況を表現するのに適しています。
観測方程式
状態方程式
ここで、
では、Pythonで簡単なサンプルデータを作り、そのサンプルデータに対しローカルレベルモデルを実装してみます。
以下、コードです。
import numpy as np
from statsmodels.tsa.statespace.structural import UnobservedComponents
import matplotlib.pyplot as plt
import japanize_matplotlib
# データ生成（新商品の日次売上をシミュレーション）
np.random.seed(123)
n = 50 # 50日分のデータ
true_popularity = np.cumsum(np.random.normal(0, 5, n)) # 真の人気度
daily_sales = true_popularity + np.random.normal(0, 10, n) # 観測される日次売上
# モデルの学習
model = UnobservedComponents(
daily_sales, # 観測された売上
level='local level' # ローカルレベルモデルを指定
)
res = model.fit()
# 結果のプロット
res.plot_components(figsize=(12,6))
plt.tight_layout()
plt.show()
以下、実行結果です。
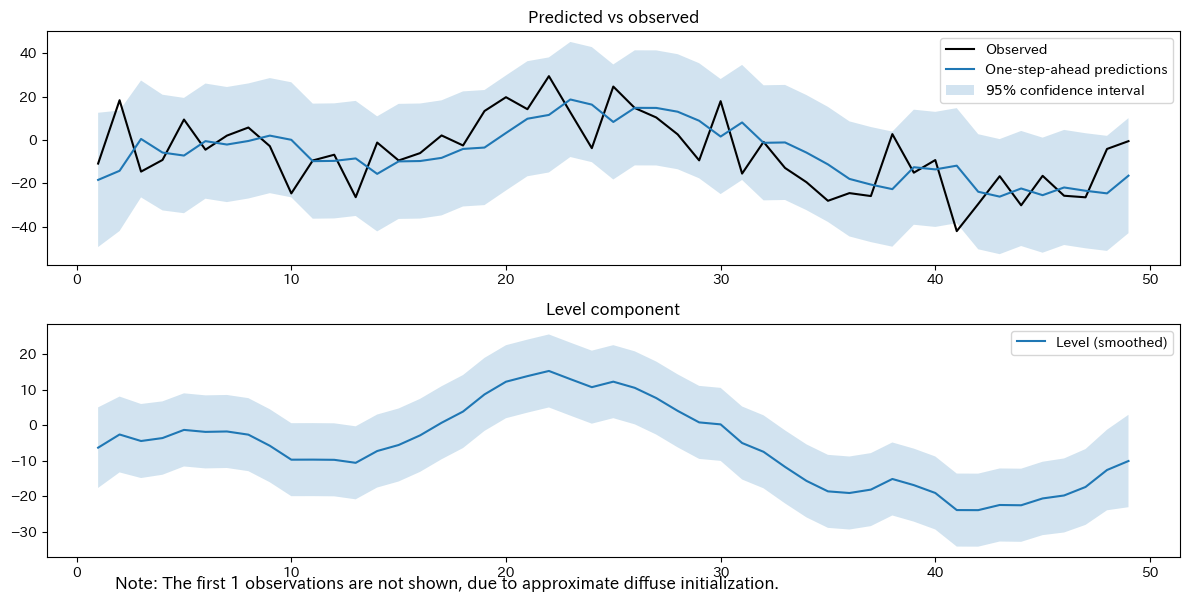
上のグラフは目的変数の実測値（Observed、観測されたデータ）と推定値（1期先予測の結果）を比較したものです。
下のグラフは水準（level）の平滑化の結果で、時点tでの売上水準
このモデルを使い将来予測をします。
以下、コードです。
# 1週間分の予測
forecast_steps = 7
forecast = res.get_forecast(steps=forecast_steps)
forecast_ci = forecast.conf_int()
# 結果のプロット
plt.figure(figsize=(12,6))
plt.plot(
daily_sales,
label='観測された売上')
plt.plot(
res.fittedvalues,
label='推定された売上',
linestyle='--')
plt.plot(
np.arange(n, n + forecast_steps),
forecast.predicted_mean, # 予測値
linestyle=':', color='r',
label='予測')
plt.fill_between(
np.arange(n, n + forecast_steps),
forecast_ci[:, 0], forecast_ci[:, 1], # 予測区間
color='r', alpha=0.1,
label='予測区間')
plt.legend()
plt.title('新商品の売上予測：ローカルレベルモデル')
plt.xlabel('発売からの日数')
plt.ylabel('売上')
plt.show()
以下、実行結果です。
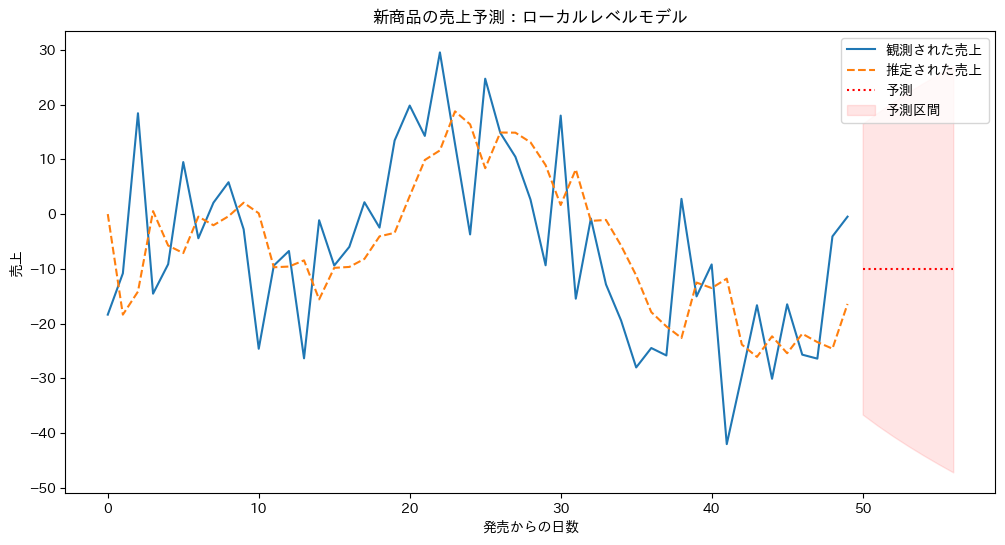
このモデルを使用することで、日々の売上の変動から売上水準の状態（真の人気度など）を推定し、将来の売上を予測することができます。
ローカル線形トレンドモデル
成長中のスタートアップ企業の売上を予測する場合を考えましょう。売上には上昇トレンドがありますが、その成長率（売上の増加速度）が時間とともに変動する可能性もあります。このような場合、ローカル線形トレンドモデルを用いることで売上をより正確に表現することができます。
観測方程式
状態方程式
ここで、
は時点tでの売上水準 は成長率（売上の増加速度）
トレンドは、状態方程式の中で
では、Pythonで簡単なサンプルデータを作り、そのサンプルデータに対しローカル線形トレンドモデルを実装してみます。
以下、コードです。
import numpy as np
from statsmodels.tsa.statespace.structural import UnobservedComponents
import matplotlib.pyplot as plt
import japanize_matplotlib
# データ生成（スタートアップの月次売上をシミュレーション）
np.random.seed(123)
n = 36 # 3年分の月次データ
true_level = np.zeros(n)
true_trend = np.zeros(n)
true_level[0] = 100 # 初期売上
true_trend[0] = 5 # 初期成長率
for t in range(1, n):
true_level[t] = true_level[t-1] + true_trend[t-1] + np.random.normal(0, 10)
true_trend[t] = true_trend[t-1] + np.random.normal(0, 0.5)
monthly_sales = true_level + np.random.normal(0, 5, n)
# モデルの適用
model = UnobservedComponents(
monthly_sales, # 観測された売上
level='local linear trend' # ローカル線形トレンドモデルを指定
)
res = model.fit()
# 結果のプロット
res.plot_components(figsize=(12,6))
plt.tight_layout()
plt.show()
以下、実行結果です。
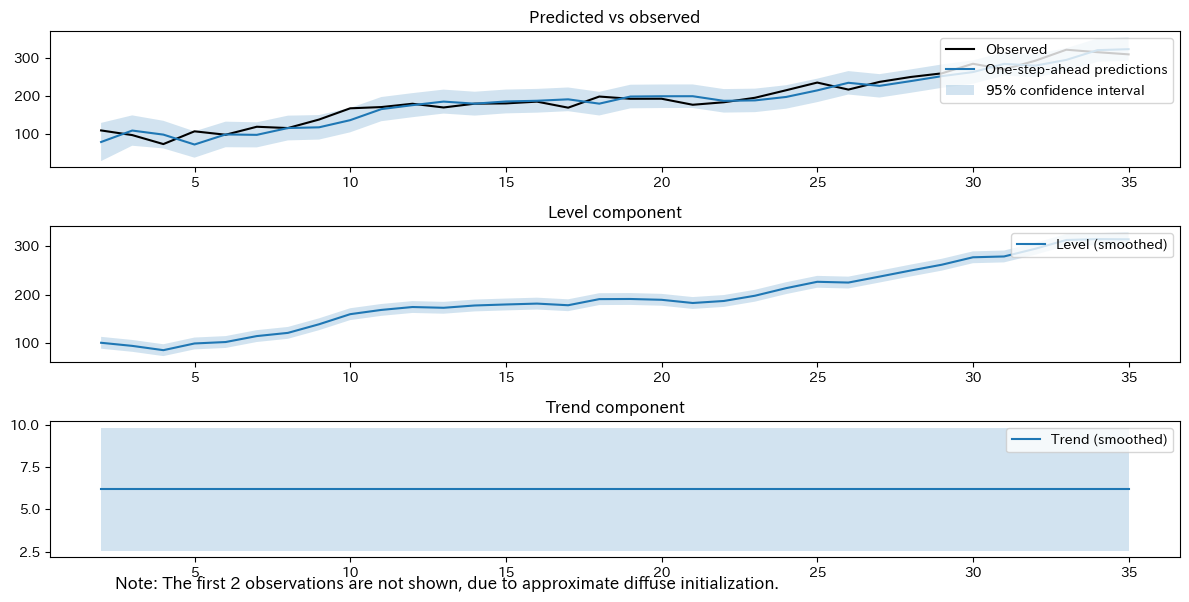
1番目のグラフは目的変数の実測値（Observed、観測されたデータ）と推定値（1期先予測の結果）を比較したものです。
2番目のグラフは水準（level）の平滑化の結果で、時点tでの水準
3番目（一番下）のグラフはトレンド（Trend）の平滑化の結果で、時点tでの
このモデルを使い将来予測をします。
以下、コードです。
# 1年分の予測
forecast_steps = 12
forecast = res.get_forecast(steps=forecast_steps)
forecast_ci = forecast.conf_int()
# 結果のプロット
plt.figure(figsize=(12,6))
plt.plot(
monthly_sales, # 観測された売上
label='観測された売上')
plt.plot(
res.fittedvalues,
label='推定された売上',
linestyle='--')
plt.plot(
np.arange(n, n + forecast_steps), # 予測期間
forecast.predicted_mean, # 予測値
linestyle=':', color='r', label='予測')
plt.fill_between(
np.arange(n, n + forecast_steps), # 予測期間
forecast_ci[:, 0], forecast_ci[:, 1], # 予測区間
color='r', alpha=0.1, label='予測区間')
plt.legend()
plt.title('スタートアップの売上予測：ローカル線形トレンドモデル')
plt.xlabel('月')
plt.ylabel('売上')
plt.show()
以下、実行結果です。
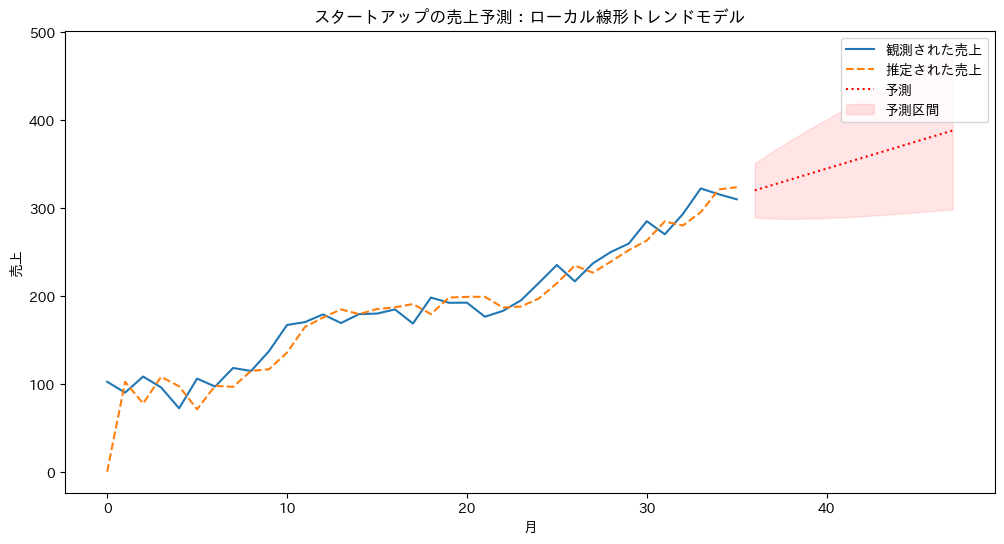
このモデルを使用することで、企業の現在の売上水準だけでなく、成長率の変化も捉えることができます。これにより、より正確な将来予測が可能になります。
季節性を含むモデル
多くの小売業では、売上に季節性があります。例えば、アイスクリーム店の売上は夏に増加し、冬に減少するでしょう。このような季節変動を持つデータは、季節性を含む状態空間モデルで分析できます。
観測方程式
状態方程式
ここで、
は基本的な売上水準 は季節成分 は季節の周期（例：月次データなら12）
では、Pythonで簡単なサンプルデータを作り、そのサンプルデータに対し季節性を含むローカルレベルモデルを実装してみます。
以下、コードです。
import numpy as np
from statsmodels.tsa.statespace.structural import UnobservedComponents
import matplotlib.pyplot as plt
import japanize_matplotlib
# データ生成（アイスクリーム店の月次売上をシミュレーション）
np.random.seed(123)
n = 60 # 5年分の月次データ
trend = np.linspace(0, 20, n) # 緩やかな上昇トレンド
seasonal = 50 * np.sin(np.linspace(0, 2*np.pi*5, n)) # 季節性（夏に高く、冬に低い）
monthly_sales = trend + seasonal + np.random.normal(0, 5, n) + 100
# モデルの適用
model = UnobservedComponents(
monthly_sales, # 観測された売上
level='local level', # ローカルレベルモデルを指定
seasonal=12 # 季節成分を指定
)
res = model.fit()
# 結果のプロット
res.plot_components(figsize=(12,6))
plt.tight_layout()
plt.show()
以下、実行結果です。
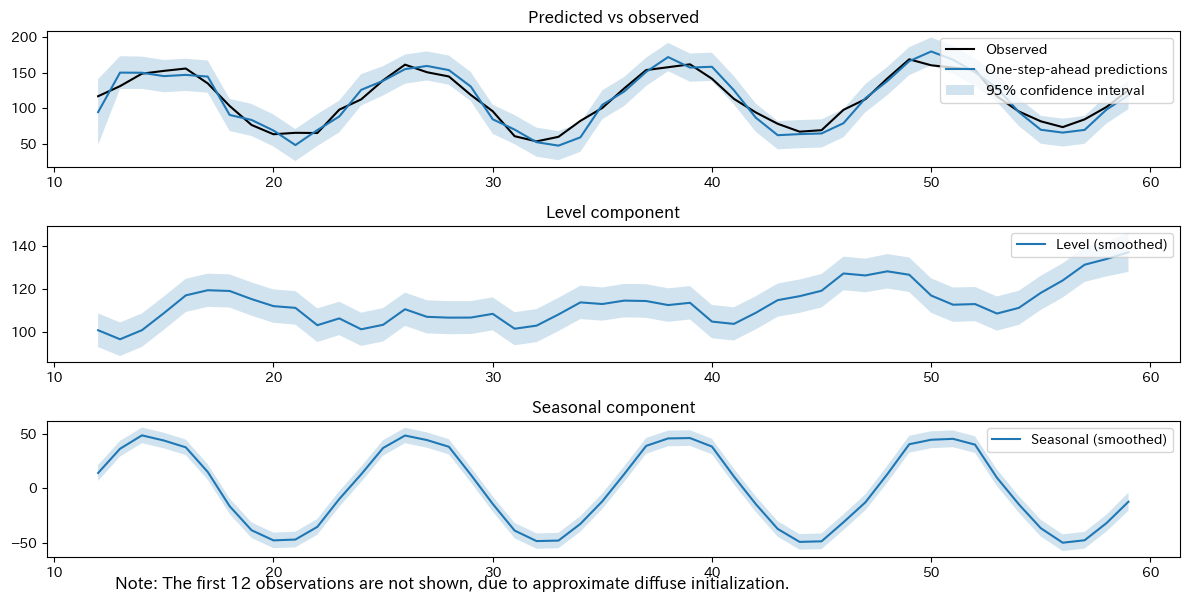
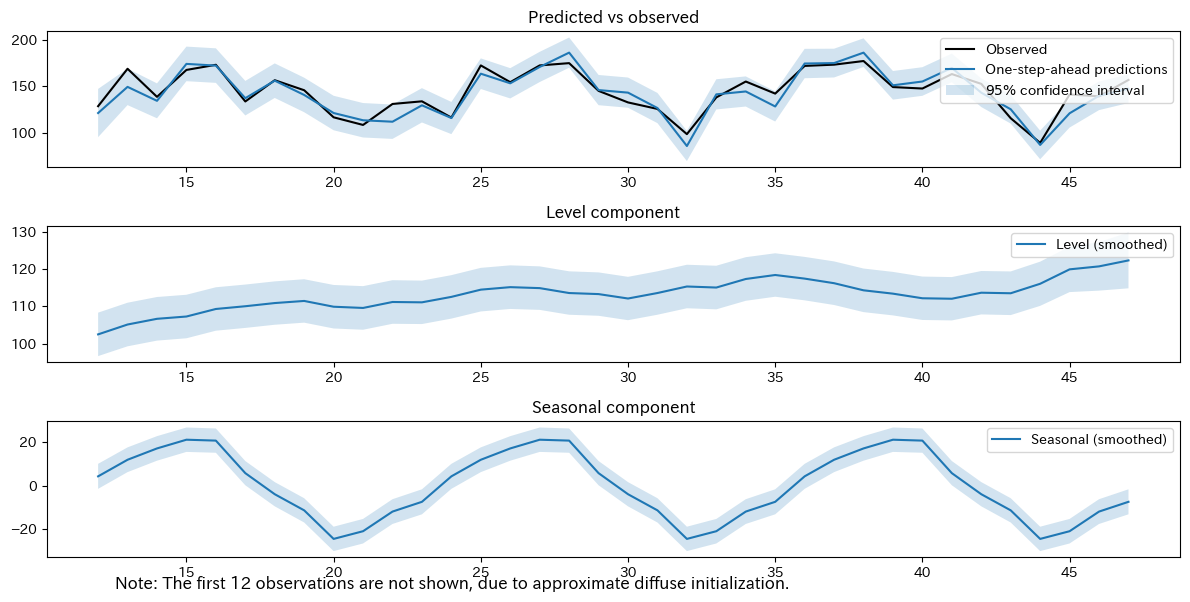
1番目のグラフは目的変数の実測値（Observed、観測されたデータ）と推定値（1期先予測の結果）を比較したものです。
2番目のグラフは水準（level）の平滑化の結果で、時点tでの水準
3番目（一番下）のグラフは季節成分（Seasonal）の平滑化の結果で、時点tでの
このモデルを使い将来予測をします。
以下、コードです。
# 1年分の予測（12ヶ月分）
forecast_steps = 12
forecast = res.get_forecast(steps=forecast_steps)
forecast_ci = forecast.conf_int()
# 結果のプロット
plt.figure(figsize=(12,6))
plt.plot(
monthly_sales,
label='観測された売上')
plt.plot(
res.fittedvalues,
label='推定された売上',
linestyle='--')
plt.plot(
np.arange(n, n + forecast_steps),
forecast.predicted_mean,
linestyle=':', color='r', label='予測')
plt.fill_between(
np.arange(n, n + forecast_steps),
forecast_ci[:, 0], forecast_ci[:, 1],
color='r', alpha=0.1, label='予測区間')
plt.legend()
plt.title('アイスクリーム店の売上予測：季節性を含むモデル')
plt.xlabel('月')
plt.ylabel('売上')
plt.show()
以下、実行結果です。
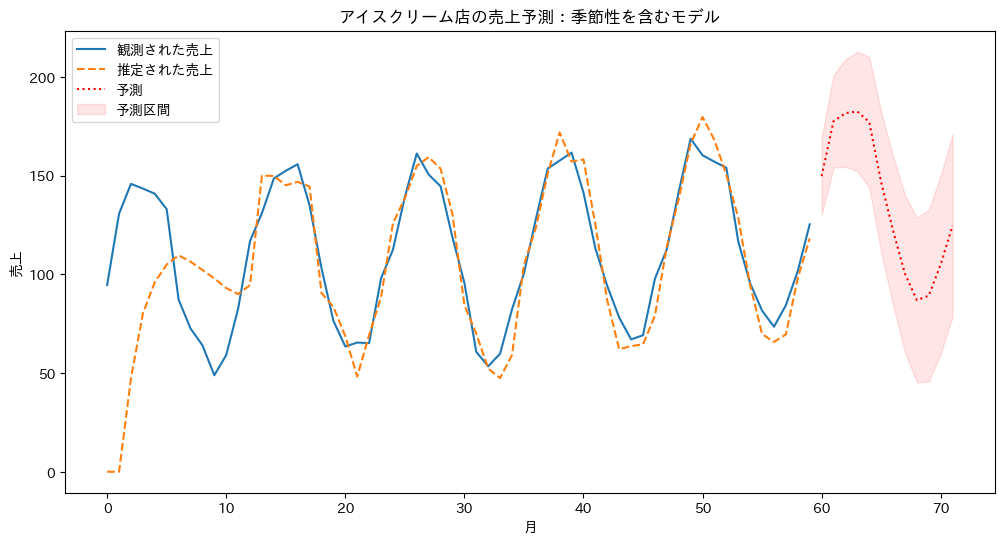
このモデルを使用することで、基本的な売上水準と季節変動を分離して分析できます。これにより、季節調整済みの売上トレンドや、各月の季節効果を正確に把握することができます。
外生変数を組み込んだモデル
多くのビジネスシーンでは、売上などの目的変数が、広告費や経済指標といった外部要因（外生変数）の影響を受けることがあります。状態空間モデルは、こうした外生変数の影響も考慮に入れることができます。
例えば、ある企業の月次売上が、基本的なトレンドと季節性に加えて、広告費の影響を受けていると仮定しましょう。このような状況は、以下のようなモデルで表現できます：
観測方程式
状態方程式
ここで、
は時点tでの売上 は基本的な売上水準 は季節成分 は広告費（外生変数） は広告費の効果を表す係数 は季節の周期（例：月次データなら12） , , はそれぞれのノイズ項
このモデルでは、売上が基本水準、季節性、広告費の影響、そしてランダムなノイズによって決定されると考えています。
では、Pythonで簡単なサンプルデータを作り、そのサンプルデータに対し外生変数と季節性のあるローカルレベルモデルを実装してみます。
以下、コードです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.structural import UnobservedComponents
# データ生成（月次売上と広告費をシミュレーション）
np.random.seed(123)
n = 48 # 4年分の月次データ
trend = np.linspace(0, 20, n) # 緩やかな上昇トレンド
seasonal = 20 * np.sin(np.linspace(0, 2*np.pi*4, n)) # 季節性
ad_spend = np.random.randint(0, 100, n) # 広告費
# 広告費の効果を加味した売上を生成
sales = trend + seasonal + 0.5 * ad_spend + np.random.normal(0, 5, n) + 100
# データフレームの作成
df = pd.DataFrame({
'sales': sales,
'ad_spend': ad_spend
})
# モデルの適用
model = UnobservedComponents(
df['sales'], # 観測された売上
exog=df[['ad_spend']], # 広告費を説明変数として指定
level='local level', # ローカルレベルモデルを指定
seasonal=12, # 季節成分の周期を指定
)
res = model.fit()
# 結果のプロット
res.plot_components(figsize=(12,6))
plt.tight_layout()
plt.show()
# 推定された係数（coef）の出力
print(res.summary().tables[1])
以下、実行結果です。
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 24.7217 10.739 2.302 0.021 3.674 45.770
sigma2.level 10.2892 9.775 1.053 0.293 -8.869 29.448
sigma2.seasonal 1.824e-08 4.281 4.26e-09 1.000 -8.390 8.390
beta.ad_spend 0.5111 0.047 10.952 0.000 0.420 0.603
====================================================================================
広告費（外生変数）の係数（coef）は0.5111で、p値（P>|z|）が0.05未満であることより有意であることが分かります。
このモデルを使い将来予測をします。
以下、コードです。
# 予測対象期間の設定（今回は12ヶ月分）
forecast_steps = 12
# 予測対象期間の新しい広告費を設定（今回は一定値を仮定）
future_ad_spend = np.full(forecast_steps, df['ad_spend'].mean())
# 予測の実施
forecast = res.get_forecast(steps=forecast_steps, exog=future_ad_spend.reshape(-1, 1))
forecast_ci = forecast.conf_int()
# 結果のプロット
plt.figure(figsize=(12,6))
plt.plot(df['sales'], label='観測された売上')
plt.plot(res.fittedvalues, label='推定された売上', linestyle='--')
plt.plot(
np.arange(len(df), len(df) + forecast_steps),
forecast.predicted_mean,
linestyle=':', color='r', label='予測')
plt.fill_between(
np.arange(len(df), len(df) + forecast_steps),
forecast_ci.iloc[:, 0], forecast_ci.iloc[:, 1],
color='r', alpha=0.1, label='予測区間')
plt.legend()
plt.title('広告費を考慮した売上予測モデル')
plt.xlabel('月')
plt.ylabel('売上')
plt.show()
以下、実行結果です。
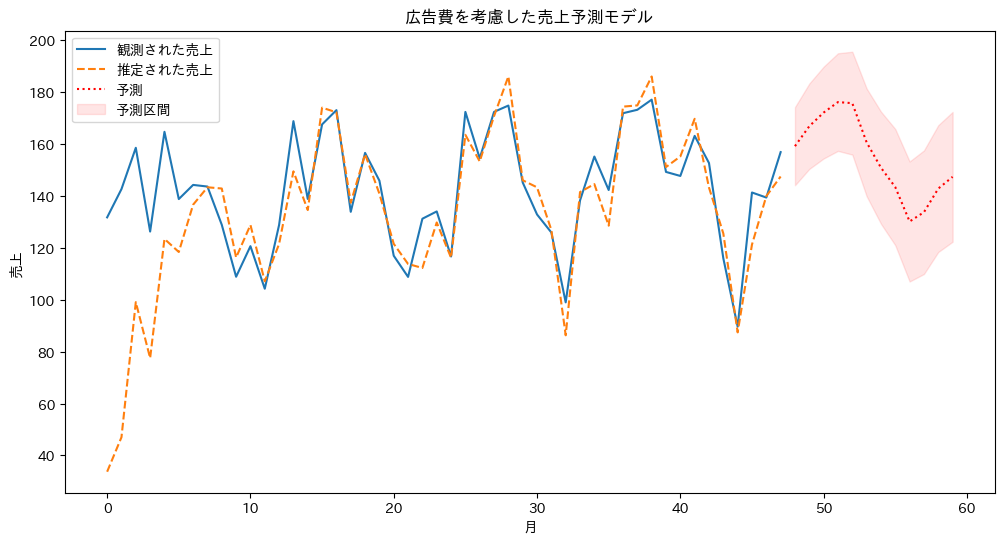
このように、外生変数を組み込んだ状態空間モデルは、ビジネスの複雑な現実をより正確に捉え、意思決定に役立つ洞察を提供することができます。
ARIMA系モデルとのつながり
時系列モデルと言えば、ARIMA系のモデルです。状態空間モデルと何がどう異なるのでしょうか。
状態空間モデルは、ARIMA系モデルに比べて柔軟で、トレンドの性質を簡単に変更できます。また、時系列の構成要素を明示的にモデル化できるため、結果の解釈が容易です。さらに、状態空間モデルは欠損値や不規則なデータにも自然に対応でき、カルマンフィルタやスムーザーといった効率的なアルゴリズムにより、大規模なデータでも計算効率が高いです。さらに、状態空間モデルは多変量時系列にも自然に拡張可能で、複数の時系列を同時にモデル化できます。
ARIMA系モデルと状態空間モデルは一見異なる方法論に見えますが、実際には密接に関連しています。ARIMA系モデルは、適切な状態変数を定義することで、状態空間表現に変換できます。ARIMAモデルを状態空間フレームワークで扱うことが可能になり、カルマンフィルタなどの強力なアルゴリズムを適用できます。
ここまでのPythonのコード例から、状態空間モデルを実装するときstatsmodels.tsa.statespace.structuralを利用していることが分かると思います。ちなみに、ARIMA系モデルを実装するときstatsmodels.tsa.statespace.sarimaxを利用するケースが多いです。どちらもstatsmodels.tsa.statespace モジュールの一部です。statespaceは状態空間を意味します。要するに、Statsmodelsライブラリは、ARIMA系モデルを状態空間表現で実装しています。
状態空間モデルは、ARIMA系モデルの機能を包含しつつ、より柔軟で解釈可能なモデリングを可能にします。実務では、データの性質や分析の目的に応じて、適切なモデルを選択することが重要です。
状態空間モデルを実装するときstatsmodels.tsa.statespace.structuralのUnobservedComponentsクラスを利用していました。ただ、基本的な線形状態空間モデルしか実装できません。より柔軟かつ自由にモデル化したい場合には、statsmodels.tsa.statespace.mlemodelのMLEModelクラスを利用します。
まとめ
状態空間モデルは、ビジネスの複雑なデータに対して柔軟かつ効果的に対応できる強力な分析ツールです。
ローカルレベルモデルや季節性を含むモデル、外生変数を考慮したモデルなど、さまざまなアプローチを活用することで、売上予測や在庫管理、広告効果の分析など、実務に直結した予測と意思決定が可能になります。
また、Pythonを用いた実装は、比較的簡単に行えるため、データサイエンス初心者にも取り組みやすいです。状態空間モデルを活用して、より精度の高い予測を行い、ビジネスに役立つ洞察を得ましょう。
