スマートフォンの利用状況、ECサイトの売上、工場の生産量など、私たちの周りには時間とともに変化するデータが溢れています。
こうした「時系列データ」を分析する際、単純にグラフを眺めるだけでは見えてこない重要な情報が隠れていることがあります。
今回は、時系列データを分解して深く理解するための手法「STL分解」(季節性が1つ)と「MSTL分解」(季節性が複数)についてお話しします。
Contents [hide]
- 3つの要素を知れば分析が見えてくる
- 時系列データとは?
- 時系列データを構成する3つの要素
- 簡単例でお話しすると……
- STL分解入門
- STL分解とは何か
- 必要なライブラリの準備
- STL分解の実践例
- Step 1: データの読み込みと準備
- Step 2: STL分解の実行
- Step 3: 季節性の強さを確認
- Step 4: 季節性の寄与度を確認
- Step 5: 季節調整済みデータの作成
- MSTL分解:複数の季節性を持つデータを理解する
- MSTL分解とは?
- MSTL分解の実践例
- Step 1: データの読み込みと準備
- Step 2: MSTL分解の実行
- Step 3: 季節性の強さを確認
- Step 4: 季節性の寄与度を確認
- Step 5: 季節調整済みデータの作成
- まとめ
3つの要素を知れば分析が見えてくる
スマートフォンの1日の使用時間、オンラインショップの月間売上、株価の値動き……
これらはすべて「時系列データ」と呼ばれるものです。
では、なぜこうしたデータを分析する必要があるのでしょうか?
時系列データとは?
時系列データとは、時間の経過とともに記録された一連の数値データのことです。
例えば、毎月の売上データであれば、4月は100万円、5月は120万円、6月は95万円…… というように時間軸に沿ってデータが並んでいきます。
このようなデータを見るとき、私たちはつい「先月より売上が減った」「去年より伸びている」といった単純な比較をしがちです。
しかし、時系列データはもっと豊かな情報を含んでいます。
時系列データを構成する3つの要素
一般的に、時系列データ
ここで……
:トレンド成分(長期的な変化傾向) :季節性成分(一定の周期で繰り返される変動) :残差成分(トレンドと季節性では説明できない変動)
を表します。
トレンド成分
長期的な変化の傾向を表します。例えば、「ここ5年間で少しずつ売上が伸びている」といった変化です。景気の変動や企業の成長などが影響します。
季節性成分
一定の周期で繰り返される変動のことです。例えば、「毎年12月は売上が増える」「毎週月曜日はアクセスが多い」といった規則的な変化がこれにあたります。
残差成分
上記の2つでは説明できない変動のことです。予期せぬイベントの影響や、ランダムな変動が含まれます。例えば、「突然の天候不良で売上が落ち込んだ」といった変化です。
簡単例でお話しすると……

例えば、あるアイスクリームショップの月間売上データを考えてみましょう。
- トレンド成分:年々少しずつ売上が増加(店舗の認知度向上)
- 季節性成分:夏場は売上が増加し、冬場は減少
- 残差成分:突然の猛暑や雨天による売上の変動
このように分解して考えることで、「夏場の売上は良いが、それを差し引いても実は着実に成長している」といった、より深い洞察を得ることができます。
時系列データは、一見シンプルに見えて実は複雑な構造を持っています。
3つの要素を理解し、適切に分解して分析することで、データに隠れた重要な情報を見つけ出すことができます。
STL分解入門
時系列データを分析していると、「売上は増えているけど、季節要因の影響をどう考えればいいんだろう?」「本当の成長トレンドを知りたい」といった悩みに直面します。
そんなとき活用できるのが「STL分解」です。これは、時系列データを以下の3つの要素に分解する統計手法です。
- トレンド成分:長期的な変化傾向
- 季節性成分:一定周期で繰り返される変動
- 残差成分:上記以外の変動
STL分解とは何か
STLは「Seasonal and Trend decomposition using Loess」の略で、「ローエス(LOESS)を使用した季節性とトレンドの分解」という意味です。
ローエス(LOESS)は「LOcally Estimated Scatterplot Smoothing」の略で、日本語では「局所推定散布図平滑化」と訳されたりします。これは、データの傾向を滑らかな曲線で表現するための統計的手法です。
難しく聞こえるかもしれませんが、簡単に言えば「時系列データを主要な3つの部分にいい感じに分ける手法」ということです。
このSTL分解は以下のような状況で特に効果を発揮します。
季節変動の影響を除きたいとき
- 実質的な業績の伸びを評価したい
- 前年同月比較をより正確に行いたい
異常値を検出したいとき
- システムの異常アクセスを見つけたい
- 売上の急激な変動を分析したい
将来予測の精度を上げたいとき
- 季節パターンを定量化したい
- トレンドの変化を正確に把握したい
より詳細なことを知りたい方は、以下の記事を参考にして頂ければと思います。
それでは、実際にPythonを使ってSTL分解を実践してみましょう。
必要なライブラリの準備
まずは必要なライブラリをインストールしましょう。
以下のコマンドを実行します。
pip install pandas numpy matplotlib statsmodels pmdarima pip install japanize-matplotlib # 日本語表示用
STL分解の実践例
Step 1: データの読み込みと準備
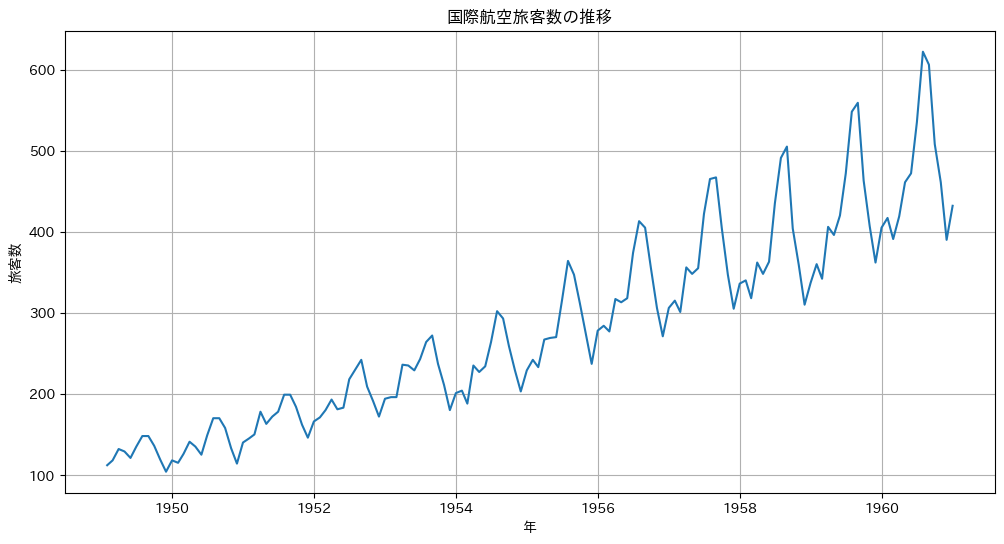
最初に、サンプルデータとして国際線乗客数データを使用します。このデータは、1949年から1960年までの月次の航空旅客数を記録したものです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from pmdarima.datasets import load_airpassengers
# データの読み込み
data = load_airpassengers()
# データフレームに変換
df = pd.DataFrame(
data,
columns=['passengers'] # 列名を設定
)
# インデックスを日付に変更
df.index = pd.date_range(
start='1949-01-01', # 開始日
periods=len(df), # データ数
freq='M' # データ間隔(M:月次)
)
# 元のデータをプロット
plt.figure(figsize=(12, 6))
plt.plot(df.index, df['passengers'])
plt.title('国際航空旅客数の推移')
plt.xlabel('年')
plt.ylabel('旅客数')
plt.grid(True)
plt.show()
以下、実行結果です。
Step 2: STL分解の実行
次に、このデータをSTL分解してみましょう。
from statsmodels.tsa.seasonal import STL
# STL分解の実施
stl = STL(df['passengers'], period=12) # 12ヶ月の季節性を指定
result = stl.fit()
# 結果のプロット
fig = plt.figure(figsize=(12, 10))
ax = fig.subplots(4, 1) # 4行1列のサブプロット
# 観測データ
result.observed.plot(ax=ax[0], title='観測データ')
ax[0].set_xlabel('')
# トレンド成分
result.trend.plot(ax=ax[1], title='トレンド成分')
ax[1].set_xlabel('')
# 季節性成分
result.seasonal.plot(ax=ax[2], title='季節性成分')
ax[2].set_xlabel('')
# 残差成分
result.resid.plot(ax=ax[3], title='残差成分')
plt.tight_layout()
plt.show()
ここでは、statsmodelsライブラリのSTLクラスを使用して分解を行っています。period=12は、12ヶ月の季節性を想定していることを示します。
以下、実行結果です。
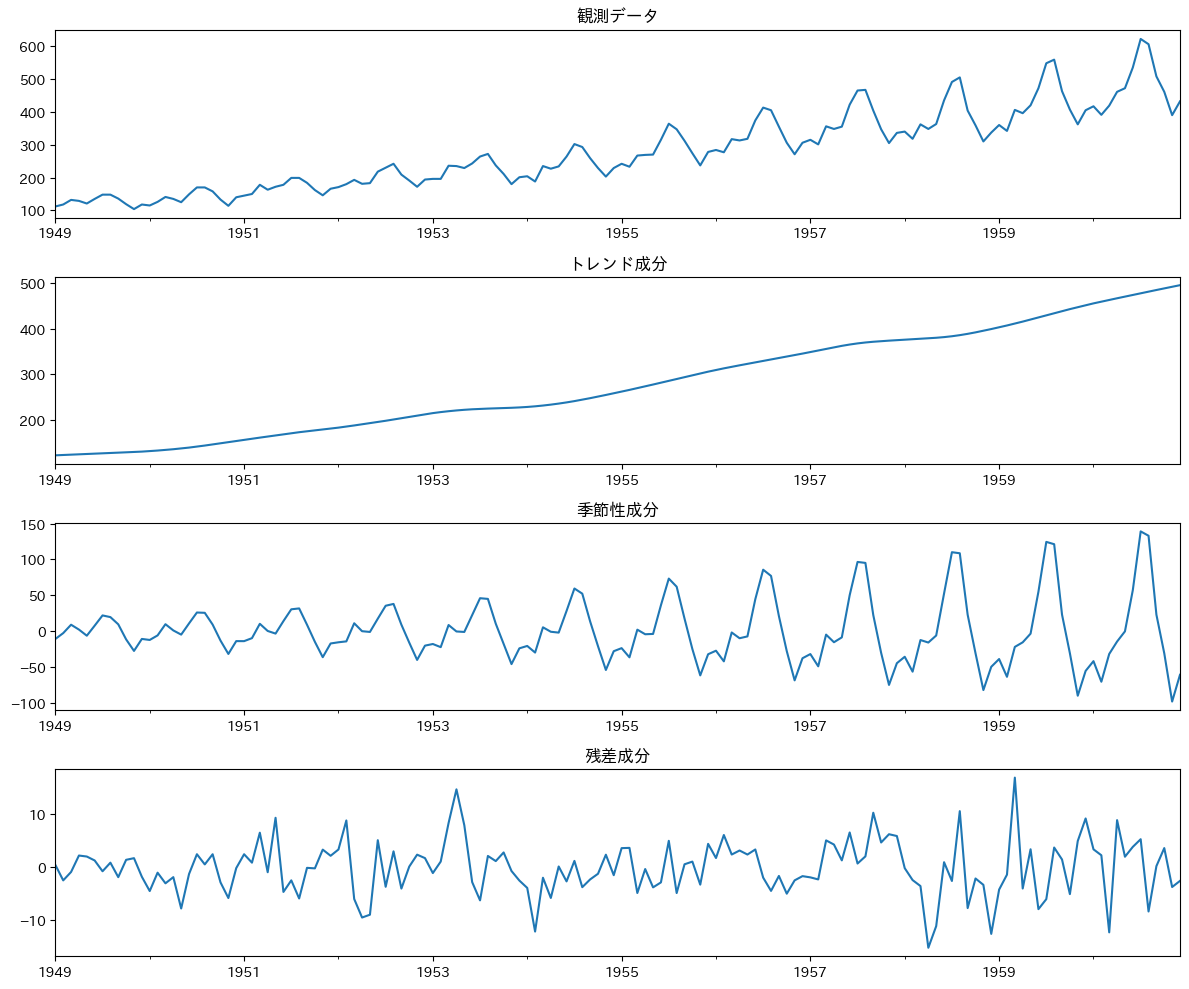
分解結果を見てみましょう。
トレンド成分ですが、なめらかな上昇カーブを描いていることが分かります。
季節性成分ですが、明確な12ヶ月周期のパターンが見られ、振幅が年々大きくなっている(季節変動が強まっている)様子が伺えます。
残差成分ですが、比較的小さな変動が中心で、特定の時期に大きな変動も見られることから、トレンド成分と季節成分だけでは説明できない要因がありそうなことが分かります。
Step 3: 季節性の強さを確認
季節性が意味のあるパターンなのか、単なるノイズなのかを判断するために、各季節性がランダムな変動(残差)に比べてどれくらい強いかを評価します。
具体的には、季節性とノイズの標準偏差の比較を行います。標準偏差は、データのばらつきの大きさを示す指標です。
- 季節性成分の標準偏差 → 季節変動の振幅(大きさ)を表す
- 残差成分の標準偏差 → ランダムな変動の大きさを表す
これらの比(seasonal_std / resid_std)を取ることで、「ランダムな変動に対して、季節変動がどれだけ大きいか」を数値化できます。
- 比率が1より大きい → 季節変動がノイズより大きい
- 比率が1より小さい → ノイズが季節変動より大きい
例えば、比率が2以上なら意味のあるパターンと判断します。
以下、コードです。
# 季節性の強さを確認
resid_std = result.resid.std() # 残差の標準偏差
seasonal_std = result.seasonal.std() # 季節性成分の標準偏差
seasonal_strength = seasonal_std / resid_std # 季節性の強さ
print(f"季節性の強さ: {seasonal_strength:.2f}")
以下、実行結果です。
季節性の強さ: 8.63
季節性が強いことが分かります。
では、この季節性がデータ全体をどれだけ説明しているのでしょうか?
Step 4: 季節性の寄与度を確認
意味のあると判断された季節性について、複数の季節性の中でどれを重視すべきか判断するために、全体に対する寄与度を把握していきます。予測モデルの構築時に、どの季節性を優先的に含めるべきか決めるためです。
分散を使い、データの全体(トレンド+季節性+残差)の変動のうち各季節性がどれくらいの割合を占めているかを評価します。
以下、コードです。
# データ全体に対する季節性の寄与度
total_variance = result.observed.var() # 全体の分散
seasonal_variance = result.seasonal.var() # 季節性成分の分散
seasonal_ratio = seasonal_variance / total_variance # 季節性分散の割合
print(f"季節性の寄与度: {seasonal_ratio:.2%}")
以下、実行結果です。
季節性の寄与度: 13.22%
季節性成分が、データ全体の変動の約13%を占めていることが分かりました。無視できる割合ではありません。
Step 5: 季節調整済みデータの作成
季節性の影響を除いた「季節調整済みデータ」を作成してみましょう。
# 季節調整済みデータの作成
plt.figure(figsize=(12, 6))
# 元のデータ
plt.plot(
df.index,
df['passengers'],
label='元のデータ'
)
# 季節調整済みデータ
seasonally_adjusted = df['passengers'] - result.seasonal
plt.plot(
df.index,
seasonally_adjusted,
linestyle=':',
label='季節調整済みデータ'
)
plt.title('元のデータと季節調整済みデータの比較')
plt.legend()
plt.grid(True)
plt.show()
以下、実行結果です。
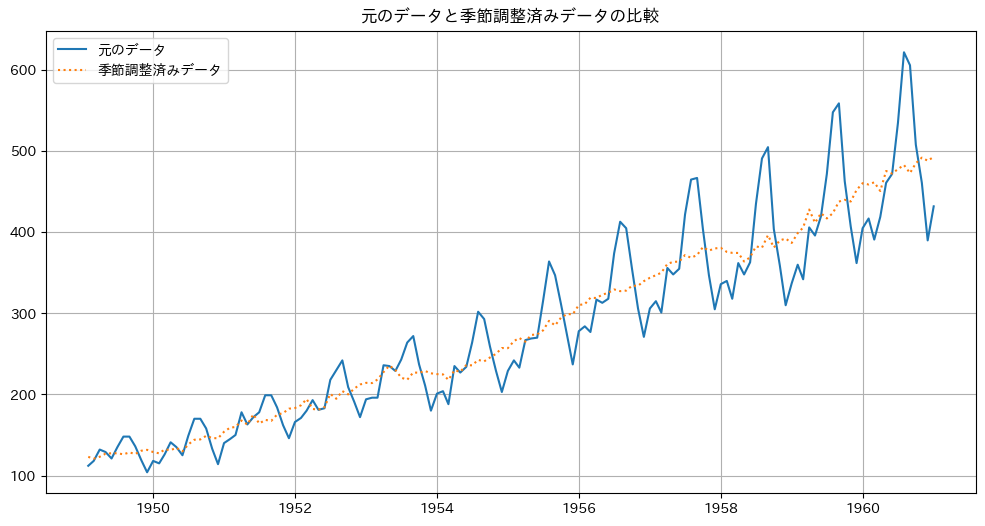
以下の理由から、このような季節調整済みデータを作ることは重要です。
- より滑らかなトレンドが見えやすくなります
- 前年同月比較などがより意味のある分析になります
- 異常値の検出が容易になります
MSTL分解:複数の季節性を持つデータを理解する
MSTL分解とは?
実際の時系列データには、複数の周期による季節性が存在することがあります。例えば、あるECサイトのアクセス数には以下のような複数の季節パターンが含まれることがあります。
- 24時間周期(1日の中での変動)
- 7日周期(週単位の変動)
- 365日周期(年単位の変動)
このような複数の季節性を持つデータに対しては、通常のSTL分解ではなく、MSTL分解を使用します。数式で表現すると、MSTL分解は次のようになります。
ここで……
:トレンド成分 :i番目の季節性成分(i = 1, …, k) :残差成分 - k:季節性の数
あるECサイトのアクセス数には、以下のような複数の周期が存在します。
- 1日の中での変動
- 朝:通勤・通学時にピーク
- 昼:お昼休みに小さなピーク
- 夜:帰宅後に大きなピーク
- 週単位の変動
- 平日:仕事の合間の利用
- 週末:ゆっくり買い物を楽しむ人が増加
- 年間の変動
- 夏:季節商品の需要増加
- 冬:クリスマス・年末商戦
STL分解では1つの周期しか指定できません。例えば、24時間(1日)の周期のみを指定してしまうと、週単位や年単位の変動を見落としてしまいます。
MSTL分解では複数の周期を指定できるます。例えば、24時間(日)、168時間(週)、8760時間(年)の周期を同時に分析するじことが可能です。
この例の場合、次のような成分に分解されます。
トレンド成分
- 長期的な増加・減少傾向
- 例:ECサイトの成長に伴う全体的なアクセス数の増加
複数の季節性成分
- 日次の変動パターン
- 週次の変動パターン
- 年次の変動パターン
残差成分
- 上記では説明できないランダムな変動
- 予期せぬイベントの影響など
MSTL分解は、複雑な時系列データを理解するための強力なツールです。特に以下のような場合に効果を発揮します。
- データに複数の周期性が存在する
- それぞれの周期の影響度を知りたい
- より精度の高い予測を行いたい
初めて時系列分析を行う場合は、まずSTL分解で基本を理解し、複数の周期性が見つかった場合にMSTL分解を検討するというステップを踏むことをお勧めします。
MSTL分解の実践例
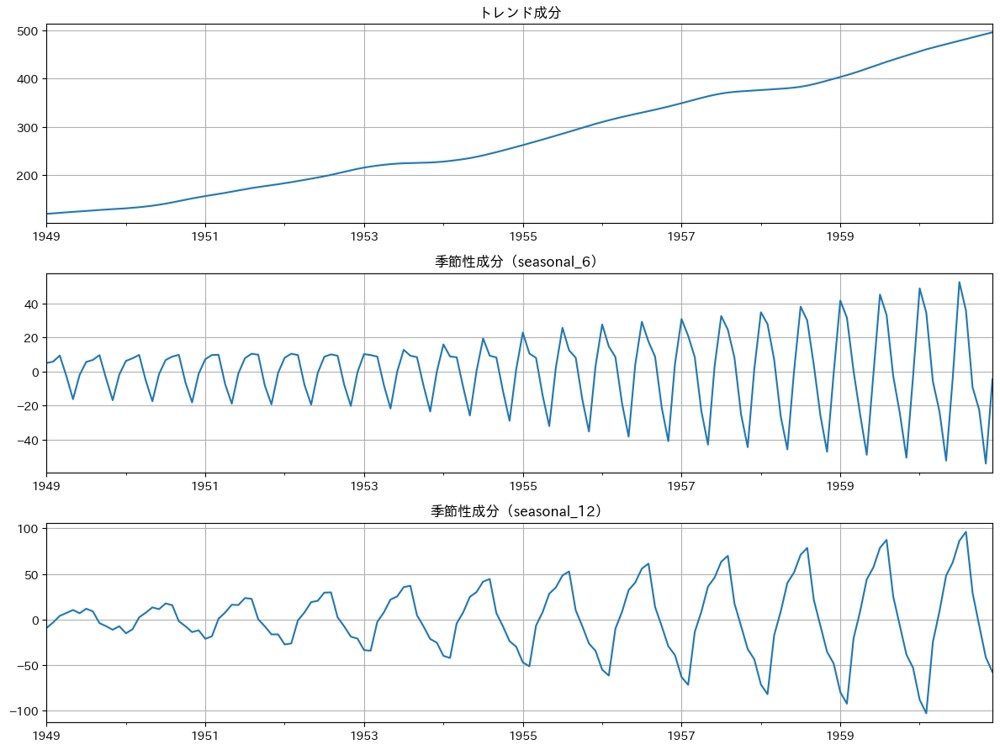
STL分解で利用した航空旅客数データに対して6ヶ月周期と12ヶ月周期の2つの季節性を想定して分析します。
Step 1: データの読み込みと準備
STL分解の実践例と同じコードなので割愛し、データセットは読み込まれているものとして話しを進めます。
Step 2: MSTL分解の実行
次に、このデータをMSTL分解してみましょう。
以下、コードです。
from statsmodels.tsa.seasonal import MSTL
# MSTL分解の実施(6ヶ月周期と12ヶ月周期を指定)
mstl = MSTL(df['passengers'], periods=[6, 12])
result = mstl.fit()
# 結果のプロット
num_seasonal = len(result.seasonal.columns) # 季節成分の数
num_rows = 3 + num_seasonal # プロット数
fig, ax = plt.subplots(num_rows, 1, figsize=(12, 3 * num_rows))
# 観測データ
result.observed.plot(ax=ax[0], title='観測データ')
ax[0].set_xlabel('')
ax[0].grid(True)
# トレンド成分
result.trend.plot(ax=ax[1], title='トレンド成分')
ax[1].set_xlabel('')
ax[1].grid(True)
# 季節性成分
for i, col in enumerate(result.seasonal.columns):
result.seasonal[col].plot(ax=ax[2 + i], title=f'季節性成分({col})')
ax[2 + i].set_xlabel('')
ax[2 + i].grid(True)
# 残差成分
result.resid.plot(ax=ax[2 + num_seasonal], title='残差成分')
ax[2 + num_seasonal].grid(True)
plt.tight_layout()
plt.show()
以下、実行結果です。
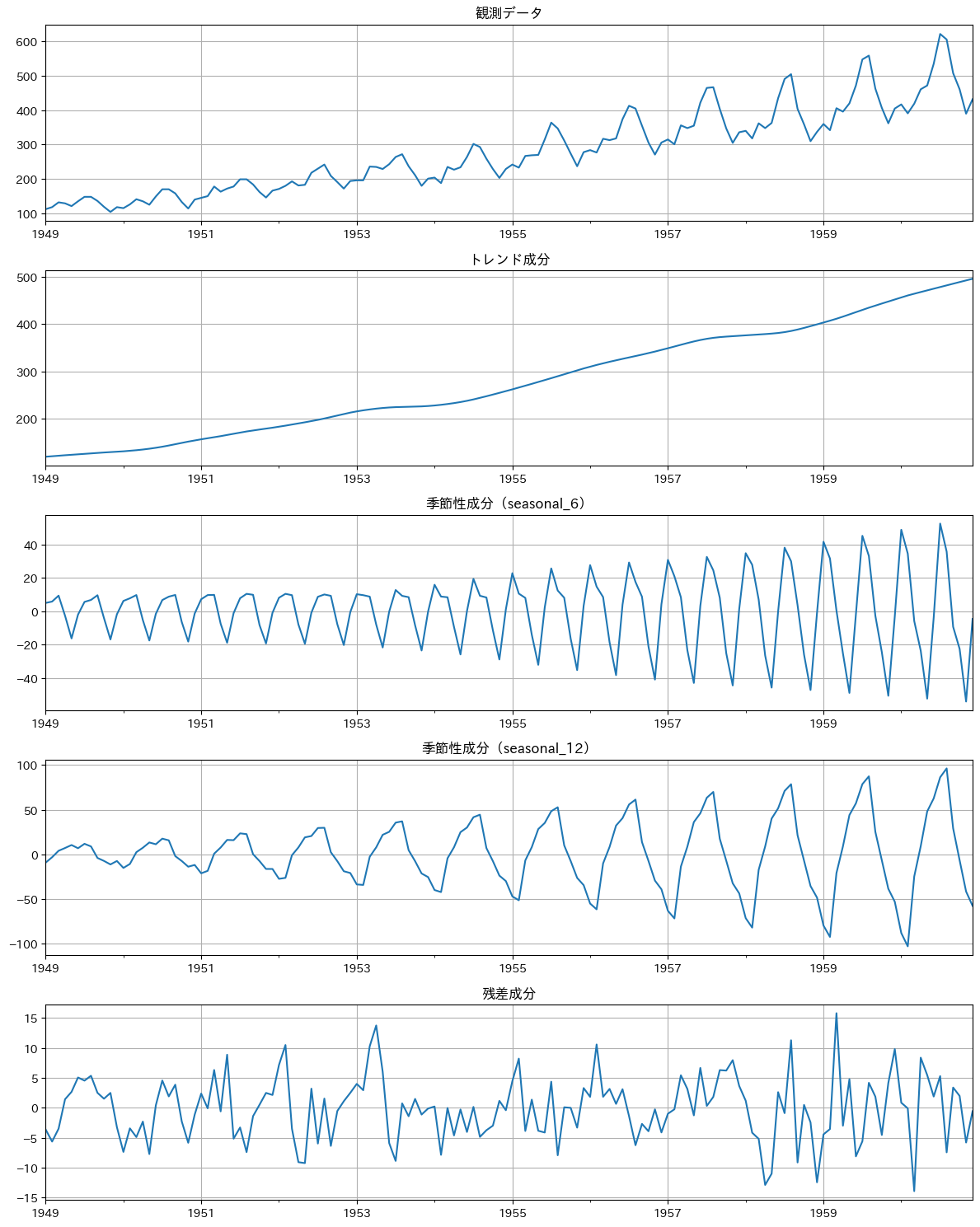
Step 3: 季節性の強さを確認
各季節性が意味のあるパターンかを確認します。目安としては、比率が2以上なら意味のあるパターンと判断します。
- 目的: 各季節性が、ランダムな変動(残差)に比べてどれくらい強いかを評価
- 特徴: 季節性とノイズの比較を行う
- 使うべき場面: 季節性が意味のあるパターンなのか、単なるノイズなのかを判断したい場合
以下、コードです。
# 季節性の強さを確認
resid_std = result.resid.std() # 残差の標準偏差
for col in result.seasonal.columns:
seasonal_std = result.seasonal[col].std() # 季節性成分の標準偏差
print(f"{col}の季節性の強さ: {seasonal_std/resid_std:.2f}")
以下、実行結果です。
seasonal_6の季節性の強さ: 3.97 seasonal_12の季節性の強さ: 7.11
2つの季節成分とも考慮した方がよさそうです。
Step 4: 季節性の寄与度を確認
意味のあると判断された季節性について、その重要度を評価していきます。全体に対する影響度です。
- 目的: データの全体の変動のうち、各季節性がどれくらいの割合を占めているかを評価
- 特徴: データ全体(トレンド+季節性+残差)に対する各季節性の相対的な重要度を示す
- 使うべき場面: 複数の季節性の中で、どれが最も影響力が大きいかを知りたい場合
以下、コードです。
# 季節性の寄与度を確認
total_var = result.observed.var() # 全体の分散
for col in result.seasonal.columns:
seasonal_var = result.seasonal[col].var() # 季節性成分の標準偏差
print(f"{col}の季節性の寄与度: {seasonal_var/total_var:.2%}")
以下、実行結果です。
seasonal_6の季節性の寄与度: 3.14% seasonal_12の季節性の寄与度: 10.04%
Step 5: 季節調整済みデータの作成
季節性の影響を除いた「季節調整済みデータ」を作成してみましょう。
以下、コードです。
# 季節調整済みデータの作成(全ての季節成分を調整)
plt.figure(figsize=(12, 6))
# 元のデータ
plt.plot(
df.index,
df['passengers'],
label='元のデータ'
)
# 季節調整済みデータ(全ての季節成分を調整する)
seasonally_adjusted = df['passengers'] - result.seasonal.sum(axis=1)
plt.plot(
df.index,
seasonally_adjusted,
linestyle=':',
label='季節調整済みデータ(全ての季節成分を調整)'
)
plt.title('元のデータと季節調整済みデータの比較(全ての季節成分を調整)')
plt.legend()
plt.grid(True)
plt.show()
以下、実行結果です。
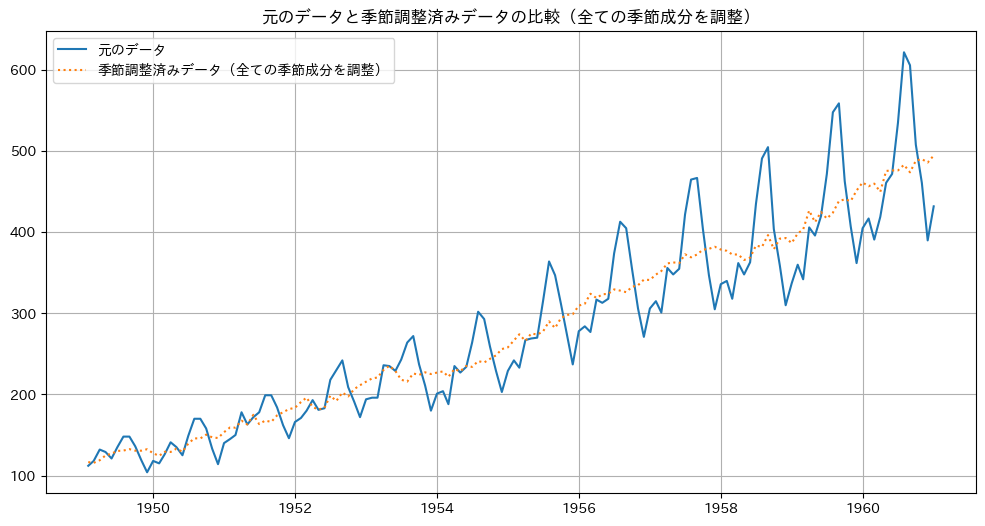
まとめ
時系列データは「トレンド」「季節性」「残差」の3要素から構成されています。分析の第一歩は、これらの要素を理解し、データの特徴を把握することです。
時系列データの分析には、まずSTL分解が基本となります。STL分解では、データを3つの要素に分解することで、長期的な変化傾向(トレンド)、周期的な変動(季節性)、そして説明できない変動(残差)を把握できます。
複数の周期を持つデータ(例:日次と週次の両方のパターン)に対しては、MSTL分解を使用します。これにより、複数の季節性を同時に分析することが可能です。
いずれの手法を選ぶ場合も、まずはデータの特徴をしっかりと観察し、ビジネスの文脈に沿って解釈することが重要です。分析の目的は、データの中に隠れたパターンを見つけ出し、より良いビジネス判断につなげることにあります。