時系列データ分析は、特定の期間における変化を捉え、将来の動向を予測するための重要な手法です。
前回の記事では、mlforecastライブラリを使用して基本的な時系列予測モデルを構築する方法と、モデル性能を向上させるためのハイパーパラメータ調整について解説しました。
しかし、時系列予測モデルの性能は単にアルゴリズムやハイパーパラメータに依存するだけではありません。
モデルに入力されるデータ、特にその特徴量(データから抽出される説明変数)や目標変数の適切な変換が非常に重要です。
データの特徴を正確に捉え、モデルがその構造を理解できるようにすることで、より良い予測を可能にします。
今回は、時系列データ特有の特徴量エンジニアリング(時系列特徴量)と目標変数の変換について解説し、それをmlforecastで実現する方法を紹介します。
以下のような具体的な疑問に答えることを目指します。
- 過去のデータをどう活用すれば、将来の予測に役立つか?
- 季節性やトレンドなど、時系列特有の構造をどのようにモデルに取り込むか?
- 目標変数をどのように変換すれば、モデル性能が向上するか?
Contents [hide]
- 時系列特徴量とは?
- 特徴量エンジニアリングの重要性
- 主な時系列特徴量
- 特徴量の作成における注意点
- 時系列機械学習モデルの構築のながれ
- サンプルデータの読み込み
- 機械学習モデルの構築
- 予測の実行
- MLForecastでの時系列特徴量の設定
- ラグ特徴量
- ローリング特徴量とエクスパンディング特徴量
- カレンダー特徴量
- MLForecastでの目的変数変換
- target_transformsとは?
- ローカル変換
- グローバル変換
- Optunaによるハイパラの自動化
- Optunaのハイパラ探索インスタンスの生成
- 時系列機械学習のモデル構築
- 予測の実行
- lightgbm版
- xgboost版
- 時系列予測モデルの作り方の検証
- 利用する機械学習モデルのインスタンスの生成
- 学習データとテストデータ(直近1年)に分割
- 学習データでモデル構築
- テストデータで精度検証
- まとめ
時系列特徴量とは?
時系列データの特徴量エンジニアリングは、モデルが予測に必要な重要な情報を学習できるようにするためのステップです。
特に、時系列データは時間的な依存性や周期性、トレンドといった特有の構造を持つため、それらを的確に捉える特徴量を作成することが重要です。
特徴量エンジニアリングの重要性
機械学習モデルの性能は、モデルに入力されるデータの質に大きく依存します。
時系列予測では、以下の理由から特徴量エンジニアリング(時系列特徴量の生成)が特に重要です。
- 時間的依存性の把握:過去のデータが将来の予測にどのような影響を与えるかをモデルが学習できるようにする。
- パターンの強調:季節性やトレンドといった時系列特有のパターンを数値化し、モデルが利用可能にする。
- 外部要因の反映:カレンダー情報や天候データなど、時系列データ以外の影響要因を統合する。
主な時系列特徴量
ラグ特徴量
ラグ特徴量とは、過去のデータポイントをそのまま特徴量として使用する方法です。
これは、時間的依存性をモデルに取り込むための最も基本的な手法です。
- 例:
- 今日の売上を予測するために、1日前や7日前の売上を特徴量として利用
- 用途:
- 短期的な依存関係のモデリング
- 繰り返し発生するパターン(例: 週次の売上トレンド)の捉え方
ローリング特徴量
移動平均や移動標準偏差といったローリング特徴量は、過去のデータの変動や傾向を滑らかに捉える特徴量です。
- 例:
- 過去3日間の平均売上(移動平均)
- 過去7日間の売上変動(移動標準偏差)
- 用途:
- 短期的な変動の平滑化
- データのノイズ除去
エクスパンディング特徴量
累積平均や累積合計といったエクスパンディング特徴量は、データの全体的な変動を特徴量として捉えます。
- 例:
- これまでの累積売上の平均
- 今までの累積売上の合計
- 用途:
- 長期的なトレンドを反映
- 過去の蓄積の影響
カレンダー特徴量
日付情報そのものを利用して特徴量を作成します。これにより、時間的なパターンを捉えやすくなります。
- 例:
- 曜日(Monday, Tuesday…)
- 月(January, February…)
- 四半期(1Q, 2Q…)
- 祝日フラグ(外部データが必要)
- 用途:
- 曜日や月ごとの周期性を表現
- 特定のイベント(祝日やセール期間)の影響
外生変数(説明変数)
天候や経済指標、SNSのトレンドといった外部要因などを特徴量として追加します。
- 例:
- 気温(アイスクリームの売上などに影響)
- 為替レート(輸出入に影響)
- 用途:
- 時系列データに影響を与える外部要因の反映
特徴量の作成における注意点
データのリーク防止
特徴量作成の際に、未来のデータが含まれないよう注意が必要です。
モデルの複雑性の管理
特徴量を増やしすぎると、モデルが過剰適合するリスクがあります。特徴量の選択は慎重に行いましょう。
特徴量の正規化やスケーリング
特にローリング特徴量やエクスパンディング特徴量などは、スケールの違いを補正するための前処理が必要になる場合があります。
時系列機械学習モデルの構築のながれ
サンプルデータの読み込み
とある小売店の売上データのサンプルデータを読み込みます。
データは以下からダウンロードできます
sales_data.csv
以下、コードです。
import pandas as pd
# sales_data.csvを読み込み
data = pd.read_csv(
'sales_data.csv', # 読み込むファイル
parse_dates=['date'], # date列をdatetime型に変換
)
print(data)
以下、実行結果です。
date sales store area_id 0 2018-01-31 117.483571 A 1 1 2018-02-28 117.968933 A 1 2 2018-03-31 123.238443 A 1 3 2018-04-30 126.275403 A 1 4 2018-05-31 113.829233 A 1 .. ... ... ... ... 175 2022-08-31 142.796170 C 3 176 2022-09-30 140.065009 C 3 177 2022-10-31 145.927924 C 3 178 2022-11-30 133.676716 C 3 179 2022-12-31 143.600846 C 3 [180 rows x 4 columns]
このサンプルデータは、2018年1月から2022年12月までの5年間にわたる月次の売上データを示しています。
データには以下の4つの列があります。
- date: 各データポイントの日付を表し、月末の日付が記録されています
- sales: 各月の売上高を示す数値データです
- store: データがどの店舗に属するかを示す識別子(A, B, Cの3店舗)
- area_id: 各店舗が属するエリアを示す識別子(1, 2, 3の3エリア)
どのようなデータなのかを視覚的に見ていきます。
以下、コードです。
import matplotlib.pyplot as plt
# 店舗IDを取得
stores = data['store'].unique()
# 店舗ごとにプロットを分けて折れ線グラフを描画
fig, axes = plt.subplots(
len(stores),
1,
figsize=(10, 4 * len(stores))
)
for ax, store in zip(axes, stores):
# 各店舗ごとのデータを抽出
store_data = data[data['store'] == store]
# 各店舗の折れ線グラフを描画
ax.plot(
store_data['date'],
store_data['sales'],
marker='o',
label=store,
)
ax.set_title(f'Store: {store}', fontsize=12)
ax.set_ylabel('Sales', fontsize=12)
ax.grid(True)
plt.xlabel('Date', fontsize=12)
plt.tight_layout()
plt.show()
以下、実行結果です。
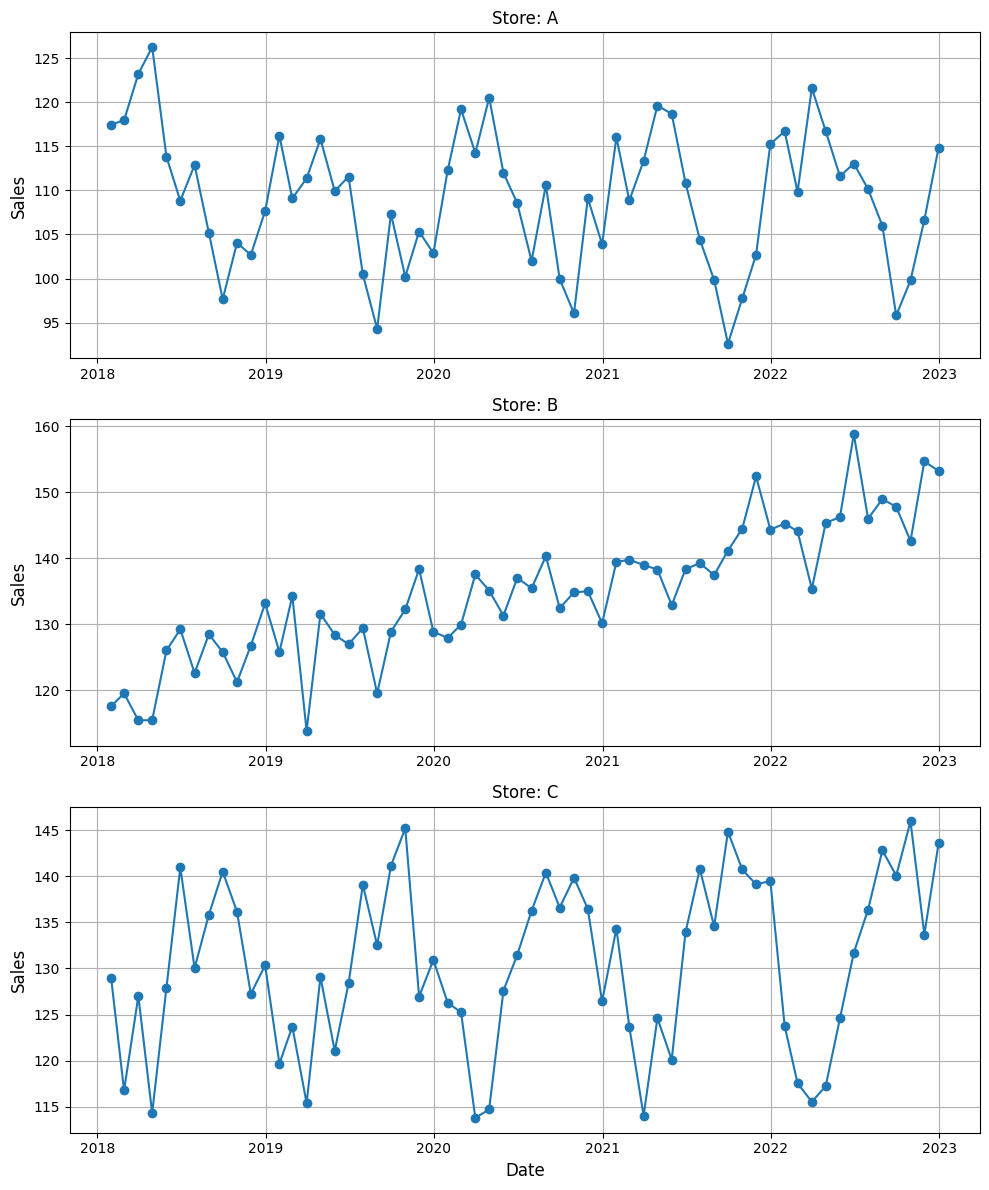
機械学習モデルの構築
次に、時系列予測モデルのもとになる、テーブルデータ系の機械学習モデルのインスタンスを作ります。今回は、ランダムフォレストモデルを使用します。
以下、コードです。
from sklearn.ensemble import RandomForestRegressor
# 利用する機械学習モデル
model = {
"TS_model": RandomForestRegressor(
n_estimators=100, # 木の数
max_depth=3, # 木の深さ
min_samples_leaf=5, # 1つの木の最小サンプル数
random_state=42, # 乱数シード
n_jobs=-1, # 並列処理
),
}
この機械学習モデルを利用し、時系列予測モデルをMLForecastで構築していきます。
MLForecastのインスタンスの生成から学習までの処理を関数にまとめています。
その関数を使い、時系列機械学習モデルを構築します。
以下、コードです。
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from mlforecast.lag_transforms import ExpandingMean
from mlforecast.lag_transforms import RollingMean
from mlforecast.utils import PredictionIntervals
# 時系列機械学習モデルを構築する関数
def create_and_train_forecast_model(data, model):
"""
MLForecastのインスタンスを作成し、提供されたデータで学習する。
パラメータ:
- data (DataFrame): 学習データセット。
- model (dict): 使用するモデルが含まれた辞書。
戻り値:
- MLForecast: 学習済みのMLForecastインスタンス。
"""
# MLForecastのインスタンスを作成
fcst = MLForecast(
models=model,
freq='M', # 月単位
lags=[1,12], # ラグ特徴量(過去1期前と12期前まで)
lag_transforms={
1: [
RollingMean(window_size=3), #ローリング特徴量(1期前までの過去3期移動平均)
ExpandingMean(), #エクスパンディング特徴量(1期前までの累積平均)
],
4: [RollingMean(window_size=3)], #ローリング特徴量(4期前までの過去3期移動平均)
},
date_features=['dayofweek', 'month'], # カレンダー特徴量(曜日と月)
target_transforms=[Differences([1])], # 差分処理(過去1期からの差分)
)
# 学習
fcst.fit(
data, # 学習データ(時系列データフレーム)
id_col='store', # ID列(ユニークな識別子、ここでは店舗ID)
time_col='date', # 時間列(時系列データの日時情報)
target_col='sales', # 目的変数(予測対象の値、ここでは売上)
static_features=['area_id'], # 静的特徴量(IDごとに固定される特徴量、今回は地域)
dropna=True, # 欠損値の削除(Trueの場合、欠損値を含む行を削除)
fitted=True, # モデルを学習後に予測値を保存する場合はTrue
# 予測区間の指定(Conformal Prediction理論で推定)
prediction_intervals=PredictionIntervals(
n_windows=2, # 分割数
h=12, #予測するステップ数
),
)
return fcst
# 時系列機械学習モデルの構築
fcst = create_and_train_forecast_model(data, model)
この時系列機械学習モデルは、幾つかの時系列特徴量を含むデータセットを入力とし、予測モデルを構築しています。
以下は、このモデルで考慮した時系列特徴量と目的変数変換などです。
- ローリング特徴量(1期前までの過去3期移動平均)
- エクスパンディング特徴量(1期前までの累積平均)
- ローリング特徴量(4期前までの過去3期移動平均)
- カレンダー特徴量(曜日と月)
- 差分処理(過去1期からの差分)
これらの特徴量などは、後で解説します。
ここでは、その時系列特徴量を含むデータセットが、どのようなデータなのかを視覚的に確認します。
以下、コードです。
# データの前処理状況の確認
preprocessed_df = fcst.preprocess(
data, # 学習データ(時系列データフレーム)
id_col='store', # ID列(ユニークな識別子、ここでは店舗ID)
time_col='date', # 時間列(時系列データの日時情報)
target_col='sales', # 目的変数(予測対象の値、ここでは売上)
static_features=['area_id'], # 静的特徴量(IDごとに固定される特徴量、今回は地域)
dropna=True, # 欠損値の削除(Trueの場合、欠損値を含む行を削除)
)
print(preprocessed_df)
以下、実行結果です。
date sales store area_id lag1 lag12 \
13 2019-02-28 -7.115959 A 1 8.538460 0.485362
14 2019-03-31 2.281558 A 1 -7.115959 5.269510
15 2019-04-30 4.473406 A 1 2.281558 3.036961
16 2019-05-31 -5.912972 A 1 4.473406 -12.446170
17 2019-06-30 1.635392 A 1 -5.912972 -4.999918
.. ... ... ... ... ... ...
175 2022-08-31 6.412716 C 3 4.677694 -6.236135
176 2022-09-30 -2.731161 C 3 6.412716 10.260038
177 2022-10-31 5.862915 C 3 -2.731161 -4.092722
178 2022-11-30 -12.251209 C 3 5.862915 -1.613858
179 2022-12-31 9.924130 C 3 -12.251209 0.373664
rolling_mean_lag1_window_size3 expanding_mean_lag1 \
13 4.052422 -0.106147
14 2.136980 -0.645363
15 1.234687 -0.436297
16 -0.120332 -0.108984
17 0.280664 -0.471733
.. ... ...
175 6.374253 0.137561
176 6.060560 0.251655
177 2.786417 0.198390
178 3.181490 0.297768
179 -3.039818 0.081406
rolling_mean_lag4_window_size3 dayofweek month
13 -2.947839 3 2
14 -0.831336 6 3
15 3.339574 1 4
16 4.052422 4 5
17 2.136980 6 6
.. ... ... ...
175 -2.170788 2 8
176 2.347809 4 9
177 5.384444 0 10
178 6.374253 2 11
179 6.060560 5 12
[141 rows x 11 columns]
本来は未来を予測するものですが、この構築したモデルが学習で利用したデータセットを、どの程度予測するかを視覚的に確認します。
精度指標として、次の2つを合わせて計算します。
- MAPE(Mean Absolute Percentage Error): 予測値と実際の値の相対誤差の平均(%)
- MAE(Mean Absolute Error): 予測値と実際の値の絶対誤差の平均
精度指標の計算からグラフのプロットまでの処理を関数として定義し、それらを呼び出します。
以下、コードです。
from sklearn.metrics import (
mean_absolute_percentage_error,
mean_absolute_error,
)
import matplotlib.pyplot as plt
# 実際の売上と予測された売上(対 学習データ)をプロットする関数
def plot_actual_vs_predicted_by_store(fcst,stores):
"""
店舗別に実際の売上と予測された売上をプロットし、MAPE、MAEを計算します。
パラメータ:
fcst (MLForecast): 予測と実際のデータを含む学習済みのMLForecastモデル。
stores (list): 店舗名のリスト。
"""
# 店舗ごとにデータを分ける
stores = fcst.fcst_fitted_values_['store'].unique()
# 各グラフの y 軸のスケールを統一するための範囲を計算
global_y_min = fcst.fcst_fitted_values_['sales'].min()*0.9
global_y_max = fcst.fcst_fitted_values_['sales'].max()*1.1
# プロットを作成
fig, axes = plt.subplots(len(stores), 1, figsize=(10, 4 * len(stores)))
if len(stores) == 1:
axes = [axes] # サブプロットが1つの場合、axesをリストとして扱う
for i, store in enumerate(stores):
# 店舗ごとのデータを抽出
store_data = fcst.fcst_fitted_values_[
fcst.fcst_fitted_values_['store'] == store
]
# 実際の値と予測値
actual = store_data['sales']
predicted = store_data['TS_model']
# 精度指標の計算
mape = mean_absolute_percentage_error(actual, predicted) * 100
mae = mean_absolute_error(actual, predicted)
# サブプロットに実際の値(actual)と予測値(predicted)の折れ線グラフを作成
axes[i].plot(
store_data['date'],
actual,
label='Actual',
marker='o'
)
axes[i].plot(
store_data['date'],
predicted,
label='Predicted',
linestyle='--',
marker='*'
)
axes[i].set_title(f'Actual vs Predicted Sales for Store {store}')
axes[i].set_xlabel('Date')
axes[i].set_ylabel('Sales')
axes[i].set_ylim(global_y_min, global_y_max)
# MAPE, MAEをグラフ内に表示
axes[i].text(
0.02,
0.95,
f"MAPE: {mape:.2f}%\nMAE: {mae:.2f}",
transform=axes[i].transAxes,
verticalalignment='top',
bbox=dict(
boxstyle="round",
facecolor="white",
alpha=0.5
)
)
axes[i].legend(loc='upper right')
axes[i].grid()
plt.tight_layout()
plt.show()
# 店舗別の実際の値と予測値の折れ線グラフを作成
plot_actual_vs_predicted_by_store(fcst,stores)
以下、実行結果です。
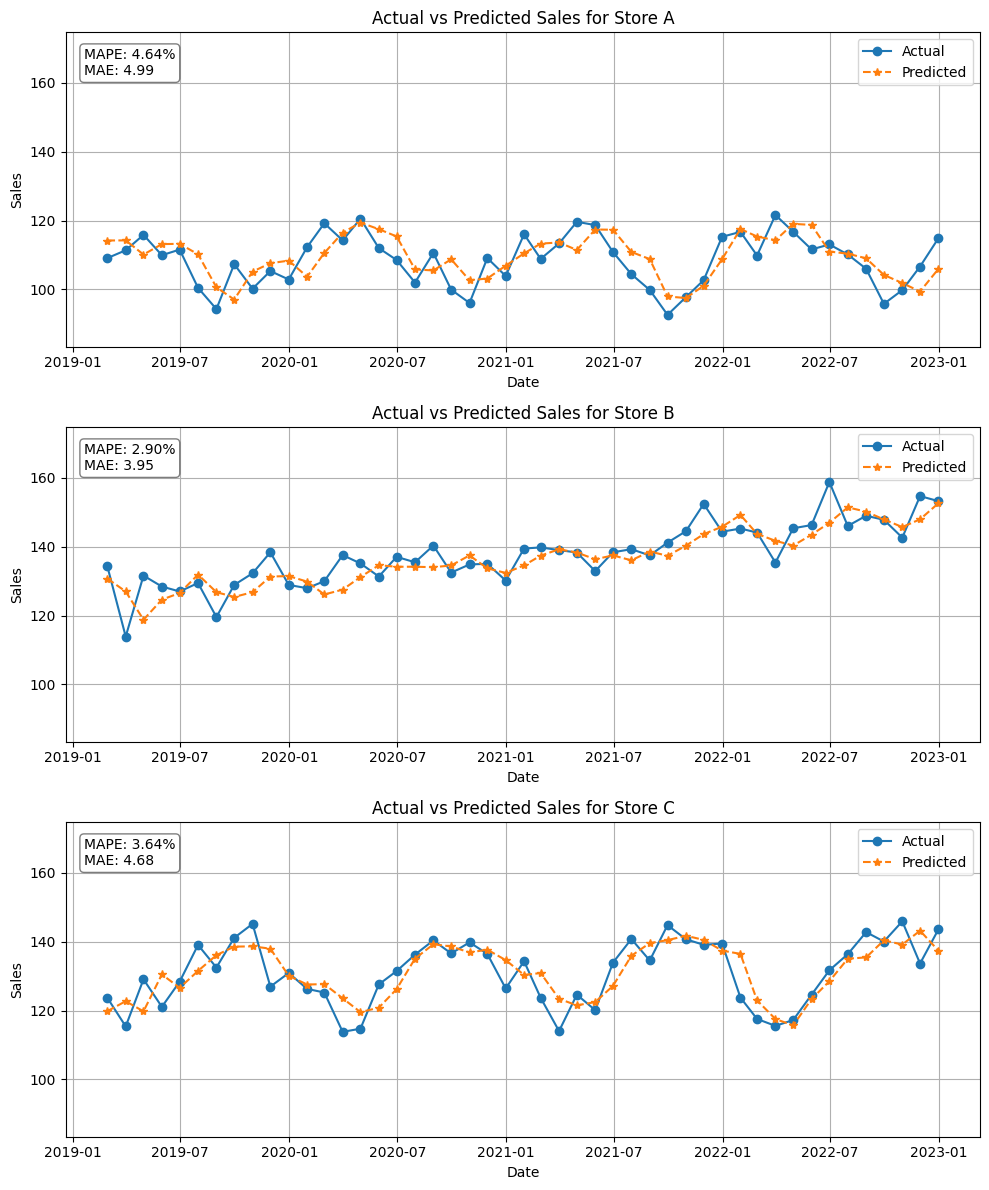
予測の実行
このモデルを使い、1年先の予測を実行します。
以下、コードです。
# 1年先の予測を実行
future_df = fcst.predict(
h=12, # 予測するステップ数(12か月先)
level=[95], # 95%予測区間
)
# storeごとに予測結果を表示
stores = future_df['store'].unique()
for store in stores:
print(f"Store: {store}")
store_data = future_df[future_df['store'] == store]
print(store_data.head())
以下、実行結果です。
Store: A store date TS_model TS_model-lo-95 TS_model-hi-95 0 A 2023-01-31 117.994082 109.221379 126.766785 1 A 2023-02-28 118.618306 112.437182 124.799430 2 A 2023-03-31 117.238918 108.791742 125.686093 3 A 2023-04-30 115.242626 100.179649 130.305603 4 A 2023-05-31 113.102772 97.881994 128.323549 Store: B store date TS_model TS_model-lo-95 TS_model-hi-95 12 B 2023-01-31 156.962450 149.969495 163.955404 13 B 2023-02-28 155.494055 146.541003 164.447107 14 B 2023-03-31 154.000388 143.914829 164.085947 15 B 2023-04-30 152.881045 143.792764 161.969326 16 B 2023-05-31 150.481163 146.718754 154.243572 Store: C store date TS_model TS_model-lo-95 TS_model-hi-95 24 C 2023-01-31 141.333963 126.951732 155.716194 25 C 2023-02-28 139.029097 119.380931 158.677264 26 C 2023-03-31 139.795260 119.278156 160.312364 27 C 2023-04-30 137.557935 120.395730 154.720141 28 C 2023-05-31 137.342671 126.977140 147.708203
予測結果をプロットする関数を定義し、実行します。
以下、コードです。
# 予測結果をプロットする関数
def plot_forecast(data, future_df, stores):
"""
予測結果をプロットする関数。
パラメータ:
data (DataFrame): 実際のデータ。
future_df (DataFrame): 予測されたデータ。
stores (list): 店舗名のリスト。
"""
# 全店舗のデータを使用してグラフの y 軸のスケールを計算
global_y_min = min(data['sales'].min(), future_df['TS_model-lo-95'].min())*0.9
global_y_max = max(data['sales'].max(), future_df['TS_model-hi-95'].max())*1.1
# プロットを作成
fig, axes = plt.subplots(
len(stores),
1,
figsize=(10, 4 * len(stores))
)
for ax, store in zip(axes, stores):
# 各店舗ごとのデータを抽出
store_data = data[data['store'] == store]
future_data = future_df[future_df['store'] == store]
# 実際のデータをプロット
ax.plot(
store_data['date'],
store_data['sales'],
marker='o',
label='Actual',
)
# 予測データをプロット
ax.plot(
future_data['date'],
future_data['TS_model'],
marker='*',
linestyle='--',
label='Forecast',
)
# 予測区間を影の帯で表示
ax.fill_between(
future_data['date'],
future_data['TS_model-lo-95'],
future_data['TS_model-hi-95'],
color='gray',
alpha=0.3,
label='Prediction Interval (95%)',
)
ax.set_title(f'Store: {store}', fontsize=12)
ax.set_ylabel('Sales', fontsize=12)
ax.set_ylim(global_y_min, global_y_max)
ax.grid(True)
ax.legend(loc='upper left')
plt.xlabel('Date', fontsize=12)
plt.tight_layout()
plt.show()
# 予測結果をプロット
plot_forecast(data, future_df, stores)
以下、実行結果です。
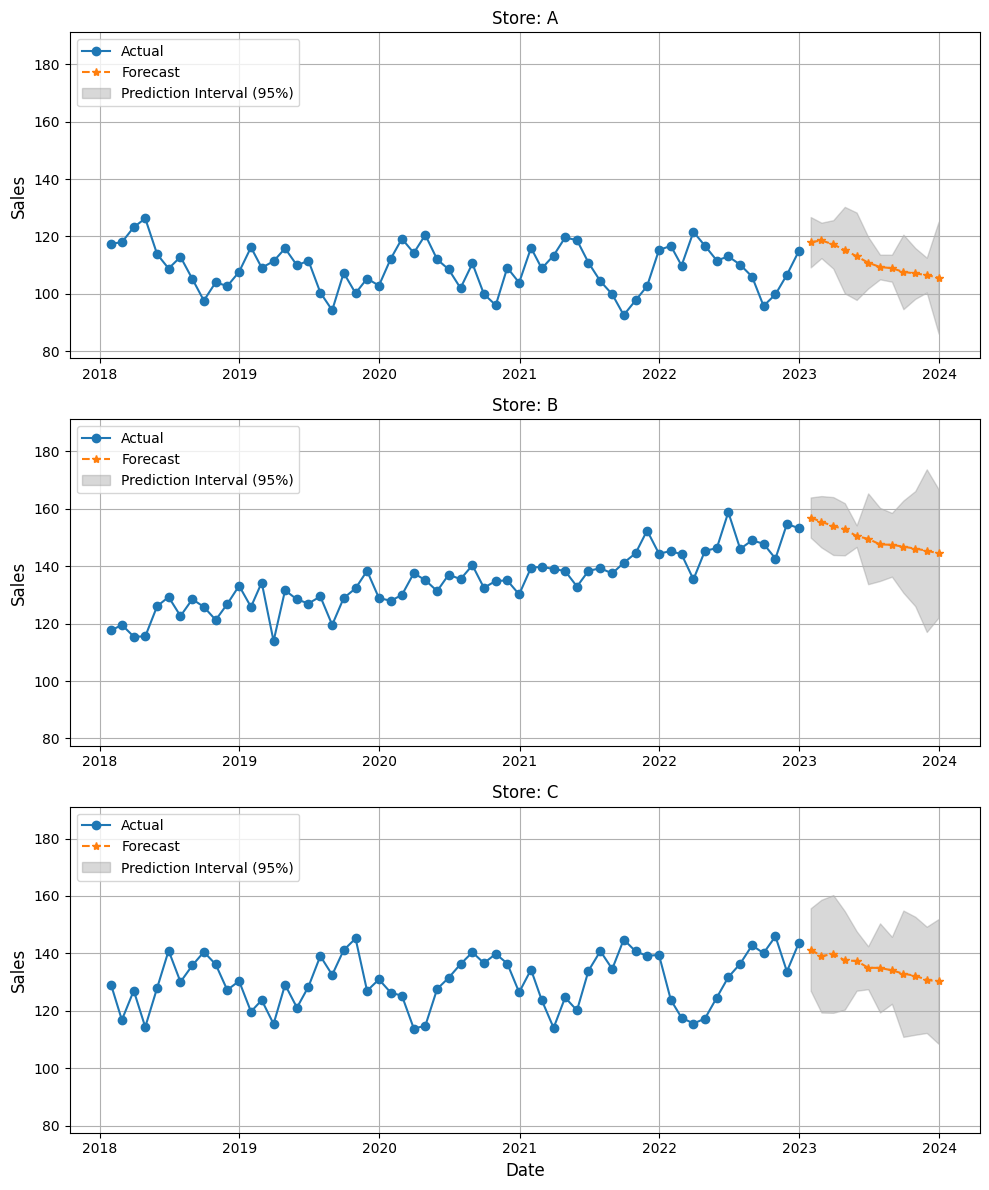
予測区間は Conformal Prediction 理論で推定したものです。
補足すると、Conformal Prediction (CP) 理論は、予測モデルが出力する予測値に対して予測区間などを求める手法です。
伝統的な統計モデルなどではない機械学習モデルも推定できるのが特徴です。
基本的な考え方は、過去のデータを利用して予測の誤差分布を推定し、その分布に基づいて新しいデータの予測区間を構築することです。
参考文献
Shafer, G., & Vovk, V. (2008). “A Tutorial on Conformal Prediction.” Journal of Machine Learning Research. Link
Angelopoulos, A. N., & Bates, S. (2021). “A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification.” Link
MLForecastでの時系列特徴量の設定
ここからは、MLForecast で時系列データに対して時系列特徴量を生成する方法について説明します。
ラグ特徴量
MLForecastでは、lagsパラメータを使用して目的変数のラグ特徴量を生成することができます。
ラグ特徴量は、時系列データにおいて過去の値を特徴量として利用するために重要です。
lagsはリスト形式で指定し、過去のどの時点の値を特徴量として使用するかを指定します。
例えば、過去1期から3期のラグ特徴量を生成する場合、以下のように設定します。
fcst = MLForecast(
models=model,
freq='M', # 月単位
lags=[1, 2, 3] # 過去1期、2期、3期のラグ特徴量
)
ARモデルのように、連続したラグを生成することも可能です。
例えば、以下は過去1期から7期のラグ特徴量を生成する場合です。
fcst = MLForecast(
models=model,
freq='M',
lags=[i+1 for i in range(7)] # 過去1期から7期のラグ特徴量
)
ローリング特徴量とエクスパンディング特徴量
MLForecastでは、lag_transformsパラメータを使用して、特定のラグに対してローリング特徴量やエクスパンディング特徴量を生成することができます。
これにより、時系列データの過去の値を基にした統計的な特徴量を簡単に追加することが可能です。
lag_transformsは辞書形式で指定します。
キーにはラグを指定し、値にはそのラグに適用する変換(ローリング特徴量やエクスパンディング特徴量など)のリストを指定します。
以下のコードは……
- 1期前の値に対して、
- 過去3期の移動平均(ローリング特徴量RollingMean)
- 累積平均(エクスパンディング特徴量ExpandingMean)
- 4期前の値に対して過去3期の移動平均(ローリング特徴量RollingMean)
……を計算する例です。
from mlforecast.lag_transforms import ExpandingMean, RollingMean
fcst = MLForecast(
models=model,
freq='M', # 月単位
lag_transforms={
# 1期前の値に対して変換
1: [
RollingMean(window_size=3),
ExpandingMean()
],
# 4期前の値に対して変換
4: [RollingMean(window_size=3)]
}
)
以下のコードは、1期前の値に対して……
- 過去3期の移動平均(ローリング特徴量RollingMean)
- 過去3期の移動標準偏差(ローリング特徴量RollingStd)
- 累積平均(エクスパンディング特徴量ExpandingMean)
- 累積標準偏差(エクスパンディング特徴量ExpandingStd)
……を計算する例です。
from mlforecast.lag_transforms import ExpandingMean, RollingMean, ExpandingStd, RollingStd
fcst = MLForecast(
models=model,
freq='M',
lag_transforms={
1: [
RollingMean(window_size=3), # 過去3期の移動平均
RollingStd(window_size=3), # 過去3期の移動標準偏差
ExpandingMean(), # 累積平均
ExpandingStd() # 累積標準偏差
]
}
)
以下は、Lag Transforms の一覧表です。
| 変換名 | 説明 | 引数と説明 |
|---|---|---|
| RollingQuantile | 過去の一定期間のデータに基づいてローリング分位数を計算します。 | window: ローリングウィンドウのサイズ(整数)。quantile: 計算する分位数(0から1の間の小数)。 |
| RollingMax | 過去の一定期間のデータに基づいてローリング最大値を計算します。 | window: ローリングウィンドウのサイズ(整数)。 |
| RollingMin | 過去の一定期間のデータに基づいてローリング最小値を計算します。 | window: ローリングウィンドウのサイズ(整数)。 |
| RollingStd | 過去の一定期間のデータに基づいてローリング標準偏差を計算します。 | window: ローリングウィンドウのサイズ(整数)。 |
| RollingMean | 過去の一定期間のデータに基づいてローリング平均を計算します。 | window: ローリングウィンドウのサイズ(整数)。 |
| SeasonalRollingQuantile | 季節性を考慮したローリング分位数を計算します。 | window: ローリングウィンドウのサイズ(整数)。quantile: 計算する分位数(0から1の間の小数)。season_length: 季節の長さ(整数)。 |
| SeasonalRollingMax | 季節性を考慮したローリング最大値を計算します。 | window: ローリングウィンドウのサイズ(整数)。season_length: 季節の長さ(整数)。 |
| SeasonalRollingMin | 季節性を考慮したローリング最小値を計算します。 | window: ローリングウィンドウのサイズ(整数)。season_length: 季節の長さ(整数)。 |
| SeasonalRollingStd | 季節性を考慮したローリング標準偏差を計算します。 | window: ローリングウィンドウのサイズ(整数)。season_length: 季節の長さ(整数)。 |
| SeasonalRollingMean | 季節性を考慮したローリング平均を計算します。 | window: ローリングウィンドウのサイズ(整数)。season_length: 季節の長さ(整数)。 |
| ExpandingQuantile | データの開始点から現在までの累積分位数を計算します。 | quantile: 計算する分位数(0から1の間の小数)。 |
| ExpandingMax | データの開始点から現在までの累積最大値を計算します。 | 該当なし |
| ExpandingMin | データの開始点から現在までの累積最小値を計算します。 | 該当なし |
| ExpandingStd | データの開始点から現在までの累積標準偏差を計算します。 | 該当なし |
| ExpandingMean | データの開始点から現在までの累積平均を計算します。 | 該当なし |
| ExponentiallyWeightedMean | 指数加重移動平均を計算します。 | alpha: 平滑化係数(0から1の間の小数)。 |
| Offset | シリーズを指定したラグだけシフトさせた後、変換を適用します。 | lags: シフトするラグの数(整数)。 |
| Combine | 2つのラグ変換を指定した演算子で組み合わせます。 | op: 演算子(例: +, -, *, /)。transform1: 最初の変換。transform2: 2番目の変換。 |
カレンダー特徴量
MLForecastでは、date_featuresパラメータを使用して、カレンダー特徴量を生成し、モデルに追加することができます。
カレンダー特徴量は、時系列データの日時情報を特徴量として活用するために重要です。
date_featuresには、以下のようなpandasの日時属性や、DatetimeIndexを入力として数値を返す独自の関数を指定できます。
| 特徴量名 | 説明 |
|---|---|
year |
年を整数で返します。例: 2024 |
quarter |
四半期を整数(1から4)で返します。例: 1 |
month |
月を整数(1から12)で返します。例: 11 |
day |
日を整数(1から31)で返します。例: 28 |
dayofweek |
曜日を整数(0から6)で返します。0が月曜日、6が日曜日を表します。例: 4(木曜日) |
dayofyear |
年初からの日数を整数(1から366)で返します。例: 333 |
is_month_start |
月初であればTrue、そうでなければFalseを返します。例: False |
is_month_end |
月末であればTrue、そうでなければFalseを返します。例: True |
is_quarter_start |
四半期の開始日であればTrue、そうでなければFalseを返します。例: False |
is_quarter_end |
四半期の終了日であればTrue、そうでなければFalseを返します。例: True |
is_year_start |
年始であればTrue、そうでなければFalseを返します。例: False |
is_year_end |
年末であればTrue、そうでなければFalseを返します。例: True |
また、独自の特徴量を作成するために、DatetimeIndexを入力として数値を返す関数を定義し、date_featuresに渡すことも可能です。
例えば、偶数日かどうかを判定する関数を以下のように定義できます。
def is_even_day(dates):
return dates.day % 2 == 0
この関数をdate_featuresに追加することで、偶数日であるかどうかの情報を特徴量としてモデルに提供できます。
以下は、曜日(dayofweek)と月(month)をカレンダー特徴量として追加する例です。
fcst = MLForecast(
models=model,
freq='M',
date_features=['dayofweek', 'month'], # カレンダー特徴量(曜日と月)
)
上記の設定を行うと、データフレームに以下のようなカレンダー特徴量が追加されます。
| date | sales | dayofweek | month |
|---|---|---|---|
| 2020-01-31 | 107.5 | 4 | 1 |
| 2020-02-29 | 108.0 | 5 | 2 |
| 2020-03-31 | 113.2 | 1 | 3 |
数字がそのまま設定(例:1月であれば1と設定)されます。
0-1変数のカレンダー特徴量を追加する場合には、別途OneHotEncoderを使用する必要があります。
MLForecastでの目的変数変換
MLForecastでは、target_transformsパラメータを使用して、目的変数を変換することができます。
この機能を活用することで、時系列データの特性に応じた前処理を簡単に行うことが可能です。
target_transformsとは?
target_transformsは、目的変数に適用する変換処理をリスト形式で指定する引数です。
これにより、モデルのトレーニング時に目的変数を変換し、予測後に元のスケールに戻す逆変換が自動的に適用されます。
以下は、主な変換処理です。
- 差分(Differences)
指定したラグに基づいて差分を計算します。 - ログ変換(LogTransform)
データのスケールを縮小するために使用されます。 - カスタム変換
独自の変換関数を定義することも可能です。
このtarget_transformsには、ローカル変換とグローバル変換があります。
ローカル変換
- 各時系列データ(例えば、店舗や製品ごと)の単位で個別に適用される変換。
- 例として、各時系列の平均値を引くことでデータを中心化する操作などが含まれる。
グローバル変換
- 全ての時系列データに対して一括で適用される変換。
- 例として、全データに対する標準化や対数変換などが含まれる。
ローカル変換
各時系列データ(例えば、店舗や製品ごと)の単位で個別に適用される変換です。
差分(Differences)
以下は、過去1期からの差分を計算する例です。
from mlforecast.target_transforms import Differences
fcst = MLForecast(
models=model,
freq='M',
target_transforms=[Differences([1])], # 差分処理(過去1期からの差分)
)
この設定により、目的変数が過去1期との差分に変換されます。
複数の差分を指定することも可能です。
例えば、過去1期と過去12期の差分を計算する場合は、以下のように設定します。
from mlforecast.target_transforms import Differences
fcst = MLForecast(
models=model,
freq='M',
target_transforms=[Differences([1, 12])], # 過去1期と過去12期の差分
)
MLForecastのtarget_transformsを使用して目的変数を変換する方法について説明します。
target_transformsは、時系列データの特性を捉えやすくするために使用されます。以下に、主要な変換方法とそのコード例を示します。
LocalStandardScaler(局所的な標準化)
各時系列データ(例えば、店舗や製品ごと)の単位で個別に標準化します。
from mlforecast.target_transforms import LocalStandardScaler
fcst = MLForecast(
models=model,
freq='M',
target_transforms=[LocalStandardScaler()],
)
もちろん、差分処理と組み合わせることもできます。
以下は、差分を取った後に標準化を適用する例です。
from mlforecast.target_transforms import Differences, LocalStandardScaler
fcst = MLForecast(
models=model,
freq='M',
target_transforms=[Differences([1, 24]), LocalStandardScaler()],
)
カスタム変換
独自の変換関数を定義して、目的変数を変換することもできます。
以下は、目的変数を単純に2倍に変換し、予測結果を元に戻す例です。
from mlforecast.target_transforms import BaseTargetTransform
class DoubleTransform(BaseTargetTransform):
"""目的変数を2倍にスケーリングします。"""
def fit_transform(self, df):
df[self.target_col] = df[self.target_col] * 2
return df
def inverse_transform(self, df):
df[self.target_col] = df[self.target_col] / 2
return df
fcst = MLForecast(
models=[],
freq='M',
target_transforms=[DoubleTransform()], # カスタム変換を適用
)
このカスタム変換では、目的変数が2倍にスケーリングされた後にモデルの学習を行います。
予測時には自動的に元のスケールに戻ります。
これにより、独自の変換ロジックを簡単に組み込むことが可能です。
グローバル変換
全ての時系列データに対して一括で適用される変換です。
GlobalSklearnTransformerを使います。
import numpy as np
from sklearn.preprocessing import FunctionTransformer
from mlforecast.target_transforms import GlobalSklearnTransformer
sk_log1p = FunctionTransformer(
func=np.log1p, # 対数変換
inverse_func=np.expm1, # 逆対数変換
)
fcst = MLForecast(
models=model,
freq='M',
target_transforms=[GlobalSklearnTransformer(sk_log1p)],
)
この例では、すべての値に対して対数変換(log(x+1))を適用します。
Optunaによるハイパラの自動化
時系列予測で利用する機械学習モデルには、ハイパーパラメータがあります。
学習データで求めるのがモデルパラメータで、ハイパーパラメータはモデルを構築する人が、モデルを学習する前に決めるものです。不運なことに、ハイパーパラメータの設定の仕方で、モデルの予測精度に影響があります。
そこで登場したのが、ハイパーパラメータも学習データを使いながら探索するメソドロジーです。そのためのライブラリの一つが、Optunaです。
Optunaは、ハイパーパラメータの探索を自動化することを目的としています。使い方については以下を参考にしてください。
ここでは、幾つかの機械学習モデルに対し、Optunaを用いてハイパーパラメータの探索を行い、時系列予測モデルを構築していきます。
今回登場する機械学習モデルは以下です。
- ランダムフォレスト
- XGBoost
- LightGBM
いずいれも、決定木系のモデルです。
Optunaのハイパラ探索インスタンスの生成
機械学習モデルとして、ランダムフォレストを使用する場合は、以下のようにインスタンスを生成します。
時系列のクロスバリデーションを使用しながら、Optunaのハイパラ探索を行います。
以下、コードです。
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import TimeSeriesSplit
from optuna.integration import OptunaSearchCV
from optuna.distributions import IntDistribution
# 時系列データに対応した TimeSeriesSplit を作成
time_series_cv = TimeSeriesSplit(n_splits=5)
# OptunaSearchCVのインスタンス作成
optuna_search = OptunaSearchCV(
# チューニング対象のモデルを指定(ここではランダムフォレスト)
estimator=RandomForestRegressor(random_state=42),
# 探索するハイパーパラメータの分布を指定
param_distributions={
# 決定木の数(10から1000の範囲で探索)
'n_estimators': IntDistribution(10, 1000),
# 決定木の最大深さ(2から100の範囲で探索)
'max_depth': IntDistribution(2, 100),
# ノードを分割するための最小サンプル数(2から20の範囲で探索)
'min_samples_split': IntDistribution(2, 20),
# リーフノードに必要な最小サンプル数(1から10の範囲で探索)
'min_samples_leaf': IntDistribution(1, 10),
},
cv=time_series_cv, # 時系列分割を使用したクロスバリデーション
n_trials=100, # 試行回数
scoring='neg_mean_absolute_error',
random_state=12,
timeout=600, # 制限時間(秒)
n_jobs=-1, # パラメータチューニングを並列処理
refit=True, # 最良モデルを最終モデルとして使用
)
# 利用する機械学習のインスタンスの生成
model = {
"TS_model": optuna_search
}
Optunaを用いてハイパーパラメータの探索を行う際に、param_distributionsで探索するハイパーパラメータの範囲を指定します。
辞書形式で設定します。今回はこの辞書に、以下のように各ハイパーパラメータの名前とその探索範囲を記述しました。
n_estimators
- 決定木の数を指定します。
- ランダムフォレストは複数の決定木を組み合わせて予測を行うモデルで、このパラメータはその決定木の数を表します。
- 探索範囲: 10から1000の間で探索します。少ないとモデルが単純になりすぎ、多すぎると計算コストが増加します。
max_depth
- 各決定木の最大深さを指定します。
- 深さが深いほど複雑なモデルになりますが、過学習のリスクも高まります。
- 探索範囲: 2から100の間で探索します。浅い深さは単純なモデル、深い深さは複雑なモデルを表します。
min_samples_split
- ノードを分割するために必要な最小サンプル数を指定します。
- この値が大きいほど、ノードの分割が制限され、モデルが単純化されます。
- 探索範囲: 2から20の間で探索します。小さい値は分割を許容し、大きい値は分割を制限します。
min_samples_leaf
- リーフノード(末端ノード)に必要な最小サンプル数を指定します。
- この値が大きいほど、リーフノードが大きくなり、モデルが単純化されます。
- 探索範囲: 1から10の間で探索します。小さい値はリーフノードを小さく、大きい値はリーフノードを大きくします。
これらのパラメータはランダムフォレストの性能に大きく影響を与えるため、適切な範囲で探索することが重要です。
探索範囲は、モデルの複雑さと計算コストのバランスを考慮して設定されています。
時系列機械学習のモデル構築
時系列機械学習モデルの構築を行い、その結果をプロットしてみましょう。
# 時系列機械学習モデルの構築 fcst = create_and_train_forecast_model(data, model) # 店舗別の実際の値と予測値の折れ線グラフを作成 plot_actual_vs_predicted_by_store(fcst,stores)
以下、実行結果です。
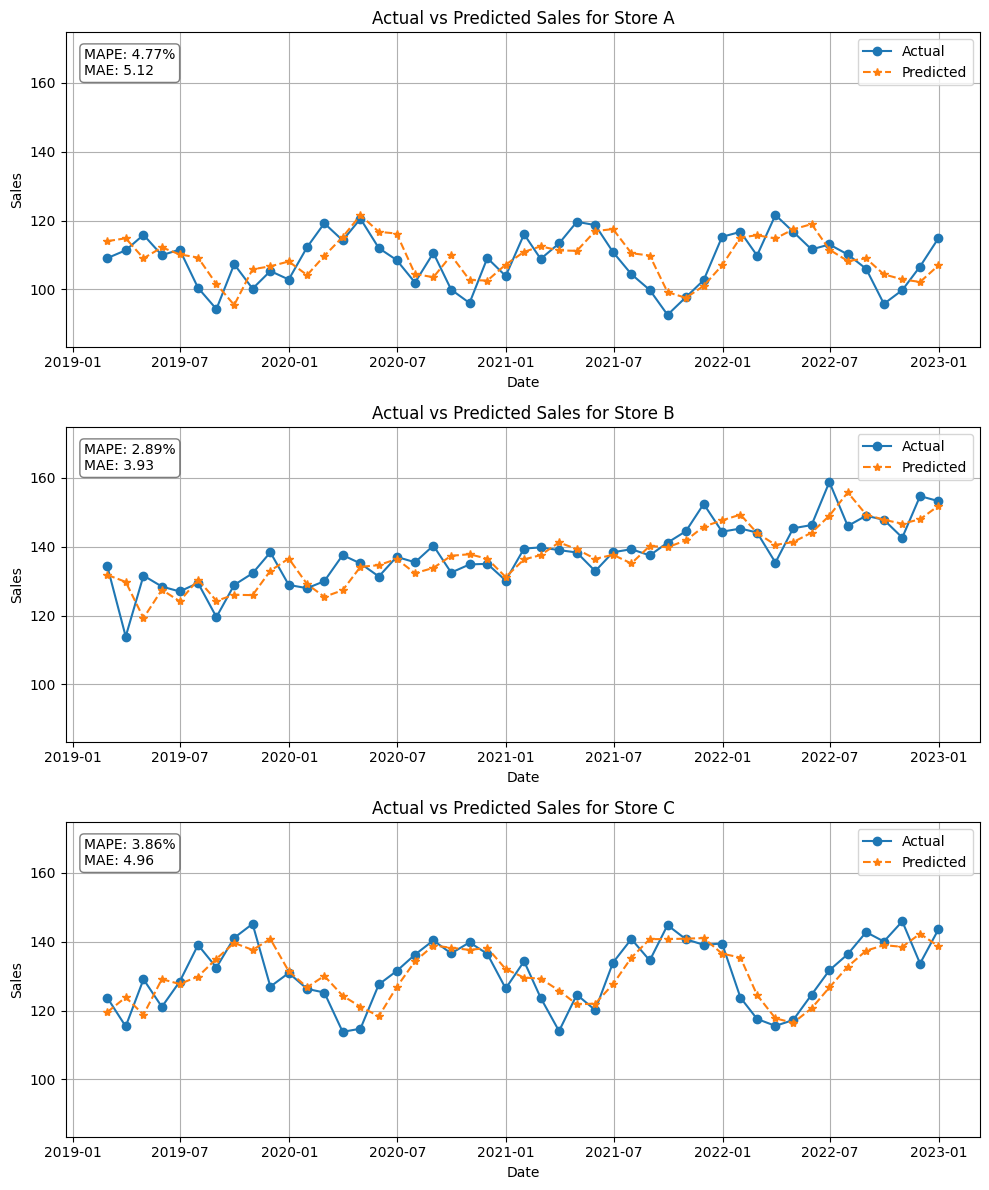
予測の実行
時系列機械学習モデルの予測を実行し、結果をプロットしてみましょう。
# 1年先の予測を実行 future_df = fcst.predict(h=12, level=[95]) # 予測結果をプロット plot_forecast(data, future_df, stores)
以下、実行結果です。
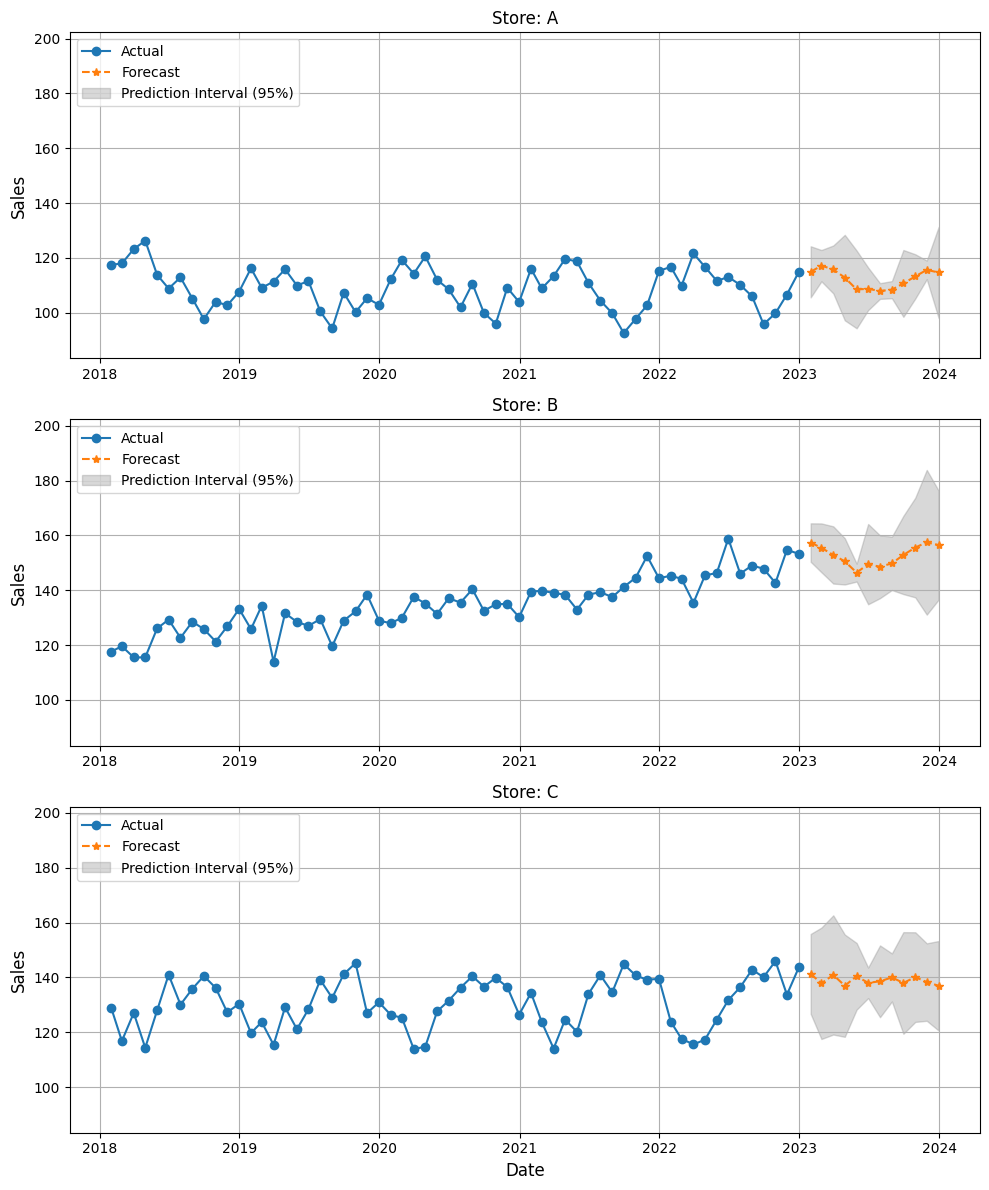
lightgbm版
LightGBMを使用して、時系列機械学習モデルを構築してみましょう。
from lightgbm import LGBMRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import TimeSeriesSplit
from optuna.integration import OptunaSearchCV
from optuna.distributions import IntDistribution
from optuna.distributions import FloatDistribution
# 時系列データに対応した TimeSeriesSplit を作成
time_series_cv = TimeSeriesSplit(n_splits=5)
# OptunaSearchCVのインスタンス作成
optuna_search = OptunaSearchCV(
# チューニング対象のモデルを指定(ここではLIGHTGBM)
estimator=LGBMRegressor(random_state=42),
# 探索するハイパーパラメータの分布を指定
param_distributions={
# 学習率(0.01から0.3の範囲で探索)
'learning_rate': FloatDistribution(0.01, 0.3),
# 決定木の数(10から1000の範囲で探索)
'n_estimators': IntDistribution(10, 1000),
# 決定木の最大深さ(2から100の範囲で探索)
'max_depth': IntDistribution(2, 100),
# リーフごとの最小データ数(1から50の範囲で探索)
'min_child_samples': IntDistribution(1, 50),
# データのサブサンプリング率(0.5から1.0の範囲で探索)
'subsample': FloatDistribution(0.5, 1.0),
# 特徴量のサブサンプリング率(0.5から1.0の範囲で探索)
'colsample_bytree': FloatDistribution(0.5, 1.0)
},
cv=time_series_cv, # 時系列分割を使用したクロスバリデーション
n_trials=100, # 試行回数
scoring='neg_mean_absolute_error',
random_state=12,
timeout=600, # 制限時間(秒)
n_jobs=-1, # パラメータチューニングを並列処理
refit=True, # 最良モデルを最終モデルとして使用
)
# 利用する機械学習のインスタンスの生成
model = {
"TS_model": optuna_search
}
# 時系列機械学習モデルの構築
fcst = create_and_train_forecast_model(data, model)
# 店舗別の実際の値と予測値の折れ線グラフを作成
plot_actual_vs_predicted_by_store(fcst,stores)
以下、実行結果です。
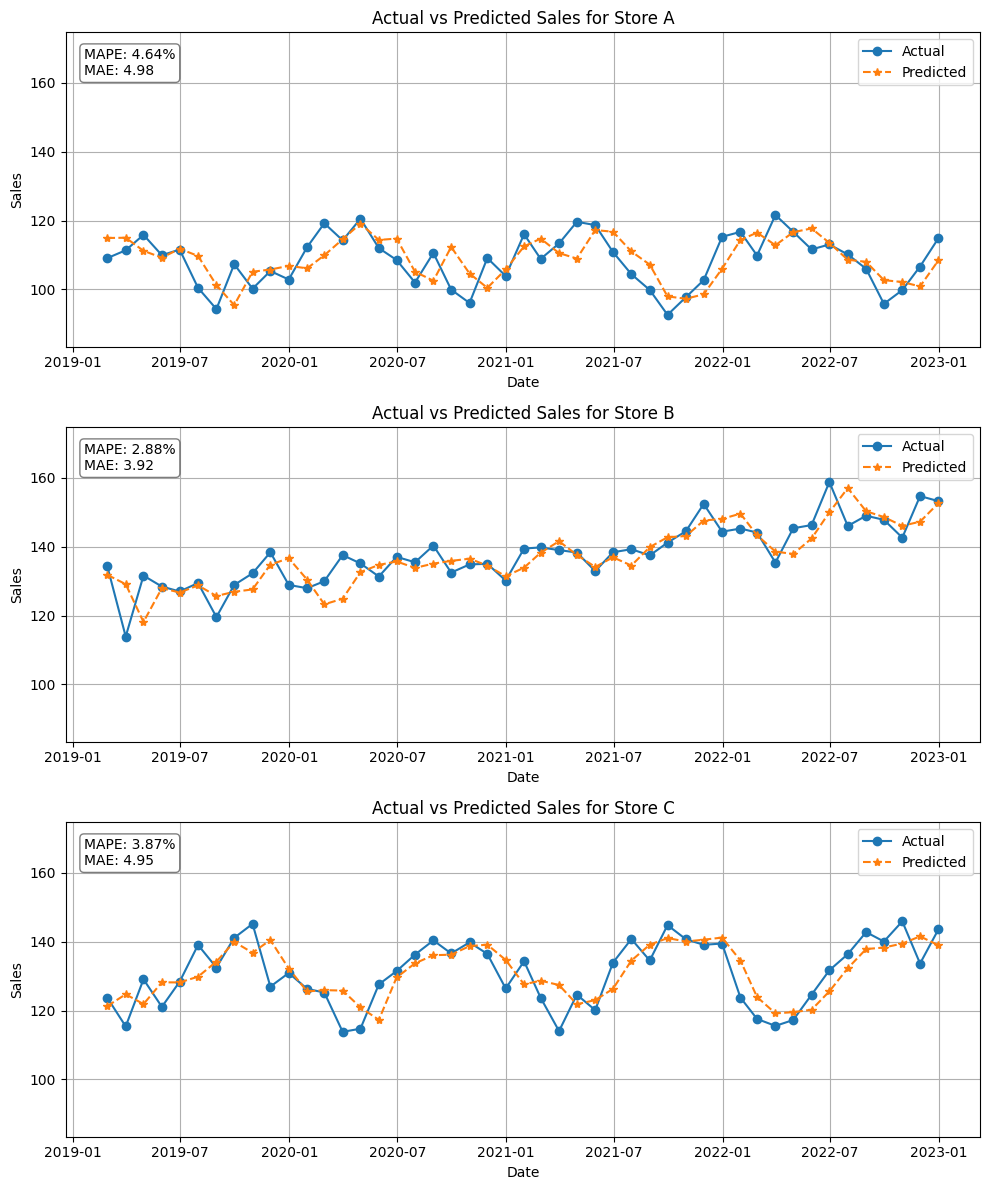
このモデルを使って予測を実行し、結果をプロットしてみましょう。
# 1年先の予測を実行 future_df = fcst.predict(h=12, level=[95]) # 予測結果をプロット plot_forecast(data, future_df, stores)
以下、実行結果です。
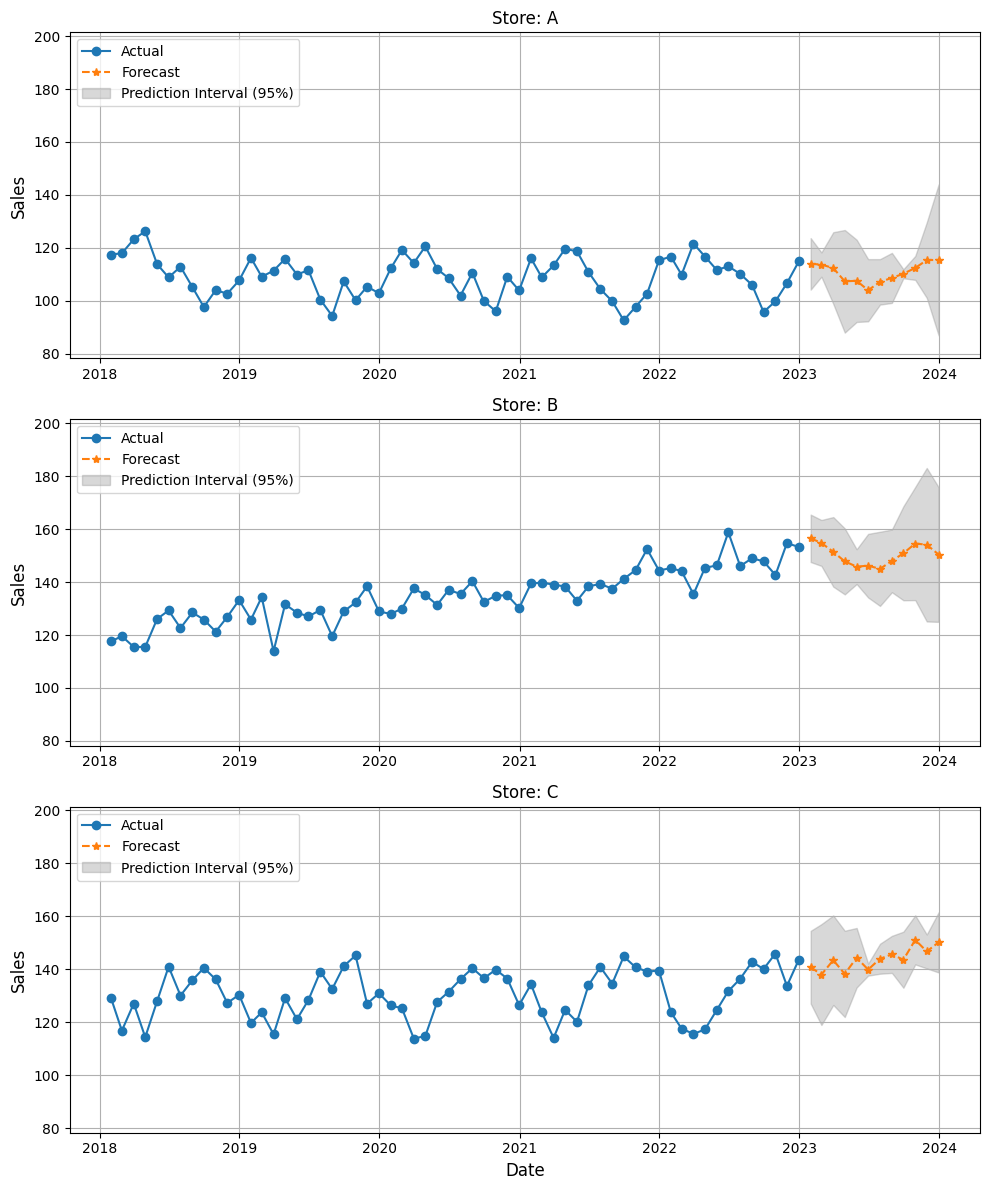
xgboost版
XGBoostを使用して、時系列機械学習モデルを構築してみましょう。
from xgboost import XGBRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import TimeSeriesSplit
from optuna.integration import OptunaSearchCV
from optuna.distributions import IntDistribution
from optuna.distributions import FloatDistribution
# 時系列データに対応した TimeSeriesSplit を作成
time_series_cv = TimeSeriesSplit(n_splits=5)
# OptunaSearchCVのインスタンス作成
optuna_search = OptunaSearchCV(
# チューニング対象のモデルを指定(ここではXGBoost)
estimator=XGBRegressor(random_state=42),
# 探索するハイパーパラメータの分布を指定
param_distributions={
# 学習率(0.01から0.3の範囲で探索)
'learning_rate': FloatDistribution(0.01, 0.3),
# 決定木の数(10から1000の範囲で探索)
'n_estimators': IntDistribution(10, 1000),
# 決定木の最大深さ(2から100の範囲で探索)
'max_depth': IntDistribution(2, 100),
# リーフごとの最小データ数(1から50の範囲で探索)
'min_child_weight': IntDistribution(1, 50),
# データのサブサンプリング率(0.5から1.0の範囲で探索)
'subsample': FloatDistribution(0.5, 1.0),
# 特徴量のサブサンプリング率(0.5から1.0の範囲で探索)
'colsample_bytree': FloatDistribution(0.5, 1.0)
},
cv=time_series_cv, # 時系列分割を使用したクロスバリデーション
n_trials=100, # 試行回数
scoring='neg_mean_absolute_error',
random_state=12,
timeout=600, # 制限時間(秒)
n_jobs=-1, # パラメータチューニングを並列処理
refit=True, # 最良モデルを最終モデルとして使用
)
# 利用する機械学習のインスタンスの生成
model = {
"TS_model": optuna_search
}
# 時系列機械学習モデルの構築
fcst = create_and_train_forecast_model(data, model)
# 店舗別の実際の値と予測値の折れ線グラフを作成
plot_actual_vs_predicted_by_store(fcst,stores)
以下、実行結果です。
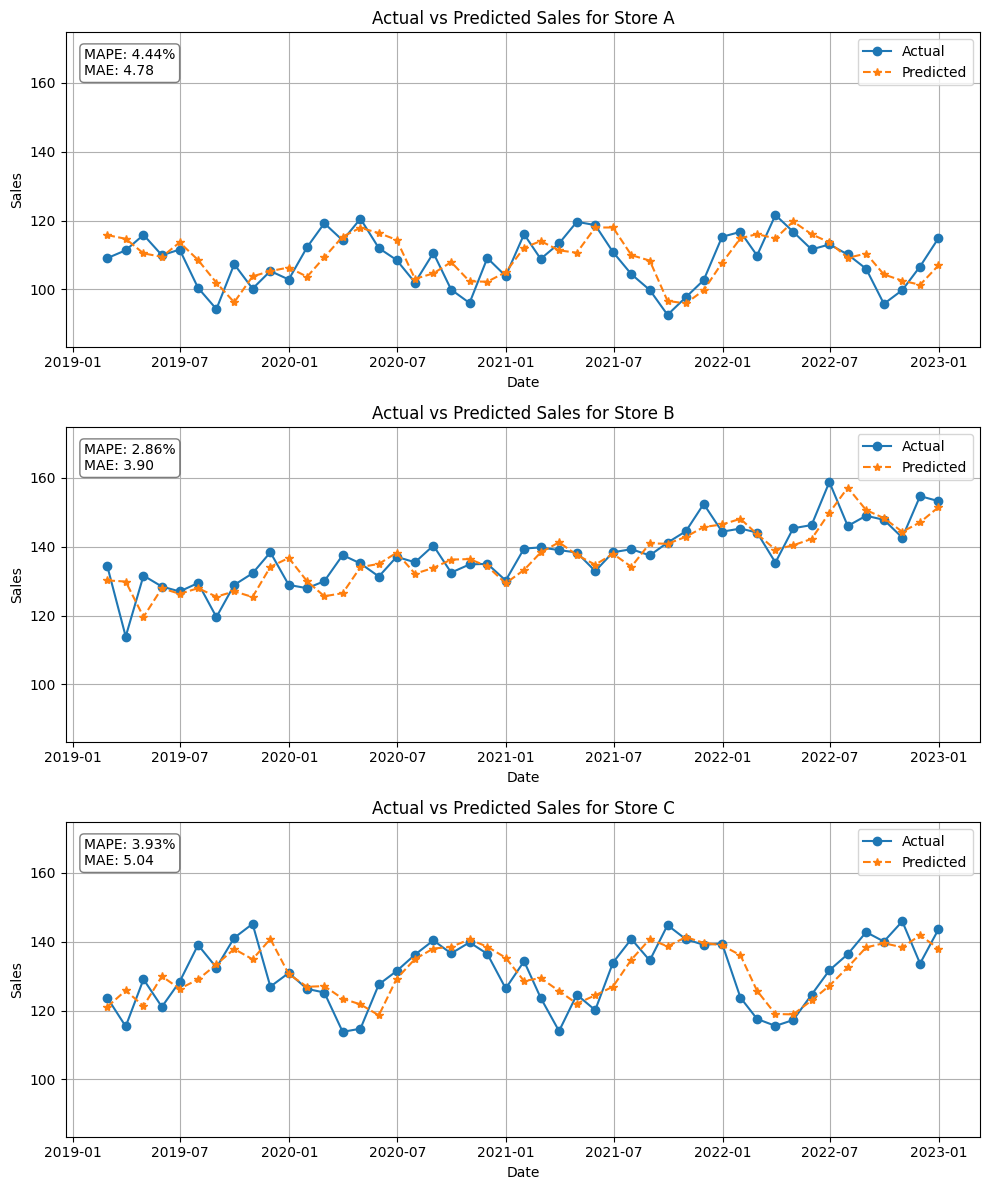
このモデルを使って予測を実行し、結果をプロットしてみましょう。
# 1年先の予測を実行 future_df = fcst.predict(h=12, level=[95]) # 予測結果をプロット plot_forecast(data, future_df, stores)
以下、実行結果です。
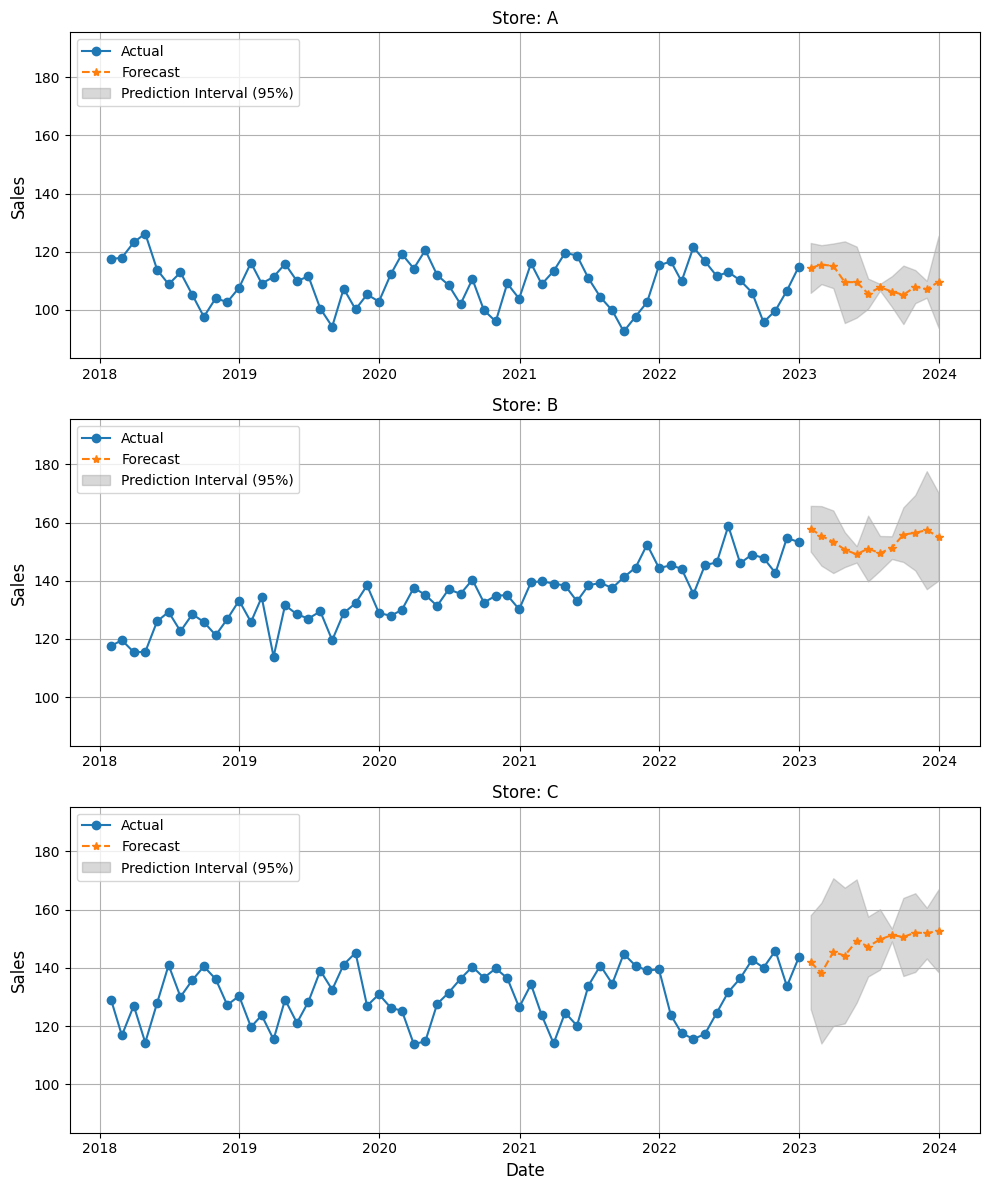
時系列予測モデルの作り方の検証
今、3つの機械学習モデルで構築した結果、lightgbmが今回の場合には最良でした。
このモデルが実務で耐えられるかどうかを、元のデータを2つに分割(学習データとテストデータ)し、学習データで構築したモデルを、テストデータで検証)してみましょう。
利用する機械学習モデルのインスタンスの生成
機械学習モデルとしてlightgbmを使用します。
時系列のクロスバリデーションを使用しながら、Optunaのハイパラ探索を行い構築するインスタンスを生成します。
以下、コードです。
from lightgbm import LGBMRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import TimeSeriesSplit
from optuna.integration import OptunaSearchCV
from optuna.distributions import IntDistribution
from optuna.distributions import FloatDistribution
# 時系列データに対応した TimeSeriesSplit を作成
time_series_cv = TimeSeriesSplit(n_splits=5)
# OptunaSearchCVのインスタンス作成
optuna_search = OptunaSearchCV(
# チューニング対象のモデルを指定(ここではLIGHTGBM)
estimator=LGBMRegressor(random_state=42),
# 探索するハイパーパラメータの分布を指定
param_distributions={
# 学習率(0.01から0.3の範囲で探索)
'learning_rate': FloatDistribution(0.01, 0.3),
# 決定木の数(10から1000の範囲で探索)
'n_estimators': IntDistribution(10, 1000),
# 決定木の最大深さ(2から100の範囲で探索)
'max_depth': IntDistribution(2, 100),
# リーフごとの最小データ数(1から50の範囲で探索)
'min_child_samples': IntDistribution(1, 50),
# データのサブサンプリング率(0.5から1.0の範囲で探索)
'subsample': FloatDistribution(0.5, 1.0),
# 特徴量のサブサンプリング率(0.5から1.0の範囲で探索)
'colsample_bytree': FloatDistribution(0.5, 1.0)
},
cv=time_series_cv, # 時系列分割を使用したクロスバリデーション
n_trials=100, # 試行回数
scoring='neg_mean_absolute_error',
random_state=12,
timeout=600, # 制限時間(秒)
n_jobs=-1, # パラメータチューニングを並列処理
refit=True, # 最良モデルを最終モデルとして使用
)
# 利用する機械学習のインスタンスの生成
model = {
"TS_model": optuna_search
}
学習データとテストデータ(直近1年)に分割
元の時系列データ(data)を、学習データ(train_data)とテストデータ(test_data)に分割します。
テストデータは、直近1年を使用します。一方、学習データ(train_data)は、直近1年を除いた全てのデータを使用します。
以下、コードです。
import pandas as pd
import numpy as np
# 各'store'の直近1年間をテストデータとし、それ以前を学習データに分割
train_data_list = []
test_data_list = []
for store in stores:
store_data = data[data['store'] == store]
cutoff_date = store_data['date'].max() - pd.DateOffset(years=1)
train_data_list.append(store_data[store_data['date'] <= cutoff_date])
test_data_list.append(store_data[store_data['date'] > cutoff_date])
train_data = pd.concat(train_data_list, ignore_index=True)
test_data = pd.concat(test_data_list, ignore_index=True)
print('学習データ\n',train_data.head())
print()
print('テストデータ\n',test_data.head())
以下、実行結果です。
学習データ
date sales store area_id
0 2018-01-31 117.483571 A 1
1 2018-02-28 117.968933 A 1
2 2018-03-31 123.238443 A 1
3 2018-04-30 126.275403 A 1
4 2018-05-31 113.829233 A 1
テストデータ
date sales store area_id
0 2022-01-31 116.718091 A 1
1 2022-02-28 109.845053 A 1
2 2022-03-31 121.620420 A 1
3 2022-04-30 116.734843 A 1
4 2022-05-31 111.615390 A 1
ここで視覚的に、学習データ(train_data)とテストデータ(test_data)の分割を確認してみましょう。
以下、コードです。
import matplotlib.pyplot as plt
# 学習データとテストデータを確認するプロット
fig, axes = plt.subplots(len(stores), 1, figsize=(10, 4 * len(stores)))
for ax, store in zip(axes, stores):
# 各店舗ごとのデータを抽出
train_store_data = train_data[train_data['store'] == store]
test_store_data = test_data[test_data['store'] == store]
# 学習データをプロット
ax.plot(
train_store_data['date'],
train_store_data['sales'],
marker='o',
label='Train Data',
)
# テストデータをプロット
ax.plot(
test_store_data['date'],
test_store_data['sales'],
marker='x',
linestyle='--',
label='Test Data',
)
ax.set_title(f'Store: {store}', fontsize=12)
ax.set_ylabel('Sales', fontsize=12)
ax.grid(True)
ax.legend(loc='upper left')
plt.xlabel('Date', fontsize=12)
plt.tight_layout()
plt.show()
以下、実行結果です。
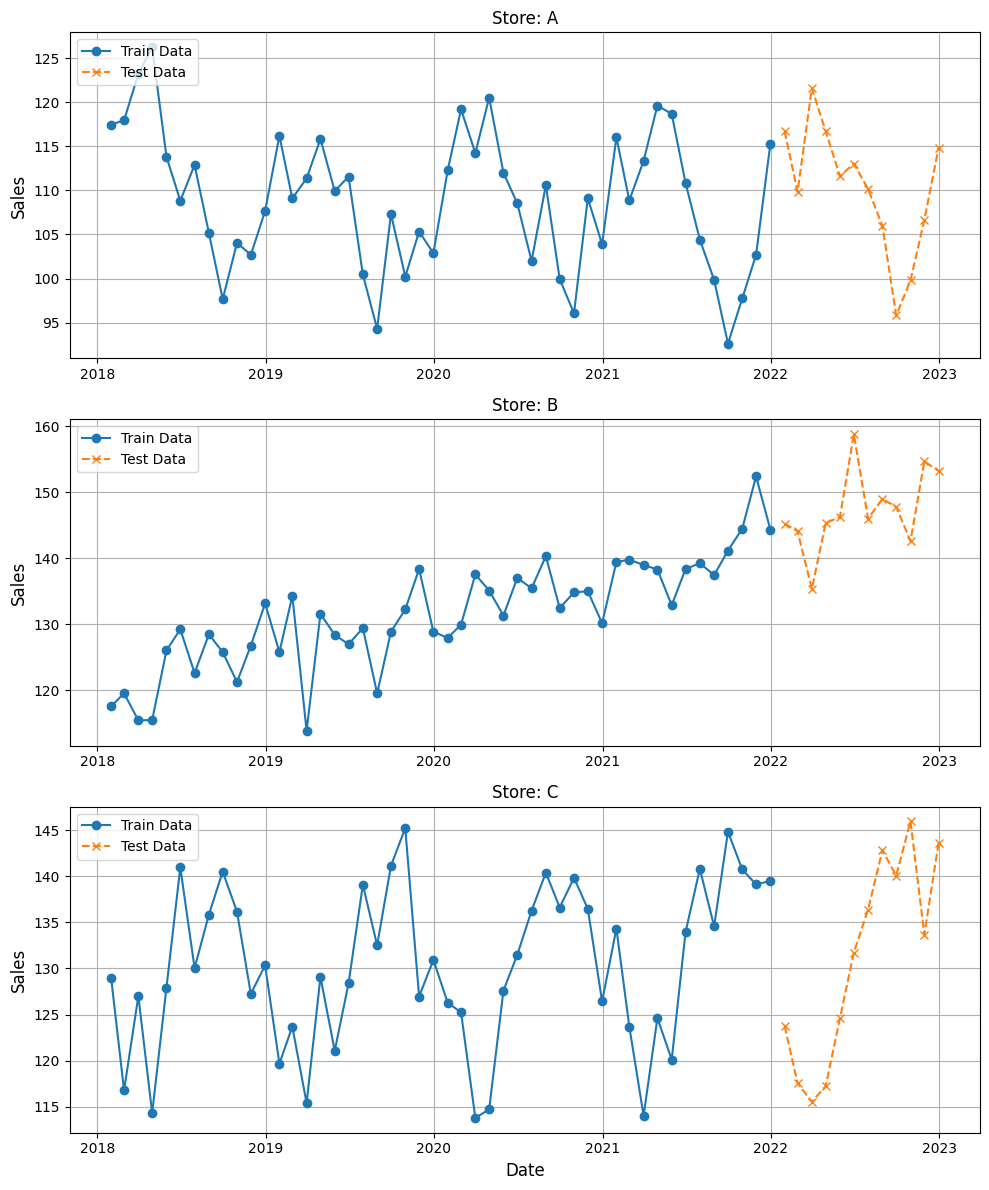
学習データでモデル構築
では、学習データ(train_data)を使ってモデルを構築します。
以下、コードです。
# 時系列機械学習モデルの構築 fcst = create_and_train_forecast_model(train_data, model) # 店舗別の実際の値と予測値の折れ線グラフを作成 plot_actual_vs_predicted_by_store(fcst,stores)
以下、実行結果です。
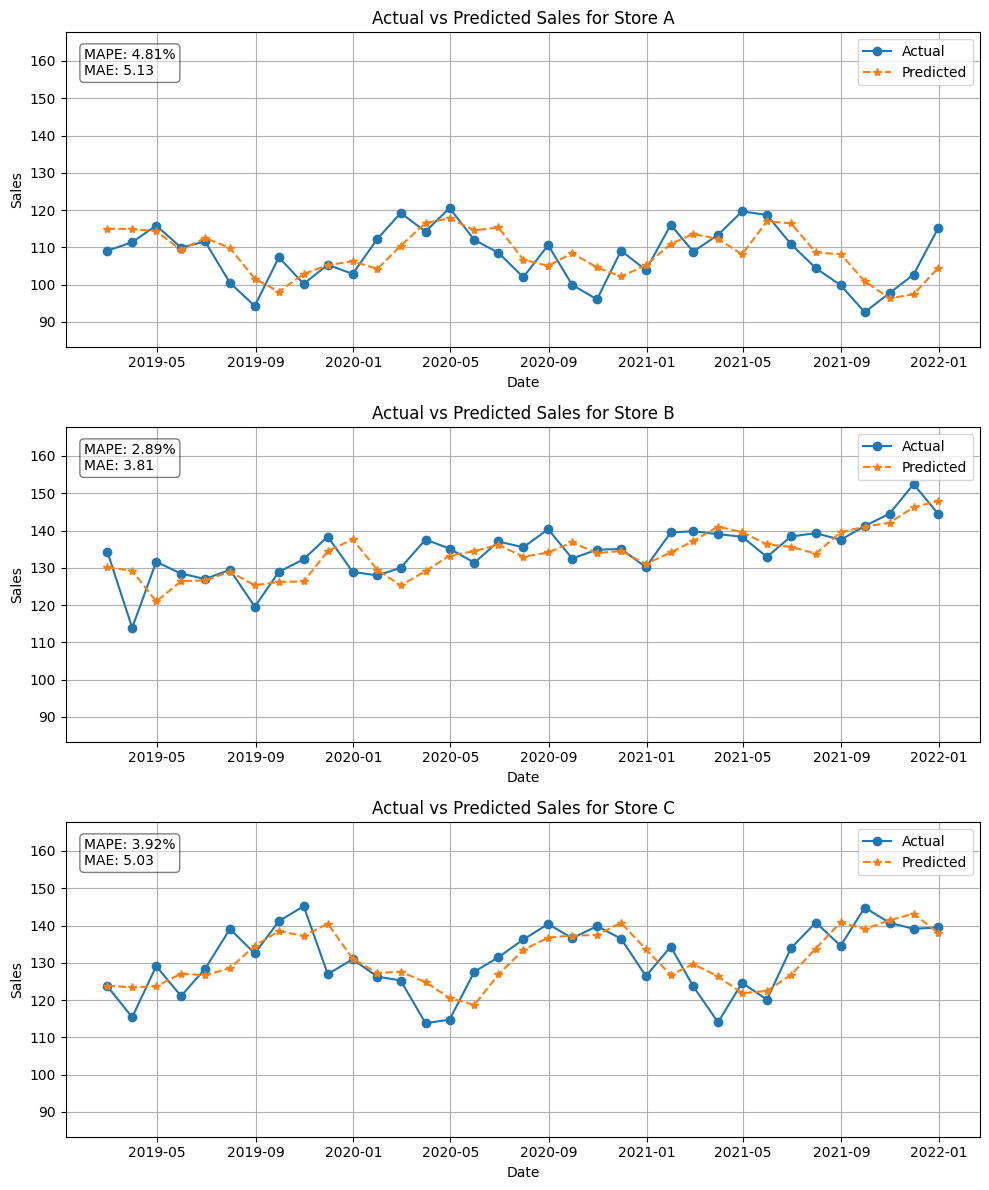
テストデータで精度検証
テストデータ(test_data)を使って、モデルの精度を検証します。
以下、コードです。
# 1年先の予測を実行 future_df = fcst.predict(h=12, level=[95]) # 予測結果をプロット plot_forecast(train_data, future_df, stores)
以下、実行結果です。
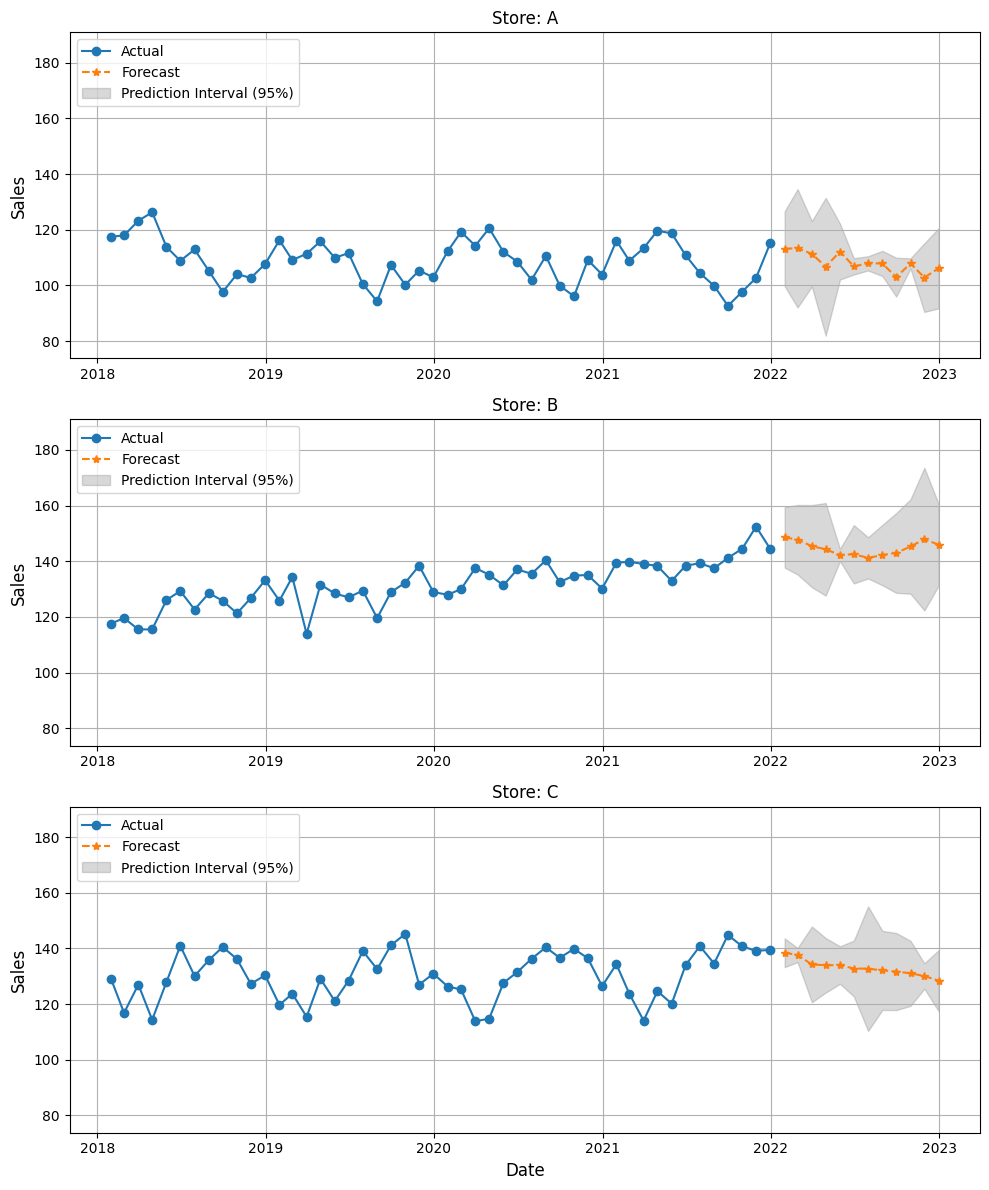
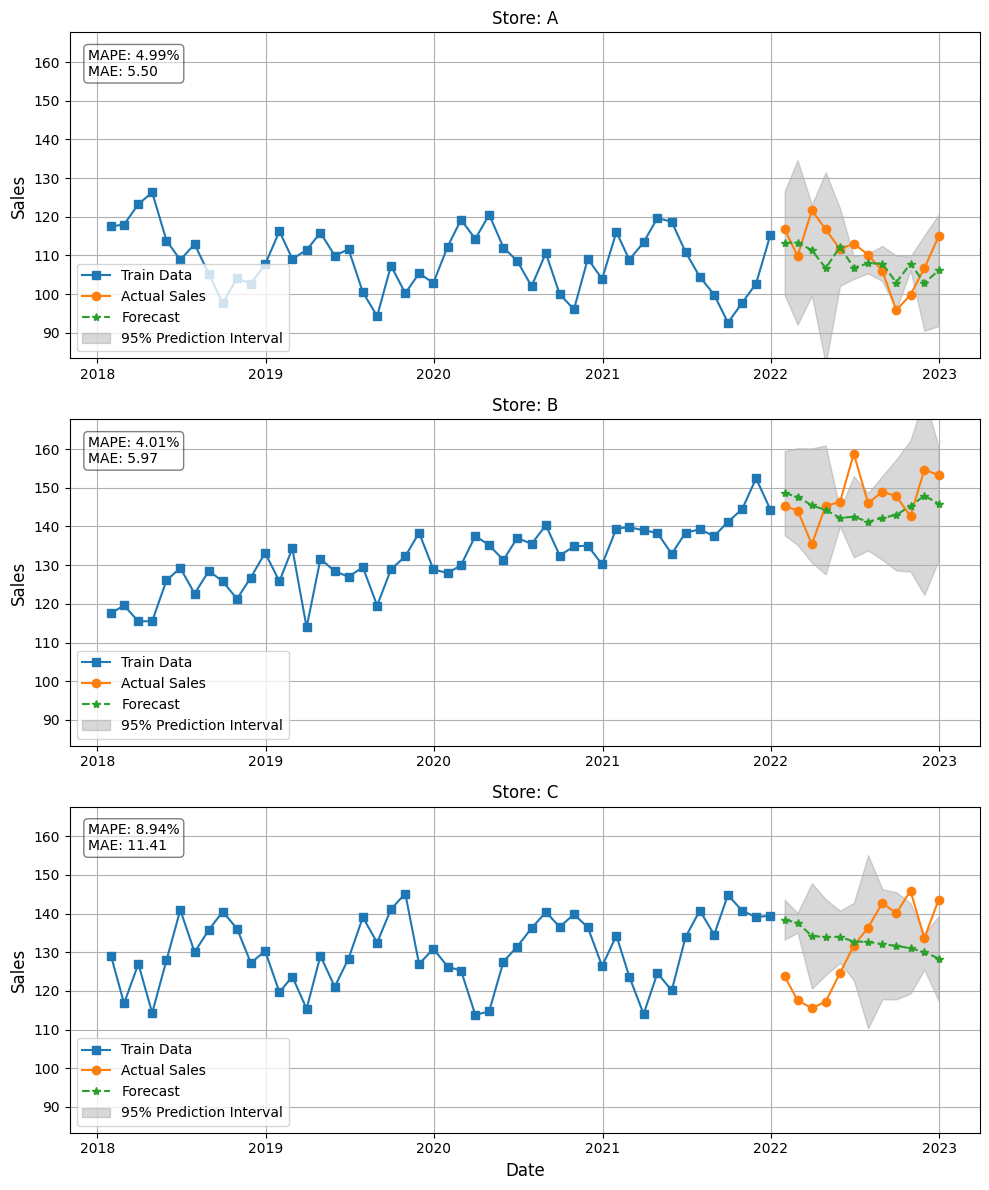
テストデータ(test_data)に対して、予測結果と精度指標を計算し、プロットもします。
以下、コードです。
import matplotlib.pyplot as plt
from sklearn.metrics import mean_absolute_error, mean_absolute_percentage_error
# 予測結果 ('future_df') とテストデータ ('test_data') を結合
test_data_merged = test_data.merge(future_df, on=['store', 'date'], how='left')
# 店舗別の精度指標を計算するリスト
store_metrics = []
# 縦軸のスケールを設定
y_min = train_data['sales'].min() * 0.9
y_max = train_data['sales'].max() * 1.1
# 各店舗ごとに学習データ、テストデータ、予測結果を計算し、プロット
fig, axes = plt.subplots(len(stores), 1, figsize=(10, 4 * len(stores)))
for ax, store in zip(axes, stores):
# 店舗ごとのデータを抽出
train_store_data = train_data[train_data['store'] == store]
test_store_data = test_data[test_data['store'] == store]
future_store_data = future_df[future_df['store'] == store]
store_data = test_data_merged[test_data_merged['store'] == store]
# 精度指標の計算
mape = mean_absolute_percentage_error(store_data['sales'], store_data['TS_model']) * 100
mae = mean_absolute_error(store_data['sales'], store_data['TS_model'])
# メトリクスをリストに追加
store_metrics.append({'store': store, 'mape': mape, 'mae': mae})
# 学習データをプロット
ax.plot(train_store_data['date'], train_store_data['sales'], label='Train Data', marker='s')
# テストデータをプロット
ax.plot(store_data['date'], store_data['sales'], label='Actual Sales', marker='o')
# 予測データをプロット
ax.plot(store_data['date'], store_data['TS_model'], label='Forecast', linestyle='--', marker='*')
# 将来予測データと予測区間をプロット
ax.fill_between(
future_store_data['date'],
future_store_data['TS_model-lo-95'],
future_store_data['TS_model-hi-95'],
color='gray',
alpha=0.3,
label='95% Prediction Interval'
)
ax.set_title(f'Store: {store}', fontsize=12)
ax.set_ylabel('Sales', fontsize=12)
ax.grid(True)
# 縦軸のスケールを統一
ax.set_ylim(y_min, y_max)
# MAPE, MAEをグラフ内に表示
ax.text(
0.02,
0.95,
f"MAPE: {mape:.2f}%\nMAE: {mae:.2f}",
transform=ax.transAxes,
verticalalignment='top',
bbox=dict(
boxstyle="round",
facecolor="white",
alpha=0.5
)
)
ax.legend(loc='lower left')
plt.xlabel('Date', fontsize=12)
plt.tight_layout()
plt.show()
以下、実行結果です。
まとめ
今回は、時系列データ特有の特徴量エンジニアリングと目的変数の変換を活用することで、モデルの予測精度を向上させる方法を具体例を交えて紹介しました。
また、Optuna を用いたハイパーパラメータの自動探索を実施し、複数の機械学習モデルを比較した結果、予測精度が高いモデルを選定しました。
これらの技術は、実務での時系列予測の効率化に大きく貢献します。ぜひ、実際のプロジェクトに応用してみてください!

