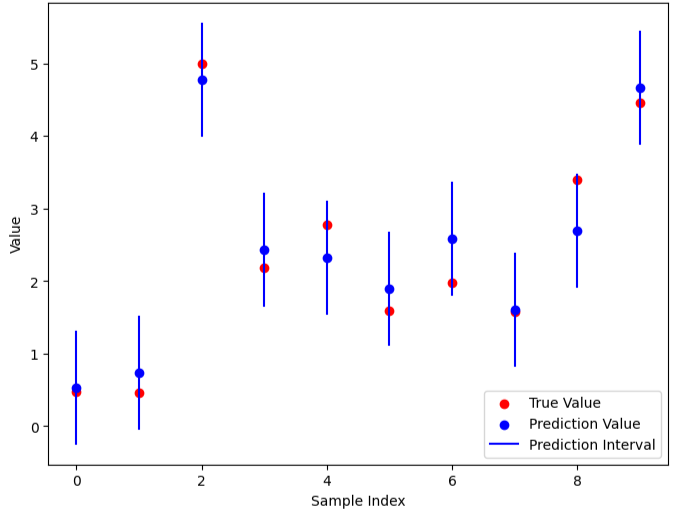
機械学習のモデルの予測値の多くは、「点」です。要は、ある数値の1点ということです。

1点予測は分かりやすいですが、現代の機械学習では、単なる点予測に加え、予測区間を用いた不確実性の評価が求められています。

今回は、Inductive Conformal Prediction (ICP) を活用して、予測区間や予測集合をどのように構築できるかを説明していきます。

ICPの枠組みはモデルに依存しないため、任意の予測モデル（例えば線形回帰、ランダムフォレスト、ニューラルネットワークなど）に対して適用可能なことが、最大の強い強みです。

Conformal Predictionとは

　不確実性の評価と予測区間の意義

従来の機械学習モデルは、入力データに対して1つの予測値やクラス確率を出力します。

しかし、需要予測の現場では、予測値のみに頼るのではなく、需要の変動や不確実性を考慮した予測区間が示されることで、過剰在庫や品切れといったリスクを軽減することが可能となります。

　CPの基本概念と予測区間の構築

CPは、各サンプルについて学習済みモデルの予測と実際の値との差（非適合度）を算出し、その分布を基にp値を導出します。

これにより、設定された有意水準に合わせた予測集合、または回帰タスクでは予測区間を構築します。

たとえば、需要予測では、モデルが予測する需要を中心に予測区間を定め、実際の需要がその区間内に収まる確率を統計的に保証します。

　CPの手法とその種類

CPには、すべてのデータを逐次使用する「オンライン型」と、データを訓練用とキャリブレーション用に分割して予測区間や予測集合を構築する「Inductive Conformal Prediction（ICP）」の2種類があります。

さらに、複数のキャリブレーション分割を組み合わせ、より堅牢な予測区間を得る手法として「Cross-Conformal Prediction」も提案されています。

いずれの場合も、データが交換可能であるという前提に基づいて、予測に統計的保証を与える点が共通しています。

　CPのメリットと留意点

CPの大きなメリットは、あらかじめ設定した信頼水準に従い、予測結果（予測区間や予測集合）に統計的な保証を与えられる点です。

これにより、需要予測の結果に対して、どの程度の不確実性があるかを明確に把握し、リスクを管理することが可能となります。

一方、交換可能性の前提や、キャリブレーション用データの適切な分割が結果に影響するため、実際のデータ特性に合わせた慎重な設定が求められます。

Inductive Conformal Prediction (ICP) の仕組み

　ICPの基本的な流れ

大きく分けて次の3つのステップになります。

　非適合度の定義と計算

ICPにおける重要な概念の一つが「非適合度（nonconformity measure）」です。

これは、各サンプルが学習済みモデルの予測結果からどれだけ逸脱しているかを定量化する指標であり、タスクの性質に応じて定義が異なります。

たとえば、回帰タスクの場合、一般的には以下のように定義されます。

$${\alpha }_i=|y_i–\hat{y}(x_i)|$$

ここで、$y_i$はキャリブレーション用セットの実際の値、$\hat{y}(x_i)$は学習済みモデルによる予測値を表します。

分類タスクの場合は、モデルが出力する各クラスの確率を利用して、正解ラベルに対する信頼度の低さ、たとえば、次のように定義されます。

$$\alpha (x,y)=1–\hat{p}(y\mid x)$$

いずれの場合も、非適合度が大きいほど、対象のサンプルが「予測から外れている」と判断されることになります。

　キャリブレーションと予測集合の構築

キャリブレーション用セットに対して各サンプルの非適合度 $\alpha_i$ を計算した後、あらかじめ設定された有意水準 $\alpha$（たとえば、$\alpha=0.05$ であれば95%の信頼保証）に対応する閾値を求めます。

具体的には、キャリブレーション用セットにおける非適合度の上位 $(1-\alpha)$ 分位点を閾値 $q_{1-\alpha}$ として定義します。

これを数式で表すと、次のようになります。

$$q_{1-\alpha }=inf\{q\in \mathbb{R}:\frac{1}{n}\sum _{i=1}^n\mathbf{1}\{{\alpha }_i\le q\}\ge 1–\alpha \}$$

ここで、$n$ はキャリブレーション用セットのサンプル数、$\mathbf{1}\{\cdot\}$ は条件が成立した場合に1を、そうでなければ0を返す指示関数です。

つまり、キャリブレーション用セット中の少なくとも $(1-\alpha) \times 100\%$ のサンプルに対して、非適合度がこの閾値以下であることを保証する閾値となります。

新たな入力 $x$ に対する予測集合 $\Gamma(x)$ は、候補となる出力 $y$ の中で、非適合度がこの閾値以下となるものすべてを含む形で定義されます。

回帰タスクの場合、非適合度の定義が先述の絶対誤差の場合には、予測集合は実質的に予測区間となります。

$$\mathrm{\Gamma }(x)=[\hat{y}(x)–q_{1-\alpha },\hat{y}(x)+q_{1-\alpha }]$$

分類タスクの場合、予測集合は次のように表現されます。

$$\mathrm{\Gamma }(x)=\{y\in \mathcal{Y}:\alpha (x,y)\le q_{1-\alpha }\}$$

ここで、$\mathcal{Y}$ は出力の可能な値の集合を示します。

このようにして構築された予測集合は、真の値 $y$ が $\Gamma(x)$ に含まれる確率が少なくとも $1-\alpha$ であることが統計的に保証されます。

　ICPの前提条件

ICPの理論的根拠は、データが交換可能（exchangeable）であるという仮定に基づいています。

交換可能性の仮定の下では、キャリブレーション用セットと新たなデータは同一の確率分布からサンプリングされているとみなすことができます。

このことで、キャリブレーション用に得られた非適合度の分布は、新たなサンプルに対しても適用可能となります。

$$\mathbb{P}(y_{new}\in \mathrm{\Gamma }(x_{new}))\ge 1–\alpha$$

この不等式は、新たな入力 $x_{new}$ に対して、対応する真の出力 $y_{new}$ が予測集合 $\Gamma(x_{new})$ に含まれる確率が、事前に設定した $1-\alpha$ 以上であることを示しています。

キャリブレーション用セットから算出された分位点 $q_{1-\alpha}$ により、この保証が成り立つ理由は、全サンプルの非適合度の中で $(1-\alpha) \times 100\%$ が閾値以下であるという事実に基づいているためです。

また、ICPの枠組みはモデルに依存しないため、任意の予測モデル（例えば線形回帰、ランダムフォレスト、ニューラルネットワークなど）に対して適用可能です。

非適合度の定義をタスクに合わせて適切に設計することで、さまざまな問題に対して信頼性のある予測集合を構築することができます。

Python実装例：回帰タスク

　回帰タスクにおけるICPの概要

回帰タスクでは、ある入力 $x$ に対してモデルが予測する出力 $\hat{y}(x)$ に対し、実際の真の値 $y$ がどの範囲に存在するか、すなわち予測区間を構築することが目的となります。

ICPを用いる場合、まずキャリブレーション用セットに対して、各サンプルの非適合度を……

$${\alpha }_i=|y_i–\hat{y}(x_i)|$$

……という絶対誤差により定義し、その分布から指定された信頼水準 $1-\alpha$ に対応する分位点 $q_{1-\alpha}$ を算出します。

新たな入力 $x$ に対しては、予測値 $\hat{y}(x)$ を中心として、次のような予測区間を構築することで、真の値 $y$ がこの区間内に含まれる確率を $1-\alpha$ と保証する、という流れとなります。

$$\mathrm{\Gamma }(x)=[\hat{y}(x)–q_{1-\alpha },\hat{y}(x)+q_{1-\alpha }]$$

　データセットの準備

ここでは、scikit-learnが提供するCalifornia Housingデータセットを用いて回帰問題に取り組みます。

まず、データセットを読み込み、全体を訓練用セットとテストセットに分割した後、訓練用セットの中からさらにキャリブレーション用セットを抽出します。

以下、コードです。

import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split

# California Housingデータセットの読み込み
data = fetch_california_housing()
X = data.data
y = data.target

# 全体を訓練用セットとテストセットに分割（テスト20%）
X_train, X_test, y_train, y_test = train_test_split(
    X, 
    y, 
    test_size=0.2, 
    random_state=42
)

# 訓練用セットをさらに、モデル学習用とキャリブレーション用に分割（キャリブレーション用に30%を使用）
X_train_model, X_calib, y_train_model, y_calib = train_test_split(
    X_train, 
    y_train, 
    test_size=0.3, 
    random_state=42
)

print("訓練データのサイズ")
print("X_train:",X_train.shape)
print(" - 学習用セットのX_train_model:",X_train_model.shape)
print(" - キャリブレーション用セットのX_calib:",X_calib.shape)
print("y_train:",y_train.shape)
print(" - 学習用セットのy_train_model:",y_train_model.shape)
print(" - キャリブレーション用セットのy_calib:",y_calib.shape)
print()
print("テストデータのサイズ")
print("X_test:",X_test.shape)
print("y_test:",y_test.shape)

以下、実行結果です。

訓練データのサイズ
X_train: (16512, 8)
 - 学習用セットのX_train_model: (11558, 8)
 - キャリブレーション用セットのX_calib: (4954, 8)
y_train: (16512,)
 - 学習用セットのy_train_model: (11558,)
 - キャリブレーション用セットのy_calib: (4954,)

テストデータのサイズ
X_test: (4128, 8)
y_test: (4128,)

　非適合度の算出

次に、回帰モデルを学習させます。ここでは、RandomForestRegressorを例として採用し、学習済みモデルを構築します。

その後、キャリブレーション用セットに対して予測を行い、各サンプルの絶対誤差を非適合度として計算します。

以下、コードです。

from sklearn.ensemble import RandomForestRegressor

# RandomForestRegressorの初期化と学習
model = RandomForestRegressor(random_state=42)
model.fit(X_train_model, y_train_model)

# キャリブレーション用セットに対して予測を実施
y_calib_pred = model.predict(X_calib)

# 各サンプルの非適合度（絶対誤差）を算出
nonconformity_scores = np.abs(y_calib - y_calib_pred)

print("非適合度(Nonconformity scores):")
print(nonconformity_scores)

以下、実行結果です。

非適合度(Nonconformity scores):
[0.05266   0.09803   2.21962   ... 0.8148796 0.19675   0.3075799]

ここで得られる非適合度の配列は、各サンプルがモデルの予測値からどれだけ逸脱しているかを示しており、この分布に基づいて予測区間の幅を決定します。

　予測区間の構築

キャリブレーション用セットの非適合度の分布から、有意水準 $\alpha$（ここでは例えば $\alpha = 0.1$、すなわち90%の信頼度）に対応する分位点 $q_{1-\alpha}$ を求めます。次に、テストデータに対して予測を行い、その予測値を中心とした予測区間を構築します。

以下、コードです。

# 有意水準の設定（α = 0.1で90%の信頼度を意味する）
alpha = 0.1

# キャリブレーション用非適合度の(1 - α)分位点を求める
q = np.quantile(nonconformity_scores, 1 - alpha)

# テストデータに対して予測を実施
y_test_pred = model.predict(X_test)

# 各サンプルに対する予測区間の構築
prediction_intervals = [(pred - q, pred + q) for pred in y_test_pred]

print("予測区間(Prediction intervals):")
print(prediction_intervals

このコードにより、各テストサンプルについて「$予測値 ± q$」という区間が得られます。

この予測区間は、真の値 $y$ がその中に含まれる確率が少なくとも90%となることが期待されています。

以下、実行結果です。

予測区間(Prediction intervals):
[(-0.23813099999999998, 1.307391), (-0.03130099999999991, 1.514221), (4.007076599999992, 5.5525985999999925),   ...   (3.8695364999999944, 5.4150584999999944), (-0.08361099999999999, 1.4619109999999997), (0.8371889999999998, 2.3827109999999996)]

　結果の評価

最後に、構築した予測区間が実際にどの程度のカバー率（真の値が区間内に含まれる割合）を達成しているか、また区間の幅がどの程度であるかを評価します。

テストデータに対して各サンプルの予測区間に真の値が含まれているかを判定し、全体のカバー率および予測区間の平均幅を算出しています。

以下、コードです。

# 真の値が予測区間に含まれているかを判定
correct = 0
interval_widths = []

for i, (lower, upper) in enumerate(prediction_intervals):
    interval_widths.append(upper - lower)
    if lower <= y_test[i] <= upper:
        correct += 1

coverage = correct / len(y_test)
avg_interval_width = np.mean(interval_widths)

print(f"Coverage (真の値が区間に含まれる割合): {coverage:.2f}")
print(f"Average Interval Width (平均予測区間幅): {avg_interval_width:.2f}")

以下、実行結果です。

Coverage (真の値が区間に含まれる割合): 0.89
Average Interval Width (平均予測区間幅): 1.55

この評価により、おおよそ「Coverage: 0.90」といった結果が得られているため、設定した信頼水準に対応する予測区間がうまく機能していることが確認できました。

なお、予測区間が広すぎる場合には、モデルの精度や非適合度の定義、あるいはキャリブレーションの手法について再検討する必要があるかもしれません。

Python実装例：分類タスク

　分類タスクにおけるICPの概要

分類タスクでは、入力 $x$ に対してモデルが各クラスに属する確率を出力し、その中から正解ラベルがどの程度信頼できるかを評価することが求められます。

ICPを用いる場合、まずキャリブレーション用セットにおいて各サンプルの非適合度を算出します。ここでは、各サンプルの正解クラスに対する予測確率 $\hat{p}(y \mid x)$ を用い、非適合度を次のような形で定義します。

$$\alpha (x,y)=1–\hat{p}(y\mid x)$$

キャリブレーション用セットにおける非適合度の分布から、あらかじめ設定した信頼水準 $1-\alpha$ に対応する分位点 $q_{1-\alpha}$ を求め、新たなサンプルに対して、各クラスごとの非適合度がこの閾値以下となるクラスを予測集合として採用します。

これにより、正解クラスが予測集合に含まれる確率が少なくとも $1-\alpha$ となることが保証されます。

　データセットの準備

実装例では、scikit-learnが提供するIrisデータセットを用いて、分類タスクに取り組みます。

まず、全体のデータセットを訓練用セットとテストセットに分割し、さらに訓練用セットの中からキャリブレーション用セットを抽出します。

以下、コードです。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# Irisデータセットの読み込み
data = load_iris()
X = data.data
y = data.target

# 全体のデータセットを訓練用セットとテストセットに分割（テスト20%）
X_train, X_test, y_train, y_test = train_test_split(
    X, 
    y, 
    test_size=0.2, 
    random_state=42
)

# 訓練用セットをさらに、モデル学習用とキャリブレーション用に分割（キャリブレーション用に30%を使用）
X_train_model, X_calib, y_train_model, y_calib = train_test_split(
    X_train, 
    y_train, 
    test_size=0.3, 
    random_state=42
)

print("訓練データのサイズ")
print("X_train:",X_train.shape)
print(" - 学習用セットのX_train_model:",X_train_model.shape)
print(" - キャリブレーション用セットのX_calib:",X_calib.shape)
print("y_train:",y_train.shape)
print(" - 学習用セットのy_train_model:",y_train_model.shape)
print(" - キャリブレーション用セットのy_calib:",y_calib.shape)
print()
print("テストデータのサイズ")
print("X_test:",X_test.shape)
print("y_test:",y_test.shape)

以下、実行結果です。

訓練データのサイズ
X_train: (120, 4)
 - 学習用セットのX_train_model: (84, 4)
 - キャリブレーション用セットのX_calib: (36, 4)
y_train: (120,)
 - 学習用セットのy_train_model: (84,)
 - キャリブレーション用セットのy_calib: (36,)

テストデータのサイズ
X_test: (30, 4)
y_test: (30,)

　非適合度の算出

次に、分類モデルを学習させます。ここでは、RandomForestClassifierを例として採用し、学習済みモデルを構築します。

その後、キャリブレーション用セットに対して各サンプルのクラスごとの予測確率を計算し、正解クラスに対する予測確率の補数を非適合度として算出します。

以下、コードです。

from sklearn.ensemble import RandomForestClassifier

# RandomForestClassifierの初期化と学習
model = RandomForestClassifier(random_state=42)
model.fit(X_train_model, y_train_model)

# キャリブレーション用セットに対して各サンプルのクラスごとの予測確率を計算
probs_calib = model.predict_proba(X_calib)

# 正解クラスの予測確率の補数を非適合度として定義（1 - 正解クラスの確率）
nonconformity_scores = 1 - np.array([
    probs_calib[i, y_calib[i]] for i in range(len(y_calib))
])

print("非適合度(Nonconformity scores):")
print(nonconformity_scores)

以下、実行結果です。

非適合度(Nonconformity scores):
[0.05 0.03 0.   0.01 0.   0.   0.49 0.02 0.05 0.   0.   0.84 0.11 0.
 0.08 0.03 0.   0.   0.   0.01 0.01 0.19 0.   0.   0.55 0.   0.01 0.
 0.   0.   0.   0.01 0.07 0.   0.02 0.07]

ここで得られる非適合度の配列は、各サンプルがモデルの予測からどの程度逸脱しているかを示しており、その分布に基づいて予測集合の構築に利用されます。

　予測集合の構築

キャリブレーション用セットの非適合度分布から、あらかじめ設定した有意水準 $\alpha$ （ここでは例えば $\alpha = 0.1$、すなわち90%の信頼度）に対応する分位点 $q_{1-\alpha}$ を求めます。

次に、テストデータに対して各サンプルのクラスごとの予測確率を算出し、各クラスの非適合度（すなわち $1 - そのクラスの予測確率$）が $q_{1-\alpha}$ 以下であるクラスを予測集合として採用します。

以下、コードです。

# 有意水準の設定（α = 0.1で90%の信頼度を意味する）
alpha = 0.1

# キャリブレーション用セットの非適合度の(1 - α)分位点を閾値として算出
q = np.quantile(nonconformity_scores, 1 - alpha)

# テストデータに対して各サンプルのクラスごとの予測確率を計算
probs_test = model.predict_proba(X_test)

# 各サンプルに対して、非適合度が閾値以下となるクラスを予測集合として構築
prediction_sets = []
for i, prob in enumerate(probs_test):
    # 各クラスに対する非適合度は 1 - そのクラスの予測確率
    nc_scores = 1 - prob
    # 非適合度が閾値以下のクラスを予測集合に採用
    pred_set = np.where(nc_scores <= q)[0]
    prediction_sets.append(pred_set)

print("予測集合(Prediction sets):")
print(prediction_sets)

このコードでは、まず np.quantile を用いてキャリブレーション用の非適合度の分布から分位点 $q$ を求め、その閾値をもとに、テストサンプルごとに非適合度が $q$ 以下となるクラスを予測集合として構築しています。

以下、実行結果です。

予測集合(Prediction sets):
[array([1]), array([0]), array([2]), array([1]), array([], dtype=int64), array([0]), array([1]), array([2]), array([], dtype=int64), array([1]), array([2]), array([0]), array([0]), array([0]), array([0]), array([1]), array([2]), array([1]), array([1]), array([2]), array([0]), array([], dtype=int64), array([0]), array([2]), array([2]), array([2]), array([2]), array([2]), array([0]), array([0])]

　結果の評価

最後に、構築した予測集合が実際にどの程度のカバー率を達成しているか、また予測集合の平均サイズがどの程度かを評価します。

ここでは、各テストサンプルにおいて、予測集合に真のクラスが含まれているかを判定し、その割合をカバー率として算出するとともに、予測集合のサイズ（含まれるクラス数）の平均を計算します。

以下、コードです。

# 予測集合に真のクラスが含まれているかを確認し、カバー率を算出
correct = 0
set_sizes = []

for i, pred_set in enumerate(prediction_sets):
    set_sizes.append(len(pred_set))
    if y_test[i] in pred_set:
        correct += 1

coverage = correct / len(y_test)
avg_set_size = np.mean(set_sizes)

print(f"Coverage (真のクラスが含まれる割合): {coverage:.2f}")
print(f"Average Prediction Set Size (予測集合の平均サイズ): {avg_set_size:.2f}")

以下、実行結果です。

Coverage (真のクラスが含まれる割合): 0.90
Average Prediction Set Size (予測集合の平均サイズ): 0.90

この評価により、おおよそ「Coverage: 0.90」といった結果が得られれば、設定した信頼水準に見合った予測集合が構築できていることが確認されます。

予測集合があまりにも広い場合は、非適合度の定義やモデルの性能を再検討する必要があるかもしれません。

発展的トピック

　ICPからCross-Conformal Predictionへ

従来のInductive Conformal Prediction（ICP）では、データを訓練用セットとキャリブレーション用セットに分割する方法が一般的ですが、分割方法に依存する部分が存在するため、結果の安定性に課題がありました。

これに対して、Cross-Conformal Predictionは、複数のキャリブレーション分割を組み合わせることで、より堅牢かつ安定した予測集合や予測区間を提供する手法です。

このアプローチにより、データ分割に起因するばらつきを低減できると期待され、特にデータ量が限られている場合に有効な可能性があります。

ただし、計算コストの増加などの課題もあり、今後の研究でさらなるアルゴリズムの改良が求められます。

　時系列予測への応用

需要予測や在庫管理などの分野では、時系列データを用いた予測が重要な役割を果たします。

従来のCPは時間的な概念が主役でない静的なデータセットを前提としていましたが、時系列予測への応用においては、データの非定常性や時間的依存性をどのように扱うかが大きな課題です。

最近では、時系列データに対するCPの拡張手法や、オンライン更新を組み合わせた手法が提案され始めており、予測区間を動的に更新することで、より実践的な需要予測やリスク管理に寄与できる可能性が示唆されています。

今後、この分野での理論的枠組みの確立と実装面での改良が期待されます。

　今後の発展の方向性

Cross-Conformal Predictionや時系列予測への応用を含むCPの発展的なアプローチは、まだ多くの研究余地を残しています。

例えば、非適合度の定義を各予測タスクに最適化する方法や、データの時間的変動に柔軟に対応するオンラインアルゴリズムの開発、さらには他の不確実性評価手法（例えば、ベイズ推定や分位点回帰）とのハイブリッド化など、多方面での改良が検討されています。

これらの研究は、実務での応用範囲をさらに広げ、より信頼性の高い予測システムの構築に寄与することが期待されます。

　主要な参考文献

この分野における、ことはじめ的な文献として、以下の書籍や論文が挙げられます。

• Shafer, G., & Vovk, V. (2008). A tutorial on conformal prediction.
• Papadopoulos, H., Vovk, V., & Gammerman, A. (2014). Conformal prediction for reliable machine learning: Theory, adaptations and applications.
• Vovk, V., Gammerman, A., & Shafer, G. (2022). Algorithmic Learning in a Random World, Second Edition.

最近のCross-Conformal Predictionや時系列データへの応用に関する論文も、各分野の国際会議や専門誌で発表されており、今後の動向に注目する価値があります。

まとめ

今回は、Inductive Conformal Prediction (ICP) を用いて、統計的な保証付きの予測区間や予測集合を構築する方法について説明しました。

まず、ICPの理論的背景や非適合度の計算方法、キャリブレーションを活用した閾値決定の仕組みを数式を交えて説明し、その後、分類タスクと回帰タスクに対する具体的なPython実装例を通じて、実際の予測区間や予測集合の構築手順を示しました。

より安定した機械学習モデルの予測区間を求めるcross-conformal-predictionをPythonで実施してみよう