機械学習の世界では、予測の精度を高めるだけでなく、その予測がどの程度信頼できるかを示す「不確実性の評価」がますます重要視されています。
そこで近年注目を集めているのが、学習データから得られる非適合性スコアを用いて、各予測に対する予測区間を導き出す「Conformal Prediction」というアプローチです。
以下の記事で、最もシンプルなConformal Predictionの1つである、Inductive Conformal Prediction (ICP)について触れました。
今回は、Conformal Predictionの中でもK-fold分割に基づき、より安定した予測区間を提供する「Cross-Conformal Prediction (CCP)」を取り上げます。
Contents [hide]
- ICPのおさらい
- CCPの基本概念
- STEP 1 : データのK-fold分割
- STEP 2 : 各フォールドでのモデル学習と非適合性スコアの計算
- STEP 3 : 新規サンプルに対するp値の算出
- STEP 4 : p値の統合
- STEP 5 : 予測信頼区間の決定
- Python実装例:回帰タスク
- データセットの準備
- 各フォールドでの学習とキャリブレーション
- 統合と予測区間の構築
- 結果の評価
- Python実装例:分類タスク
- データセットの準備
- CCPによる各フォールドでの学習とキャリブレーション
- 予測集合の構築
- 結果の評価
- 発展的トピック
- Conformal Predictionの最新動向
- Conformalized Quantile Regression (CQR)
- Online Conformal Prediction / Adaptive Conformal Inference
- 他タスクへの拡張とハイブリッドアプローチ
- 時系列データへの応用
- 時系列特有の非適合度(Nonconformity Measure)の工夫
- クロス検証とローリングウィンドウ
- マルチステップ予測への拡張
- まとめ
ICPのおさらい
Inductive Conformal Prediction (ICP)は、学習済みモデルに対して各予測の予測区間を求めるために、非適合性スコア (nonconformity score)を用いる手法です。
非適合性スコアは、たとえば回帰タスクの場合、一般的には以下のように定義されます。
ここで、
分類タスクの場合は、モデルが出力する各クラスの確率を利用して、正解ラベルに対する信頼度の低さ、たとえば、次のように定義されます。
いずれの場合も、非適合度が大きいほど、対象のサンプルが「予測から外れている」と判断されることになります。
このような非適合性スコア (nonconformity score)を用い予測区間を求める流れです。
| 処理内容 | 説明 | |
|---|---|---|
| STEP 1 | データセットの分割とモデル学習 | 利用可能なデータを「モデルの訓練(トレーニング)用のセット」とキャリブレーション用のセット」に分割し、モデルを学習する。 |
| STEP 2 | キャリブレーション用セットで非適合度計算 | キャリブレーション用セットの各サンプルに対して、モデルの予測と実際の値との差などを基に非適合度を計算する。 |
| STEP 3 | 新たなサンプルへの予測集合構築 | キャリブレーション用セットから得られた非適合度の分布を用い、指定された信頼水準(例:95%)に基づく予測集合(または予測区間)を構築する。 |
新規サンプルに対するスコアを
ここで、
ある有意水準
……と定義されます。
すなわち、候補
詳細は以下の記事を確認してください。
CCPの基本概念
CCP(Cross-Conformal Prediction)は、従来のICPが持つ「1つのキャリブレーションセットに依存する」という問題を解決するために、データ全体を複数のフォールドに分割し、各フォールドで独立に非適合性スコアとp値を計算する手法です。
簡単に流れを説明します。
STEP 1 : データのK-fold分割
データセット
各フォールド
- 訓練セット:
- キャリブレーションセット:
STEP 2 : 各フォールドでのモデル学習と非適合性スコアの計算
各フォールド
学習済みモデルを用い、キャリブレーションセット内の各サンプル
ここで、
この関数とは、回帰タスクの場合には、たとえば以下のように定義されます。
分類タスクの場合は、たとえば次のように定義されます。
いずれの場合もICPで登場したものですが、別の関数でも構いません。
STEP 3 : 新規サンプルに対するp値の算出
新規サンプル
続いて、各フォールドにおいて以下のようにp値を算出します。
ここまでは、ICPで実施したようなことを、各フォールド
STEP 4 : p値の統合
各フォールド
STEP 5 : 予測信頼区間の決定
最終的なp値である
例えば、
このように、CCPは各フォールドで独立に得られた情報を統合することで、単一のキャリブレーションセットに依存する場合のばらつきを低減し、より安定した予測信頼度の評価を可能にします。
Python実装例:回帰タスク
California Housingデータセットを用いた回帰タスクにおいて、Cross-Conformal Prediction (CCP) を実装する方法を説明します。
従来のICPでは、学習データを訓練用とキャリブレーション用に分割して非適合度の分布から分位点を求め、予測区間を構築していました。
これに対し、CCPでは訓練データ全体をK-fold分割し、各フォールドで個別にモデルの学習とキャリブレーションを行い、その結果を統合し、より安定した予測区間が得られる手法となります。
RandomForestRegressorを用いて各フォールドでモデルを学習し、キャリブレーション用セットにおける非適合度(絶対誤差)の分布から分位点を算出します。各フォールドでのテストサンプルの予測結果と分位点を統合し、最終的な予測値を中心とする予測区間を構築していきます。
データセットの準備
まず、California Housingデータセットを読み込み、全体を訓練セットとテストセットに分割します。
以下、コードです。
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
# California Housingデータセットの読み込み
data = fetch_california_housing()
X = data.data
y = data.target
# 全体を訓練用セットとテストセットに分割(テスト20%)
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
test_size=0.2,
random_state=42
)
print("訓練データのサイズ:")
print("X_train:", X_train.shape)
print("y_train:", y_train.shape)
print()
print("テストデータのサイズ:")
print("X_test:", X_test.shape)
print("y_test:", y_test.shape)
print()
上記のコードでは、全体データを80%の訓練データと20%のテストデータに分割しています。
以下、実行結果です。
訓練データのサイズ: X_train: (16512, 8) y_train: (16512,) テストデータのサイズ: X_test: (4128, 8) y_test: (4128,)
各フォールドでの学習とキャリブレーション
CCPでは、訓練セット全体に対してK-fold分割を行い、各フォールドで以下の処理を実施します。
- フォールドごとに訓練用セットとキャリブレーション用セットに分割
- RandomForestRegressorを用いてモデルを学習
- キャリブレーション用セットに対して予測を行い、非適合度(絶対誤差)を計算
- (1 – α)分位点を算出
ここでは、K=5および有意水準α=0.1(90%予測区間)を設定しています。
以下、コードです。
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import KFold
# CCPのK-fold分割の設定
K = 5 # K-fold分割数
alpha = 0.1 # 有意水準 (α=0.1 → 90%予測区間)
kf = KFold(
n_splits=K,
shuffle=True,
random_state=42
)
# 各フォールドでのテストサンプルに対する予測値(shape: (K, n_test))を保存するリスト
test_preds_folds = []
# 各フォールドでの分位点q(スカラー)を保存するリスト
quantiles_folds = []
# 各フォールドでの処理
for train_index, calib_index in kf.split(X_train):
# フォールドごとに訓練用セットとキャリブレーション用セットに分割
X_train_fold, X_calib = X_train[train_index], X_train[calib_index]
y_train_fold, y_calib = y_train[train_index], y_train[calib_index]
# モデルの学習(RandomForestRegressorを使用)
model = RandomForestRegressor(random_state=42)
model.fit(X_train_fold, y_train_fold)
# キャリブレーション用セットでの予測と非適合度(絶対誤差)の算出
y_calib_pred = model.predict(X_calib)
nonconformity_scores = np.abs(y_calib - y_calib_pred)
# キャリブレーション用非適合度の (1 - α) 分位点 q を算出
q_k = np.quantile(nonconformity_scores, 1 - alpha)
# テストサンプルに対する予測値を算出
y_test_pred_fold = model.predict(X_test)
# 結果を保存
test_preds_folds.append(y_test_pred_fold)
quantiles_folds.append(q_k)
# 各フォールドでの予測値を表示
print("各フォールドでのテストデータに対する予測値:")
for i in range(K):
print(f"フォールド {i+1} :",test_preds_folds[i])
# 各フォールドでの分位点を表示
print("各フォールドでの分位点:")
print(quantiles_folds)
各フォールドで得られた分位点
以下、実行結果です。
各フォールドでのテストデータに対する予測値: フォールド 1 : [0.50914 0.81707 4.8325074 ... 4.7265481 0.70922 1.5898 ] フォールド 2 : [0.53321 0.79979 4.7676259 ... 4.8813088 0.68591 1.68557 ] フォールド 3 : [0.47251 0.78223 4.9774071 ... 4.8278688 0.71798 1.59335 ] フォールド 4 : [0.49804 0.73734 4.7348646 ... 4.8855086 0.71636 1.67201 ] フォールド 5 : [0.54424 0.74905 4.8202061 ... 4.9208792 0.71483 1.70512 ] 各フォールドでの分位点: [0.8101599199999999, 0.7718039000000012, 0.7776130000000012, 0.7785464800000022, 0.7578354000000008]
統合と予測区間の構築
各フォールドで得られたテストサンプルの予測値と分位点を統合します。
ここでは、以下の統合方法を採用しています。
- 予測値の統合:各フォールドでの予測値の平均を最終的な予測値とする
- 分位点の統合:各フォールドで算出された分位点
の平均を、最終的な分位点とする
これにより、各テストサンプルについて、最終的な予測区間は次のようになります。
以下、コードです。
# 各フォールドでのテストサンプルの予測値を配列に変換(shape: (K, n_test))し、平均をとる
test_preds_folds = np.array(test_preds_folds)
aggregated_test_preds = np.mean(test_preds_folds, axis=0)
# 各フォールドの分位点の平均を算出
quantiles_folds = np.array(quantiles_folds)
aggregated_q = np.mean(quantiles_folds)
# 各テストサンプルに対する予測区間の構築
prediction_intervals = [
(pred - aggregated_q, pred + aggregated_q) for pred in aggregated_test_preds
]
print("Aggregated Quantile (q):", aggregated_q)
print("\n予測区間 (最初の10件):")
for i, interval in enumerate(prediction_intervals[:10]):
print(f"Test sample {i}: {interval}")
以下、実行結果です。
Aggregated Quantile (q): 0.779191740000001 予測区間 (最初の10件): Test sample 0: (-0.26776374000000125, 1.2906197400000008) Test sample 1: (-0.002095740000001123, 1.556287740000001) Test sample 2: (4.047330479999993, 5.605713959999995) Test sample 3: (1.7835862599999983, 3.3419697400000006) Test sample 4: (1.57236226, 3.130745740000002) Test sample 5: (0.9469322599999994, 2.5053157400000012) Test sample 6: (1.6123542599999985, 3.1707377400000007) Test sample 7: (0.8767722599999992, 2.4351557400000012) Test sample 8: (1.8812626599999989, 3.4396461400000007) Test sample 9: (4.070972339999989, 5.629355819999991)
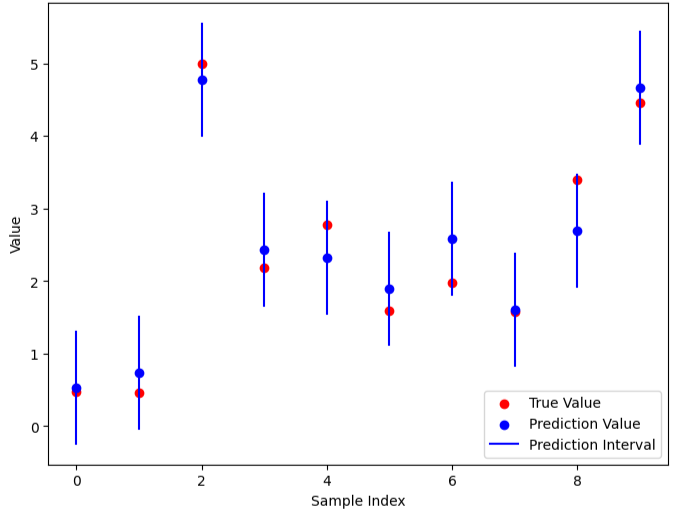
結果の評価
最後に、構築した予測区間がテストサンプルの真の値をどの程度カバーしているかを評価します。
各テストサンプルごとに予測区間内に真の値が含まれているかをチェックし、全体のカバー率と予測区間の平均幅を算出します。
以下、コードです。
# テストサンプルに対して、真の値が予測区間に含まれるかを確認し、カバー率と平均区間幅を算出
coverage_count = 0
interval_widths = []
for i, (lower, upper) in enumerate(prediction_intervals):
interval_widths.append(upper - lower)
if lower <= y_test[i] <= upper:
coverage_count += 1
coverage = coverage_count / len(y_test)
avg_interval_width = np.mean(interval_widths)
print(f"\nCoverage (真の値が区間に含まれる割合): {coverage:.2f}")
print(f"Average Interval Width (平均予測区間幅): {avg_interval_width:.2f}")
以下、実行結果です。
Coverage (真の値が区間に含まれる割合): 0.90 Average Interval Width (平均予測区間幅): 1.56
Python実装例:分類タスク
Irisデータセットを用いた分類タスクにおいて、従来のICPから発展したCross-Conformal Prediction (CCP) の手法を実装例として紹介します。
今回説明するCCPでは、訓練データ全体をK-foldに分割し、各フォールドごとにモデルを学習し、キャリブレーション用セットから各フォールドごとに非適合度(ここでは「1 − 正解クラスの予測確率」)を算出して分位点を求めます。
さらに、各フォールドの結果を統合することで、安定した予測集合(Prediction Set)を構築します。
データセットの準備
まず、Irisデータセットを読み込み、全体のデータを訓練セットとテストセットに分割します。
以下、コードです。
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Irisデータセットの読み込み
data = load_iris()
X = data.data
y = data.target
# 全体のデータセットを訓練用セットとテストセットに分割(テスト20%)
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
test_size=0.2,
random_state=42
)
print("訓練データのサイズ")
print("X_train:", X_train.shape)
print("y_train:", y_train.shape)
print("\nテストデータのサイズ")
print("X_test:", X_test.shape)
print("y_test:", y_test.shape)
以下、実行結果です。
訓練データのサイズ X_train: (120, 4) y_train: (120,) テストデータのサイズ X_test: (30, 4) y_test: (30,)
CCPによる各フォールドでの学習とキャリブレーション
ここでは、K-Fold分割(例:K=5)を用いて、各フォールドで次の処理を行います。
- フォールドごとに訓練用セットとキャリブレーション用セットに分割
- RandomForestRegressorを用いてモデルを学習
- キャリブレーション用セットに対して予測を行い、非適合度(絶対誤差)を計算
- (1 – α)分位点を算出
以下、コードです。
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import KFold
# CCPのK-fold分割の設定
K = 5 # K-fold分割数
alpha = 0.1 # 有意水準 (α=0.1 → 90%予測区間)
kf = KFold(
n_splits=K,
shuffle=True,
random_state=42
)
# 各フォールドでのテストサンプルに対する予測確率 (shape: (n_test, n_classes))を保存するリスト
test_probs_folds = []
# 各フォールドでの分位点q(スカラー)を保存するリスト
quantiles_folds = []
for train_index, calib_index in kf.split(X_train):
# 各フォールドでの訓練用セットとキャリブレーション用セットに分割
X_train_fold, X_calib = X_train[train_index], X_train[calib_index]
y_train_fold, y_calib = y_train[train_index], y_train[calib_index]
# RandomForestClassifierの学習
model = RandomForestClassifier(random_state=42)
model.fit(X_train_fold, y_train_fold)
# キャリブレーション用セットに対して各サンプルのクラスごとの予測確率を計算
probs_calib = model.predict_proba(X_calib)
# 非適合度: 各サンプルの正解クラスに対する (1 - 予測確率)
calib_nonconformity = np.array([
1 - probs_calib[i, y_calib[i]] for i in range(len(y_calib))
])
# キャリブレーション用非適合度の(1 - alpha)分位点 q を算出
q_k = np.quantile(calib_nonconformity, 1 - alpha)
quantiles_folds.append(q_k)
# テストデータに対して各サンプルのクラスごとの予測確率を計算
probs_test = model.predict_proba(X_test)
test_probs_folds.append(probs_test)
# 各フォールドでの予測値を表示
print("各フォールドでのテストデータに対する予測値(最初の3件):")
for i in range(K):
print(f"フォールド {i+1} :\n", test_probs_folds[i][:3]) # Fixed by correcting the slicing syntax
# 各フォールドでの分位点を表示
print("各フォールドでの分位点:")
print(quantiles_folds)
以下、実行結果です。
各フォールドでのテストデータに対する予測値(最初の3件): フォールド 1 : [[0. 0.99 0.01] [0.99 0.01 0. ] [0. 0. 1. ]] フォールド 2 : [[0. 1. 0. ] [0.97 0.03 0. ] [0. 0. 1. ]] フォールド 3 : [[0. 1. 0. ] [0.98 0.02 0. ] [0. 0. 1. ]] フォールド 4 : [[0. 0.96 0.04] [1. 0. 0. ] [0. 0.05 0.95]] フォールド 5 : [[0. 0.99 0.01] [0.95 0.05 0. ] [0. 0. 1. ]] 各フォールドでの分位点: [0.13899999999999996, 0.09999999999999994, 0.15899999999999986, 0.61, 0.08899999999999995]
予測集合の構築
各フォールドで得られたテストデータの予測確率と分位点を統合します。
ここでは、各フォールドの予測確率を平均し、分位点も平均して統合した値を用います。
- 統合予測確率: 各フォールドの予測確率の平均
- 統合分位点: 各フォールドの分位点
の平均 - 予測集合の構築: 各テストサンプルに対し、各クラスに対する非適合度は
として、統合された分位点 以下となるクラスを予測集合に採用します。
以下、コードです。
# 各フォールドの予測確率を平均して統合
test_probs_folds = np.array(test_probs_folds) # shape: (K, n_test, n_classes)
aggregated_probs = np.mean(test_probs_folds, axis=0) # shape: (n_test, n_classes)
# 各フォールドの分位点の平均を算出
aggregated_q = np.mean(quantiles_folds)
# 各テストサンプルに対する予測集合を構築
prediction_sets = []
for i, probs in enumerate(aggregated_probs):
# 各クラスの非適合度は 1 - そのクラスの予測確率
nc_scores = 1 - probs
# 非適合度が統合分位点 aggregated_q 以下のクラスを予測集合に採用
pred_set = np.where(nc_scores <= aggregated_q)[0]
prediction_sets.append(pred_set)
print("Aggregated Quantile (q):", aggregated_q)
print("予測集合 (Prediction Sets):")
for i, ps in enumerate(prediction_sets):
print(f"Test sample {i}: {ps}")
以下、実行結果です。
Aggregated Quantile (q): 0.21939999999999996 予測集合 (Prediction Sets): Test sample 0: [1] Test sample 1: [0] Test sample 2: [2] Test sample 3: [1] Test sample 4: [1] Test sample 5: [0] Test sample 6: [1] Test sample 7: [2] Test sample 8: [1] Test sample 9: [1] Test sample 10: [2] Test sample 11: [0] Test sample 12: [0] Test sample 13: [0] Test sample 14: [0] Test sample 15: [1] Test sample 16: [2] Test sample 17: [1] Test sample 18: [1] Test sample 19: [2] Test sample 20: [0] Test sample 21: [2] Test sample 22: [0] Test sample 23: [2] Test sample 24: [2] Test sample 25: [2] Test sample 26: [2] Test sample 27: [2] Test sample 28: [0]
結果の評価
最後に、構築した予測集合がテストサンプルの真のクラスをどの程度カバーしているか、また予測集合の平均サイズを評価します。
以下、コードです。
# 予測集合に真のクラスが含まれているかを確認し、カバー率と平均集合サイズを算出
correct = 0
set_sizes = []
for i, pred_set in enumerate(prediction_sets):
set_sizes.append(len(pred_set))
if y_test[i] in pred_set:
correct += 1
coverage = correct / len(y_test)
avg_set_size = np.mean(set_sizes)
print(f"\nCoverage (真のクラスが含まれる割合): {coverage:.2f}")
print(f"Average Prediction Set Size (予測集合の平均サイズ): {avg_set_size:.2f}")
以下、実行結果です。
Coverage (真のクラスが含まれる割合): 1.00 Average Prediction Set Size (予測集合の平均サイズ): 1.00
発展的トピック
Conformal Predictionの最新動向
Conformalized Quantile Regression (CQR)
近年注目を集めているのが、Conformalized Quantile Regression (CQR) という手法です。
従来のConformal Predictionフレームワークに分位点回帰(Quantile Regression)を組み合わせ、予測区間の幅をより効率的に制御します。
分位点回帰によって推定した下限・上限を、Conformal Predictionのキャリブレーション手続きを用いて統計的に妥当な(高カバレッジ率を持つ)予測帯(区間や集合など)を保証するイメージです。
Online Conformal Prediction / Adaptive Conformal Inference
従来のConformal Predictionは、静的なデータセットを想定する場合が多くありました。しかし、近年は以下のような枠組みも研究されています。
Online Conformal Predictionとは、ストリーミングデータやリアルタイムで到着するデータに対して、逐次的に予測区間を更新する手法です。
Adaptive Conformal Inferenceとは、データ分布が時間とともに変化する(概念漂移が起きる)状況で、適応的に予測区間を修正する手法です。
他タスクへの拡張とハイブリッドアプローチ
当初は回帰や分類タスクが中心でしたが、異常検知、テキスト生成、画像認識などへの応用事例も増えています。
次のように他の不確実性推定手法と組み合わせるハイブリッドアプローチも提案されています。
- ベイズ推論との統合
- ブートストラップとの組み合わせ
- その他アンサンブル学習との併用
これらを活用することで、予測のばらつきをさらに低減し、精度を高めることが可能になります。
時系列データへの応用
時系列データは、各サンプルが相互に依存しているため、独立同分布(i.i.d.)を仮定する従来のConformal Predictionをそのまま適用するのは難しい場合があります。
そこで、Time Series Conformal Prediction と呼ばれる手法群が開発され、次のような観点で研究が進められています。
時系列特有の非適合度(Nonconformity Measure)の工夫
回帰や分類タスクでは残差や予測確率を用いることが一般的ですが、時系列には以下のような特徴的なパターンが見られることが多いです。
- 自己回帰構造:過去の値が将来の値に影響を与える
- 季節性:一定周期でデータが似た動きを繰り返す
- トレンド:長期的に増加や減少傾向を示す
これらを考慮した非適合度を設計することで、より信頼度の高い予測区間を導くことができます。
クロス検証とローリングウィンドウ
Conformal Predictionの基本手順であるICP(Inductive Conformal Prediction)やCCP(Cross-Conformal Prediction)は、i.i.d.を前提としたランダム分割を行う仕組みになっています。
時系列データでは、この前提が成り立たないため工夫が必要です。
スライディングウィンドウ方式
訓練期間とキャリブレーション期間の長さを固定しながら、ウィンドウ全体をスライドしていくアプローチです。
たとえば、ウィンドウサイズを36、テスト区間を12に設定すると、1回目はインデックス 0〜35 を訓練に使い、36〜47 をテストに。次はインデックス 1〜36 を訓練に使い、37〜48 をテストに…… という形で進行します。
常に最新の一定量のデータで訓練するため、時間が進むにつれて古いデータを切り捨てたい場合に有効です。
ただし、古いデータを全く使わないため、長期的な履歴を反映しづらくなる場合があります。
ローリングウインドウ方式(もしくはウォークフォワード方式)
最初の訓練区間を固定した状態で、キャリブレーション区間を順次前にずらしていくアプローチです。
たとえば、初期訓練期間を36に設定し、キャリブレーション区間を12にすると、1回目はインデックス 0〜35 を訓練に使い、36〜47 をテストに。次は 0〜36 を訓練に使い、37〜48 をテストに…… といった形で進んでいきます。
訓練データが少しずつ拡大するため、より多くの履歴を活用しながら最新のデータに追随できます。
ただし、ウィンドウサイズを固定したい場合はあまり向いていません。また、訓練データがどんどん増えるため、計算コストが高くなるケースもあります。
マルチステップ予測への拡張
多ステップ先予測では、将来をさらに先まで見通そうとするため、一般に予測区間が徐々に広がる傾向にあります。
ステップごとに独立したキャリブレーション
1ステップ先、2ステップ先、といった予測ごとに非適合度(Nonconformity Measure)を再計算し、その都度予測区間をキャリブレーションします。
マルチステップ対応のConformal Prediction
多ステップ先予測を一括でモデル化したうえで、Conformal Predictionを適用する設計も提案されています。
まとめ
今回は、Inductive Conformal Prediction (ICP)の基礎を踏まえたうえで、Cross-Conformal Prediction (CCP)の理論やPython実装例を紹介しました。
Inductive Conformal Prediction (ICP)については、以下を参考にしてください。
CCPはK-fold分割による複数のキャリブレーション結果を統合することで、単一のキャリブレーションセットに依存するICPのばらつきを低減し、より安定した予測信頼度を提供します。
さらに、Quantile Regressionを組み合わせたCQRなど、近年の研究では多様な拡張が進められており、時系列データやオンライン学習などの分野でも実用が広がっています。
予測性能だけでなく、その不確実性を定量的に評価するための強力なフレームワークとして、Conformal Predictionは今後もさまざまな分野で活躍が期待されるでしょう。