Conformal Prediction とは、特定のモデルに依存せず、あらゆる機械学習モデルに対して予測区間を提供する手法です。

従来の統計モデル（例：線形回帰モデル）では、ある程度の確率分布（多くの場合は正規分布など）を仮定することで予測区間を求めることが可能でした。

しかし、非線形かつ複雑な機械学習モデルでは、そのような分布仮定が成立しにくいため、従来の手法だけでは十分な予測区間の算出が困難でした。

そこで登場するのが Conformal Prediction です。詳細については、以下の参考文献をご覧ください。

一方で、現状の多くの Conformal Prediction アルゴリズムは、時系列データに対応していないという課題があります。

時系列データに対応した Conformal Prediction の研究も、この10年間で盛んに進められてきました。

今回は、時系列データにおける再帰的マルチステップ予測（つまり、1つの予測モデルで複数先まで予測する手法）を例に、Cross-Conformal Prediction（CCP）の手法を発展させたアプローチにより、将来予測の予測区間を算出する例を紹介します。

紹介するアプローチは、複雑なアルゴリズムではなく、極めてシンプルで直感的な実装方法を採用している点が特徴です。

従来のCPと時系列データでの壁

　Conformal Prediction（CP）とは

従来の統計モデル、たとえば線形回帰やガウス過程といった手法では、あらかじめ誤差分布（多くの場合、正規分布など）の仮定に基づいて予測区間を求めることが可能でした。

しかし、機械学習モデルはその柔軟性や非線形性により、明確な分布仮定を置くことが難しく、直接的に予測区間を算出する手法が確立されていませんでした。

そこで登場するのがConformal Predictionです。

CPは、モデルに依存しない分布フリーの枠組みを提供することで、ブラックボックスな機械学習モデルに対しても、キャリブレーションデータから計算された非適合性スコアを活用し、予測区間を構築することを可能にします。

これにより、従来の統計モデルでのみ実現できた予測区間の計算を、機械学習モデルにも拡張できるという大きな革新が実現されました。

　ICPとCCPの簡単な復習

CPには色々ありますが、ベーシックなものとして、Inductive Conformal Prediction（ICP） と Cross-Conformal Prediction（CCP） の2種類があります。

　　ICP（Inductive Conformal Prediction）

ICPでは、学習データを「訓練用データ」と「キャリブレーション用データ」に分割します。

まず、訓練用データを用いてモデルを学習し、次にキャリブレーション用データを使って非適合性スコアを計算します。

新たなサンプルに対しては、この非適合性スコアの分布に基づいて予測区間を導出します。

計算効率が高くシンプルな実装が可能な一方で、キャリブレーションデータに用いるデータ量が少なくなるというデメリットがあります。

詳細を知りたい方は、以下です。

機械学習モデルの予測区間を求めるInductive Conformal PredictionをPythonで実装してみよう

　　CCP（Cross-Conformal Prediction）

CCPは、クロスバリデーションの枠組みを用いることで、学習データ全体を複数の分割で再利用しながら非適合性スコアを計算します。

各分割で得られたスコアを統合することで、より安定した予測区間が得られるようになります。

ただし、分割間の依存関係の扱いには、理論的な検証や実務上の工夫が求められる場合もあります。

詳細を知りたい方は、以下です。

より安定した機械学習モデルの予測区間を求めるcross-conformal-predictionをPythonで実施してみよう

　時系列予測特有の課題とCPが有効な理由

時系列データは、前後の観測値が強く依存するため、独立同分布（i.i.d.）を前提とした従来のCPの枠組みでは十分な保証が得られない場合があります。

時系列予測特有の課題としては、以下の点が挙げられます。

時間依存性と自己相関
時系列データは、隣接するデータ間に強い依存性が存在するため、各サンプルが独立していないという性質を持ちます。これにより、従来のCP手法が前提とする独立性が破られ、予測区間の保証に影響を及ぼす可能性があります。

再帰的マルチステップ予測における誤差伝播
時系列予測では、1ステップ先の予測結果を次の入力として再利用する再帰的な手法が一般的です。このため、予測誤差が次のステップに伝播し、予測区間が次第に広がってしまうリスクがあります。

非定常性（トレンドや季節性）の存在
実世界の時系列データは、トレンドや季節性、突発的な変動などの非定常な性質を持つことが多く、モデルの学習や予測区間の構築において、追加の工夫が求められます。

これらの課題に対して、CPは分布に依存しない予測区間の構築手法を提供するため、たとえモデルがブラックボックスであっても、キャリブレーションデータから得られる非適合性スコアを活用して、現実的な不確実性の評価が可能となります。

特に、再帰的マルチステップ予測においては、各ステップごとのエラーを丁寧に捉え、適切な予測区間を調整することができるため、従来の統計モデルでは難しかった複雑な時系列データの予測に対しても有効なアプローチとなります。

CPの時系列データへの応用

　再帰的マルチステップ予測の数式的アプローチ

時系列予測においては、1ステップ先予測モデル $f$ を用いて、次のように再帰的に未来の値を予測します。

まず、1ステップ先の予測は……

$${\hat{y}}_{t+1}=f({\mathbf{x}}_{t+1})$$

……となります。

ここで、$\mathbf{x}_{t+1}$ は、時刻 $t+1$ における特徴量ベクトル（説明変数）であり、通常は過去の実測値や場合によっては外生変数などが含まれます。

再帰的マルチステップ予測では、この1ステップ先の予測結果を次の入力に反映させ、次のように $H$ ステップ先まで予測を行います。

$${\hat{y}}_{t+h}=f({\mathbf{x}}_{t+h}({\hat{y}}_{t+1},{\hat{y}}_{t+2},\dots ,{\hat{y}}_{t+h-1})),h=1,2,\dots ,H$$

このように、再帰的予測では既に予測された値が特徴量に組み込まれるため、予測誤差が次の予測に伝播するリスクが存在します。

これが、マルチステップ予測で予測区間が拡大する主な理由の一つです。

　キャリブレーションデータを用いた予測区間幅の推定

再帰的マルチステップ予測における各ステップ $h$ での不確実性を評価するため、時系列クロスバリデーションで利用する分割手法を用いて、複数の分割におけるキャリブレーションデータ上の予測誤差を収集します。

各分割 $i$ における $h$ ステップ先の予測誤差は、以下のように定義されます。

$$e_{i,h}=y_{t+h}–{\hat{y}}_{t+h}$$

ここで $y_{t+h}$ は実際の観測値、$\hat{y}_{t+h}$ は予測値です。

この誤差 $e_{i,h}$ の絶対値 $|e_{i,h}|$ を各分割から集計し、全体の ($1-\alpha$) 分位点として、予測区間の幅 $\Delta_h$ を算出します。

$${\mathrm{\Delta }}_h=Q_{1-\alpha }(\{|e_{i,h}|\mid i=1,2,\dots ,K\})$$

ここで $K$ はクロスバリデーションでの分割数、$Q_{1-\alpha}$ は ($1-\alpha$) 分位数（たとえば $\alpha=0.05$ の場合は95パーセンタイル）を示します。

得られた $\Delta_h$ を用いれば、各ステップの最終的な予測区間は以下のように構築されます。

$$[{\hat{y}}_{t+h}–{\mathrm{\Delta }}_h,{\hat{y}}_{t+h}+{\mathrm{\Delta }}_h]$$

このアプローチにより、再帰的な予測過程でのエラー伝播を数値的に補正し、各ステップで現実的な予測区間を算出することが可能となります。

　アルゴリズムの全体像

アルゴリズムのフローとして整理すると以下のようになります。

STEP １：データ準備

• 時系列データ $y$ と、必要に応じた外生変数 $X$ を用意。
• 各時刻 $t$ に対して、ラグ特徴量や外生変数を組み合わせた特徴量ベクトル $\mathbf{x}_t$ を生成。

STEP ２：時系列データ分割

• 時系列クロスバリデーションの分割アプローチを用いて、複数の訓練データとキャリブレーションデータの組み合わせを生成。

STEP ３：1ステップ先予測モデルの学習と再帰的予測

• 各分割で、1ステップ先予測モデル $f$ を学習する。
• キャリブレーションデータに対して、再帰的に $H$ ステップ先の予測を行い、各ステップごとの予測誤差 $e_{i,h}$ を記録する。

STEP ４：予測区間幅の推定

• 各ステップ $h$ において、キャリブレーションデータ上の誤差の絶対値の ($1-\alpha$) 分位数 $\Delta_h$ を計算する。

STEP ５：最終予測と予測区間の構築

• 学習済みモデルを用いて、テストデータに対する再帰的な予測を行う。
• 各予測 $\hat{y}_{t+h}$ に対し、$\Delta_h$ を用いて$\left[\hat{y}_{t+h} - \Delta_h,\, \hat{y}_{t+h} + \Delta_h\right]$ という形で予測区間を構築する。

この数式とアルゴリズムの流れにより、従来の統計モデルで容易に実現されていた予測区間の算出を、機械学習モデルに対しても分布フリーな方法で実装することが可能となります。

また、時系列データに特有のエラー伝播問題にも対応できるため、実務上の予測リスクをより現実的に管理できる点が大きな強みとなります。

Pythonによる実装概要

　時系列CP関数と補助関数

　　時系列CP関数 ccp_recursive_multi_step_general

最も重要な役割を担う関数が ccp_recursive_multi_step_general です。

時系列クロスバリデーションのデータ分割アプローチで複数の訓練データとキャリブレーションデータを生成し、訓練データでモデル構築しキャリブレーションデータ上で再帰的なマルチステップ予測を実施して予測誤差を収集します。

その誤差の絶対値から (1−α) 分位点を算出し、各ステップの予測区間幅を求めるという、時系列CPの中心的アルゴリズムを担います。

from typing import Optional, Tuple, Iterator

# 再帰的マルチステップ予測と誤差計算を行う関数
def ccp_recursive_multi_step_general(
    y: np.ndarray,  # 目的変数の時系列データ (1次元配列)
    X: Optional[np.ndarray],  # 外生変数 (2次元配列または None)
    cv_splits: Iterator[Tuple[np.ndarray, np.ndarray]],  # クロスバリデーションの分割情報 (学習・テストインデックス)
    H: int = 3,          # 何ステップ先まで予測するか (h=1..H)
    alpha: float = 0.1,  # 予測区間の計算における信頼レベル (0.0-1.0)
    use_lags: bool = True,  # yのラグ特徴量を使用するか
    max_lag: int = 2,  # ラグ特徴量として使用する最大サイズ
    use_exog: bool = True,  # 外生変数を使用するか
    model_class = LinearRegression,  # 学習モデルのクラス (デフォルトは線形回帰)
    **model_kwargs  # モデルに渡す追加のパラメータ
):
    """
    再帰的マルチステップ予測と複数分割学習 (CCP) を用いて誤差分布を推定する。
    各先行ステップごとに予測区間幅を算出する。
    
    戻り値:
    width_h: 各ステップhについての(1-alpha)予測区間幅リスト
    residuals_h: 誤差の履歴を各ステップについて記録したリストのリスト
    """

    # 各予測ステップについての残差リストを初期化
    residuals_h = [[] for _ in range(H)]

    # 各分割 (学習・テストセット)について処理を行う
    for (train_idx, test_idx) in cv_splits:
        if len(train_idx) == 0 or len(test_idx) == 0:
            continue  # データ分割が空の場合はスキップ

        train_start, train_end = train_idx[0], train_idx[-1]  # 学習データ範囲
        cal_start, cal_end = test_idx[0], test_idx[-1]  # テストデータ範囲

        # 学習データセット (X, y) を構築
        X_train, y_train = make_train_xy(y, X, train_idx, use_lags, max_lag, use_exog)

        # 回帰モデルを初期化して学習
        model = model_class(**model_kwargs)
        if len(X_train) > 0:
            model.fit(X_train, y_train)  # モデルを学習
        else:
            continue  # 学習データがない場合はスキップ

        # 校正期間で再帰的な予測を実施し、誤差を記録
        y_known = y.copy()  # 更新可能な既知のデータを初期化

        # 各予測ステップ h=1..H について処理
        for t in range(cal_start, cal_end + 1):
            for h in range(1, H + 1):
                future_t = t + h
                if future_t >= len(y):
                    break  # データ範囲を超えた場合
                try:
                    fv = build_feature_vector(
                        future_t, y_known, X,
                        use_lags, max_lag, use_exog
                    )  # 特徴量を生成
                except IndexError:
                    break  # ラグ不足でエラーが発生した場合も終了

                y_hat = model.predict(fv)[0]  # 予測値を算出
                e = y[future_t] - y_hat  # 誤差 = 真の値 - 予測値
                residuals_h[h - 1].append(e)  # hステップ目の残差を記録

                y_known[future_t] = y_hat  # 再帰的予測用にy_knownを更新

    # 予測区間幅を計算してリストに格納
    width_h = []
    for h in range(1, H + 1):
        abs_res = np.abs(residuals_h[h - 1])  # 残差の絶対値を取得
        if len(abs_res) == 0:
            width_h.append(0.0)  # 残差がない場合は幅0に設定
        else:
            q = np.quantile(abs_res, 1 - alpha)  # 与えられた信頼水準から分位点を計算
            width_h.append(q)

    # 予測区間幅と残差リストを返す
    return width_h, residuals_h

　　補助関数 build_feature_vector と make_train_xy

build_feature_vector と make_train_xy は、時系列モデルが必要とする特徴量や学習用データを整形するための補助的な関数です。

• build_feature_vector：指定時点 $t$ のラグ特徴量および外生変数（必要に応じて）をまとめ、 $t$ 時点の特徴量を生成します
• make_train_xy：与えられた時間範囲（連続した複数時点）に対しbuild_feature_vector を用い特徴量行列 $X$ を作成、同じ範囲の目的変数 $y$ を取り出し、 $X$ と $y$ のセット作ります

マルチステップ予測では、常に特徴量を作り直す必要があるため、このような補助関数が必要になりますし、作っておいた方が楽です。

from typing import Optional, Tuple, Iterator

# 指定された時刻 t の特徴量ベクトルを構築する関数
def build_feature_vector(
    t: int,  # 現在の時刻インデックス (整数値)
    y_array: np.ndarray,  # 目的変数の時系列データ (1次元配列)
    X_array: Optional[np.ndarray],  # 外生変数 (2次元配列または None)
    use_lags: bool,  # ラグ特徴量を使用するか (True/False)
    max_lag: int,  # 最大のラグサイズ (整数値)
    use_exog: bool  # 外生変数データを使用するか (True/False)
) -> np.ndarray:
    """ 指定の時間点の特徴量ベクトル配列を生成する """
    feats = []

    # 1) y のラグ特徴量を追加
    if use_lags and max_lag > 0:
        for lag in range(1, max_lag + 1):
            feats.append(y_array[t - lag])  # ラグされた値を特徴量に追加

    # 2) 外生変数 X を追加
    if use_exog and (X_array is not None):
        feats.extend(X_array[t].tolist())  # 外生変数を特徴量として追加

    return np.array(feats, dtype=float).reshape(1, -1)  # 1行に整形して返す

# 学習データセット(X, y)を構築する関数
def make_train_xy(
    y_array: np.ndarray,  # 目的変数データ (1次元配列)
    X_array: Optional[np.ndarray],  # 外生変数データ (2次元配列または None)
    idx_array: np.ndarray,  # 学習データのインデックス配列 (1次元配列)
    use_lags: bool,  # yのラグ特徴量を使用するか (True/False)
    max_lag: int,  # 最大ラグサイズ
    use_exog: bool  # 外生変数を使用するか (True/False)
):
    """
    指定インデックス範囲に基づき、特徴量行列 X と目的変数ベクトル y を生成する。
    """
    if len(idx_array) == 0:
        return np.empty((0, 0)), np.empty((0,))  # 空のデータを返す

    start_t, end_t = idx_array[0], idx_array[-1]  # インデックスの始点と終点

    # 特徴量データとターゲット変数データを保持するリストを初期化
    X_list, y_list = [], []

    # ラグが必要な場合は開始インデックスを調整
    offset = max_lag if use_lags else 0

    for t in range(start_t + offset, end_t + 1):
        fv = build_feature_vector(
            t, y_array, X_array,
            use_lags, max_lag, use_exog
        )  # 特徴量を生成

        X_list.append(fv.ravel())  # 特徴量ベクトルをリストに追加
        y_list.append(y_array[t])  # 対応するy値をリストに追加

    if len(X_list) == 0:
        return np.empty((0, 0)), np.empty((0,))  # 空データを返す

    # リストを配列に変換して返す
    X_mat = np.array(X_list)
    y_vec = np.array(y_list)
    return X_mat, y_vec

　RollingForecastCV と SlidingWindowForecastCV

時系列データでは、一般的なランダム分割のクロスバリデーションとは異なる方法が必要です。ここでは、Pythonの時系列分析ライブラリpmdarimaで提供される2種類の時系列クロスバリデーションを紹介します。

この2つのアプローチを知りたい方は、以下を参考にしてください。

時系列データのホールドアウト法とクロスバリデーション

この2つの時系列クロスバリデーション手法を使い複数の訓練データとキャリブレーションデータの組み合わせを生成し、時系列のCPを実施します。

　　RollingForecastCV

ローリングウインドウ方式（もしくはウォークフォワード方式）と呼ばれ、最初の学習区間を固定した状態で、テスト区間を順次前にずらしていくアプローチです。

たとえば、初期学習期間を36に設定し、テスト区間を12にすると、1回目はインデックス 0〜35 を学習に使い、36〜47 をテストに。次は 0〜36 を学習に使い、37〜48 をテストに……　といった形で進んでいきます。

学習データが少しずつ拡大するため、より多くの履歴を活用しながら最新のデータに追随できます。

ただし、ウィンドウサイズを固定したい場合はあまり向いていません。また、学習データがどんどん増えるため、計算コストが高くなるケースもあります。

　　SlidingWindowForecastCV

スライディングウィンドウ方式と呼ばれ、学習期間とテスト期間の長さを固定しながら、ウィンドウ全体をスライドしていくアプローチです。

たとえば、ウィンドウサイズを36、テスト区間を12に設定すると、1回目はインデックス 0〜35 を学習に使い、36〜47 をテストに。次はインデックス 1〜36 を学習に使い、37〜48 をテストに……　という形で進行します。

常に最新の一定量のデータで学習するため、時間が進むにつれて古いデータを切り捨てたい場合に有効です。

ただし、古いデータを全く使わないため、長期的な履歴を反映しづらくなる場合があります。

　　ccp_recursive_multi_step_general との連携

ccp_recursive_multi_step_general では、これらの時系列クロスバリデーションから返される (train_idx, test_idx) の組を用いて訓練・キャリブレーションを行います。

• 訓練データ：train_idx に基づいて make_train_xy で特徴量とターゲットを生成し、モデルを学習する。
• キャリブレーションデータ：test_idx を再帰的に予測し、残差を収集する。

どちらのCV手法を選ぶかは、取り扱う時系列の性質や実務上の要件次第です。

実装例とデモ

ここまで解説した理論とコード構造を踏まえ、実際の時系列データに対してConformal Prediction（CP）を適用する手順をデモンストレーションします。

ここでは、RollingForecastCV と SlidingWindowForecastCV の2種類の時系列クロスバリデーション手法を使った実装例を順に紹介します。

最初はサンプルとして生成した合成データを用い、その後に有名な時系列データセット（AirPassengers）での例を示します。

　合成データでの実装（RollingForecastCV を利用）

まずは、乱数を用い目的変数yと外生変数Xを2つによるデータセットを生成をします。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt
from pmdarima.model_selection import train_test_split
from pmdarima.model_selection import RollingForecastCV
from sklearn.linear_model import LinearRegression

# シードを指定して再現性を確保
np.random.seed(0)

# データ生成: サンプル数と時系列データを作成
N = 150
# 時系列の時間データ
time = np.arange(N)
# サイン波とランダムノイズを足した目的変数データ (y)
y = np.sin(0.2 * time) + 0.3 * np.random.randn(N)+10

# 仮の外部変数の生成 (例: 2つの次元を持つ)
X = np.column_stack([
    # cos波による1つ目の外生変数
    np.cos(0.1 * time),
    # 正規分布に基づく2つ目の外生変数
    0.5 * np.random.randn(N)
])

# プロット
fig, ax = plt.subplots(3, 1, figsize=(10, 6), sharex=True, sharey=True)

# 各プロットを別々のサブプロットに描画
ax[0].plot(time, y, label='Target Variable (y)', color='blue')
ax[0].set_title('Target Variable (y)')
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Values')
ax[0].grid(True)

ax[1].plot(time, X[:, 0], label='Exogenous Variable 1 (X1)', color='orange')
ax[1].set_title('Exogenous Variable 1 (X1)')
ax[1].set_xlabel('Time')
ax[1].grid(True)

ax[2].plot(time, X[:, 1], label='Exogenous Variable 2 (X2)', color='green')
ax[2].set_title('Exogenous Variable 2 (X2)')
ax[2].set_xlabel('Time')
ax[2].grid(True)

plt.tight_layout()
plt.show()

以下、実行結果です。

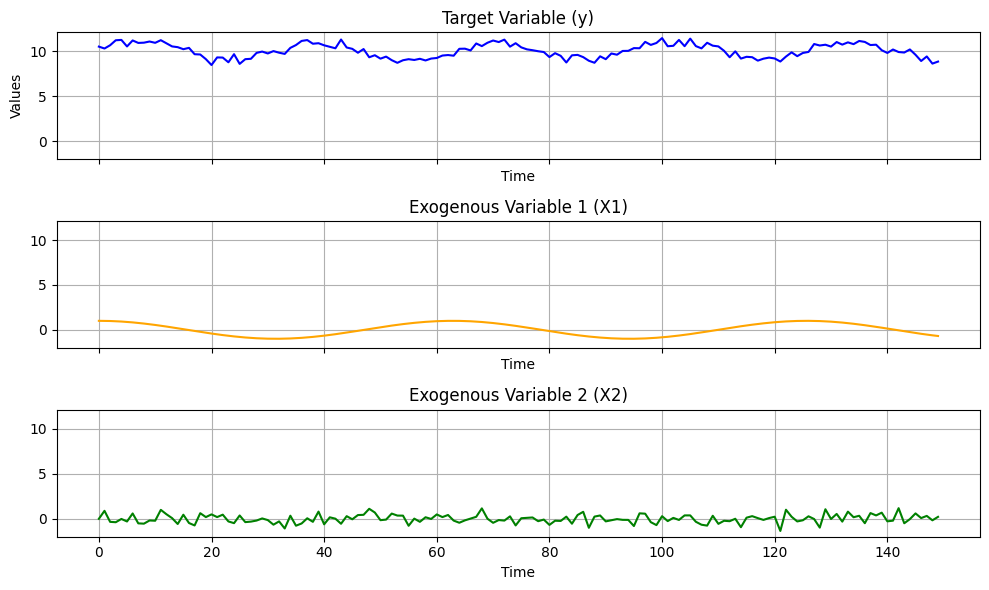
次に、学習データとテストデータに分割します。

以下、コードです。

# データ分割: 学習データとテストデータに分ける
y_train, y_test, X_train, X_test = train_test_split(y, X, test_size=12)

# 学習データとテストデータを区別してプロット
plt.figure(figsize=(10, 5))
plt.plot(range(len(y_train)), y_train, label="Train Data", marker="o")
plt.plot(range(len(y_train), len(y_train) + len(y_test)), y_test, label="Test Data", marker="o")
plt.xlabel("Time")
plt.ylabel("y values")
plt.title("Train and Test Split")
plt.legend()
plt.grid()
plt.show()

以下、実行結果です。

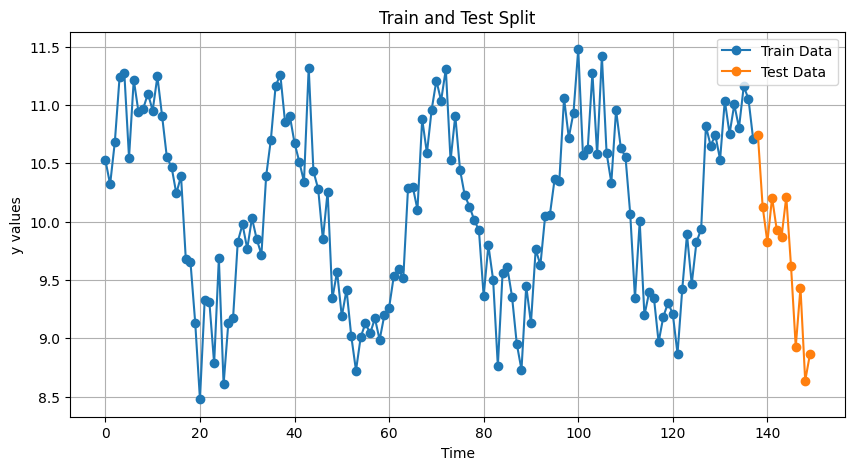
RollingForecastCVを用いCCPアルゴリズムを適用していきます。

以下、コードです。

# RollingForecastCVの設定
cv = RollingForecastCV(
    h=12,          # テスト区間の長さ (12データポイント)
    step=1,       # テスト期間をずらす間隔
    initial=36     # 最初の学習期間サイズ
)

# パラメータ設定
H = 12       # 最大予測ステップ
alpha = 0.05  # 予測区間の信頼レベル
use_lags = True  # ラグによる特徴量を使用する場合
max_lag = 12     # 最大のラグ数
use_exog = True  # 外部変数を使用するかを指定

# CCPアルゴリズムを使用して残差分布収集 => 分位点を求める
widths, residuals = ccp_recursive_multi_step_general(
    y=y_train,  # 訓練データ (ターゲット変数)
    X=X_train,  # 訓練データ (外生変数)
    cv_splits=cv.split(y_train),  # クロスバリデーション分割
    H=H,        # 最大予測ステップ
    alpha=alpha,  # 予測区間の信頼レベル
    use_lags=use_lags,  # yのラグ特徴量を使用
    max_lag=max_lag,  # 最大ラグサイズ
    use_exog=use_exog,  # 外生変数を使用
    model_class=LinearRegression  # 線形回帰モデルを使用
)

# 各ステップごとに予測区間の幅を出力
for step, width in enumerate(widths, start=1):
    print(f"{step} 先予測の予測区間の幅: {width}")

以下、実行結果です。

1 先予測の予測区間の幅: 1.135807781165176
2 先予測の予測区間の幅: 1.2666773803712696
3 先予測の予測区間の幅: 1.480940272833017
4 先予測の予測区間の幅: 1.708967798489653
5 先予測の予測区間の幅: 1.8365228171274444
6 先予測の予測区間の幅: 1.9199446239718032
7 先予測の予測区間の幅: 2.0071467763930877
8 先予測の予測区間の幅: 2.0843194231745352
9 先予測の予測区間の幅: 2.1110770668813172
10 先予測の予測区間の幅: 2.1061870717668105
11 先予測の予測区間の幅: 2.1025737708932284
12 先予測の予測区間の幅: 2.1029343943339476

キャリブレーションデータで推定した予測区間幅を用いて、テストデータ期間を再帰的に予測し、区間を付与します。

以下、コードです。

# 最終モデルのインスタンスを作成
final_model = LinearRegression()

# 学習データ全体用の特徴量行列とターゲット変数を作成
final_X_train, final_y_train = make_train_xy(
    y_array=y_train,  # 学習データのターゲット変数
    X_array=X_train,  # 学習データの外生変数
    idx_array=np.arange(len(y_train)),  # 学習データのインデックス
    use_lags=use_lags,  # ラグ特徴量を使用
    max_lag=max_lag,  # ラグサイズ
    use_exog=use_exog  # 外生変数を使用
)

# モデル学習
final_model.fit(final_X_train, final_y_train)

# テストデータ期間での予測結果を格納する配列を初期化
preds, lower_bounds, upper_bounds = [], [], []

# y_knownを既存の学習データとテストデータの予測値を結果的に保持する配列で初期化
y_known = np.concatenate([y_train, np.full(len(y) - len(y_train), np.nan)])
test_start_idx = len(y_train)  # テストデータの開始インデックス

# テストデータ期間の各時点で予測実行
for t in range(test_start_idx, test_start_idx + len(y_test)):
    # 特徴量生成: ラグと外生変数を考慮
    features = build_feature_vector(
        t=t,  # 現在の時点
        y_array=y_known,  # データ全体 (既知の情報)
        X_array=np.concatenate([X_train, X_test], axis=0),  # 訓練+テストデータ外生変数
        use_lags=use_lags,  # ラグを使用
        max_lag=max_lag,  # ラグの最大数
        use_exog=use_exog  # 外生変数を使用
    )

    # 予測値を計算
    pred = final_model.predict(features)[0]
    preds.append(pred)  # 各予測値をリストに追加

    # 予測区間の幅を取得
    step_idx = min(H - 1, t - test_start_idx)  # H以上のステップでは最大幅を使用
    interval_width = widths[step_idx]
    lower_bounds.append(pred - interval_width)  # 下限値を計算
    upper_bounds.append(pred + interval_width)  # 上限値を計算

    # 再帰的予測: y_knownに予測値を更新
    y_known[t] = pred

# 予測ごとに予測値と予測区間を出力
for i, (pred, lower, upper) in enumerate(zip(preds, lower_bounds, upper_bounds), 1):
    print(f"{i} 先予測: 予測値 = {pred}, 予測区間 = [{lower}, {upper}]")

以下、実行結果です。

1 先予測: 予測値 = 10.478600029174622, 予測区間 = [9.342792248009445, 11.614407810339799]
2 先予測: 予測値 = 10.438273405659718, 予測区間 = [9.171596025288448, 11.704950786030988]
3 先予測: 予測値 = 10.187589606674441, 予測区間 = [8.706649333841424, 11.668529879507458]
4 先予測: 予測値 = 10.18171838406449, 予測区間 = [8.472750585574838, 11.890686182554143]
5 先予測: 予測値 = 9.895632693089963, 予測区間 = [8.05910987596252, 11.732155510217407]
6 先予測: 予測値 = 9.820049662699724, 予測区間 = [7.90010503872792, 11.739994286671527]
7 先予測: 予測値 = 9.578547847318031, 予測区間 = [7.571401070924944, 11.585694623711118]
8 先予測: 予測値 = 9.434987088517602, 予測区間 = [7.3506676653430665, 11.519306511692136]
9 先予測: 予測値 = 9.295373977781338, 予測区間 = [7.184296910900021, 11.406451044662656]
10 先予測: 予測値 = 9.237972712276903, 予測区間 = [7.131785640510093, 11.344159784043715]
11 先予測: 予測値 = 9.212623231802363, 予測区間 = [7.110049460909135, 11.31519700269559]
12 先予測: 予測値 = 9.260176355436707, 予測区間 = [7.157241961102759, 11.363110749770655]

グラフ化します。

以下、コードです。

# 可視化
plt.figure(figsize=(12, 6))
# 元々の正解データをプロット
plt.plot(time, y, label="True values", color="black")
# テスト期間中の予測値をプロット
plt.plot(time[test_start_idx:], preds, label="Predictions", color="blue")
# 予測区間を描画
plt.fill_between(
    time[test_start_idx:],  # テストデータの時間範囲
    lower_bounds,  # 予測区間の下限
    upper_bounds,  # 予測区間の上限
    color="blue",
    alpha=0.2,  # 色の透明度
    label=f"{(1-alpha)*100:.1f}% Prediction Interval"
)
# ラベルとタイトルを追加
plt.legend()
plt.xlabel("Time")
plt.ylabel("Value")
plt.title("Forecast with Prediction Intervals")
plt.show()

以下、実行結果です。

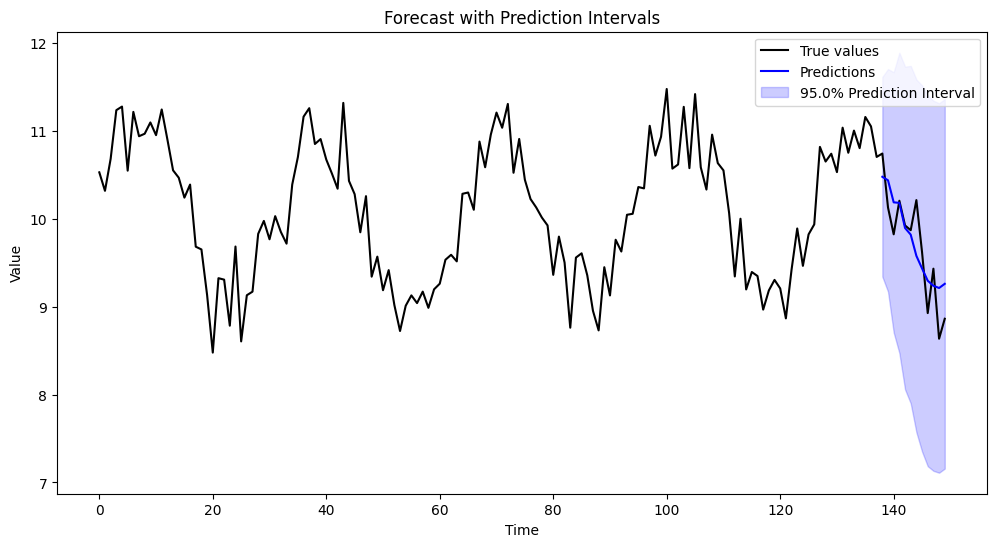
この結果、テストデータ期間での再帰的予測値（青線）と、その上限下限（青の塗りつぶし部分）が表示されます。

予測値がどの程度真の値（黒線）を捉えているか、さらに予測区間（不確実性）がどのように広がっているかを視覚的に確認できます。

　AirPassengers データでの実装（SlidingWindowForecastCV を利用）

続いて、SlidingWindowForecastCV を用いて、AirPassengers データに対して同様のアプローチを試します。

ウォークフォワード形式ではなく、一定サイズのウィンドウをスライドさせるスタイルでキャリブレーションデータを生成する点が異なります。

まずは、AirPassengers データの読み込みます。pmdarima に含まれる load_airpassengers 関数を使用します。そして読み込んだデータを、学習データとテストデータに分割します。

以下、コードです。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from pmdarima.datasets import load_airpassengers
from pmdarima.model_selection import train_test_split
from pmdarima.model_selection import SlidingWindowForecastCV

# AirPassengersデータの読み込み
data = load_airpassengers()
y = data  # 修正: data はすでに numpy 配列であるため、.values を使う必要がありません
N = len(y)  # 総データポイント数

# 時間データを生成
time = np.arange(N)

# データ分割: 学習データとテストデータに分ける
y_train, y_test = train_test_split(y, test_size=12)

# 学習データとテストデータを区別してプロット
plt.figure(figsize=(10, 5))
plt.plot(range(len(y_train)), y_train, label="Train Data", marker="o")
plt.plot(range(len(y_train), len(y_train) + len(y_test)), y_test, label="Test Data", marker="o")
plt.xlabel("Time")
plt.ylabel("y values")
plt.title("Train and Test Split")
plt.legend()
plt.grid()
plt.show()

以下、実行結果です。

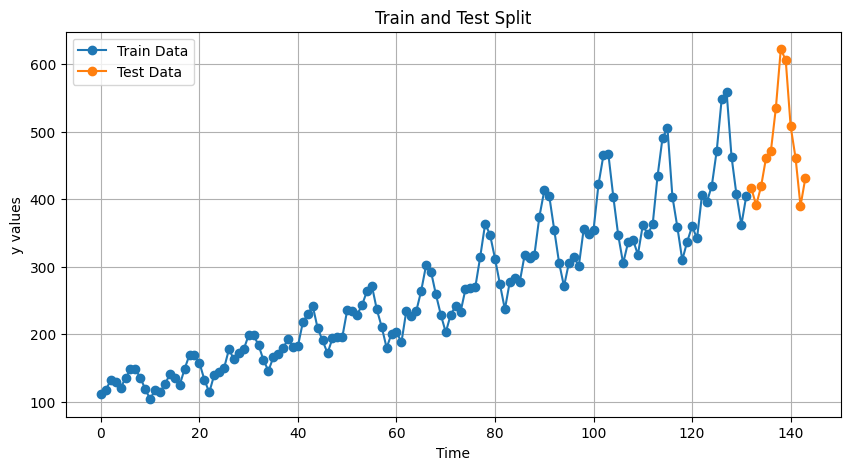
SlidingWindowForecastCVを用い、ここでCCPアルゴリズムを適用していきます。

AirPassengers には季節性が強く存在するため、現実的には季節特徴量などを組み込むほうが精度が高まりますが、ここでは単純な自己回帰（ラグのみ）を例にします。

以下、コードです。

# SlidingWindowForecastCVの設定
cv = SlidingWindowForecastCV(
    h=12,          # テスト区間の長さ (12データポイント)
    step=1,       # テスト期間をずらす間隔
    window_size=36 # スライディングウィンドウのサイズ
)

# パラメータ設定
H = 12       # 最大予測ステップ
alpha = 0.05  # 予測区間の信頼レベル
use_lags = True  # ラグによる特徴量を使用する場合
max_lag = 12     # 最大のラグ数
use_exog = False  # 外部変数は使用しない

# CCPアルゴリズムを使用して残差分布収集 => 分位点を求める
widths, residuals = ccp_recursive_multi_step_general(
    y=y_train,  # 訓練データ (ターゲット変数)
    X=None,  # 外生変数は使用しない
    cv_splits=cv.split(y_train),  # クロスバリデーション分割
    H=H,        # 最大予測ステップ
    alpha=alpha,  # 予測区間の信頼レベル
    use_lags=use_lags,  # yのラグ特徴量を使用
    max_lag=max_lag,  # 最大ラグサイズ
    use_exog=use_exog,  # 外生変数を使用しない
    model_class=LinearRegression  # 線形回帰モデルを使用
)

# 各ステップごとに予測区間の幅を出力
for step, width in enumerate(widths, start=1):
    print(f"{step} 先予測の予測区間の幅: {width}")

以下、実行結果です。

1 先予測の予測区間の幅: 66.69616612411609
2 先予測の予測区間の幅: 79.08456897463117
3 先予測の予測区間の幅: 93.55488288307745
4 先予測の予測区間の幅: 109.96479412941716
5 先予測の予測区間の幅: 124.9185735581347
6 先予測の予測区間の幅: 141.87432009057946
7 先予測の予測区間の幅: 159.126144585198
8 先予測の予測区間の幅: 182.69344639470745
9 先予測の予測区間の幅: 214.958374082699
10 先予測の予測区間の幅: 246.4246024180616
11 先予測の予測区間の幅: 275.53823309632173
12 先予測の予測区間の幅: 314.78383700288583

キャリブレーションデータで推定した予測区間幅を用いて、テストデータ期間を再帰的に予測し、区間を付与します。

以下、コードです。

# 最終モデルのインスタンスを作成
final_model = LinearRegression()

# 学習データ全体用の特徴量行列とターゲット変数を作成
final_X_train, final_y_train = make_train_xy(
    y_array=y_train,  # 訓練データのターゲット変数
    X_array=None,  # 外生変数は使用しない
    idx_array=np.arange(len(y_train)),  # 訓練データのインデックス
    use_lags=use_lags,  # ラグ特徴量を使用
    max_lag=max_lag,  # ラグサイズ
    use_exog=use_exog  # 外生変数を使用しない
)

# モデル学習
final_model.fit(final_X_train, final_y_train)

# テストデータ期間での予測 (予測区間を含む)
preds, lower_bounds, upper_bounds = [], [], []

# y_knownを既存の訓練データとテストデータの予測値を結果的に保持する配列で初期化
y_known = np.concatenate([y_train, np.full(len(y) - len(y_train), np.nan)])
test_start_idx = len(y_train)  # テストデータの開始インデックス

# テストデータ期間の各時点で予測実行
for t in range(test_start_idx, test_start_idx + len(y_test)):
    # 特徴量生成: ラグを考慮
    features = build_feature_vector(
        t=t,  # 現在の時点
        y_array=y_known,  # データ全体 (既知の情報)
        X_array=None,  # 外生変数は使用しない
        use_lags=use_lags,  # ラグを使用
        max_lag=max_lag,  # ラグの最大数
        use_exog=use_exog  # 外生変数を使用しない
    )

    # 予測値を計算
    pred = final_model.predict(features)[0]
    preds.append(pred)  # 各予測値をリストに追加

    # 予測区間の幅を取得
    step_idx = min(H - 1, t - test_start_idx)  # H以上のステップでは最大幅を使用
    interval_width = widths[step_idx]
    lower_bounds.append(pred - interval_width)  # 下限値を計算
    upper_bounds.append(pred + interval_width)  # 上限値を計算

    # 再帰的予測: y_knownに予測値を更新
    y_known[t] = pred

# 予測ごとに予測値と予測区間を出力
for i, (pred, lower, upper) in enumerate(zip(preds, lower_bounds, upper_bounds), 1):
    print(f"{i} 先予測: 予測値 = {pred}, 予測区間 = [{lower}, {upper}]")

以下、実行結果です。

1 先予測: 予測値 = 395.3439033078596, 予測区間 = [328.6477371837435, 462.04006943197567]
2 先予測: 予測値 = 380.99150121050303, 予測区間 = [301.90693223587186, 460.0760701851342]
3 先予測: 予測値 = 427.29287733323866, 予測区間 = [333.7379944501612, 520.8477602163161]
4 先予測: 予測値 = 426.4349610883223, 予測区間 = [316.47016695890517, 536.3997552177395]
5 先予測: 予測値 = 466.1151128966881, 予測区間 = [341.1965393385534, 591.0336864548228]
6 先予測: 予測値 = 512.094997423748, 予測区間 = [370.2206773331686, 653.9693175143275]
7 先予測: 予測値 = 597.5337510349831, 予測区間 = [438.4076064497851, 756.659895620181]
8 先予測: 予測値 = 607.1715539664405, 予測区間 = [424.478107571733, 789.8650003611478]
9 先予測: 予測値 = 526.982125209206, 予測区間 = [312.0237511265069, 741.940499291905]
10 先予測: 予測値 = 456.07902090975864, 予測区間 = [209.65441849169704, 702.5036233278203]
11 先予測: 予測値 = 404.1528372738321, 予測区間 = [128.6146041775104, 679.6910703701539]
12 先予測: 予測値 = 441.64429045645727, 予測区間 = [126.86045345357144, 756.4281274593432]

グラフ化します。

以下、コードです。

# 可視化
plt.figure(figsize=(12, 6))
# 元々の正解データをプロット
plt.plot(time, y, label="True values", color="black")
# テスト期間中の予測値をプロット
plt.plot(time[test_start_idx:], preds, label="Predictions", color="blue")
# 予測区間を描画
plt.fill_between(
    time[test_start_idx:],  # テストデータの時間範囲
    lower_bounds,  # 予測区間の下限
    upper_bounds,  # 予測区間の上限
    color="blue",
    alpha=0.2,  # 色の透明度
    label=f"{(1-alpha)*100:.1f}% Prediction Interval"
)
# ラベルとタイトルを追加
plt.legend()
plt.xlabel("Time")
plt.ylabel("Value")
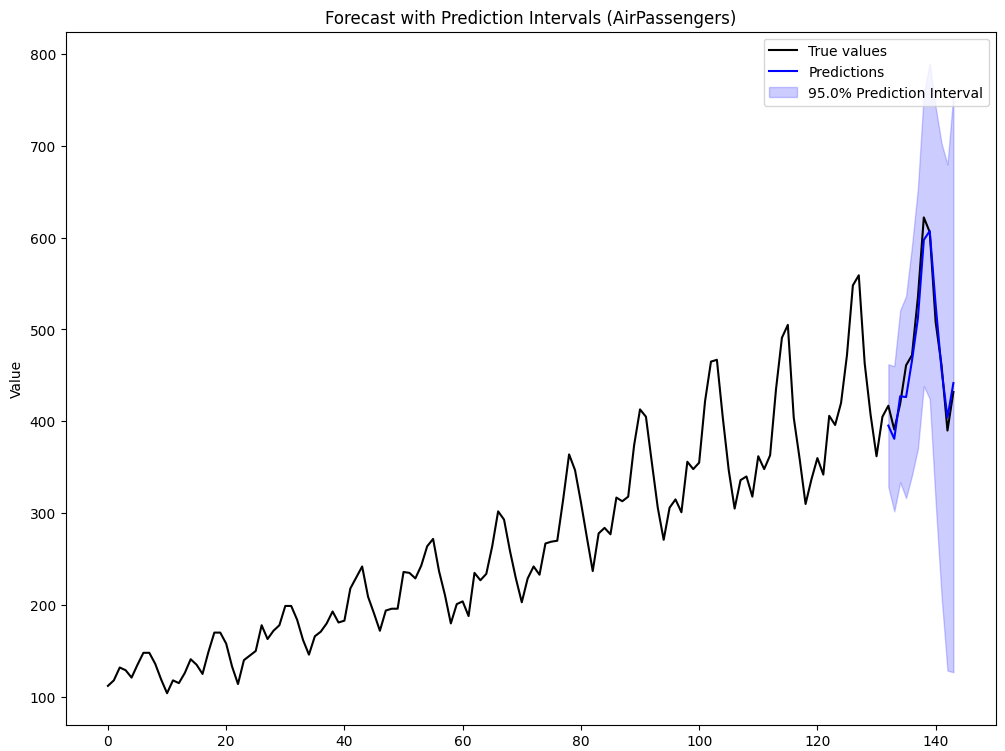
plt.title("Forecast with Prediction Intervals (AirPassengers)")
plt.show()

以下、実行結果です。

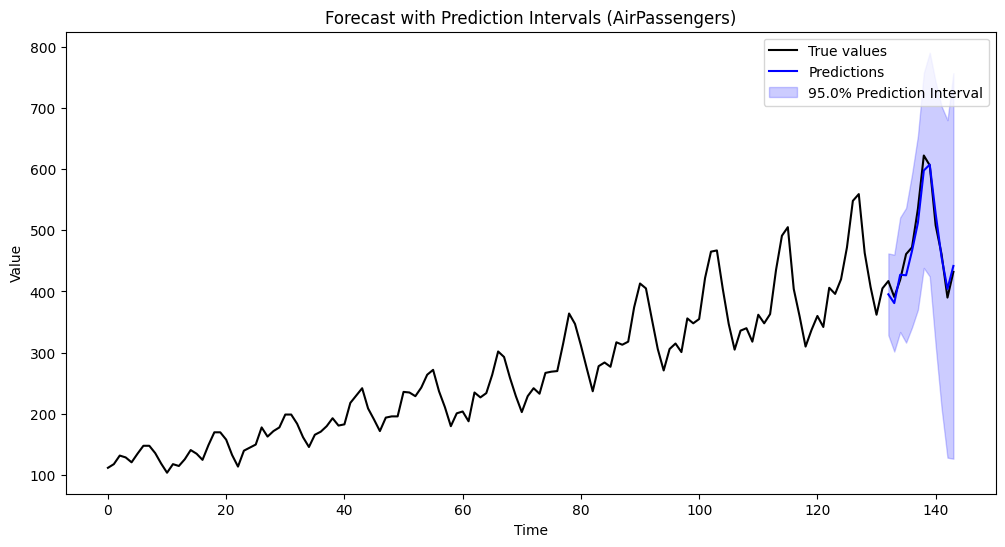
発展的なアプローチ

　Direct Multi-step 予測

本記事で取り上げたアプローチは1ステップ先モデルを再帰的に使う方式ですが、ステップごとに専用モデル（2ステップ先予測モデル、3ステップ先予測モデルなど）を用意する Direct Multi-step 方式もあります。

Conformal PredictionをDirect Multi-stepに適用するには、ステップ数分のキャリブレーションとモデル学習が増えるため計算コストはかさみますが、理論的には誤差伝播が軽減されるメリットがあります。

　オンライン学習への拡張

データが逐次追加される実務シナリオでは、学習モデルを適宜アップデートするオンライン学習手法とConformal Predictionを組み合わせる研究も進んでいます。

これにより、需要予測やリアルタイム株価予測などへの応用が期待されています。

　時系列の構造的変化への対応

ビジネス環境や社会的トレンドが大きく変化した場合、過去の誤差分布をそのまま適用することが難しくなる可能性があります。

CCPの分割やキャリブレーションルールを工夫し、急激な構造変化に適応する方法（例：逐次的に古い誤差を捨てる、ウィンドウ幅を動的に変えるなど）が検討されています。

まとめ

今回は、機械学習モデルにも適用可能なConformal Prediction（CP）を、時系列データの再帰的マルチステップ予測に活用する方法を、数式やPythonコードを交えながら解説しました。

従来の統計モデルでは誤差分布を前提に予測区間を導ける一方、機械学習のブラックボックスモデルでは同様の枠組みが難しいという課題がありました。

しかし、CPの分布フリーという強みにより、実務的に必要とされるさまざまな機械学習モデルでも予測区間の構築が可能となります。

時系列データは独立同分布（i.i.d.）ではなく、再帰的予測のエラー伝播などの特殊な事情がありますが、キャリブレーション用の時系列クロスバリデーション（RollingForecastCVやSlidingWindowForecastCV）と組み合わせることで、近似的ながらも現実的な不確実性の評価を行えます。

各ステップに応じて予測誤差を収集し、(1−α) 分位点を用いて予測区間の幅を推定する仕組みは、エラー伝播の影響を直接取り込み、より実用的な予測区間を生成してくれます。

実際のデータでは、ラグの取り方や外生変数の使用、クロスバリデーション手法の選択などを状況に応じて最適化し、予測区間のカバレッジを検証しながら運用していくことが重要です。

今後は、Direct Multi-step方式やオンライン学習への応用、季節性へのさらなる対応など、多様なアプローチが期待される分野です。CPをうまく活用することで、より信頼度の高い時系列予測を実現できるでしょう。